Large-Eddy Simulation of Plume Dispersion in the Central District of Oklahoma City by Coupling with a Mesoscale Meteorological Simulation Model and Observation
Abstract
:1. Introduction
2. Configuration of the Numerical Experiments
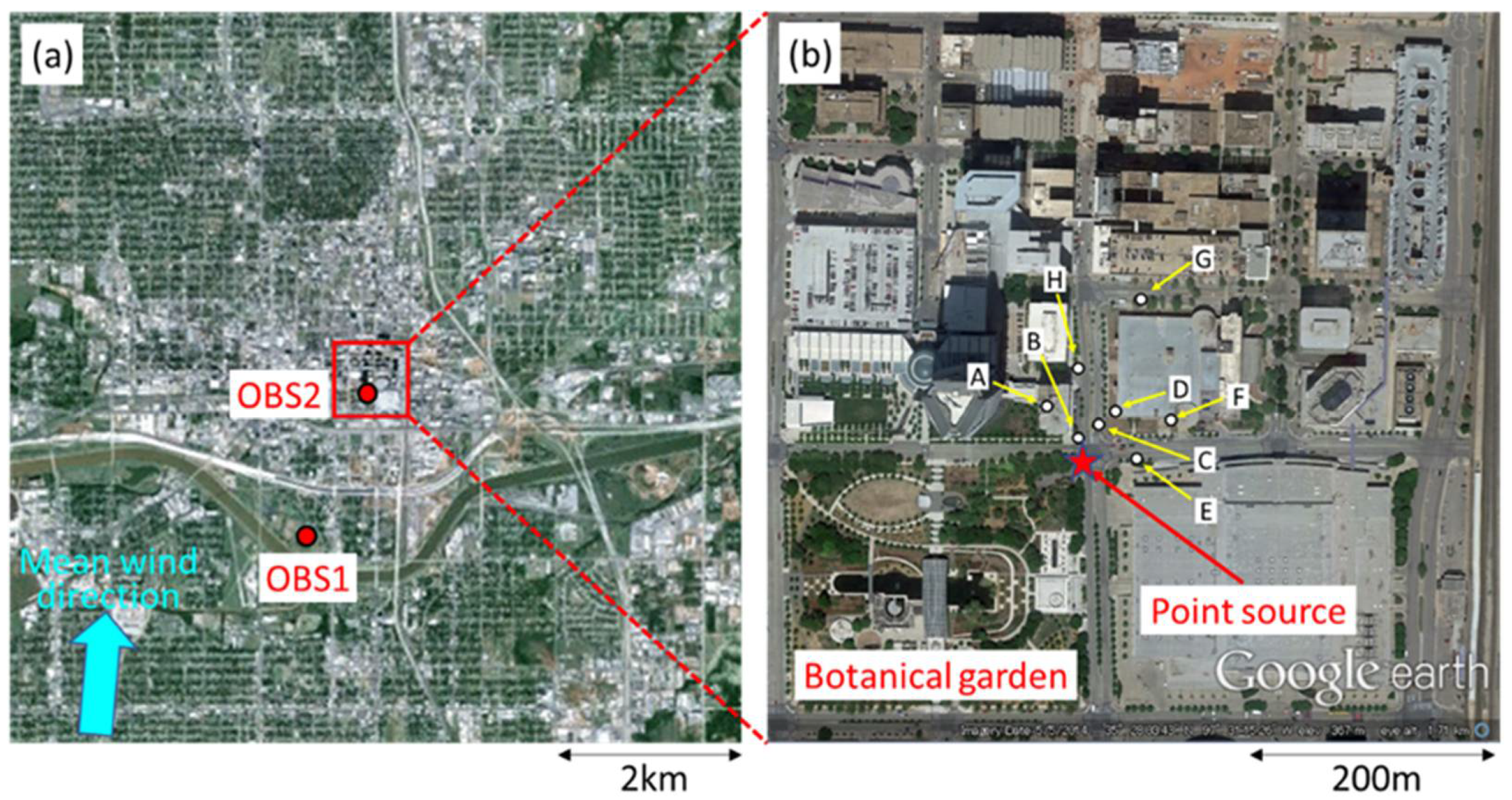
2.1. Brief Outline of JU2003 Field Experimental Dataset
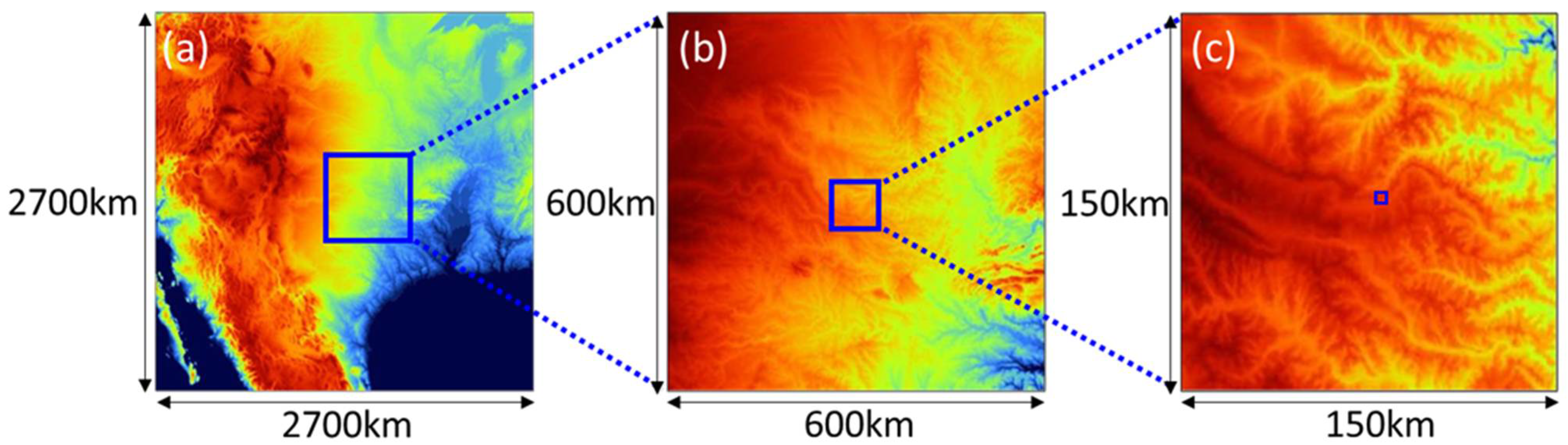
2.2. MesoScale Meteorological Simulation
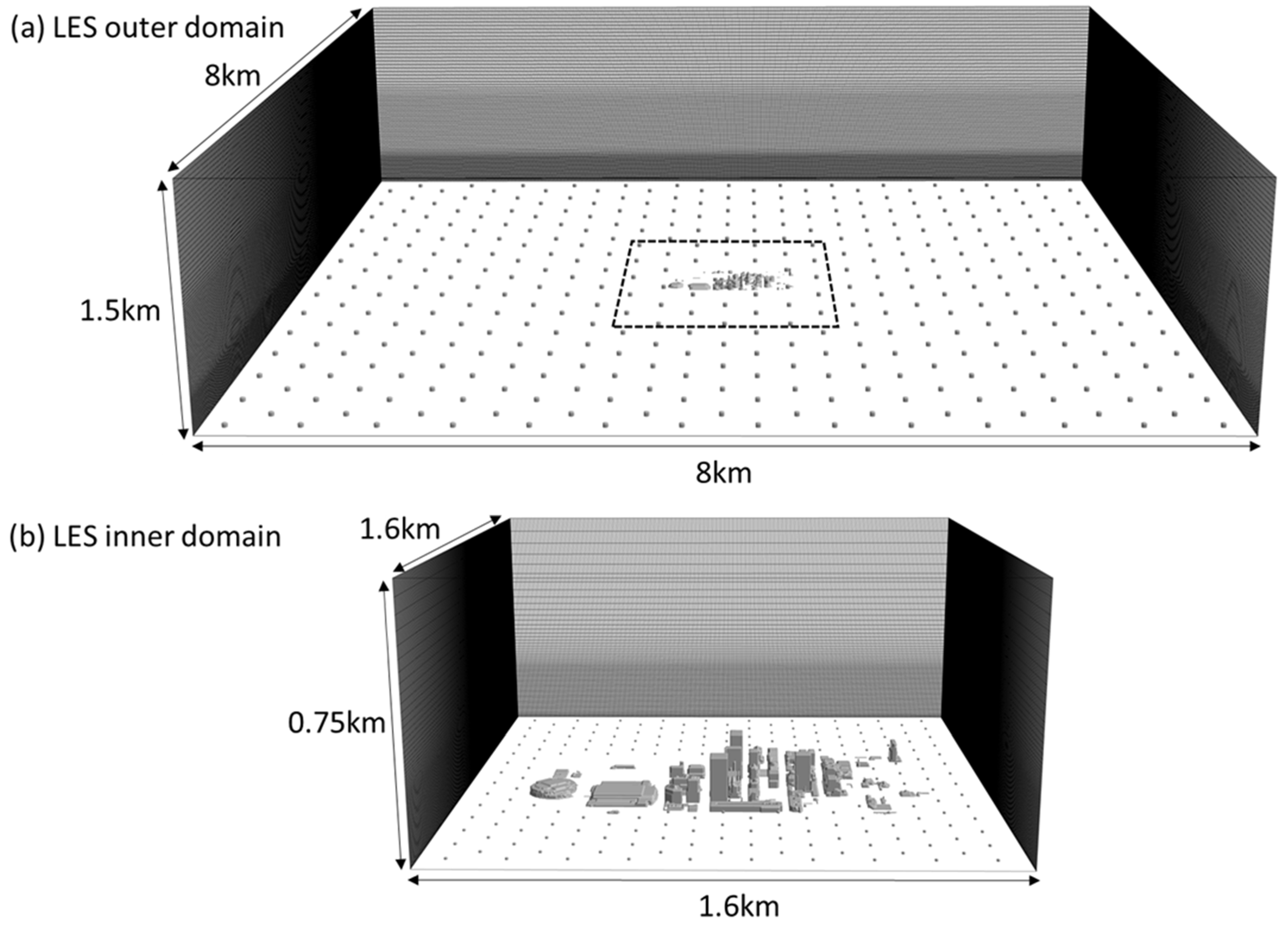
2.3. LES-Based CFD Model
3. Coupling with the MMS Model and OBS
4. Results
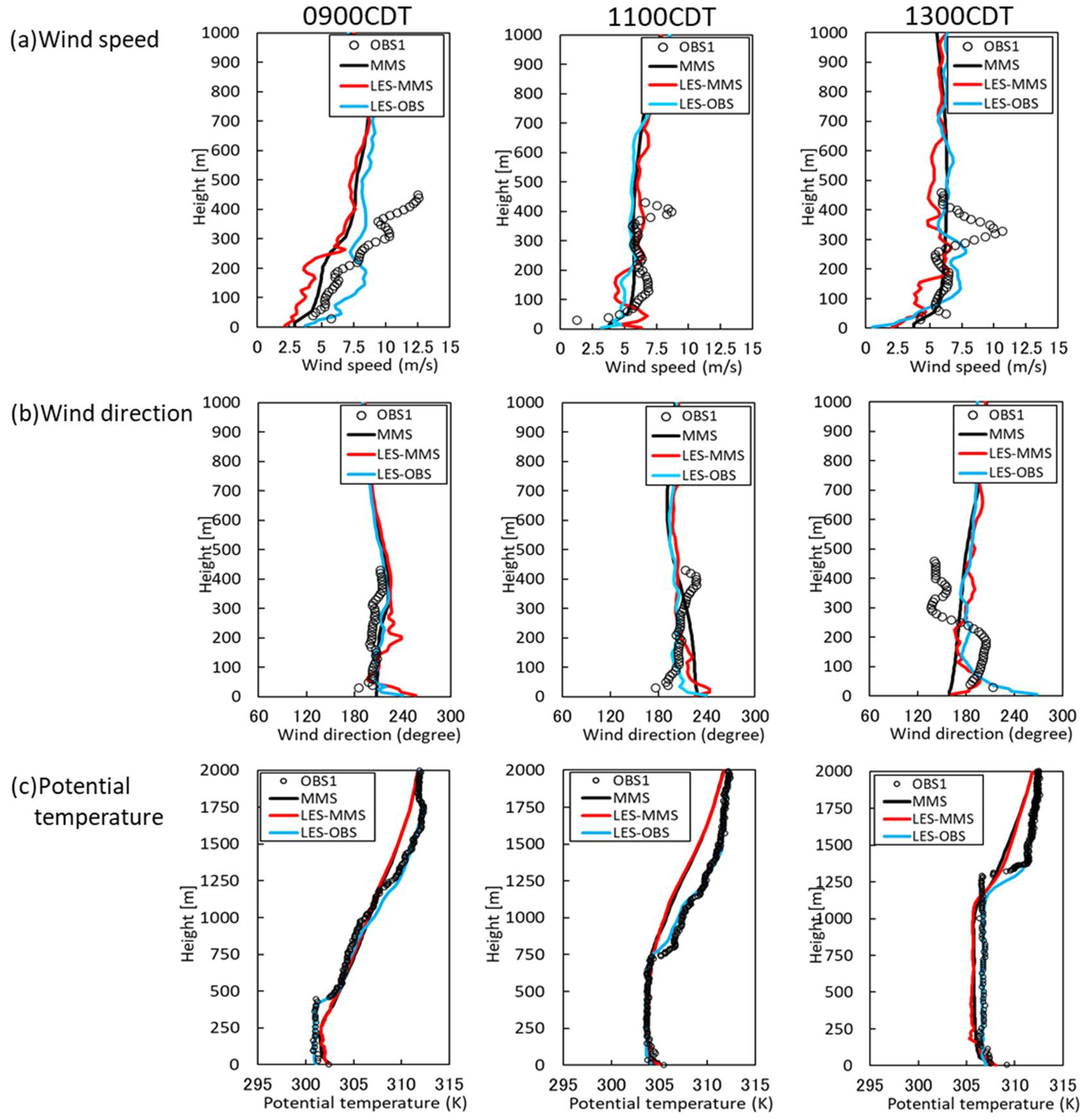
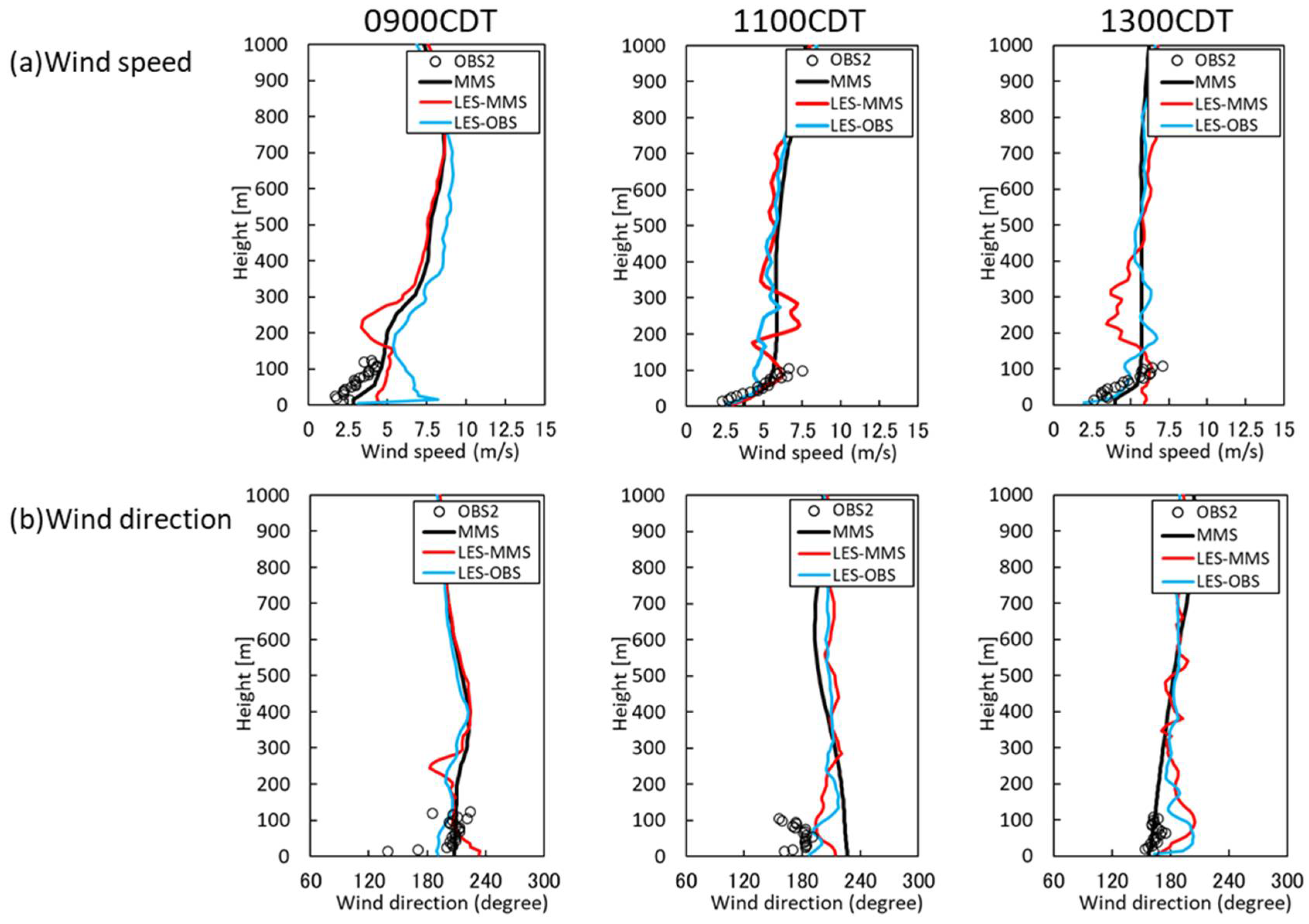
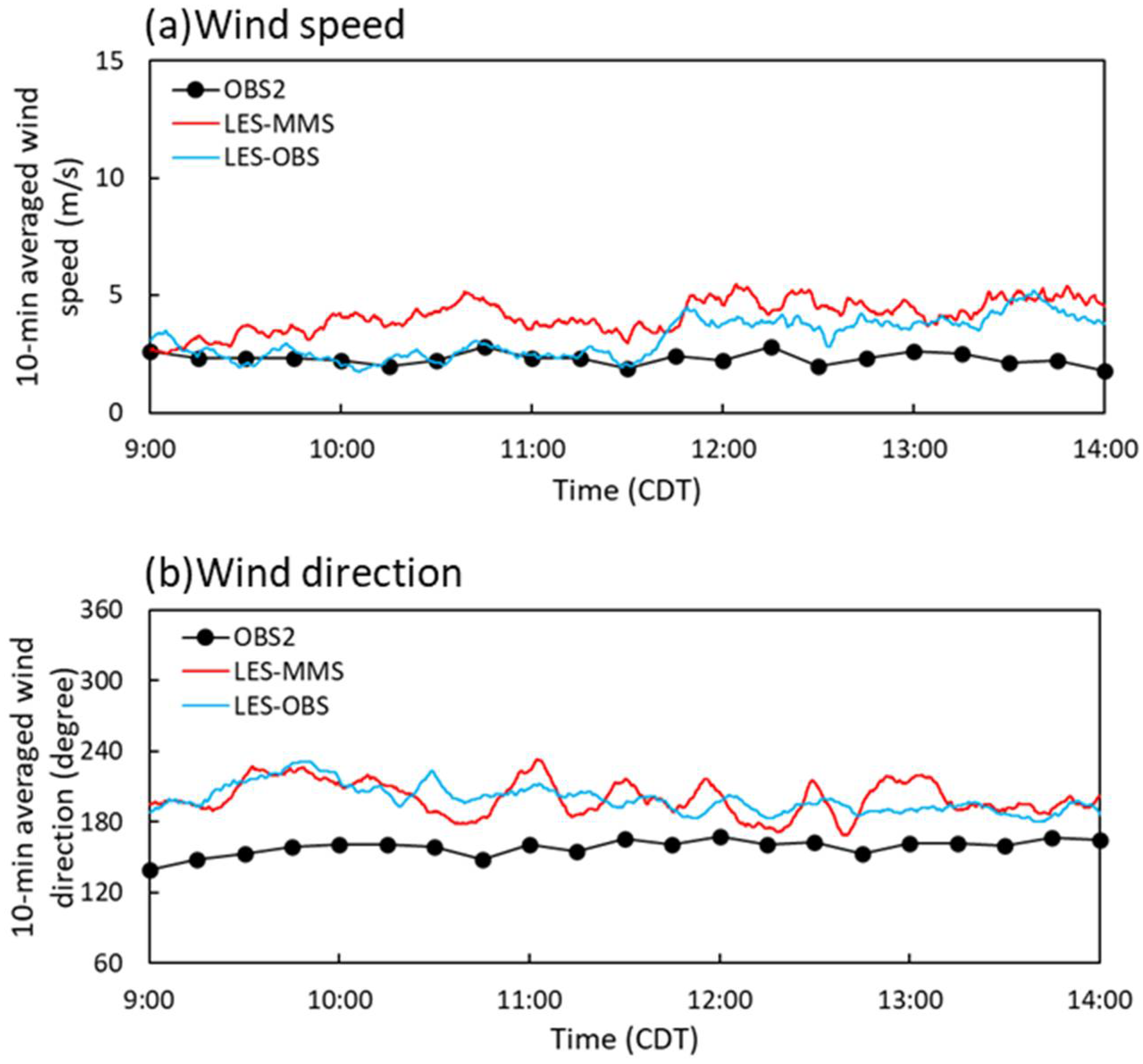
4.1. Flow Field
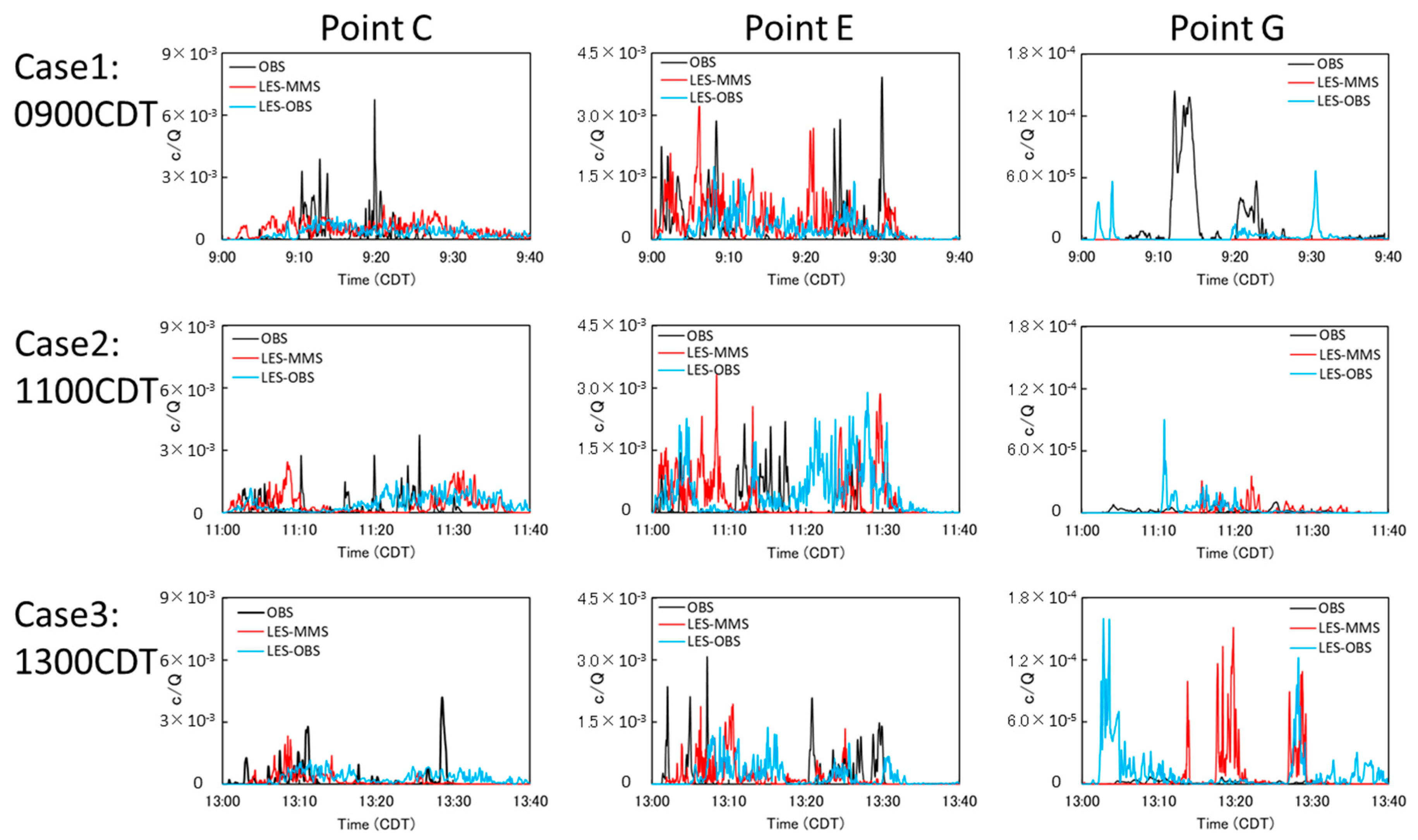
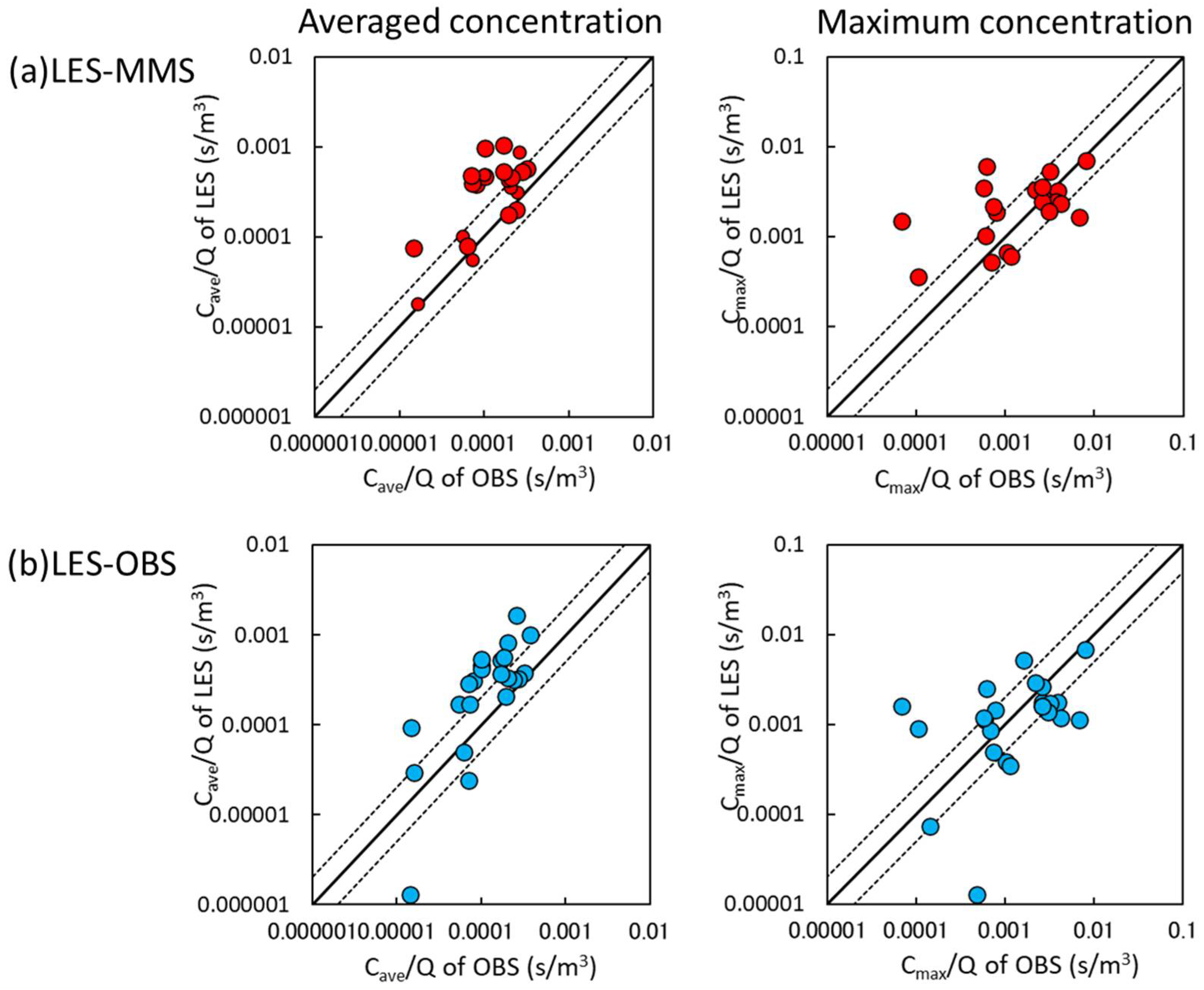
4.2. Concentration Field
5. Conclusions
- Appropriately represent aerodynamic effects of urban surfaces with the MMS model;
- Utilize multiple spatially varying wind field observations;
- Incorporate data assimilation techniques into the LES model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Inoue, T. CBRN Terrorism & Defense. J. Jpn. Soc. Saf. Eng. 2016, 55, 398–405. (In Japanese) [Google Scholar]
- Report of the United Nations Scientific Committee on the Effects of Atomic Radiation to the General Assembly, 2013 Report Vol. I. Sources, Effects and Risks of Ionizing Radiation; United Nations Scientific Committee on the Effects of Atomic Radiation: New York, NY, USA, 2013.
- World Health Organization. WHO Air Quality Guidelines for Particulate Matter, Ozone, Nitrogen Dioxide and Sulfur Dioxide: Global Update 2005: Summary of Risk Assessment; WHO: Geneva, Switzerland, 2006. [Google Scholar]
- World Health Organization. The invisible killer—Health effects of air pollution. In Proceedings of the First WHO Global Conference on Air Pollution and Health, Geneva, Switzerland, 30 October–1 November 2018; WHO: Geneva, Switzerland, 2018. [Google Scholar]
- Hanna, S.R. The exponential probability density function and concentration fluctuations in smoke plumes. Bound. Layer Meteorol. 1984, 29, 361–375. [Google Scholar] [CrossRef]
- Efthimiou, G.C.; Bartzis, J.G.; Koutsourakis, N. Modelling concentration fluctuations and individual exposure in complex urban environments. J. Wind Eng. Ind. Aerodyn. 2011, 99, 349–356. [Google Scholar] [CrossRef]
- Efthimiou, G.C.; Bartzis, J.G. Atmospheric dispersion and individual exposure of hazardous materials. J. Hazard. Mater. 2011, 188, 375–383. [Google Scholar] [CrossRef]
- Cheng, H.; Castro, I.P. Near wall flow over urban-like roughness. Bound. Layer Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Warner, S.; Platt, N.; Jeffry, T.; Heagy, J.F. Comparisons of Transport and Dispersion Model Predictions of the URBAN 2000 Field Experiment. J. Appl. Meteorol. 2004, 43, 829–846. [Google Scholar] [CrossRef] [Green Version]
- Tewari, M.; Kusaka, H.; Chen, F.; Coirier, W.J.; Kim, S.; Wyszogrodzki, A.; Warner, T. Impact of coupling a microscale computational fluid dynamics model with a mesoscale model on urban scale contaminant transport and dispersion. Atmos. Res. 2010, 96, 656–664. [Google Scholar] [CrossRef]
- Wyszogrodzki, A.; Miao, S.; Chen, F. Evaluation of the coupling between mesoscale-WRF and LES-EULAG models for simulating fine-scale urban dispersion. Atmos. Res. 2012, 118, 324–345. [Google Scholar] [CrossRef]
- Nelson, M.A.; Brown, M.J.; Halverson, S.A.; Bieringer, P.; Annunzio, A.; Bieberbach, G.; Meech, S. A case study of the weather research and forecasting model applied to the joint urban 2003 tracer field experiment. Part 1: Wind and turbulence. Bound. Layer Meteorol. 2016, 158, 285–309. [Google Scholar] [CrossRef]
- Nelson, M.A.; Brown, M.J.; Halverson, S.A.; Bieringer, P.; Annunzio, A.; Bieberbach, G.; Meech, S. A Case Study of the Weather Research and Forecasting Model Applied to the Joint Urban 2003 Tracer Field Experiment. Part 2: Gas Tracer Dispersion. Bound. Layer Meteorol. 2016, 161, 461–490. [Google Scholar] [CrossRef]
- Burman, J.; Jonsson, L.; Rutgersson, A. On possibilities to estimate local concentration variations with CFD-LES in real urban environments. Environ. Fluid Mech. 2019, 19, 719–750. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Cui, G.; Zhang, Z. A New Scheme for the Simulation of Microscale Flow and Dispersion in Urban Areas by Coupling Large-Eddy Simulation with Mesoscale Models. Bound. Layer Meteorol. 2018, 167, 145–170. [Google Scholar] [CrossRef]
- Allwine, K.J.; Flaherty, J.E. Joint Urban 2003 Study Overview and Instrument Locations; PNNL-15967; Pacific Northwest National Laboratory: Richland, WA, USA, 2003. [Google Scholar]
- Nakayama, H.; Takemi, T.; Nagai, H. Development of local-scale high-resolution atmospheric dispersion model using large-eddy simulation part5: Detailed simulation of turbulent flows and plume dispersion in an actual urban area under real meteorological conditions. J. Nucl. Sci. Technol. 2016, 53, 887–908. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Tech. Note, NCAR/TN-475+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2008; p. 1. [Google Scholar]
- Janjic, Z.I. Nonsingular Implementation of the Mellor-Yamada Level 2.5 Scheme in the NCEP Meso Model; NCEP Office Note; National Centers for Environmental Prediction: Camp Springs, MD, USA, 2002; Volume 437, p. 61. [Google Scholar]
- Meneveau, C.; Lund, T.; Cabot, W. A Lagrangian dynamic sub-grid-scale model of turbulence. J. Fluid Mech. 1996, 319, 353–385. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, D.; Handler, R.; Sirovich, L. Modeling a no-slip flow boundary with an external force field. J. Comput. Phys. 1993, 105, 354–366. [Google Scholar] [CrossRef] [Green Version]
- Franke, J.; Hellsten, A.; Schlunzen, H.; Carissimo, B. Best Practice Guideline for the CFD Simulation of Flows in the Urban Environment, COST Action 732, Quality Assurance and Improvement of Microscale Meteorological Models; Meteorological Inst.: Brussels, Belgium, 2007; ISBN 3-00-018312-4. [Google Scholar]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Nakayama, H.; Takemi, T. Large-eddy simulation studies for predicting plume concentrations around nuclear facilities using an overlapping technique. Int. J. Environ. Pollut. 2018, 64, 125–144. [Google Scholar] [CrossRef]
- Kataoka, H.; Mizuno, M. Numerical flow computation around aeroelastic 3D square cylinder using inflow turbulence. Wind Struct. 2002, 5, 379–392. [Google Scholar] [CrossRef]
- Monin, A.; Obukhov, M. Basic laws of turbulent mixing in the ground layer of the atmosphere. Tr. Akad. Nauk SSSR Geophiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Moriwaki, R.; Kanda, M. Flux-gradient profiles for momentum and heat over an urban surface. Theor. Appl. Climatol. 2006, 127–135. [Google Scholar] [CrossRef]
- Michioka, T.; Sato, A.; Sada, K. Large-eddy simulation for the tracer gas concentration fluctuation in atmospheric boundary layer. Trans. Jpn. Soc. Mech. Eng. 2003, B69, 868–875. (In Japanese) [Google Scholar] [CrossRef]
- Warner, S.; Urban, J.T.; Heagy, J.F. Comparisons of T&D model predictions of the Joint Urban 2003 field experiment. J. Appl. Meteorol. Climatol. 2008, 47, 1910–1928. [Google Scholar]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Hanna, S.R.; Hansen, O.R.; Dharmavaram, S. FLACS CFD air quality model performance evaluation with Kit Fox, MUST, Prairie Grass, and EMU observations. Atmos. Environ. 2004, 38, 4675–4687. [Google Scholar] [CrossRef]
- Hanna, S.R.; Chang, J.C. Acceptance criteria for urban dispersion model evaluation. Meteorol. Atmos. Phys. 2012, 116, 133–146. [Google Scholar] [CrossRef]
- Herring, S.; Huq, P. A review of methodology for evaluating the performance of atmospheric transport and dispersion models and suggested protocol for providing more informative results. Fluids 2018, 3, 20. [Google Scholar] [CrossRef] [Green Version]
- Martilli, A.; Clappier, A.; Rotach, M.W. An urban surface exchange parameterisation for mesoscale models. Bound. Layer Meteorol. 2002, 104, 261–304. [Google Scholar] [CrossRef]
- Kondo, H.; Tokairin, T.; Kikegawa, Y. Calculation of wind in a Tokyo urban area with a mesoscale mode lincluding a multi-layer urban canopy model. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1655–1666. [Google Scholar] [CrossRef]
- Salamanca, F.; Martilli, A.; Tewari, M.; Chen, F. A study of the urban boundary layer using different urban parameterizations and high-resolution urban canopy parameters with WRF. J. Appl. Meteorol. Climatol. 2011, 50, 1107–1128. [Google Scholar] [CrossRef]
- Nakayama, H.; Takemi, T. Development of a data assimilation method using vibration equation for large-eddy simulations of turbulent boundary layer flows. J. Adv. Model. Earth Syst. 2020, 12. [Google Scholar] [CrossRef]
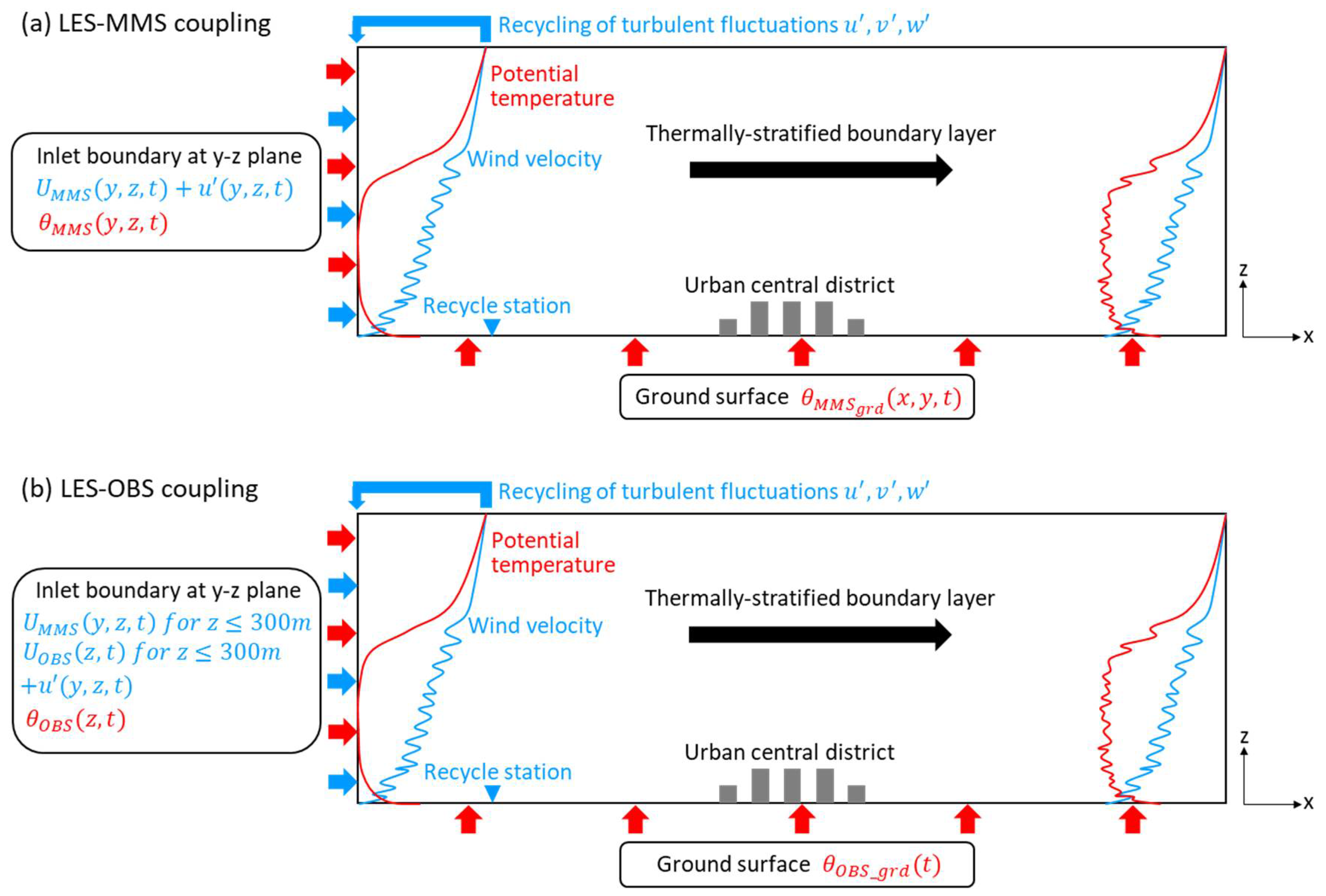

| Input Data | LES–MMS Coupling Case | LES–OBS Coupling Case | |
|---|---|---|---|
| Wind velocity field | Inlet | ||
| Ground surface | |||
| Potential temperature field | Inlet | ||
| Ground surface | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakayama, H.; Takemi, T.; Yoshida, T. Large-Eddy Simulation of Plume Dispersion in the Central District of Oklahoma City by Coupling with a Mesoscale Meteorological Simulation Model and Observation. Atmosphere 2021, 12, 889. https://doi.org/10.3390/atmos12070889
Nakayama H, Takemi T, Yoshida T. Large-Eddy Simulation of Plume Dispersion in the Central District of Oklahoma City by Coupling with a Mesoscale Meteorological Simulation Model and Observation. Atmosphere. 2021; 12(7):889. https://doi.org/10.3390/atmos12070889
Chicago/Turabian StyleNakayama, Hiromasa, Tetsuya Takemi, and Toshiya Yoshida. 2021. "Large-Eddy Simulation of Plume Dispersion in the Central District of Oklahoma City by Coupling with a Mesoscale Meteorological Simulation Model and Observation" Atmosphere 12, no. 7: 889. https://doi.org/10.3390/atmos12070889
APA StyleNakayama, H., Takemi, T., & Yoshida, T. (2021). Large-Eddy Simulation of Plume Dispersion in the Central District of Oklahoma City by Coupling with a Mesoscale Meteorological Simulation Model and Observation. Atmosphere, 12(7), 889. https://doi.org/10.3390/atmos12070889







