A Modeling Study on the Downslope Wind of “Katevatos” in Greece and Implications for the Battle of Arachova in 1826
Abstract
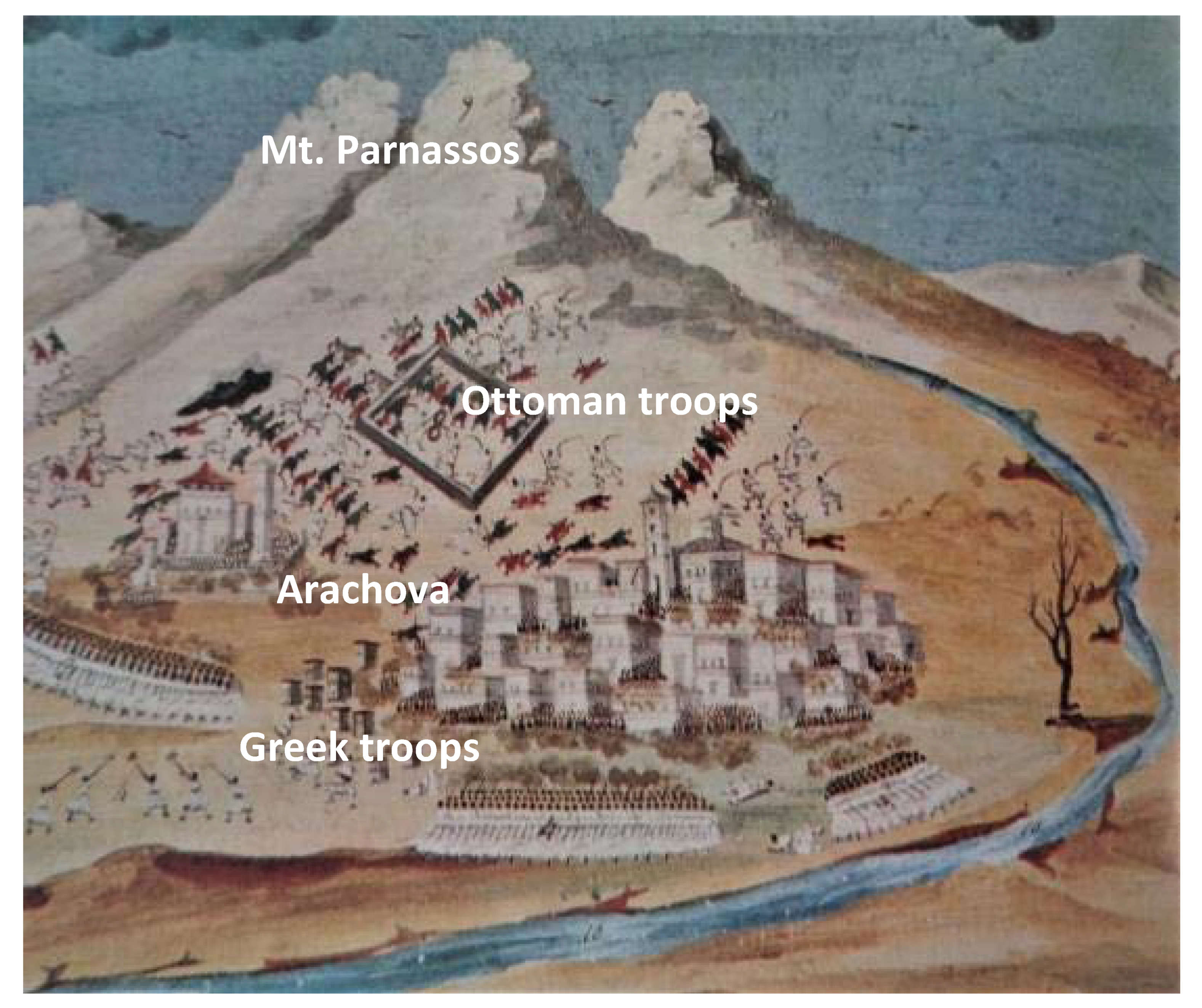
:1. Introduction
2. Theoretical Concept and Modeling Methodology
2.1. Theoretical Background
2.2. Model Configuration
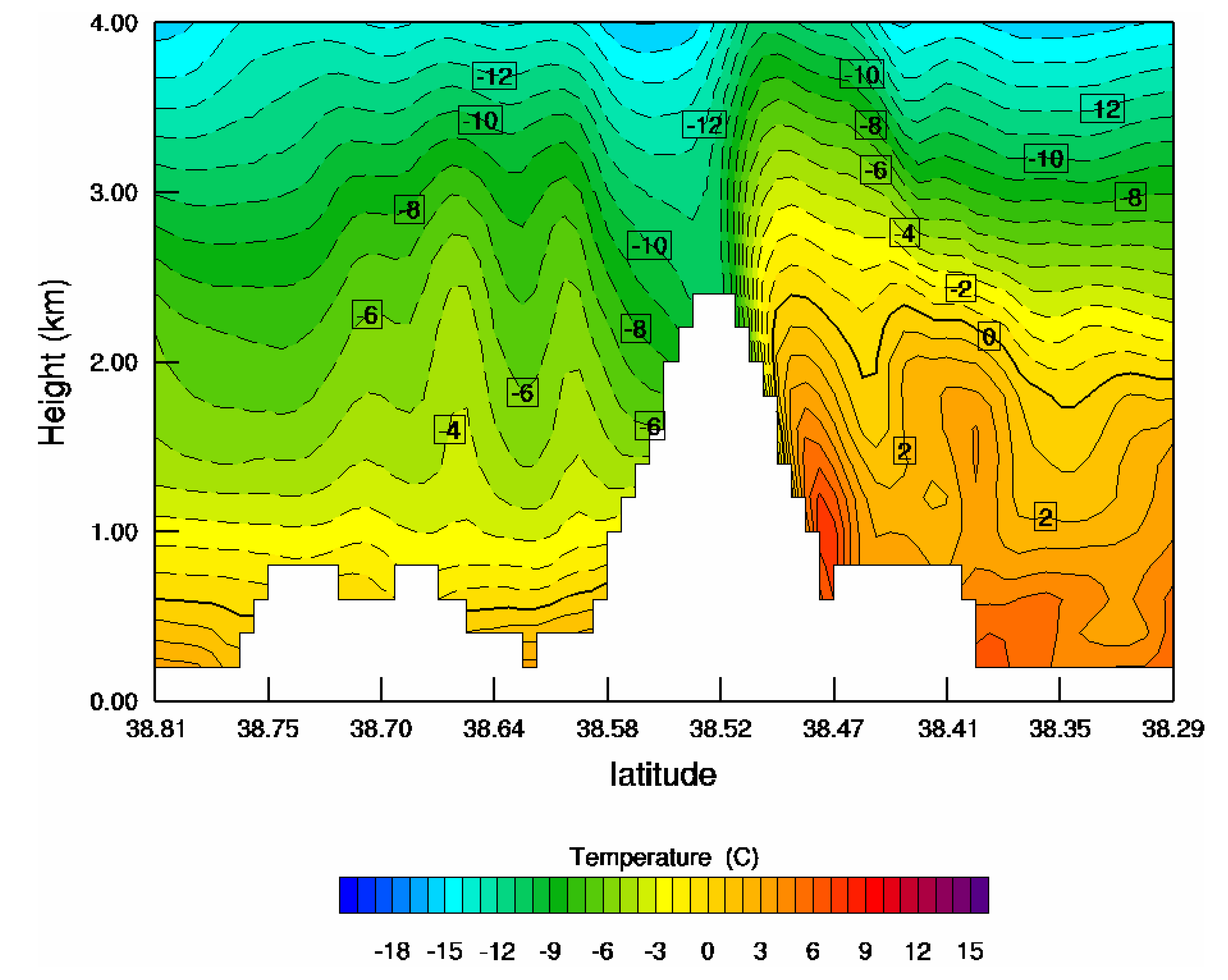
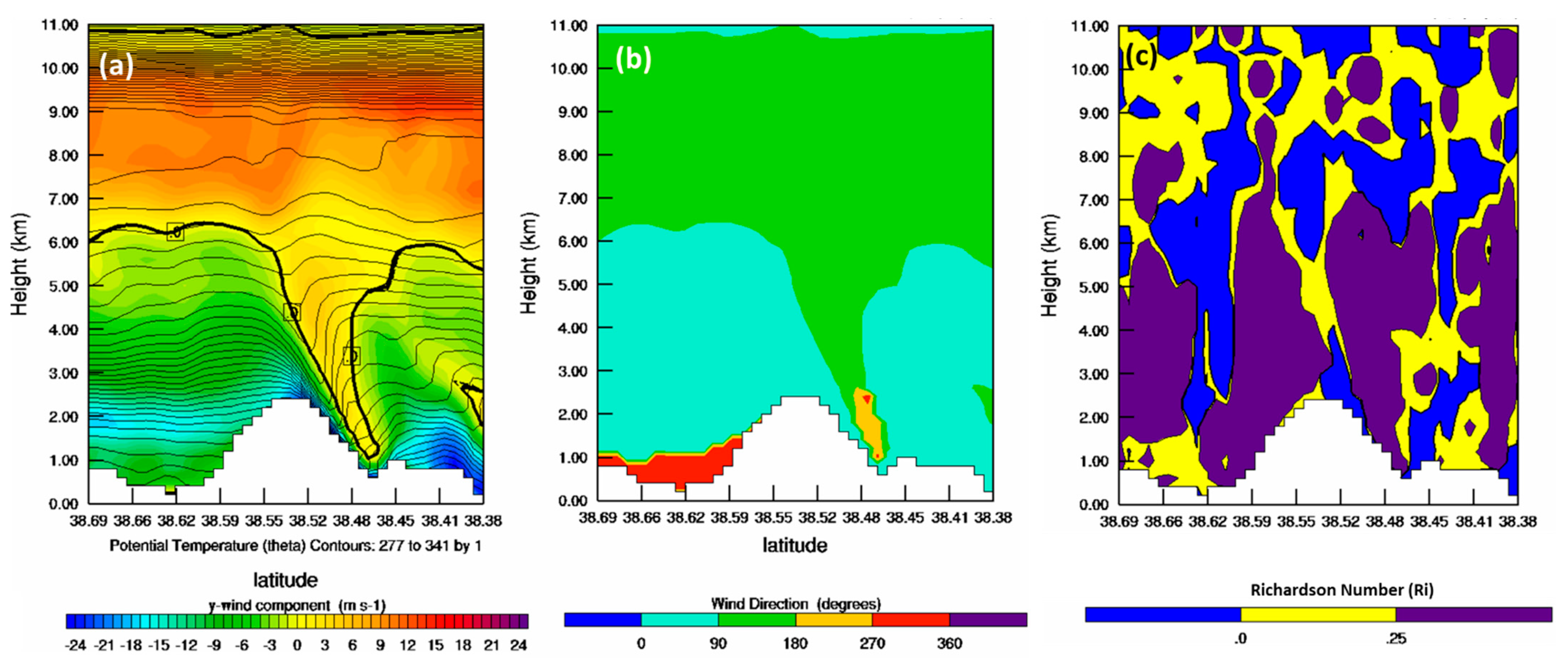
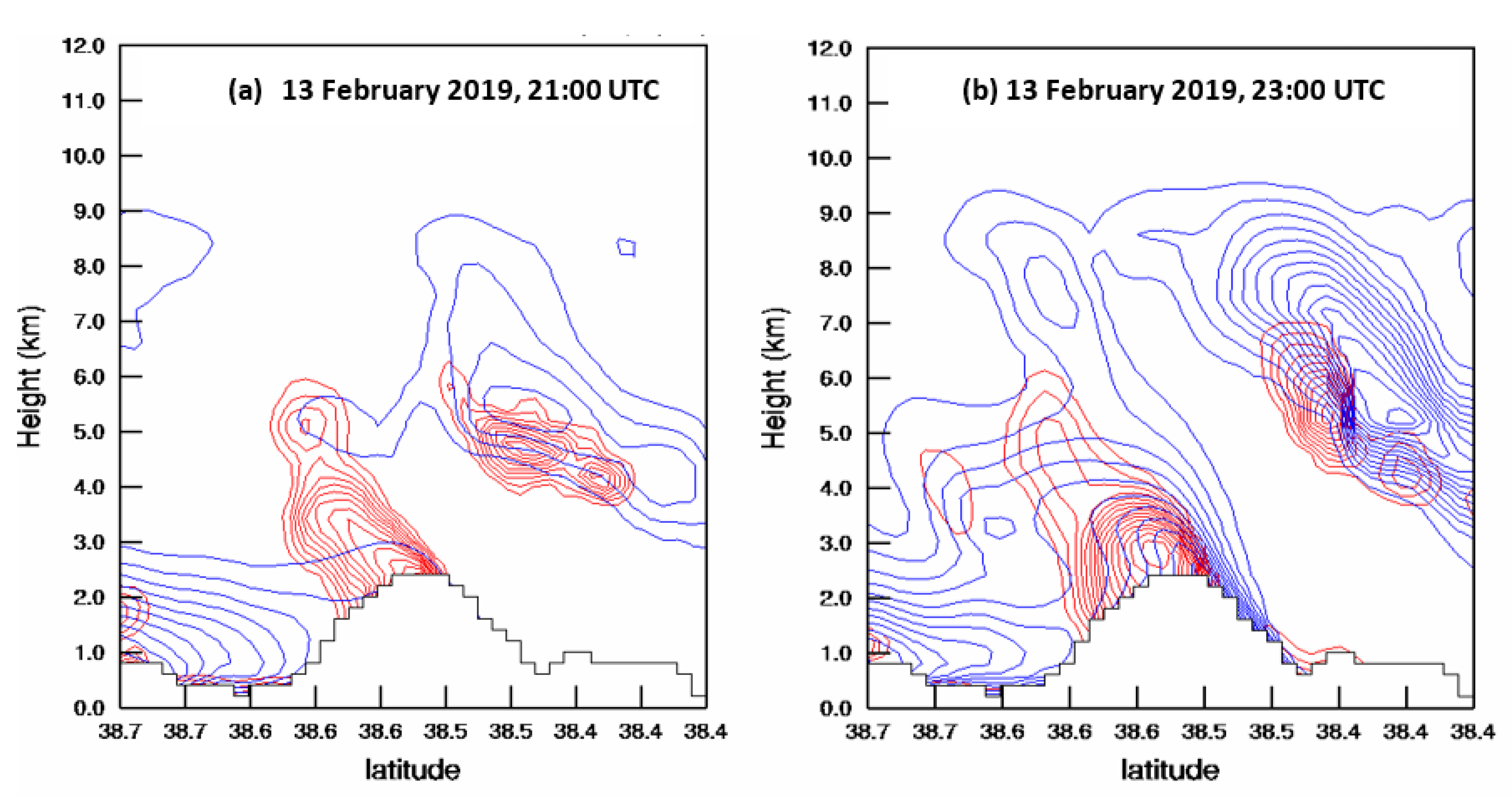
3. Modeling Results and Analysis of the Atmospheric Processes Forming “Katevatos”
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vakalopoulos, A. H Επανάσταση του Ελληνικού Έθνους [The Revolution of the Greek Nation]; Stamoulis Publications: Thessaloniki, Greece, 2016; Volume 3, pp. 671–676. [Google Scholar]
- Vakalopoulos, A.; Vakalopoulos, K.; Giannopoulos, I.; Droulia, L.; Koukkou, E.; Koumarianou, A.; Papadopoulos, S.; Sfyroeras, V. H Ελληνική Επανάσταση και η ίδρυση του Ελληνικού Κράτους [The Greek revolution and the shaping of the Greek State]. In Ιστορία του Ελληνικού Έθνους [The History of the Greek People]; Ekdotike Athenon, S.A.: Athens, Greece, 1975; Volume IB, pp. 426–429. [Google Scholar]
- Trikoupis, S. H Ιστορία της Ελληνικής Επαναστάσεως [The History of the Greek Revolution], 2nd ed.; W. Blackwood and Sons: London, UK, 1860; Volume D, pp. 90–93. [Google Scholar]
- Orlandos, A. Ναυτικά, Ήτοι Ιστορία Των Κατά Τον Υπέρ Aνεξαρτησίας Της Ελλάδοσ Aγώνα Πεπραγμένων υπό Των Τριών Ναυτικών Νήσων, Ιδίως δε των Σπετσών [Nautica, Hence Chronicles of the Actions in Support of the Struggle for Greek Independence by the Three Island Fleets, Particularly that of Spetses]; Print. Ch. N. Philadelpheos: Athens, Greece, 1869; Volume B, pp. 435–438. [Google Scholar]
- Γενική Εφημερίς Της Ελλάδος, 1826–1827, 8 [General Newspaper of Greece, 1826–1827, 8]; Provisional Administration of Greece: Aigina, Greece, 1826. Available online: https://www.searchculture.gr/aggregator/edm/KEINE/000133-181961?language=el (accessed on 20 July 2021).
- Zerefos, C.; Solomos, S.; Melas, D.; Kapsomenakis, J.; Repapis, C. The Role of Weather during the Greek–Persian “Naval Battle of Salamis” in 480 B.C. Atmosphere 2020, 11, 838. [Google Scholar] [CrossRef]
- Smith, R.B. Aerial observations of the Yugoslavian bora. J. Atmos. Sci. 1987, 44, 269–297. [Google Scholar] [CrossRef] [Green Version]
- Drobinski, P.; Bastin, S.; Guenard, V.; Caccia, J.-L.; Dabas, A.; Delville, P.; Protat, A.; Reitebuch, O.; Werner, C. Summer mistral at the exit of the Rhône valley. Q. J. R. Meteorol. Soc. 2005, 131, 353–375. [Google Scholar] [CrossRef] [Green Version]
- Glennf, C.L. The Chinook. Weatherwise 1961, 14, 175–182. [Google Scholar] [CrossRef]
- Nastos, P.T.; Bleta, A.G.; Matsangouras, I.T. Human thermal perception related to Föhn winds due to Saharan dust outbreaks in Crete Island, Greece. Theor. Appl. Climatol. 2017, 128, 635–647. [Google Scholar] [CrossRef]
- Cao, Y.; Fovell, G.R. Downslope windstorms of San Diego County. Part I: A case study. Mon. Weather Rev. 2016, 144, 529–552. [Google Scholar] [CrossRef]
- Solomos, S.; Kalivitis, N.; Mihalopoulos, N.; Amiridis, V.; Kouvarakis, G.; Gkikas, A.; Binietoglou, I.; Tsekeri, A.; Kazadzis, S.; Kottas, M.; et al. From Tropospheric Folding to Khamsin and Foehn Winds: How Atmospheric Dynamics Advanced a Record-Breaking Dust Episode in Crete. Atmosphere 2018, 9, 240. [Google Scholar] [CrossRef] [Green Version]
- Holton, J.R. An Introduction to Dynamic Meteorology, 2nd ed; Academic Press: New York, NY, USA, 1979; p. 391. [Google Scholar]
- Smith, R. On severe downslope winds. J. Atmos. Sci. 1985, 42, 2597–2603. [Google Scholar] [CrossRef] [Green Version]
- Durran, D.R.; Klemp, J.B. Another look at downslope winds. Part II: Nonlinear amplification beneath wave-overturning layers. J. Atmos. Sci. 1987, 44, 3402–3412. [Google Scholar] [CrossRef] [Green Version]
- Durran, D.R. Mountain waves and downslope winds. In Atmospheric Process over Complex Terrain; Blumen, W., Ed.; American Meteorological Society: Boston, MA, USA, 1990; pp. 59–81. [Google Scholar]
- Richard, E.; Mascart, P.; Nickerson, E.C. The role of surface friction in downslope windstorms. J. Appl. Meteor. 1989, 28, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Mercer, A.; Richman, M.; Bluestein, H.; Brown, J. Statistical modeling of downslope windstorms in Boulder, Colorado. Weather Forecast. 2008, 23, 1176–1194. [Google Scholar] [CrossRef] [Green Version]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Zhiquan, L.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; Tech. Note NCAR/TN-475+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2019; p. 145. [Google Scholar]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The weather research and forecasting model: Overview, system efforts, and future directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of Cloud Microphysics on the Development of Trailing Stratiform Precipitation in a Simulated Squall Line: Comparison of One– and Two–Moment Schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef] [Green Version]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long–lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Jimenez, P.A.; Dudhia, J.; Gonzalez–Rouco, J.F.; Navarro, J.; Montavez, J.P.; Garcia–Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef] [Green Version]
- Tewari, M.F.; Chen, W.; Wang, J.; Dudhia, M.A.; LeMone, K.; Mitchell, M.; Ek, G.; Gayno, J.; Wegiel, J.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 12–16 January 2004; pp. 11–15. [Google Scholar]
- Song–You, H.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Grell, G.A. Prognostic Evaluation of Assumptions Used by Cumulus Parameterizations. Mon. Weather Rev. 1993, 121, 764–787. [Google Scholar] [CrossRef] [Green Version]
- Grell, G.A.; Devenyi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29, 1693. [Google Scholar] [CrossRef] [Green Version]
- Lagouvardos, K.; Kotroni, V.; Bezes, A.; Koletsis, I.; Kopania, T.; Lykoudis, S.; Mazarakis, N.; Papagiannaki, K.; Vougioukas, S. The automatic weather stations NOANN network of the National Observatory of Athens: Operation and database. Geosci. Data J. 2017, 4, 4–16. [Google Scholar] [CrossRef]
- Lilly, D.K. A severe downslope windstorm and aircraft turbulence event induced by a mountain wave. J. Atmos. Sci. 1978, 35, 59–77. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.B. The steepening of hydrostatic mountain waves. J. Atmos. Sci. 1977, 34, 1634–1654. [Google Scholar] [CrossRef] [Green Version]
- Lilly, D.K.; Klemp, J.B. The effects of terrain shape on nonlinear hydrostatic mountan waves. J. Fluid Mech. 1979, 95, 241–261. [Google Scholar] [CrossRef]
- Hoinka, K.P. A comparison of numerical simulations of hydrostatic flow over mountains and observations. Mon. Weather Rev. 1985, 113, 719–735. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solomos, S.; Nastos, P.T.; Emmanouloudis, D.; Koutsouraki, A.; Zerefos, C. A Modeling Study on the Downslope Wind of “Katevatos” in Greece and Implications for the Battle of Arachova in 1826. Atmosphere 2021, 12, 993. https://doi.org/10.3390/atmos12080993
Solomos S, Nastos PT, Emmanouloudis D, Koutsouraki A, Zerefos C. A Modeling Study on the Downslope Wind of “Katevatos” in Greece and Implications for the Battle of Arachova in 1826. Atmosphere. 2021; 12(8):993. https://doi.org/10.3390/atmos12080993
Chicago/Turabian StyleSolomos, Stavros, Panagiotis T. Nastos, Dimitrios Emmanouloudis, Antonia Koutsouraki, and Christos Zerefos. 2021. "A Modeling Study on the Downslope Wind of “Katevatos” in Greece and Implications for the Battle of Arachova in 1826" Atmosphere 12, no. 8: 993. https://doi.org/10.3390/atmos12080993
APA StyleSolomos, S., Nastos, P. T., Emmanouloudis, D., Koutsouraki, A., & Zerefos, C. (2021). A Modeling Study on the Downslope Wind of “Katevatos” in Greece and Implications for the Battle of Arachova in 1826. Atmosphere, 12(8), 993. https://doi.org/10.3390/atmos12080993









