Extreme Months: Multidimensional Studies in the Carpathian Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Creation of a Representative Database
2.2. Data
3. Norm Method Based on Probability Distribution
3.1. Mathematical Model in General Case
3.2. “Basic” Questions and Problems
- –
- Which vector variable may be considered extreme?
- –
- How is it possible to test the null hypothesis of the identical distribution of the vector variables on the basis of the analysis of extremes?
3.3. Transformation of the Vector Components
3.4. Definition of the Multidimensional Extreme
3.5. Two-Dimensional Case: The SPTI Index
3.5.1. SPI (Standardized Precipitation Index)
3.5.2. STI (Standardized Temperature Index)
3.5.3. SPTI (Standardized Precipitation and Temperature Index)
3.6. Statistical Tests Used
3.6.1. Test 1
- –
- Calculate the SPTI(t) norms and then determine the frequency of norms exceeding the Cr1 value for the total period. This frequency is denoted by ν.
- –
- If the null hypothesis is true, then ν ∈ B(n,p), where B(n,p) denotes the binomial distribution with parameters n and p, specifically n = 150 and p = 0.1.
- –
- Consequently, according to the central limit theorem, the standardized value TS1 of the frequency ν converges to the standard normal distribution.
3.6.2. Test 2
3.6.3. Test 3
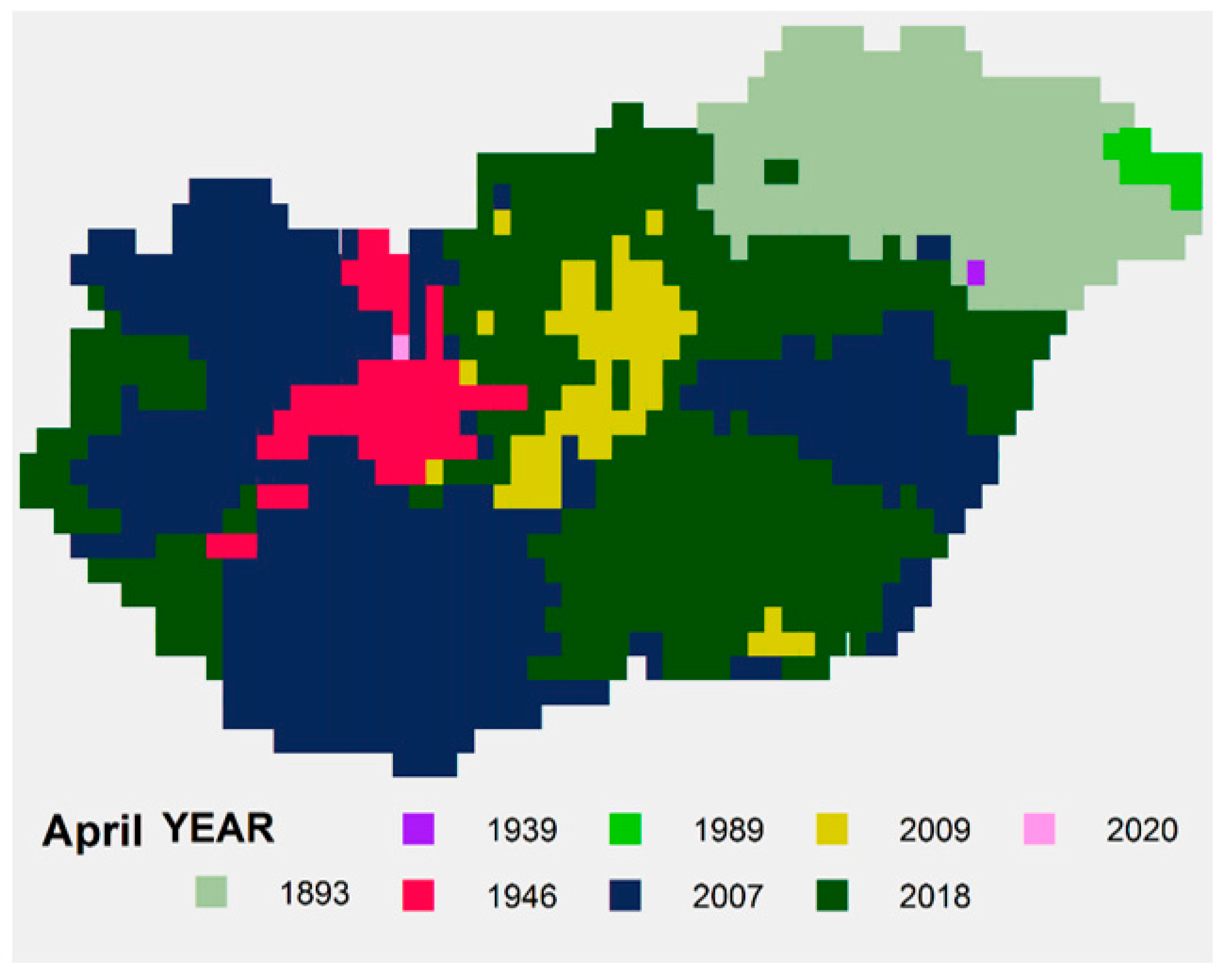
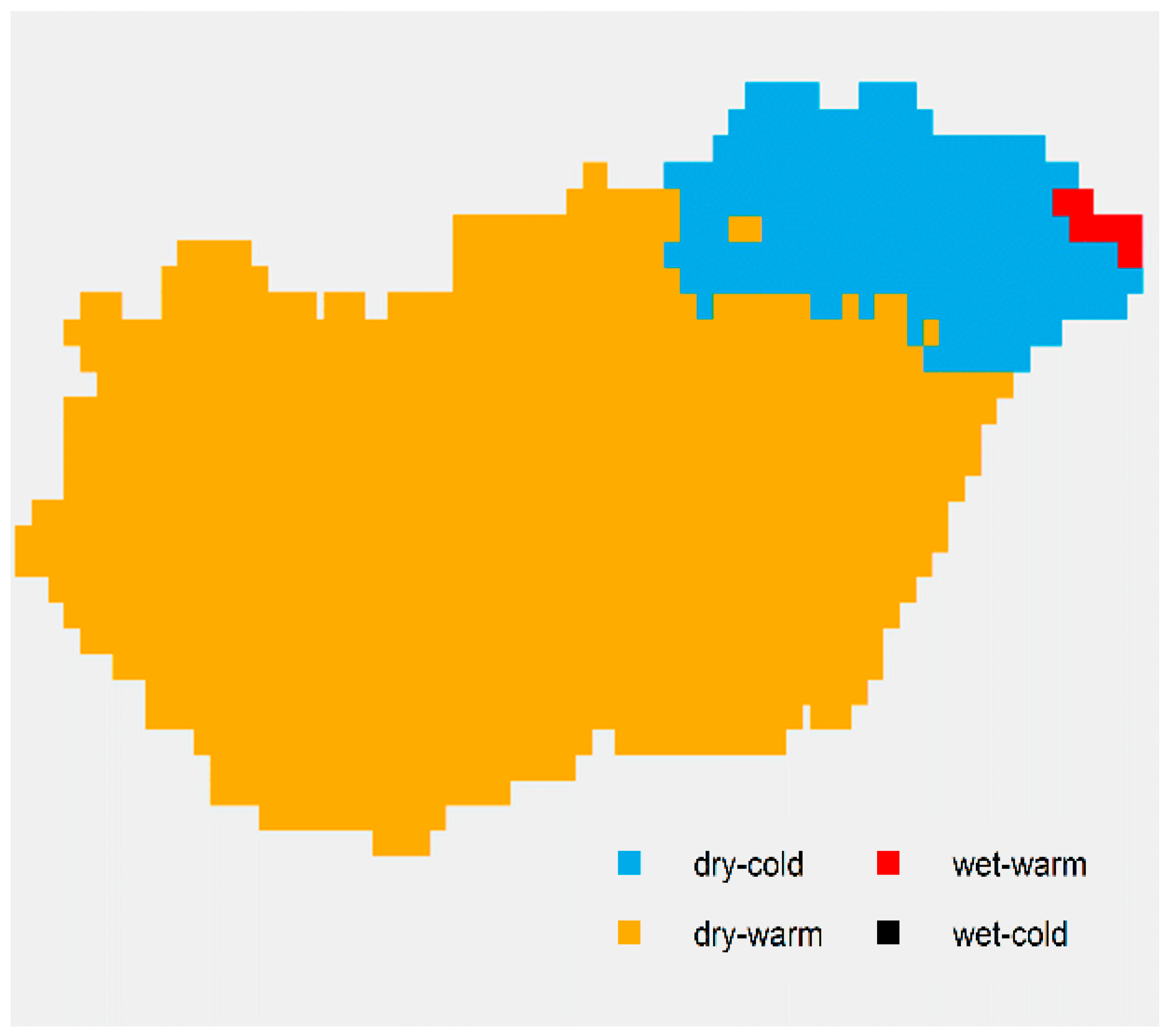
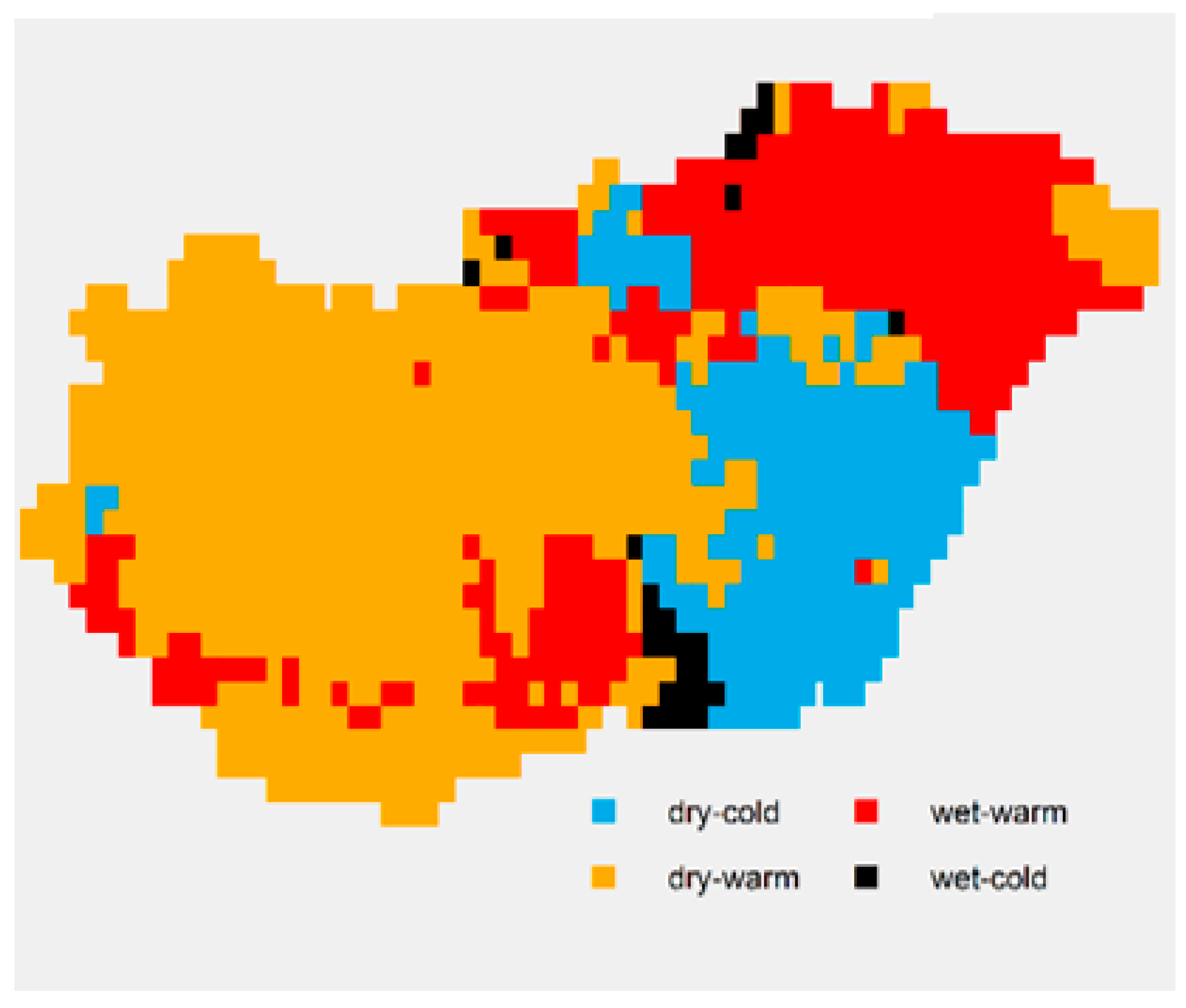
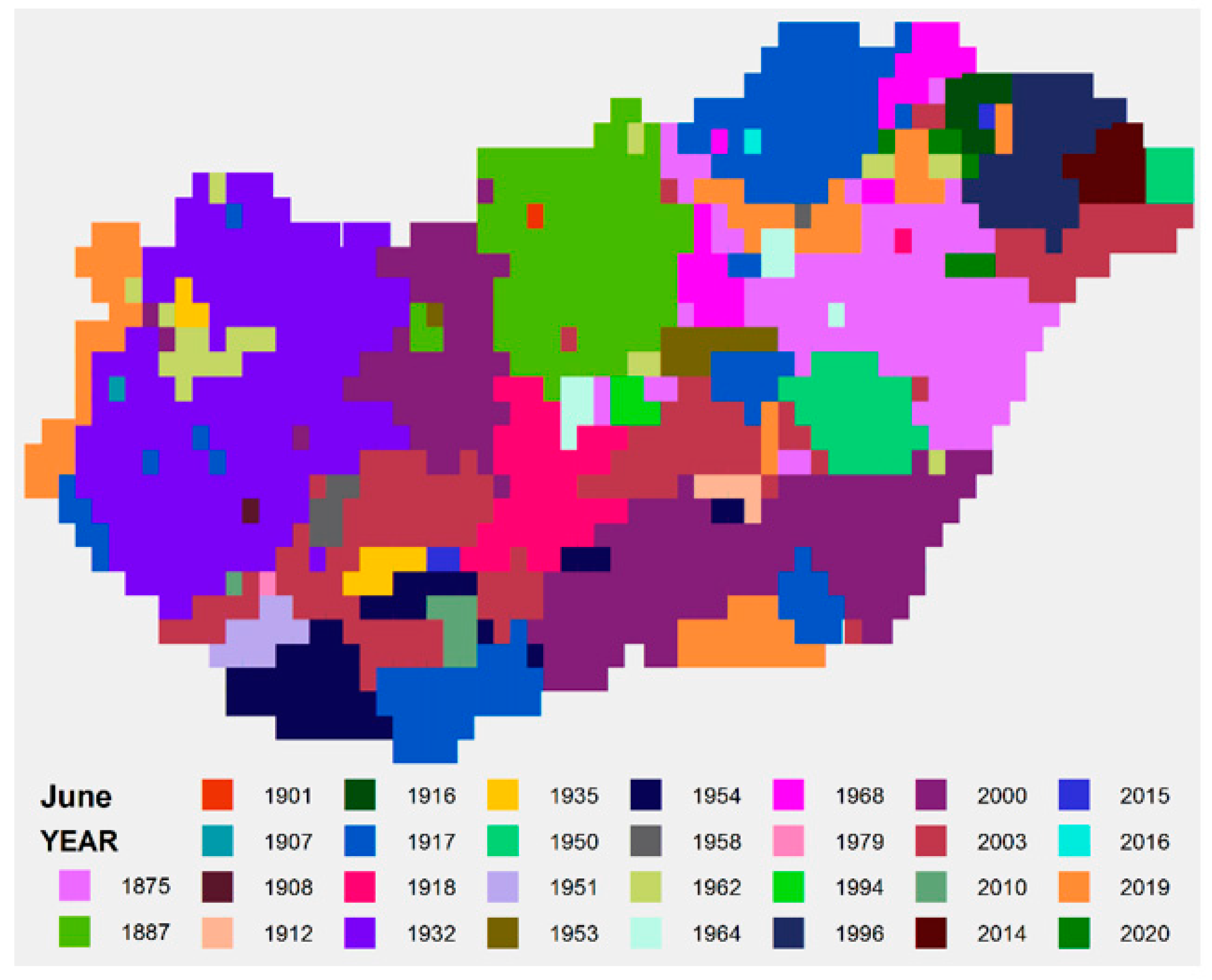
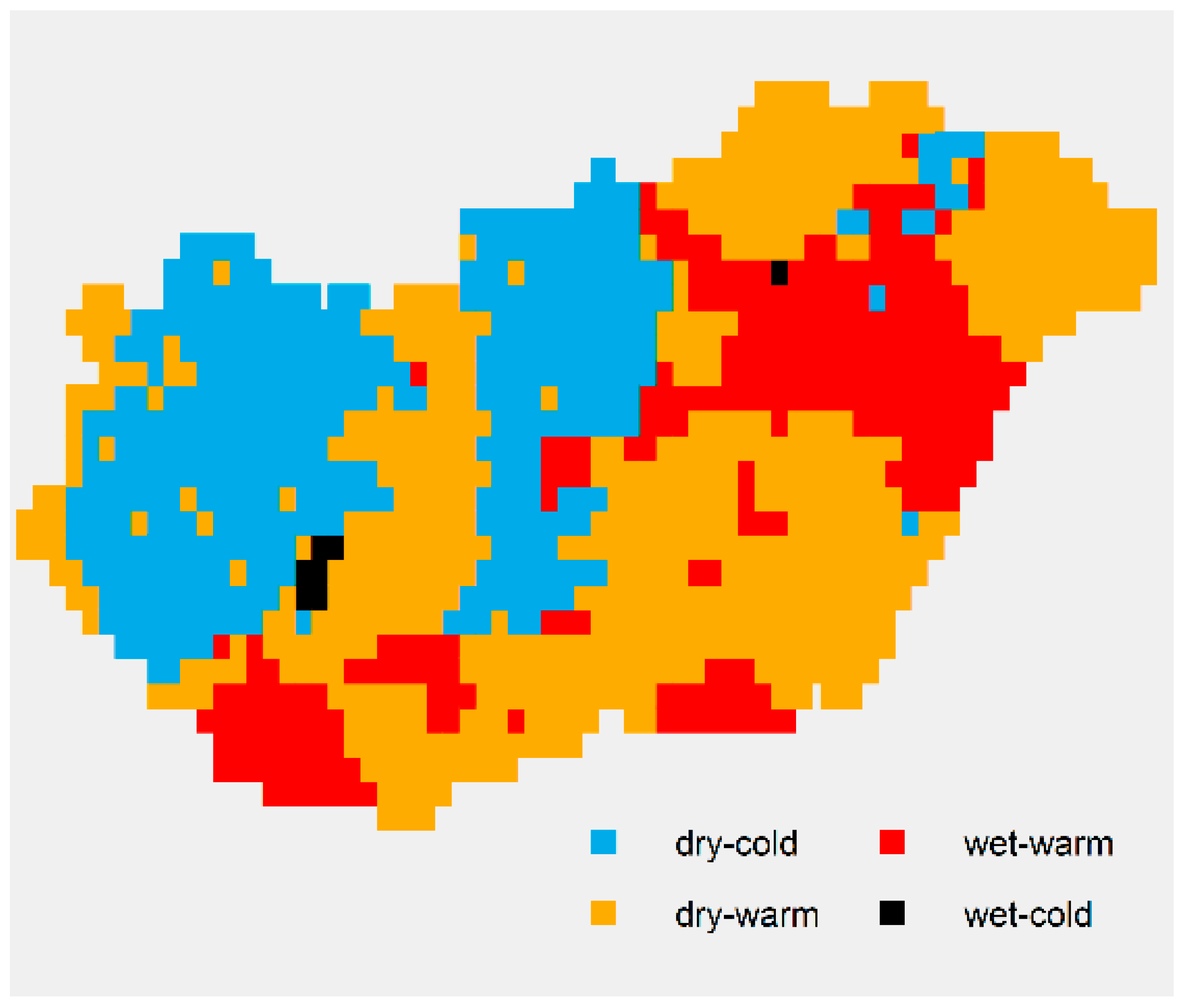
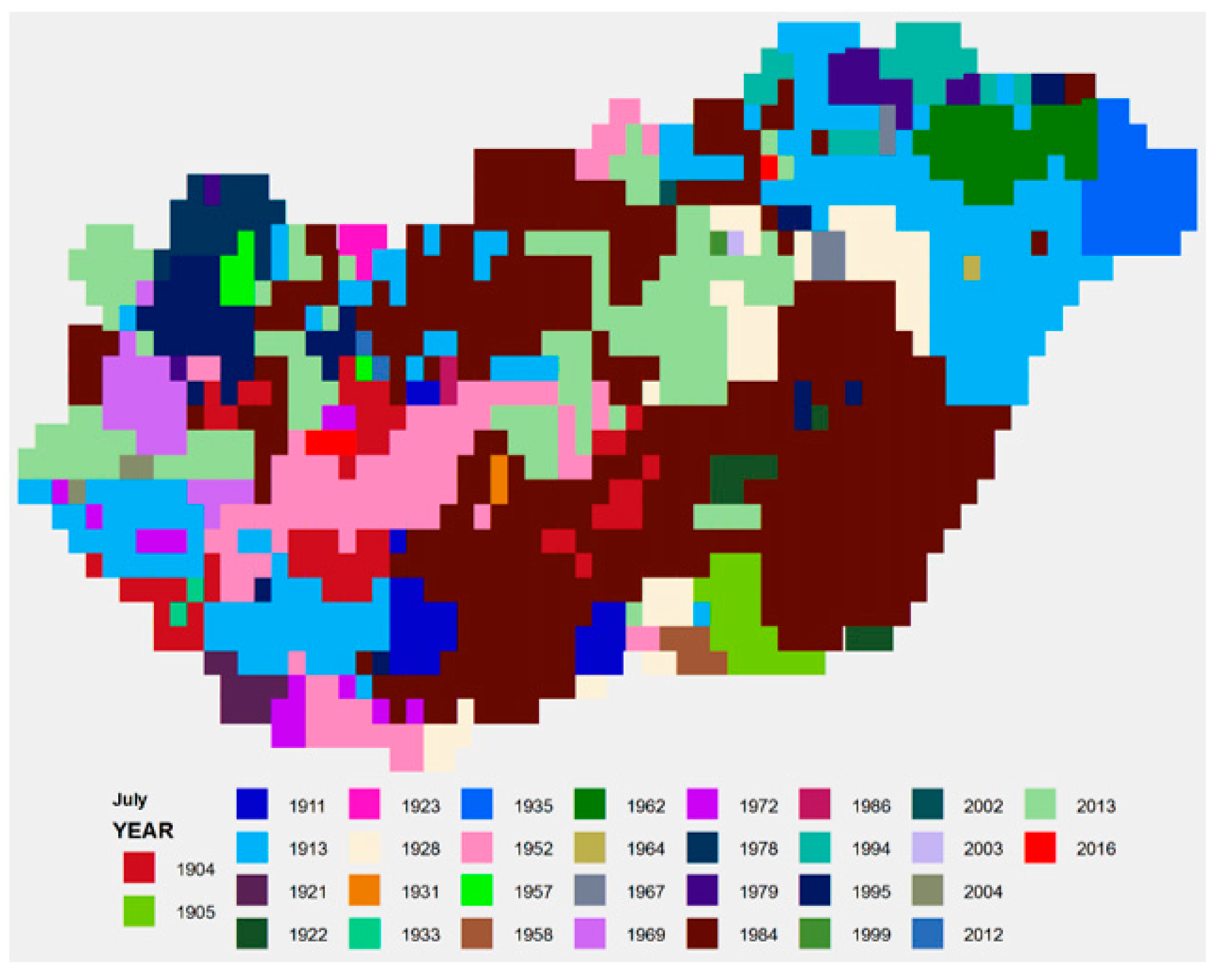
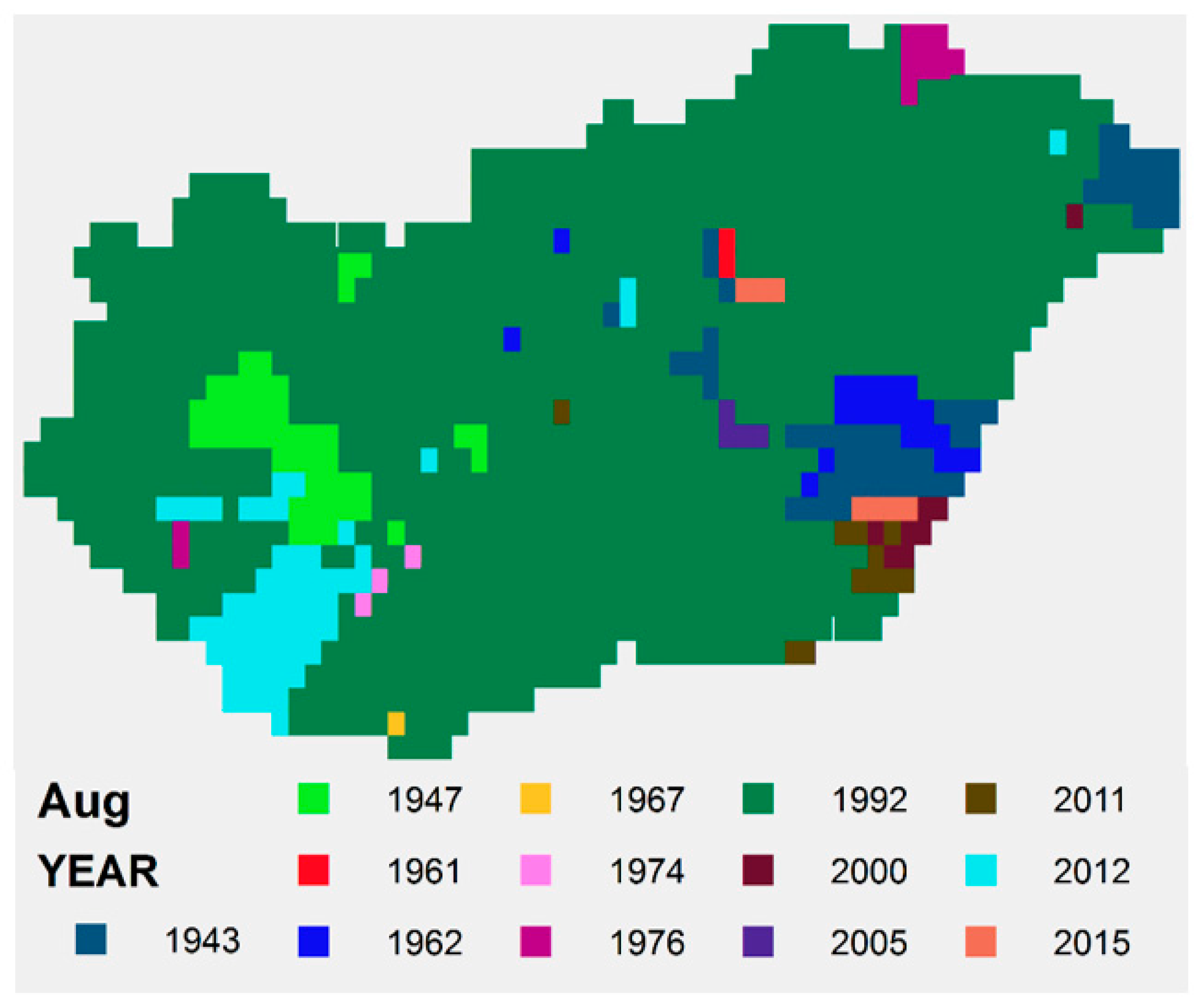
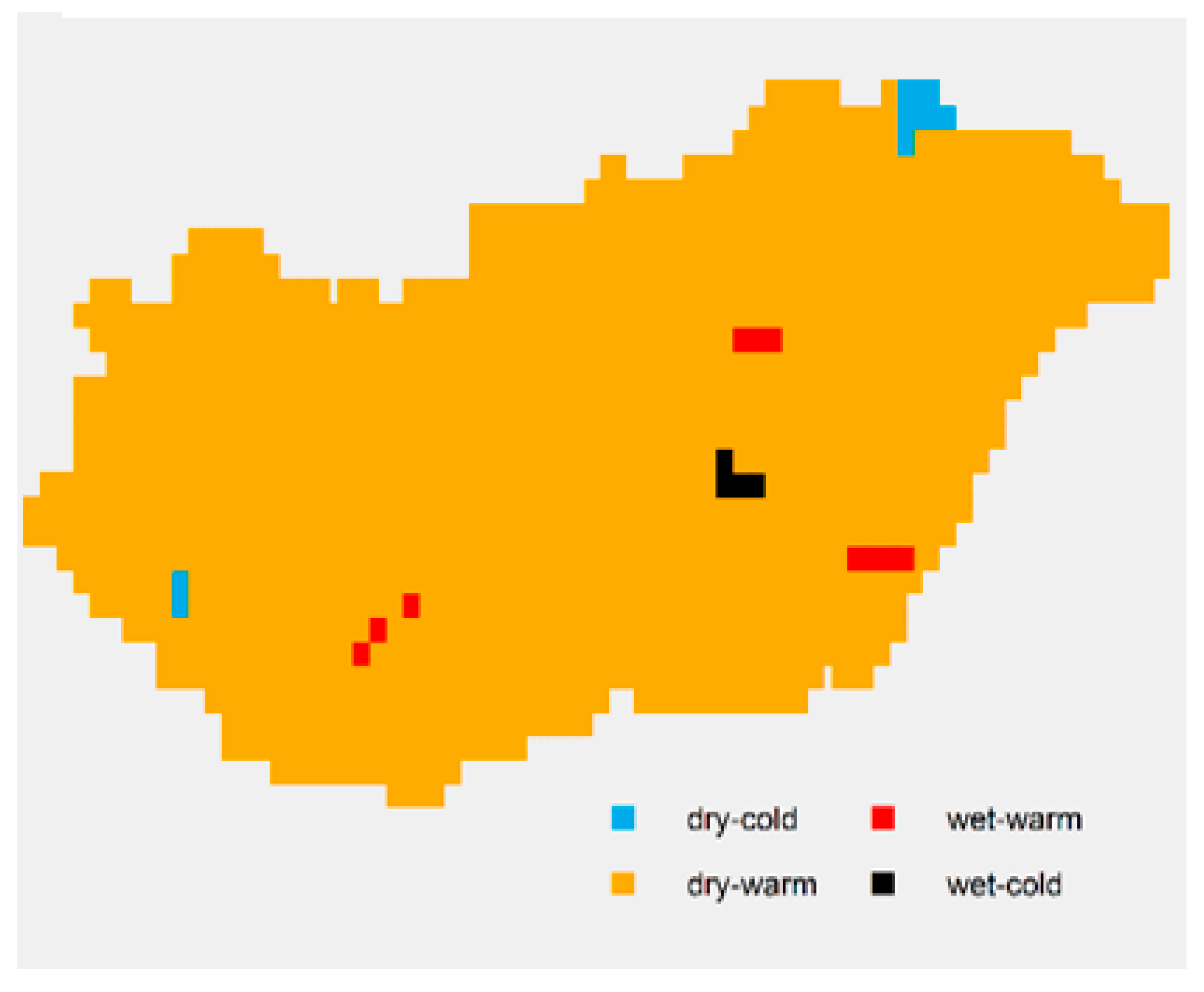
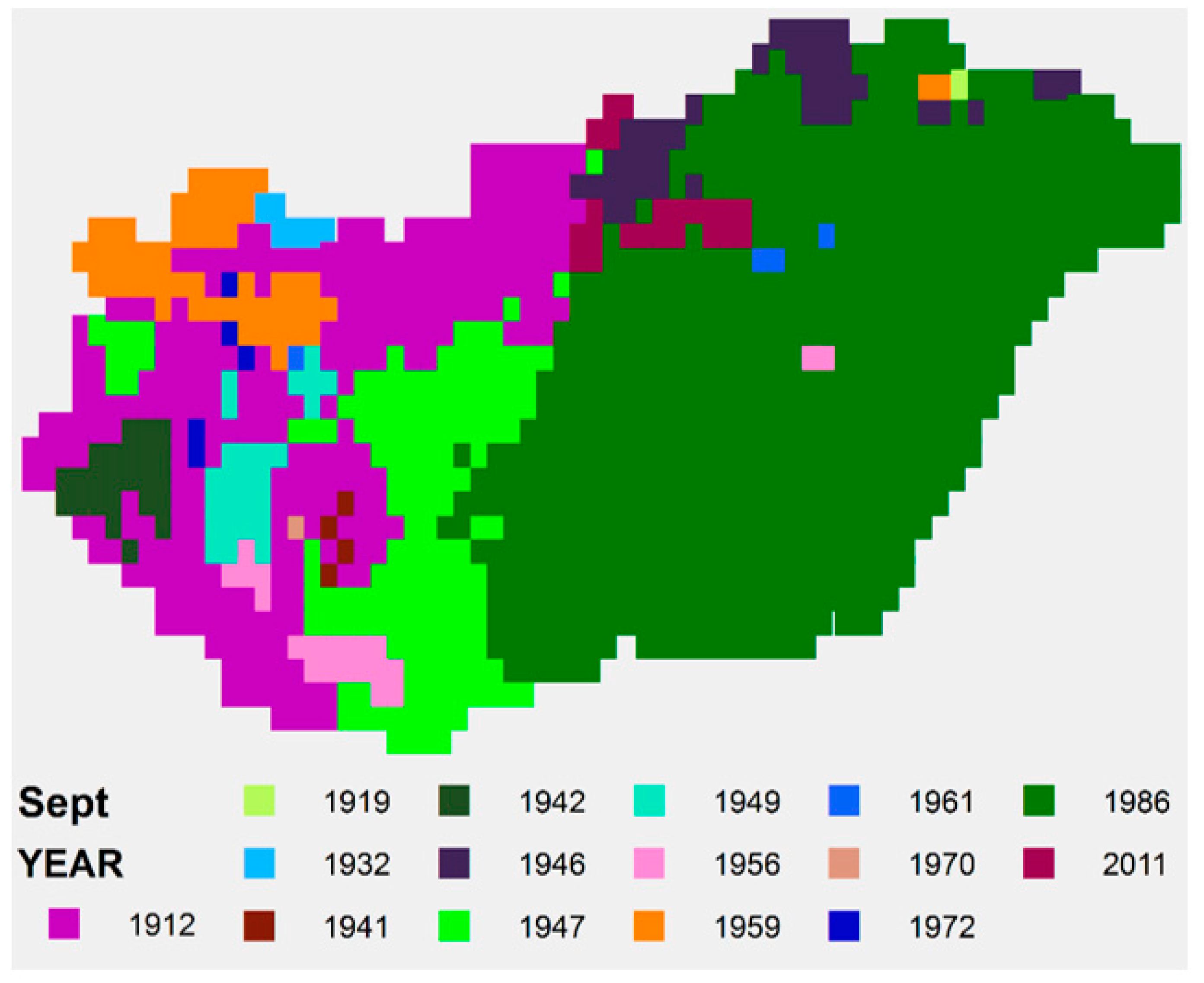
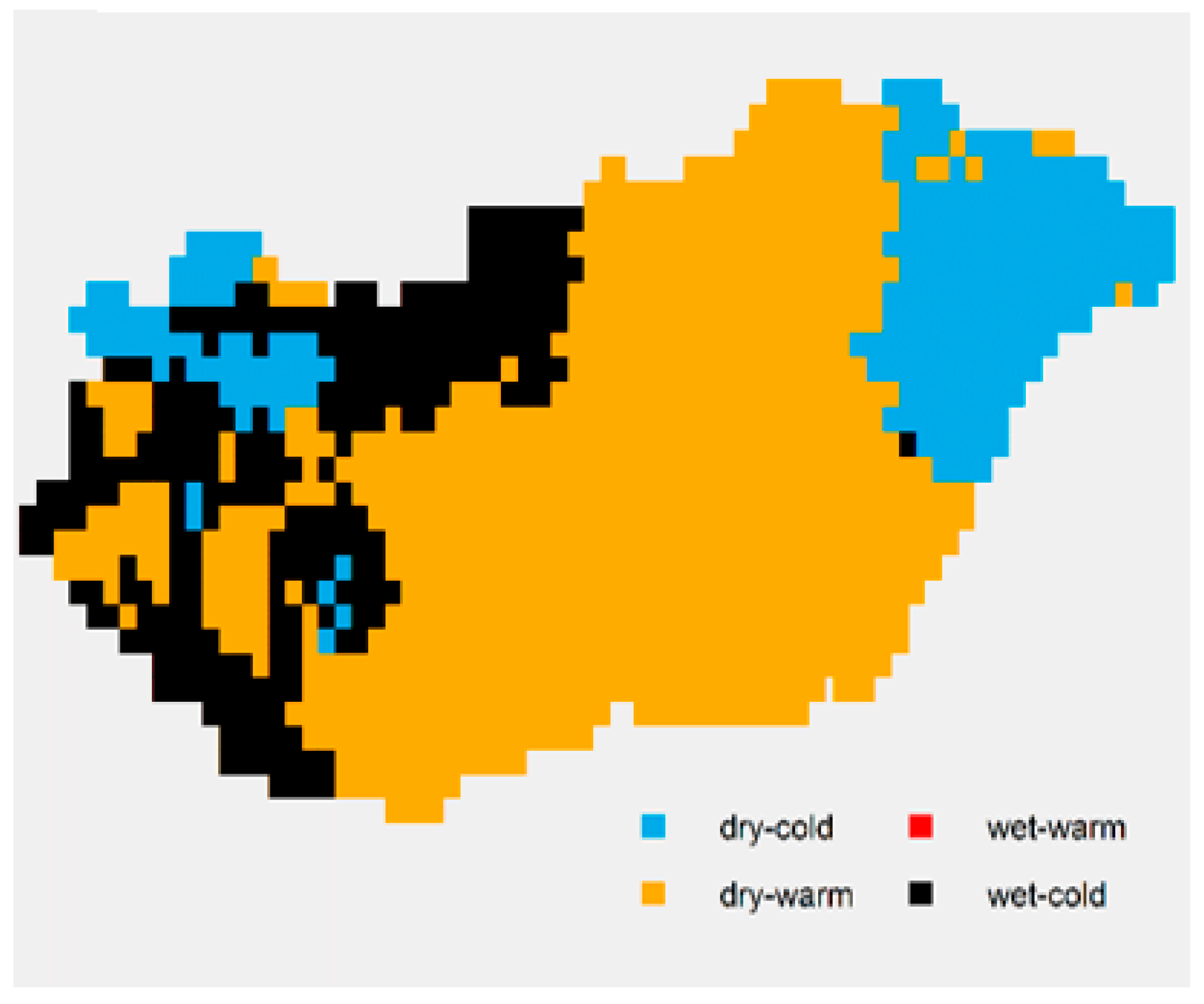
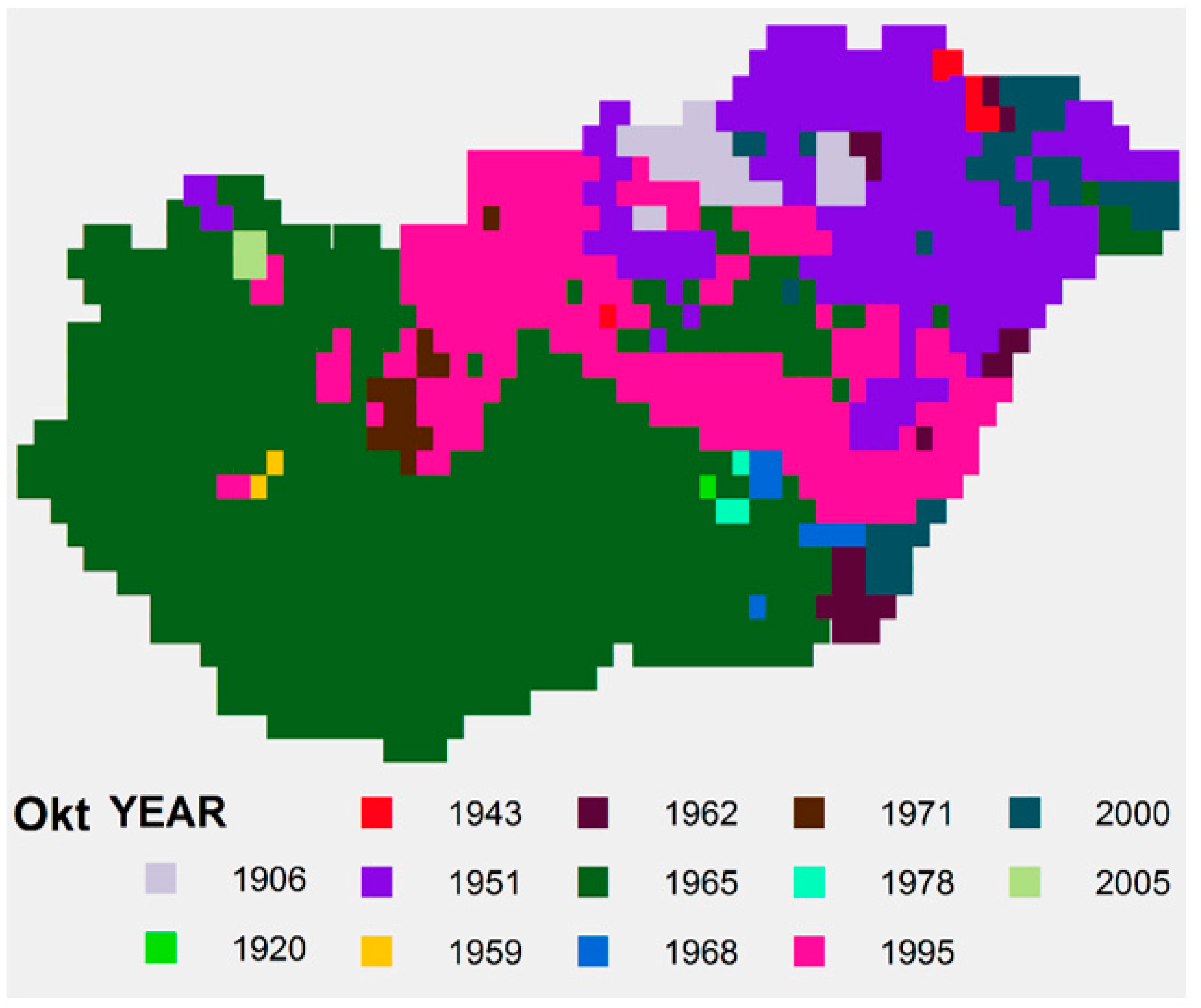
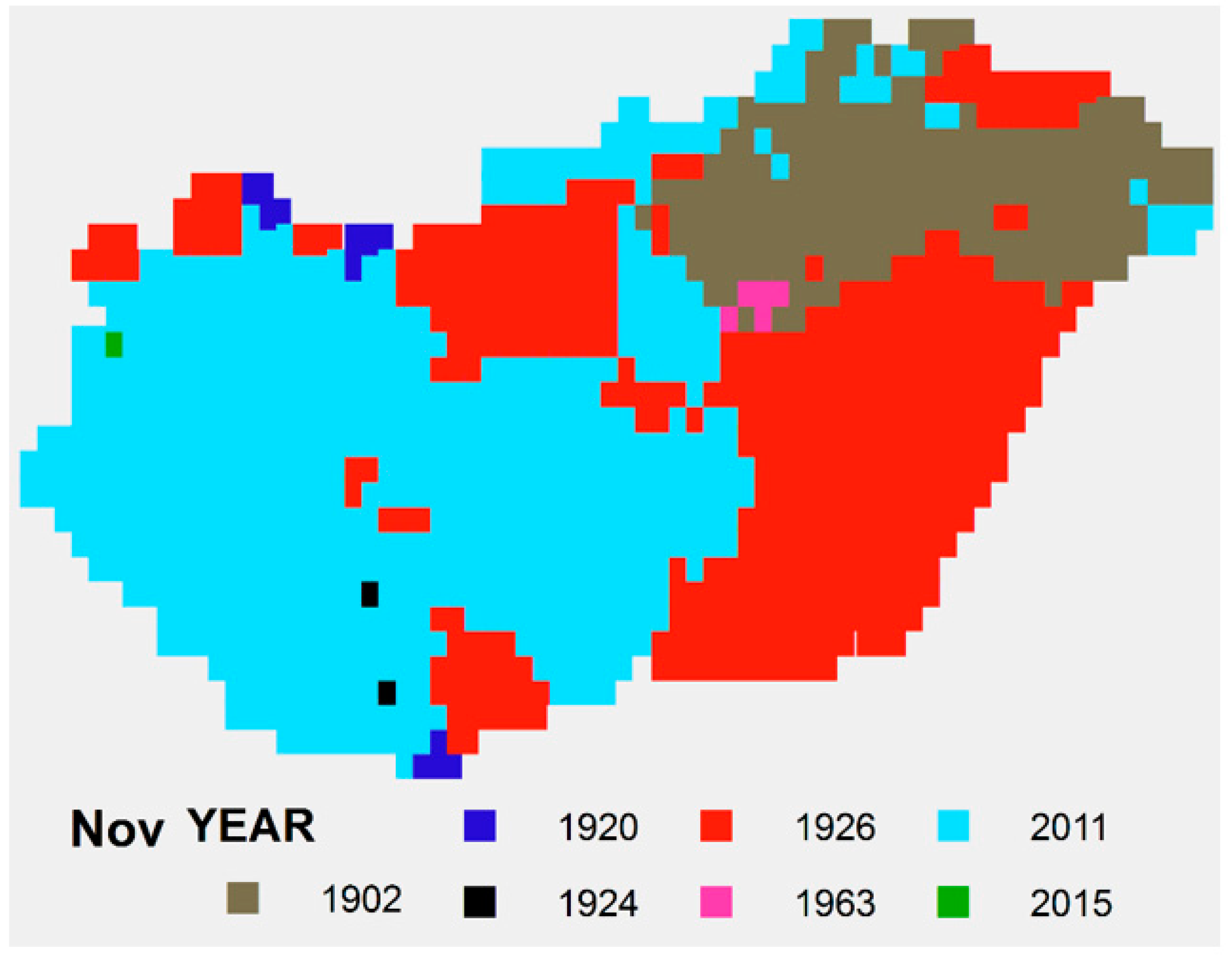
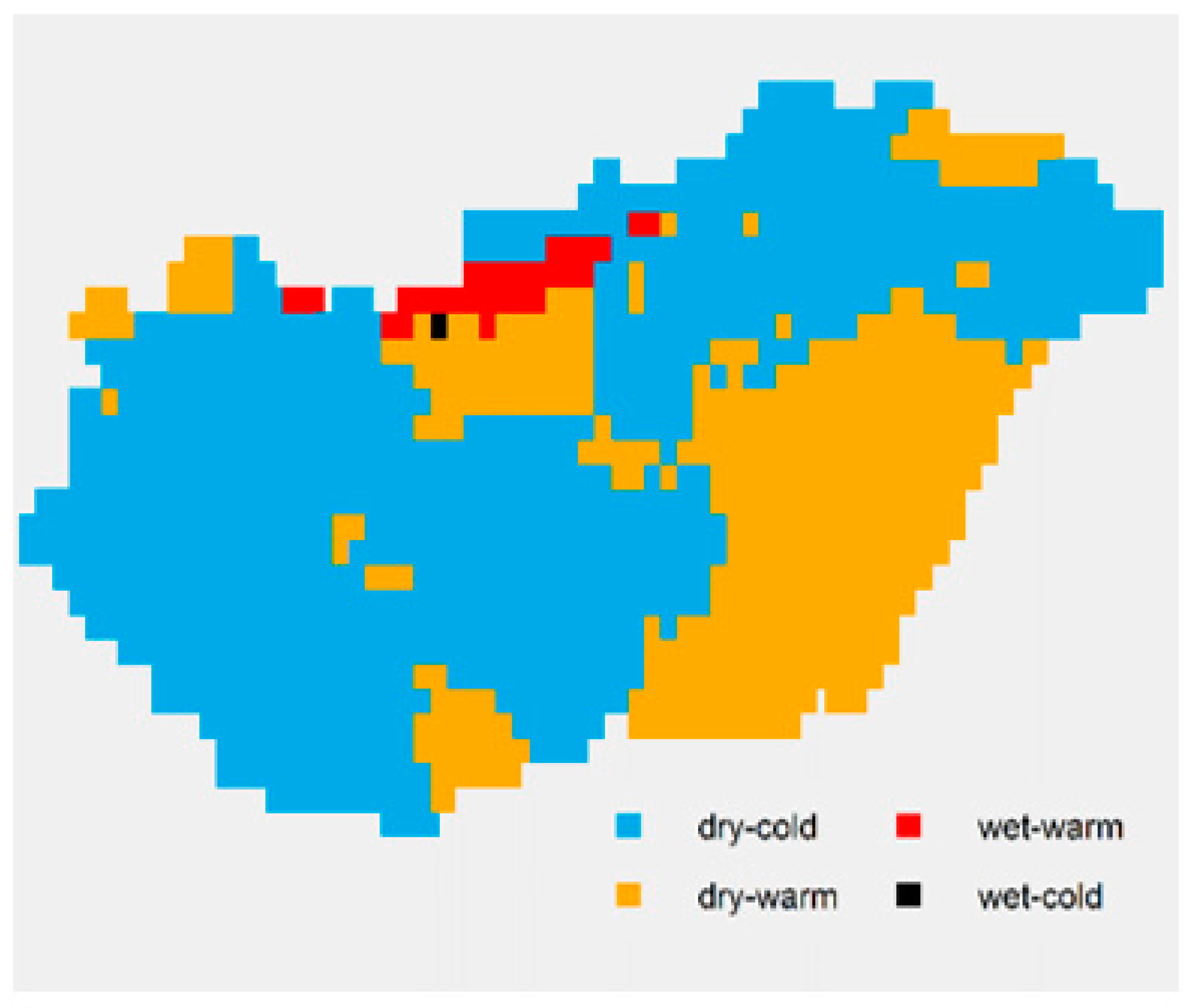
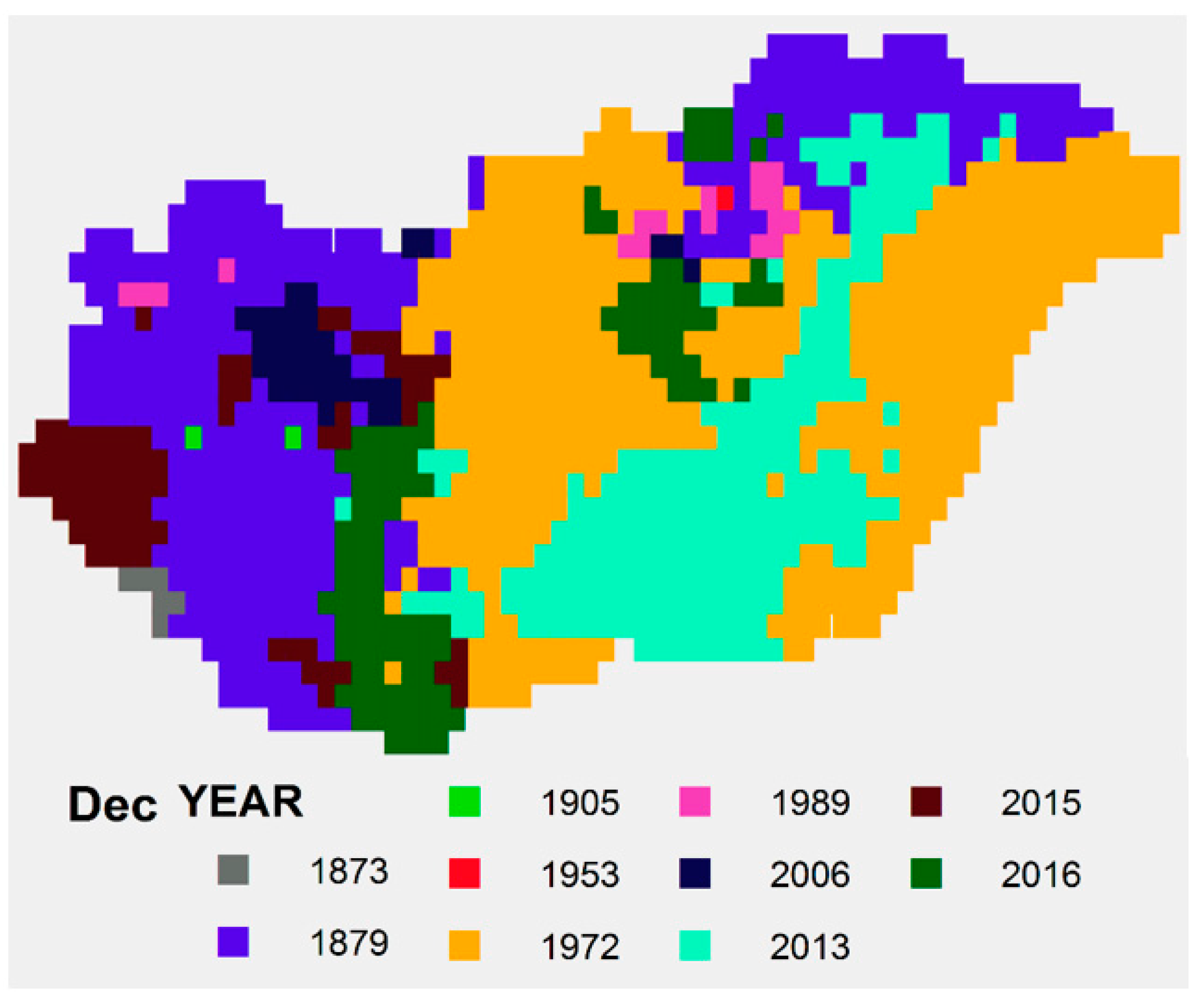
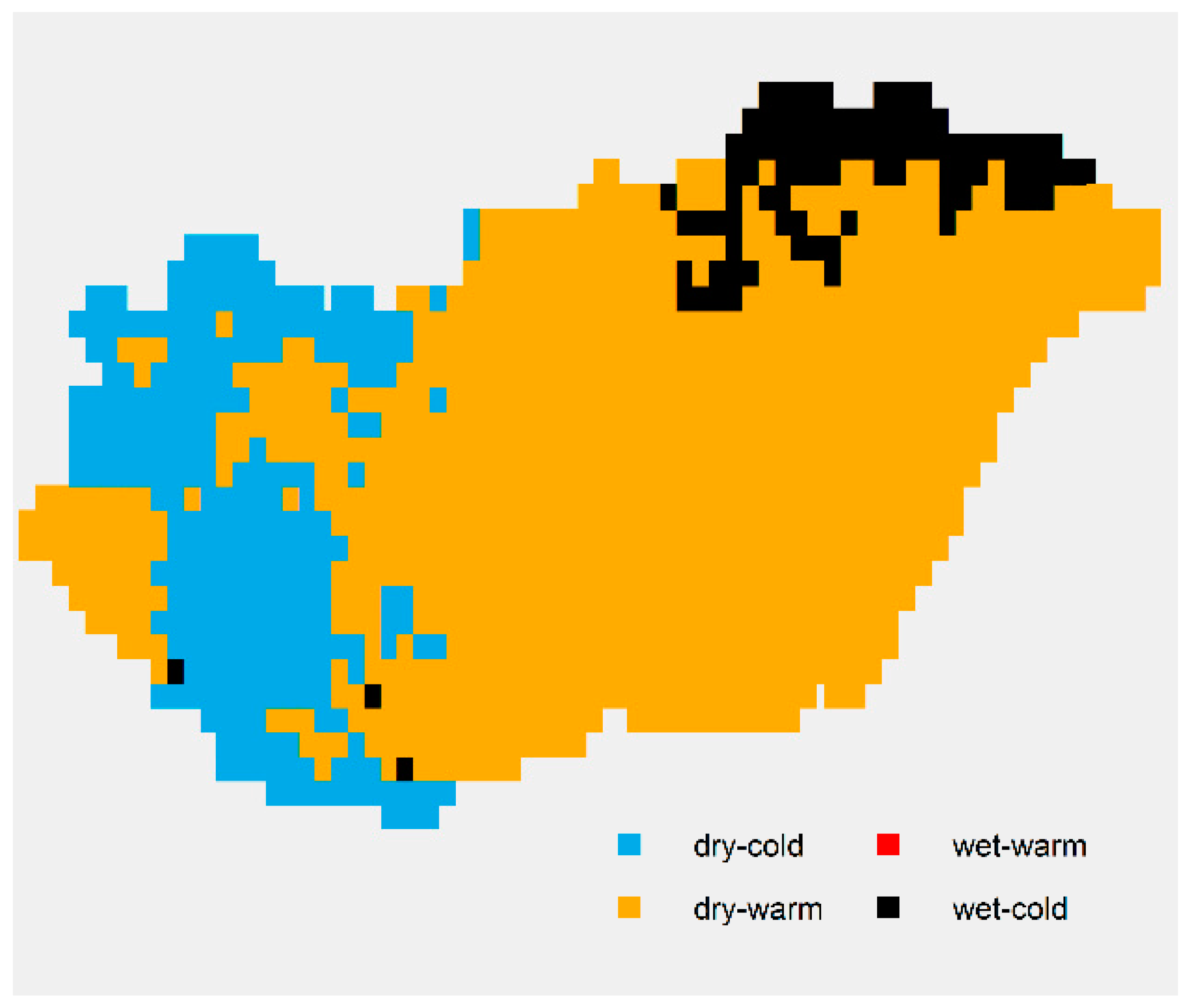
4. Results
4.1. Spatial Average
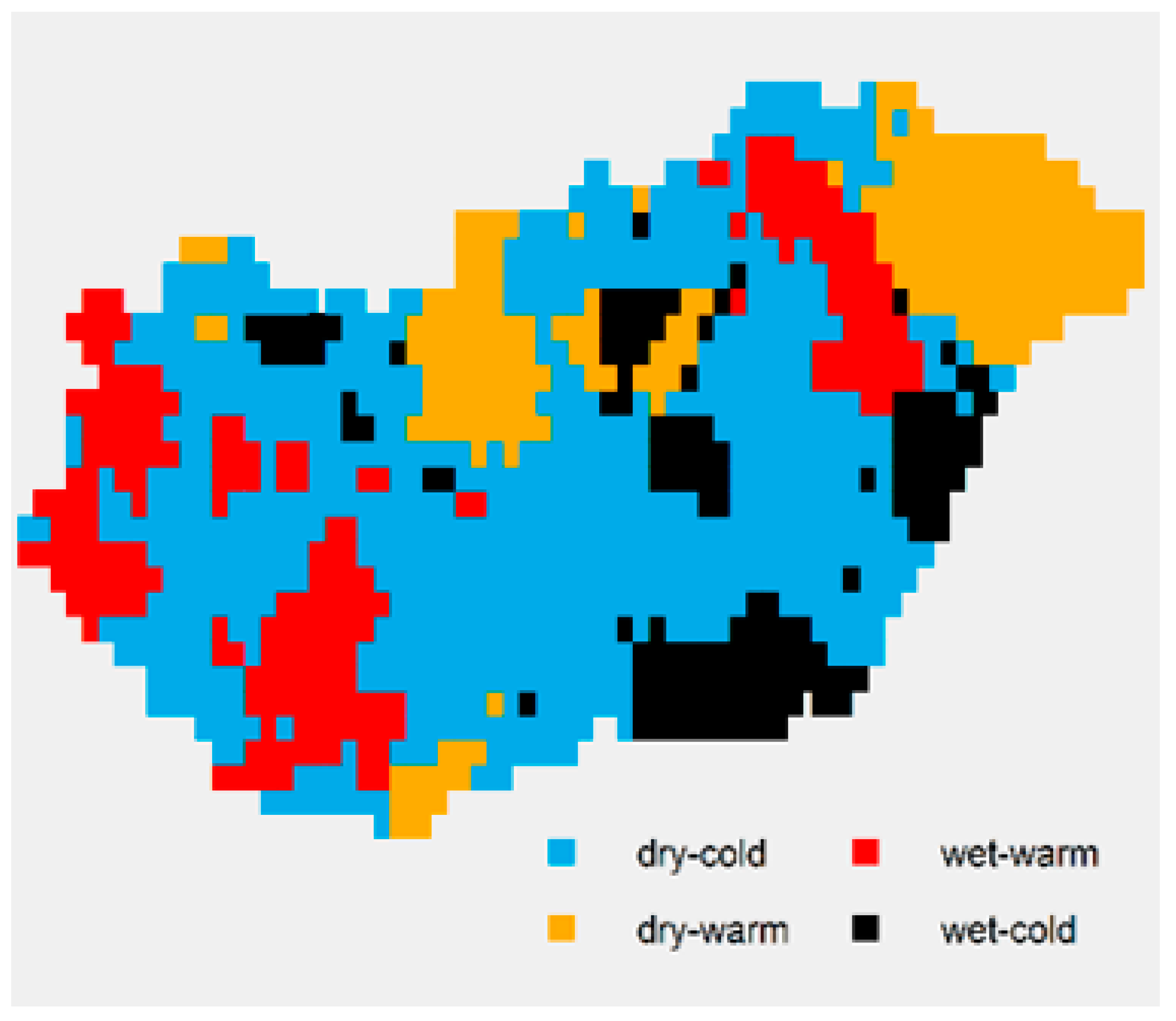
4.2. Analysis of Spatial SPTI Values
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological events. Quart. J. Roy. Meteorol. Soc. 1955, 81, 158–172. [Google Scholar] [CrossRef]
- Naveau, P.; Hannart, A.; Ribes, A. Statistical Methods for Extreme Event Attribution in Climate Science. Ann. Rev. Stat. Appl. 2020, 7, 1–22. [Google Scholar] [CrossRef] [Green Version]
- de Oliveira, J.T. Extreme values and meteorology. Theor. Appl. Climatol. 1986, 37, 184–193. [Google Scholar] [CrossRef]
- Dutfoy, A.; Parey, S.; Roche, N. Multivariate Extreme Value Theory—A Tutorial with Applications to Hydrology and Meteorology. Depend. Model. 2014, 2, 30–48. [Google Scholar] [CrossRef] [Green Version]
- Hoogewind, K.A.; Baldwin, M.E.; Trapp, R.J. The Impact of Climate Change on Hazardous Convective Weather in the United States: Insight from High-Resolution Dynamical Downscaling. J. Climate 2017, 30, 10081–10100. [Google Scholar] [CrossRef]
- Demski, C.; Capstick, S.; Pidgeon, N.; Sposato, R.G.; Spence, A. Experience of extreme weather affects climate change mitigation and adaptation responses. Clim. Chang. 2017, 140, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Carter, D.J.T.; Challeron, P.G. Estimating return values of environmental parameters. Quart. J. Roy. Meteorol. Soc. 1981, 107, 259–266. [Google Scholar] [CrossRef]
- Lakatos, M.; Izsák, B.; Szentes, O.; Hoffmann, L.; Kircsi, A.; Bihari, Z. Return values of 60-minute extreme rainfall for Hungary. Időjárás 2020, 124, 143–156. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Zwiers, F.W.; Zhang, X. Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation; World Meteorological Organization: Geneva, Switzerland, 2009; Climate data and monitoring WCDMP-No. 72; WMO-TD No. 1500. [Google Scholar]
- Szentimrey, T. Többdimenziós Éghajlati Idősorok “Extrémumainak” Vizsgálata. (Examination of "Extremes" in Multidimensional Climate Time Series); Meteorológiai Tudományos Napok’99 Kiadványa: Budapest, Hungary, 1999; pp. 77–88. (In Hungarian) [Google Scholar]
- Matyasovszky, I. Extreme temperature and precipitation years in Hungary during last century. Időjárás 2001, 105, 157–164. [Google Scholar]
- Szentimrey, T.; Izsák, B. Joint examination of climate time series based on a statistical definition of multidimensional extreme. Időjárás 2022, 126, 159–184. [Google Scholar] [CrossRef]
- Kiriliouk, A.; Naveau, P. Climate extreme event attribution using multivariate peaks-over-thresholds modeling and counterfactual theory. Ann. Appl. Stat. 2020, 14, 1342–1358. [Google Scholar] [CrossRef]
- Cooley, D.; Thibaud, E. Decompositions of dependence for high-dimensional extremes. Biometrika 2019, 106, 587–604. [Google Scholar] [CrossRef]
- Trenberth, K.; Shea, D. Relationship between precipitation and surface temperature. Geophys. Res. Lett. 2005, 32, L14703. [Google Scholar] [CrossRef]
- Zhao, W.; Khalil, M.A.K. The Relationship between Precipitation and Temperature over the Contiguous United States. J. Climate 1993, 6, 1232–1236. [Google Scholar] [CrossRef]
- Parzen, E. On the estimation of probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Rosenblatt, M. On some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Lakatos, M.; Matyasovszky, I. Analysis of the extremity of precipitation intensity using the POT method. Időjárás 2004, 108, 163–171. [Google Scholar]
- de Oliviera, J.T. Bivariate Models for Extremes. In Statistical Extremes and Applications; Reidel: Dortrecht, Holland, 1984; pp. 131–153. [Google Scholar]
- Wazneh, H.; Arain, M.; Coulibaly, P.; Gachon, P. Evaluating the Dependence between Temperature and Precipitation to Better Estimate the Risks of Concurrent Extreme Weather Events. Adv. Meteorol. 2020, 2020, 8763631. [Google Scholar] [CrossRef]
- Zhao, N.; Lin, W.T. A copula entropy approach to correlation measurement at the country level. Appl. Math. Comput. 2011, 218, 628–642. [Google Scholar] [CrossRef]
- Ohlwein, C.; Friederichs, P. Multivariate non-normally distributed random variables in climate research—Introduction to the copula approach. Nonlinear Proc. Geophys. 2008, 15, 761–772. [Google Scholar]
- Renard, B.; Lang, M. Use of a Gaussian copula for multivariate extreme value analysis: Some case studies in hydrology. Adv. Water Resour. 2007, 30, 897–912. [Google Scholar] [CrossRef] [Green Version]
- Yan, J. Enjoy the Joy of Copulas: With a Package copula. J. Stat. Software 2007, 21, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Gudendorf, G.; Segers, J. Extreme-Value Copulas. Lecture Notes in Statistics. LNSP 2010, 198, 127–145. [Google Scholar]
- Wang, J.; Rong, G.; Li, K.; Zhang, J. Analysis of Drought Characteristics in Northern Shaanxi Based on Copula Function. Water 2021, 13, 1445. [Google Scholar] [CrossRef]
- Ferreira, A.; de Haan, L. On the block maxima method in extreme value theory: PWM estimators. Ann. Statist. 2015, 43, 276–298. [Google Scholar] [CrossRef] [Green Version]
- Izsák, B.; Szentimrey, T. To what extent does the detection of climate change in Hungary depend on the choice of statistical methods? GEM—Int. J. Geomath. 2020, 11, 17. [Google Scholar] [CrossRef]
- Szentimrey, T. Manual of Homogenization Software MASHv3.03; Hungarian Meteorological Service: Budapest, Hungary, 2014. [Google Scholar]
- Szentimrey, T.; Bihari, Z.; Lakatos, M. Quality control procedures in MISH-MASH systems, 10th EMS Annual Meeting. In Proceedings of the 10th European Conference on Applications of Meteorology (ECAM) Abstracts, Zürich, Switzerland, 13–17 September 2010. [Google Scholar]
- Szentimrey, T. Theoretical questions of daily data homogenization. Időjárás 2013, 117, 113–122. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Szentimrey, T.; Bihari, Z. Manual of Interpolation Software MISHv1.03; Hungarian Meteorological Service: Budapest, Hungary, 2014; p. 89. [Google Scholar]
- Szentimrey, T.; Bihari, Z.; Lakatos, M.; Szalai, S. Mathematical, methodological questions concerning the spatial interpolation of climate elements. Időjárás 2011, 115, 1–11. [Google Scholar]
- Lakatos, M.; Szentimrey, T.; Bihari, Z.; Szalai, S. Creation of a homogenized climate database for the Carpathian region by applying the MASH procedure and the preliminary analysis of the data. Időjárás 2013, 117, 143–158. [Google Scholar]
- Spinoni, J.; Szalai, S.; Szentimrey, T.; Lakatos, M.; Bihari, Z.; Nagy, A.; Németh, Á.; Kovács, T.; Mihic, D.; Dacic, M.; et al. Climate of the Carpathian Region in the period 1961–2010: Climatologies and trends of 10 variables. Int. J. Climatol. 2015, 35, 1322–1341. [Google Scholar] [CrossRef] [Green Version]
- Venema, V.; Mestre, O.; Aguilar, E.; Auer, I.; Guijarro, J.A.; Domonkos, P.; Vertacnik, G.; Szentimrey, T.; Štěpánek, P.; Zahradnicek, P.; et al. Benchmarking monthly homogenization algorithms. Clim. Past. 2012, 8, 89–115. [Google Scholar] [CrossRef] [Green Version]
- Gutowski, W.J., Jr.; Ullrich, P.A.; Hall, A.; Leung, L.R.; O’Brien, T.A.; Patricola, C.M.; Arritt, R.W.; Bukovsky, M.S.; Calvin, K.V.; Feng, Z.; et al. The Ongoing Need for High-Resolution Regional Climate Models: Process Understanding and Stakeholder Information. Bull. Am. Meteorol. Soc. 2020, 101, E664–E683. [Google Scholar] [CrossRef] [Green Version]
- Bandhauer, M.; Isotta, F.; Lakatos, M.; Lussana, C.; Båserud, L.; Izsák, B.; Szentes, O.; Tveito, O.E.; Frei, C. Evaluation of daily precipitation analyses in E-OBS (v19.0e) and ERA5 by comparison to regional high-resolution datasets in European regions. Int. J. Climatol. 2021, 42, 727–747. [Google Scholar] [CrossRef]
- Izsák, B.; Szentimrey, T.; Lakatos, M.; Pongrácz, R.; Szentes, O. Creation of a representative climatological database for Hungary from 1870 to 2020. Időjárás 2022, 126, 1–26. [Google Scholar] [CrossRef]
- HuClim Database. Available online: https://odp.met.hu/climate/ (accessed on 9 August 2021).
- WMO-No. 1090; Standardized Precipitation Index User Guide. WMO: Geneva, Switzerland, 2012; 24p, ISBN 978-92-63-11090-9.
- Szentimrey, T.; Lakatos, M.; Bihari, Z. Joint examination of climate variables, Standardized Precipitation and Temperature Index (SPTI). In Proceedings of the European Conference on Applied Climatology (ECAC), Prague, Czech Republic, 5–10 October 2014. [Google Scholar]
- Hildreth, W.; Fierstein, J. The Novarupta-Katmai eruption of 1912—Largest eruption of the twentieth century; centennial perspectives: U.S. Geol. Surv. Prof. Pap. 2012, 1791, 259. [Google Scholar]
- Harangi, S. Vulkánkitörések klímaváltoztató hatása: A kicsi is számít! Magy. Tudomány 2017, 188, 664–674. (In Hungarian) [Google Scholar]

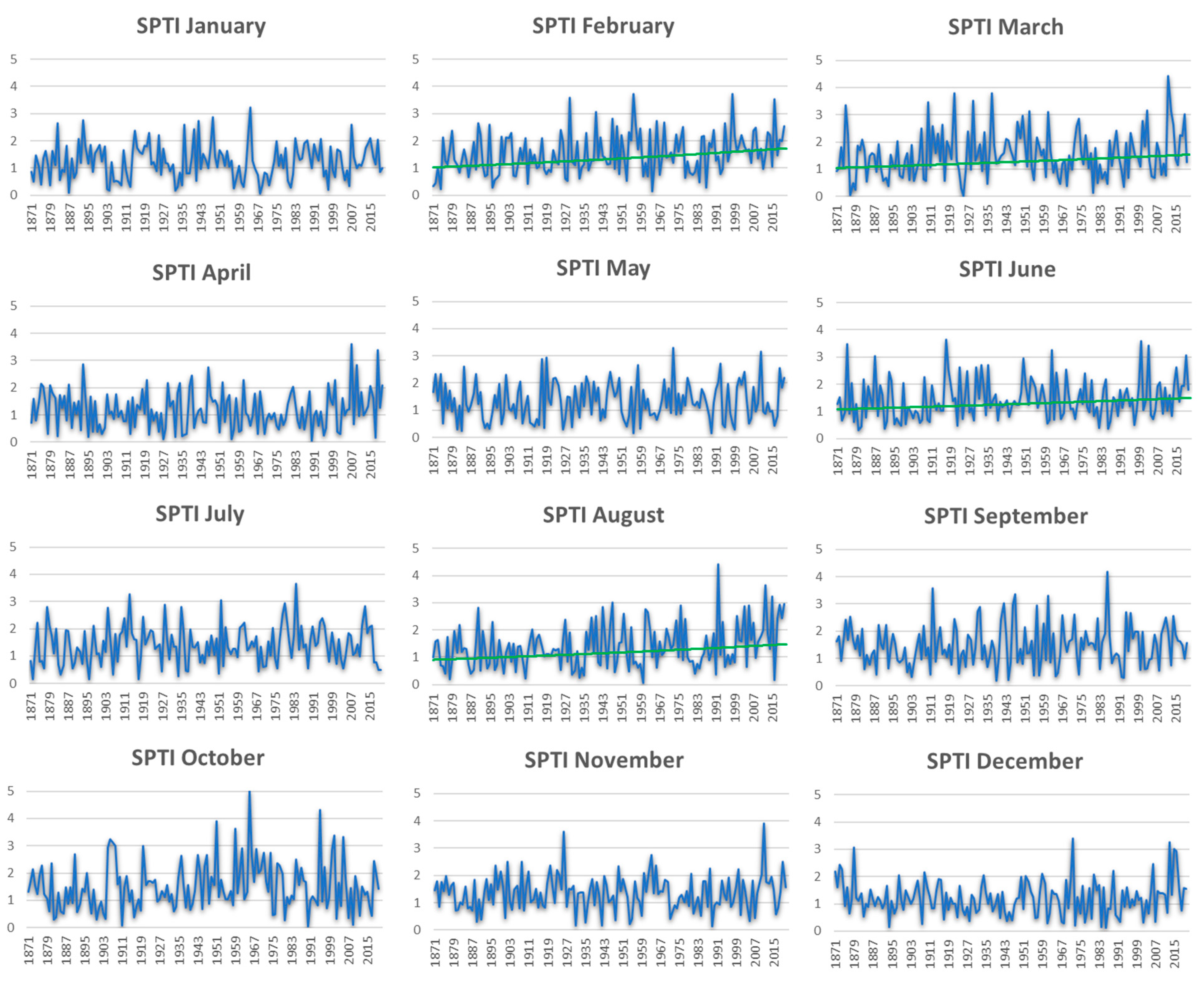
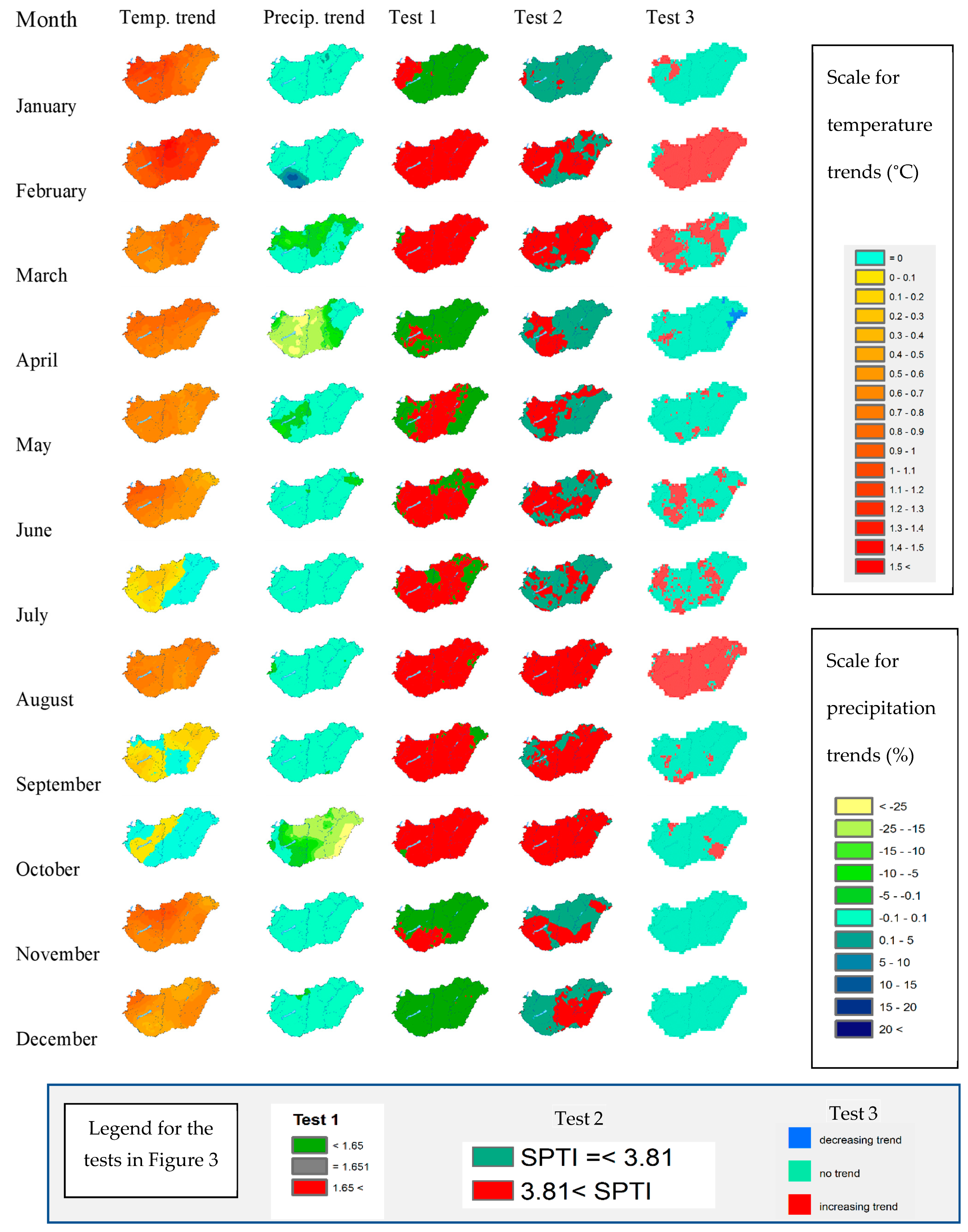
| MONTH | R Trend | T Trend | Test 1 (Cr3 = 1.65) | Test 2 (Cr2 = 3.81) | Test 3 |
|---|---|---|---|---|---|
| January | - | 2.16 °C | −1.09 | 3.23 | - |
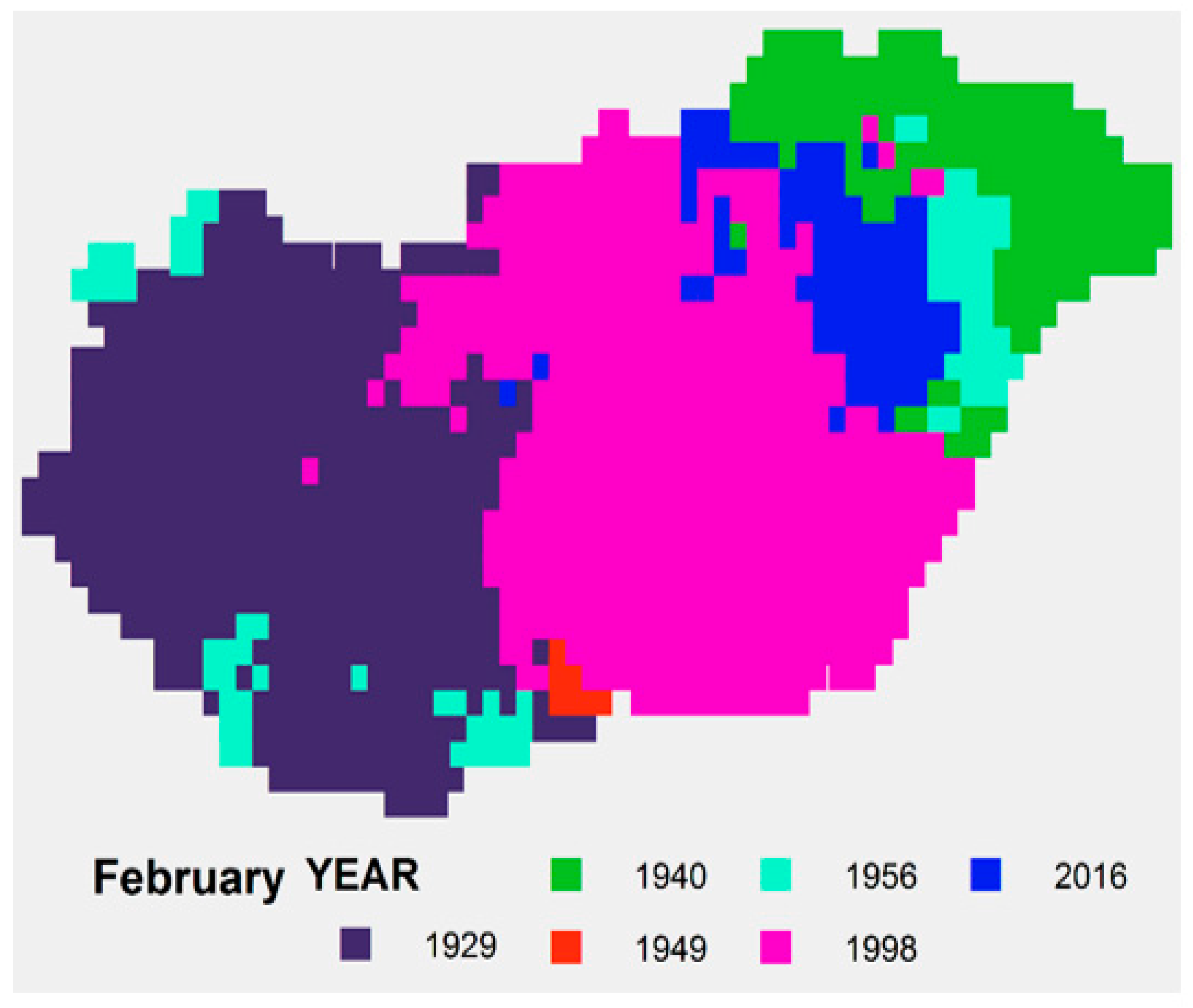
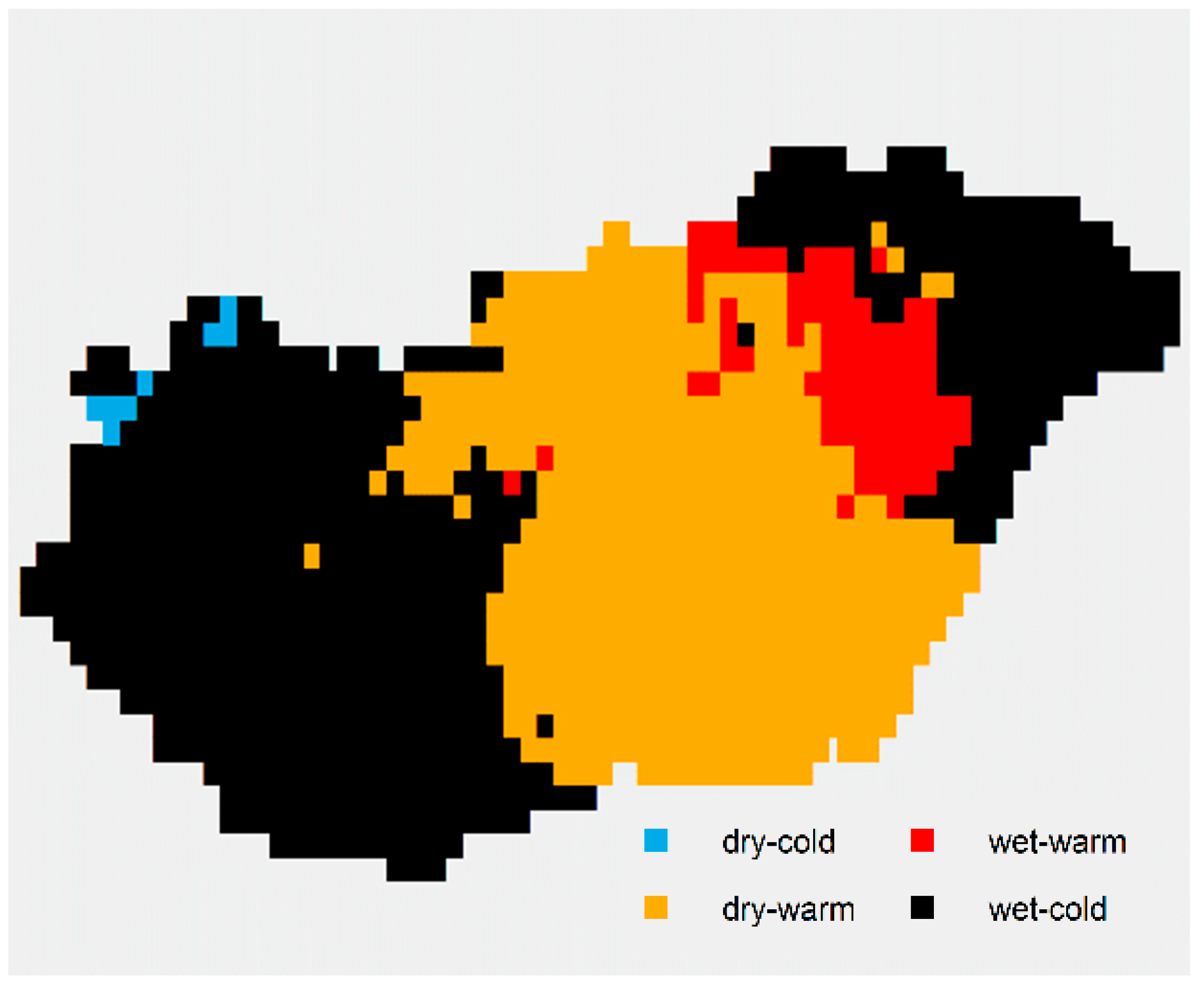
| February | - | 2.47 °C | 9.25 | 3.73 | 68% |
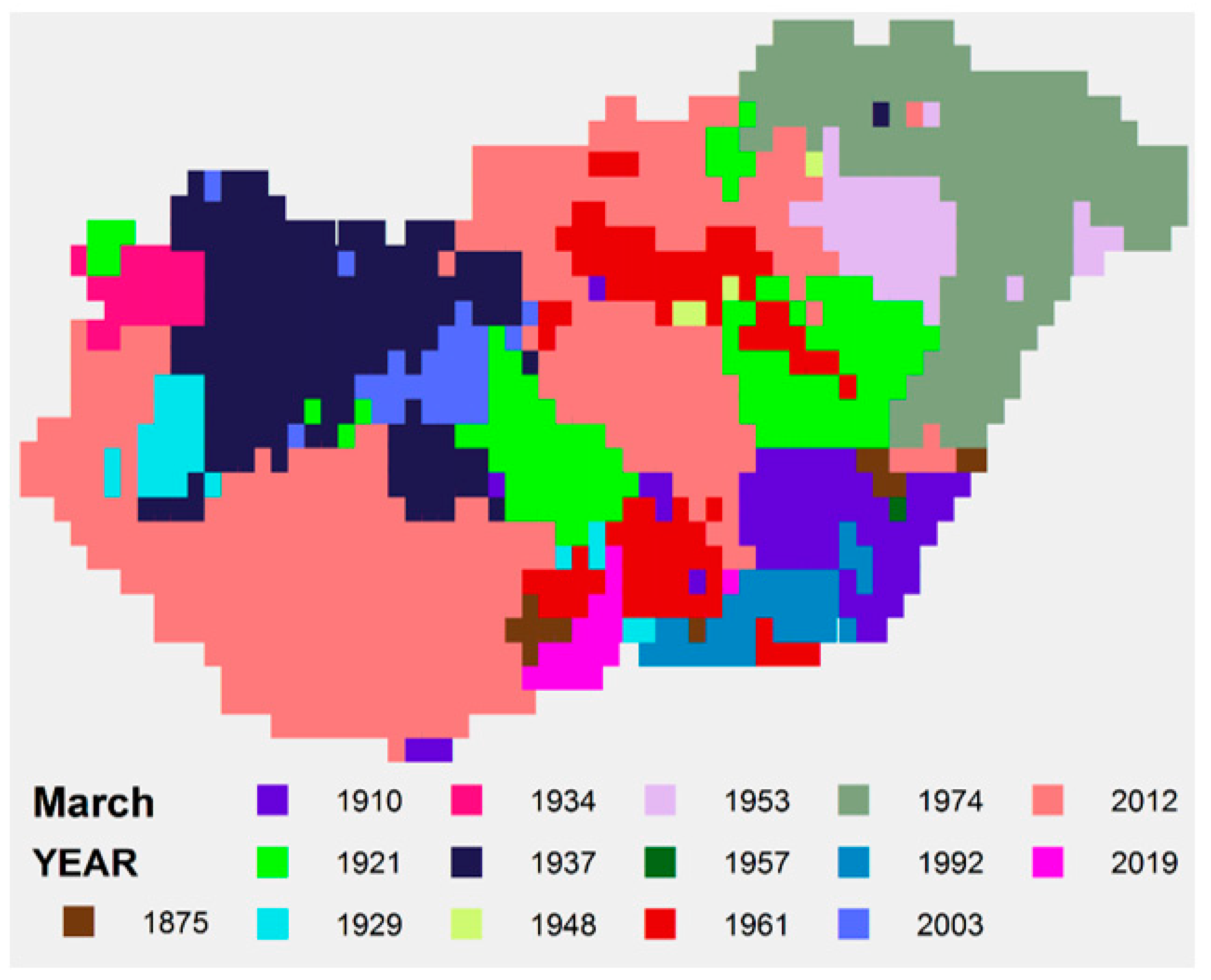
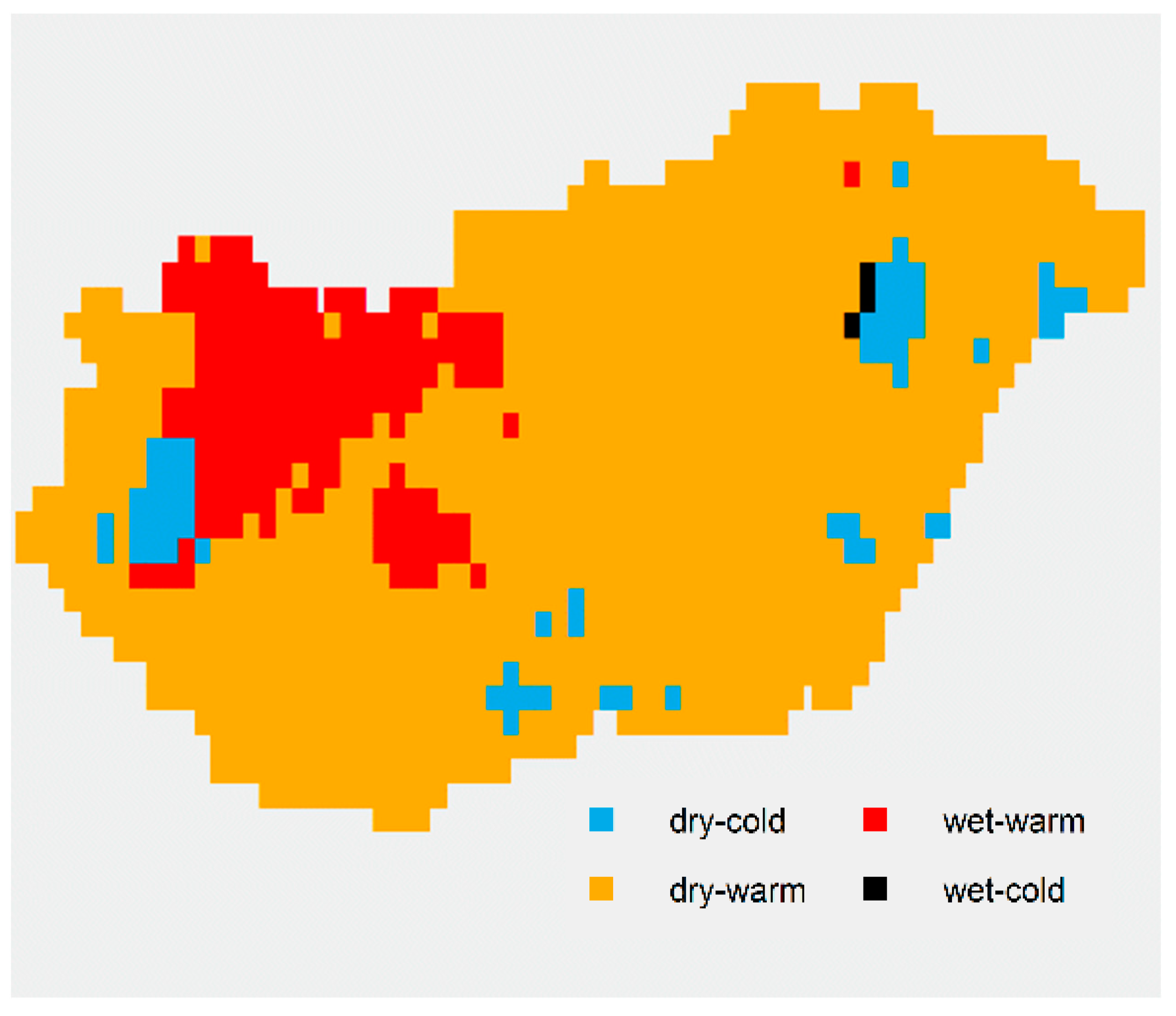
| March | - | 1.69 °C | 4.35 | 4.43 | 47% |
| April | −33% | 1.51 °C | 1.63 | 3.61 | - |
| May | - | 0.97 °C | 1.91 | 3.3 | - |
| June | - | 0.92 °C | 2.45 | 3.64 | 40% |
| July | - | - | 0.54 | 3.66 | - |
| August | - | 1.45 °C | 3.27 | 4.42 | 63% |
| September | - | 0.80 °C | 2.99 | 4.18 | - |
| October | −42% | - | 4.08 | 4.99 | - |
| November | - | 1.84 °C | −0.27 | 3.91 | - |
| December | - | 1.72 °C | 1.09 | 3.41 | - |
| Jan | Feb | Mar | Apr | May | June | July | Aug | Sept | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPTI | 3.23 | 3.73 | 4.43 | 3.61 | 3.3 | 3.64 | 3.66 | 4.42 | 4.18 | 4.99 | 3.91 | 3.41 |
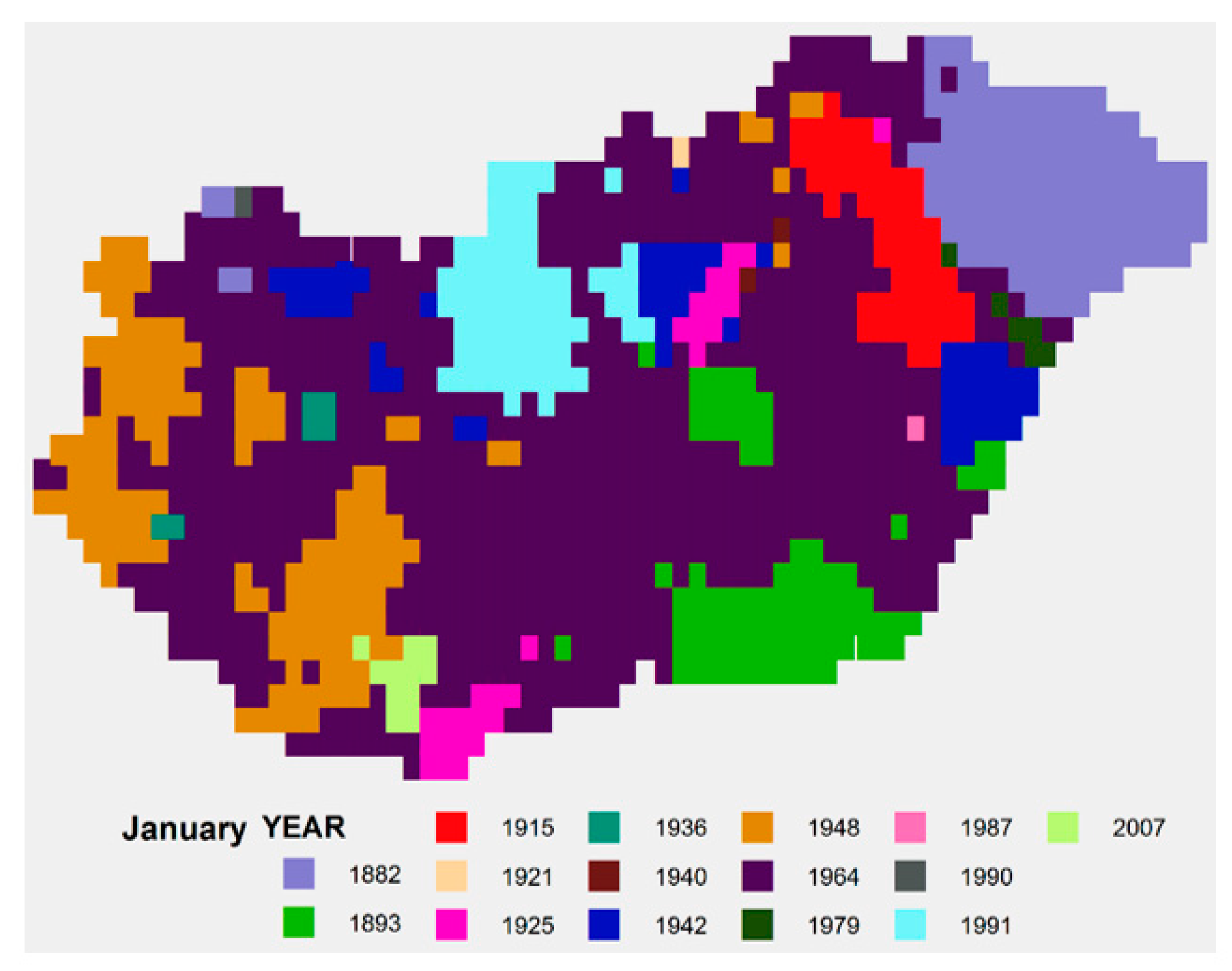
| YEAR SPTI | 1964 | 1956 | 2012 | 2007 | 1973 | 1917 | 1984 | 1992 | 1986 | 1965 | 2011 | 1972 |
| SPI | −2.57 | −2.72 | −4.39 | −3.61 | −3.13 | −3.64 | −3.06 | −3.62 | −3.75 | −4.79 | −3.9 | −3.2 |
| YEAR SPI | 1964 | 1998 | 2012 | 2007 | 1973 | 1917 | 1952 | 2012 | 1986 | 1965 | 2011 | 1972 |
| STI | −2.63 | −3.45 | −2.29 | 3.33 | 2.55 | 2.91 | −3.24 | 4.07 | −3.58 | 2.62 | 3.21 | −3.05 |
| YEAR STI | 1942 | 1929 | 1875 | 2018 | 1958 | 2019 | 1913 | 1992 | 1912 | 1966 | 1926 | 1879 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izsák, B.; Szentimrey, T.; Lakatos, M.; Pongrácz, R. Extreme Months: Multidimensional Studies in the Carpathian Basin. Atmosphere 2022, 13, 1908. https://doi.org/10.3390/atmos13111908
Izsák B, Szentimrey T, Lakatos M, Pongrácz R. Extreme Months: Multidimensional Studies in the Carpathian Basin. Atmosphere. 2022; 13(11):1908. https://doi.org/10.3390/atmos13111908
Chicago/Turabian StyleIzsák, Beatrix, Tamás Szentimrey, Mónika Lakatos, and Rita Pongrácz. 2022. "Extreme Months: Multidimensional Studies in the Carpathian Basin" Atmosphere 13, no. 11: 1908. https://doi.org/10.3390/atmos13111908
APA StyleIzsák, B., Szentimrey, T., Lakatos, M., & Pongrácz, R. (2022). Extreme Months: Multidimensional Studies in the Carpathian Basin. Atmosphere, 13(11), 1908. https://doi.org/10.3390/atmos13111908





