Spatiotemporal Characteristics of Droughts and Their Propagation during the Past 67 Years in Northern Thailand
Abstract
:1. Introduction
2. Data and Study Area
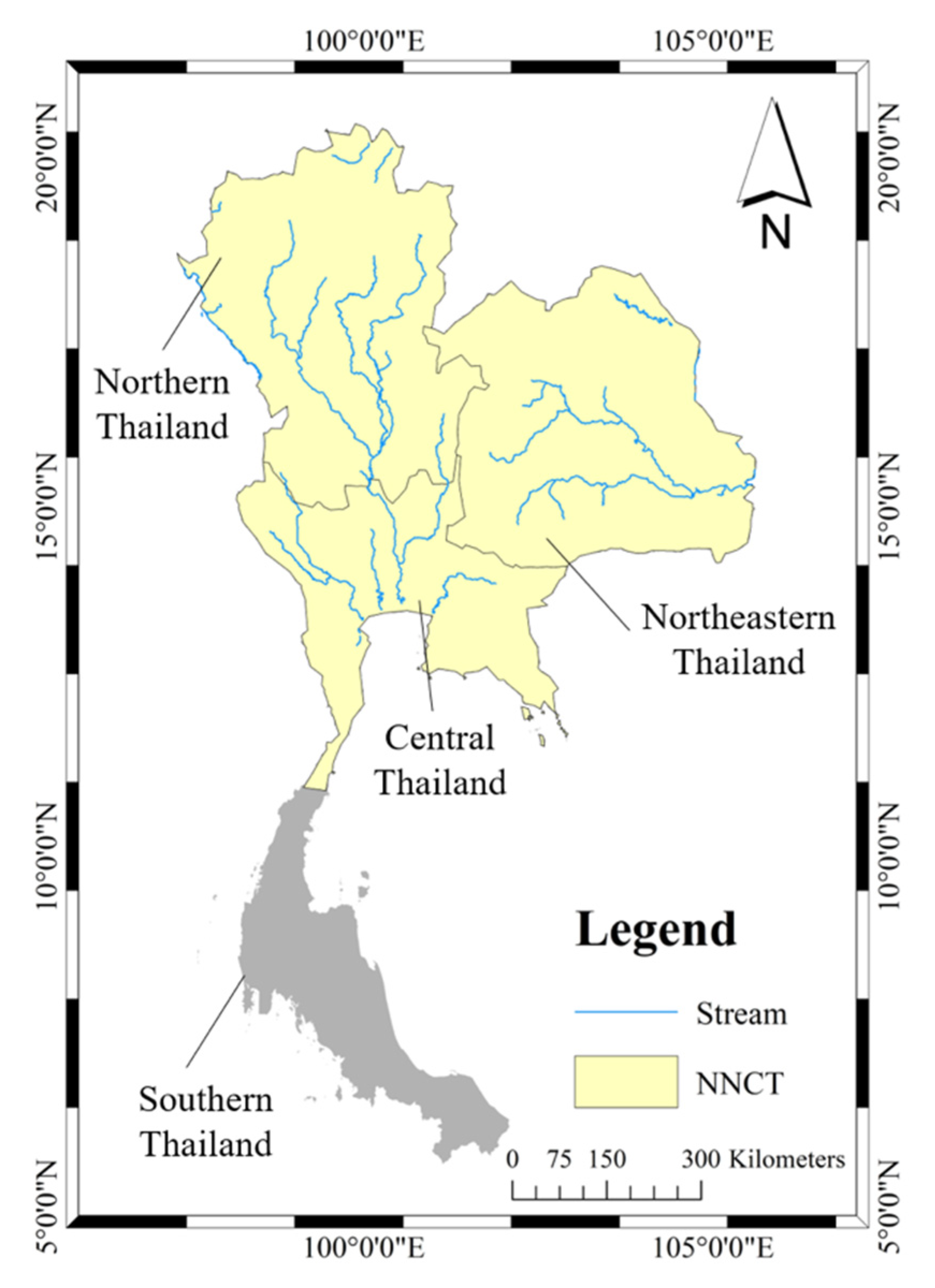
2.1. Study Area
2.2. Data Used in the Study
3. Methodology
3.1. Drought Indices Used in the Study
3.2. Three-Dimensional Identification of Drought
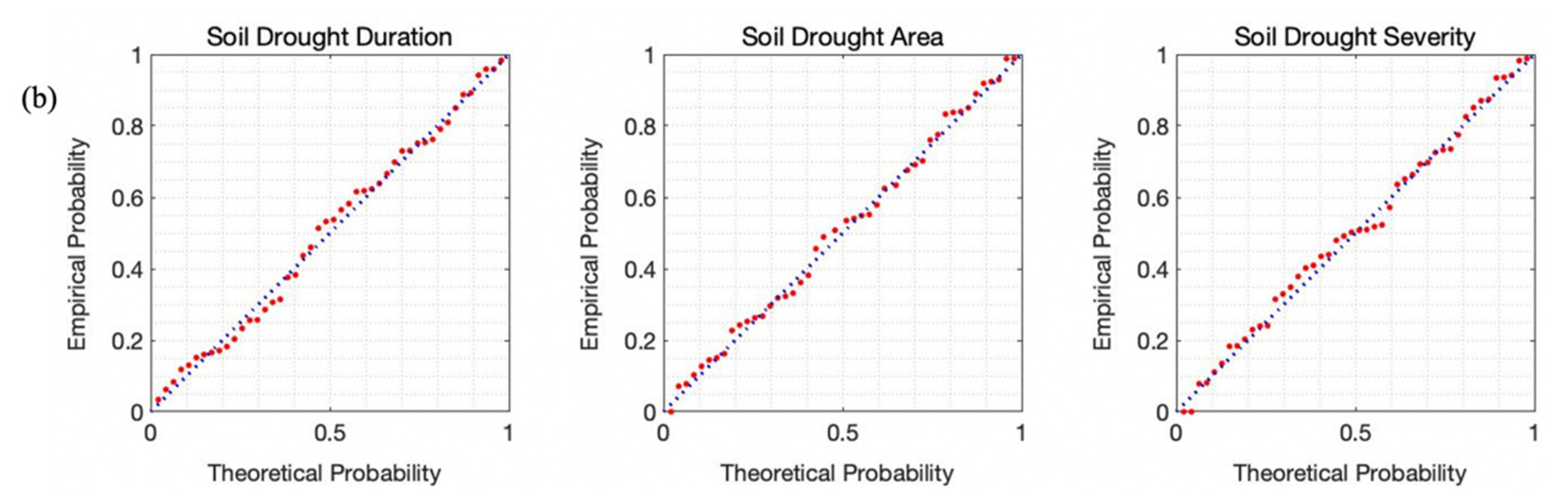
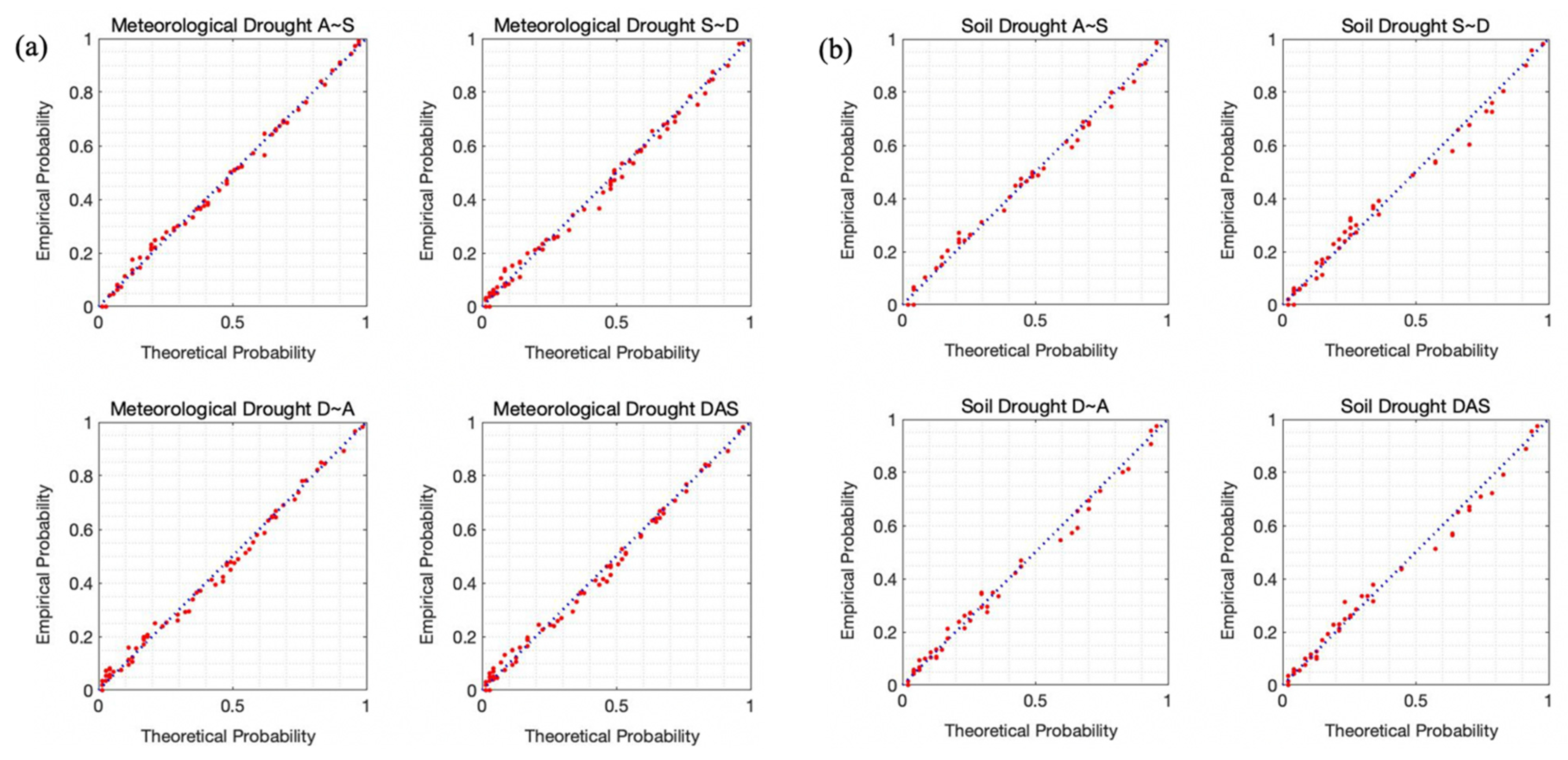
3.3. Probability Distributions of Drought and Return Period
3.4. Drought Propagation
3.5. Temporal Analysis of Historical Droughts
4. Result
4.1. A Description of Historical Soil and Meteorological Droughts
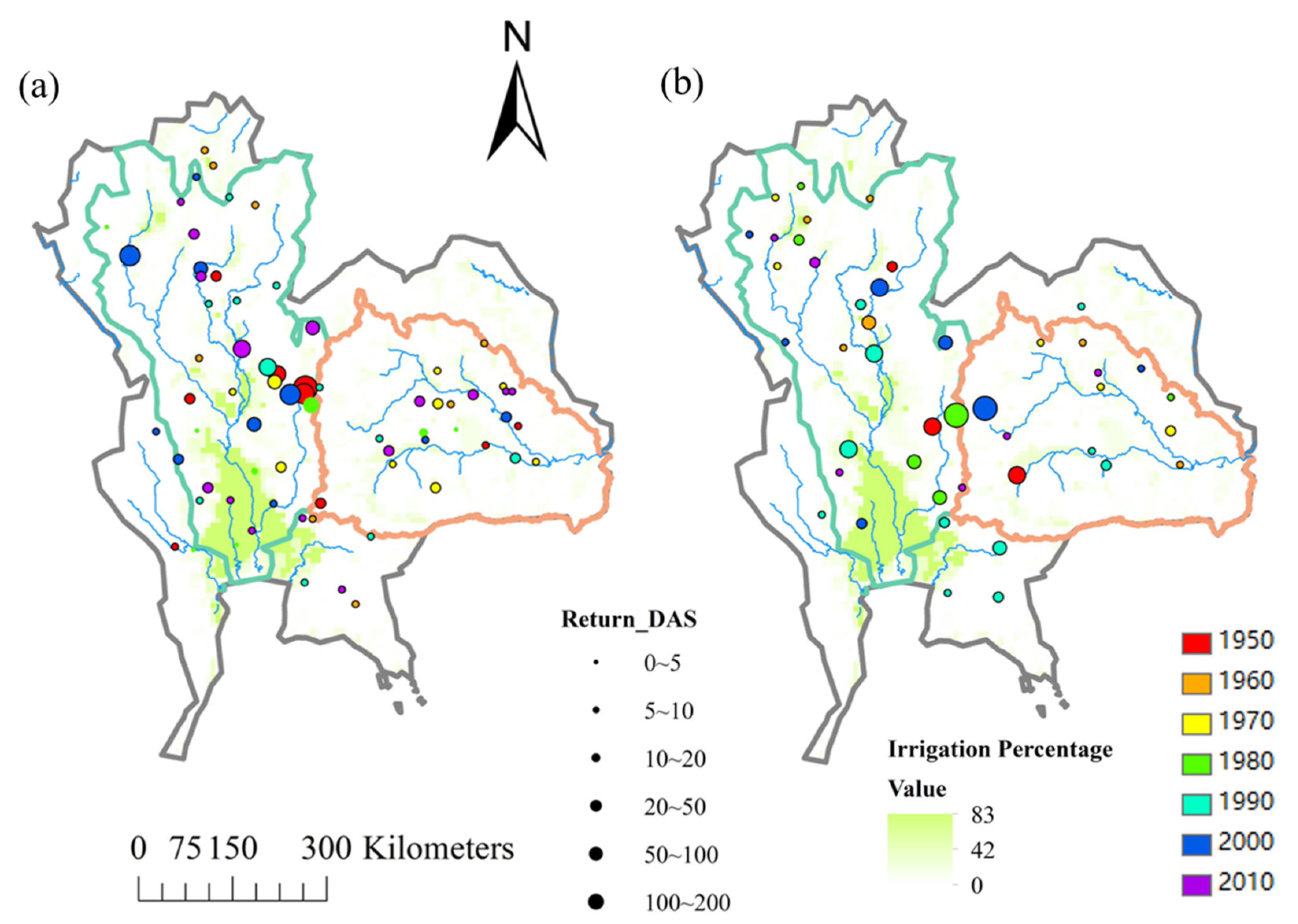
4.1.1. Drought Events and the Return Period from 1948 to 2014
4.1.2. Spatiotemporal Patterns of Historical Droughts
4.1.3. Drought Propagation
4.2. The Change in Drought Characteristics during 1948–2014
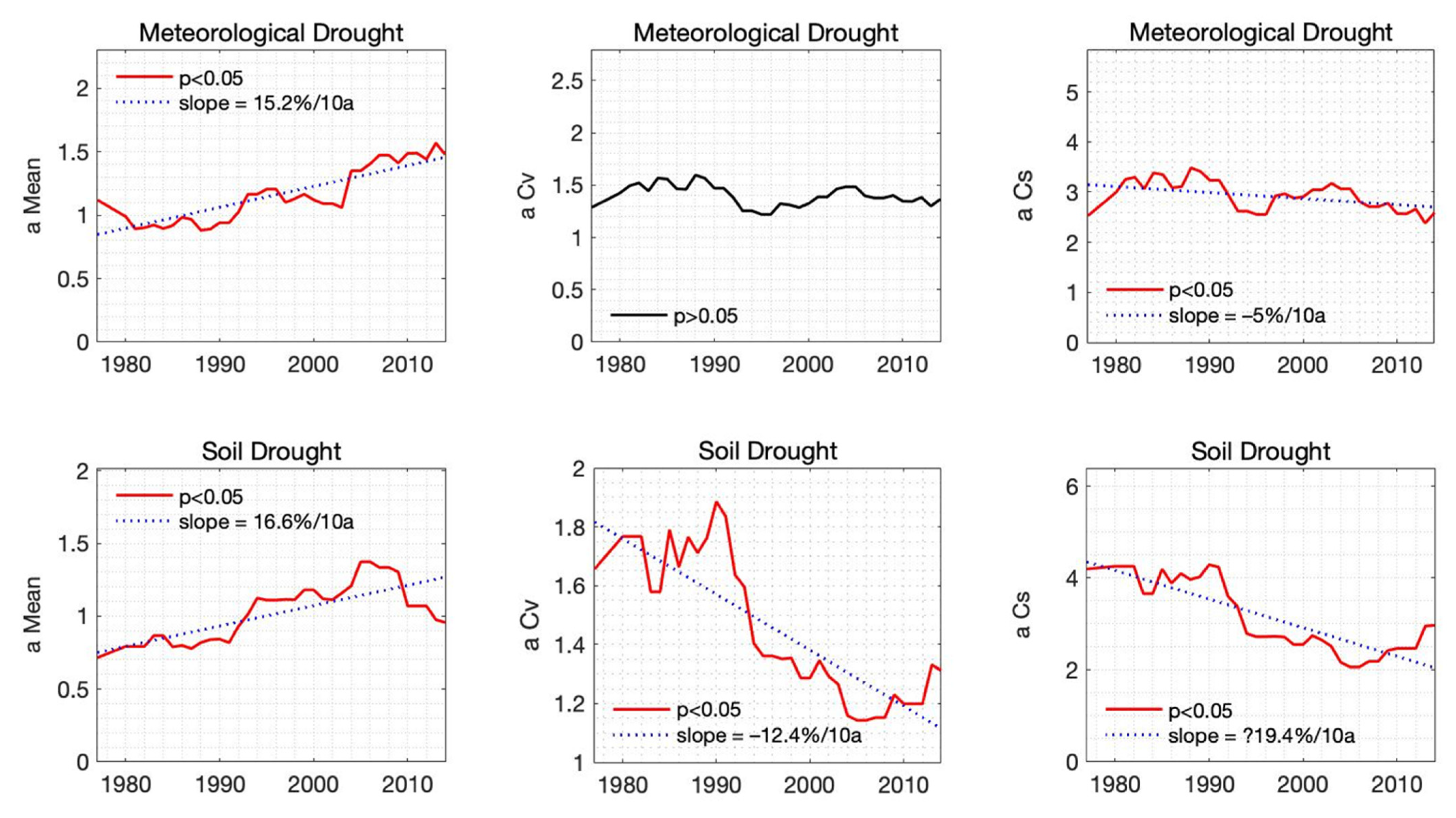
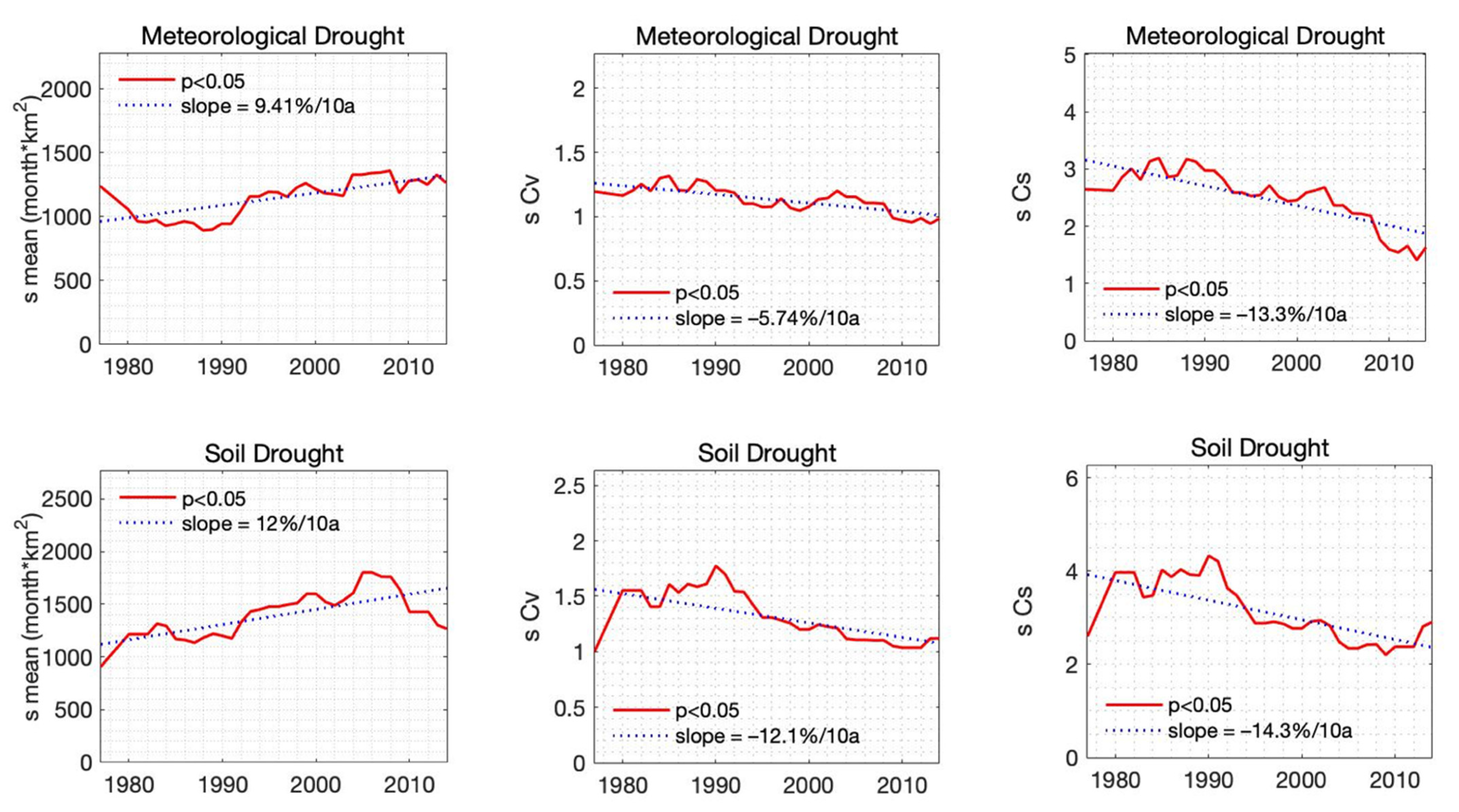
4.2.1. Change of the Drought Probability Distribution
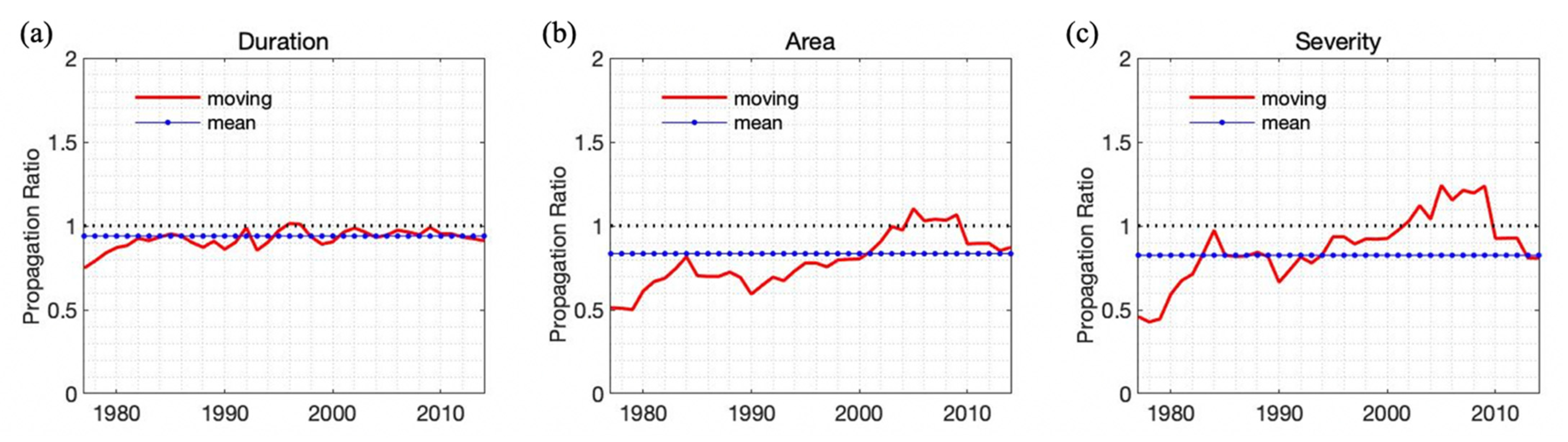
4.2.2. Change in Drought Propagation
5. Discussion
5.1. The Impacts of Climate Change on Drought Propagation
5.2. The Implications of Change in Historical Drought Characteristics
5.3. Uncertainties and Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, A. Drought under global warming: A review. WIREs Clim. Chang. 2010, 2, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Wood, E.F.; Sheffield, J. Global Trends and Variability in Soil Moisture and Drought Characteristics, 1950–2000, from Observation-Driven Simulations of the Terrestrial Hydrologic Cycle. J. Clim. 2008, 21, 432–458. [Google Scholar]
- Xu, K.; Yang, D.; Yang, H.; Li, Z.; Qin, Y.; Shen, Y. Spatio-temporal variation of drought in China during 1961–2012: A climatic perspective. J. Hydrol. 2015, 526, 253–264. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Wang, W.; Zhou, H. Propagation of soil moisture droughts in a hotspot region: Spatial pattern and temporal trajectory. J. Hydrol. 2021, 593, 125906. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B. A spatio-temporal structure-based approach to drought characterisation. Int. J. Climatol. 2012, 32, 406–418. [Google Scholar] [CrossRef] [Green Version]
- Andreadis, K.M.; Clark, E.A.; Wood, A.W.; Hamlet, A.F.; Lettenmaier, D.P. Twentieth-Century Drought in the Conterminous United States. J. Hydrometeorol. 2005, 6, 985–1001. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Ren, L.; Singh, V.P.; Yong, B.; Jiang, S.; Yuan, F.; Yang, X. Understanding the Spatiotemporal Links Between Meteorological and Hydrological Droughts from a Three-Dimensional Perspective. J. Geophys. Res. Atmos. 2019, 124, 3090–3109. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Van Lanen, H.A.J. A process-based typology of hydrological drought. Hydrol. Earth Syst. Sci. 2012, 16, 1915–1946. [Google Scholar] [CrossRef] [Green Version]
- Konapala, G.; Mishra, A. Quantifying Climate and Catchment Control on Hydrological Drought in the Continental United States. Water Resour. Res. 2020, 56, e2018WR024620. [Google Scholar] [CrossRef]
- Haslinger, K.; Koffler, D.; Schöner, W.; Laaha, G. Exploring the link between meteorological drought and streamflow: Effects of climate-catchment interaction. Water Resour. Res. 2014, 50, 2468–2487. [Google Scholar] [CrossRef]
- Wu, J.; Miao, C.; Zheng, H.; Duan, Q.; Lei, X.; Li, H. Meteorological and Hydrological Drought on the Loess Plateau, China: Evolutionary Characteristics, Impact, and Propagation. J. Geophys. Res. Atmos. 2018, 123, 11569–11584. [Google Scholar] [CrossRef]
- Apurv, T.; Sivapalan, M.; Cai, X. Understanding the Role of Climate Characteristics in Drought Propagation. Water Resour. Res. 2017, 53, 9304–9329. [Google Scholar] [CrossRef] [Green Version]
- Apurv, T.; Cai, X. Drought Propagation in Contiguous U.S. Watersheds: A Process-Based Understanding of the Role of Climate and Watershed Properties. Water Resour. Res. 2020, 56, e2020WR027755. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Climate change—Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Yang, Y.; Roderick, M.L.; Yang, D.; Wang, Z.; Ruan, F.; McVicar, T.R.; Zhang, S.; Beck, H.E. Streamflow stationarity in a changing world. Environ. Res. Lett. 2021, 16, 064096. [Google Scholar] [CrossRef]
- Apurv, T.; Cai, X. Evaluation of the stationarity assumption for meteorological drought risk estimation at the multi-decadal scale in contiguous US. Water Resour. Res. 2019, 55, 5074–5101. [Google Scholar] [CrossRef]
- Apurv, T.; Cai, X. Regional Drought Risk in the Contiguous United States. Geophys. Res. Lett. 2021, 48, e2020GL092200. [Google Scholar] [CrossRef]
- Thailand. Available online: https://en.wikipedia.org/wiki/Thailand (accessed on 1 January 2022).
- Mateo, C.M.; Hanasaki, N.; Komori, D.; Tanaka, K.; Kiguchi, M.; Champathong, A.; Sukhapunnaphan, T.; Yamazaki, D.; Oki, T. Assessing the impacts of reservoir operation to floodplain inundation by combining hydrological, reservoir management, and hydrodynamic models. Water Resour. Res. 2014, 50, 7245–7266. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z.; Zhou, T. Human Influence on the Increasing Drought Risk Over Southeast Asian Monsoon Region. Geophys. Res. Lett. 2021, 48, e2021GL093777. [Google Scholar] [CrossRef]
- Takahashi, H.G.; Yasunari, T. A climatological monsoon break in rainfall over Indochina—A singularity in the seasonal march of the Asian summer monsoon. J. Clim. 2006, 19, 1545–1556. [Google Scholar] [CrossRef] [Green Version]
- Spennemann, P.C.; Rivera, J.A.; Saulo, A.C.; Penalba, O.C. A Comparison of GLDAS Soil Moisture Anomalies against Standardized Precipitation Index and Multisatellite Estimations over South America. J. Hydrometeorol. 2015, 16, 158–171. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Wang, W. Inter-comparison of satellite-retrieved and Global Land Data Assimilation System-simulated soil moisture datasets for global drought analysis. Remote Sens. Environ. 2019, 220, 1–18. [Google Scholar] [CrossRef]
- Sanchez-Lorenzo, A.; Morán-Tejeda, E.; Revuelto, J.; Azorin-Molina, C.; López-Moreno, J.I.; Camarero, J.J.; Lorenzo-Lacruz, J.; Beguería, S.; Vicente-Serrano, S.M. Performance of Drought Indices for Ecological, Agricultural, and Hydrological Applications. Earth Interact. 2012, 16, 1–27. [Google Scholar]
- Hao, Z.; AghaKouchak, A. Multivariate Standardized Drought Index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Wang, A.; Lettenmaier, D.P.; Sheffield, J. Soil Moisture Drought in China, 1950–2006. J. Clim. 2011, 24, 3257–3271. [Google Scholar] [CrossRef]
- Marsaglia, G.; Tsang, W.W.; Wang, J. Evaluating Kolmogorov’s distribution. J. Stat. Softw. 2003, 8, 1–4. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Salvadori, G.; De Michele, C.; Durante, F. On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 2011, 15, 3293–3305. [Google Scholar] [CrossRef] [Green Version]
- Bonaccorso, B.; Cancelliere, A.; Rossi, G. An analytical formulation of return period of drought severity. Stoch. Environ. Res. Risk Assess. 2003, 17, 157–174. [Google Scholar] [CrossRef]
- Shiau, J.T. Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Vinnarasi, R.; Dhanya, C.T. Bringing realism into a dynamic copula-based non-stationary intensity-duration model. Adv. Water Resour. 2019, 130, 325–338. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; C. Griffin: London, UK, 1948; 160p. [Google Scholar]
- Nagaraj, D.; Proust, E.; Todeschini, A.; Rulli, M.C.; D’Odorico, P. A new dataset of global irrigation areas from 2001 to 2015. Adv. Water Resour. 2021, 152, 103910. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. EOS Trans. 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Fernandes, R.; Leblanc, S.G. Parametric (modified least squares) and non-parametric (Theil–Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Houghton, J. Global warming. Rep. Prog. Phys. 2005, 68, 1343–1403. [Google Scholar] [CrossRef]
- Kanae, S.; Oki, T.; Musiake, K. Impact of Deforestation on Regional Precipitation over the Indochina Peninsula. J. Hydrometeorol. 2001, 2, 51–70. [Google Scholar] [CrossRef] [Green Version]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied hydrology Journal of Engineering Education. J. Eng. Educ. 1962, 308, 1959. [Google Scholar]
- Woods, R.A. Analytical model of seasonal climate impacts on snow hydrology: Continuous snowpacks. Adv. Water Resour. 2009, 32, 1465–1481. [Google Scholar] [CrossRef]
- Woods, R.A. The relative roles of climate, soil, vegetation and topography in determining seasonal and long-term catchment dynamics. Adv. Water Resour. 2003, 26, 295–309. [Google Scholar] [CrossRef]
- Ziegler, A.D.; Sheffield, J.; Maurer, E.P.; Nijssen, B.; Wood, E.F.; Lettenmaier, D.P. Detection of Intensification in Global- and Continental-Scale Hydrological Cycles: Temporal Scale of Evaluation. J. Clim. 2003, 16, 535–547. [Google Scholar] [CrossRef] [Green Version]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Cao, G.; Han, D.; Song, X. Evaluating actual evapotranspiration and impacts of groundwater storage change in the North China Plain. Hydrol. Process. 2014, 28, 1797–1808. [Google Scholar] [CrossRef]
- Vasconcelos, V.V.; Koontanakulvong, S.; Suthidhummajit, C.; Junior, P.P.M.; Hadad, R.M. Analysis of spatial–temporal patterns of water table change as a tool for conjunctive water management in the Upper Central Plain of the Chao Phraya River Basin, Thailand. Appl. Water Sci. 2014, 7, 245–262. [Google Scholar] [CrossRef] [Green Version]



| ||||||
| Exp | Gam | Gev | Gpd | Lgt | P3 | |
| Soil Drought Duration | 0.962 | 0.416 | 0.854 | 0.979 | 0.714 | 0.974 |
| Meteorological Drought Duration | 0.574 | 0.119 | 0.704 | 0.924 | 0.625 | 0.510 |
| Soil Drought Area | 0.029 | 0.035 | 0.969 | 0.999 | 0.948 | 0.124 |
| Meteorological Drought Area | 0.002 | 0.013 | 0.818 | 0.974 | 0.741 | 0.033 |
| Soil Drought Severity | 0.000 | 0.000 | 0.861 | 0.982 | 0.875 | 0.001 |
| Meteorological Drought Severity | 0.001 | 0.002 | 0.557 | 0.955 | 0.520 | 0.040 |
| ||||||
| Exp | Gam | Gev | Gpd | Lgt | P3 | |
| Soil Drought Duration | 0.023 | 0.056 | 0.036 | 0.022 | 0.042 | 0.022 |
| Meteorological Drought Duration | 0.031 | 0.072 | 0.030 | 0.019 | 0.035 | 0.029 |
| Soil Drought Area | 0.092 | 0.083 | 0.029 | 0.021 | 0.030 | 0.074 |
| Meteorological Drought Area | 0.098 | 0.079 | 0.032 | 0.022 | 0.035 | 0.074 |
| Soil Drought Severity | 0.158 | 0.153 | 0.025 | 0.027 | 0.026 | 0.147 |
| Meteorological Drought Severity | 0.093 | 0.082 | 0.037 | 0.022 | 0.038 | 0.059 |
| ||||||
| Normal | t | Clayton | Frank | Gumbel | Joe | |
| Duration-Area | 0.030 | 0.030 | 0.037 | 0.027 | 0.028 | 0.028 |
| Area-Severity | 0.017 | 0.017 | 0.021 | 0.017 | 0.016 | 0.017 |
| Severity-Duration | 0.028 | 0.029 | 0.038 | 0.026 | 0.026 | 0.027 |
| Duration-Area-Severity | 0.030 | 0.030 | 0.036 | 0.022 | 0.021 | 0.023 |
| ||||||
| Normal | t | Clayton | Frank | Gumbel | Joe | |
| Duration-Area | 0.029 | 0.029 | 0.034 | 0.030 | 0.027 | 0.027 |
| Area-Severity | 0.023 | 0.023 | 0.030 | 0.023 | 0.021 | 0.020 |
| Severity-Duration | 0.033 | 0.032 | 0.039 | 0.034 | 0.029 | 0.027 |
| Duration-Area-Severity | 0.032 | 0.031 | 0.055 | 0.045 | 0.039 | 0.041 |
| MNo | TDuration | TArea | TSeverity | TA-S | TS-D | TD-A | TD-A-S |
|---|---|---|---|---|---|---|---|
| 31 | 76 | 133 | 58 | 133 | 76 | 133 | 157 |
| 2 | 51 | 47 | 72 | 51 | 72 | 72 | 112 |
| 3 | 10 | 38 | 43 | 38 | 43 | 43 | 75 |
| 48 | 58 | 2 | 3 | 59 | 59 | 3 | 67 |
| 55 | 7 | 32 | 22 | 37 | 24 | 33 | 66 |
| 56 | 8 | 15 | 15 | 21 | 19 | 18 | 42 |
| 4 | 3 | 17 | 14 | 17 | 14 | 17 | 28 |
| 42 | 2 | 16 | 14 | 16 | 14 | 16 | 26 |
| 27 | 15 | 6 | 12 | 15 | 15 | 12 | 19 |
| 25 | 2 | 13 | 4 | 13 | 4 | 13 | 16 |
| SNo | TDuration | TArea | TSeverity | TA-S | TS-D | TD-A | TD-A-S |
|---|---|---|---|---|---|---|---|
| 18 | 97 | 129 | 135 | 129 | 135 | 136 | 179 |
| 38 | 44 | 136 | 87 | 136 | 87 | 136 | 144 |
| 37 | 44 | 22 | 24 | 44 | 44 | 24 | 50 |
| 25 | 5 | 20 | 26 | 20 | 26 | 26 | 30 |
| 3 | 10 | 19 | 23 | 19 | 23 | 23 | 29 |
| 1 | 21 | 10 | 7 | 21 | 21 | 10 | 27 |
| 30 | 17 | 5 | 9 | 17 | 17 | 9 | 23 |
| 17 | 6 | 14 | 12 | 14 | 12 | 14 | 17 |
| 19 | 4 | 10 | 12 | 10 | 12 | 12 | 15 |
| 36 | 2 | 9 | 5 | 9 | 5 | 9 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Yang, D.; Yang, S.; Santisirisomboon, J. Spatiotemporal Characteristics of Droughts and Their Propagation during the Past 67 Years in Northern Thailand. Atmosphere 2022, 13, 277. https://doi.org/10.3390/atmos13020277
Zhao B, Yang D, Yang S, Santisirisomboon J. Spatiotemporal Characteristics of Droughts and Their Propagation during the Past 67 Years in Northern Thailand. Atmosphere. 2022; 13(2):277. https://doi.org/10.3390/atmos13020277
Chicago/Turabian StyleZhao, Baoxu, Dawen Yang, Shuyu Yang, and Jerasorn Santisirisomboon. 2022. "Spatiotemporal Characteristics of Droughts and Their Propagation during the Past 67 Years in Northern Thailand" Atmosphere 13, no. 2: 277. https://doi.org/10.3390/atmos13020277
APA StyleZhao, B., Yang, D., Yang, S., & Santisirisomboon, J. (2022). Spatiotemporal Characteristics of Droughts and Their Propagation during the Past 67 Years in Northern Thailand. Atmosphere, 13(2), 277. https://doi.org/10.3390/atmos13020277






