Next Article in Journal
Effect of Diesel Soot on the Heterogeneous Reaction of NO2 on the Surface of γ-Al2O3
Previous Article in Journal
Intercomparison of Ambient Nitrous Acid Measurements in a Shanghai Urban Site
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 13
Issue 2
10.3390/atmos13020331
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study of an Asymmetric and Anticyclonic Bow Echo Near Taiwan

by
Chung-Chieh Wang
1,
Jou-Ping Hou
2,*,
Chun-Hsiang Tseng
3,4,
Pao-Liang Chang
4 and
Dong-In Lee
5
1
Department of Earth Sciences, National Taiwan Normal University, Taipei 11677, Taiwan
2
Department of Environmental Information and Engineering, Chung Cheng Institute of Technology, National Defense University, Taoyuan 33551, Taiwan
3
Department of Atmospheric Sciences, Chinese Culture University, Taipei 11114, Taiwan
4
Central Weather Bureau, Taipei 100006, Taiwan
5
Department of Environmental Atmospheric Sciences, Pukyong National University, Busan 48513, Korea
*
Author to whom correspondence should be addressed.
Atmosphere 2022, 13(2), 331; https://doi.org/10.3390/atmos13020331
Submission received: 24 December 2021 / Revised: 26 January 2022 / Accepted: 31 January 2022 / Published: 16 February 2022
(This article belongs to the Section Meteorology)
Browse Figures
Versions Notes

Abstract

:
On 2 April 2007, a strong bow echo struck southern Taiwan, with a peak surface wind speed of 26 m s−1. On observation, the rear inflow jet (RIJ) was located at the northern flank and only one anticyclonic vortex dominated behind the bow structure. This case was different from commonly occurring cyclonic–anticyclonic pairs of bookend vortices, and was investigated through data analysis, model simulation, and vorticity budget diagnostics. The present bow echo formed at the leading edge of a cold front, with favorable ingredients of instability, large west-southwesterly vertical wind shear, and dry air aloft. Farther behind the front, however, stable conditions could not support deep convection and the portion north of the RIJ was therefore missing. Within a frontal flow structure, the developing mechanism of the anticyclonic vortex also differed from typical cases. As the low-level (west-southwesterly) vertical shear pointed from right to left of the line, and the tilting effect of updrafts generated positive (negative) vorticity at the front (rear) side. South of and below the RIJ, the anticyclonic vorticity was enhanced by the stretching and tilting effect of system-generated horizontal vorticity via a sinking motion. These sources of vorticity were then advected downward and southwestward by the postfrontal flow near the surface.

1. Introduction

Bow echoes are bow-shaped lines of convective cells that are often associated with swaths of damaging straight-line winds and small tornadoes (p. 97, [1]), and are thus a particular type of severe weather at the mesoscale (p. 677, [1]) [2,3,4,5] (Figure 1, adapted from [6]). Often evolving from squall lines [5,7,8,9], bow echoes share a common conducive environment with these convective lines, including high instability to convection with abundant moisture near the surface, strong low-level vertical wind shear, and, preferably, relatively dry conditions further aloft at mid-levels [5,6,7,8,9,10,11]. Bow echoes are most commonly observed over the Great Plains and Midwest of the United States of America (USA) in spring and summer, and they have a horizontal scale of roughly 20–200 km and can last for 3–6 h or longer [3,4,5,6,7,8,9].
When fully developed, bow echoes also have a similar structure to squall lines. The main features include a pair of tilted updraft and downdraft [12,13,14]. As the downdraft can sink and extend forward to form the gust front at the leading edge, such a configuration can reinforce the pair and, at the same time, maintain a balance with the environmental vertical wind shear, thus promoting the longevity and severity of the system [15,16]. In a system-relative sense, other structural features include a low-level front-to-rear (FTR) inflow, which feeds the warm and moist air into the updraft [5,12,13,14], an FTR outflow as an extension of the updraft toward the back in the upper troposphere, and a rear-to-front (RTF) inflow at mid-levels that develops in response to the pressure decrease behind the line due to the coupling of the rising (buoyant) updraft and the sinking (negatively buoyant) downdraft [also 17]. Associated with the FTR outflow, a stratiform precipitation region also forms with condensates falling into the downdraft and RTF inflow. The evaporative cooling subsequently enhances the downdraft and forms a surface cold pool that extends to the gust front (e.g., [17,18]). In cases where the RTF inflow is particularly strong, a rear inflow jet (RIJ) may form, which causes that segment of the line to propagate faster and bulge forward, thus forming a bow-shaped echo with a protruding apex [5,8,9,17,18,19,20,21,22,23]. This is when a section of a squall line evolves into a bow echo (Figure 1) [6]. As the RIJ descends to the surface, it can produce downbursts and damaging winds up to 30–50 m s−1 and cause serious hazards (e.g., [3,4,5,6,7,8,9,23,24,25]).
Besides the RIJ, which is needed to form the bow shape, another distinction from squall lines is that bow echoes possess a pair of “bookend vortices” at the mid-levels towards their backside (Figure 1) [6,8,9,22,26]. Typically, a cyclonic vortex is located at the northern section and an anticyclonic one at the southern section of the bow echo, with the RIJ in the middle behind the line (e.g., [17,18,19,20,21]). The simulation results of Weisman and Davis [27] suggest that at an early stage, the bookend vortices form due to the tilting of the environmental vertical wind shear as a result of the downdraft. As the bow echo matures, however, further vorticity generation occurs mainly through the tilting of system-generated horizontal vorticity (between the updraft–downdraft pair) by the updraft. This pair of vortices also acts to focus the RIJ, and therefore they enhance the lifting at the gust front and lengthen the duration of the bow echo [19,20,26,27,28]. While the bookend vortices are often quite symmetric after they develop, the Coriolis effect tends to enhance the cyclonic vortex and suppress the anticyclonic one, and thus the former often becomes more dominant with time. As a result, the bow echo typically evolves into a comma echo with a rotating head at the late stage (Figure 1) [3,6,8,9,27,28,29].
Outside the USA, bow echoes are also observed in other regions around the world (e.g., [30,31,32,33]). In the subtropics, conditions tend to be more suitable for them during frontal passages in winter and spring, since a strong vertical wind shear (i.e., large temperature gradient) is required [4,5,8,9,10,26]. For example, a bow echo occurred in November 1997 inside a squall line along a cold front near northern Taiwan [34]. This case was about 60–90 km in length, exhibited a rather symmetric pair of cyclonic and anticyclonic bookend vortices, and produced a peak surface wind speed of 18.5 m s−1 at the gust front. On 2 April 2007, another event of over 200 km in size developed and propagated across the Taiwan Strait to hit southern Taiwan (cf. Figure 2c), with a recorded maximum wind speed of 26 m s−1. Not only was this latter event bigger and stronger, as will be illustrated later, it had only one bookend vortex that rotated clockwise, i.e., in the anticyclonic direction. Hence, the bow echo in April 2007 was unique in its asymmetric structure, which had not been seen previously in the literature. Therefore, it is the subject of our investigation in the present study, and our main objective is to understand how and why such an asymmetric structure formed on the backside of this bow echo.
Below, in Section 2, the data, methodology, numerical model, and experiment used are described. In Section 3, the bow echo on 2 April 2007 is reviewed, including its environmental conditions, evolution, and, of course, its asymmetric structure. With the bow echo successfully reproduced, the model results are then used to study the event in Section 4, and the formation of the bookend vortex through vorticity budget diagnostics in Section 5. Finally, the conclusions are given in Section 6.

2. Data, Methodology, and Numerical Experiment

2.1. Data and Methodology

The observational data for the case period used in this study include the following: surface and upper-level weather maps every 6 h for the purpose of synoptic analysis, sounding data for the thermodynamic conditions of the environment, land-based radar observation and composites for the formation, evolution, and internal structure of the bow echo, and continuous and hourly records at selected surface stations for the associated weathers, respectively. All the above data were provided by the Central Weather Bureau (CWB) of Taiwan. In addition, for the cloud-resolving model experiment, the initial and boundary conditions (IC/BCs) were provided by the National Centers for Environmental Prediction (NCEP) global analyses and will be described below. For the purpose of verification and comparison with the model results, some of the observational data listed above are also used.

2.2. The CReSS Model and the Experiment

In this study, the Cloud-Resolving Storm Simulator (CReSS; [35,36]) was used for our numerical experiment. Developed at Nagoya University, Japan, it is a cloud-resolving model that employs a non-hydrostatic and compressible equation set, as well as a height-based terrain-following vertical coordinate [35,36]. In CReSS, all clouds are treated explicitly using a bulk cold-rain microphysical scheme [37,38,39,40,41], with a total of six species (vapor, cloud water, cloud ice, rain, snow, and graupel). Physical processes parameterized at the subgrid-scale include turbulent mixing in the planetary boundary layer (PBL) [36,42], and radiation and momentum/energy fluxes at the surface [43,44,45]. With a single domain (no nesting), this model was designed to run at high resolution [35,36] and has been used to study convective storms around Taiwan in spring and early summer (e.g., [46,47,48]) as well as for real-time forecasts (e.g., [49,50,51,52]).
The CReSS experiment in this study was performed using a horizontal grid spacing of 2 km and a (x, y, z) dimension of 540 × 480 × 60 grid points (Table 1, cf. Figure 2c). As mentioned, the NCEP analyses using the Global Forecast System (GFS; 1° × 1° and 26 levels from the surface to 10 hPa, every 6 h) [53,54,55] served as the IC/BCs of the model run, providing necessary variables of pressure, geopotential height, temperature, horizontal winds (u and v components), and moisture content (relative humidity). The model experiment was from 0600 UTC 1 to 0000 UTC 3 April 2007 (for a length of 42 h). At the lower boundary, the real terrain at 30 s (or 1/120°) resolution (roughly 900 m) and the observed weekly sea surface temperature (also 1° × 1°) were provided [56]. The model configuration and major physical package of the experiment are summarized in Table 1.

2.3. Vorticity Budget Diagnosis

As will be shown, the present bow echo exhibited an interesting and atypical characteristic in its structure on its backside, namely, it did not possess a pair of bookend vortices with the RIJ at the middle, and instead, the RIJ was located near the northern end behind the leading bow and only one predominant anticyclonic vortex appeared. Its structure was thus highly asymmetric, and this characteristic was well reproduced in our high-resolution model results. To shed light on the formation mechanism of this unique structure, a vorticity budget diagnosis in a quasi-Lagrangian (system-relative) framework in the z coordinate was carried out [29,57,58,59] using model outputs, as
δ ζ δ t = ω H · ∇ H w + ζ ∂ w ∂ z + F ζ − ( u − u s ) ∂ ζ ∂ x − ( v − v s ) ∂ ζ ∂ y − w ∂ ζ ∂ z   , LT TIL ST FR HAD VAD
where ζ is relative vorticity (i.e., the vertical component of the vorticity vector ω, ωH = (ξ, η) is the horizontal (x and y) components of ω, ∇H is the horizontal (2D) gradient operator, w is the vertical velocity, Fζ is the friction effect (FR), v = (u, v) is the horizontal wind vector, and c = (us, vs) is the system motion vector, respectively. With the acronym of each term labeled to facilitate later discussion, Equation (1) states that the local tendency of ζ(LT) in a system-relative frame can come from the tilting effect [TIL, = ξ(∂w/∂x) + η(∂w/∂y)], stretching effect (ST), FR, system-relative horizontal advection [HAD, = (v − c) · ∇H ζ], and vertical advection of ζ (VAD). In Equation (1), both x and y components of HAD are shown. With FR (and the solenoidal effect) neglected, the sum of the first two terms on the right-hand side (TIL + ST) also equals the total tendency of ζ (TT = dζ/dt), i.e., the full Lagrangian tendency following 3D air motion. Later, in Section 5, Equation (1) and the above method will be used to investigate the contribution of each term toward the generation of ζ in the backside of the bow echo, and to explain the formation of the asymmetric, anticyclonic vortex in the present case.

3. Case Overview

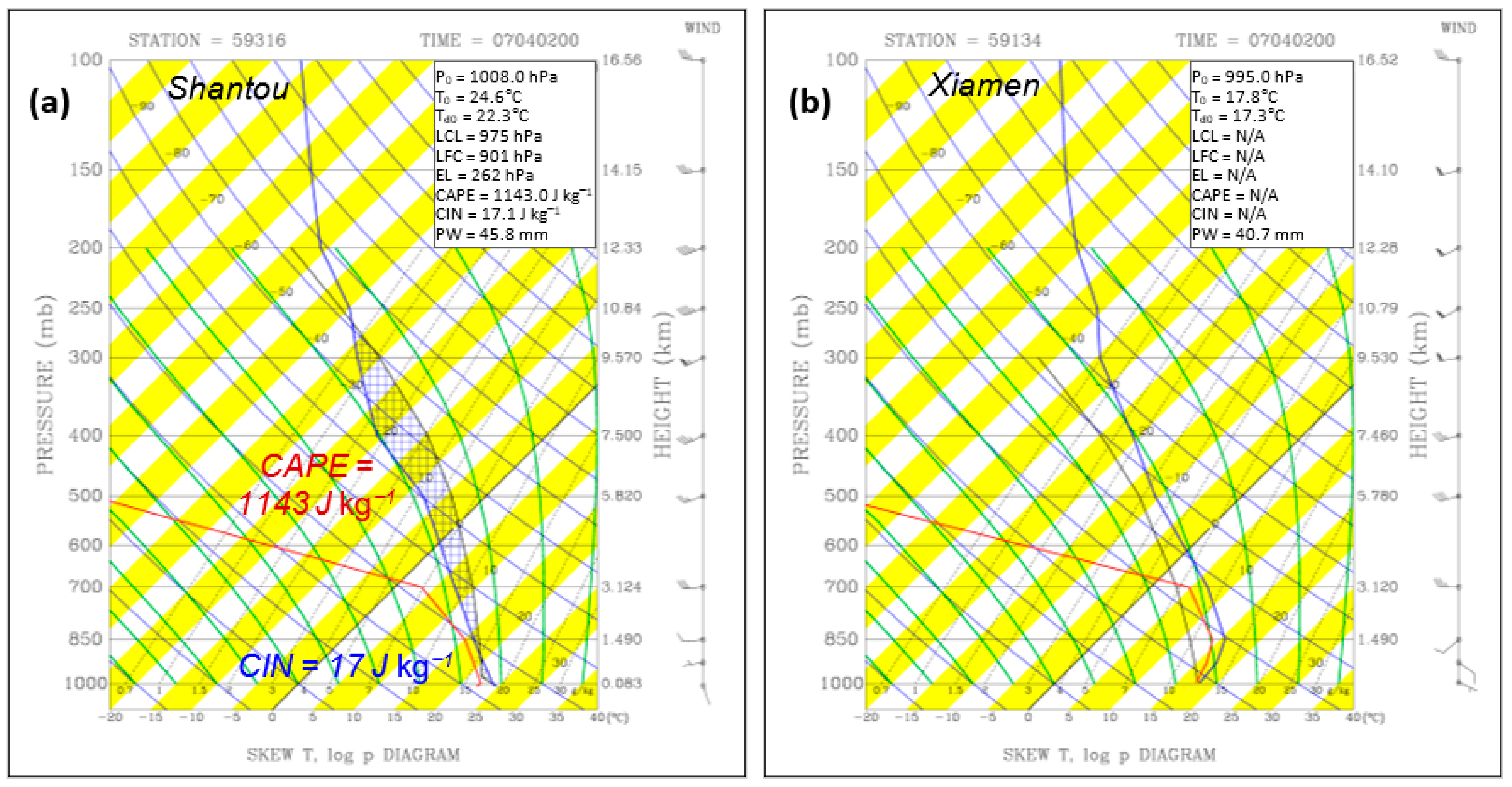
3.1. Synoptic and Thermodynamic Conditions

In this section, an overview is given on the bow echo that hit Taiwan on 2 April 2007. Figure 2 shows the synoptic environment in which the bow echo formed and evolved. At 0000 UTC (or 0800 LST) 2 April, much of China was controlled by the continental cold high-pressure system, with a central pressure of 1042 hPa near Mongolia, and a surface front was passing through Taiwan (Figure 2a). Behind the front, northerly flow prevailed over central and southern China and the East China Sea, at both surface and 850 hPa (Figure 2b), and westerly flow existed south of the front/trough. The surface front and low-level trough tilted northwestward with a height of up to 500 hPa, indicating a baroclinic structure that was consistent with the large north-south temperature gradient across the front at 850 hPa. Thus, the flow over central and southern China had turned into strong west-southwesterlies at 500 hPa (Figure 2c). In the upper troposphere at 200 hPa, the mid-latitude jet was located near 38° N, with its core over the Korean Peninsula, while a subtropical jet was stretching right across Taiwan (Figure 2d), with its core just offshore of eastern Taiwan. Thus, both the southern Taiwan Strait and southern Taiwan were located under the rear-right quadrant of this jet streak (with divergence aloft) and conducive to convection. Near Taiwan, the surface front was moving rapidly, and was moving into southern Taiwan at 0600 UTC (1400 LST) and further into the Bashi Channel by 1200 UTC (2000 LST, not shown).
The skew T-log p diagram from the sounding observation at Shantou, south of the surface front at 0800 LST 2 April, is shown in Figure 3a. At this location (cf. Figure 2a), the near-surface environment was moist, but became very dry above 700 hPa. With a lifting condensation level (LCL) at 975 hPa (310 m), a level of free convection (LFC) at 901 hPa (995 m), a convective potential available energy (CAPE) of 1143 J kg−1, and a convective inhibition (CIN) of merely 17 J kg−1 for a surface air parcel, convection could be triggered easily and indeed occurred. At slightly over 1000 J kg−1, such a CAPE is comparable to the case in northern Taiwan reviewed in Section 1 [34] and some events with moderate instability in the USA [5,9], where much larger CAPE values are possible [8,9,10,11]. Large vertical wind shear was also present at low levels, as the wind was weak at the surface but the westerlies increased to 30 kts at 700 hPa (Figure 3a). Coupled with the dry condition aloft, such a vertical shear would aid in the development of the RIJ [5,8,9,17,18,19,20,21] and the bookend vortices via the tilting effect [19,20,21,22,26,27], as reviewed. Several thermodynamic indices (not shown) also suggested high potential for deep convection (e.g., [60]). On the other hand, north of the surface front at Xiamen (cf. Figure 2a), the sounding observation taken at the same time (Figure 3b) revealed contrasting properties near the surface, although similar conditions existed above 700 hPa. Only about 200 km from Shantou (also cf. Figure 4d), there were easterly winds below 850 hPa at Xiamen. Also, the surface air was almost 7 °C colder, with no CAPE and thus no possibility for convection. Even uplifted from the most unstable level of 850 hPa, an air parcel would not reach LFC until about 650 hPa with a limited amount of CAPE. Thus, the low-level environment behind the front was very stable and convection could not develop.

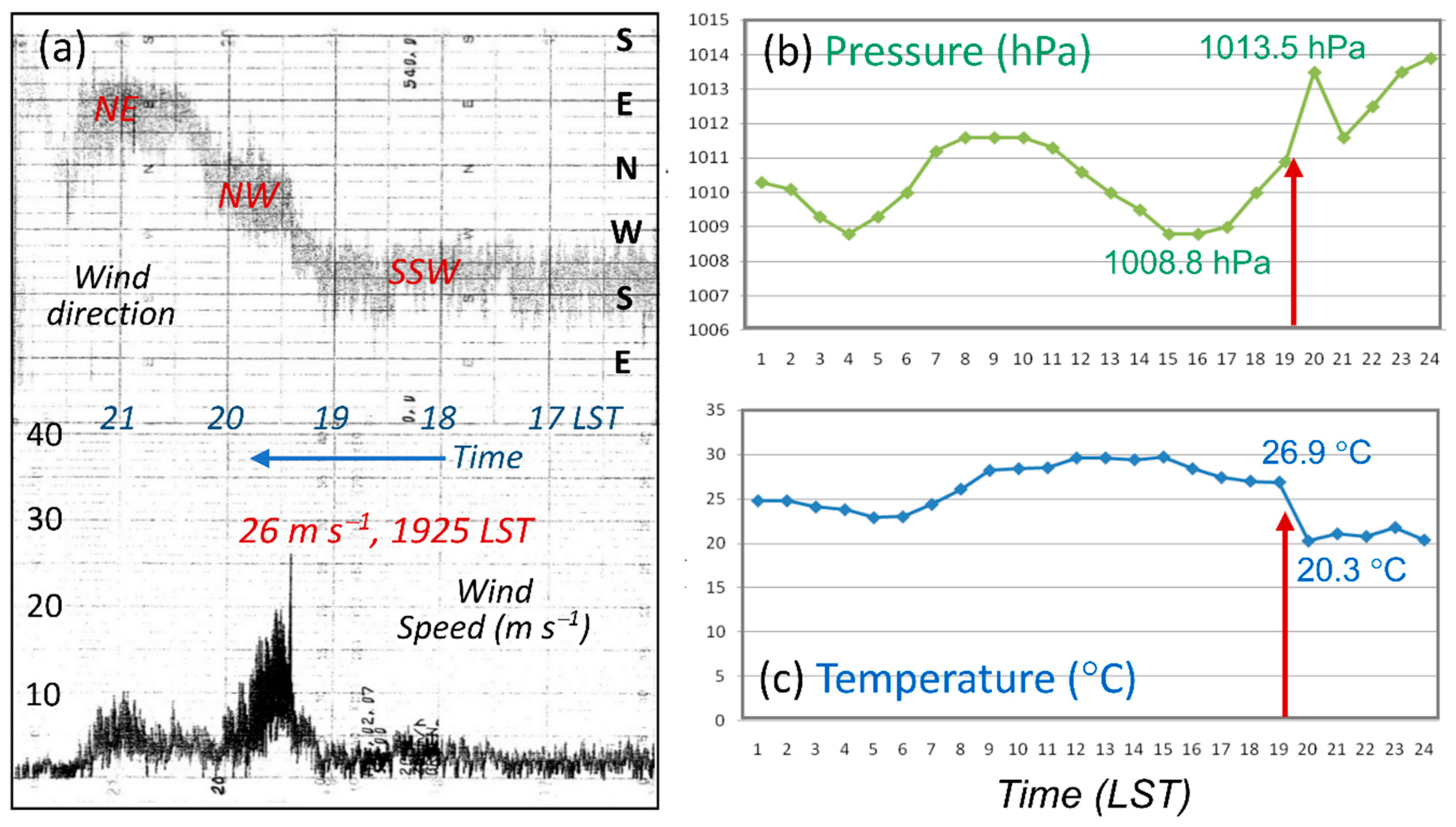
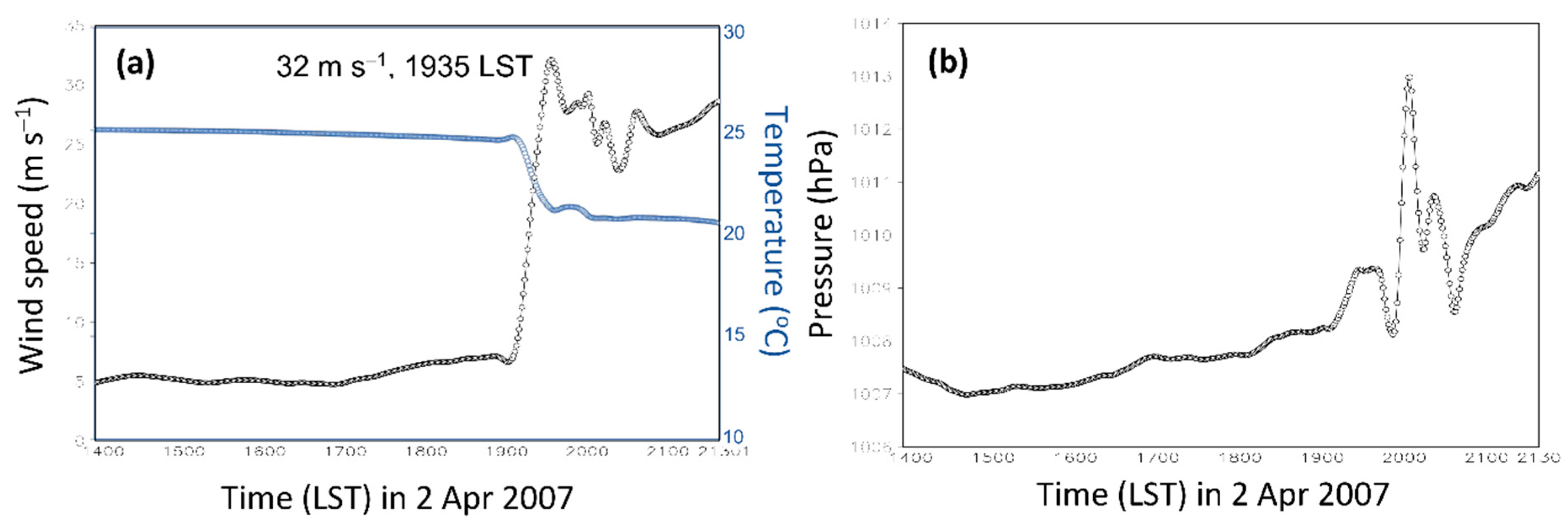
3.2. Evolution of the Bow Echo and Associated Weather

The composites of vertical maximum reflectivity from four CWB S-band land-based radars (details and limitations in [61,62]) in Taiwan during 2 April 2007 are shown in Figure 4. Up to 1 km in resolution [62], they can depict the development and evolution of the present bow echo event. At 1400 LST in the afternoon, convection was first seen to develop along the coast of southeastern China (Figure 4a), and gradually grew upscale and organized into a line-shaped squall line with a north-south alignment at around 1600 LST (Figure 4b). While moving rapidly eastward across the Taiwan Strait, a portion of the echo bulged forward into a bow shape (Figure 4c), and the system reached maturity at around 1800 LST, with peak echo reaching 60 dBZ (Figure 4d). The bow shape with a protruding apex was most apparent near 1900 LST (Figure 4e), when the total length of the echo was about 200 km. During the mature stage, a weak-echo region and stratiform area could be seen to trail the leading bow, which was about 20 km in width. Before 2000 LST (Figure 4f), the bow echo had made landfall in southwestern Taiwan. Afterwards, the system gradually weakened and eventually dissipated off southeastern Taiwan (not shown). Overall, this convective system lasted for about 10 h.
Figure 5a shows the trace of wind recorded by the anemometer during the event at the surface station in Kaoshiung, a harbor city and the second largest city in Taiwan (cf. Figure 4d for location). As the bow echo passed through, the automated and continuous record registered a peak gust of 26 m s−1 at around 1925 LST (Figure 5a), accompanied by a sudden shift in wind direction from (prefrontal) south-southwesterly to northwesterly behind the gust front. After the gusty winds, 10 mm of rain fell heavily in only 5 min. After 2030 LST, the northwesterly wind turned into a northeasterly, consistent with near-surface post-frontal flow without the severe disturbance. The peak gust at Kaoshiung reached number 10 on the Beaufort wind scale and lasted for 2 min, causing 15 injuries and much damage to structures and properties. For this event, the CWB issued a strong-wind and heavy-rain warning 3 h before its landfall. Hourly data at the surface station also indicated a rapid rise in pressure by several hPa (Figure 5b) and a sudden drop in air temperature of 6.6 °C, from 26.9 °C to 20.3 °C (Figure 5c), in association with the passage of the bow echo.

3.3. Asymmetric and Anticyclonic Structure of the Bow Echo

Besides being a rare and exceptionally strong event in Taiwan, further analysis of the Doppler radar observations reveals an interesting and unique structural characteristic of the present bow echo, namely, its asymmetric and predominantly anticyclonic circulation, as shown in Figure 6. At 1828 LST, when the bow echo had reached maturity and was rapidly approaching southwestern Taiwan, the Doppler radar at Chigu on the southwestern coast of Taiwan (cf. Figure 4a for location) observed the clear bow structure of the intense echo (dotted curve) at an elevation angle of 0.5°, with a trailing weak echo and stratiform areas, as noted earlier (Figure 6a). When an estimated moving speed of 20 m s−1 toward the east was subtracted from the radial wind field, a clear anticyclonic circulation was revealed behind the leading bow segment and to the north of the presumed apex (Figure 6b). At this lowest elevation angle (0.5°), the height of the radar beam at a distance of 90 km (first circle) was about 1.4 km above the sea level (Figure 6b), where the inbound speed of 12 m s−1 would indicate a RIJ of roughly 32 m s−1 (relative to the ground, with system motion added). South of the RIJ, an area with an outbound speed of about 6–10 m s−1 existed, forming a clear anticyclonic circulation behind the bow segment. Half an hour later at 1858 LST, when the bow echo had almost reached Chigu, its leading bow was also well depicted by the radar at an elevation angle of 2.4° (Figure 6c). At this angle, the height of the beam at the range of 60 km reached about 2.8 km, where the inbound speed of the RIJ was even stronger (Figure 6d). At both elevation angles, the anticyclonic circulation was clearly depicted, and this asymmetric structure is quite atypical to bow echoes in mid-latitudes in the literature [3,5,6,7,8,9]. Compared to typical and rather symmetric bow echoes (Figure 1), the present case near Taiwan had its RIJ located near the northern end behind the bow structure (where a cyclonic bookend vortex typically resides), and thus anticyclonic circulation dominated much of the backside of the bow echo. In other words, the bow segment north of the RIJ, where a cyclonic bookend vortex would have existed, appeared to be missing in the present case.

4. Results of Numerical Experiment

4.1. Model Results and Validation

Following the method described in Section 2.2, the 2-km CReSS experiment successfully reproduced the bow echo. The model results near the surface between 1600 and 2000 LST on 2 April 2007 are shown in Figure 7a–c. With strong convergence, a convective line developed in the model prior to 1600 LST off the coast of southeastern China, near the leading edge of the front (Figure 7a). With time, this system’s bow structure became more pronounced as it extended in length and moved across the Taiwan Strait (Figure 7b).
By 2000 LST (Figure 7c), the northern portion of the bow echo had made landfall in Taiwan while its southern segment was collocated with the front, behind which northeasterly flow with considerable temperature gradient prevailed. South of the front, the low-level flow was mainly from the southwest to west-southwest (cf. Figure 2a). Using plots of column-maximum upward motion similar to Figure 7a–c, the leading edge of the bow echo can be identified every 30 min (plotted in Figure 7d) to reveal its movement throughout its lifespan, from 1400 to 2200 LST, in the model. As shown, while its northern edge remained near 24° N, the modeled bow echo grew in length toward the south and southwest, so the system as a whole moved toward the east-southeast at a mean speed of 14.8 m s−1 (Figure 7d). Toward the later stage, the system also tended to propagate faster. From our results thus far, the question of why the northern portion of a complete bow echo was missing can be answered. Since the bow echo developed along the cold front, it could not extend farther north because the surface cold air behind the front would become too thick and the CAPE would vanish, as shown in Figure 3b. Thus, no convection too far to the north could develop.
While the overall simulation of the bow echo was successful, some differences between model results and observations still exist. First, the modeled bow echo appeared to be slightly displaced to the north, by about 50 km, and thus did not reach Kaoshiung until a later time (after 2030 LST) and with a gap in the bow segment. Second, the alignment of the bow echo was almost north-south in the observation (Figure 4), but was in a more northeast-southwest direction in the model except for its northernmost portion (Figure 7). Third, in the mature stage, minor arc-shaped lines that resemble the old tails (cf. Figure 1) appeared near the southwestern end of the main bow in the model (Figure 7). While some indication of such minor bows exists in the satellite imageries (not shown), if they indeed existed, they were most likely too far and too low in elevation to be captured by either the Chigu or RCKT radars (cf. Figure 4).
Bearing in mind the above differences, the structure of the modeled bow echo can be compared with the observation. In Figure 8, the range-height indicator (RHI) of reflectivity and system-relative radial wind speed (positive for outbound, i.e., toward the left) observed by the Chigu radar looking west at 1828 LST (Figure 8b) is compared with the vertical cross-section along line BB’ (cf. Figure 7b for location) from the model results (Figure 8a). While the two panels are scaled to be the same, note that for easy comparison the image in Figure 8b has been reversed so that the radar is located at the far right at point A. Along section AA’ (100 km in length), the leading convective line at 1828 LST was about 53 km from the radar and could reach 50 dBZ in reflectivity (cf. Figure 6a,b). Behind the leading line, a weak echo region existed (near 80 km) and was followed by the stratiform area (≥85 km), which is consistent with earlier studies (e.g., [12,15,16,17,18,19,20,21,22]). With a maximum system-relative inbound speed of about −8 m s−1, the RIJ was descending from about 3 km near point A’ down toward the surface (Figure 8b). In Figure 8a, where the baseline is 120 km (60% of line BB’), the leading convective line is also trailed by a weak echo zone and the stratiform region at comparable distances in the model. Further west, the modeled RIJ at 1828 LST was at about 5 km in height, but descended also to about 3 km below the stratiform area (near 119.1° E). It had a peak system-relative speed of more than 15 m s−1 and thus over 30 m s−1 in ground speed. In the model, the RIJ is also seen to descend right down to the surface behind the gust front (Figure 8a).
Only 10 min later, at 1838 LST, the observed bow echo has a similar profile (Figure 8d), but the RIJ now appears to have descended down to about 1 km as the system moved closer to the radar. In the corresponding model result (Figure 8c), the leading convective line intensifies considerably, with a peak mixing ratio of precipitating hydrometeors close to 5 g kg−1, compared to barely over 3 g kg−1 just 10 min ago. The weak echo region also becomes more evident, so that the stratiform region seems more detached from the leading line (Figure 8c). The two plots only 10 min apart suggest that the convective cells inside the bow echo exhibit rapid development cycles in the model, also consistent with many previous studies (e.g., [8,14,18,26,47,63]).
The time series from 1-min model results at the apex of the bow echo over the ocean (cf. Figure 7d) is presented in Figure 9, as the result at Kaoshiung is not ideal. In this figure, one sees that when the bow echo passed through, the surface wind speed increased dramatically, from about 7 to 32 m s−1, while the temperature dropped from 25 °C to 19 °C (Figure 9a). The surface pressure, meanwhile, exhibited a gradual rise beforehand and a small jump from about 1008 to 1009.5 hPa when the gust front passed through (Figure 9b). Immediately after the minor jump, the pressure dropped, rose rapidly again by more than 5 hPa to 1013 hPa, and decreased to 1008.5 hPa in response to the meso-high and wake low, respectively, over a period of roughly 45 min (Figure 9b). The above changes in pressure and temperature are also in good agreement with Figure 5b,c and many earlier observational studies (e.g., [5,8,9,13,17,18,64,65,66]).

4.2. Structure of the Anticyclonic Bow Echo

From the model results at 1900 LST, the streamlines of the system-relative flow (using a system moving speed of 14.8 m s−1 toward the east-southeast) at two different heights of 3149 and 2313 m are shown in Figure 10 to depict the circulation of the bow echo in a quasi-Lagrangian (system-relative) coordinate. To help identify the location of the bow, the column-maximum upward motion and the full wind speed are also plotted. At 3149 m (Figure 10a), it is confirmed that the modeled bow echo was also accompanied by an anticyclonic (clockwise) circulation in the backside, with the RIJ located near the far north, in a configuration in close agreement with the radar observations presented in Figure 6.
At this height, the second and third bow structure each exhibited a similar configuration, with predominantly anticyclonic circulation behind the leading bow line. At the lower elevation of about 2.3 km, the anticyclonic circulations associated with the bow segments became less clear (Figure 10b) and their centers were shifted toward the southwest compared to those at 3149 m (more apparent for the larger ones). Since the asymmetric and anticyclonic vortices were also reproduced nicely by the model, we can move on to investigate their formation mechanisms using the model results in the next section.

5. Vorticity Budget Diagnosis on the Bow Echo

The vorticity budget diagnosis of the bow echo was performed following the method described in Section 2.3. All terms (except FR) in Equation (1) were calculated from the model outputs, and the results are presented and discussed here. Figure 11 shows the results near 4-km height over a region roughly 150 km × 150 km at 0800 UTC (1600 LST) 2 April 2007, which was before the bow echo reached maturity (cf. Figure 7d). From the system-relative flow field (Figure 11a), the RIJ at this level can be clearly identified and it was associated with strong anticyclonic vorticity (ζ < 0, gray areas) on its south side, as expected. The leading convective line was mostly accompanied by cyclonic vorticity (ζ > 0) along its length, while anticyclonic vorticity existed on the backside, in agreement with the observation (cf. Figure 6 and Figure 10). System-relative local vorticity generation (LT = δζ/δt > 0, red contours) occurred along the leading line, and negative local tendency (LT < 0, dotted blue contours) also took place over regions with existing anticyclonic vorticity (Figure 11a). This means that the anticyclonic vorticity at the backside of the bow echo could be maintained and even gradually strengthened with time, also as observed.
At 1600 LST, the tilting effect (TIL) at a height near 4 km acted to generate positive (negative) vorticity immediately ahead of (behind) the leading convective line (Figure 11b). The horizontal vorticity vectors [HVV = ω H = (ξ, η)] on the x-y plane along the line, as shown, were mostly pointing toward the northwest to reflect the environmental vertical wind shear (increasing southwesterly winds with height). Thus, the updrafts along the line tilted the HVVs into pointing upward (downward) ahead of (behind) the line, to generate cyclonic (anticyclonic) vorticity. Due to the present bow echo formed along the front, such an FTR direction of environmental HVVs differed significantly from that seen in mid-latitudes (parallel to the line and from right to left). It was also different from the system-generated HVVs between the updraft–downdraft pair in typical and symmetric cases in [27,29], where they point from left to right of the bow and the updrafts create anticyclonic vorticity to the south. In Figure 11b, the local HVVs near the RIJ, also generated by the bow echo itself, were pointing in a similar direction (toward the southwest, from left to right) due to their decreasing strength upward (cf. Figure 8). However, the strong descending motion of the RIJ in this region acted to produce negative ζ on the north side and positive ζ on the south side through the tilting effect (Figure 11b). Below RIJ, the HVVs reversed in direction (cf. Figure 8) and the sinking produced ζ < 0 (ζ > 0) to the south (north). This process also differed from [27], as the vertical shear below the RIJ was system-generated here, whereas it came from the westerly environment and operated at an early stage in [27]. Thus, the tilting effect can be more complicated than previously thought also [29], despite the fact that it also produces anticyclonic vorticity to the south when in operation.
Next, in Figure 11c, the stretching effect (ST) indicated considerable enhancement in both positive vorticity along the leading convective line and negative vorticity behind the bow near 4 km at 1600 LST. For the latter, this happened when downdrafts accelerated downward in regions with ζ < 0 due to evaporative cooling and the drag of precipitation (cf. Figure 11b for w), causing the vortex tubes to stretch vertically. In some regions immediately ahead of the leading line (Figure 11c), however, ST contributed negatively (while both ζ > 0 and w > 0), indicating that the upward motion was decelerating with height across 4 km (likely above the gust front). The combined effect of TIL + ST is the total tendency (TT) following air motion and shown in Figure 11d. In this panel, one can see that in most regions along the leading line, cyclonic vorticity was being strengthened. Likewise, behind the bow and near the RIJ, anticyclonic vorticity was also being enhanced following air motion. The latter was mainly due to the tilting of HVVs in the frontal environment by the updrafts along the leading line, the tilting of HVVs below the RIJ by downdrafts, and the stretching effect of existing anticyclonic vorticity south of the RIJ (Figure 11b–d).
The two remaining terms in Equation (1) are the horizontal advection of ζ (HAD) by the system-relative flow (v − c) and the vertical advection of ζ (VAD), respectively. These two terms differ from the generation terms of TIL and ST in that they only advect and redistribute ζ in existence. In Figure 11e, HAD is seen as larger where stronger system-relative winds blew across regions with a greater horizontal vorticity gradient, i.e., near the leading convective line and the RIJ. Across the line, the FTR inflow (cf. Figure 8a,c) advected cyclonic vorticity backward along the line (Figure 11e), while the RIJ tended to advect the anticyclonic vorticity southward. Finally, VAD along the leading line (with w > 0) were mostly positive near 4 km at 1600 LST (Figure 11f). In regions with ζ < 0 and w < 0 near the RIJ (also cf. Figure 11d), on the other hand, VAD was positive and indicated that the anticyclonic vorticity there was also stronger below the level of 4 km. Overall, the four terms, TIL, ST, HAD, and VAD (Figure 11b,c,e,f), all contributed toward the local vorticity tendency (LT; Figure 11a) in the quasi-Lagrangian (system-relative) framework.
The vorticity budget results for a lower elevation of near 1 km and a later time of 1800 LST, when the modeled bow echo was moving across the southern Taiwan Strait (cf. Figure 7d), are shown in Figure 12. At this level, regions to the immediate backside of the line and further behind (and to the south) were all dominated by anticyclonic vorticity (Figure 12a). While the FTR inflow was from the east, there was post-frontal northeasterly flow behind the line. Again, the LT term in the quasi-Lagrangian frame near 1 km was positive along the leading line and negative immediately behind it, mainly due to the tilting effect (TIL, Figure 12c) of HVVs in the frontal environment by the updrafts along the line. Inside the updrafts (with positive buoyancy), its cyclonic vorticity was also enhanced by the ST effect through upward acceleration, as expected (Figure 12d). However, close to the surface, there was little indication of negative vorticity enhancement behind the line via stretching. When TIL and ST are combined, the TT following air motion (Figure 12a) thus exhibited a pattern similar to that of LT but generally with greater magnitudes.
When the vorticity pattern near 1 km at 1800 LST (Figure 12a) is compared with that near 4 km at 1600 LST (Figure 11a), one can see that immediately ahead of and behind the leading line, respectively, the tilting effect can act to locally generate positive and negative vorticity, which is then vertically stretched and enhanced. The anticyclonic vorticity in regions further behind, however, is generated mainly through the development of the RIJ and the stretching and tilting effects of the downdrafts below the RIJ (Figure 11a,c) above the boundary layer (not close to the surface). Therefore, the near-surface anticyclonic vorticity in the general backside region (not immediately behind the convective line and produced by TIL) must come from the negative vorticity associated with the RIJ aloft, through 3D advection, including the sinking motion of downdrafts, and horizontal advection toward the southwest by the post-frontal flow. Obviously, the advection of anticyclonic vorticity toward the southwest at low levels in the present case was only significant due to the frontal flow configuration, and would not be in operation in a typical, more symmetric bow echo. Overall, the frontal environment here dictated the extent of the bow echo and the direction of the HVVs, and the asymmetric anticyclonic vortex formed through the combined effects of tilting, stretching, and advection in a way that is different from typical, symmetric bow echoes. The major differences are summarized in Table 2.

6. Conclusions

On the evening of 2 April 2007, a bow echo struck the harbor city of Kaoshiung in southern Taiwan and produced a peak surface wind speed of 26 m s−1, a temperature drop of 6.6 °C, and a pressure rise of nearly 5 hPa. While it was intense, at over 200 km in length and with a lifespan of 10 h, this bow echo was atypical and unique from radar observations in that it possessed only one anticyclonic vortex on its backside with the RIJ located at the northern end behind the bow segment, as shown in the schematic in Figure 13, in contrast to a rather symmetric and typical structure with two bookend vortices in most cases (cf. Figure 1). Therefore, this rare event is investigated in this study through data analysis and high-resolution model simulation with a grid size of 2 km.
The analysis showed that the north-south oriented bow echo developed at the leading edge of an advancing cold front over the Taiwan Strait, with favorable ingredients of large vertical wind shear and very dry middle and upper levels. The environment near to and south of the front was unstable, with a moderate amount of CAPE (about 1150 J kg−1) and minimal CIN to support deep convection and bow echo development. To the north, behind the front, however, the lack of CAPE even above the surface cold northeasterly flow made it impossible for convection (Figure 13). Therefore, the portion of the bow north of the RIJ, where a cyclonic bookend vortex would reside in typical bow echoes, did not form and was missing.
The 2-km model experiment successfully reproduced this bow echo and its unique structure in good agreement with the observation. The RIJ in the model was slightly stronger than that which was observed, and produced a peak wind speed of 32 m s−1, a temperature drop of 6 °C, and a pressure rise of over 5 hPa at the surface at its apex during the mature stage. Also lasting over 8 h, the bow echo in the model was, however, slightly further north (by ~50 km) and aligned more in a northeast-southwest direction.
The reasons for the unique structural configuration of the bow echo were examined through a vorticity budget diagnosis in a storm-relative framework using model outputs. The results indicate that the anticyclonic vortex behind the leading bow in the present case formed and strengthened through the combined effects of tilting, stretching, and 3D advection, in a manner also quite different from symmetric events (synthesized in Table 2). Due to the northeasterly flow at the surface and increasing west-southwesterly winds with height aloft in the frontal environment, the horizontal vorticity vectors were pointing toward the northwest, from front to rear across the bow line, and the tilting due to updrafts produced anticyclonic vorticity at the backside (and cyclonic vorticity at the front side). On the other hand, the RIJ was associated with strong anticyclonic vorticity to its south, which was enhanced by stretching and advected downward. Below the RIJ, local horizontal vorticity vectors pointed toward the northeast (from right to left of line) and were also tilted into anticyclonic vorticity by the sinking motion to the south of the RIJ. Eventually, 3D advection by the low-level postfrontal flow carried the above anticyclonic vorticity toward the south and the backside of the bow structure. Thus, only the anticyclonic vortex became dominant. While our results indicated a somewhat complicated formation mechanism of vorticity in the present case, the main differences between the above processes and those found in symmetric bow echoes in the literature were also discussed in Section 5 and summarized in Table 2.

Author Contributions

Conceptualization, C.-C.W.; Formal analysis, C.-C.W., J.-P.H., C.-H.T. and P.-L.C.; Funding acquisition, C.-C.W. and D.-I.L.; Investigation, C.-C.W., J.-P.H., C.-H.T. and D.-I.L.; Methodology, C.-C.W. and C.-H.T.; Project administration, C.-C.W.; Software, C.-H.T. and P.-L.C.; Supervision, C.-C.W.; Visualization, C.-C.W., C.-H.T. and P.-L.C.; Writing—original draft, C.-C.W. and J.-P.H.; Writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported jointly by the Ministry of Science and Technology (MOST) of Taiwan (grants MOST-108-2111-M-003-005-MY2 and MOST-110-2111-M-003-004) and by the Korea Meteorological Institute (grand KMI 2021-03413).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The CReSS model and its user’s guide are open to researchers and available at http://www.rain.hyarc.nagoya-u.ac.jp/~tsuboki/cress_html/index_cress_eng.html (accessed on 2 April 2017), and the NCEP GFS data are available at http://rda.ucar.edu/datasets/ds335.0/#!description (accessed on 2 April 2007).

Acknowledgments

The authors thank the three anonymous reviewers for their valuable comments and suggestions. The original plots of Figure 2, Figure 4, Figure 5a, Figure 6, and Figure 8b,d are produced and provided by the CWB, and the help from T.-K. Chiou (CWB) is also appreciated and acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Glickman, T.S. (Ed.) Glossary of Meteorology; American Meteorological Society: Boston, MA, USA, 2000; 855p. [Google Scholar]
  2. Nolen, R.H. A radar pattern associated with tornadoes. Bull. Am. Meteorpl. Soc. 1959, 40, 277–279. [Google Scholar] [CrossRef] [Green Version]
  3. Fujita, T.T. Manual of Downburst Identification for Project NIMROD; Satellite and Mesometeorology Research Paper No.156; Department of Geosciences, University of Chicago: Chicago, IL, USA, 1978; 104p. [Google Scholar]
  4. Johns, R.H.; Hirt, W.D. Derechos: Widespread convectively induced wind-storms. Weather Forecast. 1987, 2, 32–49. [Google Scholar] [CrossRef]
  5. Przybylinski, R.W. The bow echo: Observations, numerical simulations, and severe weather detection methods. Weather Forecast. 1995, 10, 203–218. [Google Scholar] [CrossRef]
  6. Wakimoto, R.M.; Murphey, H.V.; Nester, A.; Jorgensen, D.P.; Atkins, N.T. High winds generated by bow echoes. Part I: Overview of the Omaha bow echo 5 July 2003 Storm during BAMEX. Mon. Weather Rev. 2006, 134, 2793–2812. [Google Scholar] [CrossRef] [Green Version]
  7. Burgess, D.W.; Ray, P.S. Principle of Radar. In Mesoscale Meteorology and Forecasting; Ray, P.S., Ed.; American Meteorological Society: Boston, MA, USA, 1986; pp. 85–117. [Google Scholar]
  8. Weisman, M.L. Bow echoes: A tribute to T. T. Fujita. Bull. Am. Meteorol. Soc. 2001, 82, 97–116. [Google Scholar] [CrossRef] [Green Version]
  9. Davis, C.; Atkins, C.; Bartels, D.; Bosart, L.; Coniglio, M.; Bryan, G.; Cotton, W.; Dowell, D.; Jewett, B.; Johns, R.; et al. The Bow Echo and MCV Experiment. Observations and opportunities. Bull. Am. Meteorol. Soc. 2004, 85, 1075–1093. [Google Scholar] [CrossRef] [Green Version]
  10. Johns, R.H. Meteorological conditions associated with bow echo development in convective storms. Weather Forecast. 1993, 8, 294–299. [Google Scholar] [CrossRef] [Green Version]
  11. Johns, R.H.; Howard, K.W.; Maddox, R.A. Conditions associated with long-lived derechos—An examination of the large-scale environment. In 16th Conference on Severe Local Storms, Kananaskis Park, AB, Canada; American Meteorological Society: Boston, MA, USA, 1990; pp. 408–412. [Google Scholar]
  12. Smull, B.F.; Houze, R.A., Jr. A midlatitude squall line with a trailing region of stratiform rain: Radar and satellite observations. Mon. Weather Rev. 1985, 113, 117–133. [Google Scholar] [CrossRef] [Green Version]
  13. Houze, R.A., Jr.; Rutledge, S.A.; Biggerstaff, M.I.; Smull, B.F. Interpretation of Doppler radar displays of mid-latitude mesoscale convective systems. Bull. Am. Meteorol. Soc. 1989, 70, 608–619. [Google Scholar] [CrossRef] [Green Version]
  14. Funk, T.W.; Darmofal, K.E.; Kirkpatrick, J.D.; DeWald, V.L.; Przybylinski, R.W.; Schmocker, G.K.; Lin, Y.-J. Storm reflectivity and mesocyclone evolution associated with the 15 April 1994 squall line over Kentucky and southern Indiana. Weather Forecast. 1999, 14, 976–993. [Google Scholar] [CrossRef]
  15. Rotunno, R.; Klemp, J.B.; Weisman, M.L. A theory for strong, long-lived squall line. J. Atmos. Sci. 1988, 45, 463–485. [Google Scholar] [CrossRef] [Green Version]
  16. Skamarock, W.C.; Weisman, M.L.; Klemp, J.B. Three-dimensional evolution of simulated long-lived squall lines. J. Atmos. Sci. 1994, 51, 2563–2584. [Google Scholar] [CrossRef] [Green Version]
  17. Smull, B.F.; Houze, R.A., Jr. Rear inflow in squall-lines with trailing stratiform precipitation. Mon. Weather Rev. 1987, 115, 2869–2889. [Google Scholar] [CrossRef] [Green Version]
  18. Braun, S.A.; Houze, R.A., Jr. The evolution of the 10–11 June 1985 PRE-STORM squall line: Initiation, development of rear inflow, and dissipation. Mon. Weather Rev. 1997, 125, 478–504. [Google Scholar] [CrossRef]
  19. Weisman, M.L. The role of convectively generated rear-inflow jets in the evolution of long-lived mesoconvective systems. J. Atmos. Sci. 1992, 49, 1826–1847. [Google Scholar] [CrossRef] [Green Version]
  20. Weisman, M.L. The genesis of severe, long-lived bow-echoes. J. Atmos. Sci. 1993, 50, 645–670. [Google Scholar] [CrossRef]
  21. James, R.P.; Markowski, P.M.; Fritsch, J.M. Bow echo sensitivity to ambient moisture and cold pool strength. Mon. Weather Rev. 2006, 134, 950–964. [Google Scholar] [CrossRef] [Green Version]
  22. Jorgensen, D.P.; Smull, B.F. Mesovortex circulations seen by airborne Doppler radar within a bow-echo mesoscale convective system. Bull. Am. Meteorol. Soc. 1993, 74, 2146–2157. [Google Scholar] [CrossRef] [Green Version]
  23. Atkins, N.T.; Arnott, J.M.; Przybylinski, R.W.; Wolf, R.A.; Ketcham, B.D. Vortex structure and evolution within bow echoes. Part I: Single-Doppler and damage analysis of the 29 June 1998 derecho. Mon. Weather Rev. 2004, 132, 2224–2242. [Google Scholar] [CrossRef] [Green Version]
  24. Fujita, T.T. Tornadoes and downbursts in the context of generalized planetary scales. J. Atmos. Sci. 1981, 38, 1511–1524. [Google Scholar] [CrossRef] [Green Version]
  25. Lee, W.-C.; Wakimoto, R.M.; Carbone, R.E. The evolution and structure of a “bow-echo-microburst” event. Part II: The bow echo. Mon. Weather Rev. 1992, 120, 2211–2225. [Google Scholar] [CrossRef] [Green Version]
  26. Weisman, M.L.; Trapp, R.J. Low-level mesovortices within squall lines and bow echoes. Part I: Overview and dependence on environmental shear. Mon. Weather Rev. 2003, 131, 2779–2803. [Google Scholar] [CrossRef] [Green Version]
  27. Weisman, M.L.; Davis, C. Mechanisms for the generation of mesoscale vortices within quasi-linear convective systems. J. Atmos. Sci. 1998, 55, 2603–2622. [Google Scholar] [CrossRef] [Green Version]
  28. French, A.J.; Parker, M.D. Numerical simulations of bow echo formation following a squall line–supercell merger. Mon. Weather Rev. 2014, 142, 4791–4822. [Google Scholar] [CrossRef]
  29. Atkins, N.T.; St. Laurent, M. Bow echo mesovortices. Part II: Their genesis. Mon. Weather Rev. 2009, 137, 1514–1532. [Google Scholar] [CrossRef] [Green Version]
  30. Businger, S.; Birchard, T., Jr.; Kodoma, K.; Jendrowski, P.A.; Wang, J.J. A bow echo and severe weather associated with a Kona Low in Hawaii. Weather Forecast. 1998, 13, 576–591. [Google Scholar] [CrossRef]
  31. Schmid, W.; Schiesser, H.H.; Furger, M.; Jenni, M. The origin of severe winds in a tornadic bow-echo storm over northern Switzerland. Mon. Weather Rev. 2000, 128, 192–207. [Google Scholar] [CrossRef]
  32. Kang, Y.; Jeong, J.-H.; You, C.H.; Lee, D.-I. Structure and evolution of a convective system with bow echo associated with terrain on Jeju Island, Korea. J. Meteorol. Soc. Jpn. 2018, 96, 447–460. [Google Scholar] [CrossRef] [Green Version]
  33. Surowiecki, A.; Taszarek, M. A 10-year radar-based climatology of mesoscale convective system archetypes and derechos in Poland. Mon. Weather Rev. 2020, 148, 3471–3488. [Google Scholar] [CrossRef]
  34. Chen, G.T.-J.; Wang, C.-C.; Chou, H.-C. Case study of a bow echo near Taiwan during wintertime. J. Meteorol. Soc. Jpn. 2007, 85, 233–253. [Google Scholar]
  35. Tsuboki, K.; Sakakibara, A. Large-scale parallel computing of cloud resolving storm simulator. In High Performance Computing; Zima, H.P., Joe, K., Sato, M., Seo, Y., Shimasaki, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 243–259. [Google Scholar]
  36. Tsuboki, K.; Sakakibara, A. Numerical Prediction of High-Impact Weather Systems: The Textbook for the Seventeenth IHP Training Course in 2007; Hydrospheric Atmospheric Research Center, Nagoya University, and UNESCO: Nagoya, Japan, 2007; 273p. [Google Scholar]
  37. Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef] [Green Version]
  38. Cotton, W.R.; Tripoli, G.J.; Rauber, R.M.; Mulvihill, E.A. Numerical simulation of the effects of varying ice crystal nucleation rates and aggregation processes on orographic snowfall. J. Clim. Appl. Meteorol. 1986, 25, 1658–1680. [Google Scholar] [CrossRef] [Green Version]
  39. Murakami, M. Numerical modeling of dynamical and microphysical evolution of an isolated convective cloud—The 19 July 1981 CCOPE cloud. J. Meteorol. Soc. Jpn. 1990, 68, 107–128. [Google Scholar] [CrossRef] [Green Version]
  40. Ikawa, M.; Saito, K. Description of a nonhydrostatic model developed at the Forecast Research Department of the MRI. MRI Technol. Rep. 1991, 28, 238. [Google Scholar]
  41. Murakami, M.; Clark, T.L.; Hall, W.D. Numerical simulations of convective snow clouds over the Sea of Japan: Two-dimensional simulation of mixed layer development and convective snow cloud formation. J. Meteorol. Soc. Jpn. 1994, 72, 43–62. [Google Scholar] [CrossRef] [Green Version]
  42. Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound.-Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
  43. Kondo, J. Heat balance of the China Sea during the air mass transformation experiment. J. Meteorol. Soc. Jpn. 1976, 54, 382–398. [Google Scholar] [CrossRef] [Green Version]
  44. Louis, J.F.; Tiedtke, M.; Geleyn, J.F. A short history of the operational PBL parameterization at ECMWF. In Workshop on Planetary Boundary Layer Parameterization; ECMWF: Reading, UK, 1981; pp. 59–79. [Google Scholar]
  45. Segami, A.; Kurihara, K.; Nakamura, H.; Ueno, M.; Takano, I.; Tatsumi, Y. Operational mesoscale weather prediction with Japan Spectral Model. J. Meteorol. Soc. Jpn. 1989, 67, 907–924. [Google Scholar] [CrossRef] [Green Version]
  46. Wang, C.-C.; Chen, G.T.-J.; Chen, T.-C.; Tsuboki, K. A numerical study on the effects of Taiwan topography on a convective line during the Mei-yu season. Mon. Weather Rev. 2005, 133, 3217–3242. [Google Scholar] [CrossRef]
  47. Wang, C.-C.; Hsu, J.C.-S.; Chen, G.T.-J.; Lee, D.-I. A study of two propagating heavy-rainfall episodes near Taiwan during SoWMEX/TiMREX IOP-8 in June 2008. Part I: Synoptic evolution, episode propagation, and model control simulation. Mon. Weather Rev. 2014, 142, 2619–2643. [Google Scholar] [CrossRef]
  48. Wang, C.-C.; Chiou, B.-K.; Chen, G.T.-J.; Kuo, H.-C.; Liu, C.-H. A numerical study of back-building process in a quasistationary rainband with extreme rainfall over northern Taiwan during 11–12 June 2012. Atmos. Chem. Phys. 2016, 16, 12359–12382. [Google Scholar] [CrossRef] [Green Version]
  49. Wang, C.-C. The more rain, the better the model performs—The dependency of quantitative precipitation forecast skill on rainfall amount for typhoons in Taiwan. Mon. Weather Rev. 2015, 143, 1723–1748. [Google Scholar] [CrossRef]
  50. Wang, C.-C.; Huang, S.-Y.; Chen, S.-H.; Chang, C.-S.; Tsuboki, K. Cloud-resolving typhoon rainfall ensemble forecasts for Taiwan with large domain and extended range through time-lagged approach. Weather Forecast. 2016, 31, 151–172. [Google Scholar] [CrossRef]
  51. Wang, C.-C.; Chuang, P.-Y.; Chang, C.-S.; Tsuboki, K.; Huang, S.-Y.; Leu, G.-C. Evaluation of mei-yu heavy-rainfall quantitative precipitation forecasts in Taiwan by a cloud-resolving model for three seasons of 2012–2014. Nat. Hazards Earth Syst. Sci. 2022, 22, 23–40. [Google Scholar] [CrossRef]
  52. Wang, C.-C.; Li, M.-S.; Chang, C.-S.; Chuang, P.-Y.; Chen, S.-H.; Tsuboki, K. Ensemble-based sensitivity analysis and predictability of an extreme rainfall event over northern Taiwan in the Mei-yu Season: The 2 June 2017 Case. Atmos. Res. 2021, 259, 105684. [Google Scholar] [CrossRef]
  53. Kanamitsu, M. Description of the NMC global data assimilation and forecast system. Weather Forecast. 1989, 4, 335–342. [Google Scholar] [CrossRef] [Green Version]
  54. Kalnay, E.; Kanamitsu, M.; Baker, W.E. Global numerical weather prediction at the National Meteorological Center. Bull. Am. Meteorol. Soc. 1990, 71, 1410–1428. [Google Scholar] [CrossRef]
  55. Moorthi, S.; Pan, H.L.; Caplan, P. Changes to the 2001 NCEP Operational MRF/AVN Global Analysis/Forecast System. In NWS Technical Procedures Bulletin; National Weather Service Office of Meteorology: Silver Spring, MD, USA, 2001; 14p. [Google Scholar]
  56. Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
  57. Klemp, J.B. Dynamics of tornadic thunderstorms. Annu. Rev. Fluid Mech. 1987, 19, 369–402. [Google Scholar] [CrossRef]
  58. Weisman, M.L.; Rotunno, R. The use of vertical wind shear versus helicity in interpreting supercell dynamics. J. Atmos. Sci. 2000, 57, 1452–1472. [Google Scholar] [CrossRef] [Green Version]
  59. Chancibault, K.; Ducrocq, V.; Lafore, J.-P. A numerical study of a nontornadic supercell over France. Mon. Weather Rev. 2003, 131, 2290–2311. [Google Scholar] [CrossRef] [Green Version]
  60. Maddox, R.A. Large-scale meteorological conditions associated with mid-latitude, mesoscale convective complexes. Mon. Weather Rev. 1983, 111, 1475–1493. [Google Scholar] [CrossRef] [Green Version]
  61. Chang, P.-L.; Lin, P.-F.; Jou, B.J.-D.; Zhang, J. An application of reflectivity climatology in constructing radar hybrid scans over complex terrain. J. Atmos. Ocean. Technol. 2009, 26, 1315–1327. [Google Scholar] [CrossRef]
  62. Chang, P.-L.; Zhang, J.; Tang, Y.-S.; Tang, L.; Pin-Lin, P.-F.; Langston, C.; Kaney, B.; Chen, C.-R.; Howard, K. An operational multi-radar multi-sensor QPE system in Taiwan. Bull. Am. Meteorol. Soc. 2021, 102, E555–E577. [Google Scholar] [CrossRef]
  63. Tao, W.-K.; Simpson, J.; Soong, S.-T. Numerical simulation of a subtropical squall line over the Taiwan Strait. Mon. Weather Rev. 1991, 119, 2699–2723. [Google Scholar] [CrossRef] [Green Version]
  64. Schaefer, J.T.; Hoxit, L.R.; Chappell, C.F. Thunderstorms and their mesoscale environment. In Thunderstorm Morphology and Dynamics; Kessler, E., Ed.; U.S. Government Printing Office: Washington, DC, USA, 1985; pp. 113–130. [Google Scholar]
  65. Johnson, R.H.; Hamilton, P.J. The relationship of surface pressure features to the precipitation and air flow structure of an intense midlatitude squall line. Mon. Weather Rev. 1988, 116, 1444–1472. [Google Scholar] [CrossRef] [Green Version]
  66. Adams-Selin, R.D.; Johnson, R.H. Mesoscale surface pressure and temperature features associated with bow echoes. Mon. Weather Rev. 2010, 138, 212–227. [Google Scholar] [CrossRef] [Green Version]
Atmosphere 13 00331 g001 550
Figure 1. A schematic diagram of the life cycle of a bow echo based on a figure in [3]. Black arrows represent the approximate location of the RIJ, and dots denote the location of tornadoes. (Adopted from [6], © American Meteorological Society, used with permission).
Figure 1. A schematic diagram of the life cycle of a bow echo based on a figure in [3]. Black arrows represent the approximate location of the RIJ, and dots denote the location of tornadoes. (Adopted from [6], © American Meteorological Society, used with permission).
Atmosphere 13 00331 g001
Atmosphere 13 00331 g002 550
Figure 2. The CWB weather charts at 0000 UTC (0800 LST) 2 April 2007, of (a) mean sea-level pressure (isobars every 4 hPa) and surface front, and of geopotential height (gpm, solid contours) and temperature (°C, dashed isotherms) at (b) 850 hPa (intervals: 30 gpm and 3 °C), (c) 500 hPa (intervals: 60 gpm and 4 °C), and (d) 200 hPa (intervals: 120 gpm and 5 °C), respectively. The troughs in (b–d) and upper-level jets in (d) are labeled. The two triangles in (a) depict the location of Shantou (orange) and Xiamen (purple). The region of the bow echo (green dashed box), surrounding geography, and model domain (orange dashed box) are marked in (c).
Figure 2. The CWB weather charts at 0000 UTC (0800 LST) 2 April 2007, of (a) mean sea-level pressure (isobars every 4 hPa) and surface front, and of geopotential height (gpm, solid contours) and temperature (°C, dashed isotherms) at (b) 850 hPa (intervals: 30 gpm and 3 °C), (c) 500 hPa (intervals: 60 gpm and 4 °C), and (d) 200 hPa (intervals: 120 gpm and 5 °C), respectively. The troughs in (b–d) and upper-level jets in (d) are labeled. The two triangles in (a) depict the location of Shantou (orange) and Xiamen (purple). The region of the bow echo (green dashed box), surrounding geography, and model domain (orange dashed box) are marked in (c).
Atmosphere 13 00331 g002
Atmosphere 13 00331 g003 550
Figure 3. The skew T-log p diagrams from sounding observations at (a) Shantou (59316) and (b) Xiamen (59134) at 0000 UTC (0800 LST) 2 April 2007. Some relevant parameters are given to the top right, and the values of CAPE and CIN for a surface air parcel are also labeled in (a).
Figure 3. The skew T-log p diagrams from sounding observations at (a) Shantou (59316) and (b) Xiamen (59134) at 0000 UTC (0800 LST) 2 April 2007. Some relevant parameters are given to the top right, and the values of CAPE and CIN for a surface air parcel are also labeled in (a).
Atmosphere 13 00331 g003
Atmosphere 13 00331 g004 550
Figure 4. The vertical maximum reflectivity composite (dBZ) from CWB land-based radars in Taiwan on 2 April 2007, at (a) 1400 LST and 1-h intervals from (b) 1600 to (f) 2000 LST, respectively. Marked by (enlarged) blue dots in (a), the four radars are coded as RCCG (located at Chigu), RCWF, RCHL, and RCKT. In (d), the locations of Shantou, Xiamen, and Kaoshiung are marked.
Figure 4. The vertical maximum reflectivity composite (dBZ) from CWB land-based radars in Taiwan on 2 April 2007, at (a) 1400 LST and 1-h intervals from (b) 1600 to (f) 2000 LST, respectively. Marked by (enlarged) blue dots in (a), the four radars are coded as RCCG (located at Chigu), RCWF, RCHL, and RCKT. In (d), the locations of Shantou, Xiamen, and Kaoshiung are marked.
Atmosphere 13 00331 g004
Atmosphere 13 00331 g005 550
Figure 5. (a) Continuous records of wind direction and speed (m s−1) by the automated anemometer, and hourly surface observations of (b) pressure (hPa) and (c) temperature (°C) during 2 April 2007 at Kaoshiung, Taiwan. The time goes from right to left in (a), and the vertical arrows in (b,c) mark the time of rapid change.
Figure 5. (a) Continuous records of wind direction and speed (m s−1) by the automated anemometer, and hourly surface observations of (b) pressure (hPa) and (c) temperature (°C) during 2 April 2007 at Kaoshiung, Taiwan. The time goes from right to left in (a), and the vertical arrows in (b,c) mark the time of rapid change.
Atmosphere 13 00331 g005
Atmosphere 13 00331 g006 550
Figure 6. The point-position indicator (PPI) of (a) echo reflectivity (dBZ, scale on top, every five dBZ from −10 to 65 dBZ) and (b) radial wind (m s−1, every 4 m s−1 from −26 to +26 m s−1) observed by the CWB Chigu Doppler radar at 0.5° elevation angle at 1828 LST 2 April 2007. (c,d) are the same as (a,b) except at 1858 LST and (d) at an elevation angle of 2.4°. The leading edge of the bow echo, RIJ, and its associated circulation are labeled. In (b,d), an eastward system moving speed of 20 m s−1 has been subtracted.
Figure 6. The point-position indicator (PPI) of (a) echo reflectivity (dBZ, scale on top, every five dBZ from −10 to 65 dBZ) and (b) radial wind (m s−1, every 4 m s−1 from −26 to +26 m s−1) observed by the CWB Chigu Doppler radar at 0.5° elevation angle at 1828 LST 2 April 2007. (c,d) are the same as (a,b) except at 1858 LST and (d) at an elevation angle of 2.4°. The leading edge of the bow echo, RIJ, and its associated circulation are labeled. In (b,d), an eastward system moving speed of 20 m s−1 has been subtracted.
Atmosphere 13 00331 g006
Atmosphere 13 00331 g007 550
Figure 7. Model results of streamlines, potential temperature (cyan contours every 1 °C), and convergence (10−4 s−1, color for convergence and magenta contours for divergence, scale at bottom) over the Taiwan Strait, at the height of 645 m at (a) 1600, (b) 1800, and (c) 2000 LST 2 April 2007. The cross-section used in Figure 8a,c is marked in (b). (d) Position and movement of modeled bow echo at 30-min intervals from 1400 to 2200 LST, as determined from the leading edge of upward motion. The data location used in Figure 9 is also marked (open circle) in (d).
Figure 7. Model results of streamlines, potential temperature (cyan contours every 1 °C), and convergence (10−4 s−1, color for convergence and magenta contours for divergence, scale at bottom) over the Taiwan Strait, at the height of 645 m at (a) 1600, (b) 1800, and (c) 2000 LST 2 April 2007. The cross-section used in Figure 8a,c is marked in (b). (d) Position and movement of modeled bow echo at 30-min intervals from 1400 to 2200 LST, as determined from the leading edge of upward motion. The data location used in Figure 9 is also marked (open circle) in (d).
Atmosphere 13 00331 g007
Atmosphere 13 00331 g008 550
Figure 8. Vertical cross-section of (a) wind vector (m s−1, reference vector at upper right) on section plane, wind speed (isotachs every 5 m s−1), and mixing ratio of total precipitation (g kg−1, rain + snow + graupel, color) along line B-B’ (cf. Figure 7b) at 1828 LST 2 April 2007 in model experiment. (b) RHI of reflectivity (dBZ) and radial wind speed (m s−1, positive for outbound) observed by the CWB Chigu radar (located at point A) looking west at 1828 LST. (c,d) are the same as (a,b) but at 1838 LST in both panels. All winds are system relative (system moving speed is 14.8 m s−1 in model and 20 m s−1 in observation).
Figure 8. Vertical cross-section of (a) wind vector (m s−1, reference vector at upper right) on section plane, wind speed (isotachs every 5 m s−1), and mixing ratio of total precipitation (g kg−1, rain + snow + graupel, color) along line B-B’ (cf. Figure 7b) at 1828 LST 2 April 2007 in model experiment. (b) RHI of reflectivity (dBZ) and radial wind speed (m s−1, positive for outbound) observed by the CWB Chigu radar (located at point A) looking west at 1828 LST. (c,d) are the same as (a,b) but at 1838 LST in both panels. All winds are system relative (system moving speed is 14.8 m s−1 in model and 20 m s−1 in observation).
Atmosphere 13 00331 g008
Atmosphere 13 00331 g009 550
Figure 9. Time evolution of (a) wind speed (m s−1, black, axis on left side) and temperature (°C, blue, axis on right side) and (b) pressure (hPa), all at the surface, at the location marked in Figure 7d during 2 April 2007 in the model experiment.
Figure 9. Time evolution of (a) wind speed (m s−1, black, axis on left side) and temperature (°C, blue, axis on right side) and (b) pressure (hPa), all at the surface, at the location marked in Figure 7d during 2 April 2007 in the model experiment.
Atmosphere 13 00331 g009
Atmosphere 13 00331 g010 550
Figure 10. Model result of system-relative stream lines (gray) and wind speed (m s−1, color, scale at bottom) at (a) 3149 m and (b) 2313 m, and column-maximum upward motion (light green and purple contours at 1 and 5 m s−1, respectively) at 1900 LST 2 April 2007. The mesoscale vortices inside the bow echo and the RIJ are marked.
Figure 10. Model result of system-relative stream lines (gray) and wind speed (m s−1, color, scale at bottom) at (a) 3149 m and (b) 2313 m, and column-maximum upward motion (light green and purple contours at 1 and 5 m s−1, respectively) at 1900 LST 2 April 2007. The mesoscale vortices inside the bow echo and the RIJ are marked.
Atmosphere 13 00331 g010
Atmosphere 13 00331 g011 550
Figure 11. Vorticity budget terms (solid red/blue dotted contours for positive/negative values) and relevant parameters computed from model results at the height of 4012 m at 0800 UTC (1600 LST) 2 April 2007. (a) Relative vorticity (ζ, 10−3 s−1, color with white contours), storm-relative horizontal wind vectors (v − c, m s−1), and local tendency of vorticity (LT) in quasi-Lagrangian frame (δζ/δt, solid red/dotted blue contours every +6/−4 × 10−6 s−2), (b) vertical velocity (w, m s−1, color with white contours), horizontal vorticity vectors [HVV, = (ξ, η), 10−3 s−1)] associated with vertical wind shear, and tilting term (TIL, every ±2 × 10−6 s−2), (c) ζ, v − c, and stretching term (ST, every ±2 × 10−6 s−2), (d) w, HVV, and total tendency (TT) of vorticity in full Lagrangian frame (dζ/dt, every ±5 × 10−6 s−2), (e) ζ, v − c, and horizontal advection term (HAD, every ±5 × 10−6 s−2), and (f) w, v − c, and vertical advection term (VAD, every ±4 × 10−6 s−2), respectively.
Figure 11. Vorticity budget terms (solid red/blue dotted contours for positive/negative values) and relevant parameters computed from model results at the height of 4012 m at 0800 UTC (1600 LST) 2 April 2007. (a) Relative vorticity (ζ, 10−3 s−1, color with white contours), storm-relative horizontal wind vectors (v − c, m s−1), and local tendency of vorticity (LT) in quasi-Lagrangian frame (δζ/δt, solid red/dotted blue contours every +6/−4 × 10−6 s−2), (b) vertical velocity (w, m s−1, color with white contours), horizontal vorticity vectors [HVV, = (ξ, η), 10−3 s−1)] associated with vertical wind shear, and tilting term (TIL, every ±2 × 10−6 s−2), (c) ζ, v − c, and stretching term (ST, every ±2 × 10−6 s−2), (d) w, HVV, and total tendency (TT) of vorticity in full Lagrangian frame (dζ/dt, every ±5 × 10−6 s−2), (e) ζ, v − c, and horizontal advection term (HAD, every ±5 × 10−6 s−2), and (f) w, v − c, and vertical advection term (VAD, every ±4 × 10−6 s−2), respectively.
Atmosphere 13 00331 g011
Atmosphere 13 00331 g012 550
Figure 12. As in Figure 11, but showing vorticity budget terms (solid red/blue dotted contours) and relevant parameters at the height of 1060 m at 1000 UTC (1800 LST) 2 April 2007. (a) ζ (10−3 s−1, color), v − c, (m s−1, vectors), and LT in quasi-Lagrangian frame (δζ/δt, red/blue contours every +6/−4 × 10−6 s−2), (b) w, HVV, and TT in full Lagrangian frame (dζ/dt, every ±5 × 10−6 s−2), (c) w, HVV, and tilting term TIL (every ±2 × 10−6 s−2), and (d) ζ, v − c, and stretching term ST (every ±2 × 10−6 s−2), respectively.
Figure 12. As in Figure 11, but showing vorticity budget terms (solid red/blue dotted contours) and relevant parameters at the height of 1060 m at 1000 UTC (1800 LST) 2 April 2007. (a) ζ (10−3 s−1, color), v − c, (m s−1, vectors), and LT in quasi-Lagrangian frame (δζ/δt, red/blue contours every +6/−4 × 10−6 s−2), (b) w, HVV, and TT in full Lagrangian frame (dζ/dt, every ±5 × 10−6 s−2), (c) w, HVV, and tilting term TIL (every ±2 × 10−6 s−2), and (d) ζ, v − c, and stretching term ST (every ±2 × 10−6 s−2), respectively.
Atmosphere 13 00331 g012
Atmosphere 13 00331 g013 550
Figure 13. A schematic diagram of the bow echo, its structure, and associated horizontal vorticity (left side) in this study. The system developed along a cold front and its backside was dominated by anticyclonic vorticity. The formation mechanism of the vortex is summarized in Table 2.
Figure 13. A schematic diagram of the bow echo, its structure, and associated horizontal vorticity (left side) in this study. The system developed along a cold front and its backside was dominated by anticyclonic vorticity. The formation mechanism of the vortex is summarized in Table 2.
Atmosphere 13 00331 g013
Table
Table 1. The CReSS model domain configuration and major physical package used in this study.
Table 1. The CReSS model domain configuration and major physical package used in this study.
ProjectionLambert conformal (centered at 120° E, secant at 10° N and 40° N)
Grid spacing2.0 km × 2.0 km × 100–980 m (350 m) *
Grid dimension (x, y, z)540 × 480 × 60
Domain size1080 km × 960 km × 21 km
IC/BCsNCEP GFS analyses (1° × 1°, 26 pressure levels, every 6 h)
Integration period0600 UTC 1 to 0000 UTC 3 April 2007 (42 h)
Output frequency10 min (1 min during 0600–1500 UTC 2 April 2007)
Cloud microphysicsBulk cold-rain scheme (six species)
PBL parameterization1.5-order closure with prediction of turbulent kinetic energy
Surface processesEnergy/momentum fluxes, shortwave and longwave radiation
Substrate model41 levels, every 5 cm to 2 m in depth
* The vertical grid spacing (Δz) of CReSS is stretched (smallest at bottom) and the averaged value is given in the parentheses.
Table
Table 2. The major differences between the formation mechanism(s) of bookend vortices in typical and symmetric bow echoes (cf. Figure 1), mainly from [27,29], and the asymmetric and anticyclonic case (cf. Figure 13) in this study. Terms are in system-relative frame.
Table 2. The major differences between the formation mechanism(s) of bookend vortices in typical and symmetric bow echoes (cf. Figure 1), mainly from [27,29], and the asymmetric and anticyclonic case (cf. Figure 13) in this study. Terms are in system-relative frame.
SymmetricA pair of cyclonic (northern) and anticyclonic (southern) vortices
Location of RIJRoughly in the middle of bow line
Environmental shearWesterly shear (RTF): HVVs pointing from right to left of line
System-induced vorticity Between updraft and downdraft: HVVs pointing from left to right
Formation mechanismTilting of environmental shear by downdraft (early stage), and tilting of system-induced HVVs by updraft (mature stage)
Asymmetric (this study)Only one anticyclonic vortex behind the line
Location of RIJNear the northern end of bow line
Environmental shear (front)Southwesterly shear: HVVs pointing FTR across the line
System-induced vorticityBelow RIJ: HVVs pointing from right to left of line
Formation mechanismTilting of environmental shear by updraft, tilting of system-induced vorticity by downdraft, stretching, and 3D advection by frontal flow
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Wang, C.-C.; Hou, J.-P.; Tseng, C.-H.; Chang, P.-L.; Lee, D.-I. Study of an Asymmetric and Anticyclonic Bow Echo Near Taiwan. Atmosphere 2022, 13, 331. https://doi.org/10.3390/atmos13020331

AMA Style

Wang C-C, Hou J-P, Tseng C-H, Chang P-L, Lee D-I. Study of an Asymmetric and Anticyclonic Bow Echo Near Taiwan. Atmosphere. 2022; 13(2):331. https://doi.org/10.3390/atmos13020331

Chicago/Turabian Style

Wang, Chung-Chieh, Jou-Ping Hou, Chun-Hsiang Tseng, Pao-Liang Chang, and Dong-In Lee. 2022. "Study of an Asymmetric and Anticyclonic Bow Echo Near Taiwan" Atmosphere 13, no. 2: 331. https://doi.org/10.3390/atmos13020331

APA Style

Wang, C. -C., Hou, J. -P., Tseng, C. -H., Chang, P. -L., & Lee, D. -I. (2022). Study of an Asymmetric and Anticyclonic Bow Echo Near Taiwan. Atmosphere, 13(2), 331. https://doi.org/10.3390/atmos13020331

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop