One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models
Abstract
:1. Introduction
2. The Lorenz 1963 and 1969 Models
2.1. The L63 Limited-Scale, Nonlinear Model
2.2. The L69 Multiscale, Linear Model
3. Discussions
3.1. Features of the L63 Model
3.1.1. Physical vs. Numerical Instability within a Linear 2nd-Order ODE
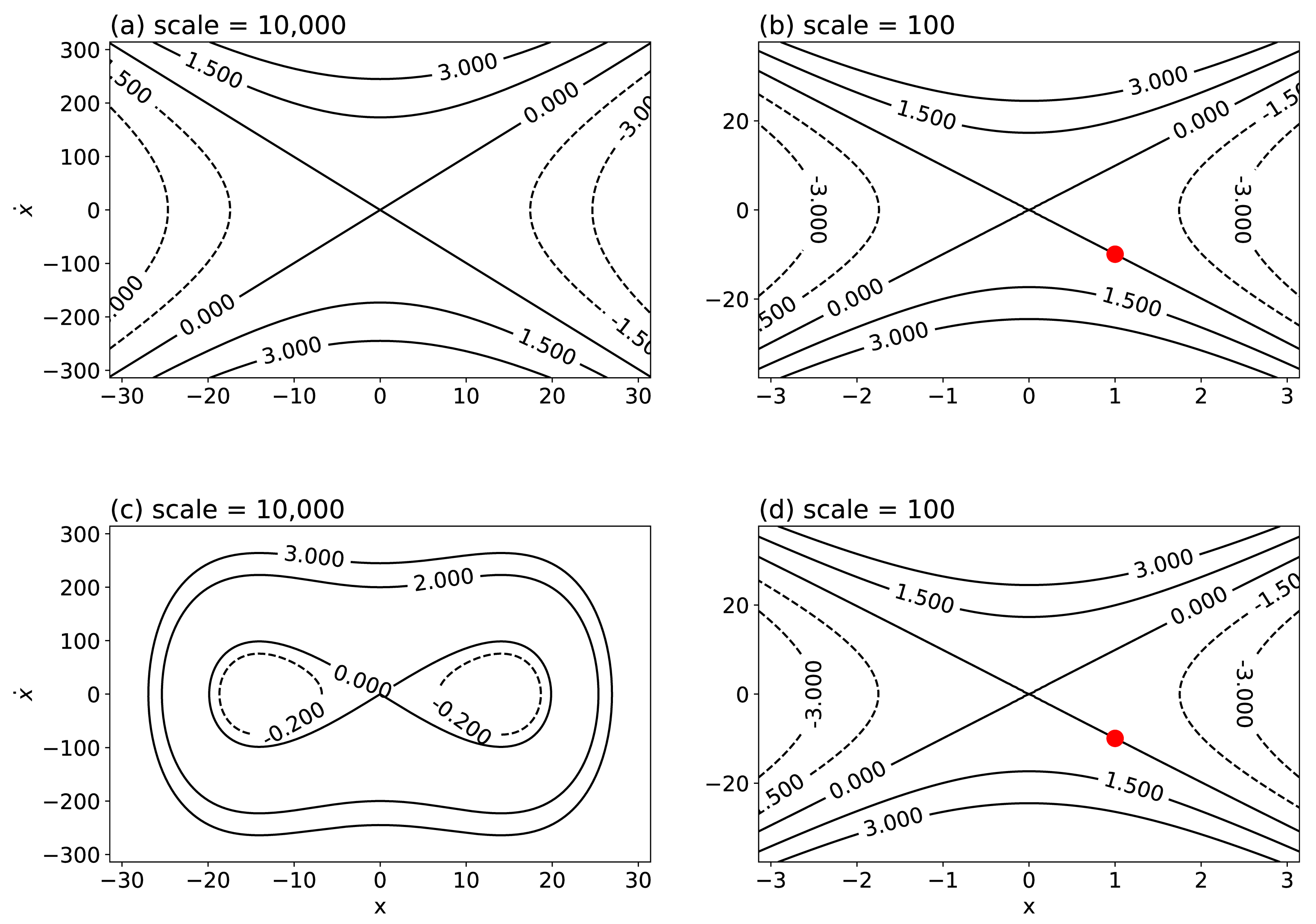
3.1.2. A Perspective of Dynamical Systems: Phase Space and a Saddle Point
3.1.3. Periodicity and Centers Enabled by Nonlinearity
3.1.4. (Computational) Limit Chaos Associated with a Homoclinic Orbit
3.1.5. Spiral Sinks Associated with an Additional Dissipative Term ()
3.1.6. SDIC and Finite Predictability Within the L63 Model
3.2. Features of the L69 Model
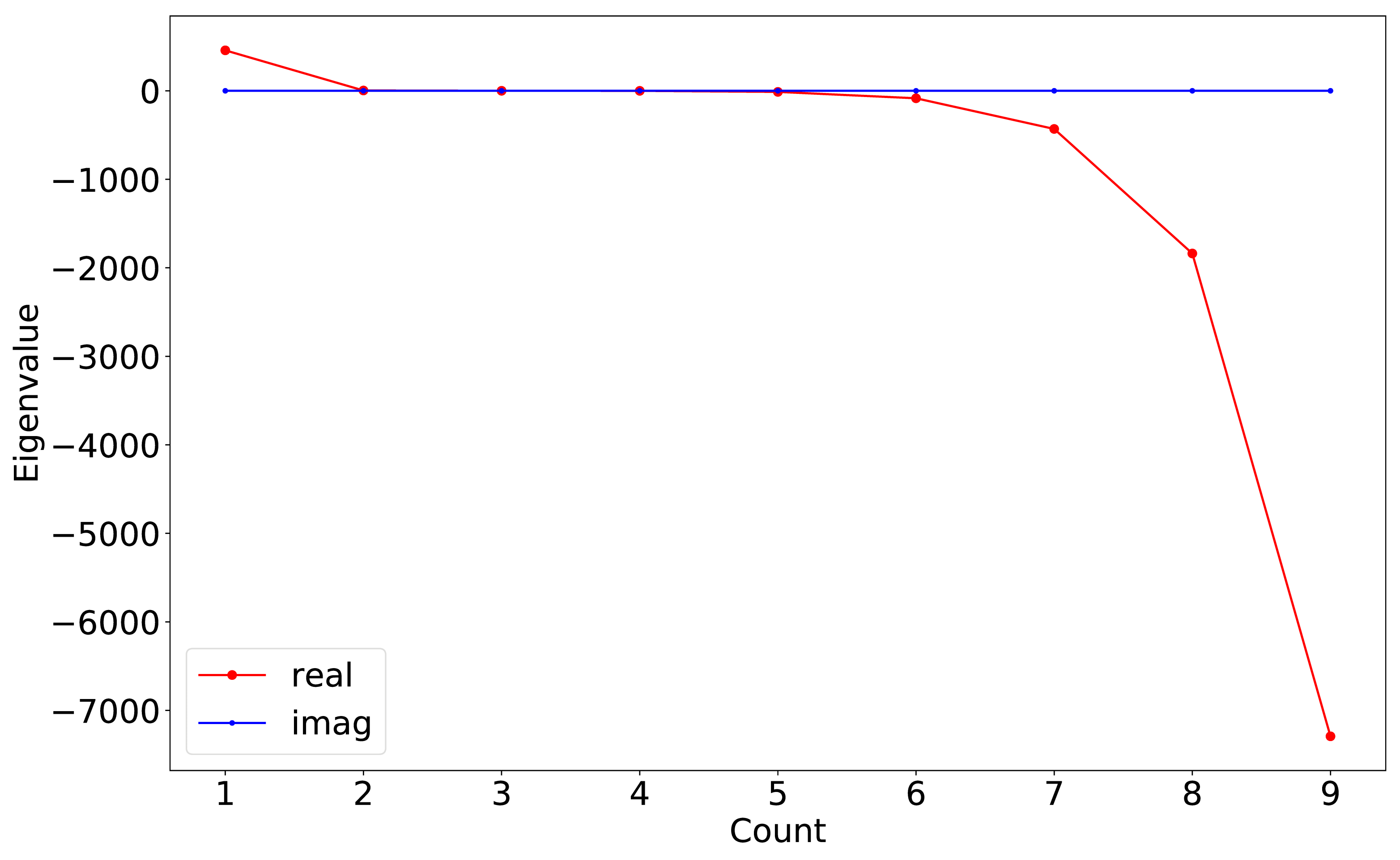
3.2.1. Eigenvalues and Eigenvectors
3.2.2. A Conceptual Model for a Chain Process
3.2.3. Numerical Instability Associated with Large Eigenvalues
3.2.4. Ill-Conditioning Associated with Large Condition Numbers
3.2.5. Solutions in Terms of Eigenvalues and Eigenvectors of the L69 Model
- (1)
- The model is closure-based, physically multiscale, mathematically linear, and numerically ill-conditioned.
- (2)
- The model possesses multiple positive and negative eigenvalues, and, thus, produces growing and decaying components and oscillatory components. However, the model may easily capture unstable modes due to numerical errors and large growth rates.
- (3)
- Since the system is linear and homogeneous, the only equilibrium point is a trivial equilibrium (or critical) point at . The critical point is a saddle point that contains multiple pairs of stable and unstable eigenvectors associated with multiple positive eigenvalues.
3.2.6. Finite Predictability within the L69 Model
Except for the smallest scales retained, where the effect of omitting still smaller scales is noticeable, and the very largest scales, where does not conform to a law, successive differences differ by a factor of about . If one chooses to reevaluate by summing the terms of the sequence , , ⋯, one is effectively summing a truncated geometric series.
3.2.7. A Comparison of Monostability and Multistability
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Lorenz 1963 Model and Its Simplified Systems
- (a)
- and (i.e., the L63 model):The system has a for the onset of chaos.
- (b)
- and (i.e., the simplest Lorenz-type model for chaos):The system has a for the onset of chaos.
- (c)
- (an uncoupled 2D system with ):The above system is briefly analyzed in the main text, yielding spiral sink solutions.
- (d)
- (i.e., the non-dissipative L63 model with ):
- (e)
- No nonlinear term in Equation (A11) (i.e., a linear system with ):The above system represents the most fundamental 2nd order ODE with stable and unstable solutions.
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Predictability: Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? In Proceedings of the 139th Meeting of AAAS Section on Environmental Sciences, New Approaches to Global Weather, GARP, AAAS, Cambridge, MA, USA, 29 December 1972. [Google Scholar]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993; 227p. [Google Scholar]
- Lighthill, J. The recently recognized failure of predictability in Newtonian dynamics. Proc. R. Soc. Lond. A 1986, 407, 35–50. [Google Scholar]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Wu, M.-L. African Easterly Waves in 30-day High-resolution Global Simulations: A Case Study during the 2006 NAMMA Period. Geophys. Res. Lett. 2010, 37, L18803. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.-W.; Tao, W.-K.; Green, B. Coupling Advanced Modeling and Visualization to Improve High-Impact Tropical Weather Prediction(CAMVis). IEEE Comput. Sci. Eng. (CiSE) 2011, 13, 56–67. [Google Scholar] [CrossRef]
- Shen, B.-W. On the predictability of 30-day global mesoscale simulations of multiple African easterly waves during summer 2006: A view with a generalized Lorenz model. Geosciences 2019, 9, 281. [Google Scholar] [CrossRef] [Green Version]
- Judt, F. Atmospheric Predictability of the Tropics, Middle Latitudes, and Polar Regions Explored through Global Storm-Resolving Simulations. J. Atmos. Sci. 2020, 77, 257–276. [Google Scholar] [CrossRef]
- Carroll, M. Predictability Limit: Scientists Find Bounds of Weather Forecasting. 2019. Available online: https://www.sciencedaily.com/releases/2019/04/190415154722.htm (accessed on 26 April 2022).
- Shen, B.-W. Aggregated negative feedback in a generalized Lorenz model. Int. J. Bifurc. Chaos 2019, 29, 1950037. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.-W.; Reyes, T.; Faghih-Naini, S. Coexistence of chaotic and non-chaotic orbits in a new nine-dimensional Lorenz model. In 11th Chaotic Modeling and Simulation International Conference; Springer Proceedings in Complexity; Skiadas, C., Lubashevsky, I., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Reyes, T.; Shen, B.-W. A recurrence analysis of chaotic and non-chaotic solutions within a generalized nine-dimensional Lorenz model. Chaos Solitons Fractals 2019, 125, 1–12. [Google Scholar] [CrossRef]
- Cui, J.; Shen, B.-W. A Kernel Principal Component Analysis of Coexisting Attractors within a Generalized Lorenz Model. Chaos Solitons Fractals 2021, 146, 110865. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is weather chaotic? coexistence of chaos and order within a generalized Lorenz model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. Available online: https://journals.ametsoc.org/view/journals/bams/102/1/BAMS-D-19-0165.1.xml (accessed on 29 January 2021). [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R.; Reyes, T.A. Is Weather Chaotic? Coexisting Chaotic and Non-Chaotic Attractors within Lorenz Models. In The 13th Chaos International Conference CHAOS 2020; Springer Proceedings in Complexity; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Curry, J.H. Generalized Lorenz Systems. Commun. Math. Phys. 1978, 60, 193–204. [Google Scholar] [CrossRef]
- Curry, J.H.; Herring, J.R.; Loncaric, J.; Orszag, S.A. Order and disorder in two- and three-dimensional Benard convection. J. Fluid Mech. 1984, 147, 1–38. [Google Scholar] [CrossRef]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Applied Mathematical Sciences; Springer: New York, NY, USA, 1982; 269p. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983; 459p. [Google Scholar]
- Roy, D.; Musielak, Z.E. Generalized Lorenz models and their routes to chaos. I. energy-conserving vertical mode truncations. Chaos Soliton. Fract. 2007, 32, 1038–1052. [Google Scholar] [CrossRef]
- Hirsch, M.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos, 3rd ed.; Academic Press: Waltham, MA, USA, 2013; 432p. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westpress View: Boulder, CO, USA, 2015; 513p. [Google Scholar]
- Faghih-Naini, S.; Shen, B.-W. Quasi-periodic in the five-dimensional non-dissipative Lorenz model: The role of the extended nonlinear feedback loop. Int. J. Bifurc. Chaos 2018, 28, 1850072. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.-W. Nonlinear feedback in a five-dimensional Lorenz model. J. Atmos. Sci. 2014, 71, 1701–1723. [Google Scholar] [CrossRef]
- Shen, B.-W. Nonlinear feedback in a six-dimensional Lorenz Model. Impact of an additional heating term. Nonlin. Processes Geophys. 2015, 22, 749–764. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.-W. Hierarchical scale dependence associated with the extension of the nonlinear feedback loop in a seven-dimensional Lorenz model. Nonlin. Processes Geophys. 2016, 23, 189–203. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.-W. On an extension of the nonlinear feedback loop in a nine-dimensional Lorenz model. Chaotic Modeling Simul. (CMSIM) 2017, 2, 147–157. [Google Scholar]
- Shen, B.-W. On periodic solutions in the non-dissipative Lorenz model: The role of the nonlinear feedback loop. Tellus A 2018, 70, 1471912. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.-W. Homoclinic Orbits and Solitary Waves within the non-dissipative Lorenz Model and KdV Equation. Int. J. Bifurc. Chaos 2020, 30, 15. [Google Scholar] [CrossRef]
- Shen, B.-W. Solitary Waves, Homoclinic Orbits, and Nonlinear Oscillations within the non-dissipative Lorenz Model, the inviscid Pedlosky Model, and the KdV Equation. In The 13th Chaos International Conference CHAOS 2020; Springer Proceedings in Complexity; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Rotunno, R.; Snyder, C. A generalization of Lorenz’s model for the predictability of flows with many scales of motion. J. Atmos. Sci. 2008, 65, 1063–1076. [Google Scholar] [CrossRef]
- Durran, D.R.; Gingrich, M. Atmospheric predictability: Why atmospheric butterflies are not of practical importance. J. Atmos. Sci. 2014, 71, 2476–2478. [Google Scholar] [CrossRef]
- Leith, C.E. Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 1971, 28, 145–161. [Google Scholar] [CrossRef] [Green Version]
- Leith, C.E.; Kraichnan, R.H. Predictability of turbulent flows. J. Atmos. Sci. 1972, 29, 1041–1058. [Google Scholar] [CrossRef]
- Holmes, P. Can dynamical systems approach turbulence. In Whither Turbulence? Turbulence at the Crossroads; Lecture Notes in Physics; Lumley, J.L., Ed.; Springer: Berlin/Heidelberg, Germany, 1990; Volume 357. [Google Scholar]
- Bohr, T.; Jensen, M.; Paladin, G.; Vulpiani, A. Dynamical Systems Approach to Turbulence; Cambridge Nonlinear Science Series; Cambridge University Press: Cambridge, CA, USA, 1998. [Google Scholar] [CrossRef]
- Saltzman, B. Finite amplitude free convection as an initial value problem. J. Atmos. Sci. 1962, 19, 329–341. [Google Scholar] [CrossRef] [Green Version]
- Pedlosky, J. Finite-amplitude baroclinic waves with small dissipation. J. Atmos. Sci. 1971, 28, 587–597. [Google Scholar] [CrossRef]
- Pedlosky, J. Limit cycles and unstable baroclinic waves. J. Atmos. Sci. 1972, 29, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer: New York, NY, USA, 1987; 710p. [Google Scholar]
- Pedlosky, J. The Effect of Beta on the Downstream Development of Unstable, Chaotic Baroclinic Waves. J. Phys. Oceanogr. 2019, 49, 2337–2343. [Google Scholar] [CrossRef] [Green Version]
- Pedlosky, J.; Frenzen, C. Chaotic and periodic behavior of finite-amplitude baroclinic waves. J. Atmos. Sci. 1980, 37, 1177–1196. [Google Scholar] [CrossRef] [Green Version]
- Lesieur, M. Turbulence in Fluids, 4th ed.; Springer: Berlin, Germany, 2008; 558p. [Google Scholar]
- Orszag, S.A. Analytical theories of turbulence. J. Fluid Mech. 1970, 41, 363–386. [Google Scholar] [CrossRef]
- Shen, B.-W. Lecture Slides for Linearization Theorems. Course Mater. Math. 2017. [Google Scholar] [CrossRef]
- Leung, T.Y.; Leutbecher, M.; Reich, S.; Shepherd, T.G. Atmospheric Predictability: Revisiting the Inherent Finite-Time Barrier. J. Atmos. Sci. 2019, 76, 3883–3892. [Google Scholar] [CrossRef]
- Lucarini, V.; Bodai, T. Global stability properties of the climate: Melancholia states, invariant measures, and phase transitions. Nonlinearity 2020, 33, R59. [Google Scholar] [CrossRef]
- Boyce, W.E.; Diprima, R.C. Elementary Differential Equations, 10th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Alligood, K.; Saucer, T.; Yorke, J. Chaos An Introduction to Dynamical Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. (Ser. 5) 1895, 39, 422–433. [Google Scholar] [CrossRef]
- Lighthill, J. Waves in Fluids; Cambridge University Press: Cambridge, UK, 1978; 504p. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons, Inc.: New York, NY, USA, 1974; 636p. [Google Scholar]
- Haberman, R. Applied Partial Differential Equations, with Fourier Series and Boundary Valule Problems, 5th ed.; Pearson Education, Inc.: Hoboken, NJ, USA, 2013; 756p. [Google Scholar]
- Jordan, D.W.; Smith, S. Nonlinear Ordinary Differential Equations. An Introduction for Scientists and Engineers, 4th ed.; Oxford University Press: New York, NY, USA, 2007; 560p. [Google Scholar]
- Shen, B.-W. Is Weather Chaotic? Multistability, Multiscale Instability, and Predictability within Lorenz Models; Oxford University: Oxford, UK, 11 October 2021. [Google Scholar] [CrossRef]
- Balmforth, N.J. Solitary waves and homoclinic orbits. Annu. Rev. Fluid Mech. 1995, 27, 335–373. [Google Scholar] [CrossRef]
- Boyd, J.P. Dynamical methodology: Solitary waves. In Encyclopedia of Atmospheric Sciences, 2nd ed.; Academic Press: San Diego, CA, USA, 2015; pp. 417–422. [Google Scholar]
- Guckenheimer, J.; Williams, R.F. Structural stability of Lorenz attractors. Publ. Math. IHES 1979, 50, 59–72. [Google Scholar] [CrossRef] [Green Version]
- Slingo, J.; Palmer, T. Uncertainty in weather and climate prediction. Philos. Trans. R. Soc. 2011, 369A, 4751–4767. [Google Scholar] [CrossRef]
- Nese, J.M. Quantifying local predictability in phase space. Physica D 1989, 35, 237–250. [Google Scholar] [CrossRef]
- Zeng, X.; Pielke, R.A., Sr.; Eykholt, R. Chaos theory and its applications to the atmosphere. Bull. Am. Meteor. Soc. 1993, 74, 631–644. [Google Scholar] [CrossRef]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in Systems with Many Characteristic Times: The Case of Turbulence. Phys. Rev. E 1996, 53, 2337–2349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drazin, P.G. Nonlinear Systems; Cambridge University Press: New York, NY, USA, 1992; p. 333. [Google Scholar]
- Eckhardt, B.; Yao, D. Local Lyapunov exponents in chaotic systems. Physica D 1993, 65, 100–108. [Google Scholar] [CrossRef]
- Lorenz, E.N. 1996 “Predictability—A Problem Partly Solved” (PDF). Seminar on Predictability, Vol. I, ECMWF. Available online: https://www.ecmwf.int/en/elibrary/10829-predictability-problem-partly-solved (accessed on 20 April 2022).
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.M. Lyapunov Characteristic Exponents for Smooth Dynamical Systems and for Hamiltonian Systems; A Method for Computing All of Them. Part 1: Theory. 1980. Available online: https://link.springer.com/article/10.1007/BF02128236 (accessed on 20 April 2022).
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003; 528p, Available online: http://sprott.physics.wisc.edu/chaos/lyapexp.htm (accessed on 26 April 2022).
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; p. 1113. [Google Scholar]
- Lewis, J.; Lakshmivarahan, S.; Dhall, S. Dynamic Data Assimilation: A Least Squares Approach; Cambridge University Press: Cambridge, UK, 2006; 654p. [Google Scholar]
- Palmer, T.N.; Doring, A.; Seregin, G. The real butterfly effect. Nonlinearity 2014, 27, R123–R141. [Google Scholar] [CrossRef]
- Palmer, T. The Butterfly Effect—What Does It Really Signify? 2017. Available online: https://www.youtube.com/watch?v=vkQEqXAz44I&t=1711s (accessed on 26 April 2022).
- Lorenz, E. The predictability of hydrodynamic flow. Trans. N. Y. Acad. Sci. 1963, 25, 409–432. [Google Scholar] [CrossRef]
- Schuster, H.G.; Just, W. Deterministic Chaos: An Introduction, 4th ed.; John Wiley & Sons, Inc.: Weinheim, Germany, 2005; p. 287. [Google Scholar] [CrossRef]



| Characteristics | Solutions | Critical Points | Remarks |
|---|---|---|---|
| non-oscillatory | saddle | monotonic | |
| oscillatory () | |||
| center | periodic | ||
| spiral source | |||
| spiral sink |
| Python | Matlab | Remarks | |
|---|---|---|---|
| Table 1 of RS08 | 8.319352 × 10 | 8.3194 × 10 | 2DV dynamics |
| Table 2 of RS08 | 8.446532 × 10 | 8.4465 × 10 | vs. Lorenz (1969) |
| Table 3 of RS08 | 2.791518 × 10 | 2.7915 × 10 | “unlimited predictability” |
| Table 4 of RS08 | 2.146269 × 10 | 2.1463 × 10 | SQG dynamics |
| Table A1 of DG14 | 7.967004 × 10 | 7.9670 × 10 | vs. Table 1 of RS08 |
| Table A2 of DG14 * | 9.767672 × 10 | 9.7677 × 10 | vs. Table 4 of RS08 |
| (1) The L63 Model | (2) The Geometric Model |
| (3) The Non-dissipative L63 Model | (4) The L69 Model |
| , | |
| : constant. | : matrix, |
| : a vector for N state variables. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X. One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models. Atmosphere 2022, 13, 753. https://doi.org/10.3390/atmos13050753
Shen B-W, Pielke RA Sr., Zeng X. One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models. Atmosphere. 2022; 13(5):753. https://doi.org/10.3390/atmos13050753
Chicago/Turabian StyleShen, Bo-Wen, Roger A. Pielke, Sr., and Xubin Zeng. 2022. "One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models" Atmosphere 13, no. 5: 753. https://doi.org/10.3390/atmos13050753
APA StyleShen, B.-W., Pielke, R. A., Sr., & Zeng, X. (2022). One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models. Atmosphere, 13(5), 753. https://doi.org/10.3390/atmos13050753








