Oscillatory Signatures in the Raindrop Motion Relative to the Air Medium with Terminal Velocity
Abstract
1. Introduction
2. Current State of Research
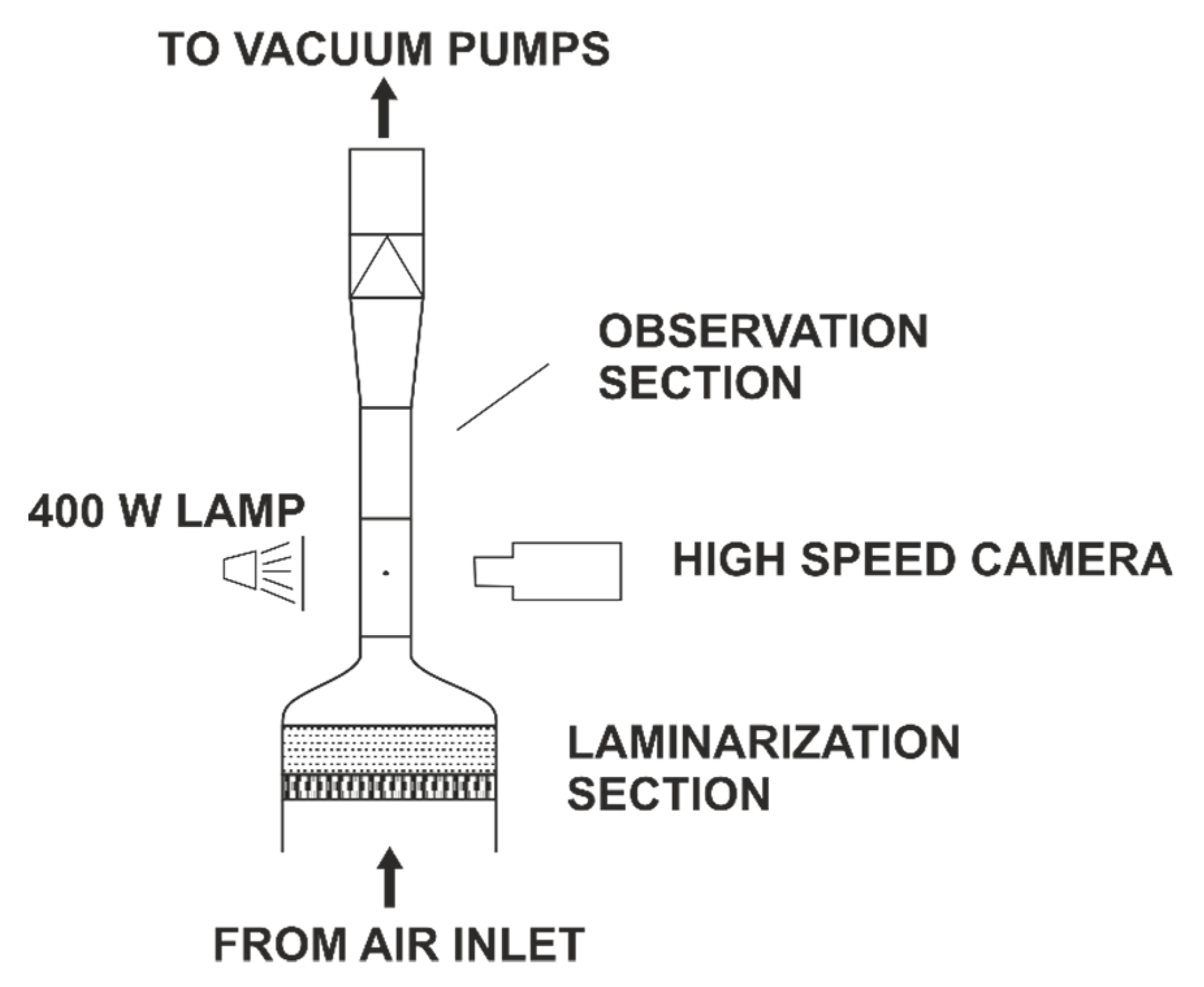
3. Experimental Setup
4. Automatic Detection of Droplets in Images
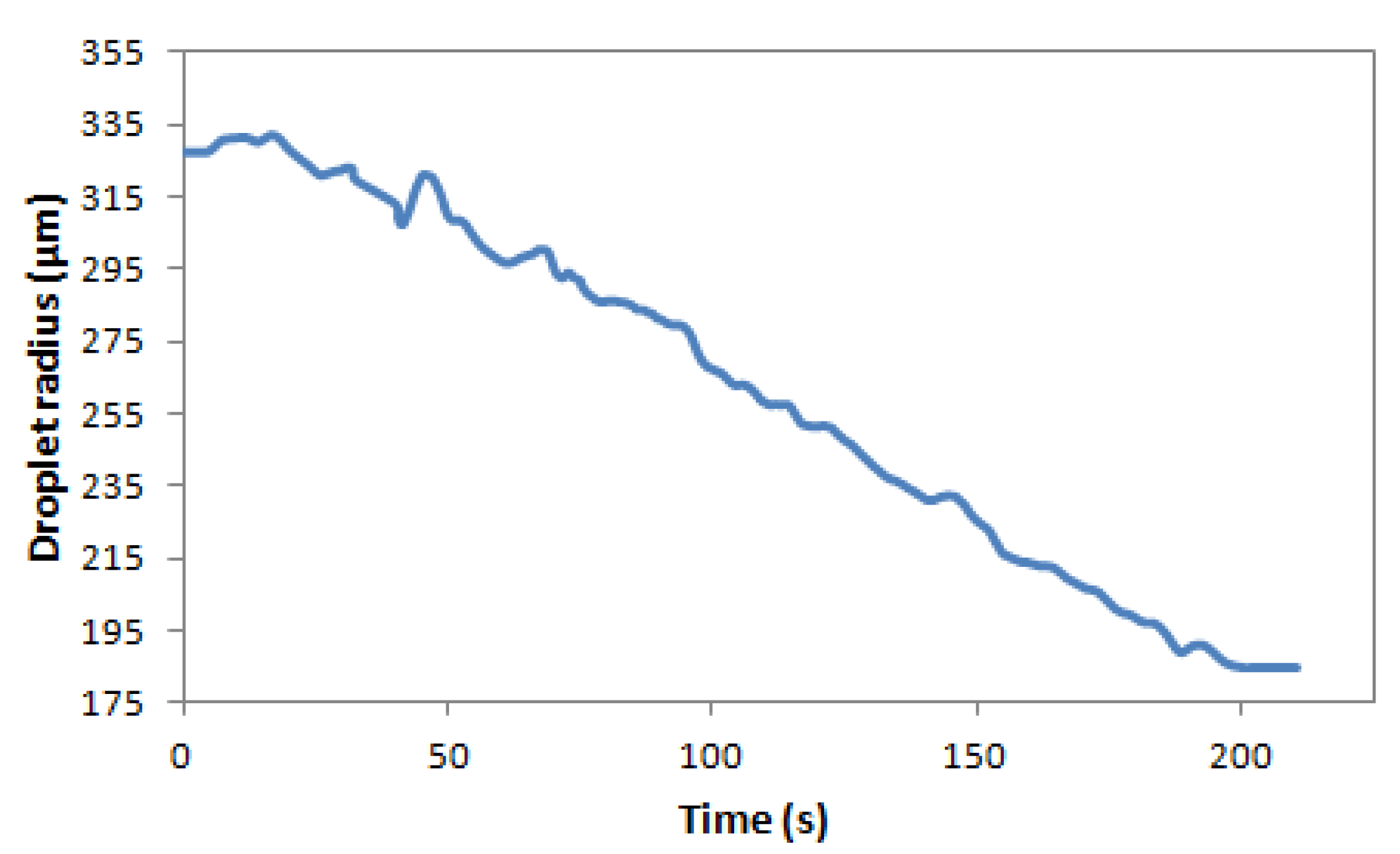
5. Data Processing
6. Fourier Analysis
6.1. Applying of the Discrete Fast Fourier Transform
6.2. Applying of the Hilbert Transform for Instantaneous Frequency Analysis
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Newton, I. The Mathematical Principles of Natural Philosophy; Motte, A., Translator; Daniel Adee: New-York, NY, USA, 1846. [Google Scholar]
- Sakamoto, H.; Haniu, H. A Study on Vortex Shedding from Spheres in a Uniform Flow. J. Fluids Eng. 1990, 112, 386. [Google Scholar] [CrossRef]
- Prządka, A.; Miedzik, J.; Gumowski, K.; Goujon-Durand, S.; Wesfreid, J.E. The wake behind the sphere; analysis of vortices during transition from steadiness to unsteadiness. Arch. Mech. 2008, 60, 467. [Google Scholar]
- Wang, P.K.; Chueh, C.-C. A numerical study on the ventilation coefficients of falling lobed hailstones. Atmos. Res. 2020, 234, 104737. [Google Scholar] [CrossRef]
- Bearman, P.W. Vortex Shedding from Oscillating Bluff Bodies. Ann. Rev. Fluid Mech. 1984, 16, 195. [Google Scholar] [CrossRef]
- Franzini, G.R.; Fujarra, A.L.C.; Meneghini, J.R.; Korkischko, I.; Franciss, R. Experimental investigation of Vortex-Induced Vibration on rigid, smooth and inclined cylinders. J. Fluid. Struct. 2009, 25, 742. [Google Scholar] [CrossRef]
- Ali, U.; Islam, M.; Janajreh, I.; Fatt, Y.; Alam, M. Flow-Induced Vibrations of Single and Multiple Heated Circular Cylinders: A Review. Energies 2021, 14, 8496. [Google Scholar] [CrossRef]
- Atkinson, J.; Chartier, Y.; Pessoa-Silva, C.L.; Jensen, P.; Li, Y.; Seto, W.-H. Natural Ventilation for Infection Control in Health-Care Settings; World Health Organisation: Geneva, Switzerland, 2009. Available online: https://www.ncbi.nlm.nih.gov/books/NBK143284/ (accessed on 20 May 2022).
- Dombrovsky, L.A.; Fedorets, A.A.; Bormashenko, E.; Nosonovsky, M. Modeling evaporation of water droplets carrying virus particles. Atmosphere 2020, 11, 965. [Google Scholar] [CrossRef]
- Joung, Y.S.; Ge, Z.; Buie, C.R. Bioaerosol generation by raindrops on soil. Nat. Commun. 2017, 8, 14668. [Google Scholar] [CrossRef]
- Joung, Y.S.; Buie, C.R. Aerosol generation by raindrop impact on soil. Nat. Commun. 2015, 6, 6083. [Google Scholar] [CrossRef]
- Kim, S.; Park, H.; Gruszewski, H.A.; Schmale, D.G.; Jung, S. Vortex-induced dispersal of a plant pathogen by raindrop impact. Proc. Natl. Acad. Sci. USA 2019, 116, 4917. [Google Scholar] [CrossRef]
- Nath, S.; Ahmadi, S.F.; Gruszewski, H.A.; Budhiraja, S.; Bisbano, C.E.; Jung, S.; Schmale, D.G.; Boreyko, J.B. ‘Sneezing’ plants: Pathogen transport via jumping-droplet condensation. J. R. Soc. Interface 2019, 16, 20190243. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, R.; Gruszewski, H.A.; Bilyeu, L.T.; David, G.; Schmale III, D.G.; Boreyko, J.B. Synergistic dispersal of plant pathogen spores by jumping-droplet condensation and wind. Proc. Natl. Acad. Sci. USA 2021, 118, e2106938118. [Google Scholar] [CrossRef] [PubMed]
- Wasserfall, J.; Figueiredo, P.; Kneer, R.; Rohlfs, W.; Pischke, P. Coalescence-induced droplet jumping on superhydrophobic surfaces: Effects of droplet mismatch. Phys. Rev. Fluids 2017, 2, 123601. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, M.; Zheng, Y.; Cheng, L.; Zhang, J.; Tee, C.A.T.H. Coalescence-Induced Droplet Jumping. Langmuir 2021, 37, 983. [Google Scholar] [CrossRef]
- Benzerara, K. Bioprecipitation. In Encyclopedia of Astrobiology; Springer: Berlin/Heidelberg, Germany, 2011; p. 200. [Google Scholar] [CrossRef]
- Baker, M.B.; Peter, T. Small-scale cloud processes and climate. Nature 2008, 451, 299. [Google Scholar] [CrossRef]
- Twomey, S. The Influence of Pollution on the Shortwave Albedo of Clouds. J. Atmos. Sci. 1977, 34, 1149. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, Cloud Microphysics, and Fractional Cloudiness. Science 1989, 245, 1227. [Google Scholar] [CrossRef]
- Venter, Z.S.; Aunan, K.; Chowdhury, S.; Lelieveld, J. COVID-19 lockdowns cause global air pollution declines. Proc. Natl. Acad. Sci. USA 2020, 117, 18984. [Google Scholar] [CrossRef]
- Titov, D.V.; Ignatiev, N.I.; McGoulgrick, K.; Wilquet, V.; Wilson, C.F. Clouds and Hazes of Venus. Space Sci. Rev. 2018, 214, 126. [Google Scholar] [CrossRef]
- Walton, L.R.; Walker, J.N. The Trajectory of an Evaporating Water Droplet Falling in an Airstream. Trans. ASAE 1970, 13, 0158. [Google Scholar] [CrossRef]
- Marchant, J.A. Calculation of spray droplet trajectory in a moving airstream. J. Agric. Eng. Res. 1977, 22, 93. [Google Scholar] [CrossRef]
- Oleskiw, M.M.; Grandia, K.L.; Rudolph, R.C. Airflow and droplet trajectory model to determine sensor placement on cloud physics research aircraft. J. Weather Mod. 1985, 17, 45. [Google Scholar]
- Finstad, K.J.; Lozowski, E.P.; Gates, E.M. A Computational Investigation of Water Droplet Trajectories. J. Atmos. Ocean. Technol. 1988, 5, 160. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibration; Krieger Publishing Company: Malabar, FL, USA, 2001. [Google Scholar]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluid. Struct. 2004, 19, 389. [Google Scholar] [CrossRef]
- Ern, P.; Risso, F.; Fabre, D.; Magnaudet, J. Wake-Induced Oscillatory Paths of Bodies Freely Rising or Falling in Fluids. Annu. Rev. Fluid Mech. 2012, 44, 97. [Google Scholar] [CrossRef]
- Tiwari, S.S.; Pal, E.; Bale, S.; Minocha, N.; Patwardhan, A.W.; Nandakumar, K.; Joshi, J.B. Flow past a single stationary sphere, 2. Regime mapping and effect of external disturbances. Powder Technol. 2020, 365, 215. [Google Scholar] [CrossRef]
- Beard, K.V.; Ochs, H.T.; Kubesh, R.J. Natural oscillations of small raindrops. Nature 1989, 342, 408. [Google Scholar] [CrossRef]
- Szakáll, M.; Mitra, S.K.; Diehl, K.; Borrmann, S. Shapes and oscillations of falling raindrops—A review. Atmos. Res. 2010, 97, 416. [Google Scholar] [CrossRef]
- Zhang, B.; Ling, Y.; Tsai, P.-H.; Wang, A.-B.; Popinet, S.; Zaleski, S. Short-term oscillation and falling dynamics for a water drop dripping in quiescent air. Phys. Rev. Fluids 2019, 4, 123604. [Google Scholar] [CrossRef]
- Miedzik, J.; Gumowski, K.; Goujon-Durand, S.; Wesfreid, J.E.; Bouchet, G. Wake behind a sphere in early transitional regimes. In Fifth Conference on Bluff Body Wakes and Vortex-Induced Vibrations; Costa de Sauípe: Bahia, Brazil, 2007. [Google Scholar]
- Horowitz, M.; Williamson, C.H.K. The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 2010, 651, 251. [Google Scholar] [CrossRef]
- Szakáll, M.; Diehl, K.; Mitra, S.K.; Borrmann, S. A Wind Tunnel Study on the Shape, Oscillation, and Internal Circulation of Large Raindrops with Sizes between 2.5 and 7.5 mm. J. Atmos. Sci. 2009, 66, 755. [Google Scholar] [CrossRef]
- Szakáll, M.; Urbich, I. Wind tunnel study on the size distribution of droplets after collision induced breakup of levitating water drops. Atmos. Res. 2018, 213, 51. [Google Scholar] [CrossRef]
- Chang, K.; Bench, J.; Brege, M.; Cantrell, W.; Chandrakar, K.; Ciochetto, D.; Mazzoleni, C.; Mazzoleni, L.R.; Niedermeier, D.; Shaw, R.A. A Laboratory Facility to Study Gas–Aerosol–Cloud Interactions in a Turbulent Environment: The Π Chamber. Bull. Am. Meteorol. Soc. 2016, 97, 2343. [Google Scholar] [CrossRef]
- Lenard, P. Rain. Q. J. R. Meteorol. Soc. 1905, 31, 62. [Google Scholar] [CrossRef]
- Davis, E.J. A History of Single Aerosol Particle Levitation. Aerosol Sci. Technol. 1997, 26, 212–254. [Google Scholar] [CrossRef]
- Andrade, M.A.B.; Pérez, N.; Adamowski, J.C. Experimental study of the oscillation of spheres in an acoustic levitator. J. Acoust. Soc. Am. 2014, 136, 1518–1529. [Google Scholar] [CrossRef]
- Moore, J.; Martin, L.L.; Maayani, S.; Kim, K.H.; Chandrahalim, H.; Eichenfield, M.; Martin, I.R.; Carmon, T. Regular oscillations and random motion of glass microspheres levitated by a single optical beam in air. Opt. Express 2016, 24, 2850–2857. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.B.; Clark, B.C. Feasibility Study for Gas-Grain Simulation Facility: NASA Contractor Report 177468; Ames Research Center, Martin Marietta Astronautics Group: Moffett Field, CA, USA, 1987. [Google Scholar]
- Gitterman, M. The Noisy Oscillator: The First Hundred Years from Einstein until Now; World Scientific: Singapore, 2005. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering. World Scientific: Singapore, 2017. [Google Scholar] [CrossRef]
- Milne-Thomson, L.M. Theoretical Hydrodynamics; The Macmillan And Company: London, UK, 1962; p. 464. Available online: https://archive.org/details/theoreticalhydro033283mbp/page/n493 (accessed on 22 May 2022).
- McDonald, K.T. Levitating beachballs. Am. J. Phys. 2000, 68, 388. [Google Scholar] [CrossRef]
- Fedorets, A.A. Droplet cluster. J. Exp. Theor. Phys. Lett. 2004, 79, 372. [Google Scholar] [CrossRef]
- Gabyshev, D.N. Damping Oscillations of Microdroplets of a Droplet Cluster in an External Electric Field. Phys. Wave Phenom. 2018, 26, 221. [Google Scholar] [CrossRef]
- Andreev, S.N.; Gabyshev, D.N. Oscillatory Motion of Microdroplets of a Droplet Cluster in a Linearly Nonuniform Electric Field. Bull. Lebedev Phys. Inst. 2018, 45, 257. [Google Scholar] [CrossRef]
- Fedorets, A.A.; Aktaev, N.E.; Gabyshev, D.N.; Bormashenko, E.; Dombrovsky, L.A.; Nosonovsky, M. Oscillatory Motion of a Droplet Cluster. J. Phys. Chem. C 2019, 123, 23572. [Google Scholar] [CrossRef]
- Fedorets, A.A.; Gabyshev, D.N.; Shcherbakov, D.; Bormashenko, E.; Dombrovsky, L.A.; Nosonovsky, M. Vertical oscillations of droplets in small droplet clusters. Colloids Surf. A 2021, 628, 127271. [Google Scholar] [CrossRef]
- Fedorets, A.A.; Frenkel, M.; Legchenkova, I.; Shcherbakov, D.V.; Dombrovsky, L.A.; Nosonovsky, M.; Bormashenko, E. Self-Arranged Levitating Droplet Clusters: A Reversible Transition from Hexagonal to Chain Structure. Langmuir 2019, 35, 15330. [Google Scholar] [CrossRef]
- Govardhan, R.N.; Williamson, C.H.K. Vortex-induced vibrations of a sphere. J. Fluid Mech. 2005, 531, 11. [Google Scholar] [CrossRef]
- Rajamuni, M.M.; Thompson, M.C.; Hourigan, K. Transverse flow-induced vibrations of a sphere. J. Fluid Mech. 2018, 837, 931. [Google Scholar] [CrossRef]
- Chizfahm, A.; Joshi, V.; Jaiman, R. Transverse flow-induced vibrations of a sphere in the proximity of a free surface: A numerical study. J. Fluids Struct. 2021, 101, 103224. [Google Scholar] [CrossRef]
- Hassanzadeh, R.; Sahin, B.; Ozgoren, M. Large eddy simulation of free-surface effects on the wake structures downstream of a spherical body. Ocean. Eng. 2012, 54, 213. [Google Scholar] [CrossRef]
- Chizfahm, A.; Jaiman, R. Data-driven stability analysis and near-wake jet control for the vortex-induced vibration of a sphere. Phys. Fluids 2021, 33, 044104. [Google Scholar] [CrossRef]
- Li, Z.; Gao, N. Experimental Study of Flow Around a Rotating Sphere at a Moderate Reynolds Number. In Proceedings of the ASME 2018 5th Joint US-European Fluids Engineering Division Summer Meeting, Montreal, QC, Canada, 15–20 July 2018. [Google Scholar] [CrossRef]
- McQueen, T.; Zhao, J.; Sheridan, J.; Thompson, M.C. Feedback control of flow-induced vibration of a sphere. J. Fluid Mech. 2020, 889, A30. [Google Scholar] [CrossRef]
- David, T.; Eshbal, L.; Rinsky, V.; van Hout, R. Flow measurements in the near wake of a smooth sphere and one mimicking a pine cone. Phys. Rev. Fluids 2020, 5, 074301. [Google Scholar] [CrossRef]
- Goyal, N.; Derksen, J.J. Direct simulations of spherical particles sedimenting in viscoelastic fluids. J. Non-Newton. Fluid Mech. 2012, 183–184, 1–13. [Google Scholar] [CrossRef]
- Amaratunga, M.; Rabenjafimanantsoa, H.A.; Time, R.W. Influence of low-frequency oscillatory motion on particle settling in Newtonian and shear-thinning non-Newtonian fluids. J. Pet. Sci. Eng. 2020, 196, 107786. [Google Scholar] [CrossRef]
- Raaghav, S.K.R.; Poelma, C.; Breugem, W.-P. Path instabilities of a freely rising or falling sphere. Int. J. Multiph. Flow 2022, 153, 104111. [Google Scholar] [CrossRef]
- Gabyshev, D.N.; Fedorets, A.A.; Shcherbakov, D. Vertical Oscillations of Water Droplets in the Supporting Vapour–Air Flow. Phys. Wave Phenom. 2021, 29, 352. [Google Scholar] [CrossRef]
- Vohl, O.; Mitra, S.K.; Wurzler, S.C.; Pruppacher, H.R. A Wind Tunnel Study of the Effects of Turbulence on the Growth of Cloud Drops by Collision and Coalescence. J. Atmos. Sci. 1999, 56, 4088. [Google Scholar] [CrossRef]
- Beard, K.V. Terminal Velocity and Shape of Cloud and Precipitation Drops Aloft. J. Atmos. Sci. 1976, 33, 851. [Google Scholar] [CrossRef]
- Szakáll, M.; Kessler, S.; Diehl, K.; Mitra, S.K.; Borrmann, S. A wind tunnel study of the effects of collision processes on the shape and oscillation for moderate-size raindrops. Atmos. Res. 2014, 142, 67–78. [Google Scholar] [CrossRef]
- Yedlin, M.J.; Margrave, G.F.; Horin, Y.B. Instantaneous frequency computation: Theory and practice. CREWES Res. Rep. 2013, 25, 85. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261. [Google Scholar] [CrossRef]
- Fielder, R.; Thomas, R.H. The unsteady motion of a lamina in an elastico-viscous liquid. Rheol. Acta 1967, 6, 306. [Google Scholar] [CrossRef]
- King, M.J.; Waters, N.D. The unsteady motion of a sphere in an elastico-viscous liquid. J. Phys. D Appl. Phys. 1972, 5, 141. [Google Scholar] [CrossRef]
- Becker, L.E.; McKinley, G.H.; Rasmussen, H.K.; Hassager, O. The unsteady motion of a sphere in a viscoelastic fluid. J. Rheol. 1994, 38, 377–403. [Google Scholar] [CrossRef][Green Version]
- Bouillant, A.; Mouterde, T.; Bourrianne, P.; Lagarde, A.; Clanet, C.; Quéré, D. Leidenfrost wheels. Nat. Phys. 2018, 14, 1188. [Google Scholar] [CrossRef]
- Loitsyanskii, L.G. Mechanics of Liquids and Gases; Pergamon: Oxford, UK, 1966. [Google Scholar]
- Lienhard, J.H. Synopsis of Lift, Drag, and Vortexes Frequency Data for Rigid Circular Cylinders; Washington State University, Technical Extension Service: Pullman, WA, USA, 1966. [Google Scholar]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Martinus Nijhoff Publishers: The Hague, The Netherlands, 1983. [Google Scholar]
- Yoon, D.-H.; Yang, K.-S. Flow-induced forces on two nearby spheres. Phys. Fluids 2007, 19, 098103. [Google Scholar] [CrossRef]
- Pranesha, T.S.; Kamra, A.K. Scavenging of aerosol particles by large water drops: 1. Neutral case. J. Geophys. Res. 1996, 101, 23373. [Google Scholar] [CrossRef]
- Wang, P.K.; Pruppacher, H.R. An Experimental Determination of the Efficiency with Which Aerosol Particles are Collected by Water Drops in Subsaturated Air. J. Atmos. Sci. 1977, 34, 1664. [Google Scholar] [CrossRef]
- Yuan, F.; Gan, F. Evolution of Aerosol Particles in the Rainfall Process via Method of Moments. Abstr. Appl. Anal. 2013, 2013, 709497. [Google Scholar] [CrossRef]
- Gonçalves, F.L.T.; Beheng, K.D.; Massambani, O.; Vautz, W.; Klockow, D. Scavenging processes of atmospheric particulate matter: A numerical modeling of case studies. Rev. Bras. de Meteorol. 2010, 25, 437. [Google Scholar] [CrossRef][Green Version]
- Davies, C.N. Definitive equations for the fluid resistance of spheres. Proc. Phys. Soc. 1945, 57, 259. [Google Scholar] [CrossRef]
- Achenbach, E. Vortex shedding from spheres. J. Fluid Mech. 1974, 62, 209. [Google Scholar] [CrossRef]
- Greenfield, S.M. Rain Scavenging of Radioactive Particulate Matter from the Atmosphere. J. Meteorol. 1957, 14, 115. [Google Scholar] [CrossRef]
- Cherrier, G.; Belut, E.; Gerardin, F.; Tanière, A.; Rimbert, N. Aerosol particles scavenging by a droplet: Microphysical modeling in the Greenfield gap. Atmos. Environ. 2017, 166, 519. [Google Scholar] [CrossRef]
- Cunningham, E. On the Velocity of Steady Fall of Spherical Particles through Fluid Medium. Proc. R. Soc. A Math. Phys. Eng. Sci. 1910, 83, 357. [Google Scholar] [CrossRef]
- Löffler, F. Staubabscheiden; Thieme: Stuttgart, Germany, 1988. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabyshev, D.N.; Szakáll, M.; Shcherbakov, D.V.; Fedorets, A.A.; Dyachkov, S.M. Oscillatory Signatures in the Raindrop Motion Relative to the Air Medium with Terminal Velocity. Atmosphere 2022, 13, 1137. https://doi.org/10.3390/atmos13071137
Gabyshev DN, Szakáll M, Shcherbakov DV, Fedorets AA, Dyachkov SM. Oscillatory Signatures in the Raindrop Motion Relative to the Air Medium with Terminal Velocity. Atmosphere. 2022; 13(7):1137. https://doi.org/10.3390/atmos13071137
Chicago/Turabian StyleGabyshev, Dmitrii N., Miklós Szakáll, Dmitrii V. Shcherbakov, Alexander A. Fedorets, and Sergey M. Dyachkov. 2022. "Oscillatory Signatures in the Raindrop Motion Relative to the Air Medium with Terminal Velocity" Atmosphere 13, no. 7: 1137. https://doi.org/10.3390/atmos13071137
APA StyleGabyshev, D. N., Szakáll, M., Shcherbakov, D. V., Fedorets, A. A., & Dyachkov, S. M. (2022). Oscillatory Signatures in the Raindrop Motion Relative to the Air Medium with Terminal Velocity. Atmosphere, 13(7), 1137. https://doi.org/10.3390/atmos13071137






