Modification of
Abstract
:1. Introduction
2. Materials and Methods
2.1. Considered Modifications of Model
2.1.1. Standard Model
2.1.2. Proposed Form of the Model
2.1.3. Alternative Length-Limited Modification
2.1.4. List of Used Turbulence Parametrizations
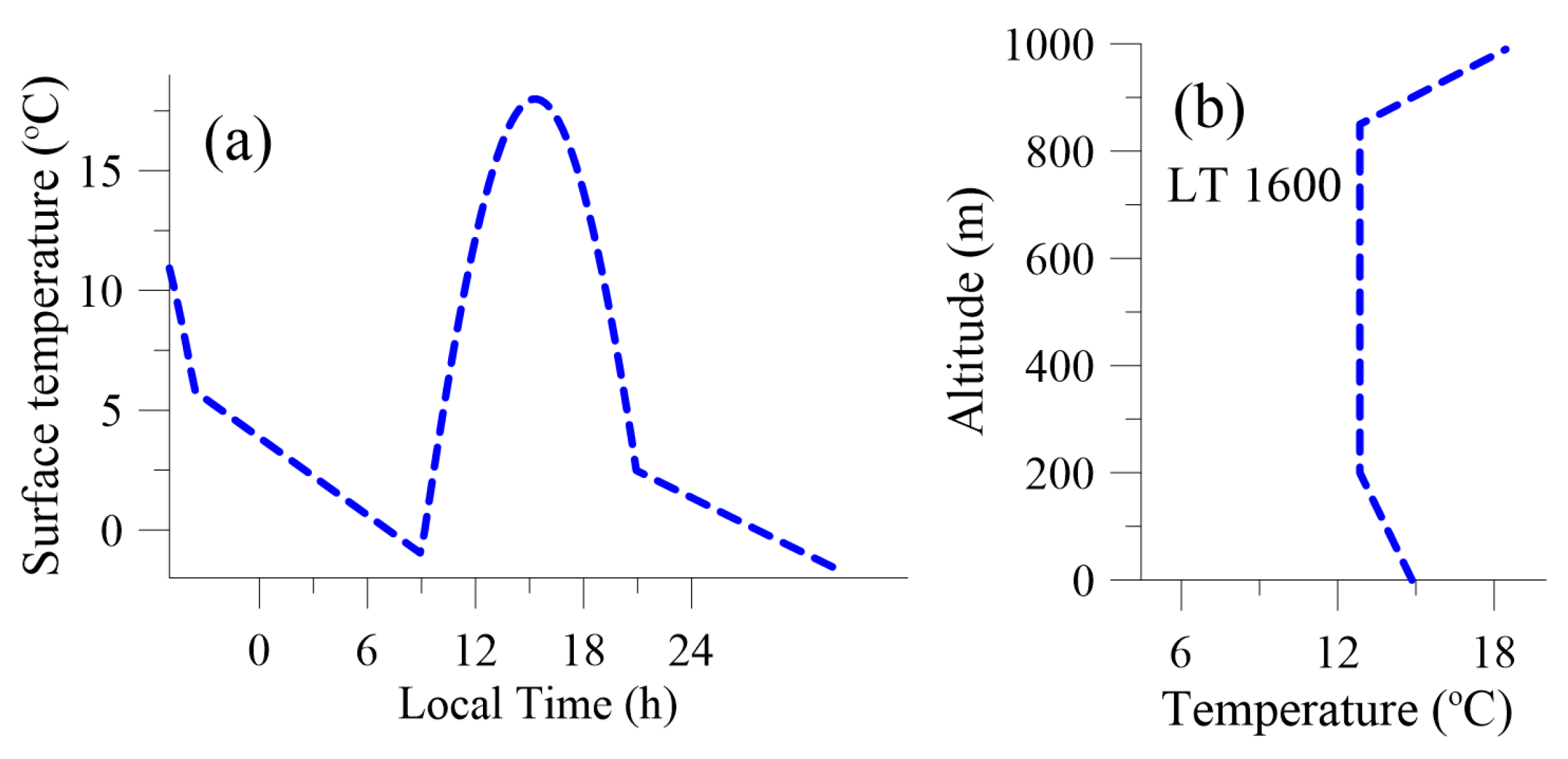
2.2. Single-Cell Formulation for Dry ABL Diurnal Cycle
2.3. Single-Column Formulation
Wall Functions
2.4. Initial and Boundary Conditions and Numerical Details
3. Simulation Results
3.1. Single-Cell Model
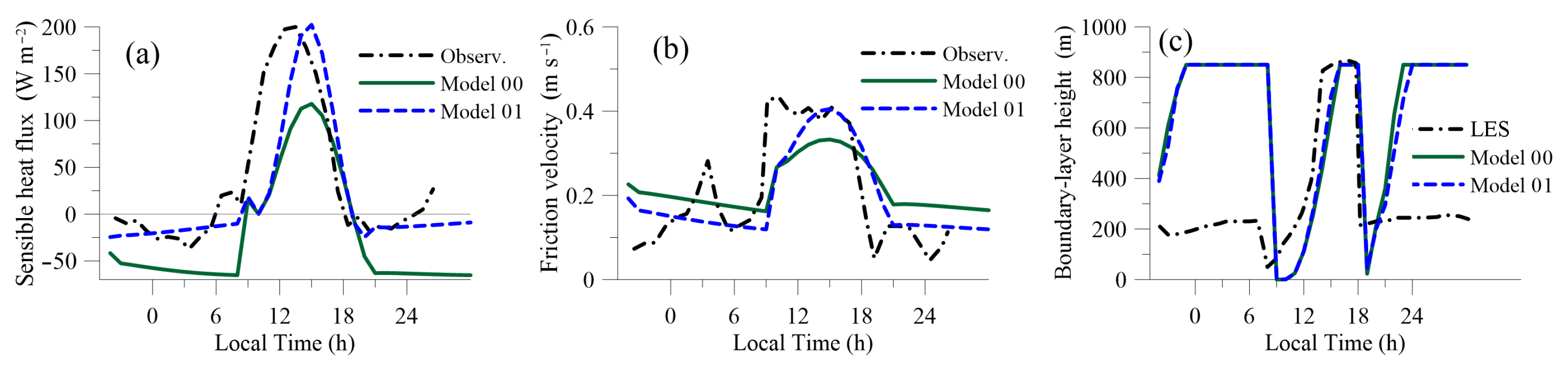
3.2. Single Column Model
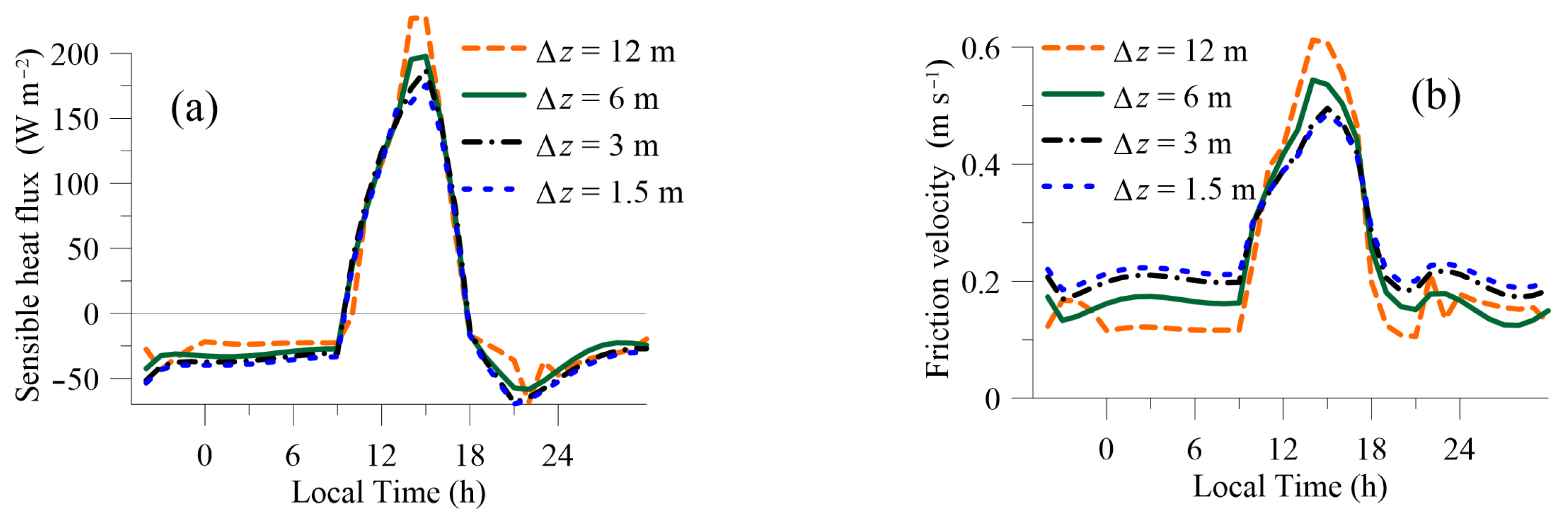
3.2.1. Numerical Resolution Effects
3.2.2. Stable Regime
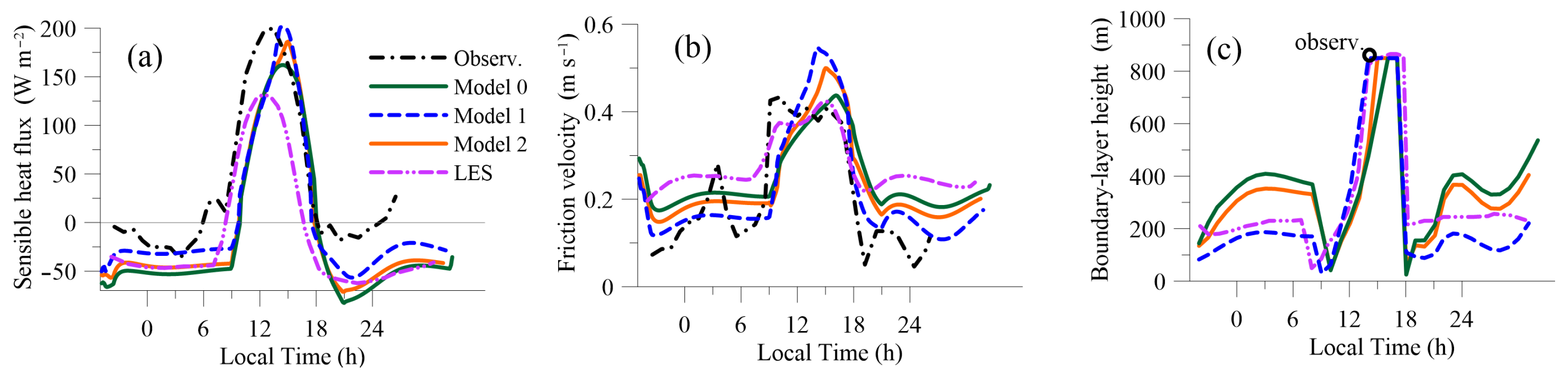
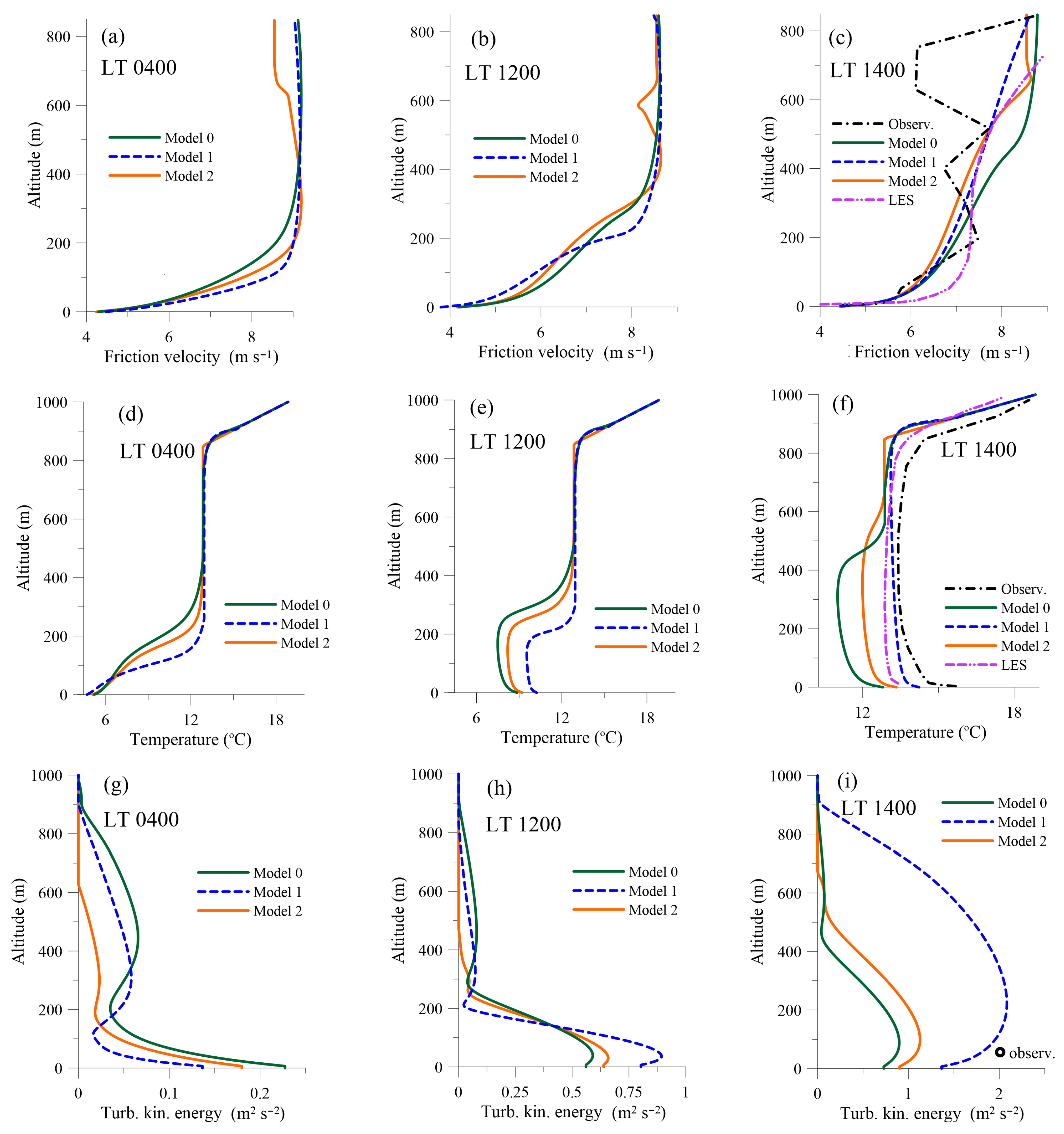
3.3. Morning Transition and Daytime Unstable Conditions
3.4. Evening Transition
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABL | Atmospheric Boundary Layer |
| RANS | Reynolds-Averaged Navier Stokes |
| LES | Large Eddy Simulation |
| TKE | Turbulence Kinetic Energy |
| CASES-99 | Cooperative Atmospheric Surface Exchange Study |
| GABLS | GEWEX Atmospheric Boundary Layer Study |
References
- Monin, A. The atmospheric boundary layer. Annu. Rev. Fluid Mech. 1970, 2, 225–250. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Garratt, J.R. The atmospheric boundary layer. Earth-Sci. Rev. 1994, 37, 89–134. [Google Scholar] [CrossRef]
- Monin, A.; Obukhov, A. Basic laws of turbulent mixing in the atmosphere near the ground. Tr. Geofiz. Inst. Akad. Nauk SSSR 1954, 24, 163–187. [Google Scholar]
- Stoll, R.; Gibbs, J.A.; Salesky, S.T.; Anderson, W.; Calaf, M. Large-eddy simulation of the atmospheric boundary layer. Bound.-Layer Meteorol. 2020, 177, 541–581. [Google Scholar] [CrossRef]
- Van Heerwaarden, C.C.; Mellado, J.P.; De Lozar, A. Scaling laws for the heterogeneously heated free convective boundary layer. J. Atmos. Sci. 2014, 71, 3975–4000. [Google Scholar] [CrossRef]
- Couvreux, F.; Bazile, E.; Rodier, Q.; Maronga, B.; Matheou, G.; Chinita, M.J.; Edwards, J.; van Stratum, B.J.; van Heerwaarden, C.C.; Huang, J.; et al. Intercomparison of large-eddy simulations of the Antarctic boundary layer for very stable stratification. Bound.-Layer Meteorol. 2020, 176, 369–400. [Google Scholar] [CrossRef]
- Van Stratum, B.J. The Influence of Misrepresenting the Nocturnal Boundary Layer on Daytime Convection in Large-Eddy Simulation. Ph.D. Thesis, Universität Hamburg, Hamburg, Germany, 2017. [Google Scholar]
- Hanjalić, K.; Launder, B.E. A Reynolds stress model of turbulence and its application to thin shear flows. J. Fluid Mech. 1972, 52, 609–638. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci. 1974, 31, 1791–1806. [Google Scholar] [CrossRef] [Green Version]
- André, J.; De Moor, G.; Lacarrere, P.; Du Vachat, R. Modeling the 24-hour evolution of the mean and turbulent structures of the planetary boundary layer. J. Atmos. Sci. 1978, 35, 1861–1883. [Google Scholar] [CrossRef] [Green Version]
- Canuto, V.; Minotti, F.; Ronchi, C.; Ypma, R.; Zeman, O. Second-order closure PBL model with new third-order moments: Comparison with LES data. J. Atmos. Sci. 1994, 51, 1605–1618. [Google Scholar] [CrossRef]
- Ilyushin, B. Simulation of the diurnal evolution of the atmospheric boundary layer. Izv. Atmos. Ocean. Phys. 2014, 50, 246–255. [Google Scholar] [CrossRef]
- Svensson, G.; Holtslag, A.; Kumar, V.; Mauritsen, T.; Steeneveld, G.; Angevine, W.; Bazile, E.; Beljaars, A.; De Bruijn, E.; Cheng, A.; et al. Evaluation of the diurnal cycle in the atmospheric boundary layer over land as represented by a variety of single-column models: The second GABLS experiment. Bound.-Layer Meteorol. 2011, 140, 177–206. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.L.; Zheng, W.Z. Diurnal cycles of surface winds and temperatures as simulated by five boundary layer parameterizations. J. Appl. Meteorol. Climatol. 2004, 43, 157–169. [Google Scholar] [CrossRef] [Green Version]
- Tjernström, M.; Žagar, M.; Svensson, G.; Cassano, J.J.; Pfeifer, S.; Rinke, A.; Wyser, K.; Dethloff, K.; Jones, C.; Semmler, T.; et al. Modelling the Arctic boundary layer: An evaluation of six ARCMIP regional-scale models using data from the SHEBA project. Bound.-Layer Meteorol. 2005, 117, 337–381. [Google Scholar] [CrossRef]
- Steeneveld, G.; Mauritsen, T.; De Bruijn, E.; Vilà-Guerau de Arellano, J.; Svensson, G.; Holtslag, A. Evaluation of limited-area models for the representation of the diurnal cycle and contrasting nights in CASES-99. J. Appl. Meteorol. Climatol. 2008, 47, 869–887. [Google Scholar] [CrossRef]
- Antoon van Hooft, J.; Baas, P.; van Tiggelen, M.; Ansorge, C.; van de Wiel, B.J. An idealized description for the diurnal cycle of the dry atmospheric boundary layer. J. Atmos. Sci. 2019, 76, 3717–3736. [Google Scholar] [CrossRef]
- Apsley, D.D.; Castro, I.P. A limited-length-scale k-ε model for the neutral and stably-stratified atmospheric boundary layer. Bound.-Layer Meteorol. 1997, 83, 75–98. [Google Scholar] [CrossRef]
- Freedman, F.R.; Jacobson, M.Z. Modification Of The Standard∈-Equation For The Stable Abl Through Enforced Consistency With Monin–Obukhov Similarity Theory. Bound.-Layer Meteorol. 2003, 106, 383–410. [Google Scholar] [CrossRef]
- Kurbatskiy, A.F.; Kurbatskaya, L.I. E − ε − <θ 2> turbulence closure model for an atmospheric boundary layer including the urban canopy. Meteorol. Atmos. Phys. 2009, 104, 63–81. [Google Scholar]
- Sumner, J.; Masson, C. The Apsley and Castro Limited-Length-Scale Model Revisited for Improved Performance in the Atmospheric Surface Layer. Bound.-Layer Meteorol. 2012, 144, 199–215. [Google Scholar] [CrossRef]
- Hanjalić, K.; Hrebtov, M. Ground boundary conditions for thermal convection over horizontal surfaces at high rayleigh numbers. Bound.-Layer Meteorol. 2016, 160, 41–61. [Google Scholar] [CrossRef]
- Kenjeres, S.; Hanjalic, K. Combined effects of terrain orography and thermal stratification on pollutant dispersion in a town valley: A T-RANS simulation. J. Turbul. 2002, 3, 026. [Google Scholar] [CrossRef]
- Kenjereš, S.; Hanjalić, K. LES, T-RANS and hybrid simulations of thermal convection at high Ra numbers. Int. J. Heat Fluid Flow 2006, 27, 800–810. [Google Scholar] [CrossRef]
- Hrebtov, M.; Hanjalić, K. Numerical study of winter diurnal convection over the city of Krasnoyarsk: Effects of non-freezing river, undulating fog and steam devils. Bound.-Layer Meteorol. 2017, 163, 469–495. [Google Scholar] [CrossRef]
- Hrebtov, M.; Hanjalić, K. River-induced anomalies in seasonal variation of traffic-emitted CO distribution over the City of Krasnoyarsk. Atmosphere 2019, 10, 407. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Multiscale model for turbulent flows. AIAA J. 1988, 26, 1311–1320. [Google Scholar] [CrossRef]
- Jones, W.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Iaccarino, G.; Mishra, A.A.; Ghili, S. Eigenspace perturbations for uncertainty estimation of single-point turbulence closures. Phys. Rev. Fluids 2017, 2, 024605. [Google Scholar] [CrossRef]
- Mishra, A.A.; Duraisamy, K.; Iaccarino, G. Estimating uncertainty in homogeneous turbulence evolution due to coarse-graining. Phys. Fluids 2019, 31, 025106. [Google Scholar] [CrossRef]
- Poulos, G.S.; Blumen, W.; Fritts, D.C.; Lundquist, J.K.; Sun, J.; Burns, S.P.; Nappo, C.; Banta, R.; Newsom, R.; Cuxart, J.; et al. CASES-99: A comprehensive investigation of the stable nocturnal boundary layer. Bull. Am. Meteorol. Soc. 2002, 83, 555–582. [Google Scholar] [CrossRef]
- Yamada, T. The critical Richardson number and the ratio of the eddy transport coefficients obtained from a turbulence closure model. J. Atmos. Sci. 1975, 32, 926–933. [Google Scholar] [CrossRef]
- Zilitinkevich, S.; Elperin, T.; Kleeorin, N.; Rogachevskii, I.; Esau, I.; Mauritsen, T.; Miles, M. Turbulence energetics in stably stratified geophysical flows: Strong and weak mixing regimes. Q. J. R. Meteorol. Soc. J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2008, 134, 793–799. [Google Scholar] [CrossRef] [Green Version]
- Freire, L.S.; Chamecki, M.; Bou-Zeid, E.; Dias, N.L. Critical flux Richardson number for Kolmogorov turbulence enabled by TKE transport. Q. J. R. Meteorol. Soc. 2019, 145, 1551–1558. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 96–116. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hrebtov, M.; Bobrov, M.
Modification of
Hrebtov M, Bobrov M.
Modification of
Hrebtov, Michael, and Maxim Bobrov.
2022. "Modification of
Hrebtov, M., & Bobrov, M.
(2022). Modification of





