The Reaction of HO2 and CH3O2: CH3OOH Formed from the Singlet Electronic State Surface
Abstract
:1. Introduction
2. Theoretical Methodologies
2.1. High-Level Coupled-Cluster Calculations
2.2. Two-Dimensional Master Equation Calculations
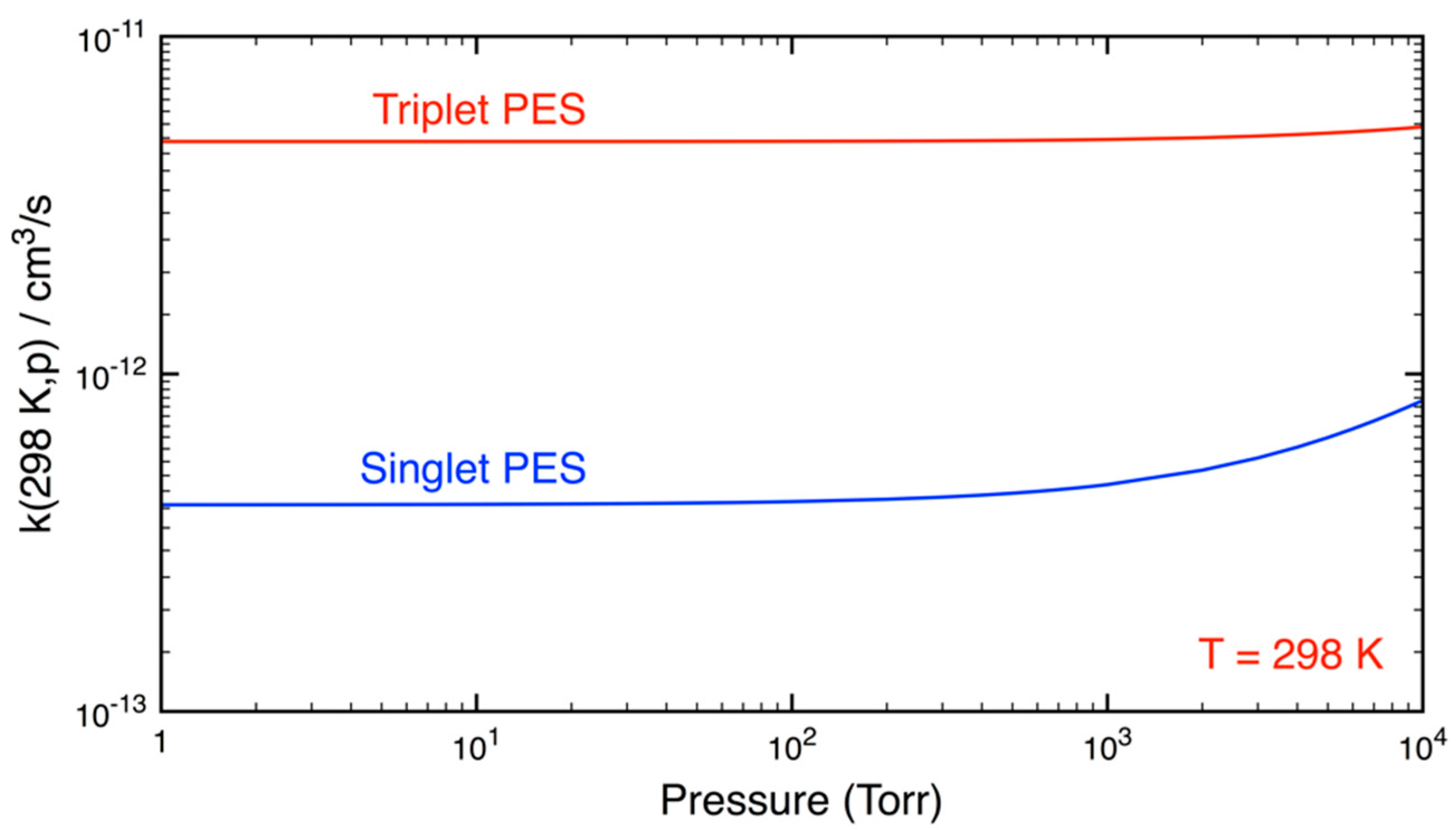
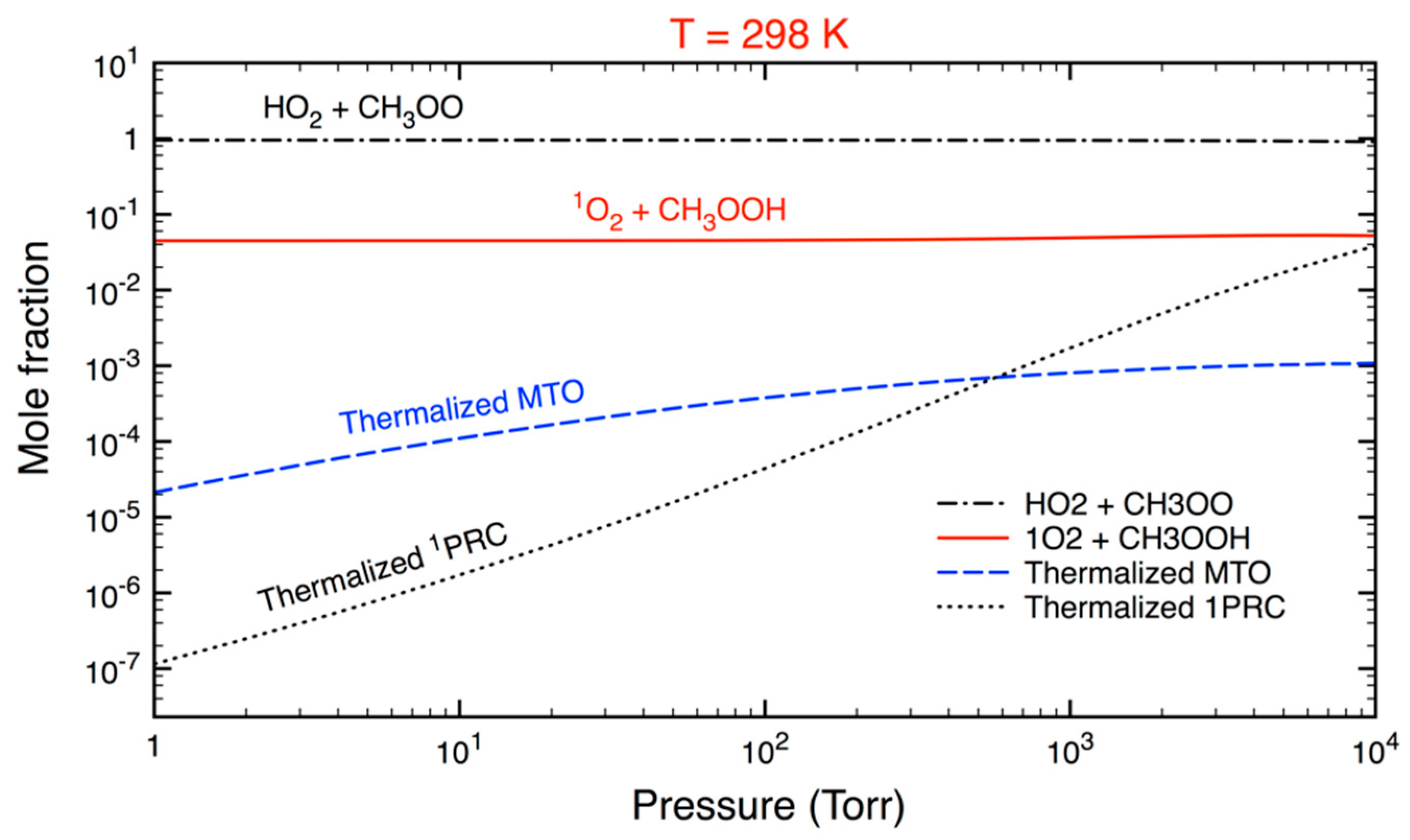
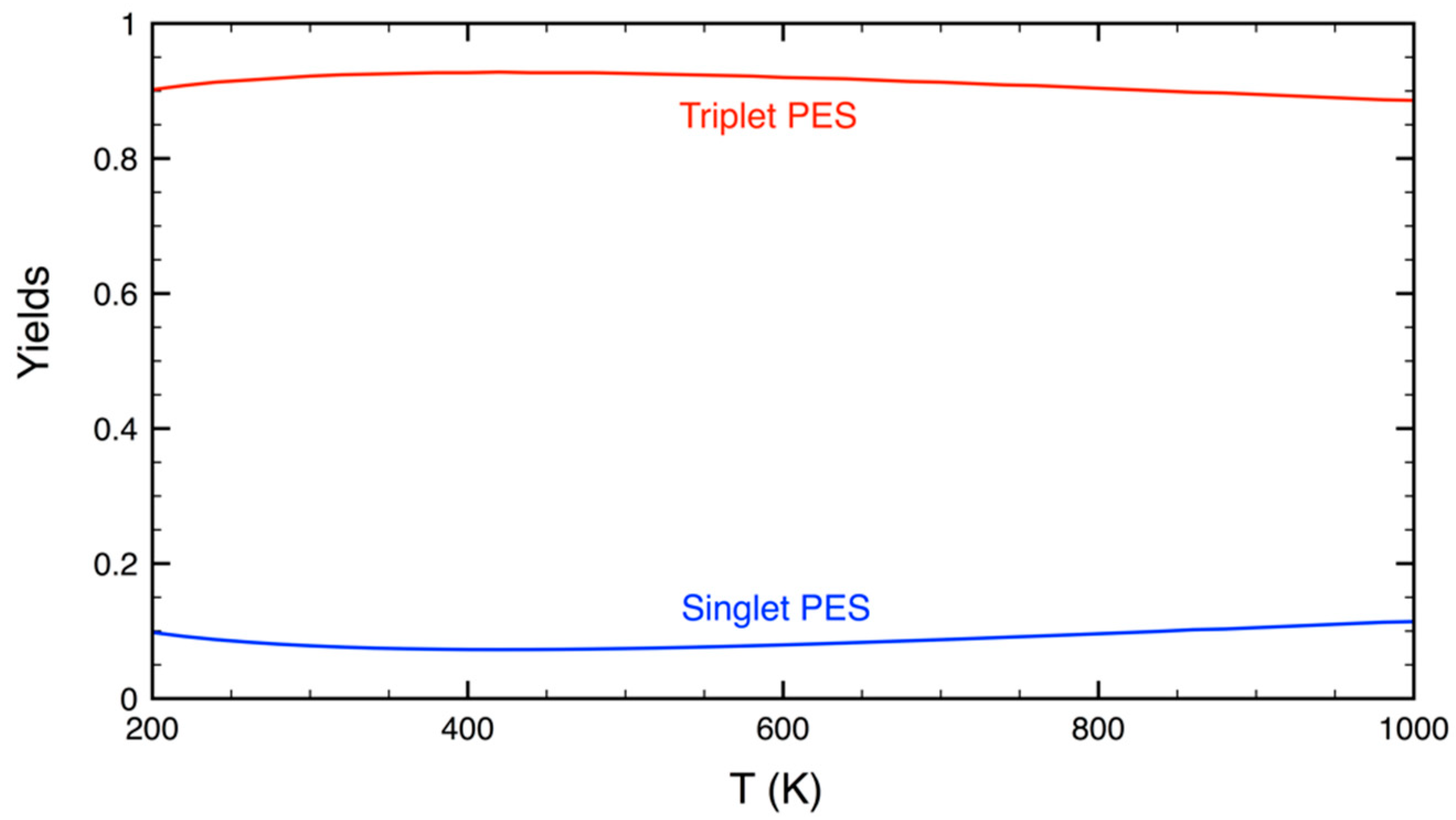
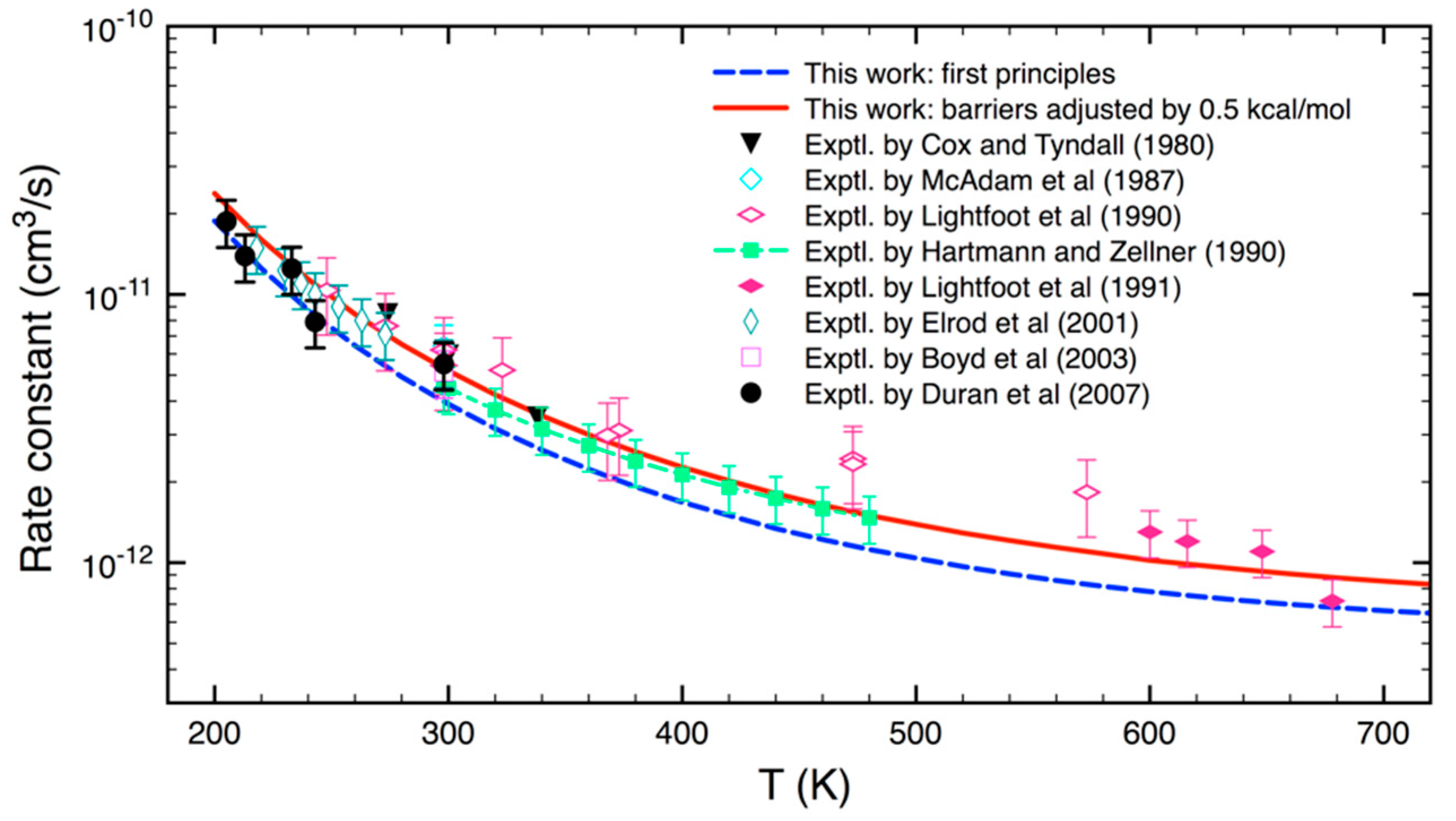
3. Results and Discussions
3.1. Reaction Mechanisms
3.2. Statistical Kinetics Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Atkinson, R. Gas-Phase Tropospheric Chemistry of Volatile Organic Compounds: 1. Alkanes and Alkenes. J. Phys. Chem. Ref. Data 1997, 26, 215–290. [Google Scholar] [CrossRef]
- Miller, J.A.; Pilling, M.J.; Troe, E. Unravelling combustion mechanisms through a quantitative understanding of elementary reactions. Proc. Combust. Inst. 2005, 30, 43–88. [Google Scholar]
- Baulch, D.L.; Bowman, C.T.; Cobos, C.J.; Cox, R.A.; Just, T.; Kerr, J.A.; Pilling, M.J.; Stocker, D.; Troe, J.; Tsang, W.; et al. Evaluated kinetic data for combustion modeling: Supplement II. J. Phys. Chem. Ref. Data 2005, 34, 757–1397. [Google Scholar]
- Orlando, J.J.; Tyndall, G.S. Laboratory studies of organic peroxy radical chemistry: An overview with emphasis on recent issues of atmospheric significance. Chem. Soc. Rev. 2012, 41, 6294–6317. [Google Scholar]
- Wallington, T.J.; Dagaut, P.; Kurylo, M.J. Ultraviolet-Absorption Cross-Sections and Reaction-Kinetics and Mechanisms for Peroxy-Radicals in the Gas-Phase. Chem. Rev. 1992, 92, 667–710. [Google Scholar]
- Tyndall, G.S.; Cox, R.A.; Granier, C.; Lesclaux, R.; Moortgat, G.K.; Pilling, M.J.; Ravishankara, A.R.; Wallington, T.J. Atmospheric chemistry of small organic peroxy radicals. J. Geophys Res.-Atmos 2001, 106, 12157–12182. [Google Scholar]
- Lightfoot, P.D.; Cox, R.A.; Crowley, J.N.; Destriau, M.; Hayman, G.D.; Jenkin, M.E.; Moortgat, G.K.; Zabel, F. Organic Peroxy-Radicals-Kinetics, Spectroscopy and Tropospheric Chemistry. Atmos. Environ. Part A Gen. Top. 1992, 26, 1805–1961. [Google Scholar]
- Onel, L.; Brennan, A.; Seakins, P.W.; Whalley, L.; Heard, D.E. A new method for atmospheric detection of the CH3O2 radical. Atmos. Meas. Tech. 2017, 10, 3985–4000. [Google Scholar]
- Cox, R.A.; Tyndall, G.S. Rate Constants for the Reactions of CH3O2 with HO2 NO and NO2 Using Molecular Modulation Spectrometry. J. Chem. Soc. Faraday Trans. 1980, 76, 153–163. [Google Scholar]
- Kurylo, M.J.; Dagaut, P.; Wallington, T.J.; Neuman, D.M. Kinetic Measurements of the Gas-Phase HO2 + CH3O2 Cross-Disproportionation Reaction at 298-K. Chem. Phys. Lett. 1987, 139, 513–518. [Google Scholar]
- Mcadam, K.; Veyret, B.; Lesclaux, R. Uv Absorption-Spectra of HO2 and CH3O2 Radicals and the Kinetics of Their Mutual Reactions at 298-K. Chem. Phys. Lett. 1987, 133, 39–44. [Google Scholar]
- Jenkin, M.E.; Cox, R.A.; Hayman, G.D.; Whyte, L.J. Kinetic-Study of the Reactions CH3O2 + CH3O2 and CH3O2 + HO2 Using Molecular Modulation Spectroscopy. J. Chem. Soc. Faraday Trans. 1988, 84, 913–930. [Google Scholar]
- Wallington, T.J. Fourier-Transform Infrared Product Study of the Reaction of CH3O2 + HO2 over the Pressure Range 15-700 Torr at 295-K. J. Chem. Soc. Faraday Trans. 1991, 87, 2379–2382. [Google Scholar]
- Lightfoot, P.D.; Roussel, P.; Caralp, F.; Lesclaux, R. Flash-Photolysis Study of the CH3O2 + CH3O2 and CH3O2 + HO2 Reactions between 60-K and 719-K-Unimolecular Decomposition of Methylhydroperoxide. J. Chem. Soc. Faraday Trans. 1991, 87, 3213–3220. [Google Scholar]
- Lightfoot, P.D.; Veyret, B.; Lesclaux, R. Flash-Photolysis Study of the CH3O2 + HO2 Reaction between 248 and 573-K. J. Phys. Chem. 1990, 94, 708–714. [Google Scholar] [CrossRef]
- Boyd, A.A.; Flaud, P.M.; Daugey, N.; Lesclaux, R. Rate constants for RO2 + HO2 reactions measured under a large excess of HO2. J. Phys. Chem. A 2003, 107, 818–821. [Google Scholar]
- Raventos-Duran, M.T.; Mcgillen, M.; Percival, C.J.; Hamer, P.D.; Shallcross, D.E. Kinetics of the CH3O2 + HO2 reaction: A temperature and pressure dependence study using chemical ionization mass Spectrometry. Int. J. Chem. Kinet. 2007, 39, 571–579. [Google Scholar]
- Moortgat, G.K.; Cox, R.A.; Schuster, G.; Burrows, J.P.; Tyndall, G.S. Peroxy Radical Reactions in the Photo-Oxidation of CH3CHO. J. Chem. Soc. Faraday Trans. 1989, 85, 809–829. [Google Scholar]
- Elrod, M.J.; Ranschaert, D.L.; Schneider, N.J. Direct kinetics study of the temperature dependence of the CH2O branching channel for the CH3O2+HO2 reaction. Int. J. Chem. Kinet. 2001, 33, 363–376. [Google Scholar]
- Hou, H.; Wang, B.S. A systematic computational study on the reactions of HO2 with RO2: The HO2+CH3O2(CD3O2) and HO2+CH2FO2 reactions. J. Phys. Chem. A 2005, 109, 451–460. [Google Scholar]
- Drougas, E. Quantum mechanical studies of the CH3O2 + HO2 reaction. Comput. Theor. Chem. 2016, 1093, 98–103. [Google Scholar]
- Anglada, J.M.; Olivella, S.; Sole, A. Mechanistic study of the CH3O2 + HO2 -> CH3O2H + O2 reaction in the gas phase. Computational evidence for the formation of a hydrogen-bonded diradical complex. J. Phys. Chem. A 2006, 110, 6073–6082. [Google Scholar] [PubMed]
- Zhang, T.L.; Wang, W.L.; Zhang, P.; Lu, J.; Zhang, Y. Water-catalyzed gas-phase hydrogen abstraction reactions of CH3O2 and HO2 with HO2: A computational investigation. Phys. Chem. Chem. Phys. 2011, 13, 20794–20805. [Google Scholar] [PubMed]
- English, A.M.; Hansen, J.C.; Szente, J.J.; Maricq, A.M. The effects of water vapor on the CH3O2 self-reaction and reaction with HO2. J. Phys. Chem. A 2008, 112, 9220–9228. [Google Scholar] [PubMed]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Headgordon, M. A 5th-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar]
- Bartlett, R.J.; Watts, J.D.; Kucharski, S.A.; Noga, J. Noniterative 5th-Order Triple and Quadruple Excitation-Energy Corrections in Correlated Methods. Chem. Phys. Lett. 1990, 165, 513–522. [Google Scholar]
- Stanton, J.F. Why CCSD(T) works: A different perspective. Chem. Phys. Lett. 1997, 281, 130–134. [Google Scholar]
- Almlof, J.; Taylor, P.R. General Contraction of Gaussian-Basis Sets. 1. Atomic Natural Orbitals for 1st-Row and 2nd-Row Atoms. J. Chem. Phys. 1987, 86, 4070–4077. [Google Scholar]
- Almlof, J.; Taylor, P.R. General Contraction of Gaussian-Basis Sets. 2. Atomic Natural Orbitals and the Calculation of Atomic and Molecular-Properties. J. Chem. Phys. 1990, 92, 551–560. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations. 1. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar]
- Thorpe, J.H.; Lopez, C.A.; Nguyen, T.L.; Baraban, J.H.; Bross, D.H.; Ruscic, B.; Stanton, J.F. High-accuracy extrapolated ab initio thermochemistry. IV. A modified recipe for computational efficiency. J. Chem. Phys. 2019, 150, 224102. [Google Scholar] [CrossRef] [PubMed]
- Ruscic, B.; Bross, D.H. Active Thermochemical Tables (ATcT) Values Based on Ver. 1.122r of the Thermochemical Network 2022. Available online: ATcT.anl.gov (accessed on 4 July 2022).
- Jeffery, S.J.; Gates, K.E.; Smith, S.C. Full Iterative Solution of the Two-Dimensional Master Equation for Thermal Unimolecular Reactions. J. Phys. Chem. 1996, 100, 7090–7096. [Google Scholar] [CrossRef]
- Robertson, S.H.; Pilling, M.J.; Green, N.J.B. Diffusion approximations of the two-dimensional master equation. Mol. Phys. 1996, 89, 1531–1551. [Google Scholar] [CrossRef]
- Miller, J.A.; Klippenstein, S.J.; Raffy, C. Solution of Some One- and Two-Dimensional Master Equation Models for Thermal Dissociation: The Dissociation of Methane in the Low-Pressure Limit. J. Phys. Chem. 2002, 106, 4904–4913. [Google Scholar] [CrossRef]
- Jasper, A.W.; Pelzer, K.M.; Miller, J.A.; Kamarchik, E.; Harding, L.B.; Klippenstein, S.J. Predictive a priori pressure-dependent kinetics. Science 2014, 346, 1212–1215. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.L.; Stanton, J.F. A Steady-State Approximation to the Two-Dimensional Master Equation for Chemical Kinetics Calculations. J. Phys. Chem. A 2015, 119, 7627–7636. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Lee, H.; Matthews, D.A.; McCarthy, M.C.; Stanton, J.F. Stabilization of the Simplest Criegee Intermediate from the Reaction between Ozone and Ethylene: A High-Level Quantum Chemical and Kinetic Analysis of Ozonolysis. J. Phys. Chem. A 2015, 119, 5524–5533. [Google Scholar]
- Nguyen, T.L.; Stanton, J.F. Pragmatic Solution for a Fully E,J-Resolved Master Equation. J. Phys. Chem. A 2020, 124, 2907–2918. [Google Scholar] [CrossRef]
- Troe, J. Theory of Thermal Unimolecular Reactions at Low-Pressures.1. Solutions of Master Equation. J. Chem. Phys. 1977, 66, 4745–4757. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Sherwood, T.K. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Neufeld, P.D.; Aziz, R.A.; Janzen, A.R. Empirical Equations to Calculate 16 of Transport Collision Integrals-Omega(L, S)’ for Lennard-Jones (12-6) Potential. J. Chem. Phys. 1972, 57, 1100. [Google Scholar] [CrossRef]
- Holbrook, K.A.; Pilling, M.J.; Robertson, S.H.; Robinson, P.J. Unimolecular Reactions, 2nd ed.; Wiley: Chichester, UK; New York, NY, USA, 1996; 417p. [Google Scholar]
- Gilbert, R.G.; Smith, S.C. Theory of Unimolecular and Recombination Reactions; Blackwell Science Publications; Publishers’ Business Services Distributor: Oxford, UK; Boston, MA, USA, 1990; 356p. [Google Scholar]
- Forst, W. Adiabatic Rotations in Unimolecular Rate Theory. J. Chem. Phys. 1968, 48, 3665. [Google Scholar] [CrossRef]
- Forst, W. Unimolecular Reactions: A Concise Introduction; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2003; 319p. [Google Scholar]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Evans, M.G.; Polanyi, M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 0875–0893. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Garrett, B.C.; Klippenstein, S.J. Current status of transition-state theory. J. Phys. Chem. 1996, 100, 12771–12800. [Google Scholar] [CrossRef]
- Hase, W.L. Variational Unimolecular Rate Theory. Acc. Chem. Res. 1983, 16, 258–264. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Garrett, B.C. Variational Transition-State Theory. Annu. Rev. Phys. Chem. 1984, 35, 159–189. [Google Scholar] [CrossRef]
- Miller, W.H. Tunneling Corrections to Unimolecular Rate Constants, with Application to Formaldehyde. J. Am. Chem. Soc. 1979, 101, 6810–6814. [Google Scholar] [CrossRef]
- Bowman, J.M. Reduced Dimensionality Theory of Quantum Reactive Scattering. J. Phys. Chem. 1991, 95, 4960–4968. [Google Scholar] [CrossRef]
- Balakrishnan, N. Quantum mechanical investigation of the O + H2 -> OH + H reaction. J. Chem. Phys. 2003, 119, 195–199. [Google Scholar] [CrossRef]
- Miller, W.H. Semiclassical Theory for Non-Separable Systems-Construction of Good Action-Angle Variables for Reaction-Rate Constants. Faraday Discuss. 1977, 62, 40–46. [Google Scholar] [CrossRef]
- Miller, W.H.; Hernandez, R.; Handy, N.C.; Jayatilaka, D.; Willetts, A. Abinitio Calculation of Anharmonic Constants for a Transition-State, with Application to Semiclassical Transition-State Tunneling Probabilities. Chem. Phys. Lett. 1990, 172, 62–68. [Google Scholar] [CrossRef]
- Hernandez, R.; Miller, W.H. Semiclassical Transition-State Theory-a New Perspective. Chem. Phys. Lett. 1993, 214, 129–136. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Stanton, J.F.; Barker, J.R. A practical implementation of semi-classical transition state theory for polyatomics. Chem. Phys. Lett. 2010, 499, 9–15. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Stanton, J.F.; Barker, J.R. Ab Initio Reaction Rate Constants Computed Using Semiclassical Transition-State Theory: HO + H2 -> H2O + H and Isotopologues. J. Phys. Chem. A 2011, 115, 5118–5126. [Google Scholar] [CrossRef]
- Wang, F.G.; Landau, D.P. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 2001, 86, 2050–2053. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.G.; Landau, D.P. Determining the density of states for classical statistical models: A random walk algorithm to produce a flat histogram. Phys. Rev. E 2001, 64, 056101. [Google Scholar] [CrossRef]
- Basire, M.; Parneix, P.; Calvo, F. Quantum anharmonic densities of states using the Wang-Landau method. J. Chem. Phys. 2008, 129, 081101. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Barker, J.R. Sums and Densities of Fully Coupled Anharmonic Vibrational States: A Comparison of Three Practical Methods. J. Phys. Chem. A 2010, 114, 3718–3730. [Google Scholar] [CrossRef]
- Baer, T.; Hase, W.L. Unimolecular Reaction Dynamics: Theory and Experiments; Oxford University Press: New York, NY, USA, 1996; 438p. [Google Scholar]
- Barker, J.R.; Nguyen, T.L.; Stanton, J.F.; Aieta, C.; Ceotto, M.; Gabas, F.; Kumar, T.J.D.; Li, C.G.L.; Lohr, L.L.; Maranzana, A.; et al. MULTIWELL Program Suite, Climate and Space Sciences and Engineering, University of Michigan. Ann. Arbor. MI 2021. [Google Scholar]


| Species | mHEAT | Anglada et al. (b) | Zhang et al. (c) | Hou et al. (d) |
|---|---|---|---|---|
| 3PRC | −5.92 ± 0.5 | −4.5 | −5.99 | −7.65 |
| 3TS1 | −2.77 ± 0.5 | −3.8 | −2.24 | −3.76 |
| 1PRC | −5.92 ± 1.0 | −4.9 | n/a | n/a |
| 1TS2 | −0.13 ± 1.0 | 5.5 | 10.72 | 8.24 |
| 1TS3 | −0.15 ± 1.0 | −1.8 | n/a | n/a |
| 1CH3OOOOH | −14.00 ± 0.5 | −6.4 | −11.29 | −9.22 |
| CH3OOH + 3O2 | −36.14 ± 0.5 (a) | −36.9 | −36.08 | −37.82 |
| CH3OOH + 1O2 | −13.57 ± 0.5 (a) | −12.6 | −5.37 | −6.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.L.; Stanton, J.F. The Reaction of HO2 and CH3O2: CH3OOH Formed from the Singlet Electronic State Surface. Atmosphere 2022, 13, 1397. https://doi.org/10.3390/atmos13091397
Nguyen TL, Stanton JF. The Reaction of HO2 and CH3O2: CH3OOH Formed from the Singlet Electronic State Surface. Atmosphere. 2022; 13(9):1397. https://doi.org/10.3390/atmos13091397
Chicago/Turabian StyleNguyen, Thanh Lam, and John F. Stanton. 2022. "The Reaction of HO2 and CH3O2: CH3OOH Formed from the Singlet Electronic State Surface" Atmosphere 13, no. 9: 1397. https://doi.org/10.3390/atmos13091397
APA StyleNguyen, T. L., & Stanton, J. F. (2022). The Reaction of HO2 and CH3O2: CH3OOH Formed from the Singlet Electronic State Surface. Atmosphere, 13(9), 1397. https://doi.org/10.3390/atmos13091397






