Simulation of Cloud-to-Ground Lightning Strikes to Wind Turbines Considering Polarity Effect Based on an Improved Stochastic Lightning Model
Abstract
:1. Introduction
2. Simulation Model
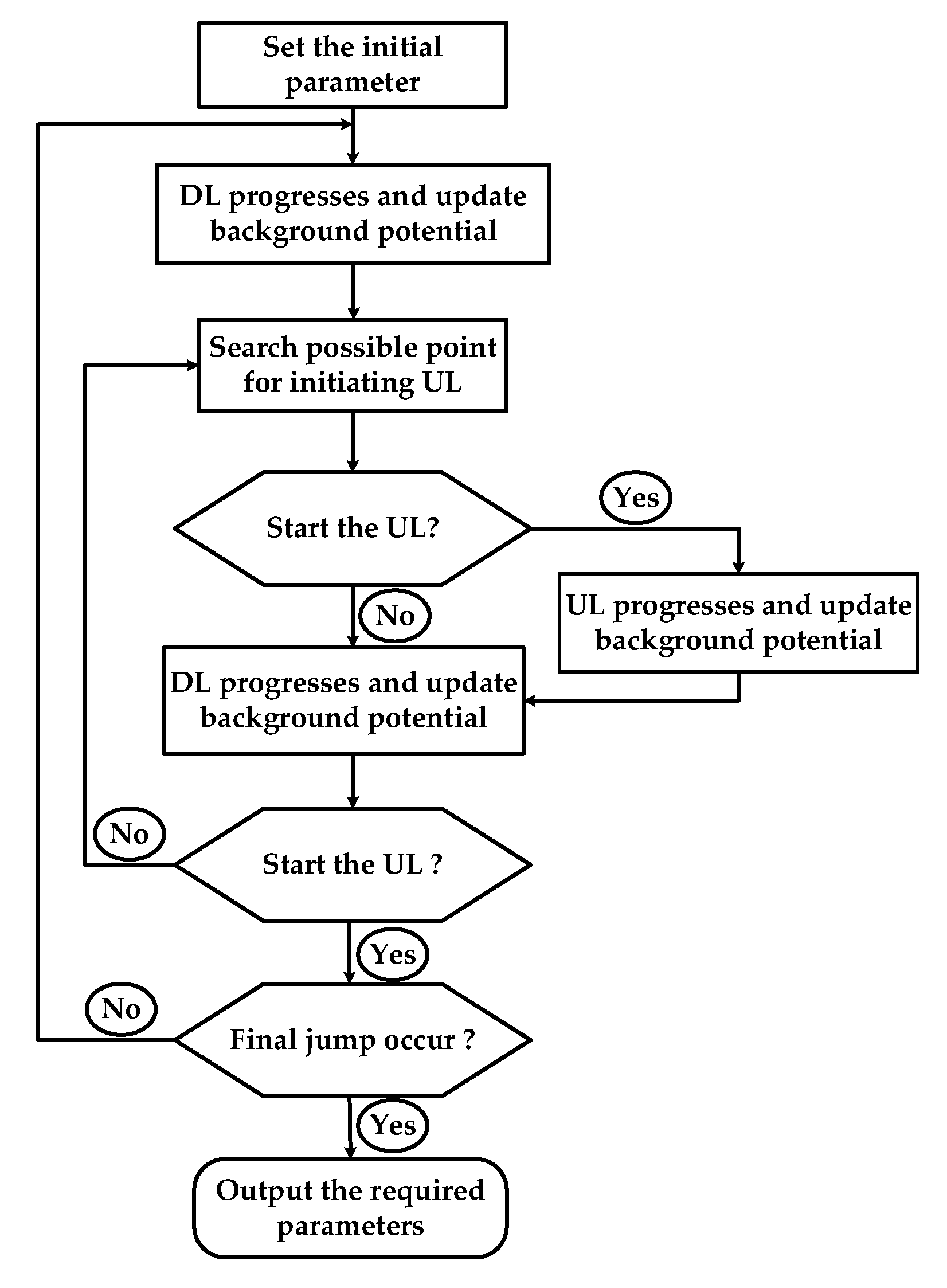
2.1. Two-Dimensional Stochastic Leader Model
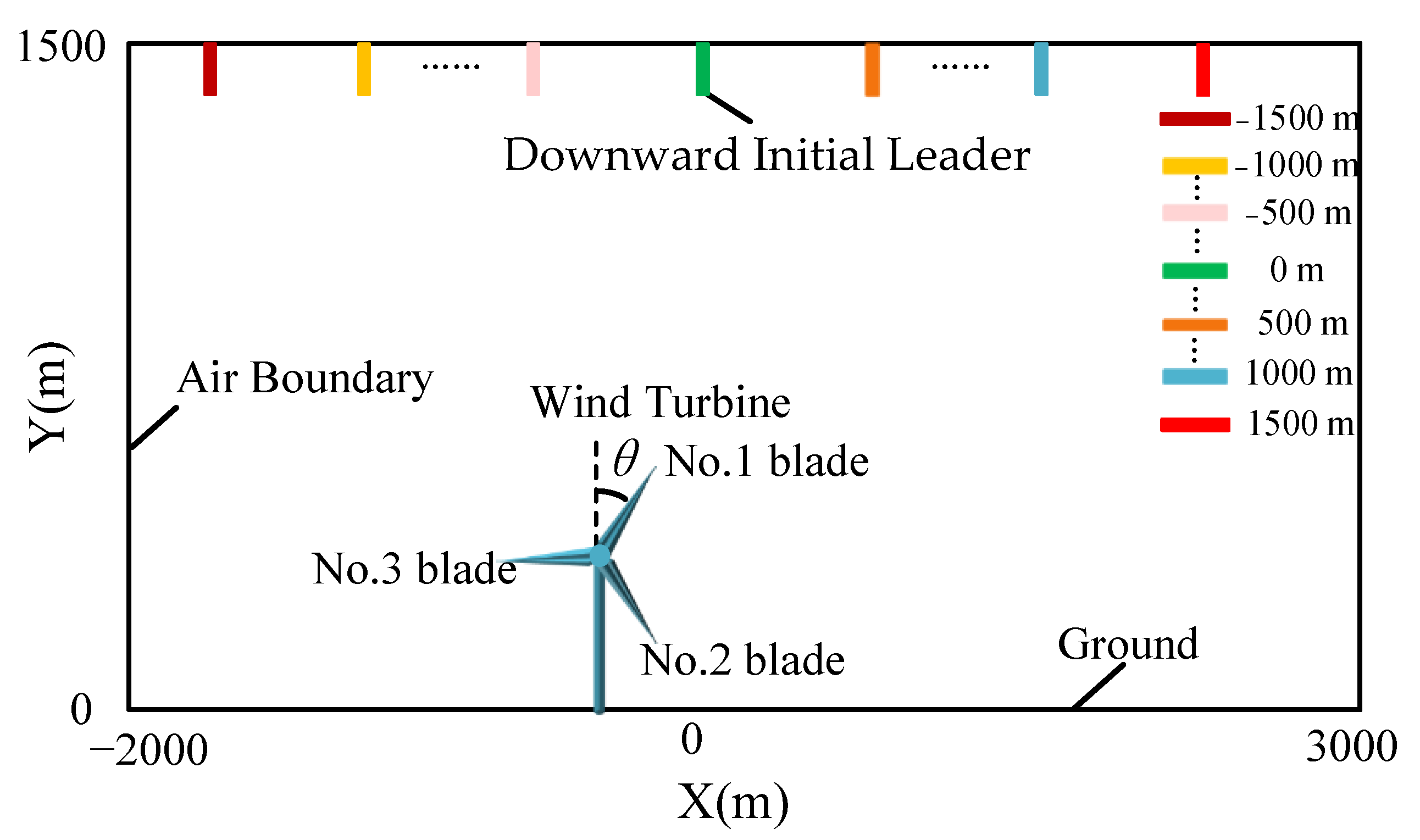
2.2. Main Parameters
2.3. Designs of Simulation
3. Modified Calculation Methods of the Annual Lightning Flash Number Considering Polarity Effect
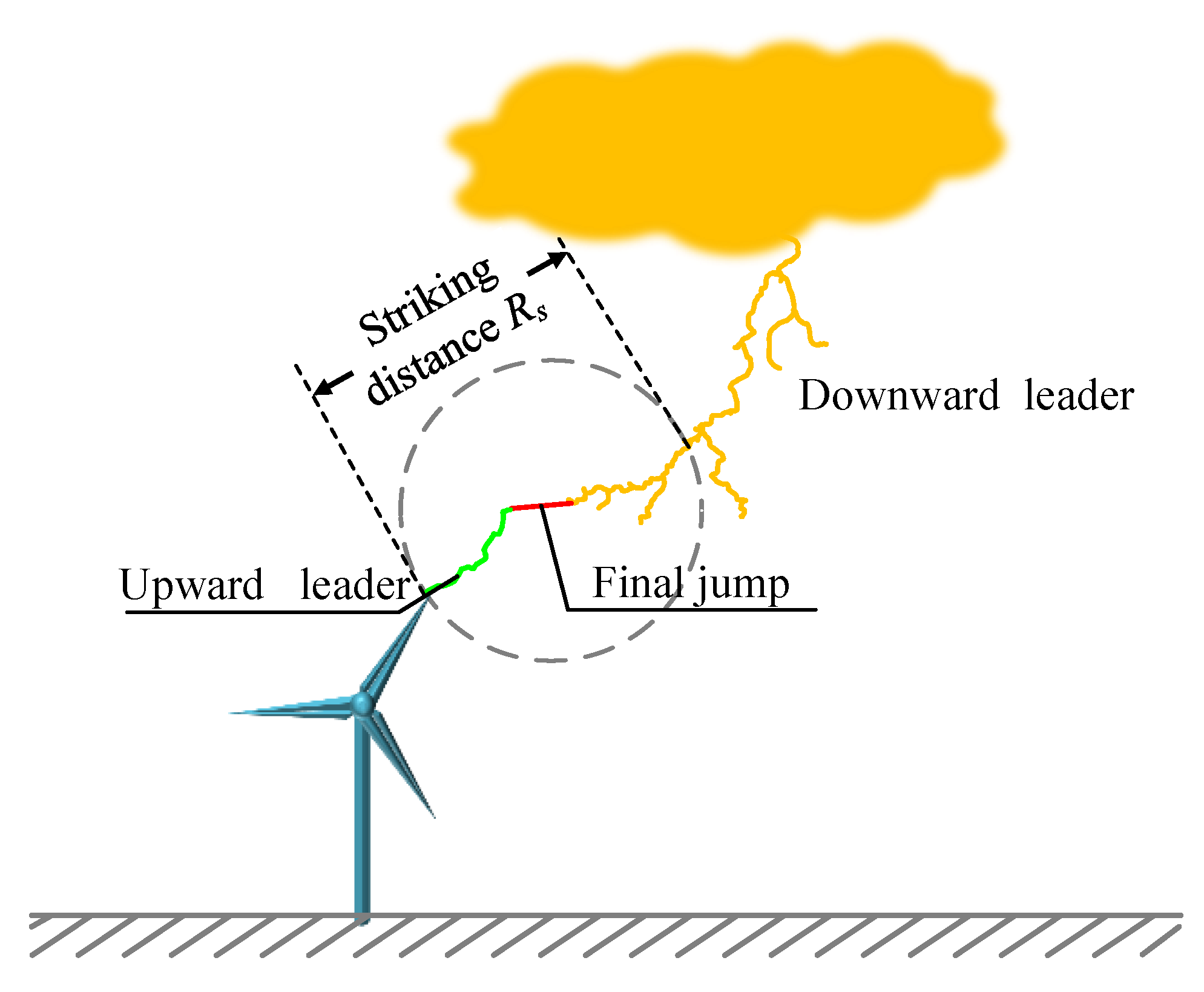
3.1. Characteristics of the Lightning Striking Distance
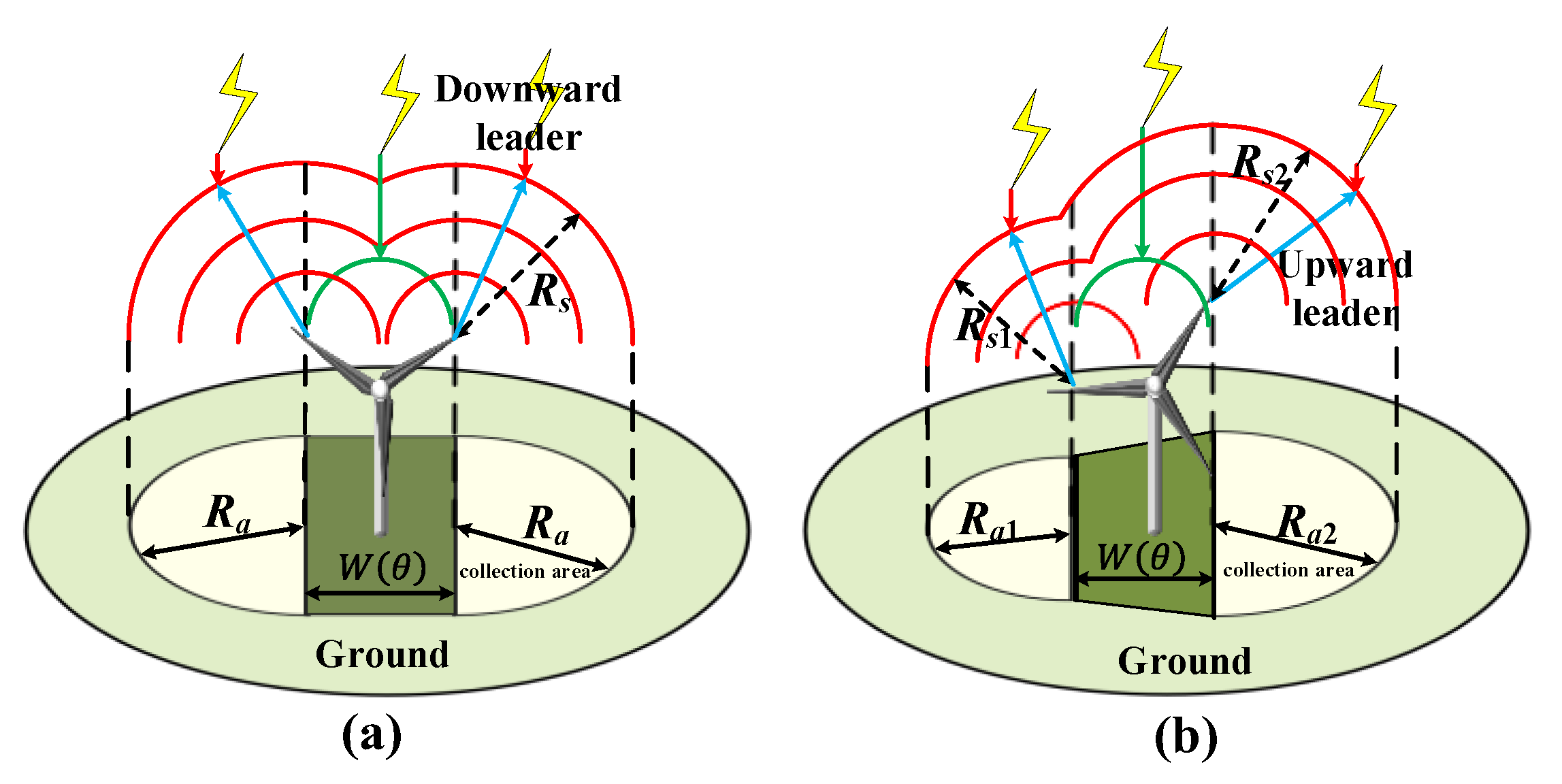
3.2. Striking Distance to the Ground in the Presence of Wind Turbines
3.3. The Calculation Method of the Annual Lightning Flash Number under the −CG Lightning
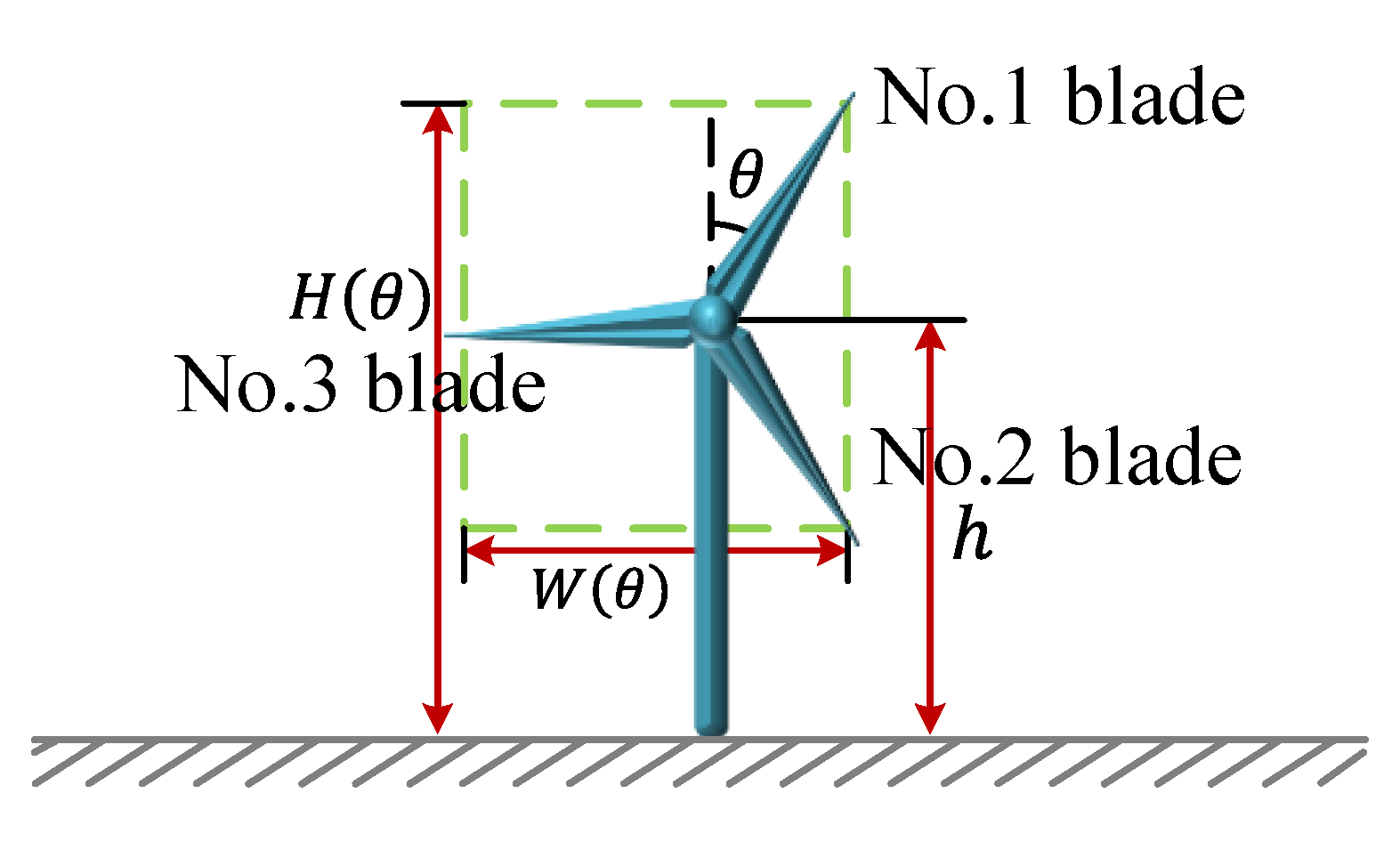
3.3.1. The Structural Model of a Wind Turbine
3.3.2. The Calculation Method
3.4. The Calculation Method of the Annual Lightning Flash Number under the +CG Lightning
4. Results and Analyses
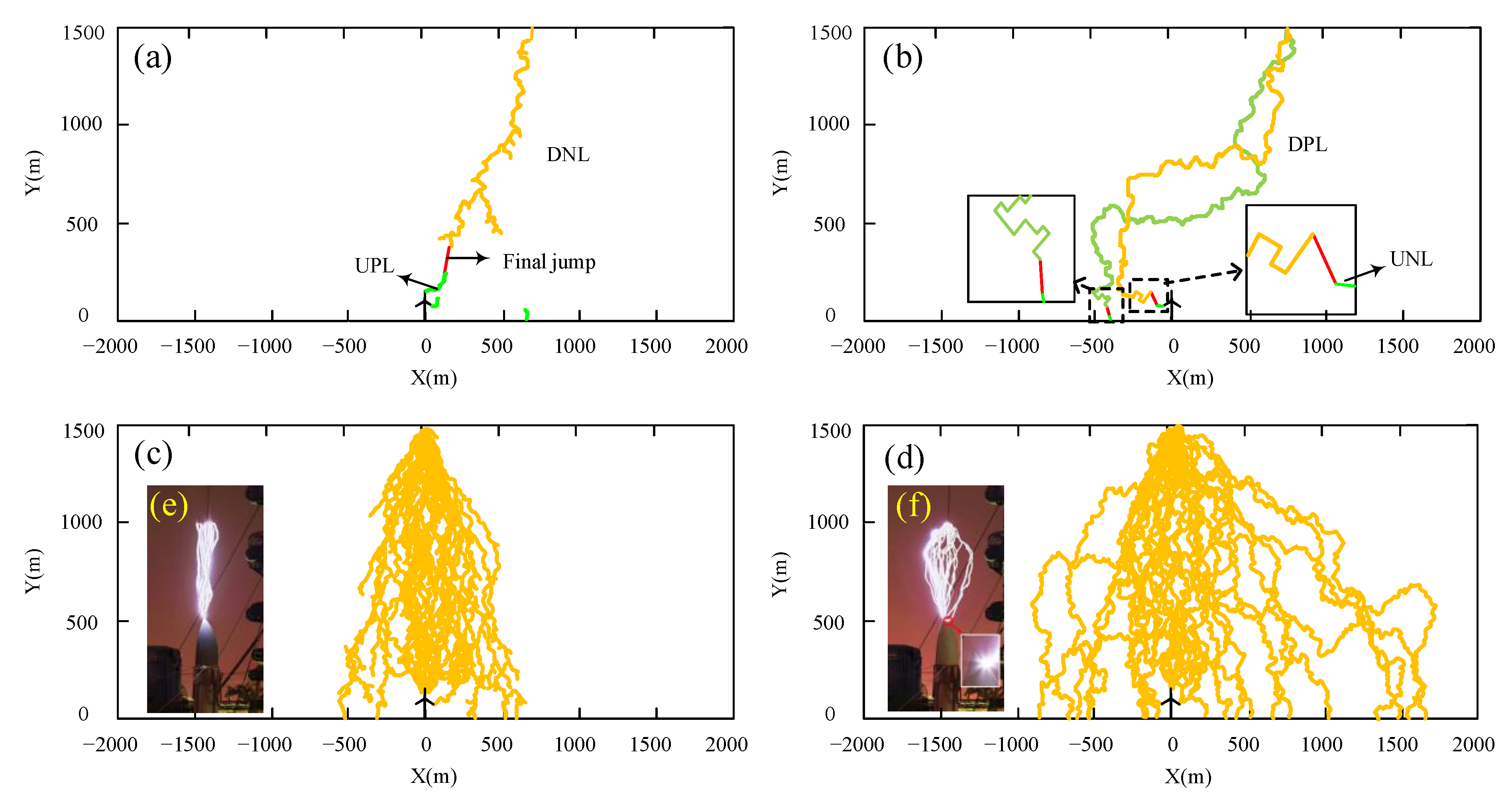
4.1. Researches on the Characteristics of the Lightning Attachment Process
4.2. Discussion of the Downward −CG Lightning Risk
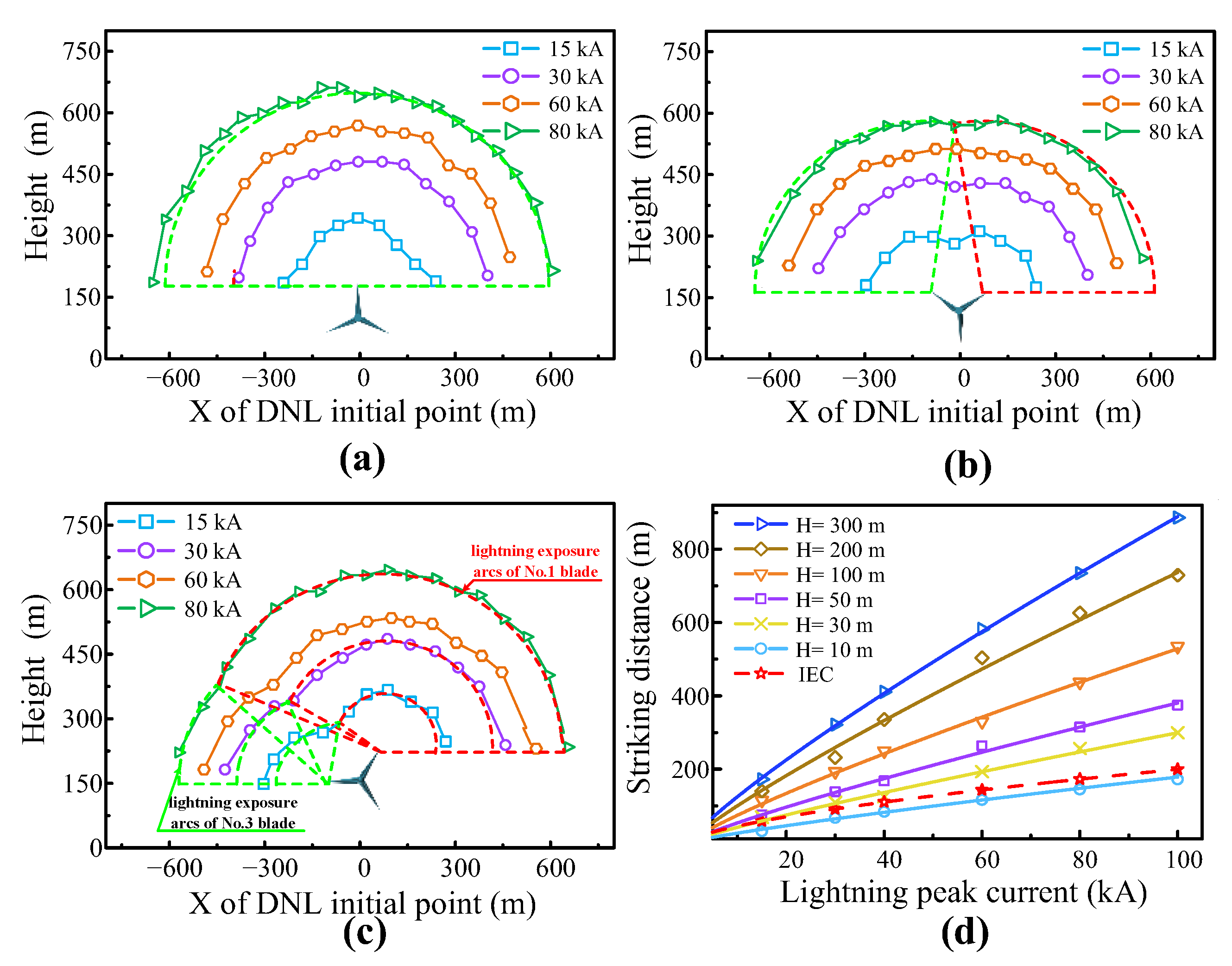
4.2.1. Influence of Blade Angles on Lightning Risk
4.2.2. Model Verification
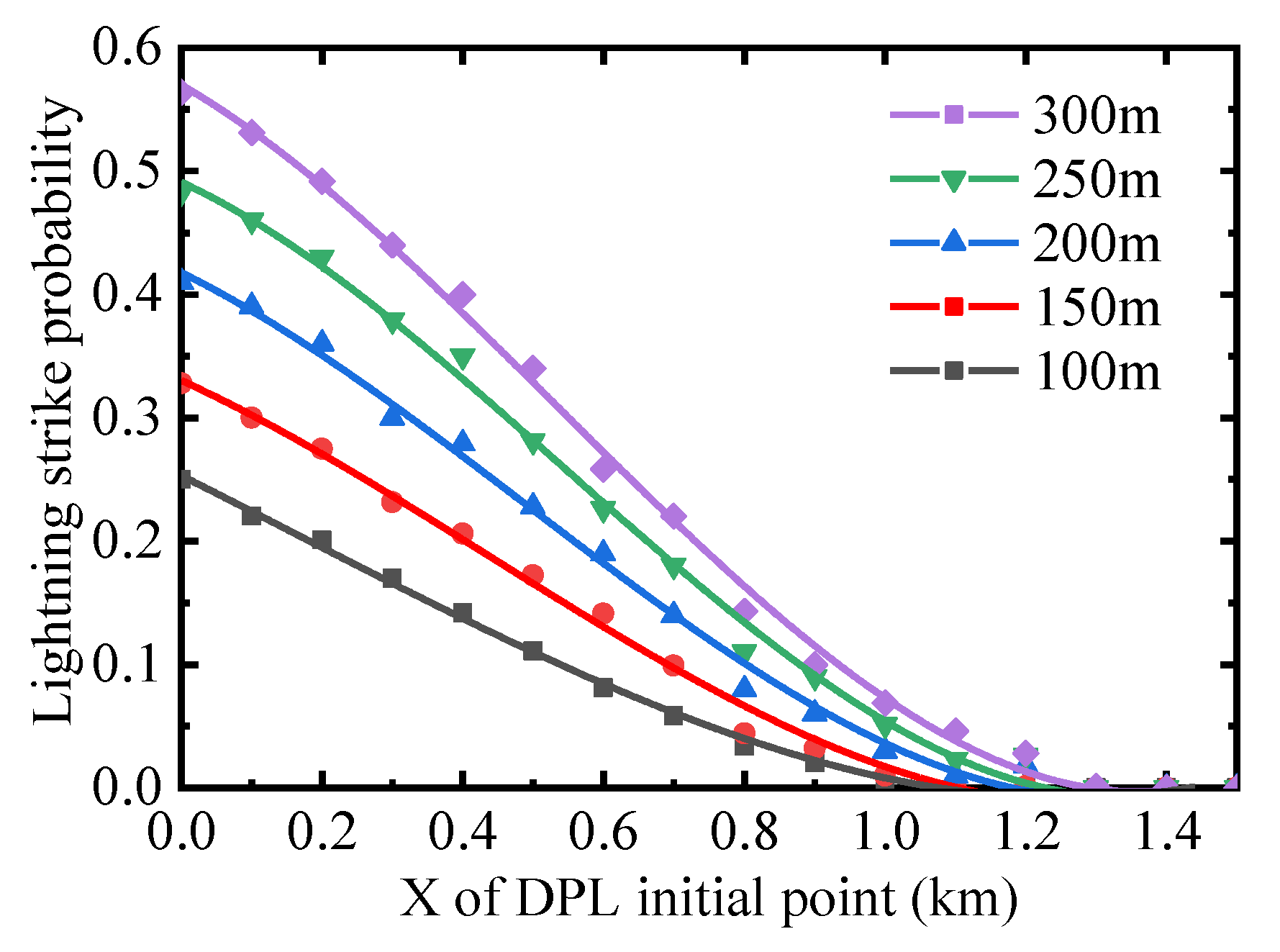
4.3. Quantitative Analysis of Downward Lightning Strike Risk for the Wind Turbine Considering Polarity Effect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marugán, A.P.; Márquez, F.P.G.; Perez, J.M.P.; Ruiz-Hernández, D. A survey of artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef] [Green Version]
- Tüfekci, M.; Tüfekci, E.; Dikicioğlu, A. Numerical investigation of the collapse of a steel truss roof and a probable reason of failure. Appl. Sci. 2020, 10, 7769. [Google Scholar] [CrossRef]
- Krausmann, E.; Renni, E.; Campedel, M.; Cozzani, V. Industrial accidents triggered by earthquakes, floods and lightning: Lessons learned from a database analysis. Nat. Hazards 2011, 59, 285–300. [Google Scholar] [CrossRef]
- Tüfekci, M.; Genel, Ö.E.; Tatar, A.; Tüfekci, E. Dynamic analysis of composite wind turbine blades as beams: An analytical and numerical study. Vibration 2020, 4, 1–15. [Google Scholar] [CrossRef]
- Ozyildiz, M.; Muyan, C.; Coker, D. Strength analysis of a composite turbine blade using puck failure criteria. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2018; Volume 1037, p. 042027. [Google Scholar]
- Wang, Y.; Deng, Y.; Liu, Y.; Qu, L.; Wen, X.; Lan, L.; Wang, J. Influence of blade rotation on the lightning stroke characteristic of a wind turbine. Wind Energy 2019, 22, 1071–1085. [Google Scholar] [CrossRef]
- Love, E.R. Improvement on Lightning Stroke Modelling and Applications to Design of EHV and UHV Transmission Lines. Master’s Thesis, University of Colorado Boulder, Boulder, CO, USA, 1973. [Google Scholar]
- Eriksson, A.J. The incidence of lightning strikes to power lines. IEEE Trans. Power Deliv. 1987, 2, 859–870. [Google Scholar] [CrossRef]
- Cooray, V.; Kumar, U.; Rachidi, F.; Nucci, C.A. On the possible variation of the lightning striking distance as assumed in the IEC lightning protection standard as a function of structure height. Electr. Power Syst. Res. 2014, 113, 79–87. [Google Scholar] [CrossRef]
- Petrov, N.I.; Petrova, G.N.; D’alessandro, F. Quantification of the probability of lightning strikes to structures using a fractal approach. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 641–654. [Google Scholar] [CrossRef]
- Guo, Z.; Li, Q.; Ma, Y.; Ren, H.; Fang, Z.; Chen, C.; Siew, W.H. Experimental study on lightning attachment manner to wind turbine blades with lightning protection system. IEEE Trans. Plasma Sci. 2018, 47, 635–646. [Google Scholar] [CrossRef] [Green Version]
- Ioannidis, A.I.; Tsovilis, T.E. Shielding Failure of High-Voltage Substations: A Fractal-Based Approach for Negative and Positive Lightning. IEEE Trans. Ind. Appl. 2021, 57, 2317–2325. [Google Scholar] [CrossRef]
- Garolera, A.C. Lightning Protection of Flap System for Wind Turbine Blades; Technical University of Denmark: Kongens Lyngby, Denmark, 2014. [Google Scholar]
- IEC 61400-24:2019; Wind Energy Generation Systems-Part 24: Lightning Protection. International Standard; International Electrotechnical Commission: Geneva, Switzerland, 2019.
- Jiang, R.; Lyu, W.; Wu, B.; Qi, Q.; Ma, Y.; Su, Z.; Tan, Y. Simulation of cloud-to-ground lightning strikes to structures based on an improved stochastic lightning model. J. Atmos. Sol.-Terr. Phys. 2020, 203, 105274. [Google Scholar] [CrossRef]
- Datsios, Z.G.; Ioannidis, A.I.; Papadopoulos, T.A.; Tsovilis, T.E. A stochastic model for evaluating the lightning performance of a− 400 kV HVDC overhead line. IEEE Trans. Electromagn. Compat. 2021, 63, 1433–1443. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, X.; Wang, B.; Hao, X.; Zheng, S.; Xie, Y.Z. A three-dimensional direct lightning strike model for lightning protection of the substation. IET Gener. Transm. Distrib. 2021, 15, 2760–2772. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, X.; Zhu, J.; Shi, Z.; Zhang, D. Influence on simulation accuracy of atmospheric electric field around a building by space resolution. Atmos. Res. 2014, 138, 301–307. [Google Scholar] [CrossRef]
- Qi, Q.; Lyu, W.; Wu, B.; Ma, Y.; Chen, L.; Liu, H. Three-dimensional optical observations of an upward lightning triggered by positive cloud-to-ground lightning. Atmos. Res. 2018, 214, 275–283. [Google Scholar] [CrossRef]
- Ioannidis, A.I.; Mikropoulos, P.N.; Tsovilis, T.E.; Karanikiotis, N. Fractal-Based Approach for Modelling Electric Breakdown of Air Gaps: An Application to a 75 cm Positive Rod-Plane Gap. In The International Symposium on High Voltage Engineering; Springer: Cham, Switzerland, 2019; pp. 1295–1305. [Google Scholar]
- Iudin, D.I.; Rakov, V.A.; Mareev, E.A.; Iudin, F.D.; Syssoev, A.A.; Davydenko, S.S. Advanced numerical model of lightning development: Application to studying the role of LPCR in determining lightning type. J. Geophys. Res. Atmos. 2017, 122, 6416–6430. [Google Scholar] [CrossRef]
- Mansell, E.R.; MacGorman, D.R.; Ziegler, C.L.; Straka, J.M. Charge structure and lightning sensitivity in a simulated multicell thunderstorm. J. Geophys. Res. Atmos. 2005, 110, D12101. [Google Scholar] [CrossRef] [Green Version]
- Becerra, M.; Cooray, V. On the velocity of positive connecting leaders associated with negative downward lightning leaders. Geophys. Res. Lett. 2008, 35, L02801. [Google Scholar] [CrossRef]
- Saba, M.M.F.; Paiva, A.R.; Schumann, C.; Ferro, M.A.S.; Naccarato, K.P.; Silva, J.C.O.; Custódio, D.M. Lightning attachment process to common buildings. Geophys. Res. Lett. 2017, 44, 4368–4375. [Google Scholar] [CrossRef]
- Guo, Z.; Li, Q.; Yu, W.; Arif, W.; Ma, Y.; Siew, W.H. Experimental study on lightning attachment manner to rotation wind turbine blade. In Proceedings of the 2018 34th International Conference on Lightning Protection (ICLP), Rzeszow, Poland, 2–7 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- IEC 62305-1: 2010; Protection against Lightning-Part 1: General Principles. International Electrotechnical Commission: Geneva, Switzerland, 2010.
- Saba, M.M.; De Paiva, A.R.; Silva, J.C.O.; Silva, L.D.; Noveline, C.; Schumann, K.P.; Naccarato, K.P. Upward connecting leaders from buildings. In Proceedings of the International Symposium on Lightning Protection (XIII SIPDA), Balneario Camboriu, Brazil, 28 September–2 October 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- IEEE Std 1243-1997; IEEE Guide for Improving the Lightning Performance of Transmission Lines. Institute of Electrical and Electronics Engineers: New York, NY, USA, 1997.
- Cooray, V.; Rakov, V.; Theethayi, N. The lightning striking distance—Revisited. J. Electrost. 2007, 65, 296–306. [Google Scholar] [CrossRef]
- Peesapati, V.; Cotton, I. Lightning protection of wind turbines-A comparison of lightning data & IEC 61400-24. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–7. [Google Scholar]
- Rizk, F.M. Modeling of lightning incidence to tall structures. I: Theory. Discussion. Author’reply. IEEE Trans. Power Deliv. 1994, 9, 162–171. [Google Scholar] [CrossRef]
- Rizk, F.A. Modeling of lightning incidence to tall structures. II. Application. IEEE Trans. Power Deliv. 1994, 9, 172–193. [Google Scholar] [CrossRef]

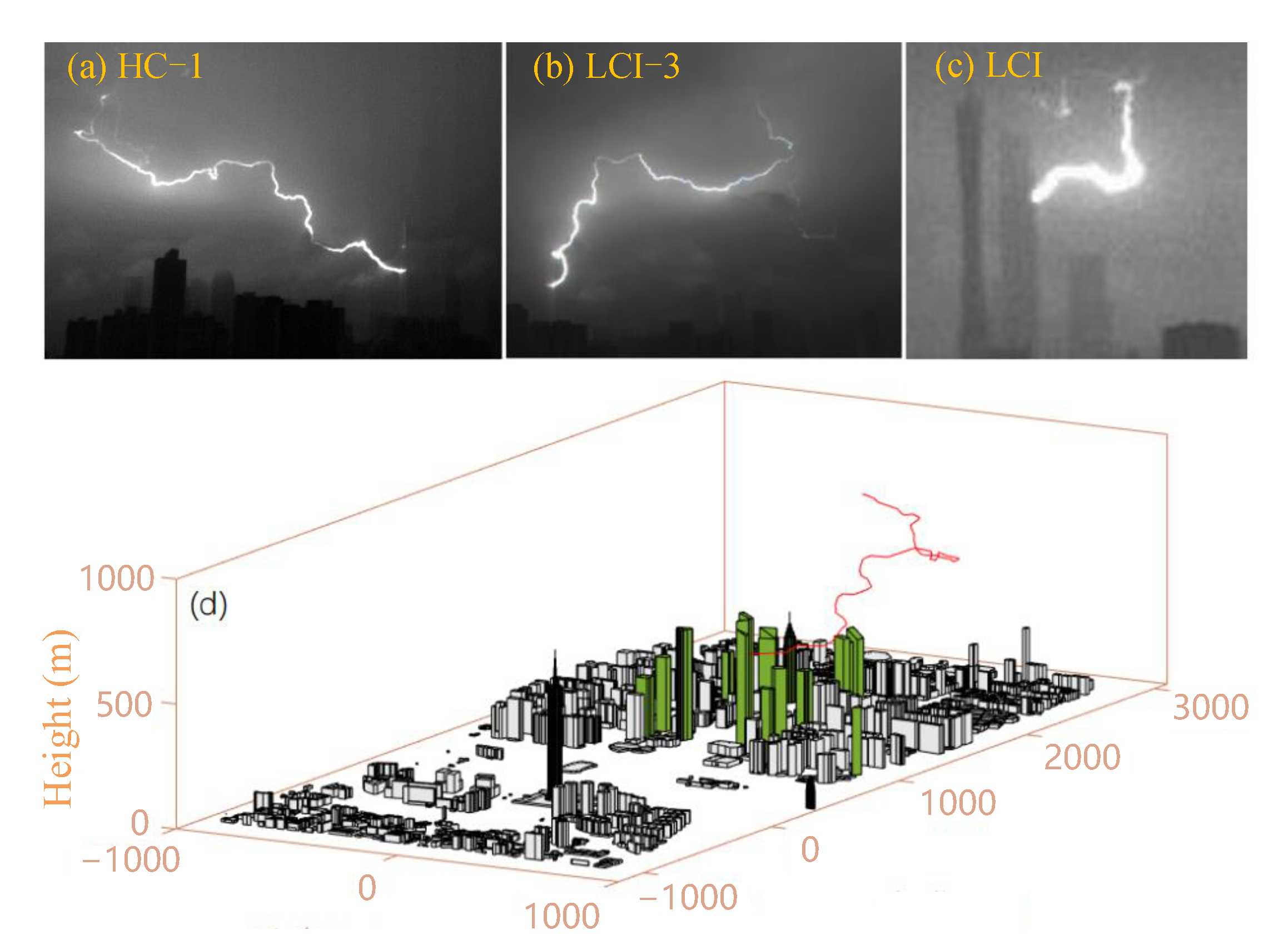
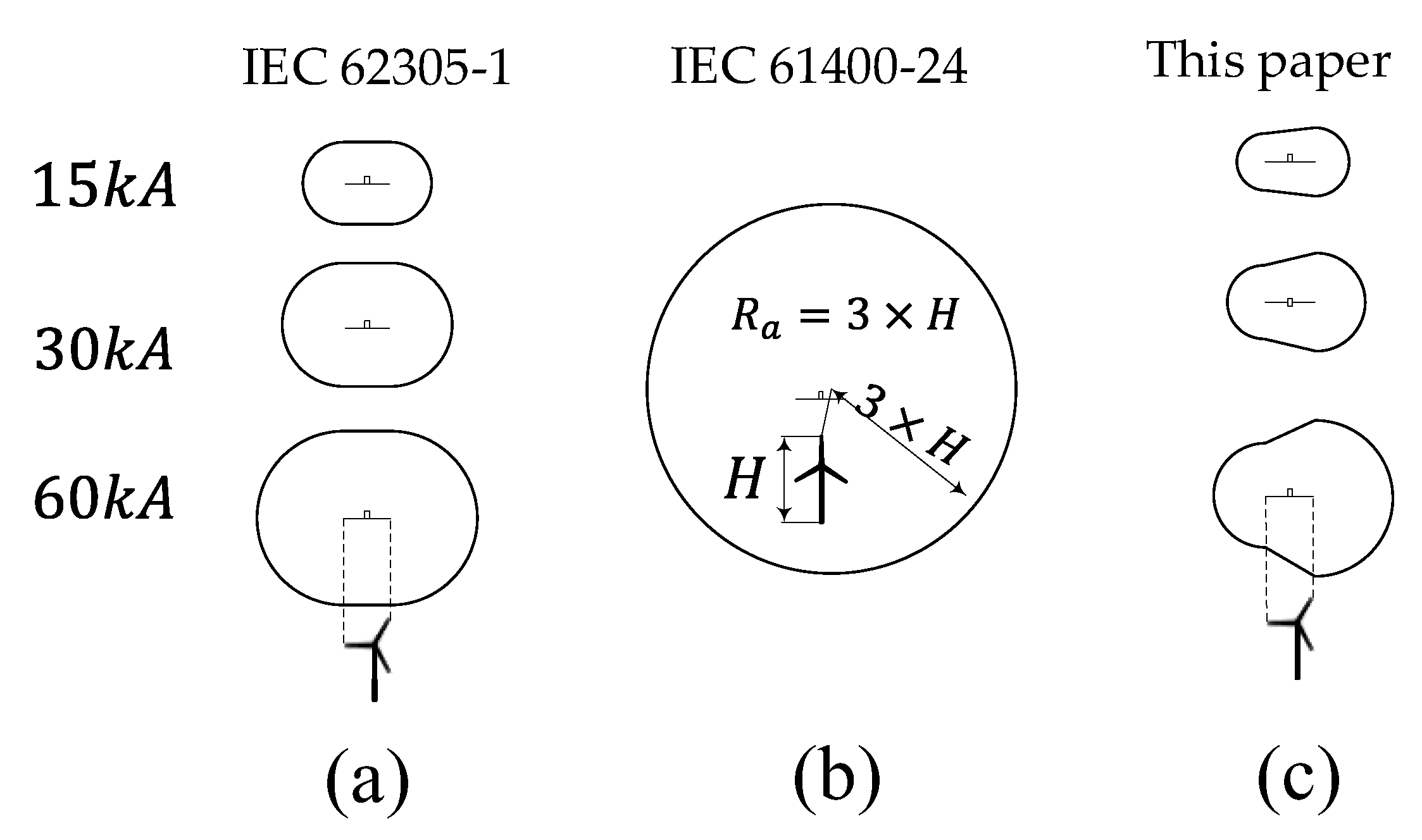

| Model Parameters | Values |
|---|---|
| Simulation area | 5000 × 1500 m |
| Field strength at the ground-level | −5 kV/m or 5 kV/m |
| Field strength at the top boundary | −90 kV/m or 90 kV/m |
| Propagation parameter η | 1 |
| Critical electric field Ecr (DNL and UPL) | 220 kV/m |
| Initiation threshold (UPL) | 400 kV/m |
| Initial length (DL) | 40 m |
| Developed probability formula | Equation (1) |
| The final attachment threshold | 500 kV/m |
| The speed ratio of DL to UL | 4:1 |
| Initiation threshold (UNL) | 750 kV/m |
| Striking Distance/m | Lightning Current Amplitude/kA | |||||
|---|---|---|---|---|---|---|
| 15 | 30 | 60 | 80 | 100 | ||
| 100 m | 108 | 187 | 396 | 475 | 540 | |
| 47 | 83 | 166 | 206 | 239 | ||
| 0.43 | 0.44 | 0.42 | 0.43 | 0.44 | ||
| 150 m | 127 | 219 | 445 | 535 | 632 | |
| 47 | 84 | 165 | 205 | 238 | ||
| 0.37 | 0.38 | 0.37 | 0.38 | 0.38 | ||
| 200 m | 140 | 242 | 494 | 648 | 729 | |
| 45 | 81 | 168 | 205 | 244 | ||
| 0.32 | 0.33 | 0.34 | 0.32 | 0.33 | ||
| Blade Angle of the Wind Turbine | IEC 61400-24 Ra = 3 × H | ||||
|---|---|---|---|---|---|
| 60° | 30° | 60° | |||
| 100 m | 0.037 | 0.042 | 0.046 | 0.342 k | |
| 0.109 | 0.111 | 0.117 | |||
| 0.477 | 0.312 | 0.483 | |||
| 150 m | 0.051 | 0.054 | 0.055 | 0.724 k | |
| 0.151 | 0.154 | 0.155 | |||
| 0.643 | 0.475 | 0.621 | |||
| 200 m | 0.062 | 0.065 | 0.071 | 1.131 | |
| 0.184 | 0.156 | 0.175 | |||
| 0.767 | 0.547 | 0.691 | |||
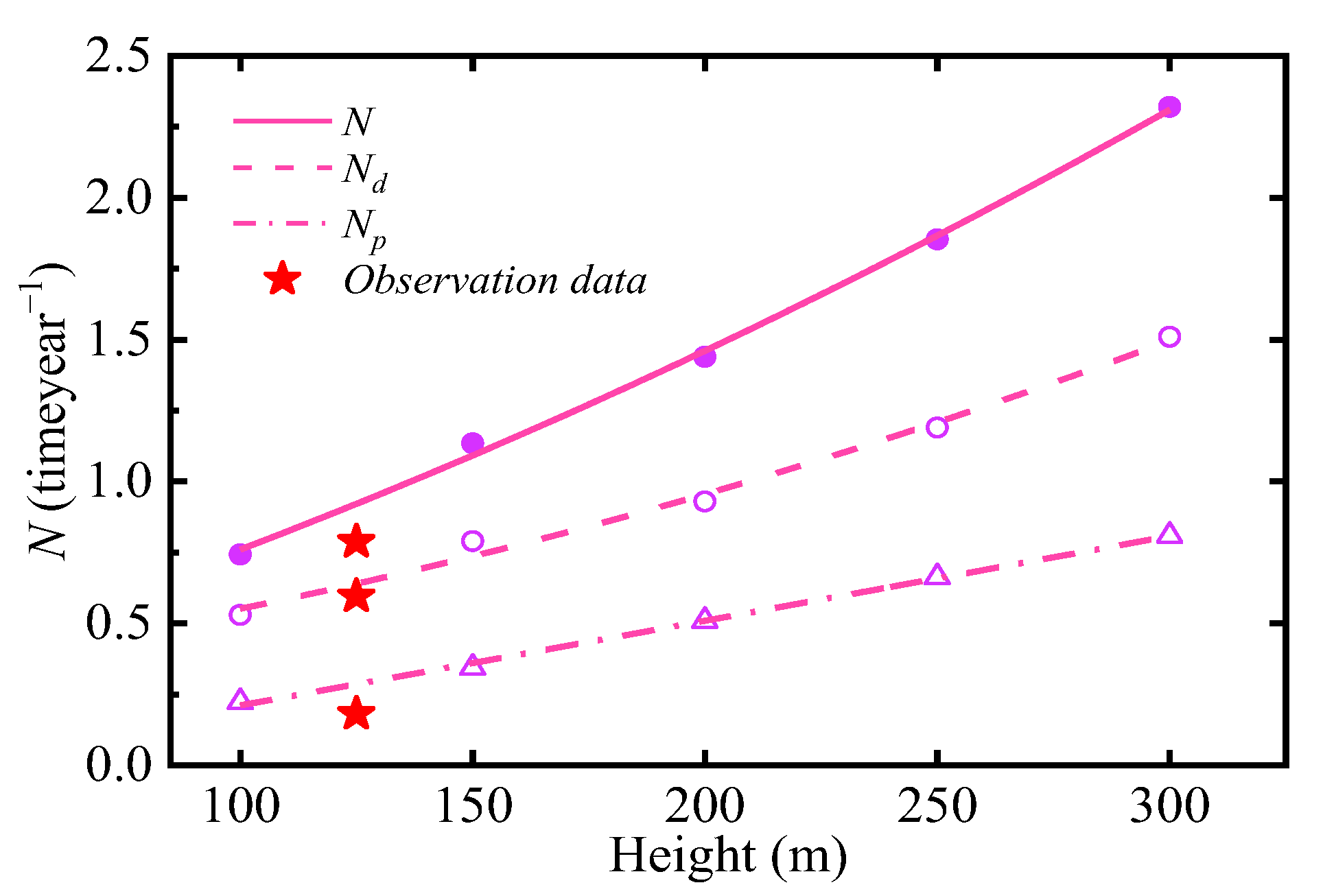
| Model | Observed Data | Difference | |
|---|---|---|---|
| IEC 61400 | 1.02 | 0.5956 (Garolera, 125 m) | 71% |
| IEC 62305 | 0.18 | −70% | |
| Eriksson | 1.16 | 95% | |
| This paper | 0.57 | 4% | |
| IEC 61400 | 2.16 | 0.5956 (Garolera, 125 m) | 263% |
| IEC (EGM) | 0.19 | −68% | |
| Eriksson | 2.45 | 311% | |
| This paper | 0.79 | 32% | |
| IEC 61400 | 3.37 | 0.5956 (Garolera, 125 m) | 466% |
| IEC (EGM) | 0.20 | −66% | |
| Eriksson | 3.83 | 543% | |
| This paper | 0.93 | 56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, X.; Wu, Y.; Zhou, Q.; Jiang, R.; Zhang, Y.; Chen, L.; Qi, Q.; Lyu, W. Simulation of Cloud-to-Ground Lightning Strikes to Wind Turbines Considering Polarity Effect Based on an Improved Stochastic Lightning Model. Atmosphere 2023, 14, 108. https://doi.org/10.3390/atmos14010108
Bian X, Wu Y, Zhou Q, Jiang R, Zhang Y, Chen L, Qi Q, Lyu W. Simulation of Cloud-to-Ground Lightning Strikes to Wind Turbines Considering Polarity Effect Based on an Improved Stochastic Lightning Model. Atmosphere. 2023; 14(1):108. https://doi.org/10.3390/atmos14010108
Chicago/Turabian StyleBian, Xiaoyan, Yong Wu, Qibin Zhou, Ruijiao Jiang, Yao Zhang, Lyuwen Chen, Qi Qi, and Weitao Lyu. 2023. "Simulation of Cloud-to-Ground Lightning Strikes to Wind Turbines Considering Polarity Effect Based on an Improved Stochastic Lightning Model" Atmosphere 14, no. 1: 108. https://doi.org/10.3390/atmos14010108
APA StyleBian, X., Wu, Y., Zhou, Q., Jiang, R., Zhang, Y., Chen, L., Qi, Q., & Lyu, W. (2023). Simulation of Cloud-to-Ground Lightning Strikes to Wind Turbines Considering Polarity Effect Based on an Improved Stochastic Lightning Model. Atmosphere, 14(1), 108. https://doi.org/10.3390/atmos14010108





