Abstract
In this paper, we explore the computational capabilities of advanced modeling tools to reveal the factors that shape the observed benzene levels and behavior under different environmental conditions. The research was based on two-year hourly data concentrations of inorganic gaseous pollutants, particulate matter, benzene, toluene, m, p-xylenes, total nonmethane hydrocarbons, and meteorological parameters obtained from the Global Data Assimilation System. In order to determine the model that will be capable of achieving a superior level of performance, eight metaheuristics algorithms were tested for eXtreme Gradient Boosting optimization, while the relative SHapley Additive exPlanations values were used to estimate the relative importance of each pollutant level and meteorological parameter for the prediction of benzene concentrations. According to the results, benzene levels are mostly shaped by toluene and the finest aerosol fraction concentrations, in the environment governed by temperature, volumetric soil moisture content, and momentum flux direction, as well as by levels of total nonmethane hydrocarbons and total nitrogen oxide. The types of conditions which provided the environment for the impact of toluene, the finest aerosol, and temperature on benzene dynamics are distinguished and described.
1. Introduction
The existing scientific evidence clearly shows that there are no air pollutant concentration limits below which the adverse health effects are excluded [1]. The current estimations warn that exposure to air pollution causes 7 million premature deaths each year globally and contributes to the early onset and exacerbations of noncommunicable diseases, including asthma and other respiratory disorders, coronary and neurodegenerative diseases, and diabetes [2]. The relevant authorities including United Nations (UN) and World Health Organization (WHO) consider air quality control and research imperative to public health and environmental sustainability. As a result, air quality is monitored in more than 6000 cities in 117 countries worldwide compared to 1100 cities in 91 countries a decade ago [3].
In addition to commonly monitored suspended particulate matter (PM) and inorganic gaseous pollutants, a group of volatile organic compounds (VOCs), represented by BTEX (benzene, toluene, ethylbenzene, and xylene) has been the focus of scientific and public interest, due to a large body of literature addressing the benzene carcinogenicity, as well as relationships of its homolog compounds with the respiratory, hematologic, reproductive, and nervous system disorders (e.g., [4,5] and references therein). Seasonal variations in BTEX concentrations have been reported worldwide, with the highest levels registered during the cold season due to the lower atmospheric boundary layer and intensified fossil fuel combustion for heating purposes. On a daily basis, both natural and anthropogenic factors result in pronounced diurnal BTEX concentration dynamics, with peaks occurring in the morning and evening, and the lower values being registered in the meantime [6].
In addition to their detrimental effects on human health, benzene and its homologs are highly reactive compounds and the key precursors for the generation of secondary organic aerosol (SOA) and tropospheric ozone in the atmosphere. Photochemical reactions in which BTEX are involved depend on the sunlight, and the presence of oxidative species such as nitrogen oxides and many short-lived radicals, e.g., OH, alkyl peroxide, and hydrogen peroxide radicals [7,8]. In photochemical reactions, VOCs act as fuel, while NO has a role of a catalyst. At low VOC/NO ratios, which is often recognized as a VOC-limited regime and observed in urban polluted areas, maximum ozone concentrations that result from initial pollutant mixtures are defined by VOC levels, whereas, at high VOC/NO ratios, the O production rate is limited by the supply of NO [9]. In the presence of suspended particles (PM), the photochemical oxidation and subsequent condensation of VOCs lead to the production of SOA. Among volatile organics, alkenes and aromatics including BTEX appeared to possess the highest O formation potential of 59.6%, and 65.3%, respectively, while aromatics also largely contribute to the SOA formation (95%), as reported by Li et al. [10]. Similarly, Zhan et al. [11] concluded that out of 51 VOCs, benzene homologs, toluene and xylenes, were the main species responsible for SOA formation, as well as that alkenes and aromatics dominantly facilitated the production of ground-level O (56.8% and 30.3%, respectively).
The nonlinear nature of BTEX behavior and the seasonal dynamics of their particle–gas partitioning require a multidisciplinary scientific approach and advanced computational capabilities of modeling tools and methods [12] which enable us to research relationships in the environment, enhance our current knowledge and provide the basis for future sustainability. Galán-Madruga and García-Cambero [13] performed multiple linear regression analysis to predict benzene concentration based on the independent atmospheric pollutants and meteorological factors, while Jephcote and Mah [14] used Bayesian multilevel models to provide analysis of benzene exposures from the petrochemical industry, connecting industrial emissions to pollution episodes and disparities in regional mortality rates. Generally, the researchers have combined a variety of methods such as eXtreme Gradient Boosting (XGBoost), Generalized AutoRegressive Conditional Heteroskedasticity (GARCH), neural networks, or light gradient boosting machine (LightGBM) algorithm to predict VOCs, PM, and PAHs concentrations, or haze hazards (e.g., [15,16,17,18,19,20]).
Machine learning methods, capable of interrelating pollutant evolution with the environmental conditions in which it occurs, require adaptations for each individual problem (dataset), which is considered to be a nondeterministic polynomial-hard (NP-hard) challenge by nature. It is extremely time-consuming if this task is done manually. Additionally, NP-hard challenges are not possible to be solved by applying traditional deterministic approaches, as it would require an impractical amount of time and resources. On the other hand, stochastic algorithms, where swarm intelligence metaheuristics algorithms belong, can be used to determine satisfactory solutions within a reasonable time. Thus, some papers have addressed the application of metaheuristic methods for the optimization and training of artificial intelligence techniques or statistical regression models, with the aim to improve their performance and reveal novel information on air quality and its impact on human health [21,22,23].
This paper proposes an XGBoost model tuned by the metaheuristics algorithms for this particular problem, as the survey of the available literature shows that it hasn’t been done before. Eight well-known metaheuristics algorithms were employed to tune the XGBoost hyperparameters with the goal to determine the model that will be capable of achieving a superior level of performance on the observed dataset. Moreover, building on our previous experience in modeling environmental phenomena and machine learning method hyperparameter optimization [15,16,17,24,25,26,27,28], this study aimed to explore the potential of coupling the advanced methodologies to capture and characterize defining factors and processes that shape benzene’s fate in an urban environment. By conducting simulations for the purpose of this research, some of the most promising metaheuristics for tackling combined integer and continuous NP-hard challenges, such as XGBoost tuning, were employed in contextualizing the air pollutant concentrations and meteorological data, and the results of the best-generated model were interpreted using SHapley Additive exPlanations (SHAP). Taking into account that there is a research gap in AI applications for environmental sciences, the proposed research represents a significant contribution to this scientific domain, especially because two families of AI methods, machine learning and metaheuristics, were coupled together to generate a model that can be used to reveal causal relationships between air pollutants and factors governing their behavior, as well as to emphasize what novel conclusions on the environmental phenomena can be drawn by a multidisciplinary approach.
2. Background and Preliminaries
2.1. The XGBoost Algorithm
The XGBoost model utilizes the adaptive training technique to tune the objective function. Accordingly, every step of the tuning procedure is depending on the previous step with respect to the result. The objective function of the XGBoost approach can be mathematically articulated as follows:
where the loss of the tth round is denoted as l, constant term C, and the regularization parameter R of XGBoost, that can be obtained by:
In general, the complexity of the XGBoost tree structure is correlated to the values of and tuning parameters. The increase of the parameters will result in a more simple tree structure of the model. The first and the second derivatives of the XGBoost, named g and h, are calculated in the following way:
Finally, the solution is determined by applying the following two equations:
where the loss function value is denoted by , while the solution’s weight values are represented by .
2.2. Metaheuristic Optimization
Metaheuristics belong to the group of stochastic algorithms, that are commonly used to address NP-hard challenges. These problems are not possible to be solved with traditional deterministic methods, due to their complexity and an impractical amount of required resources. Metaheuristics algorithms are grouped into several distinctive families, still, many authors use different classifications. The mostly adopted taxonomy classifies the metaheuristics based on the natural phenomenon that inspired the search procedure of the given algorithm [29,30,31]. According to this taxonomy, metaheuristics algorithms are classified into nature-inspired algorithms (with two distinctive subgroups, swarm intelligence and genetic algorithms), approaches inspirited by physical phenomena (for example, gravitational or electromagnetic force, waves, etc.), approaches based on human behavior (brainstorming, social networks, teaching, etc.) and mathematics-based approaches (derived from the properties of the sine, cosine, and arithmetical operators).
The swarm intelligence family is based on the animal behavior, typically exhibited by the large groups of individual beings (swarms) that tend to show very coordinated and complex actions while hunting, foraging, migrating and mating [32,33]. The methods belonging to this particular family have established themselves as very efficient optimizers that have been employed recently in a wide spectrum of practical NP-hard challenges. The most notable swarm intelligence algorithms are ant colony optimization (ACO) [34], (PSO) [35], artificial bee colony (ABC) [36], bat algorithm (BA) [37,38], and firefly algorithm (FA) [39], among many others.
The algorithms inspired by fundamental mathematical functions have recently gained popularity. The most important exemplars include the sine–cosine algorithm (SCA) [40] and the arithmetic optimization algorithm (AOA) [41]. The former mimics the mathematical fluctuation of the sine and cosine functions, and the latter relies on basic mathematical operations. Another recent metaheuristic that belongs to this family is the golden sine algorithm (Gold-SA) [42].
The biggest challenge in the application of population-based metaheuristics is summed in the no free lunch (NFL) theorem [43], stating that the universal algorithm that is capable to obtain the best results for all optimization tasks is not existing. In other words, one algorithm can be superior for one particular optimization problem, but completely fail when applied to other problems. Therefore, there is a large diversity in the metaheuristics and their implementations, and the appropriate algorithm must be tailored for every use case.
Some of the most successful contemporary applications of the population-based methods include COVID-19 case number prediction [44,45], cloud computing [46,47,48], cloud-edge computing [49], wireless sensor network tuning [50,51,52,53], feature selection task [54,55], classification of MRI scans and medical applications in general [56,57], global optimization problems [58], credit card frauds [59,60], pollution estimation [61], network security [62,63], as well as general tuning of the machine learning models [64,65,66,67].
The XGBoost model employed in this research has also been subjected to tuning by metaheuristics approaches. The paper [68] tests the classification capabilities of several metaheuristics methods alongside XGBoost, [69] utilizes PSO to address the network intrusion problem, and [70] employs the XGBoost and genetic algorithm (GA) for stock prices forecasting. Moreover, the XGBoost model optimized by metaheuristics has been extensively used as a part of intrusion detection and network security solutions [71,72,73,74].
2.3. Shapley Additive Explanations
The explainability of machine learning model behavior is crucial for understanding the process being modeled. The inability to explain the predictions derived from accurate but complex models posed a severe limitation in understanding the governing factors that shape predictions until recently.
To explain the obtained best-performing model, we applied the advanced explainable artificial intelligence method SHAP. SHAP avoids the trade-off between accuracy and interpretability and provides a straightforward and meaningful interpretation of the machine learning model-derived decisions. The method is based on Shapley values, calculated as a feature importance measure by a game theory approach that provides an impact of features on individual predictions [75]. In brief, Shapley values represent fairly distributed payouts among the cooperating players (features) depending on their contribution to the joint payout (prediction). They apportion the difference between the prediction and the average prediction among the features [76]. Thus, SHAP assigns each feature importance as a measure of its contribution to a particular prediction and interprets the impact compared to a model’s prediction if that feature took some baseline value. This way, the method provides valuable insights into a model’s behavior and (1) overcomes the main drawback of inconsistency, (2) minimizes the possibility of underestimating the importance of a feature with a specific attribution value, and (3) captures feature interaction effects based on a generalization of Shapley values and interpreting the model’s global behavior while retaining local faithfulness [24,77].
We use the relative SHAP values introduced by Stojic et al. [17] to gain insight into relative relationships among feature attributions for each prediction. Relative SHAP values show the relative influence of a feature on the prediction. They are defined as a share of absolute SHAP in total attributed importance of all features for the particular prediction.
This study used Python SHAP implementation (SHAP Python package) and TreeExplainer [77] to obtain SHAP values that we used to produce SHAP dependency plots representing the change of feature importance over its value range.
3. Materials and Methods
3.1. Data
For this study, the concentrations of inorganic gaseous pollutants (NO, NO, NO, O), particulate matter (PM, PM, and PM), and benzene, toluene, m, p-xylene, and total nonmethane hydrocarbons (TNMHC) were obtained from the station of regulatory air quality monitoring Vatrogasni Dom in Pančevo (Serbia). A two-year database (2019–2020) of air pollutants (11,368 hourly concentrations) was complemented by meteorological parameters obtained from the Global Data Assimilation System (GDAS1).
Hourly concentrations of organic (benzene, toluene, and m, p-xylene) and inorganic gaseous pollutants (NO, NO, NO, and O) were obtained using referent sampling devices, according to the European standards EN 14662-3, EN 14211, and EN 14625. GRIMM EDM 180 was used to determine hourly concentrations of particulate matter conferring the standards EN 12341 and EN 14907. Gas chromatograph Syntech Spectras GC955, which separates methane from other hydrocarbons and measures the concentration of methane and other total nonmethane hydrocarbons in the air, was used for measuring concentrations of TNMHC.
3.2. Study Area
Pančevo is a city of over 100,000 inhabitants located on the left bank of the Danube, 20 km east and northeast of Belgrade, the largest Serbian metropolitan area. The sampling site (44°51′31″ N, 20°38′56″ E), characterized as an urban background station, is situated about 500 m south of the city center, surrounded by the residential areas from E and NE sides, and small-scale industry referring scrap metal sorting and storage center, and factory for the flour production in the nearest vicinity. The E70 European corridor, with public transport and intensive vehicle flow, passes by approximately 200 m in the S-SW direction from the sampling site. The confluence of two navigable rivers, Tamiš and Danube, is located at a distance of approximately 500 m in the SW direction. Two kilometers SE stands one of the largest industrial complexes in this part of Serbia. It includes three main factories for producing artificial fertilizers (HTP Azotara), manufacturing chemical products (HTP Petrohemija), and the largest center for oil processing in Serbia (Pančevo Oil Refinery), and a few smaller chemical industrial plants.
3.3. Metaheuristics
This section describes the eight metaheuristics algorithms that were utilized to tune the XGBoost model for the purpose of this research. The chosen algorithms are well-known optimizers, that have been employed to solve various NP-hard challenges in the past, with a great deal of success. All algorithms were used in their original versions, with the control parameters’ values recommended in their respective publications.
3.3.1. Genetic Algorithm
Genetic algorithm (GA) is an evolutionary algorithm inspired by natural selection. The processes of selection, inheritance, crossover, and mutation at the level of cells are simulated. The creator of genetic algorithms to solve various optimization problems was Goldberg [78,79]. The author of the GA is Mirjalili [80].
Initial population individuals have a set of properties which represent chromosomes that are alterable and mutative. Similar to the biological evolution process, GA is modifying the population of individuals over the iterations. In every round of execution, GA takes the best solutions from the population, to produce offspring. As the iterations pass, over several generations, the population as a whole is evolving in the direction of the optimum.
Based on the individual’s fitness, the parents are selected for the creation of the individual in the next generation. Additionally, they can be crossed over by selecting two individuals and exploiting their advantages to create a better one. Finally, the process of mutation can be applied to a single individual to alter its previous properties for better fitness in the next generation. The interested reader can refer to the [80] for more details.
3.3.2. Particle Swarm Optimization
Kennedy and Eberhart developed a heuristic optimization method called Particle Swarm Optimization (PSO) in 1995 [35]. Birds and fish flocking are the main inspirations of the algorithm. The particles, which are considered individuals in the population act as search agents. Their goal is to provide satisfactory solutions for discrete and continuous optimization problems.
The collective experience is shared in search of the best solution, which consists of the individual best experience and those of neighboring solutions. After the evaluation of the gathered experiences, the next move is decided. Initially, random velocities are given to each particle in the generated population, which are represented as initial positions. The particles move over iterations and the best position of each one is stored.
The velocity with which the particle moves is a sum of three components’ weights: the old velocity, the velocity that leads in direction of the best solution so far, and the velocity toward the best solution obtained by neighboring particles.
where the shows a vector consisting of uniformly distributed random numbers in the range of 0 to , randomly generated during each iteration for each particle. The ⨂ represents the componentwise multiplication. Each component of is inside the range of . More details about this algorithm are available in [35].
3.3.3. Artificial Bee Colony
The artificial bee colony (ABC) metaheuristics were developed by Karaboga with the goal to target continuous optimization problems, based on the honey-collecting behavior of the bees [36]. The original ABC implementation puts into use three control parameters, and models three types of bees: workers, onlookers, and scouts, where 50 % of the colony is allocated as worker bees.
This approach models the food sources as the possible solutions of the problem, and each individual food source is allocated with exactly one worker bee. Workers execute the search procedure by investigating the area in the proximity of the solution (food source). The onlookers pick the food source to be exploited with respect to the data collected by workers. Lastly, if the food source is not improved after a defined number of iterations, scout bees will replace it with a novel, arbitrary food source. This procedure is controlled by the parameter, as described in [81].
As stated above, the worker investigates the neighborhood, and if it comes upon a food source, it will evaluate its fitness value. The process of discovering the novel solution in the neighborhood is modeled by ABC search equation given by Equation (8):
where denotes the jth component of the previous solution i, denotes jth component of a discovered solution k, denotes an arbitrary value in range , while denotes a control parameter that controls the modification rate. In case that the fitness of the novel solution is better than the old solution, the worker continues the exploitation of the novel food source. Worker bees share gathered data with onlookers, who will choose a food source i with a probability that is proportional to the solution’s fitness:
For more details about the entire algorithm please refer to the original publication [36].
3.3.4. Firefly Algorithm
The firefly metaheuristics was proposed in 2009 by Yang [82]. The algorithm was based on the flashing behavior exhibited by fireflies. The algorithm utilizes the brightness and attractiveness of these insects, where the brightness is calculated by the value of the objective function, while the attractiveness property is depending on the brightness. When the distance between two fireflies is reduced, the attractiveness is increasing, and vice versa.
The FA search equation defined for an arbitrary solution i, that traverses to the new position in iteration , toward the solution j that is more attractive (brighter), is provided by Equation (10):
where denotes the randomization parameter, is an arbitrary value from the Gaussian or uniform distribution, and marks the distance between solutions i and j. Common values for and parameters are determined as 1 and , respectively, and are suitable for most of the optimization problems. For more details about the entire algorithm please refer to the original publication [82].
3.3.5. Bat Algorithm
Bat algorithm (BA) was proposed in 2010 by Yang [37], and it is inspired by the hunting behavior and echolocation utilized by bats to catch prey or avoid trees and similar obstacles. Bats use sound wave reflection to estimate the distance to nearby objects and to form their images.
Bats execute the search phase by utilizing the Equation (11):
that is used to define the solution’s current position where the locations of the solution in two consecutive rounds of execution are given by and , respectively. The speed of the solution is determined by , calculated with Equation (12):
where represents the latest global best location, and specifies the frequency utilized by ith bat in the population. During the exploitation phase, the algorithm utilizes a random walk procedure to update the position of the current fittest bat. When the prey is located, the bats update their loudness by changing the pulse-emitting rate.
The exploitation relies on the random walk that updates the current best solution, described with the Equation (13):
where the mean loudness of all solutions is given by , while the is a scaling factor given as an arbitrary number in the range .
Finally, when the prey is located, the loudness of bats is updated by utilizing the Equation (14):
where describes the loudness of ith bat in round t, and r represents the pulse emission rate. The parameters and are constants. Additional information about this process is available in [37].
3.3.6. Whale Optimization Algorithm
The whale optimization algorithm was introduced by Mirjalili et al. in 2016 [83], and the algorithm mimics the unique hunting tactic of humpback whales, known as the bubble net method. While executing this maneuver, whales cooperatively dive under the flock of fish, and move upward in spirals while simultaneously blowing bubbles that trap the prey and force it to also swim toward the surface, where it can easily be caught by hunters.
The algorithm implements this bubble net strategy in the exploitation phase, while the exploration is implemented as the pseudorandom search for the fish. As the WOA is a population-based method, the latest best-candidate solution describes the prey, while the remaining solutions represent the whales.
The exploitation bubble net approach assumes that whales circle around the target by moving in the spirals and simultaneously decrease the circle radius, and it can be modeled by switching with equal probability p (determined in each iteration by a random value from 0 to 1), between two options described by the Equation (16):
where denotes the distance between the ith solution and the global best, obtainable by , and b is a fixed value used to control the dimensions of the logarithmic spiral. Finally, parameter l denotes the arbitrary value within .
While executing the exploration, each individual whale updates its location with respect to the location of a random solution rather than to the global best. Vector is employed in a way that if the produced arbitrary values are greater or equal to 1 (), the new location of the whale is directed to the random solution, thus the global search is performed. This is modeled by the Equation (17), as proposed in [83]:
where , representing the distance from the ith solution to the arbitrary solution in iteration t, is obtained as . More details about the WOA are available in the original publication [83].
3.3.7. Harris’ Hawks Optimization
The Harris’ Hawks optimization metaheuristics was inspired by a variety of hunting techniques employed by these hawks to attack and capture the prey in nature. It is one of the most recent algorithms, being introduced by Heidari et al. in 2019 [84].
During the exploration stage, the algorithm tries to discover the solution nearest to the global optimum. The solutions are arbitrarily produced on several positions, and they move closer to the prey in each step, imitating the hawks perching behavior. The algorithm makes use of two methods having the same probability, decided by the parameter q as proposed in [84]:
where q, as well as , , and , denote arbitrary values within the range , that are being updated in each round, denotes the solutions’ location in next round, while , and represent the best, current and average solutions’ locations in the current round t. Lastly, and denote the lower and upper boundaries of the search domain. The average position of the solutions is determined by:
where N is the total count of individuals and denotes the location of solution X in round t.
HHO can transit from exploitation to exploration and vice versa multiple times, with respect to the solution’s strength (representing the prey escaping energy). The strength of the solution is updated in every round in the following way:
where T denotes the maximal number of iterations and is the starting prey’s energy, changing arbitrarily inside the range.
In the exploitation stage, the hawks start attacking the prey, who is trying to flee. The hawks therefore must employ various strategies to overtire the prey for an easy catch. They are moving closer to the target, and mix between soft and hard besiege, based on the target’s remaining energy as follows. If , hawks employ the soft besiege approach, else if , hard besiege is used.
In the situation where and , the prey is still not tired, and the hawks will surround it in a soft manner to exhaust it, as described in the following equations:
where represents a vector difference from the best solution (representing the hawks’ prey) and solution position in round t. Variable J is modified randomly in every iteration to mimic the prey’s escaping technique:
where represents an arbitrary produced value in range . If and , the prey is fatigued and hawks move to a hard attack strategy, where the current locations are being updated by:
If the pray yet has a certain amount of energy remaining, the hawks will use zigzag patterns before the attack, modeled by the next equation:
followed by hawks’ dives in leapfrog patterns defined in the following way:
where D represent the dimensionality of the problem and S denotes a random vector of size, and represent the levy flight function, determined by:
Therefore, the overall strategy to update the locations of the solutions can be obtained as follows:
where Y and Z are obtained by employing the Equations (25) and (26).
Lastly, if and (denoted as hard besiege with progressive rapid dives strategy), the prey is entirely exhausted, and hawks start with a hard attack prior to the final catch of the prey. The hawks start decreasing their mean distance to the target, modeled by:
where, opposite to Equation (28), Y and Z are calculated as follows:
3.3.8. Sine Cosine Algorithm
The sine cosine algorithm (SCA) was introduced by Mirjalili in 2016 [40], and it draws inspiration from the mathematical behavior of the fundamental trigonometric functions. The locations of the solutions are being updated according to the sine and cosine functions’ fluctuations, oscillating in the proximity of the best individual. Similar to other population-based methods, the algorithm begins by producing a collection of arbitrary candidate solutions inside the limits of the search phase. The exploration and exploitation processes are steered during the run by four random modifiable variables. The SCA search equations are defined by Equation (32):
where and represent the observed solution’s location over the ith dimension at successive rounds t and , respectively, are values produced in a pseudorandom manner, the determines the target point’s location (the best currently available approximation of the optimal value) in the ith dimension. It should be stated that, for each part of every individual solution belonging to the population, the new pseudorandom numbers are produced. For more details about the entire algorithm, please refer to the original publication [40].
4. Results
4.1. Metrics
The simulation outcomes of each XGBoost model were evaluated by mean squared error (MSE) calculated as Equation (33), root mean squared error (RMSE) that can be obtained by Equation (34), mean absolute error (MAE) determined by Equation (36), and the coefficient of determination (R2) given by Equation (36).
where and denote the vectors of the observed values that are predicted and predicted values with size N, respectively. In this work, MSE was observed as the objective function that needs to be minimized.
4.2. Experimental Setup
The eight described metaheuristics algorithms were utilized to tune the XGBoost model for the observed dataset. The XGBoost hyperparameters that were tuned, together with their respective bounds and types are listed below:
- learning rate (), range: , continuous parameter,
- min_child_weight, range: , continuous parameter,
- subsample, range: , continuous parameter,
- collsample_bytree, range: , continuous parameter,
- max_depth, range: , integer parameter and
- gamma, range: , continuous parameter.
The count of parameters for softprob objective function (‘num_class’:self.no_classes) was also provided as the parameter to the XGBoost model. The rest of the XGBoost parameters were fixed in the experiments to the default XGBoost values.
The proposed approach was developed in Python programming language, and the common set of machine learning libraries was employed, including scikit-learn, scipy, numpy, and pandas. The XGBoost model was obtained from the scikit-learn package.
In the proposed implementation, the standard solutions’ encoding scheme has been employed as follows. Each metaheuristics solution has been constituted as a vector of size l, where l represents the count of tuned hyperparameters. Consequently, the l for the XGBoost solutions’ was set to six.
All metaheuristics algorithms were implemented independently by the authors, and tested with 40 individuals in the population and 20 iterations per run, over the course of 15 independent runs. As stated before, MSE was set as the objective function that is required to be minimized.
4.3. Experimental Outcomes
This section presents the results obtained through conducted simulations. Table 1 and Table 2 contain the results for the objective function and detailed metrics of the best individual runs, and the best outcomes are noted in bold.

Table 1.
Comparative results of the objective function (MSE) of the observed metaheuristics.

Table 2.
Detailed metrics for the best individual run of the observed metaheuristics.
Table 1 presents detailed comparative metrics for the objective function (MSE) achieved by XGBoost models tuned by the eight observed algorithms. It can be noted that the FA algorithm obtained the best results for all performance indicators (best, worst, mean, median, standard deviation, and variance). The second-best performing algorithm in terms of the best run metric was HHO, while SCA obtained the second-best results for worst, mean, and median indicators. Additionally, baseline XGBoost with default hyperparameters was also evaluated, and it obtained r2 of 0.8762324 with 1.3572 MSE, which is significantly worse than the models’ performance generated by metaheuristics.
Table 2 shows the detailed metrics of the best individual runs of each observed algorithm. Again, it can be noted that the FA outperformed other metaheuristics for all indicators—R2, R, MSE, MAE, and RMSE. In terms of MSE, which was used as the objective function to be minimized, FA was superior with the result of 0.933440, followed by the HHO, which achieved 0.951989, ABC that scored 0.964857, and SCA that finished fourth with the result of 0.980756.
The collection of the XGBoost hyperparameters determined by the best runs of each metaheuristics are shown in Table 3. The best performing algorithm in this scenario was FA, that determined the XGBoost model with a learning rate of 0.338502, max_child_weight of 2.465529, a subsample of 0.895580, collsample_bytree of 1.000000, max_depth of 9, and gamma value of 0.562947. The second best performing method was HHO, that obtained the XGBoost model with a learning rate of 0.365808, max_child_weight of 7.374436, a subsample of 0.943227, collsample_bytree of 0.994926, max_depth of 10, and gamma value of 0.420847.

Table 3.
Best solutions’ determined XGBoost hyperparameters set.
The visualization of the executed experiments is given in Figure 1, presenting the objective convergence graphs, box plots, and violin plots of all eight observed methods for both objective function and R2. Figure 2 first presents the swarm plots for both the objective function and R2, showing the diversity of the population in the last iteration of the best run of each algorithm. Additionally, join plots of both objective function and R2 with histograms for the two best algorithms are also shown in Figure 2.
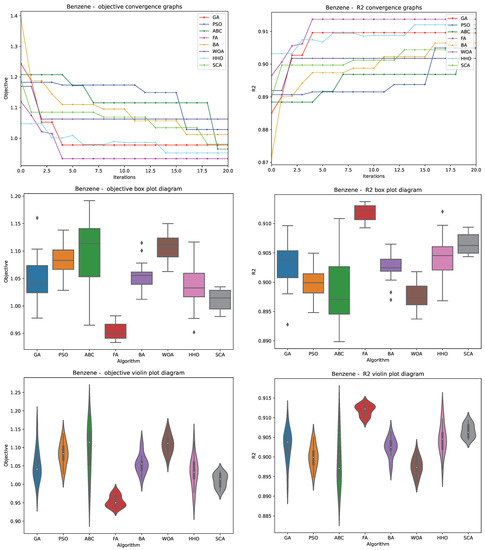
Figure 1.
Visualisations of the conducted simulations for all algorithms in terms of convergence, box plot, and violin diagrams for both objective function and R2.
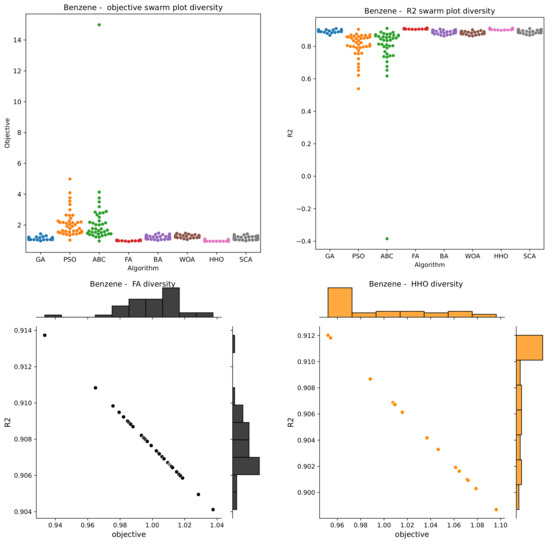
Figure 2.
Visualisations of the conducted simulations for all algorithms in terms of swarm plot diagrams for both objective function and R2, and join plots with histograms of two best methods (FA and HHO).
While observing Figure 1 and Figure 2, it can be concluded that FA algorithm exhibits the fastest converging speed, followed by the HHO algorithm. FA also achieves the most stable results, followed by the HHO and GA, as can be noted from the box plot and swarm plot diversity diagrams.
Finally, the visualization of the best-predicted results achieved by the best-produced model by each one of the eight observed algorithms is shown in Figure 3. Again, it is possible to note that the model tuned by the FA algorithm produced the best forecasts of the observed time series.

Figure 3.
Best predictions by XGBoost model tuned by each observed algorithm.
5. Discussion
Descriptive statistics for the observed pollutant concentrations is provided in Table 4, while the obtained SHAP importance is provided in Table 5. In addition to their use for air quality forecasting [19,85], machine learning models, when supplemented by explainable and model interpretability analyses, provide insight into the significance and impact of considered prediction variables. By applying deep SHAP analysis to NO LSTM forecasting, García and Aznarte [18] registered a significant influence of meteorological parameters on the modeled pollutant concentrations, which has been shown to be in compliance with the well-known natural phenomena in the investigated area. Further, Kang et al. [86] have used SHAP analysis to investigate the seasonal impacts of meteorological factors on the spatiotemporal prediction of NO and O levels. In this study, we have made a step forward by analyzing the air pollutant behavior in a certain type of environment affected by different meteorological conditions and the presence of other polluting species.

Table 4.
Descriptive statistics for the observed pollutant concentrations [g m].

Table 5.
Variable SHAP importance.
To demonstrate the potential of the applied methodology, we provide details on the three most important predictors that describe the evolution of benzene concentration. The interrelations with toluene and finest aerosol fraction dominantly shape benzene concentrations, while other important variables include meteorological parameters temperature (T02M and TMPS), volumetric soil moisture content (SOLM), and momentum flux direction (MOFD), as well as concentrations of total nonmethane hydrocarbons (TNMHC) and total nitrogen oxides (NO).
5.1. Toluene
Although benzene and toluene most often appear as copollutants sharing the same sources (traffic, petrochemical industry, commercial product manufacturing, etc.), their reactivity and atmospheric half-life differ. Namely, toluene contains an electron-releasing methyl group attached to a benzene ring, which makes it more reactive and results in different environmental behavior of toluene and benzene, which can be indicative when distinguishing between emission sources.
The results have shown that benzene and toluene are strongly interrelated, with toluene levels affecting an average of 35% of the benzene concentrations and the decrease of 1.4 g m relative to the expected levels (Table 5). According to the findings, three types of environmental conditions that shape the benzene behavior depending on the toluene concentration range can be identified.
The first environment is characterized by toluene concentrations below 2 g m (Figure 4), as well as low concentrations of all pollutants including aerosol fractions, m, p-xylenes, and NO, except ozone, with the registered values exceeding 70 g m. Within these conditions, the considerable variability of all analyzed meteorological parameters and diverse weather conditions were observed, which indicates consistent emission sources. Additionally, the obtained organic/inorganic gas relations and a toluene-to-benzene ratio above 2 (Figure 4), suggests that the majority of low benzene concentrations assigned to this environment originate from evaporation processes related to petrochemical refinery sources in the southern zone of Pančevo, including equipment leaks from valves or steam power units and leakage during the transport.
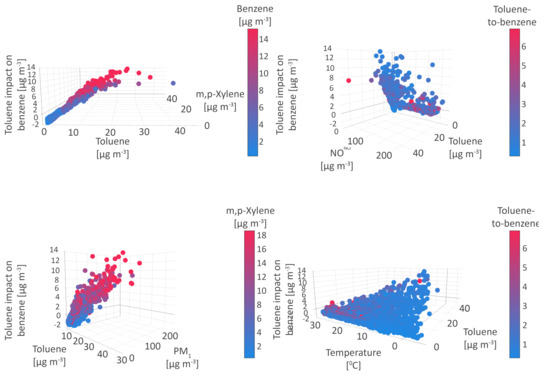
Figure 4.
Toluene impact on benzene.
The second environment refers to toluene concentrations ranging from 2 to 4.5 g m with no registered impact on benzene levels and SHAP values around zero. The belonging concentrations of NO were below 30 g m and above 100 g m, NO levels were below 100 g m and above 170 g m, while PM and TNMHC were below 64 g m and 110 g m, respectively. The observed extreme concentrations of nitrogen oxides, as well as relatively high concentrations of fine particles and lacking relationship between toluene and benzene all point to the strong and intermittent emission source, which can be attributed to HIP Azotara Pančevo, one of the most important regional plant of mineral fertilizers and nitrogen compounds, and agricultural practices on the surrounding farming areas related to heavy use of fertilizers and livestock waste.
Toluene concentrations ranging from 4.5 to 15 g m describe the third environment, which appears to be favorable for elevating benzene concentrations (Figure 4). Within the defined conditions, two subenvironments related to separate emission sources can be distinguished based on the benzene-to-toluene ratio.
The first subenvironment is characterized as highly affecting conditions responsible for driving the observed benzene concentrations up to 14 g m above the expected value. Thereby, the role of toluene seems to be of particular significance, since its relative impact on benzene concentrations increased to 55%. The high levels of benzene were accompanied by high PM, NO, and TNMHC concentrations, as well as ozone levels below 70 g m. Regarding meteorological parameters, the medium- and the highly-supporting environment was related to air temperatures below 15 °C, low wind speeds (below 2 m s), low planetary boundary layer height of 200 m, and high air humidity above 80%, all of which can be assigned to a cold period of the year. During autumn and winter months, these unfavorable meteorological conditions contribute to high concentrations of pollutants originating from fossil fuel burning for heating purposes. Additionally, reactions with photochemically produced hydroxyl radicals, which represent the principal mechanism of vapor-phase toluene and benzene atmospheric removal, are suppressed during the cold months, which results in the prolongation of pollutants’ lifetimes from a few days in the summer season to several weeks in autumn and winter.
The second sub-environment refers to conditions with a lower impact on benzene concentrations (up to 8 g m) that govern high levels of benzene (>15 g m), m, p-xylene (>14 g m), and NO (>40 g m), and above average TNMHC levels (t). Concurrently medium to high air and soil temperatures, air pressure, and humidity, as well as a toluene-to-benzene ratio in the range between 1 and 2, can be attributed to the site-specific and year-round continuous contribution of traffic (Figure 4) [87].
5.2. Particulate Matter (PM)
The aerosol fraction PM and benzene are interrelated in four environments, which define an average of 16.2% observed concentrations and lead to the average increase of about 0.6 g m (Table 5) in benzene levels. In the first case, the benzene concentrations exhibit a decrease by 1 g m, in two of the identified environments benzene levels increase by 2.5 g m, while the interrelationship with PM in the last case does not seem to affect its levels (Figure 5).
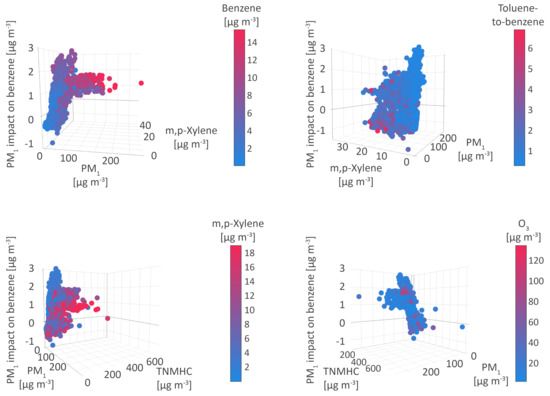
Figure 5.
PM impact on benzene.
In the first environment, the reduction of benzene concentrations by 1 g m is affected by a decrease in PM concentrations to 20 g m and complemented by low concentrations of atmospheric aerosols PM and PM (up to 30 g m) and high concentrations of O (above 70 g m). The concentrations of toluene, TNMHC, and m, p-xylenes are observed in a wide range of values, which disables drawing conclusions on the relationship between particles and VOCs, however, the calculated toluene-to-benzene ratio above 2 suggests the dominant impact of the industrial evaporation processes in this environment [88]. The observed pollutant levels have occurred under low atmospheric pressure, and medium or higher temperatures, planetary boundary layer height, humidity and momentum flux intensity, i.e., the atmospheric conditions that enable vertical mixing, pollutant dispersion and transport. Previous research has shown that, despite the constant pollutant emissions, PM levels could fluctuate up to several times with the change in influential weather variables [89,90]. Some studies have reported elevated PM concentrations under calm weather, mild wind and low planetary boundary layer height, temperature and relative humidity, while findings associating high PM levels with high wind speed and low humidity, or increased precipitations are also available. These contrasting results can be explained by the fact that aerosol water largely impacts complex heterogeneous gas/liquid/solid partitioning of freshly emitted particles and precursor gases.
Medium concentrations of benzene registered in the second environment were independent (SHAP values are zero) of PM levels ranging from 20 to 30 g m, and accompanied by moderate levels of PM, PM, and m, p-xylenes, and higher concentrations of toluene and NO. The prevailing conditions can be described by the average air humidity of 50%, air pressure of 1000 mbar, boundary layer height ranging from 300 to 500 m, and temperatures from 10 to 20 °C.
In the highly affecting environment, the increase of benzene concentrations by 2.5 g m was driven by the PM levels ranging from 30 to 92 g m, under the impact of temperatures below 10 °C, planetary boundary layer heights below 400 m, and medium or higher air pressure and humidity. These meteorological conditions and the toluene-to-benzene ratio below 1 correspond to the cold part of the year when the burning of fossil fuels can be considered the major cause of low air quality.
An additional interrelation pushes benzene levels by 1.5 g m with the PM concentrations exceeding 60 g m, in the fourth environment, defined by higher concentrations of TNMHC, m, p-xylenes, all fractions of atmospheric aerosols, NO and NO, and low O levels. The atmospheric conditions, which can be attributed to the cold part of the year, including low wind speed, temperature, and planetary boundary layer height (up to 2 m s, 10 °C and 400 m, respectively), medium and high air and soil humidity, and high air pressure, created the unfavorable environment for the production of secondary pollutants, which explains the lower concentrations of O, while slightly higher toluene-to-benzene ratio values equal or above 1 indicates the contribution of traffic emissions to high pollutant concentrations during autumn and winter season [91].
5.3. Temperature
Temperature is recognized as the third important parameter that shapes 15.8% of benzene levels, lowering its concentrations by about 0.5 g m on average. Its impact is complex but relatively symmetrical and monotonically decreasing with increasing temperature, with a pronounced positive effect at temperatures lower than 9 °C and a negative effect at temperatures higher than 14 °C (positive/negative effect refers to an increase/decrease of benzene concentrations), Figure 6.
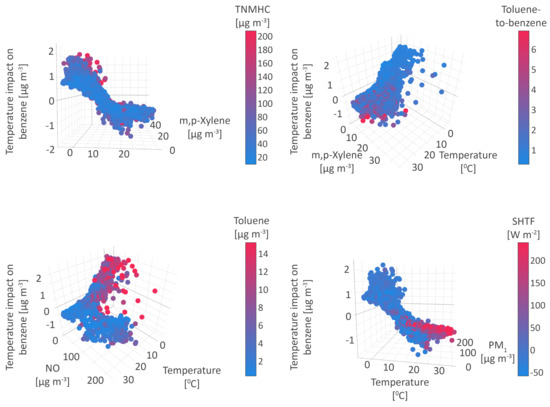
Figure 6.
Temperature impact on benzene.
Within the range of lower temperatures, two environments have been identified. In the first case, the benzene concentration increase up to 1 g m is followed by low to medium concentrations of toluene (2 g m on average), m, p-xylenes (5 g m on average), nitrogen oxides (25 g m on average) and all atmospheric aerosol fractions, low concentrations of O, as well as high cloudiness and intensity of momentum flux, low insolation and air pressure, and a very low planetary boundary layer height of 350 m.
In the second environment, which can be assigned to fossil fuel burning for heating purposes during the cold season, benzene levels increase almost linearly with the drop in temperature by 2.3 g m on average. The increase is followed by high concentrations of aerosols, nitrogen oxides, and benzene (above 12 g m for the latter), extremely low concentrations of O (below 20 g m), stable atmospheric conditions, low temperature, and planetary boundary layer, but high pressure and air humidity.
As shown in Figure 6, interrelations between benzene and temperature, which ranged from 9 to 14 ºC, were apportioned in three subenvironments. In the first case, a positive impact of temperature was accompanied by an increase in benzene concentrations and lower levels of toluene (2.5 g m on average), medium levels of m, p-xylenes (5 g m on average) and NO (38 g m on average), and medium boundary layer heights. Contrary, in the second case, temperature impact reduces to a minimum while the environment is characterized by an increase in the pollutant concentrations, approximately 25%, 35%, and 52% for VOCs, NO, and all particle fractions, respectively. Under these conditions, the elevation of SHTF for 680%, downward short-wave radiation flux (DSWF) for 54%, and LHTF for 26% was observed, while soil moisture (SOLM) and low cloud cover (LCLD) declined for 7% and 28%, respectively. Ambiances with higher PM concentrations and gaseous pollutants have been associated with ambivalent impacts on the surface temperature while an increase in water vapor induces a rise in the shortwave cloud radiative forcing [92]. In addition, SOA formation from precursors such as particles, NO and dominantly the benzene homologs, toluene, and xylene, is enhanced in the presence of water vapor with NO being the most soluble species. Prevalent temperature values in described subarea are not sufficient to render photolysis of VOCs. In the third subarea, when temperature impact is negative, the ambiance is shaped by a decrease of benzene and even higher levels of pollutants (more than 50, 40, and 80% for VOCs, NO, and PM, respectively). Much of the anticipated energy balance concept in the land–atmosphere interactions rely on soil moisture as a key variable. The content of soil moisture depends on atmospheric conditions such as precipitation, radiation, and evaporation, which further alters surface turbulent and radiative heat fluxes. Some studies witnessed that low precipitation suppressed the availability of soil moisture causing a decrease in latent heating (LHTF) and an elevation of sensible heating at the surface (SHTF). These conditions, accompanied by increased temperature, affect atmospheric thermodynamics and the structure of PBL and make the atmosphere less suitable to maintain deep convection. Causality in the coupled land/surface–atmosphere system becomes more complicated in the presence of atmospheric pollutants and variations of local meteorological conditions. For example, suspended particles scatter shortwave radiation and trap longwave radiation to a different extent, which could modify surface temperature and heat fluxes [92].
In the environment with temperatures above 14 °C, benzene concentrations, lower up to 1.5 g m on average, are accompanied by higher concentrations of PM, NO, m, p-xylenes and TNMHC, as well as by low humidity, higher air and soil surface temperatures, and planetary boundary layer heights above 1200 m. In addition to this, the toluene-to-benzene ratio over 3, reflects the industrial activities at the regional chemical plant Azotara Pančevo, which manufactures nitrogen chemicals and mineral fertilizers, but also soil preparation, maturing, and other farm production processes in the surrounding agricultural land during the spring and summer season. Besides, meteorological conditions in the warm season are favorable for benzene removal. In the troposphere, photolysis transforms VOCs or they react with OH and radicals and O. Concerning the reaction rates with the OH radical, which is a dominant loss of most VOCs, lifetimes of benzene, toluene, and xylenes in the air are up to 10 days, 2 days, and 6 hours, respectively, while their presence is up to several years regarding loss by NO radical and O. In the presence of sunlight, the reaction between VOCs and •OH yields a peroxy (•HO) and an alkyl or substituted alkyl radical (•ROO). Such produced radicals further react with NO, converting it to NO, which photolysis forms O. As evident from the presented simplified chemical mechanisms, a photo equilibrium between NO, NO, O, and kinetic reactivity of radicals and VOCs lead to no net formation or loss of O. The VOC/NO, ratio impacts the production of O as follows: (i) the occurrence of NO, sinks (NO-limited conditions) lowers the amount of formed O, and (ii) during VOC-limited conditions, a net formation or loss of OH radicals leads to an intensification or reduction of overall reactivity of all presented VOCs.
6. Conclusions
The air pollutant level dynamics in space and time is extremely intense, and thus air pollution represents a phenomenon of regional and global significance and a real challenge for scientific exploration. The behavior of polluting species in the atmosphere depends on the strength and other characteristics of emission sources, as well as on the atmospheric environment, which provides the conditions for their dispersion, transformation, and removal. Building on our previous experience in modeling environmental pollutant level dynamics, we have employed, coupled, and optimized advanced artificial intelligence modeling tools to investigate and quantify the interrelations between air pollutants and meteorological parameters, and to capture the types of environmental conditions under which air pollutant behavior exhibits certain regularities and consistency. For this study, we have used two-year air quality monitoring and meteorological data to portray types of the environment that shapes the observed benzene levels in the urban area surrounded by large industrial complexes, including plants for the manufacturing of artificial fertilizers, chemical industry, and oil refinery. Among eight algorithms that have been previously confirmed as well-known optimizers by successfully solving nondeterministic polynomial-hard challenges in the past, the firefly algorithm has been shown to achieve a superior level of performance and provide the best results for all performance indicators. As shown, the interrelations between benzene, and toluene and finest aerosol fraction are the most prominent, while the factors which shape the supportive environment for these relationships to take place include meteorological parameters temperature, volumetric soil moisture content, and momentum flux direction, as well as concentrations of total nonmethane hydrocarbons and total nitrogen oxides. Toluene, temperature, and the finest aerosol fraction were recognized to affect 35%, 16.2%, and 15.8% of benzene concentrations, respectively. The first two played role in decreasing benzene levels, while the aerosol–benzene interrelation led to an increase of benzene concentrations of about 0.6 g m. Since there is large space for improvements, considering the fact that the ML models have not been thoroughly tested for environmental datasets (challenges), as part of future research, it was planned to validate other ML models (baseline and tuned by metaheuristics) against the one used in this research and other environmental datasets.
Author Contributions
Conceptualization, A.S. and N.B.; methodology, A.S. and N.B.; software, L.J., N.B. and M.Z.; validation, G.J., M.P., N.B. and A.S.; investigation, N.B., L.J., M.Z., M.P., G.J., F.A., S.S. and A.S.; data curation, M.P.; writing—original draft preparation, N.B., M.P., G.J., F.A., S.S. and A.S.; writing—review and editing, A.S. and N.B.; visualization, A.S. and N.B.; supervision, A.S. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge funding provided by the Institute of Physics Belgrade, through the grant by the Ministry of Education, Science and Technological Development of the Republic of Serbia, the Science Fund of the Republic of Serbia GRANT No. #6524105, AI—ATLAS.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BTEX | benzene, toluene, ethylbenzene, and xylene |
| SHAP | SHapley Additive exPlanations |
| SOA | secondary organic aerosols |
| TNMHC | total non-methane hydrocarbons |
| VOCs | volatile organic compounds |
| XGBoost | eXtreme Gradient Boosting |
| Meteorological paramater | Unit | Label |
| Pressure at surface | hPa | PRSS |
| Pressure reduced to mean sea level | hPa | MSLP |
| Accumulated precipitation (6 h accumulation) | m | TPP6 |
| Momentum flux intensity (3- or 6-h average) | N m | MOFI |
| Momentum flux direction (3- or 6-h average) | ° | MOFD |
| Sensible heat net flux at surface (3- or 6-h average) | W m | SHTF |
| Downward short wave radiation flux (3- or 6-h average) | W m | DSWF |
| Relative Humidity at 2 m AGL | % | RH2M |
| Wind speed at 10 m AGL | m s | WS |
| Wind direction at 10 m AGL | ° | WD |
| Temperature at 2 m AGL | °C | TO2M |
| Total cloud cover (3- or 6-h average) | % | TCLD |
| Geopotential height | gpm * | SHGT |
| Convective available potential energy | J Kg | CAPE |
| Convective inhibition | J Kg | CINH |
| Standard lifted index | °C | LISD |
| Best 4-layer lifted index | °C | LIB4 |
| Planetary boundary layer height | m | PBLH |
| Temperature at surface | °C | TMPS |
| Accumulated convective precipitation (6 h accumulation) | m | CPP6 ** |
| Volumetric soil moisture content | frac. | SOLM |
| Categorial snow (yes = 1, no = 0) (3- or 6-h average) | CSNO | |
| Categorial ice (yes = 1, no = 0) (3- or 6-h average) | CICE | |
| Categorial freezing rain (yes = 1, no = 0) (3- or 6-h average) | CFZR | |
| Categorial rain (yes = 1, no = 0) (3- or 6-h average) | CRAI | |
| Latent heat net flux at surface (3- or 6-h average) | W/m | LHTF |
| Low cloud cover (3- or 6-h average) | % | LCLD |
| Middle cloud cover (3- or 6-h average) | % | MCLD |
| High cloud cover (3- or 6-h average) | % | HCLD |
| * geopotential meters | ||
| ** Beginning with 00 UTC 15 July 2019, CPPA (total accumulation) instead of CPP6 (6-hour accumulation) | ||
References
- Faber, P.; Drewnick, F.; Borrmann, S. Aerosol particle and trace gas emissions from earthworks, road construction, and asphalt paving in Germany: Emission factors and influence on local air quality. Atmos. Environ. 2015, 122, 662–671. [Google Scholar] [CrossRef]
- WHO. Global Air Quality Guidelines Aim to Save Millions of Lives from Air Pollution; WHO: Geneva, Switzerland, 2021; Available online: https://www.who.int/news/item/22-09-2021-new-who-global-air-quality-guidelines-aim-to-save-millions-of-lives-from-air-pollution (accessed on 1 December 2022).
- UN. Global Perspective Human Stories. 2022. Available online: https://news.un.org/en/story/2022/04/1115492 (accessed on 1 November 2022).
- Begou, P.; Kassomenos, P. One-year measurements of toxic benzene concentrations in the ambient air of Greece: An estimation of public health risk. Atmos. Pollut. Res. 2020, 11, 1829–1838. [Google Scholar] [CrossRef]
- Sekar, A.; Varghese, G.K.; Varma, M.R. Analysis of benzene air quality standards, monitoring methods and concentrations in indoor and outdoor environment. Heliyon 2019, 5, e02918. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Gao, F.; Wu, Z.; Li, L.; Li, D.; Zhang, H.; Zhang, Y.; Gao, J.; Bai, Y.; Li, H. A review of atmospheric benzene homologues in China: Characterization, health risk assessment, source identification and countermeasures. J. Environ. Sci. 2020, 95, 225–239. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, Q.; Jie Li, Y.; Zheng, Y.; Liao, K.; Huang, G. Highly oxygenated organic molecules produced by the oxidation of benzene and toluene in a wide range of OH exposure and NO x conditions. Atmos. Chem. Phys. 2021, 21, 12005–12019. [Google Scholar] [CrossRef]
- Deng, Y.; Li, J.; Li, Y.; Wu, R.; Xie, S. Characteristics of volatile organic compounds, NO2, and effects on ozone formation at a site with high ozone level in Chengdu. J. Environ. Sci. 2019, 75, 334–345. [Google Scholar] [CrossRef] [PubMed]
- National Research Council. Rethinking the Ozone Problem in Urban and Regional Air Pollution; National Academies Press: Washington, DC, USA, 1992.
- Li, J.; Deng, S.; Li, G.; Lu, Z.; Song, H.; Gao, J.; Sun, Z.; Xu, K. VOCs characteristics and their ozone and SOA formation potentials in autumn and winter at Weinan, China. Environ. Res. 2022, 203, 111821. [Google Scholar] [CrossRef]
- Zhan, J.; Feng, Z.; Liu, P.; He, X.; He, Z.; Chen, T.; Wang, Y.; He, H.; Mu, Y.; Liu, Y. Ozone and SOA formation potential based on photochemical loss of VOCs during the Beijing summer. Environ. Pollut. 2021, 285, 117444. [Google Scholar] [CrossRef]
- Whaley, C.H.; Galarneau, E.; Makar, P.A.; Moran, M.D.; Zhang, J. How much does traffic contribute to benzene and polycyclic aromatic hydrocarbon air pollution? Results from a high-resolution North American air quality model centred on Toronto, Canada. Atmos. Chem. Phys. 2020, 20, 2911–2925. [Google Scholar] [CrossRef]
- Galán-Madruga, D.; García-Cambero, J.P. An optimized approach for estimating benzene in ambient air within an air quality monitoring network. J. Environ. Sci. 2022, 111, 164–174. [Google Scholar] [CrossRef]
- Jephcote, C.; Mah, A. Regional inequalities in benzene exposures across the European petrochemical industry: A Bayesian multilevel modelling approach. Environ. Int. 2019, 132, 104812. [Google Scholar] [CrossRef]
- Stojić, A.; Maletić, D.; Stojić, S.S.; Mijić, Z.; Šoštarić, A. Forecasting of VOC emissions from traffic and industry using classification and regression multivariate methods. Sci. Total. Environ. 2015, 521, 19–26. [Google Scholar] [CrossRef]
- Perišić, M.; Maletić, D.; Stojić, S.S.; Rajšić, S.; Stojić, A. Forecasting hourly particulate matter concentrations based on the advanced multivariate methods. Int. J. Environ. Sci. Technol. 2017, 14, 1047–1054. [Google Scholar] [CrossRef]
- Stojić, A.; Jovanović, G.; Stanišić, S.; Romanić, S.H.; Šoštarić, A.; Udovičić, V.; Perišić, M.; Milićević, T. The PM2. 5-bound polycyclic aromatic hydrocarbon behavior in indoor and outdoor environments, part II: Explainable prediction of benzo [a] pyrene levels. Chemosphere 2022, 289, 133154. [Google Scholar] [CrossRef] [PubMed]
- García, M.V.; Aznarte, J.L. Shapley additive explanations for NO2 forecasting. Ecol. Inform. 2020, 56, 101039. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Zeng, H.; Zhou, F. PM2. 5 volatility prediction by XGBoost-MLP based on GARCH models. J. Clean. Prod. 2022, 356, 131898. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Zeng, H.; Yu, R. Haze Risk Assessment Based on Improved PCA-MEE and ISPO-LightGBM Model. Systems 2022, 10, 263. [Google Scholar] [CrossRef]
- Belotti, J.T.; Castanho, D.S.; Araujo, L.N.; da Silva, L.V.; Alves, T.A.; Tadano, Y.S.; Stevan, S.L., Jr.; Correa, F.C.; Siqueira, H.V. Air pollution epidemiology: A simplified Generalized Linear Model approach optimized by bio-inspired metaheuristics. Environ. Res. 2020, 191, 110106. [Google Scholar] [CrossRef]
- Yonar, A.; Yonar, H. Modeling air pollution by integrating ANFIS and metaheuristic algorithms. Model. Earth Syst. Environ. 2022, 1–11. [Google Scholar] [CrossRef]
- Drewil, G.I.; Al-Bahadili, R.J. Air pollution prediction using LSTM deep learning and metaheuristics algorithms. Meas. Sens. 2022, 24, 100546. [Google Scholar] [CrossRef]
- Stojić, A.; Stanić, N.; Vuković, G.; Stanišić, S.; Perišić, M.; Šoštarić, A.; Lazić, L. Explainable extreme gradient boosting tree-based prediction of toluene, ethylbenzene and xylene wet deposition. Sci. Total. Environ. 2019, 653, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Šoštarić, A.; Stojić, S.S.; Vuković, G.; Mijić, Z.; Stojić, A.; Gržetić, I. Rainwater capacities for BTEX scavenging from ambient air. Atmos. Environ. 2017, 168, 46–54. [Google Scholar] [CrossRef]
- Stanišić, S.; Perišić, M.; Jovanović, G.; Maletić, D.; Vudragović, D.; Vranić, A.; Stojić, A. What Information on Volatile Organic Compounds Can Be Obtained from the Data of a Single Measurement Site Through the Use of Artificial Intelligence? In Artificial Intelligence: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2021; pp. 207–225. [Google Scholar]
- Stojić, A.; Mustać, B.; Jovanović, G.; Đinović Stojanović, J.; Perišić, M.; Stanišić, S.; Herceg Romanić, S. Patterns of PCB-138 Bioaccumulation in Small Pelagic Fish from the Eastern Mediterranean Sea Using Explainable Machine Learning Prediction. In Artificial Intelligence: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2021; pp. 175–189. [Google Scholar]
- Stojić, A.; Vuković, G.; Perišić, M.; Stanišić, S.; Šoštarić, A. Urban air pollution: An insight into its complex aspects. In A Closer Look at Urban Areas; Nova Science Publishers: New York, NY, USA, 2018. [Google Scholar]
- Stegherr, H.; Heider, M.; Hähner, J. Classifying Metaheuristics: Towards a unified multi-level classification system. Nat. Comput. 2020, 21, 155–171. [Google Scholar] [CrossRef]
- Emmerich, M.; Shir, O.M.; Wang, H. Evolution strategies. In Handbook of Heuristics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 89–119. [Google Scholar]
- Fausto, F.; Reyna-Orta, A.; Cuevas, E.; Andrade, Á.G.; Perez-Cisneros, M. From ants to whales: Metaheuristics for all tastes. Artif. Intell. Rev. 2020, 53, 753–810. [Google Scholar] [CrossRef]
- Beni, G. Swarm intelligence. In Complex Social and Behavioral Systems: Game Theory and Agent-Based Models; Springer: Berlin/Heidelberg, Germany, 2020; pp. 791–818. [Google Scholar]
- Abraham, A.; Guo, H.; Liu, H. Swarm intelligence: Foundations, perspectives and applications. In Swarm Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 3–25. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Yang, X.S.; Slowik, A. Firefly algorithm. In Swarm Intelligence Algorithms; CRC Press: Boca Raton, FL, USA, 2020; pp. 163–174. [Google Scholar]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden sine algorithm: A novel math-inspired algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Zivkovic, M.; Bacanin, N.; Venkatachalam, K.; Nayyar, A.; Djordjevic, A.; Strumberger, I.; Al-Turjman, F. COVID-19 cases prediction by using hybrid machine learning and beetle antennae search approach. Sustain. Cities Soc. 2021, 66, 102669. [Google Scholar] [CrossRef] [PubMed]
- Zivkovic, M.; Venkatachalam, K.; Bacanin, N.; Djordjevic, A.; Antonijevic, M.; Strumberger, I.; Rashid, T.A. Hybrid Genetic Algorithm and Machine Learning Method for COVID-19 Cases Prediction. In Proceedings of the International Conference on Sustainable Expert Systems: ICSES 2020, Lalitpur, Nepal, 28–29 September 2020; Springer Nature: Berlin/Heidelberg, Germany, 2021; Volume 176, p. 169. [Google Scholar]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M.; Zivkovic, M. Task scheduling in cloud computing environment by grey wolf optimizer. In Proceedings of the 2019 27th Telecommunications Forum (TELFOR), Serbia, Belgrade, 26–27 November 2019; pp. 1–4. [Google Scholar]
- Bezdan, T.; Zivkovic, M.; Tuba, E.; Strumberger, I.; Bacanin, N.; Tuba, M. Multi-objective Task Scheduling in Cloud Computing Environment by Hybridized Bat Algorithm. In Proceedings of the International Conference on Intelligent and Fuzzy Systems, Izmir, Turkey, 21–23 July 2020; pp. 718–725. [Google Scholar]
- Bezdan, T.; Zivkovic, M.; Antonijevic, M.; Zivkovic, T.; Bacanin, N. Enhanced Flower Pollination Algorithm for Task Scheduling in Cloud Computing Environment. In Machine Learning for Predictive Analysis; Springer: Berlin/Heidelberg, Germany, 2020; pp. 163–171. [Google Scholar]
- Zivkovic, M.; Bezdan, T.; Strumberger, I.; Bacanin, N.; Venkatachalam, K. Improved Harris Hawks Optimization Algorithm for Workflow Scheduling Challenge in Cloud–Edge Environment. In Computer Networks, Big Data and IoT; Springer: Berlin/Heidelberg, Germany, 2021; pp. 87–102. [Google Scholar]
- Zivkovic, M.; Bacanin, N.; Tuba, E.; Strumberger, I.; Bezdan, T.; Tuba, M. Wireless Sensor Networks Life Time Optimization Based on the Improved Firefly Algorithm. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 1176–1181. [Google Scholar]
- Zivkovic, M.; Bacanin, N.; Zivkovic, T.; Strumberger, I.; Tuba, E.; Tuba, M. Enhanced Grey Wolf Algorithm for Energy Efficient Wireless Sensor Networks. In Proceedings of the 2020 Zooming Innovation in Consumer Technologies Conference (ZINC), Online, 26–27 May 2020; pp. 87–92. [Google Scholar]
- Bacanin, N.; Tuba, E.; Zivkovic, M.; Strumberger, I.; Tuba, M. Whale Optimization Algorithm with Exploratory Move for Wireless Sensor Networks Localization. In Proceedings of the International Conference on Hybrid Intelligent Systems, Sehore, India, 10–12 December 2019; pp. 328–338. [Google Scholar]
- Zivkovic, M.; Zivkovic, T.; Venkatachalam, K.; Bacanin, N. Enhanced Dragonfly Algorithm Adapted for Wireless Sensor Network Lifetime Optimization. In Data Intelligence and Cognitive Informatics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 803–817. [Google Scholar]
- Bezdan, T.; Cvetnic, D.; Gajic, L.; Zivkovic, M.; Strumberger, I.; Bacanin, N. Feature Selection by Firefly Algorithm with Improved Initialization Strategy. In Proceedings of the 7th Conference on the Engineering of Computer Based Systems, Sad Novi Sad, Serbia, 26–27 May 2021; pp. 1–8. [Google Scholar]
- Nadimi-Shahraki, M.H.; Zamani, H.; Mirjalili, S. Enhanced whale optimization algorithm for medical feature selection: A COVID-19 case study. Comput. Biol. Med. 2022, 148, 105858. [Google Scholar] [CrossRef] [PubMed]
- Bezdan, T.; Zivkovic, M.; Tuba, E.; Strumberger, I.; Bacanin, N.; Tuba, M. Glioma Brain Tumor Grade Classification from MRI Using Convolutional Neural Networks Designed by Modified FA. In Proceedings of the International Conference on Intelligent and Fuzzy Systems, Izmir, Turkey, 21 July 2020; pp. 955–963. [Google Scholar]
- Zivkovic, M.; Bacanin, N.; Antonijevic, M.; Nikolic, B.; Kvascev, G.; Marjanovic, M.; Savanovic, N. Hybrid CNN and XGBoost Model Tuned by Modified Arithmetic Optimization Algorithm for COVID-19 Early Diagnostics from X-ray Images. Electronics 2022, 11, 3798. [Google Scholar] [CrossRef]
- Strumberger, I.; Tuba, E.; Zivkovic, M.; Bacanin, N.; Beko, M.; Tuba, M. Dynamic search tree growth algorithm for global optimization. In Proceedings of the Doctoral Conference on Computing, Electrical and Industrial Systems, Costa de Caparica, Portugal, 8–10 May 2019; pp. 143–153. [Google Scholar]
- Jovanovic, D.; Antonijevic, M.; Stankovic, M.; Zivkovic, M.; Tanaskovic, M.; Bacanin, N. Tuning Machine Learning Models Using a Group Search Firefly Algorithm for Credit Card Fraud Detection. Mathematics 2022, 10, 2272. [Google Scholar] [CrossRef]
- Petrovic, A.; Bacanin, N.; Zivkovic, M.; Marjanovic, M.; Antonijevic, M.; Strumberger, I. The AdaBoost Approach Tuned by Firefly Metaheuristics for Fraud Detection. In Proceedings of the 2022 IEEE World Conference on Applied Intelligence and Computing (AIC), Sonbhadra, India, 17–19 June 2022; pp. 834–839. [Google Scholar]
- Bacanin, N.; Sarac, M.; Budimirovic, N.; Zivkovic, M.; AlZubi, A.A.; Bashir, A.K. Smart wireless health care system using graph LSTM pollution prediction and dragonfly node localization. Sustain. Comput. Inform. Syst. 2022, 35, 100711. [Google Scholar] [CrossRef]
- Bacanin, N.; Zivkovic, M.; Stoean, C.; Antonijevic, M.; Janicijevic, S.; Sarac, M.; Strumberger, I. Application of Natural Language Processing and Machine Learning Boosted with Swarm Intelligence for Spam Email Filtering. Mathematics 2022, 10, 4173. [Google Scholar] [CrossRef]
- Stankovic, M.; Antonijevic, M.; Bacanin, N.; Zivkovic, M.; Tanaskovic, M.; Jovanovic, D. Feature Selection by Hybrid Artificial Bee Colony Algorithm for Intrusion Detection. In Proceedings of the 2022 International Conference on Edge Computing and Applications (ICECAA), Coimbatore, India, 21–23 September 2022; pp. 500–505. [Google Scholar]
- Milosevic, S.; Bezdan, T.; Zivkovic, M.; Bacanin, N.; Strumberger, I.; Tuba, M. Feed-Forward Neural Network Training by Hybrid Bat Algorithm. In Proceedings of the Modelling and Development of Intelligent Systems: 7th International Conference, MDIS 2020, Sibiu, Romania, 22–24 October 2020; Revised Selected Papers 7. Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 52–66. [Google Scholar]
- Gajic, L.; Cvetnic, D.; Zivkovic, M.; Bezdan, T.; Bacanin, N.; Milosevic, S. Multi-layer Perceptron Training Using Hybridized Bat Algorithm. In Computational Vision and Bio-Inspired Computing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 689–705. [Google Scholar]
- Bacanin, N.; Stoean, C.; Zivkovic, M.; Jovanovic, D.; Antonijevic, M.; Mladenovic, D. Multi-Swarm Algorithm for Extreme Learning Machine Optimization. Sensors 2022, 22, 4204. [Google Scholar] [CrossRef]
- Jovanovic, L.; Jovanovic, D.; Bacanin, N.; Jovancai Stakic, A.; Antonijevic, M.; Magd, H.; Thirumalaisamy, R.; Zivkovic, M. Multi-Step Crude Oil Price Prediction Based on LSTM Approach Tuned by Salp Swarm Algorithm with Disputation Operator. Sustainability 2022, 14, 14616. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J.; Khandelwal, M.; Yang, H.; Yang, P.; Li, C. Performance evaluation of hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost models to predict blast-induced ground vibration. Eng. Comput. 2021, 38, 4145–4162. [Google Scholar] [CrossRef]
- Jiang, H.; He, Z.; Ye, G.; Zhang, H. Network intrusion detection based on PSO-XGBoost model. IEEE Access 2020, 8, 58392–58401. [Google Scholar] [CrossRef]
- Yun, K.K.; Yoon, S.W.; Won, D. Prediction of stock price direction using a hybrid GA-XGBoost algorithm with a three-stage feature engineering process. Expert Syst. Appl. 2021, 186, 115716. [Google Scholar] [CrossRef]
- Zivkovic, M.; Tair, M.; Venkatachalam, K.; Bacanin, N.; Hubálovskỳ, Š.; Trojovskỳ, P. Novel hybrid firefly algorithm: An application to enhance XGBoost tuning for intrusion detection classification. PeerJ Comput. Sci. 2022, 8, e956. [Google Scholar] [CrossRef]
- Zivkovic, M.; Jovanovic, L.; Ivanovic, M.; Bacanin, N.; Strumberger, I.; Joseph, P.M. XGBoost Hyperparameters Tuning by Fitness-Dependent Optimizer for Network Intrusion Detection. In Communication and Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 947–962. [Google Scholar]
- AlHosni, N.; Jovanovic, L.; Antonijevic, M.; Bukumira, M.; Zivkovic, M.; Strumberger, I.; Mani, J.P.; Bacanin, N. The XGBoost Model for Network Intrusion Detection Boosted by Enhanced Sine Cosine Algorithm. In Proceedings of the International Conference on Image Processing and Capsule Networks, Bangkok, Thailand, 20–21 May 2022; pp. 213–228. [Google Scholar]
- Tair, M.; Bacanin, N.; Zivkovic, M.; Venkatachalam, K.; Strumberger, I. XGBoost Design by Multi-verse Optimiser: An Application for Network Intrusion Detection. In Mobile Computing and Sustainable Informatics; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–16. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. Available online: https://papers.nips.cc/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf (accessed on 17 November 2022).
- Molnar, C. Interpretable Machine Learning. 2020. Available online: https://christophm.github.io/interpretable-ml-book/index.html (accessed on 17 November 2022).
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.E.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization. In Genetic Algorithms and Their Applications: Proceedings of the Second International Conference on Genetic Algorithms; Lawrence Erlbaum: Hillsdale, NJ, USA, 1987; Volume 4149. [Google Scholar]
- Goldberg, D.E.; Deb, K. A comparative analysis of selection schemes used in genetic algorithms. In Foundations of Genetic Algorithms; Elsevier: Amsterdam, The Netherlands, 1991; Volume 1, pp. 69–93. [Google Scholar]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Tuba, M.; Bacanin, N. Artificial Bee Colony Algorithm Hybridized with Firefly Algorithm for Cardinality Constrained Mean-Variance Portfolio Selection Problem. Appl. Math. Inf. Sci. 2014, 8, 2831–2844. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Proceedings of the International Symposium on Stochastic Algorithms, Sapporo, Japan, 26–28 October 2009; pp. 169–178. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Zeng, H.; Shao, B.; Bian, G.; Dai, H.; Zhou, F. A hybrid deep learning approach by integrating extreme gradient boosting-long short-term memory with generalized autoregressive conditional heteroscedasticity family models for natural gas load volatility prediction. Energy Sci. Eng. 2022, 10, 1998–2021. [Google Scholar] [CrossRef]
- Kang, Y.; Choi, H.; Im, J.; Park, S.; Shin, M.; Song, C.K.; Kim, S. Estimation of surface-level NO2 and O3 concentrations using TROPOMI data and machine learning over East Asia. Environ. Pollut. 2021, 288, 117711. [Google Scholar] [CrossRef]
- Ji, X.; Xu, K.; Liao, D.; Chen, G.; Liu, T.; Hong, Y.; Dong, S.; Choi, S.D.; Chen, J. Spatial-temporal Characteristics and Source Apportionment of Ambient VOCs in Southeast Mountain Area of China. Aerosol Air Qual. Res. 2022, 22, 220016. [Google Scholar] [CrossRef]
- Ibragimova, O.P.; Omarova, A.; Bukenov, B.; Zhakupbekova, A.; Baimatova, N. Seasonal and Spatial Variation of volatile organic compounds in ambient air of Almaty city, Kazakhstan. Atmosphere 2021, 12, 1592. [Google Scholar] [CrossRef]
- Shi, Z.; Huang, L.; Li, J.; Ying, Q.; Zhang, H.; Hu, J. Sensitivity analysis of the surface ozone and fine particulate matter to meteorological parameters in China. Atmos. Chem. Phys. 2020, 20, 13455–13466. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, X.; Wang, F.; Brasseur, G.; Chen, S.; Wang, J.; Gao, M. Observed sensitivities of PM2. 5 and O3 extremes to meteorological conditions in China and implications for the future. Environ. Int. 2022, 168, 107428. [Google Scholar] [CrossRef]
- Guo, S.; Wang, Y.; Zhang, T.; Ma, Z.; Ye, C.; Lin, W.; Yang Zong, D.J.; Yang Zong, B.M. Volatile organic compounds in urban Lhasa: Variations, sources, and potential risks. Front. Environ. Sci. 2022, 23, 1337. [Google Scholar] [CrossRef]
- Parida, B.R.; Bar, S.; Roberts, G.; Mandal, S.P.; Pandey, A.C.; Kumar, M.; Dash, J. Improvement in air quality and its impact on land surface temperature in major urban areas across India during the first lockdown of the pandemic. Environ. Res. 2021, 199, 111280. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).