1. Introduction
The tropospheric delay refers to the signal delay caused by signal propagation in the troposphere (the un-ionized part below 50 km). The troposphere represents a neutral atmospheric region in which signal propagation remains frequency-independent, rendering interfrequency differencing ineffective in mitigating delay effects [
1]. In Global Navigation Satellite System (GNSS) data processing, the delay on the signal path is generally calculated using the product of the Zenith Tropospheric Delay (ZTD) and the projection function related to the altitude angle [
2,
3]. On the one hand, tropospheric delay is an important error source in the navigation and positioning process of GNSS [
4,
5]; on the other hand, the water vapor information it contains is the basis for water vapor retrieval in GNSS meteorology [
6,
7]. Therefore, establishing a stable and reliable ZTD model is one of the current GNSS research hot spots.
ZTD models can be divided into two broad categories based on whether meteorological parameters are required. The first type of classic ZTD model requires measured meteorological parameters. Common ones include the Black, Saastamoinen, and Hopfield models [
8], but GNSS monitoring stations in many areas are not equipped with meteorological sensors and cannot obtain meteorological data. To solve this problem, many scholars began to study the second type of model which does not require meteorological parameters, namely, the empirical model, that is, through a large amount of historical empirical data to establish the mapping relationship between various influencing factors and ZTD to estimate ZTD. A series of models have been proposed one after another, such as the Global Pressure and Temperature (GPT) series of models [
9,
10,
11], the University of New Brunswick (UNB) series of models [
12], and the EGNOS model [
13]. Empirical models have gained extensive utilization; however, the simulation of Zenith Wet Delay (ZWD) within ZTD remains intricate and resistant to formulation by means of physical equations. Consequently, this particular model category continues to encounter challenges in satisfying the prerequisites of high-precision GNSS positioning, water vapor retrieving, and related applications [
14].
It is very difficult to study the physical mechanism of ZTD. Data-driven models using machine learning methods have become a popular research topic without explicitly providing physical mechanisms [
15]. Machine learning is widely used in data modeling and prediction because it can solve problems such as classification and prediction and has strong nonlinear fitting capabilities. In recent years, many scholars have used machine learning methods to conduct extensive research on regional ZTD modeling and related fields. Wang et al. used GPS network observation data and the back-propagation neural network (BPNN) algorithm to study a ZTD prediction model. The model exhibits accuracy at the centimeter level; nonetheless, there are specific stations demonstrating suboptimal predictive performance [
16]. Xiao et al. proposed an improved BP neural network, overcoming the shortcomings of over-fitting and instability of the traditional BP neural network. Nevertheless, the model fails to consider the impact of factors such as station distribution and the dimensions of the modeled area on the experimental outcomes [
17]. Yang et al. used an artificial neural network (ANN) to construct the correlation between the ZTD estimated by the GPT3 model and the ZTD calculated by GNSS observation data. The proposed model demonstrates superior performance in ZTD estimation compared to the Saastamoinen model and the GPT3 model. However, an investigation into the impacts of site quantity, site distribution, and training set data volume on the proposed model was not conducted [
18]. Li et al. used the ZTD products provided by IGS and ERA5 data to develop a new regional ZTD model based on the least-squares support vector machine (LSSVM). However, the model’s accuracy is influenced by an inadequate number of training samples and the heightened variability in climatic conditions within the surrounding area [
19]. Later, long short-term memory (LSTM) and Radical Basis Function (RBF) neural networks were used to correct the ZTD value estimated by the GPT3 model in the Antarctic region. The annual average RMSE of the ZTD value calculated by the corrected model was 15.7 mm, which was 10.2 mm smaller than the GPT3 ZTD. However, the accuracy at sites with fewer stations is lower compared to the GPT3 model [
20]. Zhang et al. used the difference between the ZTD calculated by GNSS observation data and the ZTD calculated by the periodic function model as the input dataset to train an LSTM neural network. Utilizing the estimated ZTD in static Precise Point Positioning (PPP) significantly diminishes the convergence time in comparison to conventional PPP methods [
21]. Xu et al. used ERA5 meteorological data to calculate the ZTD value of the measuring stations and proposed an improved tropospheric delay model based on the RBF neural network. The results showed that the accuracy of the ZTD value estimated by the improved model was significantly improved, and the improvement rate is related to the density of the distribution of measuring stations [
22]. Li et al. used Random Forest (RF) to fit the relationship between the residual values of GPT3 ZTD, GNSS ZTD, and spatiotemporal information, then established an improved model of GPT3 ZTD in mainland China. The improved model can more accurately capture the rapid variations in the observed ZTD, and experimental results show that the RMSE of it is 1.83 cm [
23].
While the GPT3 model has become a subject of extensive study, it continues to exhibit certain limitations, particularly when it comes to accurately modeling swift fluctuations in ZTD, frequently linked with extreme weather variations [
24]. Additional ZTD computations can be conducted through the utilization of techniques capable of capturing nonlinear variations, with machine learning methods emerging as a primary focus of research. Within the realm of machine learning algorithms, Generalized Regression Neural Networks (GRNNs) are distinguished by their robust nonlinear mapping capabilities and rapid learning pace, endowing them with a significant advantage in capturing the swift variations in ZTD values. Hence, a GRNN refined ZTD model was developed to enhance the accuracy of ZTD estimates derived from the GPT3 model. This model was built using data sourced from 53 IGS stations located within the European region. The ZTD with high accuracy was also calculated using ERA5 data in the experiments for comparative analysis [
25,
26]. In this study, the primary objective is to develop an enhanced modeling approach capable of accurately capturing the rapid fluctuations in ZTD, and it is user-friendly and does not necessitate intricate preprocessing of prior data. The performance of this model will be thoroughly analyzed and rigorously evaluated. The results are anticipated to serve as a significant reference point in the fields of water vapor inversion, extreme weather forecasting, and precise point positioning (PPP).
The remainder of this article is organized as follows.
Section 2 provides a detailed introduction to the data and methods used in this study.
Section 3 uses experiments to verify the accuracy of the proposed model by comparing it with other models. In
Section 4, based on the proposed model, their impact on modeling accuracy is explored from both spatial and temporal aspects. Finally, a concluding summary is given in
Section 5.
3. Analysis and Results
In order to assess the performance of the GRNN refined model, this study employs the two calculation methods presented in
Section 2.2.1 and
Section 2.2.2 to compute ERA5 ZTD and GPT3 ZTD for the purpose of conducting a comparative analysis. Thus, there are three types of ZTD in the experiments of this article: ERA5 ZTD, GPT3 ZTD, and GRNN ZTD, which are respectively derived from the ERA5 data, GPT3 model, and GRNN optimization model. Three statistics, i.e.,
bias,
RMSE, and Mean Absolute Error (
MAE), are selected as comparison standards. Different statistics highlight different characteristics of the results [
18].
Bias can show the systematic error, that is, the degree of deviation between the predicted value and the true value;
RMSE measures the deviation between the predicted value and the true value, and is more sensitive to outliers in the data;
MAE measures the average distance between each data point and the dataset. The more dispersed the data points, the greater the
MAE. The calculation formulas for the three statistics are as follows:
where
represents the true value,
represents the model value, and
N is the number of samples.
3.1. Preprocessing for Different ZTD
Prior to initiating the model training, it is essential to first temporally align the sample data. While IGS ZTD, GPT3 ZTD, and ERA5 ZTD data for each station have been acquired in
Section 2, they exhibit dissimilar sequence lengths and temporal resolutions. Therefore, a harmonization process is necessary to ensure consistency among these datasets. For one IGS station, the time resolution of its IGS ZTD is 5 min, and there are missing data for several days in a year (the number of missing days is different for each station, and the missing dates are also different). Its GPT3 ZTD and ERA5 ZTD have full sequence length but a temporal resolution of 1 day and 1 h, respectively. In summary, first, consider unifying the time resolutions of the three types of data. Since the GPT3 model has obvious annual and semi-annual cycles and is not sensitive to ZTD changes in a short time (within a few hours), it can be considered that the changes between two adjacent values of GPT3 ZTD are uniform. Therefore, it is reasonable that linear interpolation can be used to expand the GPT3 ZTD from 1 value per day to 24 values per day. Then, the ZTD value corresponding to each hour is extracted from the IGS ZTD, so that the time resolution of the three ZTDs is 1 h. Finally, the date of the missing data was determined based on the IGS ZTD of each station, and the GPT3 ZTD and ERA5 ZTD of the corresponding dates were removed, so that the sequence lengths of the three types of data were consistent. After the processing is completed, a total of 421,800 pieces of data will be available in 2021 from 53 IGS stations.
In accordance with the categorization of station types illustrated in
Figure 1, the consolidated dataset is segregated into two subsets: a training set and a validation set. Data from 43 stations represented by the red circular markers are employed for training the GRNN model, while data from the remaining 10 stations serve as the validation set for assessing the model’s accuracy. The specifics concerning the 10 validation stations can be found in
Table 1.
3.2. Overall Performance of the GRNN Refined Model
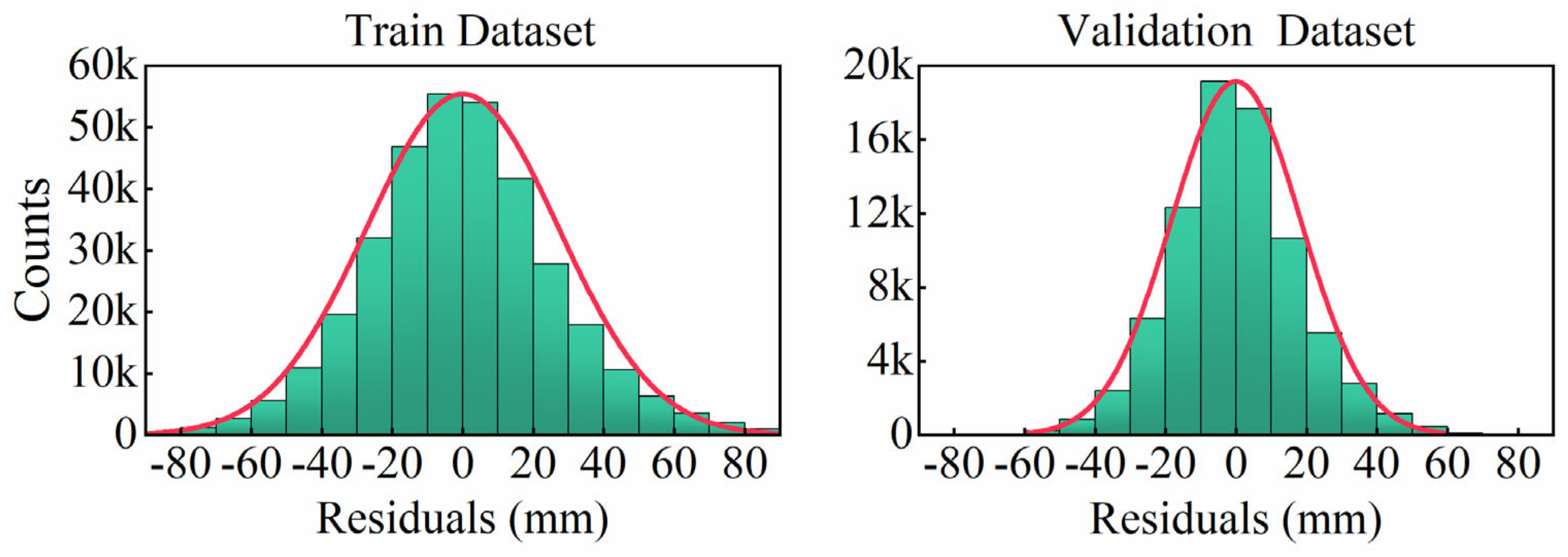
Following the training of the GRNN model with optimized parameters, the performance of the refined GRNN model is assessed for the initial time. This evaluation involves the utilization of statistical indicators derived from both the training and validation sets. The residual histograms of the training set and the test set are shown in
Figure 4. It can be seen that the absolute value of the residual of the training set is within 80 mm, and the absolute value of the residual of the validation set is within 60 mm. They all obey the normal distribution, indicating that the GRNN refined model effectively eliminates systematic deviations. In the training dataset, 52% of residuals fall within the −20 to 20 mm interval, and 86.4% of residuals are contained within the −40 to 40 mm range. And in the validation dataset, 74.75% of residuals are observed within the −20 to 20 mm interval, with 96.15% falling within the −40 to 40 mm range.
Two types of accuracy, training accuracy and validation accuracy, are defined in this experiment. Training accuracy refers to after determining the optimal parameters, the accuracy information of the optimized GRNN ZTD and IGS ZTD obtained by using the 10-fold cross-validation method on the training set. Test accuracy refers to training the final model with the data in the training set, inputting the input parameters in the verification set into the trained model to obtain the optimized ZTD, and comparing it with the IGS ZTD to obtain the accuracy information. To further verify the internal accuracy of the GRNN model, the data of the training set are divided according to the measurement stations, and the training accuracy of each training measurement station is calculated separately, that is, their three statistics of RMSE, bias, and MAE.
As shown in
Figure 5, the RMSE of the training station is mostly distributed in the range of 20–30 mm; the MAE is distributed in the range of 15–25 mm; the bias fluctuates around 0 mm, indicating that the training results of the GRNN refined model have eliminated systematic errors. None of the three statistics of the training stations showed points with large errors, which demonstrated the good performance of the GRNN refined model during model training.
To test whether there is an “over-fitting” phenomenon in the model, this article compares the training accuracy and testing accuracy of the model, as shown in
Table 2. The dataset is comprised of training data from 43 stations and validation data from 10 stations, resulting in 43 and 10 sets of respective statistical metrics. These metrics serve as the basis for deriving the mean, maximum, and minimum values for the three statistical indicators, which are used to assess the two types of accuracy.
Table 2 summarizes the average values of the three statistical indicators of training accuracy and test accuracy, and the square brackets correspond to the maximum and minimum values, respectively. Overall, the three statistical indicators of training accuracy and test accuracy are not significantly different, which shows that the accuracy of the trained model has not declined, and there is no “over-fitting” phenomenon.
3.3. Evaluating the External Accuracy of the GRNN Refined Model
To validate the external accuracy (test accuracy), data from the 10 validation stations listed in
Table 1 were employed. Due to the limited length of the article, 6 of the 10 validation stations were randomly selected for comparison of results, as shown in
Figure 6.
As can be seen from
Figure 6, the GPT3 ZTD of different verification stations can only reflect the general change trend of ZTD but cannot reflect the rapid fluctuation of ZTD. Compared with GPT3 ZTD, ERA5 ZTD and GRNN ZTD are not only more consistent with IGS ZTD but also consistent with the changing trend of IGS ZTD, which shows that they both have higher accuracy. The difference is that the peaks of ERA5 ZTD at rising and falling points are mostly higher than those of IGS ZTD, which indicates that there may be a positive bias in ERA5 ZTD compared with IGS ZTD. It is worth noting that ERA5 ZTD is closer to IGS ZTD than GRNN ZTD at many peaks. This may be due to ERA5 ZTD being calculated from 37-layer measured meteorological parameters, which can be closer to the true value during periods when ZTD changes rapidly.
To further analyze the three models, the ZTD obtained by the three models of GPT3, ERA5, and GRNN is compared with the IGS ZTD. The obtained deviations are recorded as DGPT3, DERA5, and DGRNN, respectively. The residual sequences of the six measuring stations are obtained as shown in
Figure 7. It can be seen from the figure that the change in the range from small to large is DGRNN, DERA5, and DGPT3. At some stations, DGRNN and DERA5 are not very different. Among them, the fluctuation range of DGRNN is the smallest, roughly distributed on both sides of 0 mm, and there is little difference in performance at different stations. However, the performance of DGPT3 and DERA5 at different measuring stations is quite different, which shows that GRNN ZTD has better stability than GPT3 ZTD and ERA5 ZTD. In addition, it can be seen from the figure that in some periods at the BRUX, BUCU, VILL, and WORC stations, when DGPT3 has a large deviation, the DGRNN also has a large deviation value at the corresponding time. This is because the input parameters of the GRNN refined model include GPT3 ZTD, which shows that GPT3 ZTD has a certain impact on GRNN ZTD. At the M0SE station, the fluctuations of the three deviation values are larger than those of other stations. This is because the M0SE station is close to the ocean, and the dramatic changes in water vapor lead to rapid and irregular fluctuations in ZTD. This shows that none of the three models can acutely capture this ZTD change.
The RMSE, bias, and MAE of the three models at 10 verification stations are shown in
Figure 8. It can be seen that the accuracy of measuring stations close to the ocean is relatively poor, and this performance is particularly obvious on GPT3 ZTD. Although the ZTD calculated by ERA5 data has considerable accuracy, its stability is relatively poor compared to the GRNN refined model. In
Figure 8, it can be seen from the color changes that the accuracy of ERA5 ZTD changes at several inland stations, while the GRNN ZTD is relatively stable. In general, GRNN ZTD has the highest accuracy and is the most stable. This reflects the superiority of the GRNN refined model and verifies its applicability in the entire research area.
Table 3 shows the three statistical values of the 10 verification stations and their average values. For GRNN ZTD, RMSE is between 16.40 and 20.37 mm, bias is between −0.67 and 0.66 mm, MAE is between 12.61 and 15.98 mm, and the average values are 18.33 mm, 0.07 mm, and 14.08 mm, respectively. In comparison to ERA5 ZTD and GPT3 ZTD, the introduced model achieved a significant improvement: bias was virtually eliminated, RMSE was diminished by 19.5% and 63.4%, and MAE exhibited a reduction of 24.8% and 67.1%, respectively. The above results show that the overall error of the GRNN refined model is very small, and its overall accuracy still has obvious advantages compared with the ERA5 and GPT3 models. Compared with IGS ZTD, GRNN ZTD has higher consistency and better accuracy. At the same time, it is also noted that at the measuring station M0SE close to the ocean, the accuracy of GRNN ZTD has also declined relative to the overall accuracy. This reflects a common and difficult-to-solve problem, that is, the accumulation of water vapor near the measuring station close to the ocean. The impact of rapid changes and irregular changes in ocean climate on the accuracy of ZTD modeling is difficult to eliminate.
4. Impact of Spatiotemporal Factors on Modeling Accuracy
Numerous factors influence modeling accuracy, including factors associated with the volume of training data within the model, the geographical placement of validation stations, and temporal fluctuations. Consequently, this section is dedicated to investigating the impacts of station spatial distribution and temporal variations on the accuracy of the GRNN refined model.
4.1. Impact of Spatial Factors on Modeling Accuracy
To explore the impact of the distribution of stations on modeling accuracy, this section redesigned an experiment: Selecting one station as the verification station, using the remaining 52 stations as training stations (using their data to train the model), and then using the trained GRNN refined model to verify the ZTD accuracy of this verification station. For example, the OBE4 station is used as the verification measuring station, the remaining 52 stations are used to train the model, and then the trained model is used to verify the ZTD accuracy of the OBE4 station. Experiments were conducted at 10 verification stations in sequence, and the results are shown in
Figure 9. The subfigure in the upper left corner of
Figure 9 shows the location distribution of the 53 stations, the red triangle icon represents the verification measurement station and the blue circular icon represents the training measurement station. The remaining three subfigures represent the bias, RMSE, and MAE of the 10 verification measurement stations, respectively. The darker the color, the higher the accuracy.
It can be seen from
Figure 9 that the small bias measuring stations are almost all located inside the land or in areas with a dense distribution of measuring stations, while the large bias measuring stations are close to the ocean. The GRAC station (6.921° E, 43.754° N) has the largest deviation, which is −0.615 mm. This shows that compared with the distribution of the station, whether it is close to the ocean has a greater impact on the bias of the station. The performance of RMSE and MAE at the same measuring station has good consistency. It can be seen that the accuracy of the measuring station located at the edge of the modeling area is lower than that of the measuring station located in the center of the modeling area. The highest accuracy measuring station is the OBE4 measuring station located in the center (11.277° E, 48.085° N); the RMSE and MAE are 17.36 mm and 13.39 mm, respectively, which is consistent with the experimental results in
Table 4 in
Section 3.3. Further analysis shows that in addition to the influence of the location distribution of the verification station on the accuracy of the model, the influence of the distribution of stations around the verification station on the accuracy cannot be ignored. For example, also located at the edge of the modeling area, the accuracy of the two measuring stations BUCU (26.126° E, 44.464° N) and OP71 (2.355° E, 48.386° N) is lower than the accuracy of the two measuring stations BRUX (4.359° E, 50.798° N) and VILL (3.952° W, 40.443° N). Because the latter serve as the validation station with a denser distribution of nearby stations than the former, this may have a positive impact on their accuracy.
Overall, it is evident that, within the context of regional ZTD modeling, the geographical placement of measuring stations and the density of neighboring sites surrounding the measuring station significantly influence its accuracy. The accuracy of areas located in the center of the modeling area or with dense surrounding sites is higher than in areas located at the edge of the modeling area or with sparse surrounding sites. The smallest measuring station for RMSE and MAE is OBE4, located at the center of the modeling, which is 17.36 mm and 13.39 mm, respectively; the largest measuring station for RMSE and MAE is M0SE, located at the edge of the modeling, which is 21.21 mm and 16.66 mm, respectively. However, it should also be noted that the verification accuracy of WROC measuring stations, which are in a relatively central area and are densely distributed around them, is relatively skewed. This shows that in addition to the factors of the location distribution of the measuring stations, the accuracy of the measuring stations is also affected by other spatial factors, such as latitude and elevation factors. In addition, the distance from the ocean is also a factor that affects the accuracy of the measuring station, because the closer to the ocean, the more drastic the changes in water vapor are.
4.2. Impact of Time Factors on Modeling Accuracy
Usually, climate conditions such as rainfall, temperature, humidity, etc. will change differently in an area at different times of the year. This will affect the ZTD change trend and fluctuation amplitude above the measuring station, and thus affect the accuracy of ZTD modeling. To verify whether the accuracy of the same model changes in different time periods, this section calculates the monthly MAE of 10 verification stations to reflect the error changes of each station from January to December.
Figure 10 plots the relationship between the MAE of the 10 verification stations and each month. The horizontal axis in the figure represents the 10 verification measuring stations, and the vertical axis represents the monthly MAE of a certain measuring station from January to December. Each small grid represents the monthly average absolute deviation value of a certain measuring station in a certain month. The redder the color, the greater the error. It can be intuitively seen from the figure that the red squares are mainly concentrated from June to October, which shows that the monthly average absolute deviation of each station from June to October is larger than that in other months. That is, the accuracy of the model from June to October is worse than the accuracy in other months. In addition, it is noted that the number of red squares and white squares at stations close to the ocean, such as the BRUX, M0SE, and OP71 stations, is higher than that of other stations. This also confirms the conclusion in
Section 4.1 that “the distance from the ocean is also a factor that affects the accuracy of the measurement station”, indicating that the modeling accuracy of the measurement station close to the ocean is relatively low.
For a more detailed examination of the temporal influence on model accuracy, the monthly MAE of each validation station has been collated and is presented in
Table 4. As can be seen from
Table 4, the monthly average absolute deviation values of different measuring stations vary greatly, with the maximum value exceeding 20 mm and the minimum value within 10 mm. Moreover, the monthly MAE of almost every measuring station shows a trend of first increasing and then decreasing, with the maximum values appearing from June to October, which shows that the accuracy of the model is poor from June to October. On the contrary, the minimum value of the monthly average absolute deviation of the measuring station appears from January to March. It is known that the water vapor content is notably higher and exhibits greater complexity during the summer season. These characteristics have a direct bearing on the accuracy of ZWD, leading to reduced precision during summer compared to winter. And this explains well why ZTD has the larger MAE during the summer months.
In summary, the modeling accuracy of the GRNN refined model demonstrates temporal variability. The accuracy of the model from June to October (summer and autumn) is significantly lower than that from January to March (winter) accuracy.
5. Discussion
The newly released GPT3 model has better performance in terms of accuracy and stability than the GPT2w and GPT2 models. However, it primarily portrays the overarching ZTD trend and encounters challenges in accurately capturing rapid fluctuations within a brief time frame. This is a common limitation associated with empirical models. Hence, an improved GPT3 model built upon the foundation of the GRNN is proposed, called the GRNN refined model. It successfully addresses the limitation of the GPT3 model, which struggles to capture the swift variations in ZTD. For the purpose of more extensive comparative analysis, ERA5 ZTD values were additionally computed for 53 stations within the study area using ERA5 data. As depicted in
Figure 6 and
Figure 7, it becomes evident that the GRNN ZTD and ERA5 ZTD exhibit a consistent trend and effectively capture the rapid fluctuations in IGS ZTD. However, there is a noteworthy positive deviation of ERA5 from the IGS ZTD. It is noteworthy that the procedure for ERA5 ZTD entails a substantial level of complexity and demands a significant investment of time and computational resources. This holds true for both the initial data retrieval within the study area and the subsequent ZTD computation. The GRNN refined model is characterized by its relative simplicity, necessitating the inclusion of information pertaining to IGS stations, temporal data, and IGS ZTD for training within the model. This is an absolute advantage for near real-time water vapor inversion, PPP, PPP-RTK, and others. The GRNN refined model combines the advantages of the GPT3 model and the ERA5 data. It can not only reflect the real ZTD rapid fluctuation changes as well as the ERA5 ZTD but is also easy to calculate as the GPT3 ZTD. While the GRNN ZTD exhibits inferior performance compared to ERA5 ZTD at its peak, both models share a consistent trend and effectively capture the fluctuation in ZTD. Furthermore, the GRNN model substantially mitigates bias, whereas ERA5 still retains a non-negligible bias value. Consequently, it can be asserted that the GRNN model outperforms ERA5 in capturing the rapid fluctuations of ZTD.
The experimental outcomes clearly indicate that the GRNN ZTD outperformed the GPT3 ZTD and ERA5 ZTD. The GRNN ZTD effectively eliminated bias, demonstrating an RMSE of 18.33 mm and MAE of 14.08 mm. In comparison to ERA5 ZTD and GPT3 ZTD, RMSE exhibited reductions of 19.5% and 63.4%, respectively, while MAE demonstrated reductions of 24.8% and 67.1%, respectively. As depicted in
Figure 8, it is evident that the GRNN refined model surpasses the other two models, particularly in the coastal region characterized by rapid and intricate water vapor fluctuations. This observation validates its robust and stable performance. Furthermore, an inquiry was conducted to examine the influence of two key factors, namely, spatial and temporal variables, on modeling accuracy. The findings clearly indicated that both temporal and spatial factors exert a notable impact on the accuracy of the modeling process. In the spatial context, it is observed that sites positioned within the central area of the modeled region, or those surrounded by a denser distribution of neighboring sites, typically exhibit higher levels of accuracy in contrast to sites located at the peripheries of the modeled region. For example, the modeling accuracy of OBE4 located at the center of the region (RMSE: 16.40 mm) is 17.86% higher than that of BRUX located at the edge of the region (RMSE: 19.33 mm). Concerning temporal variation, it is noteworthy that modeling accuracy tends to be comparatively lower during the period from June to October as opposed to other months. Notably, the largest monthly mean absolute deviation difference is observed at station OP71, with a magnitude of 14.49 mm. Moreover, several conclusions derived from this research align with previous findings. Specifically, the spatial distribution of stations significantly influences the model’s accuracy, with greater precision achieved through a denser distribution. Additionally, the model’s accuracy is observed to be seasonally dependent, generally exhibiting lower accuracy during summer compared to winter.
Nonetheless, it is important to acknowledge that this study does have certain limitations. Firstly, the GRNN refined model still exhibits a non-negligible error in approximating the true value at its peak, consequently impacting the precision when applying ZTD for water vapor inversion or PPP, leaving room for improvement. Secondly, the study’s reliance on just one year of data may be considered insufficient for constructing a long-term and stable model. Subsequent research endeavors should prioritize expanding the temporal scope of experimental data and exploring the implementation of deep learning models with more intricate structures for ZTD modeling. This approach will enhance the model’s stability and ensure greater alignment with actual ZTD fluctuations. Simultaneously, it will bring the predicted model values, especially at peak points, into closer proximity to the true values, thus fulfilling the exacting requirements of high precision.
6. Conclusions
In this study, a revised GPT3 model for ZTD estimation in Europe based on the GRNN (the GRNN refined model) is proposed. The model uses the spatiotemporal information of the IGS stations and the GPT3 ZTD as input terms and the IGS ZTD as the output term, and the 10-fold cross-validation method is used to determine the hyperparameters of the model. The proposed model is trained and validated employing ZTD data from 53 IGS stations in the European region for the year 2021 as the reference values. To establish the superior performance of the GRNN-derived ZTD obtained through the GRNN optimization model, we conducted comparative analyses with ERA5 ZTD and GPT3 ZTD, calculated using the ERA5 dataset and the GPT3 model, respectively. The results of the research are as follows:
- (1)
The accuracy performance of GRNN ZTD surpasses that of ERA5 ZTD and GPT3 ZTD. Specifically, the bias associated with GRNN ZTD approaches nearly 0 mm. The RMSE and MAE of GRNN ZTD are recorded at 18.33 mm and 14.08 mm, respectively. These values represent a notable increase of 19.5% and 24.8%, as well as 63.4% and 67.1%, in comparison to ERA5 ZTD and GPT3 ZTD, respectively. Moreover, the GRNN refined model demonstrates remarkable stability, notably outperforming the other two models, particularly in the coastal areas characterized by rapid and complex water vapor fluctuations.
- (2)
Both spatial and temporal factors exert a significant influence on modeling accuracy. In terms of spatial considerations, model accuracy is observed to be higher for stations situated in the central regions of the modeling area or those enveloped by a dense distribution of neighboring stations, in contrast to stations positioned at the periphery of the modeling area or surrounded by a sparser distribution of stations. The experimental findings reveal that OBE4 (located in the central region) exhibits an RMSE of 16.40 mm, which is notably 17.86% lower than that of BRUX (positioned at the edge of the region) with an RMSE of 19.33 mm. Temporally, a consistent trend is observed across all stations: the monthly mean absolute deviation exhibits an initial increase followed by a subsequent decrease, with the maximum deviation primarily occurring between June and October. Notably, the largest monthly mean absolute deviation is recorded at station OP71, reaching 14.49 mm. This underscores the influence of temporal factors on modeling accuracy, with the model demonstrating lower accuracy during the summer months in comparison to winter. This discrepancy can be attributed to the intricacies and complexity of climate changes during the summer period.
In future research, in addition to increasing the amount of training data and replacing the training model, other methods to improve accuracy should be considered. On one hand, the incorporation of parameters encompassing atmospheric humidity into the model inputs is contemplated to bring the prediction results into closer alignment with actual values. On the other hand, methodological studies can incorporate sensitivity analyses, by making a small change in the inputs and checking how much the results change and which method provides better results.