A Method for Assessing Background Concentrations near Sources of Strong CO2 Emissions
Abstract
:1. Introduction
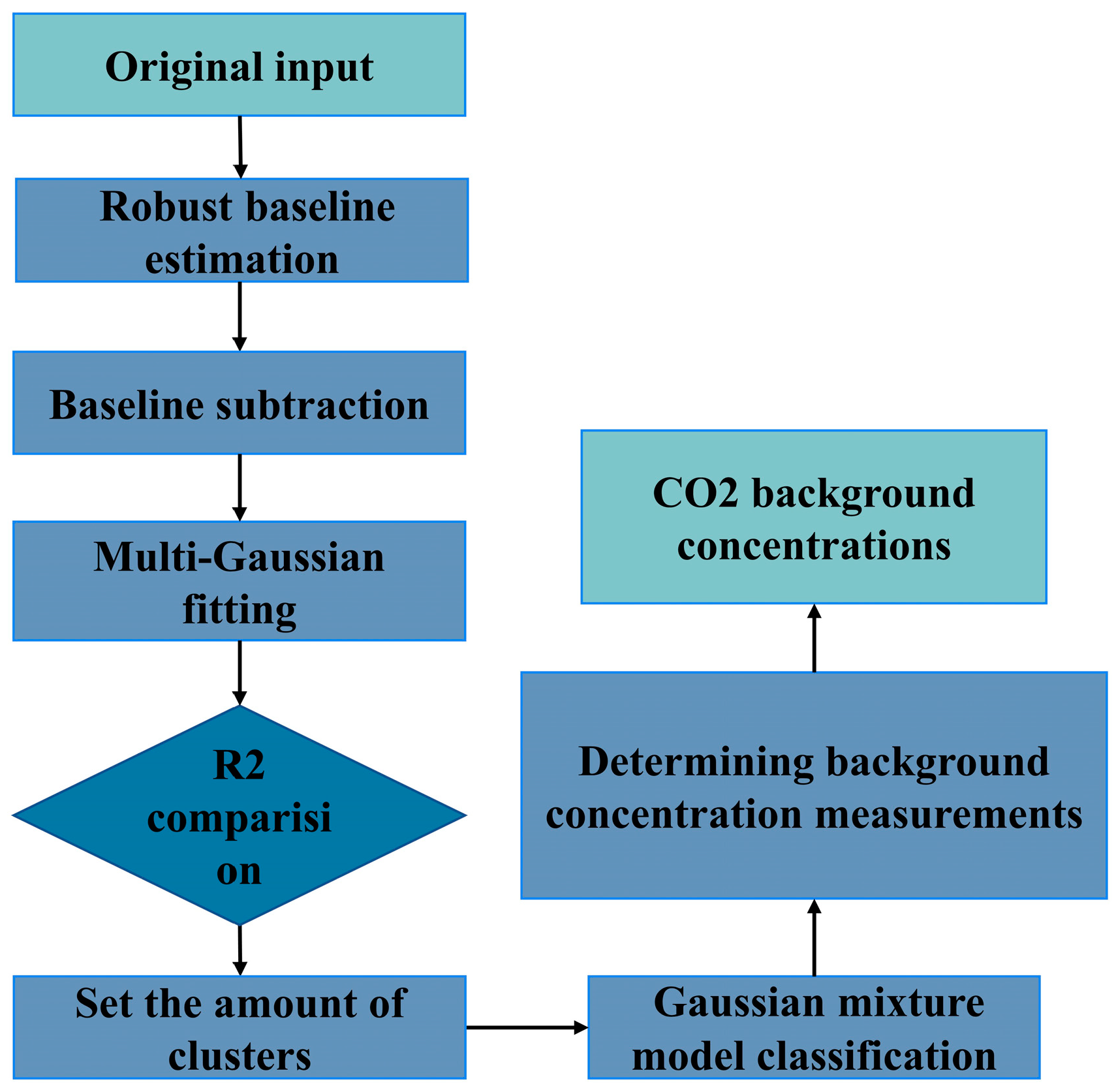
2. Methods
2.1. Robust Local Regression
2.2. Multivariate Gaussian Function Fitting
2.3. Gaussian Mixture Model Clustering
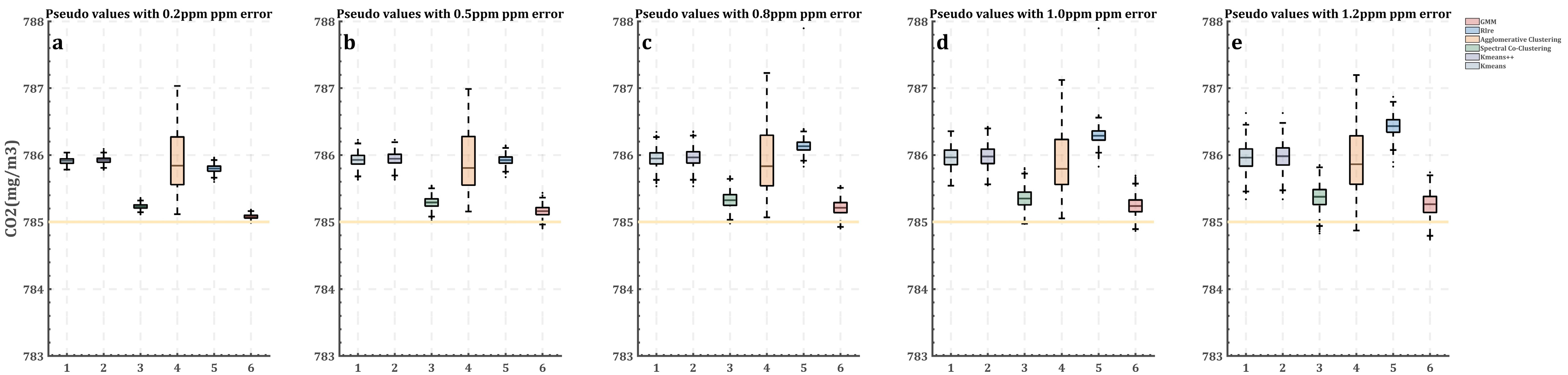
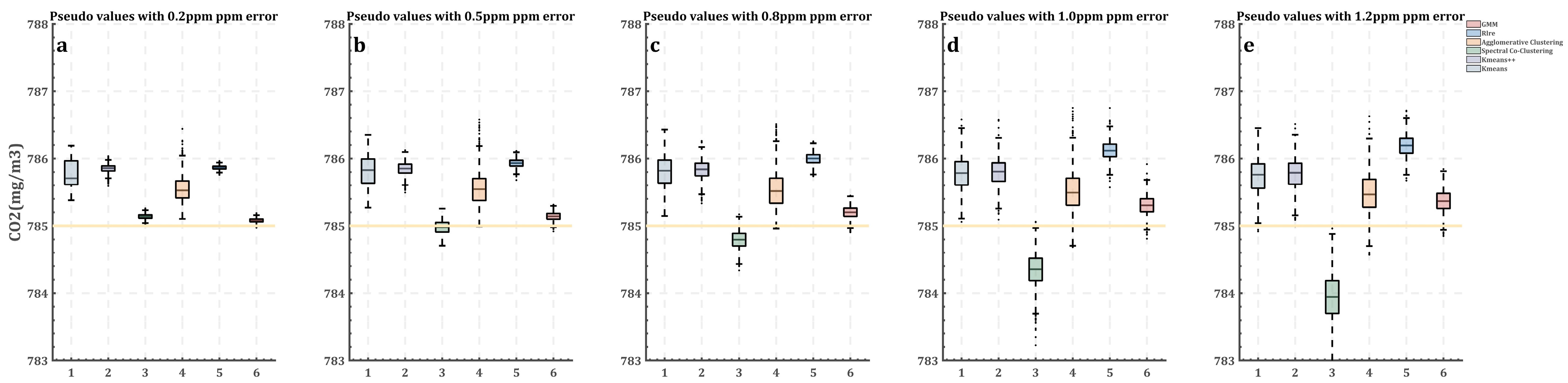
3. Results
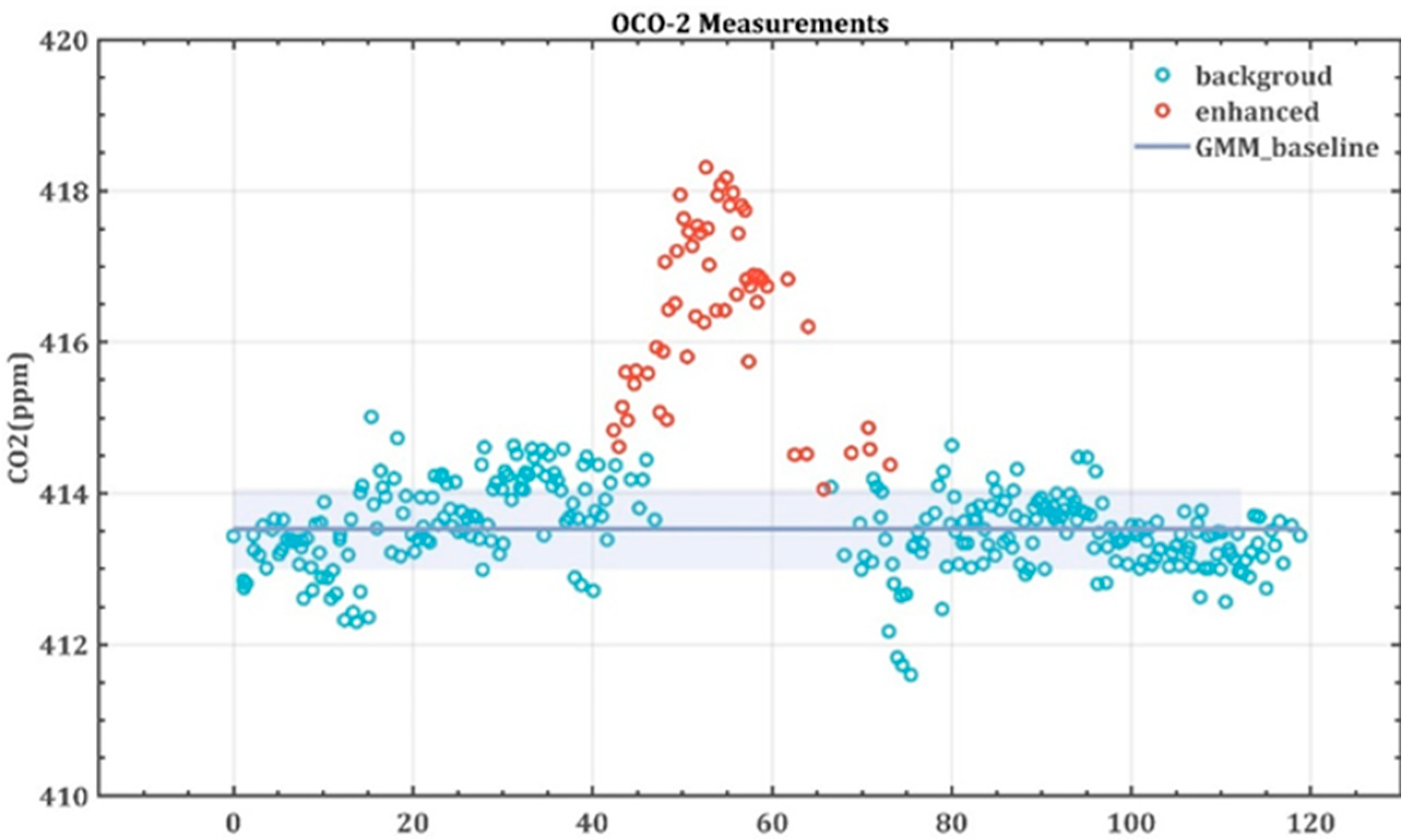
3.1. Estimated CO2 Concentration Background Measurement with 1.2 ppm Measurement Error
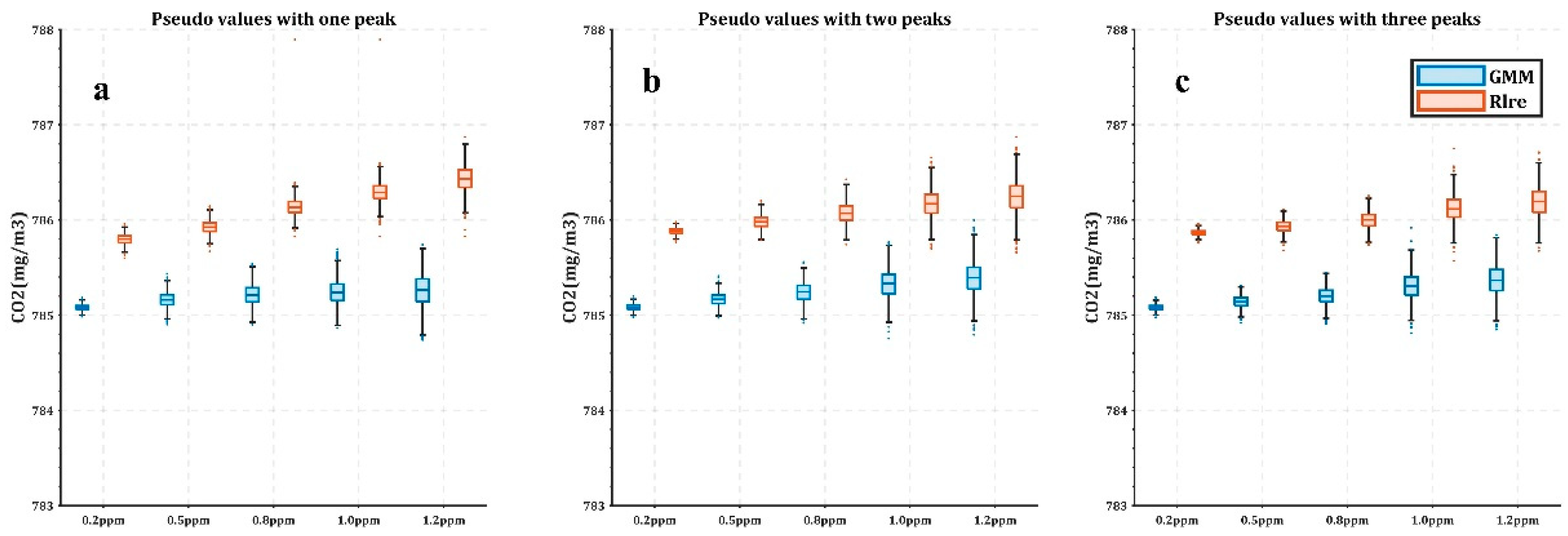
3.2. Multiple Simulation Results
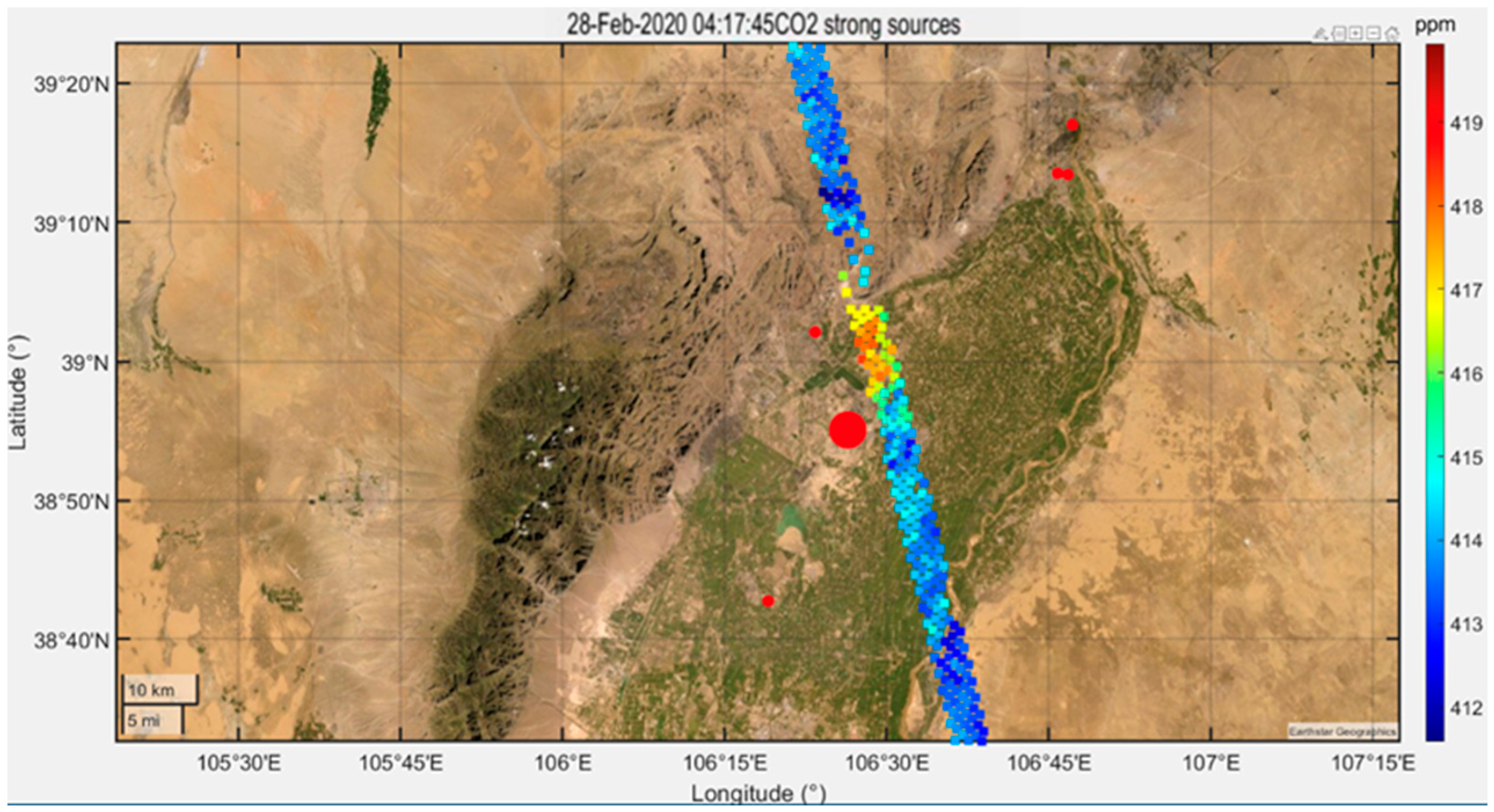
3.3. Real Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, T.; Han, G.; Ma, X.; Zhang, M.; Pei, Z.; Xu, H.; Qiu, R.; Zhang, H.; Gong, W. An inversion method for estimating strong point carbon dioxide emissions using a differential absorption Lidar. J. Clean. Prod. 2020, 271, 122434. [Google Scholar] [CrossRef]
- Zheng, B.; Chevallier, F.; Ciais, P.; Broquet, G.; Wang, Y.; Lian, J.; Zhao, Y. Observing carbon dioxide emissions over China’s cities and industrial areas with the Orbiting Carbon Observatory-2. Atmos. Chem. Phys. 2020, 20, 8501–8510. [Google Scholar] [CrossRef]
- Stocker, T.; Qin, D.; Plattner, G.; Tignor, M.; Allen, S.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, B.; Midgley, B. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2013. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhang, Y.; Hakkarainen, J.; Ju, W.; Liu, Y.; Jiang, F.; He, W. Distinguishing Anthropogenic CO2 Emissions From Different Energy Intensive Industrial Sources Using OCO-2 Observations: A Case Study in Northern China. J. Geophys. Res. Atmos. 2018, 123, 9462–9473. [Google Scholar] [CrossRef]
- Bovensmann, H.; Buchwitz, M.; Burrows, J.P.; Reuter, M.; Krings, T.; Gerilowski, K.; Schneising, O.; Heymann, J.; Tretner, A.; Erzinger, J. A remote sensing technique for global monitoring of power plant CO2 emissions from space and related applications. Atmos. Meas. Tech. 2010, 3, 781–811. [Google Scholar] [CrossRef] [Green Version]
- Cai, M.; Mao, H.; Chen, C.; Wei, X.; Shi, T. Measuring Greenhouse Gas Emissions from Point Sources with Mobile Systems. Atmosphere 2022, 13, 1249. [Google Scholar] [CrossRef]
- Shi, T.; Han, Z.; Han, G.; Ma, X.; Chen, H.; Andersen, T.; Mao, H.; Chen, C.; Zhang, H.; Gong, W. Retrieving CH 4-emission rates from coal mine ventilation shafts using UAV-based AirCore observations and the genetic algorithm–interior point penalty function (GA-IPPF) model. Atmos. Chem. Phys. 2022, 22, 13881–13896. [Google Scholar] [CrossRef]
- Cai, M.; Han, G.; Ma, X.; Pei, Z.; Gong, W. Active–passive collaborative approach for XCO2 retrieval using spaceborne sensors. Opt. Lett. 2022, 47, 4211–4214. [Google Scholar] [CrossRef]
- Shi, T.Q.; Han, G.; Ma, X.; Gong, W.; Chen, W.B.A.; Liu, J.Q.; Zhang, X.Y.; Pei, Z.P.; Gou, H.L.; Bu, L.B. Quantifying CO2 Uptakes Over Oceans Using LIDAR: A Tentative Experiment in Bohai Bay. Geophys. Res. Lett. 2021, 48, e2020GL091160. [Google Scholar] [CrossRef]
- Andersen, T.; Scheeren, B.; Peters, W.; Chen, H. A UAV-based active AirCore system for measurements of greenhouse gases. Atmos. Meas. Tech. 2018, 11, 2683–2699. [Google Scholar] [CrossRef]
- Messerschmidt, J.; Geibel, M.C.; Blumenstock, T.; Chen, H.; Deutscher, N.M.; Engel, A.; Feist, D.G.; Gerbig, C.; Gisi, M.; Hase, F.; et al. Calibration of TCCON column-averaged CO2: The first aircraft campaign over European TCCON sites. Atmos. Chem. Phys. 2011, 11, 10765–10777. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Broquet, G.; Caldow, C.; Laurent, O.; Gichuki, S.; Cropley, F.; Yver-Kwok, C.; Fontanier, B.; Lauvaux, T.; Ramonet, M.; et al. Near-field atmospheric inversions for the localization and quantification of controlled methane releases using stationary and mobile measurements. Q. J. R. Meteorol. Soc. 2022, 148, 1886–1912. [Google Scholar] [CrossRef]
- Liu, B.; Ma, X.; Ma, Y.; Li, H.; Jin, S.; Fan, R.; Gong, W. The relationship between atmospheric boundary layer and temperature inversion layer and their aerosol capture capabilities. Atmos. Res. 2022, 271, 106121. [Google Scholar] [CrossRef]
- Shi, T.; Han, Z.; Gong, W.; Ma, X.; Han, G. High-precision methodology for quantifying gas point source emission. J. Clean. Prod. 2021, 320, 128672. [Google Scholar] [CrossRef]
- Shi, T.Q.; Ma, X.; Han, G.; Xu, H.; Qiu, R.N.; He, B.; Gong, W. Measurement of CO2 rectifier effect during summer and winter using ground-based differential absorption LiDAR. Atmos. Environ. 2020, 220, 10. [Google Scholar] [CrossRef]
- Luo, B.; Yang, J.; Song, S.; Shi, S.; Gong, W.; Wang, A.; Du, L. Target Classification of Similar Spatial Characteristics in Complex Urban Areas by Using Multispectral LiDAR. Remote Sens. 2022, 14, 238. [Google Scholar] [CrossRef]
- Nathan, B.J.; Golston, L.M.; O’Brien, A.S.; Ross, K.; Harrison, W.A.; Tao, L.; Lary, D.J.; Johnson, D.R.; Covington, A.N.; Clark, N.N.; et al. Near-Field Characterization of Methane Emission Variability from a Compressor Station Using a Model Aircraft. Environ. Sci. Technol. 2015, 49, 7896–7903. [Google Scholar] [CrossRef]
- Andersen, T.; Vinkovic, K.; de Vries, M.; Kers, B.; Necki, J.; Swolkien, J.; Roiger, A.; Peters, W.; Chen, H.L. Quantifying methane emissions from coal mining ventilation shafts using an unmanned aerial vehicle (UAV)-based active AirCore system. Atmos. Environ.-X 2021, 12, 100135. [Google Scholar] [CrossRef]
- Fujinawa, T.; Kuze, A.; Suto, H.; Shiomi, K.; Kanaya, Y.; Kawashima, T.; Kataoka, F.; Mori, S.; Eskes, H.; Tanimoto, H. First Concurrent Observations of NO2 and CO2 From Power Plant Plumes by Airborne Remote Sensing. Geophys. Res. Lett. 2021, 48, e2021GL092685. [Google Scholar] [CrossRef]
- Xu, W.; Wang, W.; Wang, N.; Chen, B. A New Algorithm for Himawari-8 Aerosol Optical Depth Retrieval by Integrating Regional PM2.5 Concentrations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Toon, G.C.; Connor, B.J.; Fisher, B.; Osterman, G.B.; Frankenberg, C.; Mandrake, L.; O’Dell, C.; Ahonen, P.; et al. A method for evaluating bias in global measurements CO2 Total Columns Space. Atmos. Chem. Phys. 2011, 11, 12317–12337. [Google Scholar] [CrossRef] [Green Version]
- Qiu, R.; Li, X.; Han, G.; Xiao, J.; Ma, X.; Gong, W. Monitoring drought impacts on crop productivity of the US Midwest with solar-induced fluorescence: GOSIF outperforms GOME-2 SIF and MODIS NDVI, EVI, and NIRv. Agric. For. Meteorol. 2022, 323, 109038. [Google Scholar] [CrossRef]
- Qiu, R.N.; Han, G.; Ma, X.; Xu, H.; Shi, T.Q.; Zhang, M. A Comparison of OCO-2 SIF, MODIS GPP, and GOSIF Data from Gross Primary Production (GPP) Estimation and Seasonal Cycles in North America. Remote Sens. 2020, 12, 258. [Google Scholar] [CrossRef] [Green Version]
- Nassar, R.; Moeini, O.; Mastrogiacomo, J.-P.; O’Dell, C.W.; Nelson, R.R.; Kiel, M.; Chatterjee, A.; Eldering, A.; Crisp, D. Tracking CO2 emission reductions from space: A case study at Europe’s largest fossil fuel power plant. Front. Remote Sens. 2022, 3. [Google Scholar] [CrossRef]
- Nassar, R.; Mastrogiacomo, J.P.; Bateman-Hemphill, W.; McCracken, C.; MacDonald, C.G.; Hill, T.; O’Dell, C.W.; Kiel, M.; Crisp, D. Advances in quantifying power plant CO2 emissions with OCO-2. Remote Sens. Environ. 2021, 264, 112579. [Google Scholar] [CrossRef]
- Nassar, R.; Hill, T.G.; McLinden, C.A.; Wunch, D.; Jones, D.B.A.; Crisp, D. Quantifying CO2 Emissions From Individual Power Plants From Space. Geophys. Res. Lett. 2017, 44, 10045–10053. [Google Scholar] [CrossRef] [Green Version]
- Pei, Z.P.; Han, G.; Ma, X.; Shi, T.Q.; Gong, W. A Method for Estimating the Background Column Concentration of CO2 Using the Lagrangian Approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Pei, Z.P.; Han, G.; Ma, X.; Su, H.; Gong, W. Response of major air pollutants to COVID-19 lockdowns in China. Sci. Total Environ. 2020, 743, 140879. [Google Scholar] [CrossRef]
- Ruckstuhl, A.F.; Jacobson, M.P.; Field, R.W.; Dodd, J.A. Baseline subtraction using robust local regression estimation. J. Quant. Spectrosc. Radiat. Transf. 2001, 68, 179–193. [Google Scholar] [CrossRef]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 433–439. [Google Scholar] [CrossRef]
- Dhillon, I.S. Co-clustering documents and words using bipartite spectral graph partitioning. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 269–274. [Google Scholar]
- Murtagh, F.; Legendre, P. Ward’s hierarchical agglomerative clustering method: Which algorithms implement Ward’s criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, D.A. Gaussian mixture models. Encycl. Biom. 2009, 741, 827–832. [Google Scholar]
- Moon, T.K. The expectation-maximization algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Chen, C.; Wang, H.; Xu, N.; Liu, C.; Gao, J. A Method for Assessing Background Concentrations near Sources of Strong CO2 Emissions. Atmosphere 2023, 14, 200. https://doi.org/10.3390/atmos14020200
Sun Q, Chen C, Wang H, Xu N, Liu C, Gao J. A Method for Assessing Background Concentrations near Sources of Strong CO2 Emissions. Atmosphere. 2023; 14(2):200. https://doi.org/10.3390/atmos14020200
Chicago/Turabian StyleSun, Qingfeng, Cuihong Chen, Hui Wang, Ningning Xu, Chao Liu, and Jixi Gao. 2023. "A Method for Assessing Background Concentrations near Sources of Strong CO2 Emissions" Atmosphere 14, no. 2: 200. https://doi.org/10.3390/atmos14020200
APA StyleSun, Q., Chen, C., Wang, H., Xu, N., Liu, C., & Gao, J. (2023). A Method for Assessing Background Concentrations near Sources of Strong CO2 Emissions. Atmosphere, 14(2), 200. https://doi.org/10.3390/atmos14020200



