Next Article in Journal
Assessing the Spatial Distribution of NO2 and Influencing Factors in Urban Areas—Passive Sampling in a Citizen Science Project in Berlin, Germany
Next Article in Special Issue
Assessment of the Sea Surface Salinity Simulation and Projection Surrounding the Asian Waters in the CMIP6 Models
Previous Article in Journal
Evaluation of Atmospheric Environmental Regulations: The Case of Thermoelectric Power Plants
Previous Article in Special Issue
Numerical Study on Storm Surge Level Including Astronomical Tide Effect Using Data Assimilation Method
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 14
Issue 2
10.3390/atmos14020359
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Atlantic Meridional Mode and Associated Wind–SST Relationship in the CMIP6 Models

by
Fannyu Xia
1,2,3,
Jinqing Zuo
2,3,*,
Chenghu Sun
1 and
Ao Liu
1,3
1
State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, China Meteorological Administration, Beijing 100081, China
2
Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters (CIC-FEMD), Nanjing University of Information Science & Technology, Nanjing 210044, China
3
CMA Key Laboratory for Climate Prediction Studies, National Climate Centre, China Meteorological Administration, Beijing 100081, China
*
Author to whom correspondence should be addressed.
Atmosphere 2023, 14(2), 359; https://doi.org/10.3390/atmos14020359
Submission received: 10 January 2023 / Revised: 6 February 2023 / Accepted: 8 February 2023 / Published: 11 February 2023
(This article belongs to the Special Issue Recent Advances in Researches of Ocean Climate Variability)
Browse Figures
Versions Notes

Abstract

:
The Atlantic Meridional Mode (AMM) is the dominant mode of interannual climate variability in the tropical Atlantic, maintained primarily by the positive wind–evaporation–sea surface temperature (SST) feedback in which the wind anomalies lead the SST anomalies by ~2 months. A previous study revealed that climate models from Coupled Model Intercomparison Project Phase 5 (CMIP5) show poor performance in simulating the AMM-related wind–SST relationship, but the possible causes remain unclear. This study assesses the representation of the AMM and associated wind–SST relationship in the climate models from CMIP6. Results show that most of the CMIP6 models can reasonably reproduce the observed spatial pattern of the AMM, with significant SST and wind anomalies in the northern tropical Atlantic and weak anomalies in the equatorial–southern oceans. However, the simulated wind–SST relationship associated with the AMM varies among the models. In particular, several models fail to capture the observed wind–SST relationship; that is, the simulated wind anomalies peak in boreal spring as in the observations, but no obvious peak occurs in the corresponding SST anomalies. Further analysis suggests the models that fail to capture the observed wind–SST relationship tend to simulate a stronger mean trade wind and a thicker mixed layer in the northern tropical Atlantic, leading to a weaker ocean–atmosphere coupling and, thus, a weaker SST response to the wind forcing. Moreover, there exists a significant out-of-phase relationship between the strength of ocean–atmosphere coupling and mean mixed layer depth among the models, supporting the impact of mean state biases on the AMM variability in the models.

1. Introduction

The Atlantic Ocean shows several important climate phenomena at different time scales [1], including the Atlantic Meridional Mode (AMM), the Atlantic Niño (also referred to as the Atlantic zonal mode or Atlantic equatorial mode) and the Atlantic Multi-decadal Oscillation [2]. Among them, the AMM is the dominant coupled mode between the sea surface temperature (SST) and wind anomalies in the tropical Atlantic at an interannual time scale, which features south-to-north C-shape-like surface wind anomalies across the equator and north–south reversal of SST anomalies [3,4]. The AMM is a thermodynamic mode that is driven primarily by the wind–evaporation–SST (WES) feedback, with the wind anomalies leading the SST anomalies by approximately 1–2 months, whereas the positive subtropical stratocumulus–SST feedback may also play a role in maintaining the AMM [5,6,7,8,9,10]. The AMM is most pronounced in boreal spring and could persist into the following summer [3]. The northern lobe of the AMM is consistent with the northern tropical Atlantic (NTA) pattern [11].
Previous studies have revealed that the AMM has a considerable impact on the Atlantic hurricane activity [12] and precipitation variability in the surrounding countries [13,14,15]. Moreover, SST anomalies associated with the AMM, particularly those in the NTA region, can also modulate interannual climate variability in the region beyond the tropical Atlantic through atmospheric teleconnection [16]. For example, boreal spring warming of the NTA can trigger cold SST anomalies in the tropical Pacific in the following winter [17,18]. Through atmospheric teleconnection, the AMM can also exert an impact on the Indian summer monsoon [19,20] and the western North Pacific–East Asian climate variability [11,21,22,23,24,25,26,27]. Therefore, it is crucial to assess the ability of climate models in simulating spatiotemporal characteristics of the AMM and associated physical mechanism, as the model is an essential tool for learning the mechanisms of past climate change and predicting the future.
However, due to the complexity of the global climate system, accurate simulations of the climatological mean and climate variability in the tropical Atlantic still pose a problem for most of the current climate models [28,29,30,31,32]. Despite the coupled atmosphere–ocean models having received much improvement over the last decades, they still exhibit significant disparities from the observations [9]. Indeed, much attention has been paid to the model’s ability to simulate the climate mean states, climate variability and climate impacts in the Atlantic Ocean (e.g., [33,34,35,36]). Mean state biases in the tropical Atlantic can affect model performance in simulating the local climate variability and even that in the regions beyond through atmospheric teleconnection [37,38,39]. With a focus on the multi-model ensemble mean, the spatial pattern of the AMM and the WES feedback in maintaining the pattern in the climate models of the last generation have been evaluated in a previous study [40]. They found that the climate models that participated in Coupled Model Intercomparison Project Phase 5 (CMIP5) still have a lot of room for improvement in simulating the spatially coherent interactions between the AMM-related SST and wind anomalies in the tropical Atlantic [40]. However, the possible causes of model biases in simulating the AMM-related wind–SST relationship still remain unclear.
Therefore, the present study attempts to assess the representation of the AMM in the climate models of the current generation, and more importantly, the causes of associated model biases in simulating the AMM will be explored. Section 2 introduces the data and methods used as well as the climate models involved in this paper. Section 3 presents the spatial pattern of the AMM and associated wind–SST relationship in the CMIP6 historical simulations, followed by conclusions in Section 4.

2. Data and Methods

Historical simulations from 28 climate models that participated in Coupled Model Intercomparison Project Phase 6 (CMIP6) are used in this study [41]. The variables we used include monthly mean SST, surface wind stress, latent and sensible heat fluxes, precipitation and mixed layer depth (MLD). For the models without MLD output, we define MLD as the depth where the sea temperature is 0.5 °C lower than the surface temperature (i.e., SST) [42]. The CMIP6 historical simulations branch from piControl and are forced by observed climate forcing, including time-evolving atmospheric compositions, solar variability, volcanic aerosols and land cover/land use for the period of 1850–2014 [41]. Table 1 shows the modeling centers and resolutions for the individual models used in the present paper. All the model outputs were regridded to a 1°×1° regular grid prior to our analysis.
For comparison, we use SST data from the Met Office Hadley Centre Sea Ice and Sea Surface Temperature (HadISST) dataset on a 1° × 1° grid from 1870 to the present [43]. We obtained monthly 1° × 1° surface wind stress and MLD from the European Centre for Medium Range Weather Forecasts (ECMWF) Ocean Reanalysis System 5 (ORAS5; [44,45]) for the period 1959–2022. Zonal and meridional components of 10 m wind, precipitation and latent and sensible heat fluxes were obtained from the ERA5 reanalysis dataset on a 1° × 1° grid [46]. We limit our analysis to 1960–2014 as the observations and the CMIP6 historical simulations are both available during this period.
In this study, the AMM is obtained by applying a singular value decomposition (SVD) analysis to the monthly SST and wind anomalies in the tropical Atlantic. Prior to the SVD analysis, all fields are linearly detrended and smoothed with a 3-month running average at each grid point. The NTA and ATL3 indices are constructed as the regional-averaged SST anomalies over 5–25° N and 60° W–0° E and 3° S–3° N and 20° W–0°, respectively. In addition, we remove the linear signal of ENSO by regressing out the Nino3.4 index (5° N–5° S, 170° W–120° W) in winter (December–January–February) for the NTA index. The seasons refer to those in the Northern Hemisphere. The two-tailed Student’s t test is used to assess the statistical significance of regression coefficient as well as correlation coefficient.

3. Results

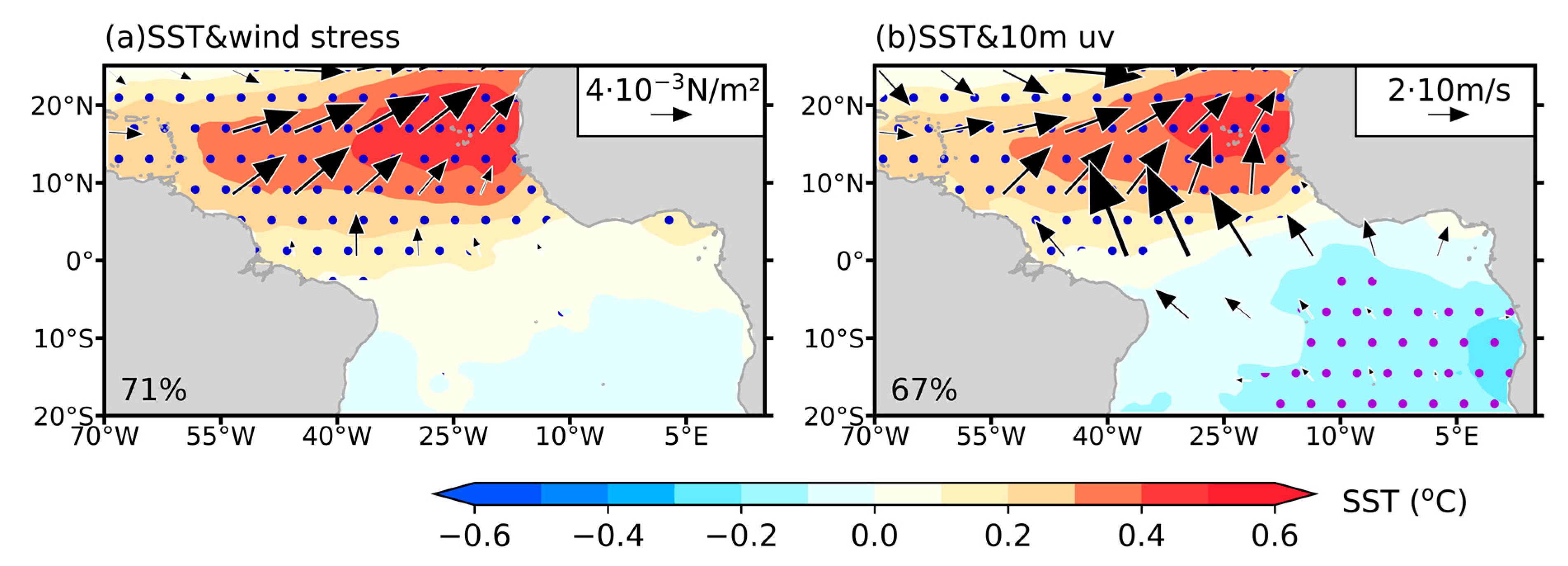
3.1. Spatial Pattern of the AMM

The spatial pattern of the AMM is generally obtained by applying an SVD analysis between monthly SST and surface wind stress or 10 m wind anomalies in the tropical Atlantic [4,40]. It is shown that the spatial pattern of the AMM obtained from the surface wind stress anomalies is basically consistent with that obtained from the 10 m wind anomalies (Figure 1a vs. Figure 1b), except that the corresponding SST anomalies in the southern tropical Atlantic are a bit more pronounced when using the 10 m wind. Due to the unavailability of 10 m wind output for some models, surface wind stress is used to obtain the AMM for both observations and model simulations in this study. Indeed, the SST anomalies in the northern tropical Atlantic are highly independent of those in the south at interannual time scale (e.g., [11,47,48,49]).
The observational result shows that the positive phase of the AMM is accompanied by significant above-normal SST and southwest wind stress anomalies in the northern tropical Atlantic (Figure 1a). This indicates that the background northeast trade winds are decelerated over the northern tropical Atlantic, leading to weaker, wind-driven evaporation and thus less heat fluxes released from the ocean into the overlying atmosphere. In this case, the ocean loses less heat and therefore the SST becomes warmer. Opposite situations can be obtained for the negative phase of the AMM. This result is in agreement with that from previous studies that the positive WES feedback acts as the primary mechanism responsible for the evolution of the AMM [22,23].
In the observations, the AMM is represented as the first leading SVD mode between the monthly SST and wind stress anomalies in the tropical Atlantic, but this may not be true for the individual model simulations. To identify the AMM in the individual model simulations, the spatial patterns of the first three leading SVD modes between the monthly simulated SST and wind stress anomalies were compared with the observed AMM pattern, and the one with the highest spatial correlation with the observed pattern was selected as the simulated AMM for each model. Figure 2 displays the spatial pattern of the AMM for the individual models. In the observations, the AMM-related SST anomalies tend to be opposite between the northern and southern tropical Atlantic, though the anomalies are relatively weak in the south (Figure 2A). For comparison purposes, we ranked the models in descending order in terms of similarity between the simulations and observations, which can be estimated by using the difference between the NTA and ATL3 SST indices as a metric. We have also examined the similarity according to the spatial correlation coefficient between the simulations and observations, but results show that the difference between NTA and ATL3 serves the purpose better. It is indicated that the simulated AMM is represented as the first leading SVD mode in all the CMIP6 models, except in CNRM-CM6-1-HR (Figure 2S), NorCPM1 (Figure 2W), CESM2-WACCM (Figure 2Y) and ACCESS-ESM1-5 (Figure 2d). Particularly for NorCPM1, the first three leading SVD modes are all obviously different from the observed AMM mode, suggesting that this model has a limited ability to capture the observed AMM mode. In contrast, most of the CMIP6 models can capture the observed maximum of AMM-related southwest wind stress and warm SST anomalies in the northern tropical Atlantic. However, more pronounced differences are observed between the observations and simulations in the equatorial and southern tropical Atlantic. Some models show opposite SST anomalies between the northern tropical Atlantic and the equatorial and/or southern oceans. These models include HadGEM3-GC31-MM, MPI-ESM1-2-HR, ACCESS-CM2, HadGEM3-GC31-LL, UKESM1-0-LL, SAM0-UNICON, MRI-ESM2-0, KACE-1-0-G, CanESM5, IPSL-CM6A-LR, FIO-ESM2-0 and EC-Earth3 (Figure 2B–M). In contrast, the remaining models tend to show warm SST anomalies across almost the entire tropical Atlantic, except that ES3M-1-0 simulates negligible SST anomalies in the southern tropical Atlantic (Figure 2N). Overall, about one-half of the models can capture the spatial pattern of the AMM similar to the observed one, with significant SST and wind stress anomalies in the tropical North Atlantic and opposite and weak anomalies in the equatorial–southern oceans. The remaining one-half tends to simulate an AMM with warm SST anomalies across almost the entire tropical Atlantic, although most of them have an SST maximum in the northern ocean. Moreover, the AMM-related SST anomalies in the equatorial and (or) southern tropical Atlantic are more obvious in the majority of the CMIP6 models than in the observations. These models tend to exhibit stronger southeasterly and (or) cross-equatorial wind stress, which leads to colder SST in the equatorial and (or) tropical southern Atlantic by modulating the surface heat flux transport. Previous studies have suggested that the wind stress can be affected by surface currents along the equatorial region [50,51] and the west African monsoon variability [9]. In the model with warm SST anomalies in the southern tropical Atlantic, however, there are almost no significant wind stress anomalies. The causes of such a model bias in simulating the spatial pattern of the AMM deserve further investigation but lie beyond the scope of this study.

3.2. AMM-Related Wind–SST Relationship in the CMIP6 Models

Figure 3 shows the month-by-month variance in the expansion coefficients of the wind stress and SST anomalies associated with the AMM in the observations and individual models. It is indicated that the variance in wind stress anomalies peaks in February, while that of the SST anomalies peaks in the following April, which is consistent with the WES feedback that variation in the AMM-related wind stress leads that in the SST [6,9]. However, the simulated wind–SST relationship varies among the models. Some models, such as HadGEM3-GC31-MM, MPI-ESM1-2-HR, ACCESS-CM2, HadGEM3-GC31-LL, MRI-ESM2-0, KACE-1-0-G, NESM3, MIROC6, CNRM-ESM2-1, CNRM-CM6-1-HR, CNRM-CM6-1, FGOALS-f3-L and CAMS-CSM1-0, have a peak in the wind and SST variances in spring, with a lead of the wind over the SST, implying that the simulated wind–SST relationship is basically consistent with the observed one. In contrast, in some other models, including UKESM1-0-LL, SAM0-UNICON, IPSL-CM6A-LR, FIO-ESM-2-0, EC-Earth3-Veg, NorESM2-LM, CESM2, CESM2-WACCM, FGOALS-g3 and GFDL-ESM4, the month-to-month variation in the AMM-related SST anomalies is relatively flat and without any obvious peak, suggesting that these models fail to capture the observed wind–SST relationship associated with the AMM.
The results emerging from Figure 2 and Figure 3 suggest that, although most of the CMIP6 models can reasonably capture the spatial pattern of the AMM similar to the observed one, some models fail to reproduce the associated wind–SST relationship. To explore the possible causes, two groups of models are selected for comparison based on a criterion to measure the wind–SST relationship. We calculated the difference in the SST variances (see Figure 3) between the month of the peak and the month preceding the peak by two months, and the ones with the largest difference represent a more similar observed wind–SST relationship and vice versa. The first six models with the largest differences in the SST variances are selected as the ones (referred to as group A) that can capture the observed spatial pattern of the AMM and the associated wind–SST relationship. In contrast, the models with a small difference in the SST variances are chosen as the ones (referred to as group B) that can capture the observed spatial pattern of the AMM but not the wind–SST relationship. There are five models in group A, namely HadGEM3-GC31-MM, MRI-ESM2-0, CNRM-CM6-1-HR, KACE-1-0-G, ACCESS-CM2 and MIROC6, and those in group B include FIO-ESM-2-0, UKESM1-0-LL, IPSL-CM6A-LR, EC-Earth3-Veg and NorESM2-LM. As shown in Figure 1e,f, the spatial patterns of the AMM for the multi-model ensemble (MME) average of group A and B both resemble the observed one well. Note here that linear regression coefficients are calculated for the individual models prior to the MME average. Moreover, the wind–SST relationship for group A (Figure 3e) is also consistent with the observed one, but for group B (Figure 3F), the month-to-month variation in the SST is relatively flat and obviously different to that for group A.
To further examine the evolution of the AMM-related thermodynamic processes, Figure 4 shows the time–latitude cross-sections of 60° W–0° E zonal-averaged surface wind stress, surface heat flux (i.e., sum of the latent and sensible heat fluxes) and SST anomalies from January to June regressed onto the spring NTA index for the observations and the MME averages of group A and group B, respectively. Here, the NTA index is used in the regression analysis since the AMM primarily highlights SST variations in the northern tropical Atlantic. The result indicates that the evolutions of surface wind stress, heat flux and SST anomalies for group A are essentially consistent with those for the observations (Figure 4b vs. Figure 4a, and Figure 4f vs. Figure 4e); that is, southeast wind stress and negative heat flux anomalies are observed over the tropical North Atlantic from the previous winter to early spring, accompanied by warm SST anomalies with a maximum in spring. For group B, however, the surface wind stress and heat flux anomalies are significantly weaker than those for group A from the previous winter to early spring (Figure 4d), which therefore implies a weaker forcing of the ocean by the wind stress in the models of group B when compared to that for group A. Due to the weaker wind stress anomalies, there is less evaporation and thus less heat flux from the sea surface into the overlying atmosphere, leading to a weaker SST response in the models of group B when compared to that for group A (Figure 4g,h). This result is consistent with the notion that the AMM-related SST anomalies in the northern tropical Atlantic are dominated by variations in the trade wind and associated heat fluxes. In other words, the models in group B tend to underestimate the WES feedback that is responsible for the evolution of the AMM.
To confirm the results regarding the AMM-related wind–SST relationship, lead–lag relationships of the spring NTA index with the NTA-regional-averaged zonal and meridional components of wind stress are further investigated (Figure 5). The observational result indicates that the spring NTA index has a significant in-phase relationship with both the zonal and meridional wind components when wind stress is leading, with a maximum correlation at a 1–2-month lead. The observed in-phase relationship drops significantly and even can be negligible for the zonal wind stress when SST is leading. The lead–lag wind–SST relationship for group A resembles that for the observations, although the simulated relationship is slightly weaker than the observed one for both the zonal and meridional wind components. For group B, however, the lead–lag wind–SST relationships are weaker for almost all the leads/lags when compared to those in group A and the observations. This confirms that the models in group B obviously underestimate the wind–SST relationship (i.e., the WES feedback) in the northern tropical Atlantic, which therefore results in weaker month-to-month variations in the SST anomalies associated with the AMM.
A question arises as to why the models in group B underestimate the AMM-related wind–SST relationship in the northern tropical Atlantic. To answer this question, mean states of the tropical Atlantic for group A and B are compared since the SST response to the wind stress forcing is modulated by the background state (e.g., [36,51,52]). Figure 6 displays the climatological means of SST and mixed layer depth in spring and surface wind stress and precipitation in the previous winter (January–February–March). Compared to those in group A, the models in group B show stronger mean trade winds and colder SSTs over the northern tropical Atlantic. The mean precipitation in group A is heavier in the deep tropical Atlantic than that in group B, which is consistent with the convergence of the mean wind there. In other words, the tropical Atlantic Intertropical Convergence Zone (ITCZ) is stronger in group A than in group B. It will be indicated later in Figure 7 and Figure 8 that almost all the models in group A show a stronger ocean–atmosphere coupling compared to those in group B. Therefore, our result is consistent with previous studies that found the stronger climatological ITCZ benefits a stronger ocean–atmosphere coupling in the tropics [53,54]. Meanwhile, the mean mixed layer depth in the northern tropical Atlantic simulated by the models in group B is deeper than that for group A, which is consistent with the stronger trade winds simulated by the former. The stronger trade winds and thus the stronger stir on the ocean could result in a thicker mixed layer. The mixed layer is an important interface for material exchange between the atmosphere and the ocean. According to the SST tendency equation, the variation in SST is inversely proportional to that in the mixed layer depth [55,56]. In other words, when the heat flux is constant, a shallower mixed layer depth corresponds to a larger fluctuation in the SST and vice versa. Therefore, the stronger mean trade winds and thus deeper mean mixed layer contribute to the underestimation of the wind–SST relationship in the northern tropical Atlantic for group B when compared to group A.
To verify the impact of the mean state biases on the AMM variability in the models, the intermodal relationship between the mean mixed layer depth and the strength of ocean–atmosphere coupling is examined. Following previous studies (e.g., [57,58]), the strength of ocean–atmosphere coupling is estimated as the regression coefficient between the wind stress and SST anomalies for the observations and individual model simulations. Figure 7 presents the binned scatter plots of the meridional component of wind stress anomalies in winter and SST anomalies in spring regional-averaged over the northern tropical Atlantic (see the box in Figure 6f), in which the slope of the linear regression is defined as the strength of ocean–atmosphere coupling in this study. The larger value of the slope is on behalf of the stronger ocean–atmosphere coupling. It is shown that the SST anomalies in spring have a linear relationship with the meridional component of wind stress anomalies in the previous winter for the observation and all the model simulations (Figure 7), consistent with the wind–SST relationship associated with the AMM. In addition, the relationship between the zonal component of wind stress anomalies in winter and SST anomalies in spring was also analyzed, and similar conclusions were obtained.
Figure 8 displays the scatter plots of the regional-averaged mean mixed layer depth versus the strength of ocean–atmosphere coupling obtained from the zonal and meridional wind stress components, respectively. Note here that SAM0-UNICON appears to be a model outlier and excluded from Figure 8. It is indicated that the strength of ocean–atmosphere coupling has a significant out-of-phase effect with the mean mixed layer depth, with a correlation coefficient reaching −0.51 (p < 0.05) and −0.49 (p < 0.05) for the zonal and meridional components of wind stress, respectively. In general, the ocean–atmosphere coupling in the models of group B is weaker than that in those of group A, consistent with the aforementioned results. This result confirms that the deeper mean mixed layer contributes to the underestimation of the wind–SST relationship in the northern tropical Atlantic in the models. Model biases in the mean mixed layer depth may be related to those in the mean northeasterly trade wind, due to stronger winds inducing more vertical mixing and entrainment [28,54,59,60], but further investigation is needed in future works.

4. Conclusions

The Atlantic Meridional Mode (AMM), peaking in boreal spring and maintained primarily by the positive WES feedback, is the dominant coupled mode between the SST and wind anomalies in the tropical Atlantic at an interannual time scale [6,16]. Although opposite and relatively weak SST anomalies tend to occur in the equatorial and southern oceans, the AMM mainly highlights SST and wind fluctuations in the northern tropical Atlantic in the observations. Many studies have been devoted to exploring the formation mechanisms and climate impacts of the AMM [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27], but fewer works are related to the model’s ability to simulate the AMM. In this study, representation of the AMM and the associated wind–SST relationship are evaluated by using historical simulations from 28 CMIP6 climate models.
An SVD analysis is applied to the monthly SST and wind stress anomalies in the tropical Atlantic to identify the AMM mode for the observations and individual model simulations. It was found that most of the CMIP6 models simulate the AMM as the first leading SVD mode, and only NorCPM1 fails to reproduce any SVD mode similar to the observed pattern of the AMM. Overall, approximately one-half of the models can capture the spatial pattern of the AMM similar to the observed one, with significant SST and wind stress anomalies in the tropical north Atlantic and opposite and weak anomalies in the equatorial–southern tropical Atlantic. The remaining one-half tend to simulate an AMM with warm SST anomalies across almost the entire tropical Atlantic although most of them have an SST maximum in the northern ocean. In all, most of the CMIP6 models can reasonably capture the spatial pattern of the AMM similar to the observed one. Moreover, the relationships of AMM-associated SST anomalies between the northern and equatorial/southern tropical Atlantic tend to be overestimated in the majority of the CMIP6 models.
Consistent with the WES feedback mechanism, AMM-related variation in the wind stress anomalies leads that in the SST anomalies by ~2 months in the observations. However, the simulated wind–SST relationship associated with the AMM varies among the CMIP6 models. In particular, several models fail to reproduce the observed wind–SST relationship. In these models, the AMM-related wind stress anomalies peak in boreal spring, but the corresponding SST anomalies show nearly flat month-to-month variation without any obvious peak. To explore the possible causes for such a model bias, two sets of models (groups A and B) were selected; that is, the models in group A can capture the observed wind–SST relationship associated with the AMM, but those in group B cannot. Compared to those in group A, a stronger mean northeast trade wind and deeper mean mixed layer are found in the northern tropical Atlantic for the multi-model ensemble average of group B. Since the SST variation is inversely related to the mean mixed layer depth, the deeper mean mixed layer in group B weakens the atmosphere–ocean coupling in the tropical Atlantic. Further analysis reveals that there exists a significant out-of-phase relationship between the strength of ocean–atmosphere coupling and mean mixed layer depth among the models, supporting the influence of the mean state biases on the AMM variability in the models. In all, the stronger mean trade wind and, thus, the deeper mean mixed layer contribute to the underestimation of the AMM-associated wind–SST relationship in the CMIP6 models. The mixed layer biases may be related to those in the mean northeasterly trade winds, due to stronger winds inducing more vertical mixing and entrainment [28,59,60]. Indeed, mean trade wind and mixed layer biases are parts of the mean state biases in the tropical Atlantic, which have been widely explored in previous studies (e.g., [36,61,62,63,64,65]) and lie beyond the scope of this study.
The present study mainly focused on the model’s ability to simulate the AMM-related wind–SST relationship in the tropical Atlantic. Note that some models show obvious biases in simulating the spatial pattern of the AMM, the causes of which are investigated in our ongoing research. In addition to the tropical Atlantic mean state biases, other factors may also have an impact on model performance in simulating the AMM and associated wind–SST relationship. For example, previous studies have revealed that the North Atlantic Oscillation (NAO) has a strong influence on the formation of the NTA and thus the AMM [66,67,68], and model performance in simulating NAO–AMM connection and associated influence on the AMM still require further examination in future works.

Author Contributions

Conceptualization and Methodology, J.Z.; Software and Validation, F.X; Formal analysis, F.X. and J.Z.; Writing Original Draft, F.X. and J.Z.; Review and Editing, C.S. and A.L.; Supervision, J.Z.; Funding and Acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research Program and Development of China (2021YFA0718000), the Science Foundations of China (41975102) and the Innovative Development Special Project of China Meteorological Administration (CXFZ2021Z011).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The CMIP6 data are available at https://pcmdi.llnl.gov/CMIP6/, accessed on 23 May 2022. ERA5 reanalysis is freely available at https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5, accessed on 18 January 2023. ORAS5 dataset is obtained from https://www.ecmwf.int/en/research/climate-reanalysis/ocean-reanalysis, accessed on 7 October 2022. The HadISST dataset is provided by the Met Office Hadley Centre at https://www.metoffice.gov.uk/hadobs/hadisst/data/download.html, accessed on 14 September 2021.

Acknowledgments

Special thanks to Gongjie Wang for useful discussions and suggestions. The authors are grateful to the four anonymous reviewers for their insightful comments, which helped us improve the quality of this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Foltz, G.R.; Brandt, P.; Richter, I.; Rodríguez-Fonseca, B.; Hernandez, F.; Dengler, M.; Rodrigues, R.R.; Schmidt, J.O.; Yu, L.; LOefevre, N.; et al. The Tropical Atlantic Observing System. Front. Mar. Sci. 2019, 6, 206. [Google Scholar] [CrossRef]
  2. Wang, C. Three-ocean interactions and climate variability: A review and perspective. Clim. Dyn. 2019, 53, 5119–5136. [Google Scholar] [CrossRef]
  3. Xie, S.P.; Carton, J.A. Tropical Atlantic variability: Patterns, mechanisms, and impacts. In Earth’s Climate: The Ocean–Atmosphere Interaction; American Geophysical Union: Washington, DC, USA, 2004; Volume 147, pp. 121–142. [Google Scholar] [CrossRef]
  4. Chiang, J.C.; Vimont, D.J. Analogous Pacifc and Atlantic meridional modes of tropical atmosphere-ocean variability. J. Clim. 2004, 17, 4143–4158. [Google Scholar] [CrossRef]
  5. Tanimoto, Y.; Xie, S.-P. Inter-hemispheric decadal variations in SST, surface wind, heat flux and cloud cover over the Atlantic Ocean. J. Meteorol. Soc. Jpn. 2002, 80, 1199–1219. [Google Scholar] [CrossRef]
  6. Chang, P.; Yamagata, T.; Schopf, P.S.; Behera, S.K.; Carton, J.; Kessler, W.S.; Meyers, G.; Qu, T.; Schott, F.; Shetye, S.; et al. Climate Fluctuations of Tropical Coupled Systems-The Role of Ocean Dynamics. J. Clim. 2006, 19, 5122–5174. [Google Scholar] [CrossRef]
  7. Mahajan, S.; Saravanan, R.; Chang, P. Free and forced variability of the tropical Atlantic Ocean: Role of the wind–evaporation–sea surface temperature feedback. J. Clim. 2010, 23, 5958–5977. [Google Scholar] [CrossRef]
  8. Evan, A.T.; Allan, A.J.; Bennartz, R.; Vimont, D.J. The modifcation of sea surface temperature anomaly linear damping time scales by stratocumulus clouds. J. Clim. 2013, 26, 3619–3630. [Google Scholar] [CrossRef]
  9. Cabos, W.; de la Vara, A.; Koseki, S. Tropical Atlantic variability: Observations and modeling. Atmosphere 2019, 10, 502. [Google Scholar] [CrossRef]
  10. Myers, T.A.; Mechoso, C.R.; DeFlorio, M.J. Importance of positive cloud feedback for tropical Atlantic interhemispheric climate variability. Clim. Dyn. 2018, 51, 1707–1717. [Google Scholar] [CrossRef]
  11. Ren, H.-C.; Zuo, J.; Li, W. The impact of tropical Atlantic SST variability on the tropical atmosphere during boreal summer. J. Clim. 2021, 34, 6705–6723. [Google Scholar] [CrossRef]
  12. Vimont, D.J.; Kossin, J.P. The Atlantic Meridional Mode and hurricane activity. Geophys Res Lett. 2007, 34, L07709. [Google Scholar] [CrossRef]
  13. Nobre, P.; Shukla, J. Variation of Sea Surface Temperature, Wind Stress and Rainfall over the Tropical Atlantic and South America. J. Clim. 1996, 9, 2464–2479. [Google Scholar] [CrossRef]
  14. Kushnir, Y.; Robinson, W.A.; Chang, P.; Robertson, A.W. The Physical Basis for Predicting Atlantic Sector Seasonal-to-Interannual Climate Variability. J. Clim. 2006, 19, 5949–5970. [Google Scholar] [CrossRef]
  15. Foltz, G.R.; Mcphaden, M.J.; Lumpkin, R. A Strong Atlantic Meridional Mode Event in 2009: The Role of Mixed Layer Dynamics. J. Clim. 2012, 25, 363–380. [Google Scholar] [CrossRef]
  16. Cai, W.; Wu, L.; Lengaigne, M.; Li, T.; McGregor, S.; Kug, J.S.; Yu, J.Y.; Stuecker, M.F.; Santoso, A.; Li, X.; et al. Pantropical climate interactions. Science 2019, 363, eaav4236. [Google Scholar] [CrossRef]
  17. Ham, Y.G.; Kug, J.S.; Park, J.Y.; Jin, F.F. Sea surface temperature in the north tropical Atlantic as a trigger for El Niño/Southern Oscillation events. Nat. Geosci. 2013, 6, 112–116. [Google Scholar] [CrossRef]
  18. Wang, L.; Yu, J.Y.; Paek, H. Enhanced biennial variability in the Pacific due to Atlantic capacitor effect. Nat. Commun. 2017, 8, 14887. [Google Scholar] [CrossRef]
  19. Kucharski, F.; Joshi, M.K. Influence of tropical South Atlantic sea-surface temperatures on the Indian summer monsoon in CMIP5 models. Q. J. R. Meteorol. Soc. 2017, 143, 1351–1363. [Google Scholar] [CrossRef]
  20. Vittal, H.; Villarini, G.; Zhang, W. Early prediction of the Indian summer monsoon rainfall by the Atlantic Meridional Mode. Clim. Dyn. 2020, 54, 2337–2346. [Google Scholar] [CrossRef]
  21. Zuo, J.; Li, W.; Sun, C.; Xu, L.; Ren, H.-L. Impact of the North Atlantic sea surface temperature tripole on the East Asian summer monsoon. Adv. Atmos. Sci. 2013, 30, 1173–1186. [Google Scholar] [CrossRef]
  22. Hong, C.-C.; Chang, T.-C.; Hsu, H.-H. Enhanced relationship between the tropical Atlantic SST and the summertime western North Pacific subtropical high after the early 1980s. J. Geophys. Res. 2014, 119, 3715–3722. [Google Scholar] [CrossRef]
  23. Chang, T.-C.; Hsu, H.H.; Hong, C.-C. Enhanced influences of tropical Atlantic SST on WNP-NIO atmosphere-ocean coupling since the early 1980s. J. Clim. 2016, 29, 6509–6525. [Google Scholar] [CrossRef]
  24. Gao, S.; Chen, Z.; Zhang, W. Impacts of tropical North Atlantic SST on western North Pacific landfalling tropical cyclones. J. Clim. 2018, 31, 853–862. [Google Scholar] [CrossRef]
  25. Li, J.P.; Zheng, F.; Sun, C.; Feng, J.; Wang, J. Pathways of influence of the Northern Hemisphere mid–high latitudes on East Asian climate: A review. Adv. Atmos. Sci. 2019, 36, 902–921. [Google Scholar] [CrossRef]
  26. Zuo, J.; Li, W.; Sun, C.; Ren, H.-C. Remote forcing of the northern tropical Atlantic SST anomalies on the western North Pacific anomalous anticyclone. Clim. Dyn. 2019, 52, 2837–2853. [Google Scholar] [CrossRef]
  27. Zhao, J.; Zhang, H.; Zuo, J.; Yang, L.; Yang, J.; Xiong, K.; Feng, G.; Dong, W. Oceanic drivers and empirical prediction of interannual rainfall variability in late summer over Northeast China. Clim. Dyn. 2022, 58, 861–878. [Google Scholar] [CrossRef]
  28. Richter, I.; Tokinaga, H. An overview of the performance of CMIP6 models in the tropical Atlantic: Mean state, variability, and remote impacts. Clim. Dyn. 2020, 55, 2579–2601. [Google Scholar] [CrossRef]
  29. Zhang, Q.; Zhu, Y.; Zhang, R. Subsurface Warm Biases in the Tropical Atlantic and Their Attributions to the Role of Wind Forcing and Ocean Vertical Mixing. J. Clim. 2022, 35, 2291–2303. [Google Scholar] [CrossRef]
  30. Worou, K.; Goosse, H.; Fichefet, T.; Kucharski, F. Weakened impact of the Atlantic Niño on the future equatorial Atlantic and Guinea Coast rainfall. Earth Syst. Dynam. 2022, 13, 231–249. [Google Scholar] [CrossRef]
  31. Wang, R.; Chen, L.; Li, T.; Luo, J. Atlantic Niño/Niña Prediction Skills in NMME Models. Atmosphere 2021, 12, 803. [Google Scholar] [CrossRef]
  32. Moreno-Chamarro, E.; Caron, L.-P.; Loosveldt Tomas, S.; Vegas-Regidor, J.; Gutjahr, O.; Moine, M.P.; Putrasahan, D.; Roberts, C.D.; Roberts, M.J.; Senan, R.; et al. Impact of increased resolution on long-standing biases in HighResMIP-PRIMAVERA climate models. Geosci. Model Dev. 2022, 15, 269–289. [Google Scholar] [CrossRef]
  33. Li, G.; Xie, S.-P. Origins of tropical-wide SST biases in CMIP multi-model ensembles. Geophys. Res. Lett. 2012, 39, L22703. [Google Scholar] [CrossRef]
  34. Liu, H.; Wang, C.; Lee, S.; Enfield, D.B. Atlantic Warm Pool Variability in the CMIP5 Simulations. J. Clim. 2013, 26, 5315–5336. [Google Scholar] [CrossRef]
  35. McGregor, S.; Stuecker, M.F.; Kajtar, J.B.; England, M.H.; Collins, M. Model tropical Atlantic biases underpin diminished Pacific decadal variability. Nat. Clim. Change 2018, 8, 493–498. [Google Scholar] [CrossRef]
  36. Voldoire, A.; Exarchou, E.; Sanchez-Gomez, E.; Demissie, T.; Deppenmeier, A.L.; Frauen, C.; Goubanova, K.; Hazeleger, W.; Keenlyside, N.; Koseki, S.; et al. Role of wind stress in driving SST biases in the Tropical Atlantic. Clim. Dyn. 2019, 53, 3481–3504. [Google Scholar] [CrossRef]
  37. Kucharski, F.; Syed, F.S.; Burhan, A.; Farah, I.; Gohar, A. Tropical Atlantic influence on Pacific variability and mean state in the twentieth century in observations and CMIP5. Clim. Dyn. 2015, 44, 881–896. [Google Scholar] [CrossRef]
  38. Ham, Y.-G.; Kug, J.-S. Role of north tropical atlantic SST on the ENSO simulated using CMIP3 and CMIP5 models. Clim. Dyn. 2015, 45, 3103–3117. [Google Scholar] [CrossRef]
  39. Zuo, J.; Sun, C.; Li, W.; Wu, J.; Ren, H. Representation of the boreal summer tropical Atlantic–western North Pacific teleconnection in AGCMs: Comparison of CMIP5 and CMIP6. Clim. Dyn. 2020, 55, 3025–3041. [Google Scholar] [CrossRef]
  40. Amaya, D.J.; DeFlorio, M.J.; Miller, A.J.; Xie, S.-P. WES feedback and the Atlantic Meridional Mode: Observations and CMIP5 comparisons. Clim. Dyn. 2017, 49, 1665–1679. [Google Scholar] [CrossRef]
  41. Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
  42. An, Y.Z.; Zhang, R.; Wang, H.Z.; Chen, J.; Chen, Y.-D. Study on calculation and spatio-temporal variations of global ocean mixed layer depth. Chin. J. Geophys. 2012, 55, 2249–2258. (In Chinese) [Google Scholar] [CrossRef]
  43. Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Ocean. 2003, 108, 4407. [Google Scholar] [CrossRef]
  44. Zuo, H.; Balmaseda, M.A.; Tietsche, S.; Mogensen, K.; Mayer, M. The ECMWF operational ensemble reanalysis–analysis system for ocean and sea ice: A description of the system and assessment. Ocean Sci. 2019, 15, 779–808. [Google Scholar] [CrossRef]
  45. Zuo, H.; Balmaseda, M.A.; de Boisseson, E.; Hirahara, S.; Chrust, M.; De Rosnay, P. A Generic Ensemble Generation Scheme for Data Assimilation and Ocean Analysis. In ECMWF Technical Memorandum; European Centre for Medium-Range Weather Forecasts, Shinfield Park: Reading, UK, 2017. [Google Scholar] [CrossRef]
  46. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  47. Enfield, D.B.; Mayer, D.A. Tropical Atlantic sea surface temperature variability and its relation to El Niño–Southern Oscillation. J. Geophys. Res. Ocean. 1997, 102, 929–945. [Google Scholar] [CrossRef]
  48. Huang, B. Remotely forced variability in the tropical Atlantic Ocean. Clim. Dyn. 2004, 23, 133–152. [Google Scholar] [CrossRef]
  49. Huang, B.; Shukla, J. Ocean–atmosphere interactions in the tropical and subtropical Atlantic Ocean. J. Clim. 2005, 18, 1652–1672. [Google Scholar] [CrossRef]
  50. Chacko, N.; Ali, M.M.; Bourassa, M.A. Impact of Ocean Currents on Wind Stress in the Tropical Indian Ocean. Remote Sens. 2022, 14, 1547. [Google Scholar] [CrossRef]
  51. Dippe, T.; Greatbatch, R.J.; Ding, H. On the relationship between Atlantic Niño variability and ocean dynamics. Clim. Dyn. 2018, 51, 597–612. [Google Scholar] [CrossRef]
  52. Park, W.; Latif, M. Resolution dependence of CO2-induced Tropical Atlantic sector climate changes. NPJ Clim. Atmos. Sci. 2020, 3, 36. [Google Scholar] [CrossRef]
  53. Zheng, Y.Q.; Chen, S.F.; Chen, W.; Yu, B. A continuing increase of the impact of the spring North Pacific Meridional Mode on the following winter El Nino and Southern Oscillation. J. Clim. 2022, 36, 585–602. [Google Scholar] [CrossRef]
  54. Zheng, Y.; Chen, W.; Chen, S. Intermodel spread in the impact of the springtime Pacific Meridional Mode on following-winter ENSO tied to simulation of the ITCZ in CMIP5/CMIP6. Geophys. Res. Lett. 2021, 48, e2021GL093945. [Google Scholar] [CrossRef]
  55. Gaspar, P. Modeling the Seasonal Cycle of the Upper Ocean. J. Phys. Ocean. 1988, 18, 161–180. [Google Scholar] [CrossRef]
  56. Deser, C.; Alexander, M.A.; Xie, S.-P.; Phillips, A.S. Sea surface temperature variability: Patterns and mechanisms. Annu. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [PubMed]
  57. Zheng, F.; Fang, X.-H.; Yu, J.-Y.; Zhu, J. Asymmetry of the Bjerknes positive feedback between the two types of El Niño. Geophys. Res. Lett. 2014, 41, 7651–7657. [Google Scholar] [CrossRef]
  58. Kumar, A.; Zhu, J. Spatial Variability in Seasonal Prediction Skill of SSTs: Inherent Predictability or Forecast Errors? J. Clim. 2018, 31, 613–621. [Google Scholar] [CrossRef]
  59. Rugg, A.; Foltz, G.R.; Perez, R.C. Role of Mixed Layer Dynamics in Tropical North Atlantic Interannual Sea Surface Temperature Variability. J. Clim. 2016, 29, 8083–8101. [Google Scholar] [CrossRef]
  60. Kataoka, T.; Kimoto, M.; Watanabe, M.; Tatebe, H. Wind–Mixed Layer–SST Feedbacks in a Tropical Air–Sea Coupled System: Application to the Atlantic. J. Clim. 2019, 32, 3865–3881. [Google Scholar] [CrossRef]
  61. Xu, Z.; Li, M.; Patricola, C.M.; Chang, P. Oceanic origin of southeast tropical Atlantic biases. Clim. Dyn. 2014, 43, 2915–2930. [Google Scholar] [CrossRef]
  62. Richter, I.; Xie, S.-P. On the origin of equatorial Atlantic biases in coupled general circulation models. Clim. Dyn. 2008, 31, 587–598. [Google Scholar] [CrossRef]
  63. Richter, I.; Xie, S.-P.; Wittenberg, A.T.; Masumoto, Y. Tropical Atlantic biases and their relation to surface wind stress and terrestrial precipitation. Clim. Dyn. 2012, 38, 985–1001. [Google Scholar] [CrossRef]
  64. Wahl, S.; Latif, M.; Park, W.; Keenlyside, N. On the tropical Atlantic SST warm bias in the Kiel climate model. Clim. Dyn. 2009, 36, 891–906. [Google Scholar] [CrossRef]
  65. Lee, T.; Waliser, D.E.; Li, J.; Landerer, F.W.; Gierach, M.M. Evaluation of CMIP3 and CMIP5 Wind Stress Climatology Using Satellite Measurements and Atmospheric Reanalysis Products. J. Clim. 2013, 26, 5810–5826. [Google Scholar] [CrossRef]
  66. Chen, S.; Wu, R.; Chen, W. Strengthened connection between springtime North Atlantic Oscillation and North Atlantic tripole SST pattern since the late-1980s. J. Clim. 2020, 35, 2007–2022. [Google Scholar] [CrossRef]
  67. Chen, S.; Wu, R.; Chen, W. The changing relationship between interannual variations of the North Atlantic Oscillation and northern tropical Atlantic SST. J. Clim. 2015, 28, 485–504. [Google Scholar] [CrossRef]
  68. Qiao, S.; Zou, M.; Tang, S.; Cheung, H.N.; Su, H.; Li, Q.; Feng, G.; Feng, G.; Dong, W. The Enhancement of the Impact of the Wintertime North Atlantic Oscillation on the Subsequent Sea Surface Temperature over the Tropical Atlantic since the Middle 1990s. J. Clim. 2020, 33, 9653–9672. [Google Scholar] [CrossRef]
Atmosphere 14 00359 g001 550
Figure 1. Spatial patterns of the AMM represented as the first leading SVD mode between the SST (shading, unit: °C) and (a) surface wind stress (vectors, unit: 10−3 N/m2) and (b) 10-m wind (vectors, unit: 10 m/s) anomalies in observations during 1960–2014. The pattern is represented as the SST and wind anomalies regressed onto the expansion coefficients of the SVD mode. Stippling indicates significance at the 95% confidence level. The percentage of explained variance from the SVD mode is shown at the bottom left. Only the vectors with significance at the 95% confidence leel are shown.
Figure 1. Spatial patterns of the AMM represented as the first leading SVD mode between the SST (shading, unit: °C) and (a) surface wind stress (vectors, unit: 10−3 N/m2) and (b) 10-m wind (vectors, unit: 10 m/s) anomalies in observations during 1960–2014. The pattern is represented as the SST and wind anomalies regressed onto the expansion coefficients of the SVD mode. Stippling indicates significance at the 95% confidence level. The percentage of explained variance from the SVD mode is shown at the bottom left. Only the vectors with significance at the 95% confidence leel are shown.
Atmosphere 14 00359 g001
Atmosphere 14 00359 g002 550
Figure 2. Comparison of the AMM spatial pattern between the (A) observation and (B–c) individual CMIP6 models and multi-model ensemble average for (d) group A and (e) group B during 1960–2014. The pattern is represented as regression between the expansion coefficients of the SVD mode and SST anomalies (shading, unit: °C) and wind stress anomalies (vectors, unit: 10−3 N/m2). Dots indicate significance at the 95% confidence level. The percentage of explained variance from the SVD mode is given at the bottom left. Only the vectors with significance at the 95% confidence level are shown. The models are ranked in descending order according to the difference in the regressed SST anomalies between the NTA and ATL3 regions.
Figure 2. Comparison of the AMM spatial pattern between the (A) observation and (B–c) individual CMIP6 models and multi-model ensemble average for (d) group A and (e) group B during 1960–2014. The pattern is represented as regression between the expansion coefficients of the SVD mode and SST anomalies (shading, unit: °C) and wind stress anomalies (vectors, unit: 10−3 N/m2). Dots indicate significance at the 95% confidence level. The percentage of explained variance from the SVD mode is given at the bottom left. Only the vectors with significance at the 95% confidence level are shown. The models are ranked in descending order according to the difference in the regressed SST anomalies between the NTA and ATL3 regions.
Atmosphere 14 00359 g002
Atmosphere 14 00359 g003 550
Figure 3. Month-by-month variance of the AMM-related wind stress (gray curve) and SST (black curve) anomalies in the (A) observation, (B–c) individual CMIP6 models and multi-model ensemble average for (d) group A and (e) group B. Dashed gray and black lines denote the month corresponding to the peak in the observed wind and SST, respectively.
Figure 3. Month-by-month variance of the AMM-related wind stress (gray curve) and SST (black curve) anomalies in the (A) observation, (B–c) individual CMIP6 models and multi-model ensemble average for (d) group A and (e) group B. Dashed gray and black lines denote the month corresponding to the peak in the observed wind and SST, respectively.
Atmosphere 14 00359 g003
Atmosphere 14 00359 g004 550
Figure 4. Time–latitude cross-sections of 60°W–0°E zonal-mean wind stress (arrows, unit: 10−2 N/m2), surface heat flux (shading, unit: J/m2; positive values represent heat released from the ocean to the atmosphere) and SST anomalies (shading, unit: °C) from January to June regressed against the spring NTA index for the (a,e) observations, the (b,f) MME of group A, the (c,g) MME of group B, and (d,h) difference between group A and B (former minus latter). Dots in d and h indicate significance at the 95% confidence level. Only the vectors with significance at the 95% confidence level are shown. To share the same color bar, wind stress and heat fluxes in (d) are magnified by a factor of 2, and SST in (h) is magnified by a factor of 6.
Figure 4. Time–latitude cross-sections of 60°W–0°E zonal-mean wind stress (arrows, unit: 10−2 N/m2), surface heat flux (shading, unit: J/m2; positive values represent heat released from the ocean to the atmosphere) and SST anomalies (shading, unit: °C) from January to June regressed against the spring NTA index for the (a,e) observations, the (b,f) MME of group A, the (c,g) MME of group B, and (d,h) difference between group A and B (former minus latter). Dots in d and h indicate significance at the 95% confidence level. Only the vectors with significance at the 95% confidence level are shown. To share the same color bar, wind stress and heat fluxes in (d) are magnified by a factor of 2, and SST in (h) is magnified by a factor of 6.
Atmosphere 14 00359 g004
Atmosphere 14 00359 g005 550
Figure 5. Lead–lag correlation coefficients of the spring NTA index with the NTA-regional-averaged (a) zonal and (b) meridional components of wind stress for the observations (black), MME average of group A (red) and group B (blue). The dashed and dashed-dotted lines denote significance at the 99% and 95% confidence levels, respectively. The lead time refers to the middle month of the 3-month-running season, and negative values indicate that the wind stress is leading.
Figure 5. Lead–lag correlation coefficients of the spring NTA index with the NTA-regional-averaged (a) zonal and (b) meridional components of wind stress for the observations (black), MME average of group A (red) and group B (blue). The dashed and dashed-dotted lines denote significance at the 99% and 95% confidence levels, respectively. The lead time refers to the middle month of the 3-month-running season, and negative values indicate that the wind stress is leading.
Atmosphere 14 00359 g005
Atmosphere 14 00359 g006 550
Figure 6. Climatological mean of the SST (shading, unit: °C) in spring and wind stress (vectors, unit: 10−2 N/m2) and precipitation (contours, unit: mm, zero and negative contours omitted) in the previous winter for the (a) observations and the MME average of (b) group A and (c) group B and (d) differences between groups A and B (former minus latter) during 1960–2014. (e–h) As in (a–d), but for the mixed layer depth (shading, unit: m) in spring. Dots in c and f indicate significance at the 95% confidence level.
Figure 6. Climatological mean of the SST (shading, unit: °C) in spring and wind stress (vectors, unit: 10−2 N/m2) and precipitation (contours, unit: mm, zero and negative contours omitted) in the previous winter for the (a) observations and the MME average of (b) group A and (c) group B and (d) differences between groups A and B (former minus latter) during 1960–2014. (e–h) As in (a–d), but for the mixed layer depth (shading, unit: m) in spring. Dots in c and f indicate significance at the 95% confidence level.
Atmosphere 14 00359 g006
Atmosphere 14 00359 g007 550
Figure 7. Binned scatter plots for the meridional component of wind stress (unit: N/m2) in winter and SST (unit: °C) anomalies in spring regional-averaged over the NTA region (black box in Figure 6f) for the (A) observation and (B–c) individual CMIP6 models. The bin range is 0.02 N/m2. The points and the error bars represent the means and the ±1 standard deviation over the averaged samples in each bin, respectively. The blue line is the linear fit in terms of least squares. The slopes of the linear regression are represented with black color text a.
Figure 7. Binned scatter plots for the meridional component of wind stress (unit: N/m2) in winter and SST (unit: °C) anomalies in spring regional-averaged over the NTA region (black box in Figure 6f) for the (A) observation and (B–c) individual CMIP6 models. The bin range is 0.02 N/m2. The points and the error bars represent the means and the ±1 standard deviation over the averaged samples in each bin, respectively. The blue line is the linear fit in terms of least squares. The slopes of the linear regression are represented with black color text a.
Atmosphere 14 00359 g007
Atmosphere 14 00359 g008 550
Figure 8. Scatter plots of the regional-averaged mean mixed layer depth in spring over the NTA region versus the strength of ocean–atmosphere coupling obtained from the (a) zonal and (b) meridional components of wind stress, respectively. The orange line denotes the line regression and R the correlation.
Figure 8. Scatter plots of the regional-averaged mean mixed layer depth in spring over the NTA region versus the strength of ocean–atmosphere coupling obtained from the (a) zonal and (b) meridional components of wind stress, respectively. The orange line denotes the line regression and R the correlation.
Atmosphere 14 00359 g008
Table
Table 1. Model information about the CMIP6 historical simulations used in this study.
Table 1. Model information about the CMIP6 historical simulations used in this study.
Model NameInstituteResolution (Lon × Lat)
AtmosphereOcean
ACCESS-CM2Commonwealth Scientific and Industrial Research Organisation and Australian Research Council Centre of Excellence for Climate System Science, Australia1.875° × 1.25°1.0° × 0.6°
ACCESS-ESM1.5Commonwealth Scientific and Industrial Research Organisation, Australia1.875° × 1.25°1.0° × 0.6°
CAMS-CSM1.0Chinese Academy of Meteorological Sciences, China1.125° × 1.125°1.0° × 0.9°
CanESM5Canadian Centre for Climate Modeling and Analysis, Canada2.8125°× 2.8125°0.998° × 0.621°
CESM2-WACCMNational Center for Atmospheric Research, USA1.25° × 0.94°1.125° × 0.47°
CESM2National Center for Atmospheric Research, USA1.25° × 0.94°1.125° × 0.47°
CNRM-CM6.1-HRCentre National de Recherches Météorologiques, France0.5° × 0. 5°0.25° × 0. 17°
CNRM-CM6.1Centre National de Recherches Météorologiques, France1.4° × 1.4°0.99° × 0. 61°
CNRM-ESM2.1Centre National de Recherches Météorologiques, France1.4° × 1.4°0.99° × 0. 61°
E3SM1.0Department of Energy, USA1.0° × 1.0°1.0° × 1.0°
EC-Earth3-VegEC-Earth consortium, Europe0.7° × 0. 7°0.99° × 0. 62°
EC-Earth3EC-Earth consortium, Europe0.7° × 0. 7°0.99° × 0. 62°
FGOALS-f3-LChinese Academy of Sciences, China1.25° × 1.0°1° × 0.83°
FGOALS-g3Chinese Academy of Sciences, China2.0° × 2.25°1° × 0.83°
FIO-ESM2.0First Institute of Oceanography, State Oceanic Administration, and Qingdao National Laboratory for Marine Science and Technology, China1.25° × 0.94°1.125° × 0.47°
GFDL-ESM4National Oceanic and Atmospheric Administration Geophysical Fluid Dynamics Laboratory, USA1.25° × 1.0°0.5° × 0.3125°
HadGEM3-GC31-LLMet Office Hadley Centre, UK1.875° × 1.25°0.83° × 0.55°
HadGEM3-GC31-MMMet Office Hadley Centre, UK0.83° × 0.56°0.25° × 0.15°
IPSL-CM6A-LRInstitut Pierre Simon Laplace, France2.5° × 1. 26°0.99° × 0. 54°
KACE1.0-GNational Institute of Meteorological Sciences, Korea1.875° × 1.25°1° × 0.9°
MIROC6JAMSTEC, AORI, NIES and RIKEN Center for Computational Science, Japan1.4° × 1.4°1° × 0.7°
MPI-ESM1-2-HRMax Planck Institute for Meteorology, Germany0.94° × 0.94°0.45° × 0.45°
MRI-ESM2.0Meteorological Research Institute, Japan1.125° × 1.125°1.0° × 0.49°
NESM3Nanjing University of Information Science and Technology, China1.875° × 1.875°0.94° × 0.497°
NorCPM1NorESM Climate modeling Consortium, Norway2.5° × 1.875°1.125° × 0.47°
NorESM2-LMNorwegian Climate Centre, Norway2.5° × 1.875°1.0° × 0.47°
SAM0-UNICONSeoul National University, Korea1.25° × 0.94°1.125° × 0.47°
UKESM1.0-LLMet Office Hadley Centre, UK1.875° × 1.25°1.0° × 0.545°
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xia, F.; Zuo, J.; Sun, C.; Liu, A. The Atlantic Meridional Mode and Associated Wind–SST Relationship in the CMIP6 Models. Atmosphere 2023, 14, 359. https://doi.org/10.3390/atmos14020359

AMA Style

Xia F, Zuo J, Sun C, Liu A. The Atlantic Meridional Mode and Associated Wind–SST Relationship in the CMIP6 Models. Atmosphere. 2023; 14(2):359. https://doi.org/10.3390/atmos14020359

Chicago/Turabian Style

Xia, Fannyu, Jinqing Zuo, Chenghu Sun, and Ao Liu. 2023. "The Atlantic Meridional Mode and Associated Wind–SST Relationship in the CMIP6 Models" Atmosphere 14, no. 2: 359. https://doi.org/10.3390/atmos14020359

APA Style

Xia, F., Zuo, J., Sun, C., & Liu, A. (2023). The Atlantic Meridional Mode and Associated Wind–SST Relationship in the CMIP6 Models. Atmosphere, 14(2), 359. https://doi.org/10.3390/atmos14020359

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop