ENSO and PDO Effect on Stratospheric Dynamics in Isca Numerical Experiments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Isca Model
2.3. Experiments Boundary Condition
- The SST values in the region [20° N–20° S, 140° E–80° W] (EN region) were extracted from the monthly mean field of the SST anomalies for the selected years.
- The values in this region have been doubled and added to the climatological mean monthly SST values from AMIP data (Equation (1)).
- The years with the maximum and minimum values of the PDO index were determined: for the positive phase, it is 1949, while, for the negative phase, it is 1941.
- For the above-mentioned area, the SST anomalies were doubled and added to the climatological mean AMIP SST fields (Figure S3).
2.4. Analysis Methods
3. Results
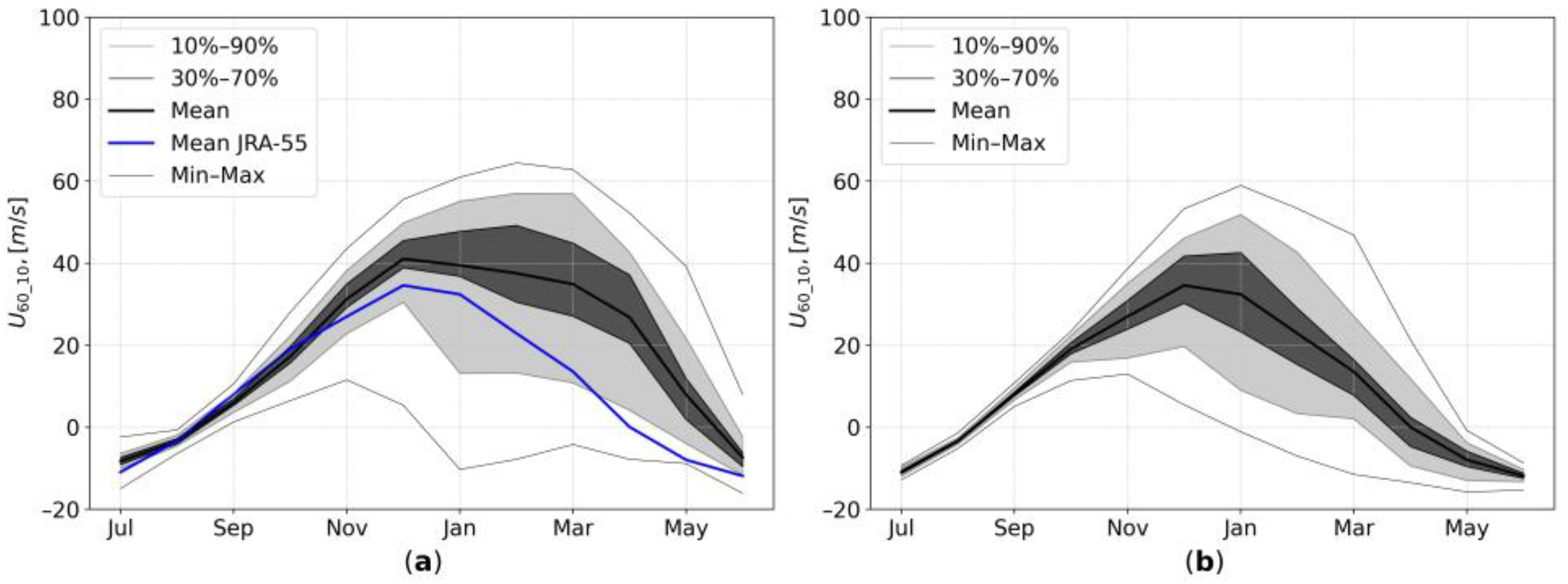
3.1. Model Validation
3.2. Intensity of the SPV
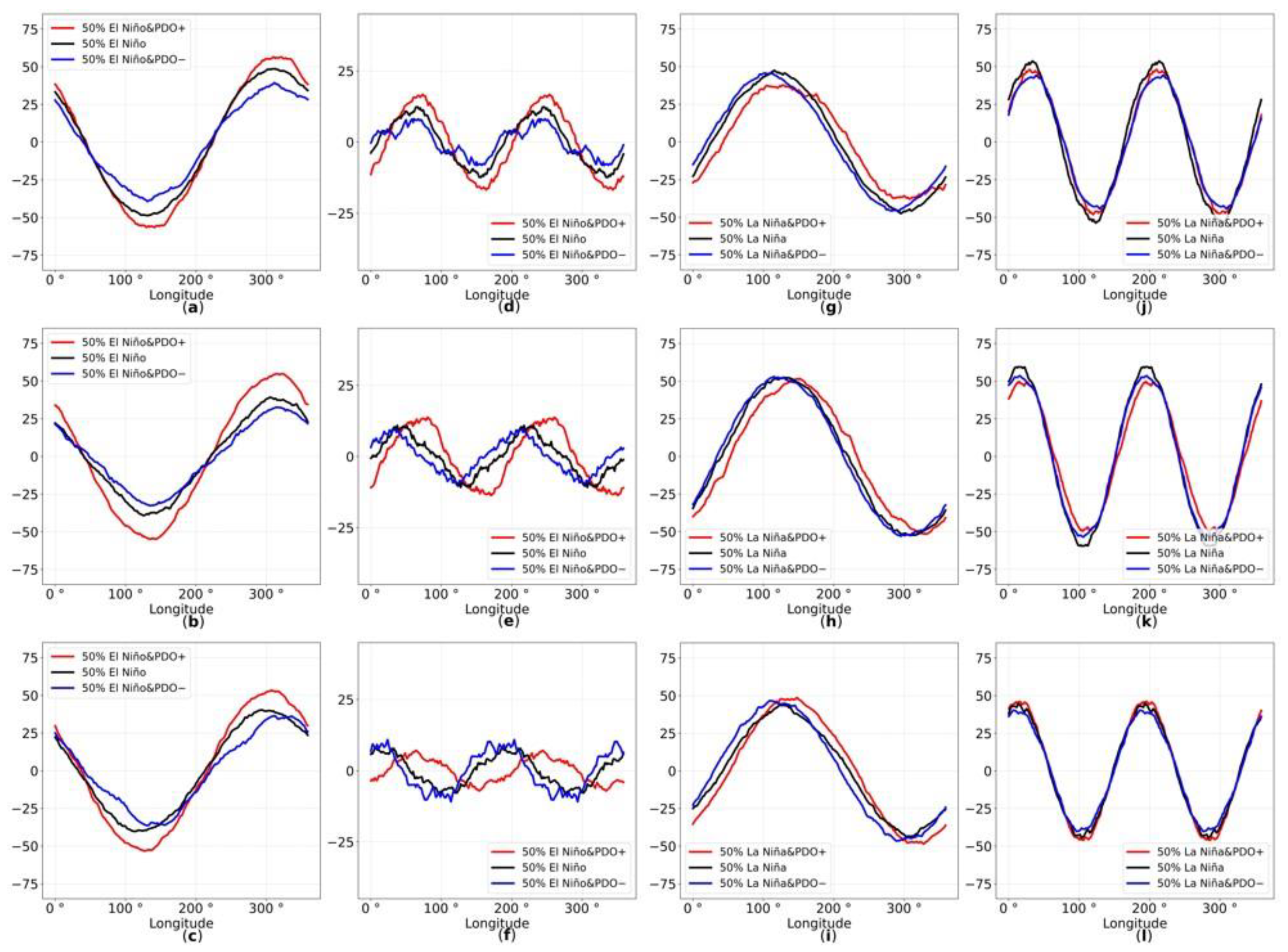
3.3. Planetary Waves Structure
3.4. Planetary Waves Activity
4. Conclusions
- It was shown that the large-scale extratropical SST anomalies do not show a statistically significant effect on the dynamics of the stratospheric polar vortex, but they significantly correct the effect of the ENSO modes when added to them. This contradicts the results obtained in [37], which show that the vortex is often weakened during the positive phase of the PDO. However, these works are based on the observational data, in which it is difficult to distinguish the influence of the various factors. It also contradicts the results obtained in the numerical experiments presented in [36].
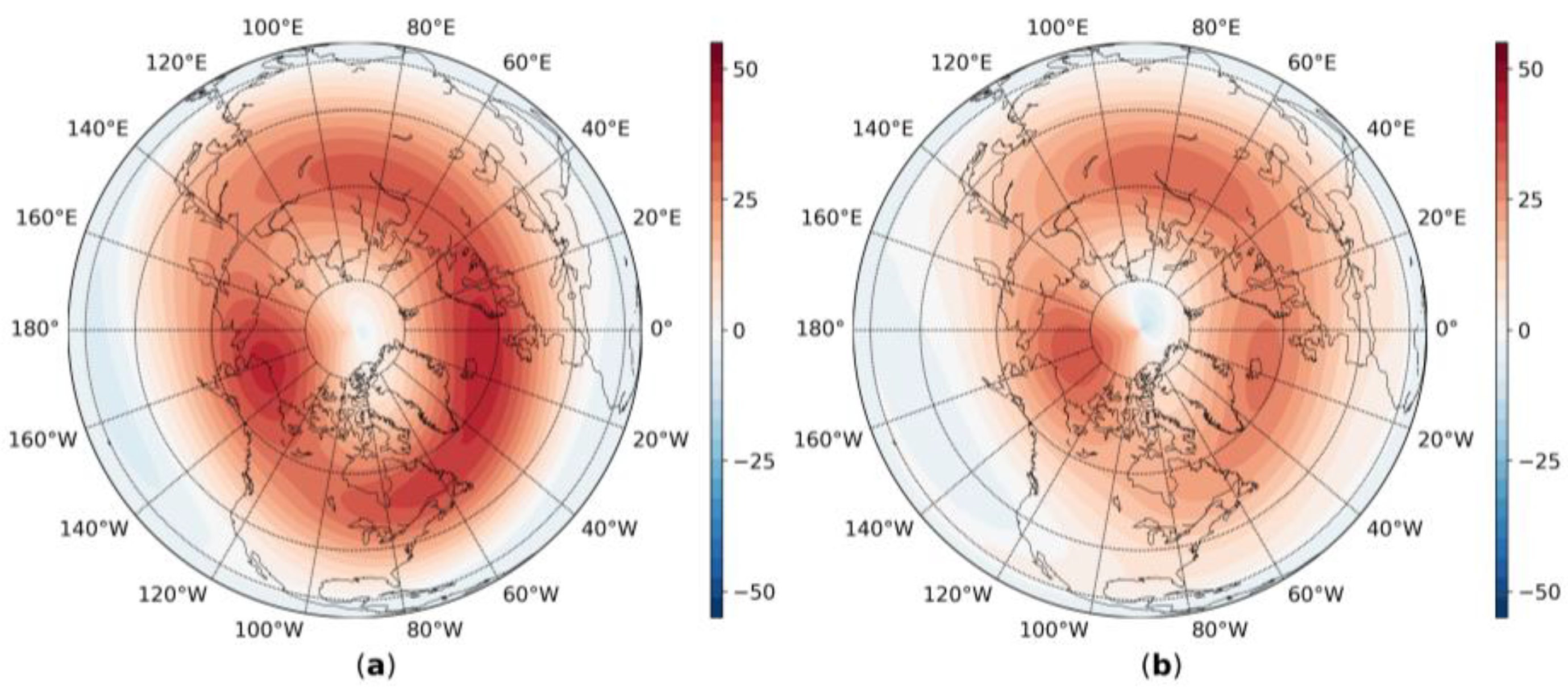
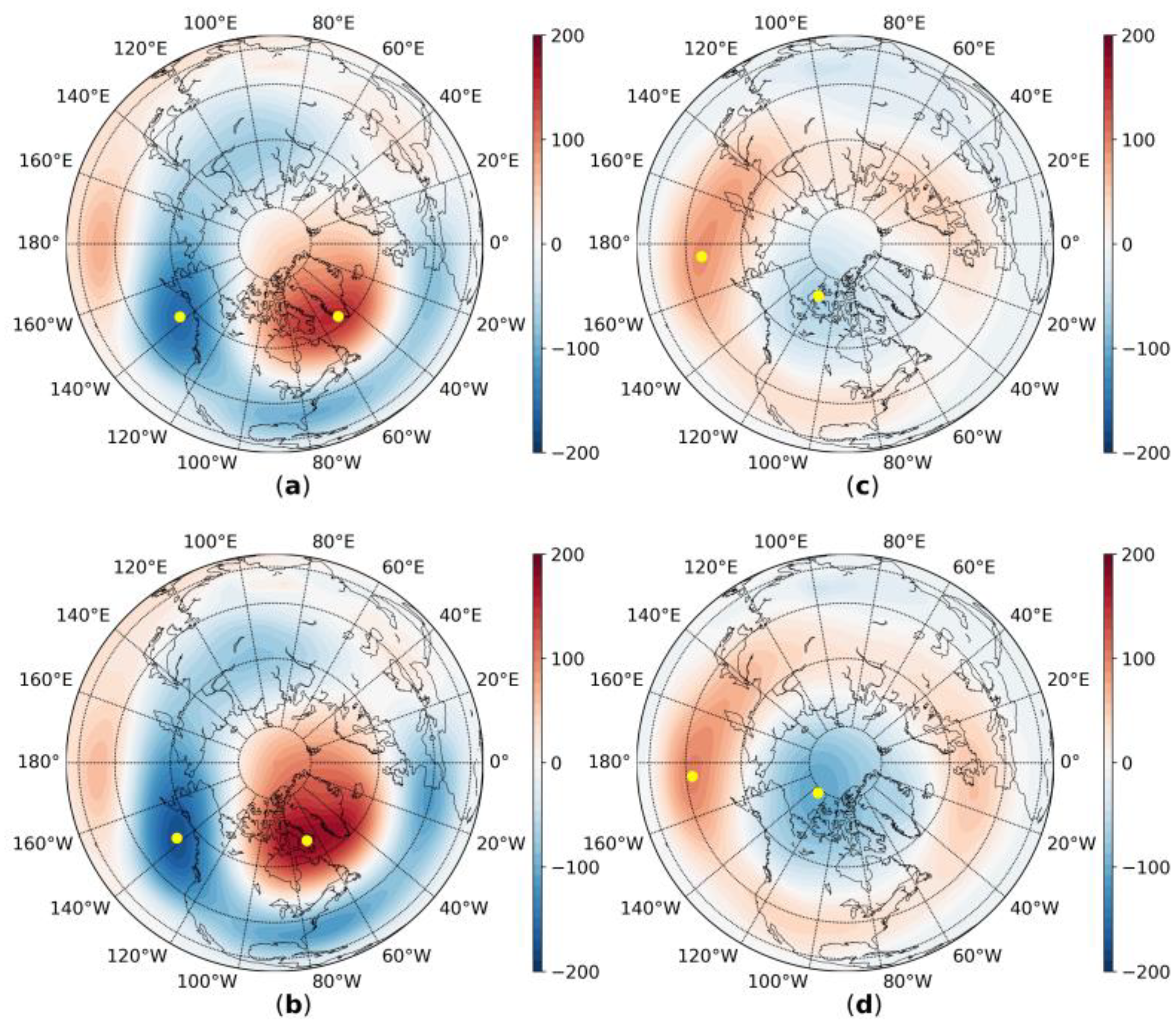
- In the middle troposphere, the El Niño leads to the PNA mode pattern pressure anomalies formation, which is consistent with the previously obtained results ([67,68,69]). At the same time, in our work, we obtained that, when the El Niño occurs during the positive PDO phase, these anomalies increase, and, during the negative phase, the anomalies weaken. The “single” La Niña experiment showed the NAM-pattern pressure anomalies and that they intensify when PDO− added. However, when PDO+ is added, the spatial pattern of the pressure field anomalies is absolutely different and we can find the features of the PNA mode there.
- The intensity of the SPV, expressed as U60_10, is weaker in both EN and LN experiments compared to the CTRL one. The previous papers have shown that, during the La Niña events, the SPV is stronger than the climatic mean [30]. This is explained by the fact that the average intensity of the vortex is lower according to the reanalysis data, compared to the CTRL experiment, since, in averaging over the observational data, weakened SPV states during the El Niño events are used. However, we showed that the effect of the El Niño and La Niña events on the SPV intensity is asymmetrical, so that, in the “single” EN experiment, the vortex is weaker by 40% than in the CTRL, and, in the “single” LN, the decrease is on average 19%. However, this characteristic is sensitive both to the intensity of the polar night jet and to the position of the SPV relative to the pole. Therefore, an additional analysis of the change in the spatial structure of the vortex and its centering over to the pole is required. Additionally, it is important to remember that, in the SST, the anomalies in this study’s experiments conducted were doubled and, in reality, the response of the stratosphere dynamics could be weaker.
- We showed that asymmetry is seen in the PDO mode’s influence on the effect of the ENSO on stratosphere dynamics. During the positive phase of the PDO, the impact of the El Niño events increases. When the negative PDO phase is added, the El Niño effect weakens: the vortex is stronger than in the “single” EN experiments, but is weaker than in the control experiment. The La Niña effect weakens during both positive and negative PDO phases.
- The formation of the SPV intensity anomalies during the El Niño events in “single” experiments occurs mainly due to planetary wave 2 variability, which explains up to 38% of the SPV intensity variability. In the case of the “merged” experiments, in EN&PDO+, wave 1 adopts the leading role in the formation of the SPV intensity anomalies, which explains up to 26% of the SPV intensity variability.
- In the “single” LN experiments, the formation of the SPV intensity anomalies occurs mainly due to wave 1 variability, which explains up to 20% of its variability. However, only in the LN&PDO− experiments can a connection between wave 2 and the SPV intensity be seen (18%).
- Our analysis showed that the dynamical response of the stratosphere-troposphere interaction is very sensitive to the meridional gradient of the SST anomalies between the tropical zone and mid-latitudes. The PDO mode can significantly correct the ENSO effect. The El Niño and positive PDO phase lead to the strongest meridional SST gradient between the tropical zone and the mid-latitudes and the strongest effect on the vortex. On the contrary, the El Niño and negative PDO phase lead to the weakest gradient and a weakening effect on the vortex.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, K.L.; Kushner, P.J. Linear interference and the initiation of extratropical stratosphere-troposphere interactions. J. Geophys. Res. 2012, 117, D13107. [Google Scholar] [CrossRef] [Green Version]
- Kidston, J.; Scaife, A.A.; Hardiman, S.C.; Mitchell, D.M.; Butchart, N.; Baldwin, M.P.; Gray, L.J. Stratospheric influence on tropospheric jet streams, storm tracks and surface weather. Nat. Geosci. 2015, 8, 433–440. [Google Scholar] [CrossRef]
- Scaife, A.A.; Comer, R.E.; Dunstone, N.J.; Knight, J.R.; Smith, D.M.; MacLachlan, C.; Martin, N.; Peterson, K.A.; Rowlands, D.; Carroll, E.B.; et al. Tropical rainfall, Rossby waves and regional winter climate predictions. Q. J. R. Meteorol. Soc. 2016, 143, 1–11. [Google Scholar] [CrossRef]
- Nie, Y.; Scaife, A.A.; Ren, H.L.; Comer, R.E.; Andrews, M.B.; Davis, P.; Martin, N. Stratospheric initial conditions provide seasonal predictability of the North Atlantic and Arctic Oscillations. Environ. Res. Lett. 2019, 14, 034006. [Google Scholar] [CrossRef]
- Xiong, X.; Liu, X.; Wu, W.; Knowland, K.E.; Yang, F.; Yang, Q.; Zhou, D.K. Impact of Stratosphere on Cold Air Outbreak: Observed Evidence by CrIS on SNPP and Its Comparison with Models. Atmosphere 2022, 13, 876. [Google Scholar] [CrossRef]
- Vitart, F.; Brown, A. S2S Forecasting: Towards Seamless Prediction. WMO Bull. 2019, 68, 70–74. [Google Scholar]
- Vitart, F.; Robertson, A.W. The sub-seasonal to seasonal prediction project (S2S) and the prediction of extreme events. NPJ Clim. Atmos. 2018, 1, 3. [Google Scholar] [CrossRef] [Green Version]
- Baldwin, M.P.; Dunkerton, T.J. Stratospheric harbingers of anomalous weather regimes. Science 2001, 294, 581–584. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.W.; Wallace, J.M. Regional climate impacts of the Northern Hemisphere annular mode. Science 2001, 293, 85–89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wallace, J.M.; Thompson, D.W. Annular modes and climate prediction. Phys. Today 2002, 55, 28–34. [Google Scholar] [CrossRef] [Green Version]
- Baldwin, M.P.; Stephenson, D.B.; Thompson, D.W.; Dunkerton, T.J.; Charlton, A.J.; O’Neill, A. Stratospheric memory and skill of extended-range weather forecasts. Science 2003, 301, 636–640. [Google Scholar] [CrossRef]
- Kolstad, E.W.; Breiteig, T.; Scaife, A.A. The association between stratospheric weak polar vortex events and cold air outbreaks in the Northern Hemisphere. Q. J. R. Meteorol. Soc. 2010, 136, 886–893. [Google Scholar] [CrossRef] [Green Version]
- Gerber, E.P.; Butler, A.; Calvo, N.; Charlton-Perez, A.; Giorgetta, M.; Manzini, E.; Perlwitz, J.; Polvani, L.M.; Sassi, F.; Scaife, A.A.; et al. Assessing and understanding the impact of stratospheric dynamics and variability on the Earth system. Bull. Am. Meteorol. Soc. 2012, 93, 845–859. [Google Scholar] [CrossRef] [Green Version]
- Tomassini, L.; Gerber, E.P.; Baldwin, M.P.; Bunzel, F.; Giorgetta, M. The role of stratosphere-troposphere coupling in the occurrence of extreme winter cold spells over northern Europe. J. Adv. Model. Earth Syst. 2012, 4. [Google Scholar] [CrossRef]
- Hitchcock, P.; Simpson, I.R. The downward influence of stratospheric sudden warmings. J. Atmos. Sci. 2014, 71, 3856–3876. [Google Scholar] [CrossRef]
- Nakamura, T.; Yamazaki, K.; Iwamoto, K.; Honda, M.; Miyoshi, Y.; Ogawa, Y.; Tomikawa, Y.; Ukita, J. The stratospheric pathway for Arctic impacts on midlatitude climate. Geophys. Res. Lett. 2016, 43, 3494–3501. [Google Scholar] [CrossRef] [Green Version]
- Charlton-Perez, A.J.; Ferranti, L.; Lee, R.W. The influence of the stratospheric state on North Atlantic weather regimes. Q. J. R. Meteorol. Soc. 2018, 144, 1140–1151. [Google Scholar] [CrossRef] [Green Version]
- Kretschmer, M.; Coumou, D.; Agel, L.; Barlow, M.; Tziperman, E.; Cohen, J. More-persistent weak stratospheric polar vortex states linked to cold extremes. Bull. Am. Meteorol. Soc. 2018, 99, 49–60. [Google Scholar] [CrossRef]
- Kretschmer, M.; Cohen, J.; Matthias, V.; Runge, J.; Coumou, D. The different stratospheric influence on cold-extremes in Eurasia and North America. NPJ Clim. Atmos. 2018, 1, 44. [Google Scholar] [CrossRef] [Green Version]
- Gerber, E.P.; Orbe, C.; Polvani, L.M. Stratospheric influence on the tropospheric circulation revealed by idealized ensemble forecasts. Geophys. Res. Lett. 2009, 36, L24801. [Google Scholar] [CrossRef] [Green Version]
- Karpechko, A.Y. Predictability of sudden stratospheric warmings in the ECMWF Extended-Range Forecast System. Mon. Weather Rev. 2018, 146, 1063–1075. [Google Scholar] [CrossRef]
- Tripathi, O.P.; Baldwin, M.; Charlton-Perez, A.; Charron, M.; Eckermann, S.D.; Gerber, E.; Harrison, R.G.; Jackson, D.R.; Kim, B.M.; Kuroda, Y.; et al. The predictability of the extratropical stratosphere on monthly time-scales and its impact on the skill of tropospheric forecasts. Q. J. R. Meteorol. Soc. 2015, 141, 987–1003. [Google Scholar] [CrossRef]
- Scaife, A.A.; Karpechko, A.Y.; Baldwin, M.P.; Brookshaw, A.; Butler, A.; Eade, R.; Gordon, M.E.; MacLachlan, C.; Martin, N.A.; Dunstone, N.; et al. Seasonal winter forecasts and the stratosphere. Atmos. Sci. Lett. 2016, 17, 51–56. [Google Scholar] [CrossRef] [Green Version]
- Volodin, E.M. Natural climate oscillations on decadal time scales. Fund. Appl. Climatol. 2015, 1, 78–95. [Google Scholar]
- Kim, H.M.; Webster, P.J.; Curry, J.A. Evaluation of short-term climate change prediction in multi-model CMIP5 decadal hindcasts. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Calvo, N.; García-Herrera, R.; Garcia, R.R. The ENSO signal in the stratosphere. Ann. N. Y. Acad. Sci. 2008, 1146, 16–31. [Google Scholar] [CrossRef] [Green Version]
- Manzini, E. ENSO and the stratosphere. Nat. Geosci. 2009, 2, 749–750. [Google Scholar] [CrossRef]
- Mo, K.C.; Livezey, R.E. Tropical-extratropical geopotential height teleconnections during the Northern Hemisphere winter. Mon. Weather Rev. 1986, 114, 2488–2515. [Google Scholar] [CrossRef]
- Manzini, E.; Giorgetta, M.A.; Esch, M.; Kornblueh, L.; Roeckner, E. The influence of sea surface temperatures on the northern winter stratosphere: Ensemble simulations with the MAECHAM5 model. J. Clim. 2006, 19, 3863–3881. [Google Scholar] [CrossRef] [Green Version]
- Rao, J.; Ren, R. Asymmetry and nonlinearity of the influence of ENSO on the northern winter stratosphere: 1. Observations. J. Geophys. Res. Atmos. 2016, 121, 9000–9016. [Google Scholar] [CrossRef] [Green Version]
- Ashok, K.; Behera, S.; Rao, A.S.; Weng, H.; Yamagata, T. El Niño Modoki and its teleconnection. J. Geophys. Res. 2007, 112, C11007. [Google Scholar] [CrossRef]
- Xie, F.; Li, J.; Tian, W.; Feng, J.; Huo, Y. Signals of El Niño Modoki in the tropical tropopause layer and stratosphere. Atmos. Chem. Phys. 2012, 12, 5259–5273. [Google Scholar] [CrossRef] [Green Version]
- Garfinkel, C.I.; Hartmann, D.L. Different ENSO teleconnections and their effects on the stratospheric polar vortex. J. Geophys. Res. Atmos. 2008, 113, D18. [Google Scholar] [CrossRef] [Green Version]
- Kushnir, Y.; Robinson, W.A.; Bladé, I.; Hall, N.M.J.; Peng, S.; Sutton, R. Atmospheric GCM response to extratropical SST anomalies: Synthesis and evaluation. J. Clim. 2002, 15, 2233–2256. [Google Scholar] [CrossRef]
- Jadin, E.A.; Wei, K.; Zyulyaeva, Y.A.; Chen, W.; Wang, L. Stratospheric wave activity and the Pacific Decadal Oscillation. J. Atmos. Sol.-Terr. Phys. 2010, 72, 1163–1170. [Google Scholar] [CrossRef]
- Hurwitz, M.M.; Newman, P.A.; Garfinkel, C.I. On the influence of North Pacific sea surface temperature on the Arctic winter climate. J. Geophys. Res. Atmos. 2012, 117, D19. [Google Scholar] [CrossRef]
- Woo, S.H.; Sung, M.K.; Son, S.W.; Kug, J.S. Connection between weak stratospheric vortex events and the Pacific Decadal Oscillation. Clim. Dyn. 2015, 45, 3481–3492. [Google Scholar] [CrossRef]
- Kren, A.C.; Marsh, D.R.; Smith, A.K.; Pilewskie, P. Wintertime Northern Hemisphere response in the stratosphere to the Pacific decadal oscillation using the Whole Atmosphere Community Climate Model. J. Clim. 2016, 29, 1031–1049. [Google Scholar] [CrossRef]
- Wang, W.; Matthes, K.; Omrani, N.E.; Latif, M. Decadal variability of tropical tropopause temperature and its relationship to the Pacific Decadal Oscillation. Sci. Rep. 2016, 6, 29537. [Google Scholar] [CrossRef] [Green Version]
- Zyulyaeva, Y.A.; Zhadin, E.A. Analysis of three-dimensional Eliassen-Palm fluxes in the lower stratosphere. Russ. Meteorol. Hydrol. 2009, 34, 483. [Google Scholar] [CrossRef]
- Brierley, C.M.; Fedorov, A.V. Relative importance of meridional and zonal sea surface temperature gradients for the onset of the ice ages and Pliocene-Pleistocene climate evolution. Paleoceanography 2010, 25. [Google Scholar] [CrossRef] [Green Version]
- Rind, D.; Suozzo, R.; Balachandran, N.K.; Prather, M.J. Climate change and the middle atmosphere. Part I: The doubled CO2 climate. J. Atmos. Sci. 1990, 47, 475–494. [Google Scholar] [CrossRef]
- Olsen, M.A.; Schoeberl, M.R.; Nielsen, J.E. Response of stratospheric circulation and stratosphere-troposphere exchange to changing sea surface temperatures. J. Geophys. Res. Atmos. 2007, 112, D16. [Google Scholar] [CrossRef] [Green Version]
- Rao, J.; Ren, R.; Xia, X.; Shi, C.; Guo, D. Combined impact of El Niño–Southern Oscillation and Pacific Decadal Oscillation on the northern winter stratosphere. Atmosphere 2019, 10, 211. [Google Scholar] [CrossRef] [Green Version]
- Bond, N.A.; Overland, J.E.; Spillane, M.; Stabeno, P. Recent shifts in the state of the North Pacific. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
- Di Lorenzo, E.; Schneider, N.; Cobb, K.M.; Franks, P.J.S.; Chhak, K.; Miller, A.J.; McWilliams, J.C.; Bograd, S.J.; Arango, H.; Curchitser, E.; et al. North Pacific Gyre Oscillation links ocean climate and ecosystem change. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Hurrell, J.W.; Hack, J.J.; Shea, D.; Caron, J.M.; Rosinski, J. A new sea surface temperature and sea ice boundary dataset for the Community Atmosphere Model. J. Clim. 2008, 21, 5145–5153. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108, D14. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Taylor, K.E.; Williamson, D.; Zwiers, F. The Sea Surface Temperature and Sea-Ice Concentration Boundary Conditions for AMIP II Simulations; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2000; Volume 28.
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Vallis, G.K.; Colyer, G.; Geen, R.; Gerber, E.; Jucker, M.; Maher, P.; Paterson, A.; Pietschnig, M.; Penn, J.; Thomson, S.I. Isca, v1. 0: A framework for the global modelling of the atmospheres of Earth and other planets at varying levels of complexity. Geosci. Model Dev. 2018, 11, 843–859. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Thomson, S.I.; Vallis, G.K. Atmospheric response to SST anomalies. Part I: Background-state dependence, teleconnections, and local effects in winter. J. Atmos. Sci. 2018, 75, 4107–4124. [Google Scholar] [CrossRef]
- Fortuin, J.P.; Langematz, U. Update on the global ozone climatology and on concurrent ozone and temperature trends. Proc. SPIE 1995, 2311, 207–216. [Google Scholar]
- Jucker, M.; Gerber, E.P. Untangling the annual cycle of the tropical tropopause layer with an idealized moist model. J. Clim. 2017, 30, 7339–7358. [Google Scholar] [CrossRef]
- Trenberth, K.E. The definition of El Niño. Bull. Am. Meteorol. Soc. 1997, 78, 2771–2778. [Google Scholar] [CrossRef]
- Kug, J.S.; Jin, F.F.; An, S.I. Two types of El Niño events: Cold tongue El Niño and warm pool El Niño. J. Clim. 2009, 22, 1499–1515. [Google Scholar] [CrossRef]
- Tseng, J.C.-H. An ISOMAP Analysis of Sea Surface Temperature for the Classification and Detection of El Niño & La Niña Events. Atmosphere 2022, 13, 919. [Google Scholar]
- Meehl, G.A.; Teng, H. Multi-model changes in El Niño teleconnections over North America in a future warmer climate. Clim. Dyn. 2007, 29, 779–790. [Google Scholar] [CrossRef]
- Hare, S.R. Low Frequency Climate Variability and Salmon Production. Ph.D. Dissertation, University of Washington, Seattle, WA, USA, 1996. [Google Scholar]
- Zhang, Y. An Observational Study of Atmosphere-Ocean Interactions in the Northern Oceans on Interannual and Interdecadal Time-Scales. Ph.D. Dissertation, University of Washington, Seattle, WA, USA, 1996. [Google Scholar]
- Plumb, R.A. On the three-dimensional propagation of stationary waves. J. Atmos. Sci. 1985, 42, 217–229. [Google Scholar] [CrossRef]
- Anstey, J.A.; Scinocca, J.F.; Keller, M. Simulating the QBO in an atmospheric general circulation model: Sensitivity to resolved and parameterized forcing. J. Atmos. Sci. 2016, 73, 1649–1665. [Google Scholar] [CrossRef]
- Lott, F.; Rani, R.; Podglajen, A.; Codron, F.; Guez, L.; Hertzog, A.; Plougonven, R. Direct comparison between a non orographic gravity wave drag scheme and constant level balloons. J. Geophys. Res. Atmos. 2022; in press. [Google Scholar]
- Matsuno, T. A dynamical model of the stratospheric sudden warming. J. Atmos. Sci. 1971, 28, 1479–1494. [Google Scholar] [CrossRef]
- Gushchina, D.; Kolennikova, M.; Dewitte, B.; Yeh, S.W. On the relationship between ENSO diversity and the ENSO atmospheric teleconnection to high-latitudes. Int. J. Climatol. 2022, 42, 1303–1325. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, T. A new paradigm for continental U.S. summer rainfall variability: Asia–North America teleconnection. J. Clim. 2016, 29, 7313–7327. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, T. Amplified contiguous United States summer rainfall variability induced by East Asian monsoon intedecadal change. Clim. Dyn. 2018, 50, 3523–3536. [Google Scholar] [CrossRef]



| Boundary Conditions | Pacific Decadal Oscillation | |||
|---|---|---|---|---|
| Neutral | Positive Phase | Negative Phase | ||
| ENSO | Neutral | + (control) | + | + |
| El Niño | + | + | + | |
| La Niña | + | + | + | |
| PC 1 | PC 2 | ||
|---|---|---|---|
| CTRL | 0.04 | 0.00 | |
| El Niño | N | 0.38 | 0.20 |
| PDO+ | 0.10 | 0.26 | |
| PDO− | 0.10 | 0.18 | |
| La Niña | N | 0.00 | 0.20 |
| PDO+ | 0.06 | 0.01 | |
| PDO− | 0.18 | 0.01 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobaeva, D.; Zyulyaeva, Y.; Gulev, S. ENSO and PDO Effect on Stratospheric Dynamics in Isca Numerical Experiments. Atmosphere 2023, 14, 459. https://doi.org/10.3390/atmos14030459
Sobaeva D, Zyulyaeva Y, Gulev S. ENSO and PDO Effect on Stratospheric Dynamics in Isca Numerical Experiments. Atmosphere. 2023; 14(3):459. https://doi.org/10.3390/atmos14030459
Chicago/Turabian StyleSobaeva, Daria, Yulia Zyulyaeva, and Sergey Gulev. 2023. "ENSO and PDO Effect on Stratospheric Dynamics in Isca Numerical Experiments" Atmosphere 14, no. 3: 459. https://doi.org/10.3390/atmos14030459
APA StyleSobaeva, D., Zyulyaeva, Y., & Gulev, S. (2023). ENSO and PDO Effect on Stratospheric Dynamics in Isca Numerical Experiments. Atmosphere, 14(3), 459. https://doi.org/10.3390/atmos14030459







