1. Introduction
According to estimates, the amount of electricity produced by solar photovoltaics (PVs) increased by 22% globally in 2021 and surpassed 1000 TWh. As a result, the global electricity market share of solar PV is currently close to 3.6% [
1]. Government support programs, technological breakthroughs, and sharp cost reductions are all responsible for this surge [
2]. The intermittence, randomness, and volatility of PV power output is caused by uncontrollable factors such as weather, seasonality, and climate [
3]. These significant constraints still hinder the large-scale integration of PVs into the power grid and interfere with the reliability and stability of existing grid-connected power systems [
4]. Therefore, PV power predictions are essential to ensure the stability, reliability, and cost effectiveness of the system [
5]. Usually, PV power prediction can be achieved through the prediction of global horizontal irradiance (GHI) or PV power output, with techniques applied to forecast PV power production being an extension of those used for predicting GHI. According to forecast horizons and model types, solar irradiance forecasting models can be broadly categorized [
6]. Forecasting horizons can be categorized as short term [
7], medium term [
8], and long term [
9]. For the real-time optimization of various grid components such as electrolyzers—which are essential for producing low-emission hydrogen—short-term forecasting (a few minutes to an hour) is used. For intraday operation optimization, medium-term (1 h to 6 h) forecasting is used. For days-ahead optimization, long-term forecasting (6 h to days ahead) is used. Furthermore, there are two main groups of solar irradiance forecasting model types, i.e., physical methods and data-driven models [
6]. Physical models use numerical weather predictions (NWPs), sky imagery, and satellite imaging to obtain information on the physical state and dynamic motion of solar radiation through the atmosphere [
10,
11]. Data-driven models, on the other hand, are based on historical data and have the capacity to extract information from the data in order to forecast time series [
12]. Finally, data-driven models are further sub-categorized into statistical or machine learning models. Statistical models include the autoregressive integrated moving average (ARIMA) [
13], the autoregressive moving average (ARMA) [
14], and the coupled autoregressive and dynamic system (CARD) [
15]. Support-vector machines (SVMs) [
8] and feed-forward neural networks (FFNNs) [
16] are examples of machine learning models, as are convolutional neural networks (CNNs) [
7] and recurrent neural networks (RNNs) [
17]. A wealth of studies demonstrate that machine learning algorithms are better than statistical models for time series forecasting.
All-sky images can be used, coupled with meteorological data, to perform short-term irradiance forecasting. These techniques are better suited for short-term forecasting since they provide real-time information on the cloud cover above the considered site.
Peng et al. [
18] employed sky images from numerous total sky imagers (TSIs) to detect clouds more effectively and make up for incorrect or excessively exposed TSI images. This technique, which is used for very-short-term forecasting (1 to 15 minutes in advance), makes use of redundant data from numerous cameras’ overlapping views to figure out the base heights and wind field of various layers. Under the majority of cloud situations, the suggested methodology offers accurate 15 min forecasts.
Kuhn et al. [
19] used multiple TSIs for temporal and spatial aggregation in order to improve very-short-term solar irradiance forecasting. Those aggregation effects are relevant only for large solar plants, covering several square kilometers. It is shown that considering aggregation effects significantly reduces forecasting errors, especially spatial aggregation that lowers the relative root mean square error from 30.9% to 23.5% on a day with variable conditions for 1 min averages and a time horizon of 15 min.
Additionally, image processing and short-term irradiance forecasting can be performed with a CNN. The 2D structure of images is utilized by this neural network to apply filters and extract significant features. Ref. [
20] employed the CNN model SUNSET for short-term PV forecasting. For a 30 kW PV system, the model forecasts the PV power output 15 min in advance with a 1 min resolution. The training was conducted on sky images captured the course of a year and PV output power. Along with the SUNSET model, deeper and more complicated CNN models were also used, as well as auto-regression techniques. Mean square error (MSE) and forecast skill (%) were two metrics used to assess the models’ accuracy. With an MSE of 4.51 kW² and forecasting skill of 26.22% and 16.11% for bright and cloudy days, respectively, the SUNSET model performs better than other models.
For very-short-term forecasting of solar irradiation, ref. [
21] employed a hybrid model combining a convolutional neural network and multilayer perceptron (CNN-MLP). Images of the sky and weather data gathered from a ground meteorological station in Morocco are processed using the suggested method. The CNN-MLP produces the best results with an RMSE ranging from 13.05 W/m² to 49 W/m², while the persistence model’s RMSE is between 45.076 W/m² and 114.19 W/m².
Other neural networks can also be used for medium-term forecasting, such as RNN, which specializes in time-series forecasting. However, the vanishing gradient issue with the classical RNN [
22] makes it impossible to learn lengthy data sequences. This issue is resolved using LSTM, a form of RNN, which enforces a continuous error flow (i.e., one that is neither exploding nor disappearing) across the internal states of the neural network’s cells [
23]. Making the LSTM neural network appropriate for long time-series forecasting. An RNN implemented by [
17] can forecast over multiple time horizons at once, including 1 h, 2 h, 3 h, and 4 h ahead. In parallel, four independent RNN models were developed for predictions that are 1 h, 2 h, 3 h, and 4 h in advance. The models were trained with two years (2010 and 2011) of meteorological data and tested on four different years (2009, 2015, 2016, 2017). With data collected at Bonville, USA, in 2009, the multi-horizon model produced a mean RMSE (across the four time horizons) of 14.6 W/m², while at the same location and time, the four independent models’ mean RMSE was 18.6 W/m². The RMSE achieved using the RNN models is lower than the RMSE for other machine learning methods, such as random forests, support-vector machine, gradient boosting, and FFNN, described in [
24].
Kumari and Toshniwal [
25] used a hybrid CNN-LSTM model for estimating solar irradiation. The model was trained using GHI values collected over a 12-year period (2006–2018). The observations were made in Alice Spring, Australia, which is notable for having a desert climate and 300 clear days per year. The models’ time horizon can be adjusted from one day to one month in advance. The CNN-LSTM model was compared with other standalone models such as CNN, LSTM, RNN, and deep neural network (DNN). The mean absolute percentage error (MAPE) was found equal to 4.84%, 6.48%, 5.84%, and 6.56% for the CNN-LSTM, LSTM, CNN, and DNN, respectively, for all simulations over one-day prediction. The results show that the hybrid CNN-LSTM model to be the best for GHI forecasting.
Kumari and Toshniwal [
26] proposed a hybrid deep learning CNN-LSTM model for hourly GHI forecasting. The training was implemented at 23 locations in California, USA. The historical data used for the training of the different forecasting models was composed of meteorological data such as GHI, temperature, precipitation, cloud cover, etc. The proposed method showed a forecast skill of about 37–45% over other standalone models such as smart persistence, SVM, ANN, LSTM, and CNN. It suggests that the proposed hybrid model is appropriate for short-term GHI forecasting, due to its high accuracy under diverse climatic, seasonal, and sky conditions.
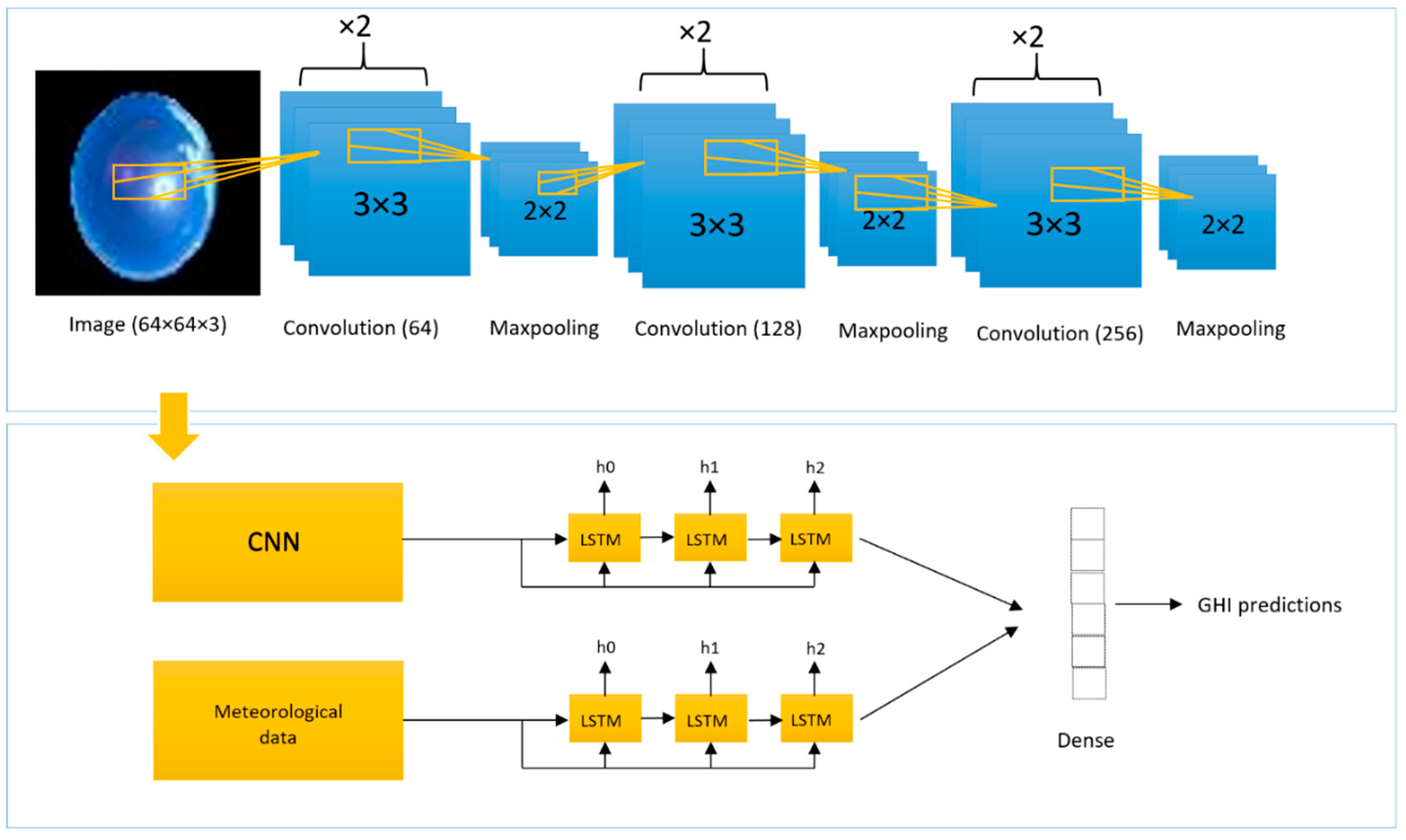
In summary, a CNN-LSTM hybrid model is an interesting and promising deep learning model for deploying point forecasts of solar irradiance. The benefit of this model is that it can simultaneously analyze sky images and meteorological data. In fact, combining feature extraction from the CNN and the ability to detect long-term dependencies from the LSTM ought to increase the accuracy of the implemented solar irradiance forecasts. In addition, one of the disadvantages of GHI point forecasts (or deterministic forecasts) is that they do not contain sufficient information about the errors that forecasting models may generate, as well as the volatility and randomness of the solar irradiance. Point forecasts are insufficient for optimizing the operation of power systems [
27].
The objective of this paper is to implement hourly probabilistic forecasts through combining quantile mapping with a hybrid model (CNN-LSTM). The analysis of hourly residuals allows the computation of prediction intervals with varying levels of confidence. The hybrid model is compared to other standalone models, namely ANN, CNN, and LSTM, for comparative purposes.
The novelty of this paper resides in the residual modeling implemented with the hybrid CNN-LSTM model to derive hourly GHI probabilistic forecasts. Through the analysis of hourly residuals, also known as quantile mapping [
28], probabilistic forecasts are obtained through the computation of prediction intervals with various levels of confidence. In this application, sky images, which are typically utilized for very-short-term forecasting (1 to 15 min), are utilized for 1 h-ahead GHI forecasting. This paper’s probabilistic forecasts account for the fact that approaching clouds are not yet visible to the TSI (on an hourly timescale). Combining probabilistic forecasts with sky images is pertinent for hourly predictions, which are typically made using satellite images [
29,
30].
In order to produce these forecasts, various forecasting tools are trained using historical meteorological data measured on site and sky images. The GHI forecasting models are intended to control a combined cold and power generation system (isolated micro-grid for electricity and cold production, such as air conditioning), with multiple energy production and storage sub-systems, all of which are solar-powered. The RECIF project’s (French acronym for micro-grid for electricity and cold cogeneration) electrolyzer must have sufficient power for at least one hour in order to function correctly and avoid potential misfires, which would reduce the component’s lifetime. Consequently, the necessity and implementation of the mean hourly forecasting models are presented in this paper. This initiative was developed within the framework of a French National Agency for Research (ANR)-funded project and is being carried out at the University of French Polynesia (UPF).
The paper is organized as follows: the data collection and data processing methods are presented in
Section 2.1, followed by the GHI forecasting models in
Section 2.2. The quantile mapping method for prediction interval computation is detailed in
Section 2.3.
Section 3 details the different metrics and reference models used for the comparison between the different deep learning algorithms. The results for point and probabilistic forecasts are detailed in
Section 4.
Section 5 provides the main achievements of the study in a summary form.
5. Conclusions
In this article, we implemented a hybrid deep learning model for mean hourly forecasting, using convolutional layers for feature extraction from images and LSTM technology for meteorological data processing and time-series forecasting. The performance of the hybrid model was compared to the performance of three other neural nets, specifically, ANN, CNN, and LSTM. The persistence model was compared to each of the implemented models. The novelty of this study resides in the residual modeling implemented with the CNN-LSTM model, which enables us to generate probabilistic forecasts from the statistical models. Overall, the testing data, for each type of day, and for all the deterministic and probabilistic metrics, the hybrid model was found to be the best performing and most accurate. Indeed, the RMSE, MAE, and R² for the CNN-LSTM were equal to 100.58 W/m², 66.09 W/m², and 0.85, respectively, which is better than the other benchmark models. For probabilistic forecasts, the CNN-LSTM has the best CWC values with 8.54, 17.04, 33.37, and 47.98, respectively, for PI(38%), PI(68%), PI(95%), and PI(99%).