Hemispheric Symmetry of Planetary Albedo: A Corollary of Nonequilibrium Thermodynamics
Abstract
1. Introduction
2. Box Model
2.1. Surface-Air Temperature
2.2. Sea-Surface Temperature
2.3. Albedo Symmetry
2.4. Cloud Partition
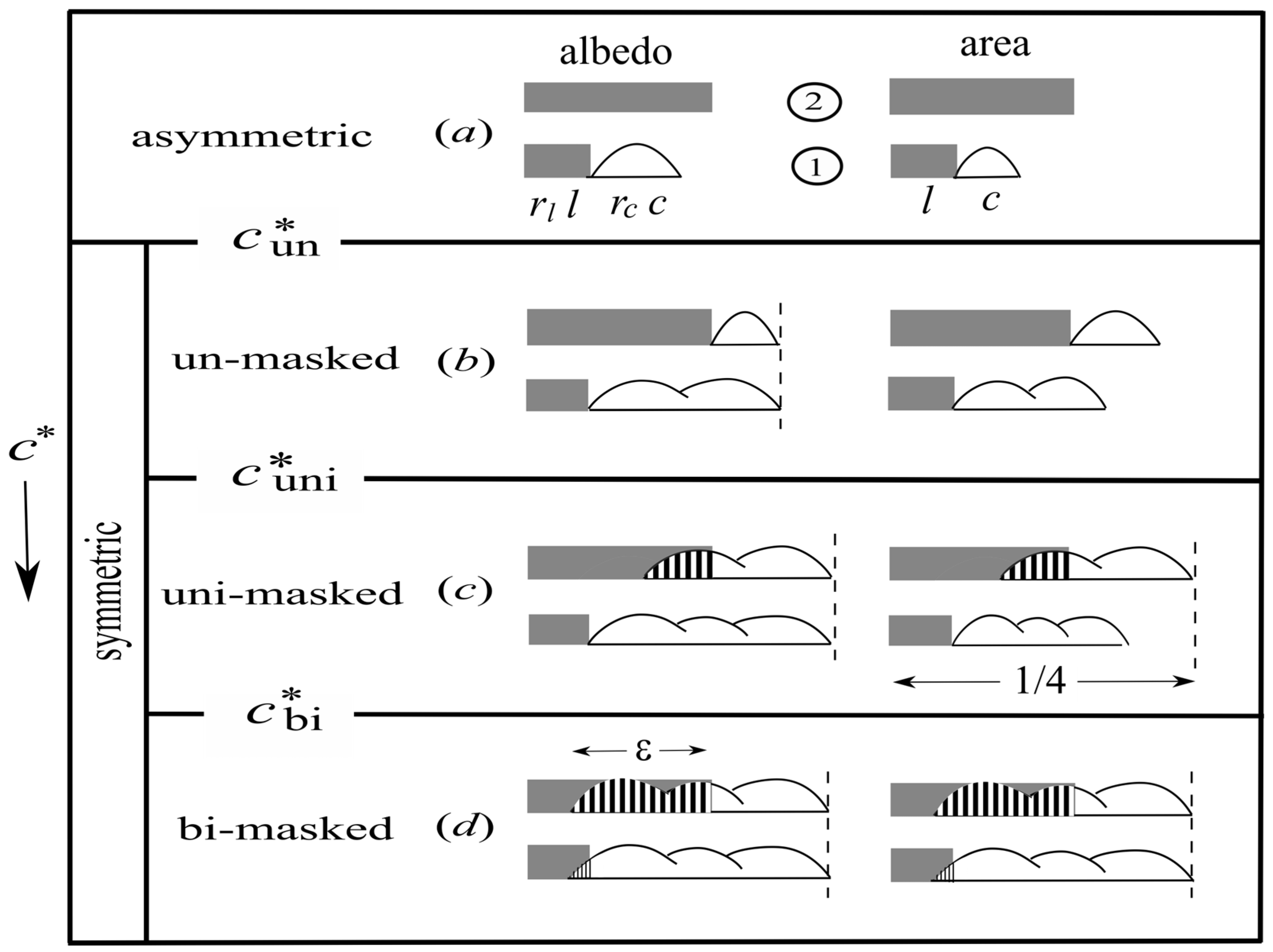
3. Model Regimes
3.1. Asymmetric Regime
3.2. Un-Masked Regime
3.3. Uni-Masked Regime
3.4. Bi-Masked Regime
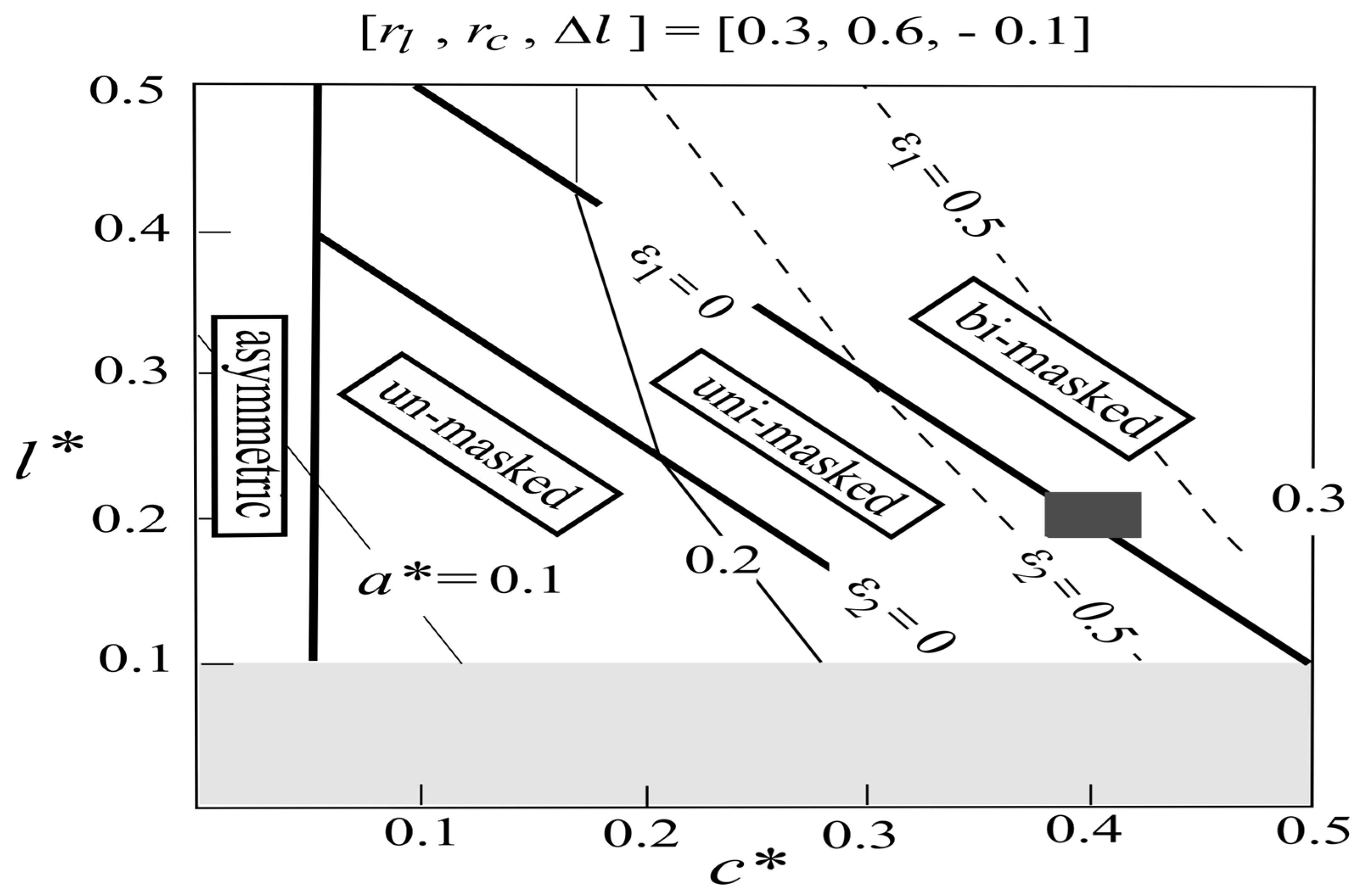
3.5. Parameter Dependence
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Planetary albedo | |
| Cloud area | |
| Polar-total cloud area | |
| Asymmetry of cloud area | |
| Un-masked threshold | |
| Uni-masked threshold | |
| Bi-masked threshold | |
| Atmosphere heat transport | |
| Ocean heat transport | |
| Land area | |
| Polar-total land area | |
| Asymmetry of land area | |
| Incident SW flux | |
| Absorbed SW flux | |
| Global mean of | |
| Deviation of ( | |
| Deviation of convective flux | |
| Asymmetry of absorbed SW flux | |
| Reflectance ratio () | |
| Cloud reflectance | |
| Land reflectance | |
| Deviation of SST | |
| Deviation of SAT | |
| Air/sea transfer coefficient | |
| Masked land area | |
| Ocean entropy production | |
| Deviation of | |
| Atmospheric entropy production | |
| Deviation of |
References
- Stephens, G.L.; O’Brien, D.; Webster, P.J.; Pilewski, P.; Kato, S.; Li, J.L. The albedo of Earth. Rev. Geophys. 2015, 53, 141–163. [Google Scholar] [CrossRef]
- Datseris, G.; Stevens, B. Earth’s albedo and its symmetry. AGU Adv. 2021, 2, e2021AV000440. [Google Scholar] [CrossRef]
- Voigt, A.; Stevens, B.; Bader, J.; Mauristen, T. The observed hemispheric symmetry in reflected shortwave irradiance. J. Clim. 2013, 26, 468–477. [Google Scholar] [CrossRef]
- Haywood, J.M.; Jones, A.; Dunstone, N.; Milton, S.; Vellinga, M.; Bodas-Salcedo, A.; Hawcroft, M.; Kravitz, B.; Cole, J.; Watanabe, S.; et al. The impact of equilibrating hemispheric albedos on tropical performance in the HadGEM2-ES coupled climate model. Geophys. Res. Lett. 2016, 43, 395–403. [Google Scholar] [CrossRef]
- Donohoe, A.; Battisti, D.S. Atmospheric and surface contributions to planetary albedo. J. Clim. 2011, 24, 4402–4418. [Google Scholar] [CrossRef]
- Kang, S.M.; Held, I.M.; Frierson, D.M.W.; Zhao, M. The response of the ITCZ to extratropical thermal forcing: Idealized slab-ocean experiments with a GCM. J. Clim. 2008, 21, 3521–3532. [Google Scholar] [CrossRef]
- Donohoe, A.; Marshall, J.; Ferreira, D.; Mcgee, D. The relationship between ITCZ location and cross-equatorial atmospheric heat transport: From the seasonal cycle to the Last Glacial Maximum. J. Clim. 2013, 26, 3597–3618. [Google Scholar] [CrossRef]
- Voigt, A.; Stevens, B.; Bader, J.; Mauritsen, T. Compensation of hemispheric albedo asymmetries by shifts of the ITCZ and tropical cloud. J. Clim. 2014, 27, 1029–1044. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 1018. [Google Scholar] [CrossRef]
- Kleidon, A. Non-equilibrium thermodynamics and maximum entropy production in the Earth system: Applications and implications. Naturwissenschaften 2009, 96, 653–677. [Google Scholar] [CrossRef]
- Dewar, R.C.; Lineweaver, C.H.; Niven, R.K.; Regenauer-Lieb, K. Beyond the second law: An overview. In Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 3–27. [Google Scholar] [CrossRef]
- Ou, H.W. Thermohaline circulation: A missing equation and its climate change implications. Clim. Dyn. 2018, 50, 641–653. [Google Scholar] [CrossRef]
- Evans, D.J.; Cohen, E.G.; Morriss, G.P. Probability of second law violations in shearing steady states. Phys. Rev. Lett. 1993, 71, 2401–2404. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.M.; Sevick, E.M.; Mittag, E.; Searles, D.J.; Evans, D.J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 2002, 89, 050601. [Google Scholar] [CrossRef]
- Shimokawa, S.; Ozawa, H. On the thermodynamics of the oceanic general circulation: Irreversible transition to a state with higher rate of entropy production. Q. J. R. Meteorolog. Soc. 2002, 128, 2115–2128. [Google Scholar] [CrossRef]
- Kleidon, A.; Fraedrich, K.; Kunz, T.; Lunkeit, F. The atmospheric circulation and states of maximum entropy production. Geophys. Res. Lett. 2003, 30, 2223. [Google Scholar] [CrossRef]
- Fraedrich, K.; Lunkeit, F. Diagnosing the entropy budget of a climate model. Tellus 2008, A60, 921–931. [Google Scholar] [CrossRef][Green Version]
- Hogg, A.M.; Gayen, B. Ocean gyres driven by surface buoyancy forcing. Geophys. Res. Lett. 2020, 47, e2020GL088539. [Google Scholar] [CrossRef]
- Colin de Verdière, A. Buoyancy driven planetary flows. J. Mar. Res. 1988, 46, 215265. [Google Scholar] [CrossRef]
- Ou, H.W. Possible bounds on the earth’s surface temperature: From the perspective of a conceptual global-mean model. J. Clim. 2001, 14, 2976–2988. [Google Scholar] [CrossRef]
- Crowley, T.J.; North, G.R. Paleoclimatology; Oxford University Press: New York, NY, USA, 1991; 339p. [Google Scholar]
- Liou, K.N. (Ed.) Chapter 8—Radiation and Climate; Int Geophys, Academic Press: Cambridge, MA, USA, 2002; Volume 84, pp. 442–521. ISSN 0074-6142. [Google Scholar]
- Kim, D.; Ramanathan, V. Solar radiation and radiative forcing due to aerosols. J. Geophys. Res. 2008, 113, D02203. [Google Scholar] [CrossRef]
- Pauluis, O.; Held, I.M. Entropy budget of an atmosphere in radiative-convective equilibrium. Part I: Maximum work and frictional dissipation. J. Atmos. Sci. 2002, 59, 125–139. [Google Scholar] [CrossRef]
- Ou, H.W. Hydrological cycle and ocean stratification in a coupled climate system: A theoretical study. Tellus 2007, 59A, 683–694. [Google Scholar] [CrossRef][Green Version]
- Peixoto, J.P.; Oort, A.H. Physics of Climate; American Institute of Physics: New York, NY, USA, 1992; 520p. [Google Scholar]
- Klein, S.A.; Hartmann, D.L. The seasonal cycle of low stratiform clouds. J. Clim. 1993, 6, 1587–1606. [Google Scholar] [CrossRef]
- Wood, R. Stratocumulus Clouds. Mon. Weather. Rev. 2012, 140, 2373–2433. [Google Scholar] [CrossRef]
- Hartmann, D.L. Global Physical Climatology; Academic Press: New York, NY, USA, 2015; 411p. [Google Scholar]
- Ramanathan, V.C.; Crutzen, P.J.; Kiehl, J.T.; Rosenfeld, D. Aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef]
- Scotese, C.R.; Golonka, J. Paleogeographic Atlas; PALEOMAP project, Department of Geology, University of Texas at Arlington: Arlington, TX, USA, 1993. [Google Scholar]
- Stephens, G.L. Cloud feedbacks in the climate system: A critical review. J. Clim. 2005, 18, 237–273. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, H.-W. Hemispheric Symmetry of Planetary Albedo: A Corollary of Nonequilibrium Thermodynamics. Atmosphere 2023, 14, 1243. https://doi.org/10.3390/atmos14081243
Ou H-W. Hemispheric Symmetry of Planetary Albedo: A Corollary of Nonequilibrium Thermodynamics. Atmosphere. 2023; 14(8):1243. https://doi.org/10.3390/atmos14081243
Chicago/Turabian StyleOu, Hsien-Wang. 2023. "Hemispheric Symmetry of Planetary Albedo: A Corollary of Nonequilibrium Thermodynamics" Atmosphere 14, no. 8: 1243. https://doi.org/10.3390/atmos14081243
APA StyleOu, H.-W. (2023). Hemispheric Symmetry of Planetary Albedo: A Corollary of Nonequilibrium Thermodynamics. Atmosphere, 14(8), 1243. https://doi.org/10.3390/atmos14081243





