Optimal Probability Distribution and Applicable Minimum Time-Scale for Daily Standardized Precipitation Index Time Series in South Korea
Abstract
:1. Introduction
2. Data and Methods
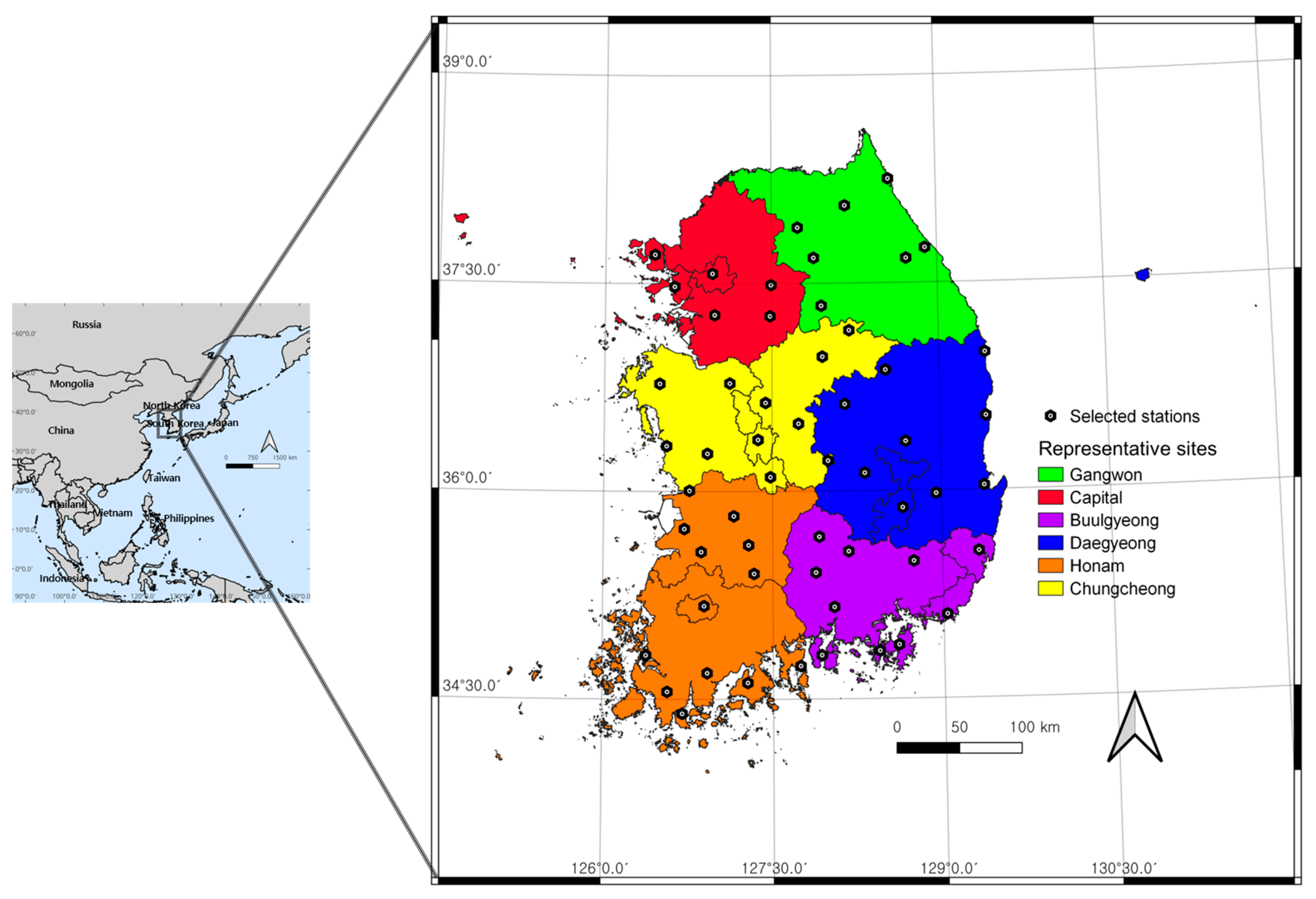
2.1. Data
2.2. Standardized Precipitation Index
2.3. Goodness-of-Fit of Probability Distribution
2.4. Normality Test
3. Results
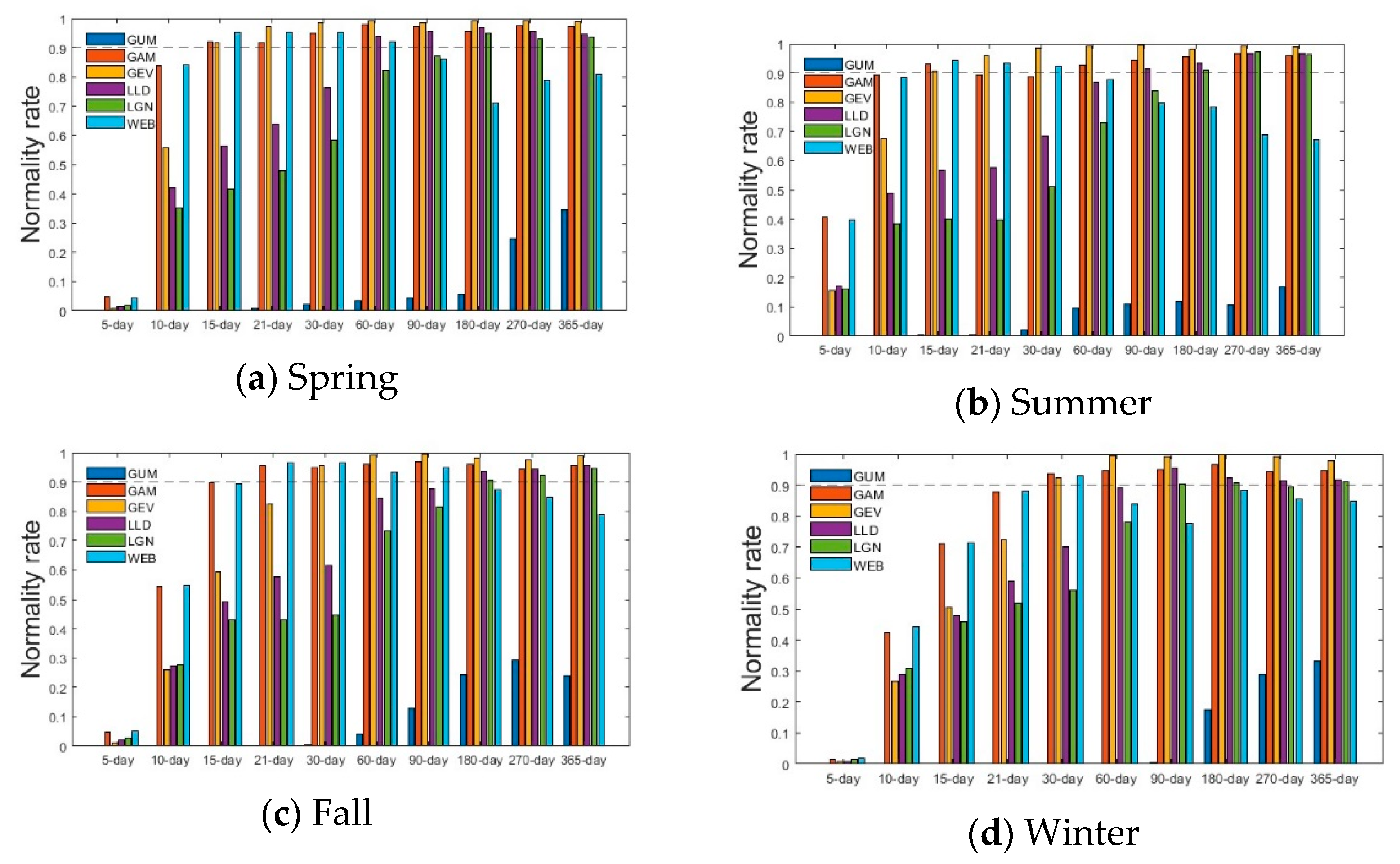
3.1. Goodness-of-Fit Test
3.2. Normality Test
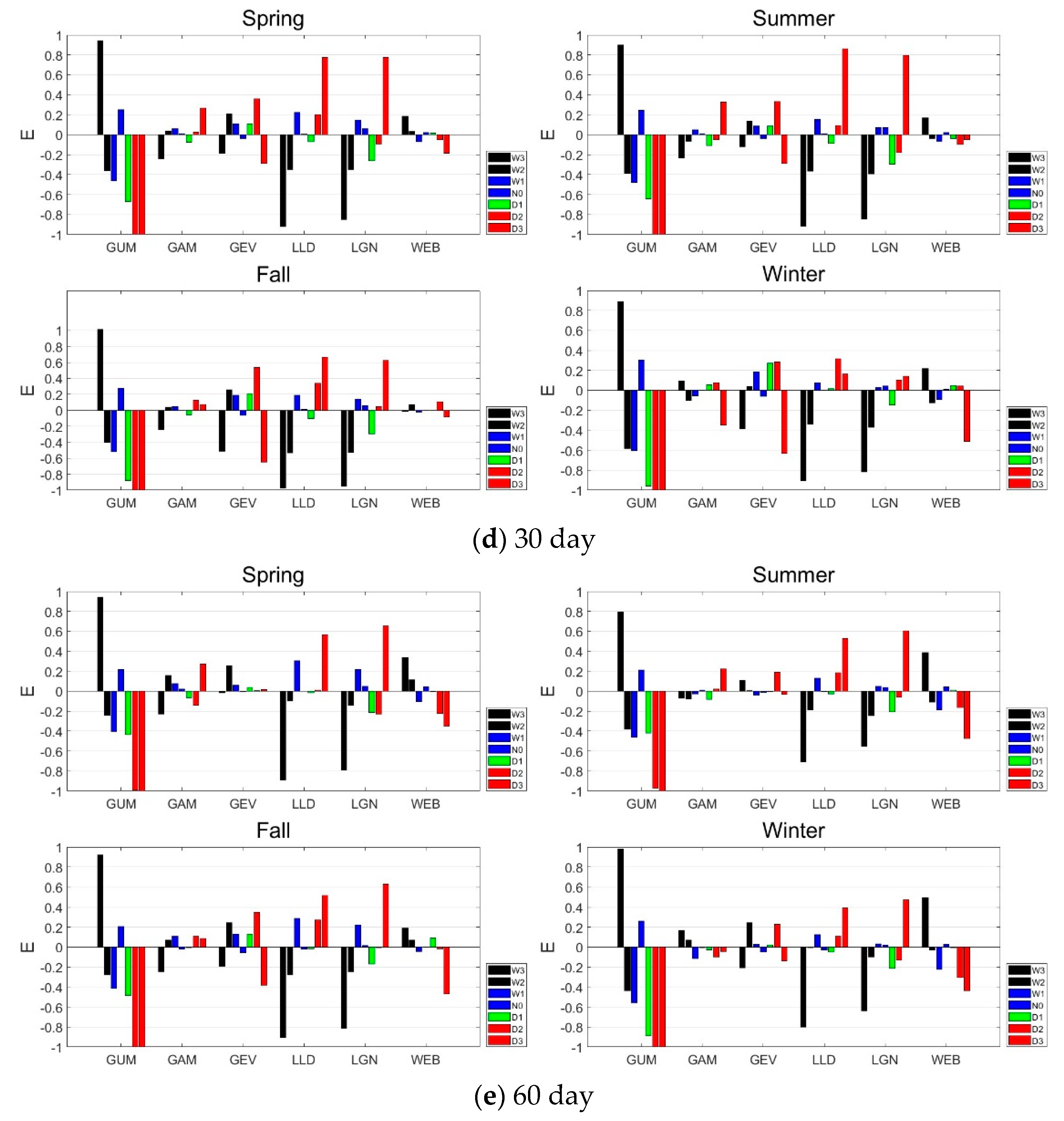
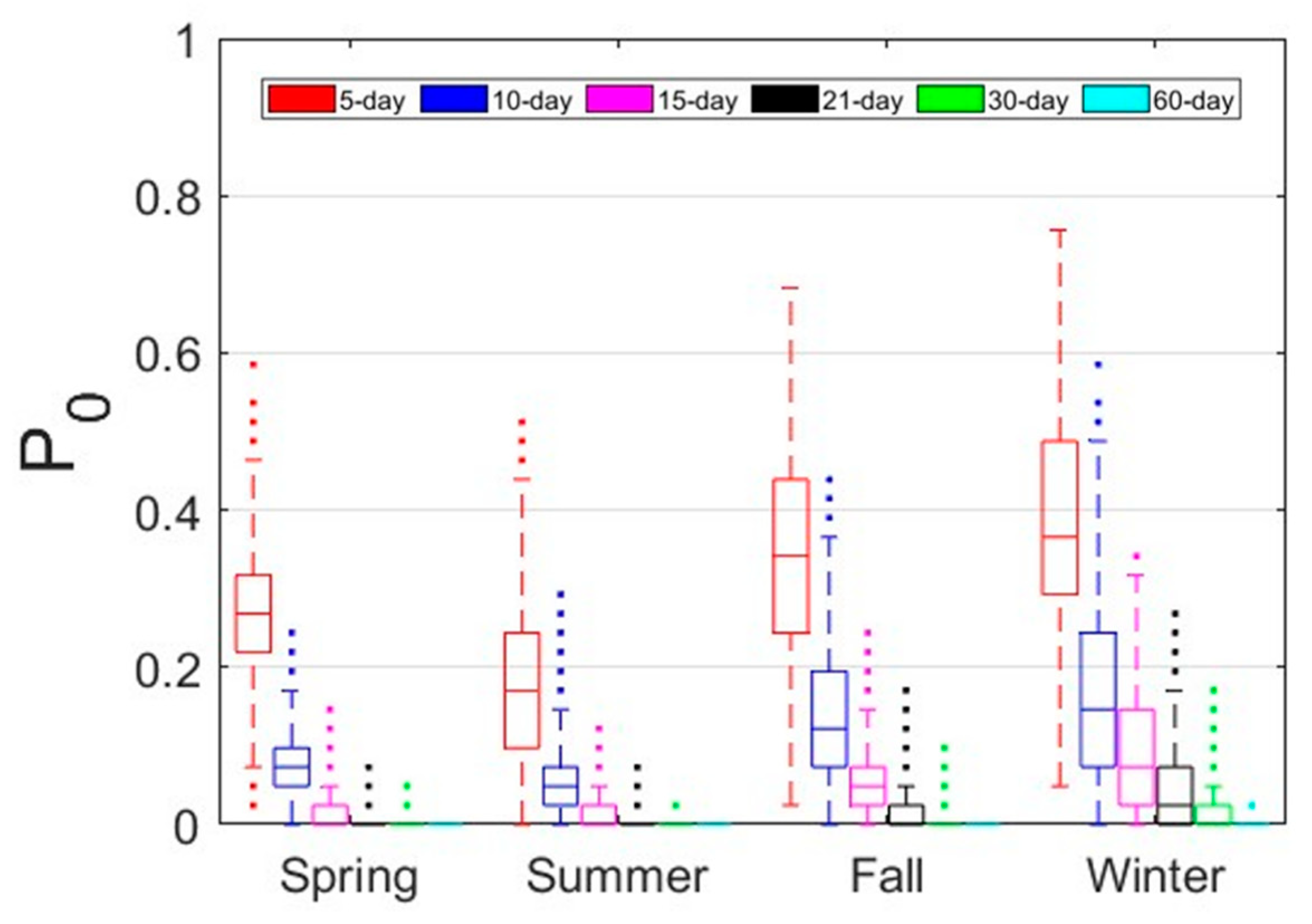
4. Discussion
4.1. Effect of Zero Precipitation Events on Minimum Time-Scales
4.2. Applicability of the GEV Distribution
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, MA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Guttman, N.B. Accepting the standardized precipitation index: A calculation algorithm. J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Kyoung, M.; Kim, S.; Kim, B.; Kim, H. Construction of hydrological drought severity-area-duration curves using cluster analysis. KSCE J. Civ. Environ. Eng. Res. 2007, 27, 267–276. [Google Scholar]
- Kim, H.; Park, J.; Yoon, J.; Kim, S. Application of SAD curves in assessing climate-change impacts on spatio-temporal characteristics of extreme drought events. KSCE J. Civ. Environ. Eng. Res. 2010, 30, 561–569. [Google Scholar]
- Sienz, F.; Bothe, O.; Fraedrich, K. Monitoring and quantifying future climate projections of dryness and wetness extremes: SPI bias. Hydrol. Earth Syst. Sci. 2012, 16, 2143–2157. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Feng, P.; Hu, P. A time-dependent drought index for non-stationary precipitation series. Water Resour. Manag. 2015, 29, 5631–5647. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Okpara, J.; Afiesimama, E.; Anuforom, A.; Owino, A.; Ogunjobi, K. The applicability of standardized precipitation index: Drought characterization for early warning system and weather index insurance in West Africa. Nat. Hazards 2017, 89, 555–583. [Google Scholar] [CrossRef]
- Blain, G.C.; de Avila, A.M.H.; Pereira, V.R. Using the normality assumption to calculate probability-based standardized drought indices: Selection criteria with emphases on typical events. Int. J. Climatol. 2018, 38, e418–e436. [Google Scholar] [CrossRef]
- Guenang, G.; Komkoua, M.; Pokam, M.; Tanessong, R.; Tchakoutio, S.; Vondou, A.; Tamoffo, A.; Djiotang, L.; Yepdo, Z.; Mkankam, K. Sensitivity of SPI to Distribution Functions and Correlation Between its Values at Different Time Scales in Central Africa. Earth Syst. Environ. 2019, 3, 203–214. [Google Scholar] [CrossRef]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012.
- Chang, Y.; Kim, S.; Choi, G. A study of drought spatio-temporal characteristics using SPI-EOF analysis. J. Korea Water Resour. Assoc. 2006, 39, 691–702. [Google Scholar] [CrossRef]
- Paulo, A.; Martins, D.; Pereira, L.S. Influence of precipitation changes on the SPI and related drought severity. An analysis using long-term data series. Water Resour. Manag. 2016, 30, 5737–5757. [Google Scholar] [CrossRef]
- Sim, H.; Ryu, J.; Ahn, J.; Kim, J.; Kim, S. Real-time drought index for determining drought conditions in natural water supply system communities. J. Korean Soc. Hazard Mitig. 2013, 13, 365–374. [Google Scholar] [CrossRef]
- Won, J.; Jang, S.; Kim, K.; Kim, S. Applicability of the evaporative demand drought index. J. Korean Soc. Hazard Mitig. 2018, 18, 431–442. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Romanowicz, R. Uncertainty in SPI calculation and its impact on drought assessment in different climate regions over China. J. Hydrometeorol. 2021, 22, 1369–1383. [Google Scholar] [CrossRef]
- Park, B.; Lee, J.; Kim, C.; Jang, H. Projection of future drought of Korea based on probabilistic approach using multi-model and multi climate change scenarios. KSCE J. Civ. Eng. Res. 2013, 33, 1871–1885. [Google Scholar] [CrossRef]
- Park, M.; Lee, O.; Park, Y.; Kim, S. Future drought projection In Korea under ar5 rcp climate change scenarios. J. Korean Soc. Hazard Mitig. 2015, 15, 423–433. [Google Scholar] [CrossRef]
- Kim, B.; Chang, I.; Sung, J.; Han, H. Projection in Future Drought Hazard of South Korea Based on RCP Climate Change Scenario 8.5 Using SPEI. Adv. Meteorol. 2016, 2016, 4148710. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, H.; Zhan, C.; Hu, S.; Ma, M.; Dong, Y. Comparative analysis of probability distributions for the Standardized Precipitation Index and drought evolution in China during. Theor. Appl. Climatol. 2020, 139, 1363–1377. [Google Scholar] [CrossRef]
- Angelidis, P.; Maris, F.; Kotsovinos, N.; Hrissanthou, V. Computation of drought index SPI with alternative distribution functions. Water Resour. Manag. 2012, 26, 2453–2473. [Google Scholar] [CrossRef]
- Pieper, P.; Dusterhus, A.; Baehr, J. A universal Standardized Precipitation Index candidate distribution function for observations and simulations. Hydrol. Earth Syst. Sci. 2020, 24, 4541–4565. [Google Scholar] [CrossRef]
- Kim, B.; Kim, S.; Lee, J.; Kim, H. Spatio-temporal characteristics of droughts in Korea: Construction of drought severity-area-duration curves. KSCE J. Civ. Environ. Eng. Res. 2006, 26, 69–78. [Google Scholar]
- Ryu, J.; Ahn, J.; Kim, S. An application of drought severity-area-duration curves using copulas-based joint drought index. J. Korea Water Resour. Assoc. 2012, 45, 1043–1050. [Google Scholar] [CrossRef]
- Wu, H.; Svoboda, M.D.; Hayes, M.J.; Wilhite, D.A.; Wen, F. Appropriate application of the Standardized Precipitation Index in arid locations and dry seasons. Int. J. Climatol. 2007, 27, 65–79. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Climatol. 2014, 34, 2792–2804. [Google Scholar] [CrossRef]
- Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Anderson, T.; Darling, D. A Test of Goodness of Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multi-Model Inference: A Practical Information-Theoretical Approacrh, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Lee, O.; Sim, I.; Kim, S. Application of the non-stationary peak-over-threshold methods for deriving rainfall extremes from temperature projections. J. Hydrol. 2020, 585, 124318. [Google Scholar] [CrossRef]
- Yoo, J.; Song, H.; Kim, T.; Ahn, J. Evaluation of Short-Term Drought Using Daily Standardized Precipitation Index and ROC Analysis. J. Korean Soc. Civ. Eng. 2013, 33, 1851–1860. [Google Scholar] [CrossRef]
- Kim, S.; Kim, B.; Ahn, T.; Kim, H. Spatio-temporal characterization of Korean drought using severity-area–duration curve analysis. Water Environ. J. 2011, 25, 22–30. [Google Scholar] [CrossRef]
- Kang, D.; Nam, D.; Kim, B. Comparison of Meteorological Drought Indices Using Past Drought Cases of Taebaek and Sokcho. J. Korean Soc. Civ. Eng. 2019, 39, 735–742. [Google Scholar]
- Won, J.; Choi, J.; Lee, L.; Kim, S. Copula-based Joint Drought Index using SPI and EDDI and its application to climate change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- DeGaetano, A.T.; Belcher, B.N.; Noon, W. Temporal and spatial interpolation of the standardized precipitation index for computational efficiency in the dynamic drought index tool. J. Appl. Meteorol. Climatol. 2015, 54, 795–810. [Google Scholar] [CrossRef]
- Carbone, G.J.; Lu, J.; Brunetti, M. Estimating uncertainty associated with the standardized precipitation index. Int. J. Climatol. 2018, 38, e607–e616. [Google Scholar] [CrossRef]


| SPI Interval | Period Classification | Probability |
|---|---|---|
| SPI ≥ 2 | W3: extremely wet | 0.0228 |
| 2 > SPI ≥ 1.5 | W2: severely wet | 0.0441 |
| 1.5 > SPI ≥ 1 | W1: moderately wet | 0.0918 |
| 1 > SPI > −1 | N0: normal | 0.6827 |
| −1 ≥ SPI > −1.5 | D1: moderately dry | 0.0918 |
| −1.5 ≥ SPI > −2 | D2: severely dry | 0.0441 |
| SPI ≤ −2 | D3: extremely dry | 0.0228 |
| Time-Scale | 5 Day | 10 Day | 15 Day | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Season | h (%) | (%) | (%) | (%) | (%) | (%) | ||||
| Spring | GUM | 0.0698 | 22.8649 | 8.6762 | 0.0515 | 22.8649 | 6.5023 | 0.0465 | 21.3703 | 5.4542 |
| GAM | 0.4387 | 89.0334 | 42.4884 | 0.3310 | 89.0334 | 24.9030 | 0.3138 | 89.5186 | 15.6250 | |
| GEV | 0.2331 | 76.5916 | 4.8331 | 0.2843 | 76.5916 | 23.0784 | 0.3036 | 83.1328 | 28.7849 | |
| LLD | 0.2670 | 71.2345 | 5.2213 | 0.2319 | 71.2345 | 8.8898 | 0.2551 | 78.8626 | 12.3253 | |
| LGN | 0.2326 | 57.4340 | 5.3571 | 0.1631 | 57.4340 | 4.8525 | 0.1748 | 63.3152 | 6.9682 | |
| WEB | 0.4480 | 89.7127 | 33.4239 | 0.3462 | 89.7127 | 31.7741 | 0.3322 | 90.5085 | 30.8424 | |
| Summer | GUM | 0.0393 | 15.1009 | 5.3183 | 0.0319 | 15.1009 | 4.2314 | 0.0360 | 16.9061 | 3.9790 |
| GAM | 0.4082 | 88.7811 | 44.4876 | 0.3403 | 88.7811 | 27.5039 | 0.3040 | 87.5970 | 17.1584 | |
| GEV | 0.2224 | 75.9511 | 7.7640 | 0.2811 | 75.9511 | 21.8750 | 0.3092 | 82.7640 | 32.4728 | |
| LLD | 0.2558 | 75.0388 | 6.7158 | 0.2557 | 75.0388 | 11.9759 | 0.2562 | 79.1925 | 13.5481 | |
| LGN | 0.2174 | 60.6366 | 5.8618 | 0.1856 | 60.6366 | 6.2694 | 0.1704 | 62.7135 | 6.7547 | |
| WEB | 0.4234 | 90.0815 | 29.8525 | 0.3549 | 90.0815 | 28.1444 | 0.3177 | 89.0722 | 26.0870 | |
| Fall | GUM | 0.0584 | 15.8948 | 6.2991 | 0.0292 | 15.8948 | 3.6107 | 0.0296 | 15.2669 | 3.6303 |
| GAM | 0.4065 | 91.8760 | 42.8571 | 0.3954 | 91.8760 | 43.2104 | 0.3583 | 90.5416 | 31.8681 | |
| GEV | 0.2038 | 62.2449 | 1.9231 | 0.2093 | 62.2449 | 7.1429 | 0.2580 | 72.9003 | 17.7983 | |
| LLD | 0.3201 | 74.5290 | 8.3595 | 0.2676 | 74.5290 | 7.1232 | 0.2656 | 77.0212 | 11.3815 | |
| LGN | 0.3195 | 69.5251 | 12.0487 | 0.2412 | 69.5251 | 8.5754 | 0.2132 | 67.5432 | 6.8681 | |
| WEB | 0.4399 | 93.0338 | 28.5126 | 0.4161 | 93.0338 | 30.3375 | 0.3768 | 91.2088 | 28.4537 | |
| Winter | GUM | 0.0699 | 17.3413 | 7.8175 | 0.0365 | 17.3413 | 4.9405 | 0.0291 | 13.6905 | 3.8492 |
| GAM | 0.3742 | 89.3849 | 33.3532 | 0.3675 | 89.3849 | 31.6468 | 0.3497 | 89.0278 | 25.6746 | |
| GEV | 0.2240 | 67.2421 | 2.2817 | 0.2410 | 67.2421 | 7.4008 | 0.2749 | 74.0278 | 15.7540 | |
| LLD | 0.3397 | 78.3929 | 10.2778 | 0.3090 | 78.3929 | 10.0794 | 0.2966 | 78.4921 | 12.4405 | |
| LGN | 0.3518 | 76.5675 | 17.4603 | 0.3014 | 76.5675 | 15.1984 | 0.2653 | 72.7579 | 12.1429 | |
| WEB | 0.4171 | 91.8452 | 28.8095 | 0.4014 | 91.8452 | 30.7341 | 0.3740 | 91.1508 | 30.1389 | |
| Time-Scale | 30 Day | 60 Day | 90 Day | |||||||
| Season | (%) | (%) | (%) | (%) | (%) | (%) | ||||
| Spring | GUM | 0.0512 | 25.4464 | 2.5815 | 0.0730 | 38.7422 | 2.4068 | 0.0768 | 38.5675 | 2.7562 |
| GAM | 0.3159 | 89.0722 | 15.3144 | 0.3480 | 92.1584 | 14.1693 | 0.3546 | 90.7997 | 15.9744 | |
| GEV | 0.2836 | 84.6273 | 21.3703 | 0.2769 | 85.5784 | 13.3152 | 0.2658 | 82.5505 | 11.8789 | |
| LLD | 0.2934 | 86.5101 | 19.7399 | 0.3450 | 91.9837 | 26.5528 | 0.3483 | 91.8284 | 27.1351 | |
| LGN | 0.2196 | 76.9410 | 9.9961 | 0.2817 | 86.8012 | 12.9658 | 0.3071 | 88.1988 | 16.4402 | |
| WEB | 0.3374 | 90.0621 | 30.9977 | 0.3426 | 90.3339 | 30.5901 | 0.3223 | 86.9565 | 25.8152 | |
| Summer | GUM | 0.0582 | 28.4744 | 3.6102 | 0.0830 | 38.3346 | 3.2609 | 0.0944 | 42.9154 | 3.7655 |
| GAM | 0.3149 | 87.7329 | 14.3439 | 0.3341 | 89.9068 | 14.7904 | 0.3637 | 92.1584 | 14.7710 | |
| GEV | 0.2933 | 85.0155 | 21.9526 | 0.2585 | 82.8804 | 9.3362 | 0.2751 | 84.8408 | 9.6079 | |
| LLD | 0.2885 | 84.3362 | 17.0613 | 0.3260 | 89.7321 | 25.5629 | 0.3608 | 92.3525 | 27.7174 | |
| LGN | 0.2157 | 72.6126 | 9.1615 | 0.2566 | 82.0264 | 10.4814 | 0.3041 | 88.1017 | 12.7329 | |
| WEB | 0.3404 | 89.6351 | 33.8703 | 0.3413 | 88.7811 | 36.5683 | 0.3336 | 86.8401 | 31.4053 | |
| Fall | GUM | 0.0404 | 19.4662 | 3.5714 | 0.0803 | 37.8728 | 3.7873 | 0.1260 | 58.0651 | 5.9066 |
| GAM | 0.3141 | 88.5008 | 15.6986 | 0.3436 | 91.7975 | 12.9906 | 0.3636 | 93.4851 | 14.5801 | |
| GEV | 0.3086 | 85.1452 | 29.5918 | 0.3028 | 87.2841 | 18.9560 | 0.2678 | 85.5377 | 8.1240 | |
| LLD | 0.2681 | 81.6523 | 13.9521 | 0.3277 | 89.5408 | 20.1727 | 0.3386 | 91.8564 | 19.8980 | |
| LGN | 0.1927 | 69.0149 | 7.0447 | 0.2686 | 84.5173 | 12.0683 | 0.2926 | 88.0298 | 12.7551 | |
| WEB | 0.3294 | 89.2661 | 30.1413 | 0.3574 | 91.3462 | 32.0251 | 0.3909 | 93.3673 | 38.7363 | |
| Winter | GUM | 0.0197 | 9.1667 | 1.4484 | 0.0166 | 9.3452 | 0.1786 | 0.0372 | 20.1587 | 1.2103 |
| GAM | 0.3144 | 88.1746 | 16.0119 | 0.3358 | 90.9921 | 12.8571 | 0.3437 | 91.2500 | 15.0595 | |
| GEV | 0.3521 | 87.7183 | 34.4643 | 0.3473 | 89.0079 | 30.7738 | 0.3119 | 86.9841 | 23.3730 | |
| LLD | 0.3038 | 84.7421 | 15.5357 | 0.3545 | 91.9841 | 25.7937 | 0.3452 | 91.2698 | 23.4722 | |
| LGN | 0.2423 | 74.8810 | 10.4365 | 0.2922 | 84.2857 | 13.8095 | 0.3043 | 87.9762 | 16.0913 | |
| WEB | 0.3141 | 88.7500 | 22.1032 | 0.3020 | 87.3413 | 16.5873 | 0.3043 | 86.0714 | 20.7937 | |
| Time-Scale | 180 Day | 270 Day | 365 Day | |||||||
| Season | (%) | (%) | (%) | (%) | (%) | (%) | ||||
| Spring | GUM | 0.0851 | 41.2073 | 2.9697 | 0.1501 | 59.2391 | 5.9006 | 0.1854 | 67.2943 | 7.4534 |
| GAM | 0.3796 | 92.9542 | 14.9068 | 0.3797 | 93.4006 | 17.7019 | 0.4030 | 92.9542 | 19.8758 | |
| GEV | 0.2925 | 86.0248 | 15.2562 | 0.2782 | 84.4720 | 9.1033 | 0.2925 | 85.7337 | 8.1716 | |
| LLD | 0.3770 | 94.0023 | 27.3098 | 0.3637 | 92.8183 | 24.7671 | 0.3837 | 92.8960 | 21.5062 | |
| LGN | 0.3543 | 91.9449 | 19.1576 | 0.3337 | 90.6444 | 15.1009 | 0.3652 | 91.5955 | 14.5380 | |
| WEB | 0.2984 | 84.3944 | 20.3998 | 0.3428 | 89.1498 | 27.4262 | 0.3534 | 89.1304 | 28.4550 | |
| Summer | GUM | 0.1015 | 45.2446 | 4.4837 | 0.0991 | 45.2640 | 4.4061 | 0.1548 | 58.7716 | 6.5149 |
| GAM | 0.3676 | 91.4014 | 17.4884 | 0.3864 | 93.4589 | 17.4301 | 0.4034 | 93.9168 | 21.5071 | |
| GEV | 0.2499 | 81.6770 | 7.2399 | 0.2757 | 84.8797 | 9.9573 | 0.2926 | 85.2630 | 8.2025 | |
| LLD | 0.3597 | 91.7314 | 29.4449 | 0.3854 | 93.9635 | 31.6770 | 0.3873 | 93.4458 | 27.0408 | |
| LGN | 0.3258 | 89.1304 | 13.2764 | 0.3611 | 92.4884 | 17.6048 | 0.3544 | 92.0722 | 10.5769 | |
| WEB | 0.3144 | 85.8307 | 28.0668 | 0.2830 | 83.3851 | 18.9247 | 0.3334 | 88.4027 | 26.1578 | |
| Fall | GUM | 0.1645 | 65.6201 | 7.2214 | 0.1712 | 65.0903 | 7.6334 | 0.1879 | 68.0952 | 6.8452 |
| GAM | 0.4016 | 91.8956 | 19.1523 | 0.3940 | 92.4254 | 17.5235 | 0.3864 | 91.7460 | 19.7024 | |
| GEV | 0.2819 | 84.4976 | 2.8257 | 0.2744 | 84.0659 | 3.5322 | 0.2841 | 82.7778 | 7.4008 | |
| LLD | 0.3770 | 91.9741 | 22.8414 | 0.3656 | 92.4451 | 26.0008 | 0.3526 | 91.1706 | 22.5992 | |
| LGN | 0.3447 | 90.0510 | 13.9914 | 0.3425 | 90.3061 | 11.3619 | 0.3354 | 88.6706 | 10.9325 | |
| WEB | 0.3766 | 89.6193 | 33.9678 | 0.3646 | 88.2064 | 33.9482 | 0.3561 | 89.5040 | 32.5198 | |
| Winter | GUM | 0.1299 | 55.3175 | 5.0992 | 0.1531 | 60.9325 | 6.1111 | 0.1531 | 60.9325 | 6.1111 |
| GAM | 0.3671 | 92.5794 | 14.3651 | 0.3493 | 89.2262 | 16.2103 | 0.3493 | 89.2262 | 16.2103 | |
| GEV | 0.2785 | 85.7341 | 11.1706 | 0.2556 | 78.9881 | 5.0992 | 0.2556 | 78.9881 | 5.0992 | |
| LLD | 0.3428 | 91.7262 | 16.8651 | 0.3345 | 88.9286 | 21.0913 | 0.3345 | 88.9286 | 21.0913 | |
| LGN | 0.3298 | 90.7341 | 17.0437 | 0.3128 | 85.8532 | 12.3214 | 0.3128 | 85.8532 | 12.3214 | |
| WEB | 0.3679 | 92.1032 | 35.4563 | 0.3415 | 88.8294 | 39.1667 | 0.3415 | 88.8294 | 39.1667 | |
| Time-Scale | 5 Day | 10 Day | 15 Day | 21 Day | 30 Day | |
|---|---|---|---|---|---|---|
| GAM | 0.8549 | 0.9303 | 0.9318 | 0.8945 | 0.8532 | |
| WEB | 0.9036 | 0.9526 | 0.9563 | 0.9346 | 0.8879 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Seo, J.; Won, J.; Kim, S. Optimal Probability Distribution and Applicable Minimum Time-Scale for Daily Standardized Precipitation Index Time Series in South Korea. Atmosphere 2023, 14, 1292. https://doi.org/10.3390/atmos14081292
Lee C, Seo J, Won J, Kim S. Optimal Probability Distribution and Applicable Minimum Time-Scale for Daily Standardized Precipitation Index Time Series in South Korea. Atmosphere. 2023; 14(8):1292. https://doi.org/10.3390/atmos14081292
Chicago/Turabian StyleLee, Chaelim, Jiyu Seo, Jeongeun Won, and Sangdan Kim. 2023. "Optimal Probability Distribution and Applicable Minimum Time-Scale for Daily Standardized Precipitation Index Time Series in South Korea" Atmosphere 14, no. 8: 1292. https://doi.org/10.3390/atmos14081292
APA StyleLee, C., Seo, J., Won, J., & Kim, S. (2023). Optimal Probability Distribution and Applicable Minimum Time-Scale for Daily Standardized Precipitation Index Time Series in South Korea. Atmosphere, 14(8), 1292. https://doi.org/10.3390/atmos14081292







