Computational Fluid Dynamics Analysis of Wet Dust Removal in High-Gravity Countercurrent Rotating Packed Bed
Abstract
:1. Introduction
2. CFD Model
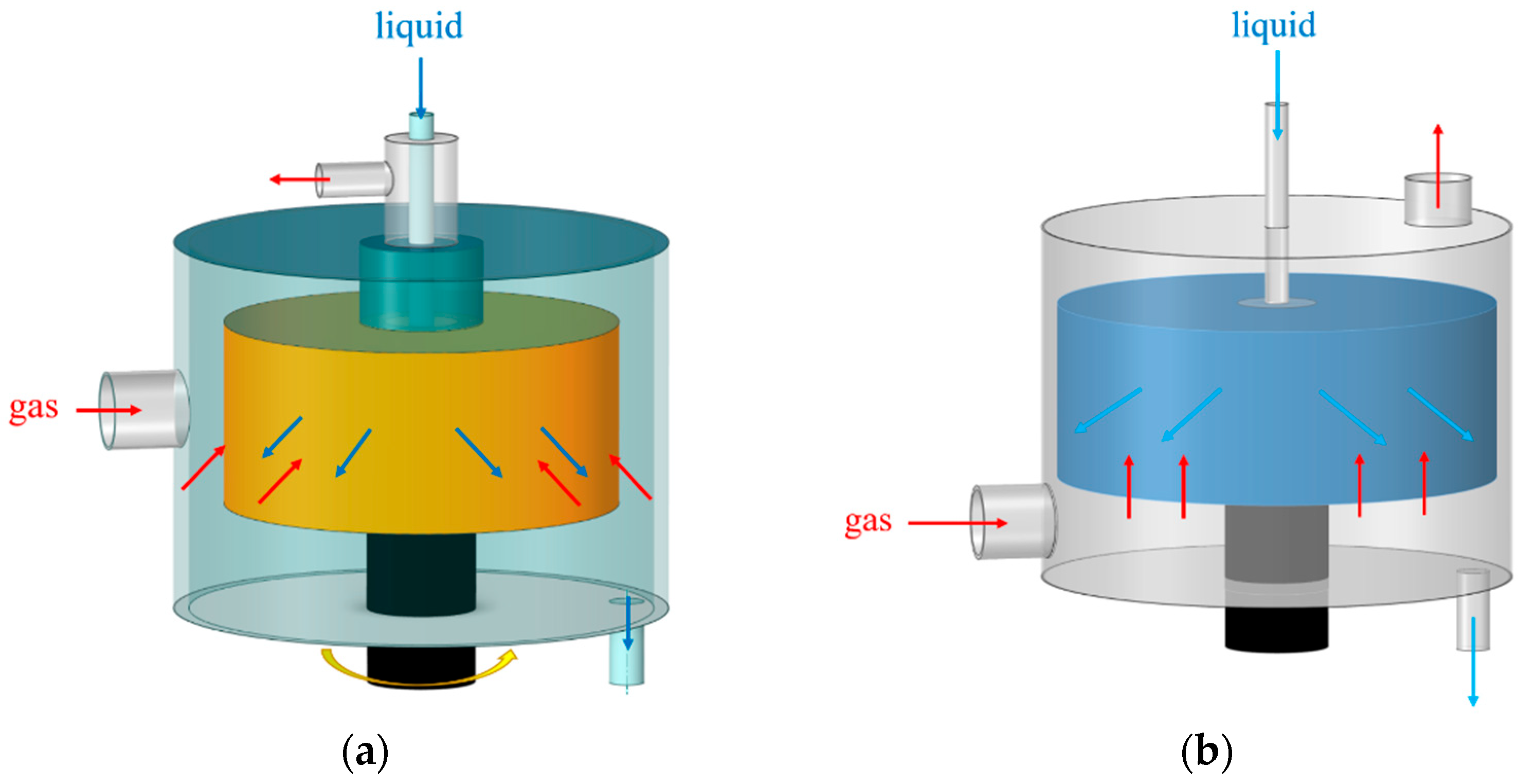
2.1. Geometrical Model
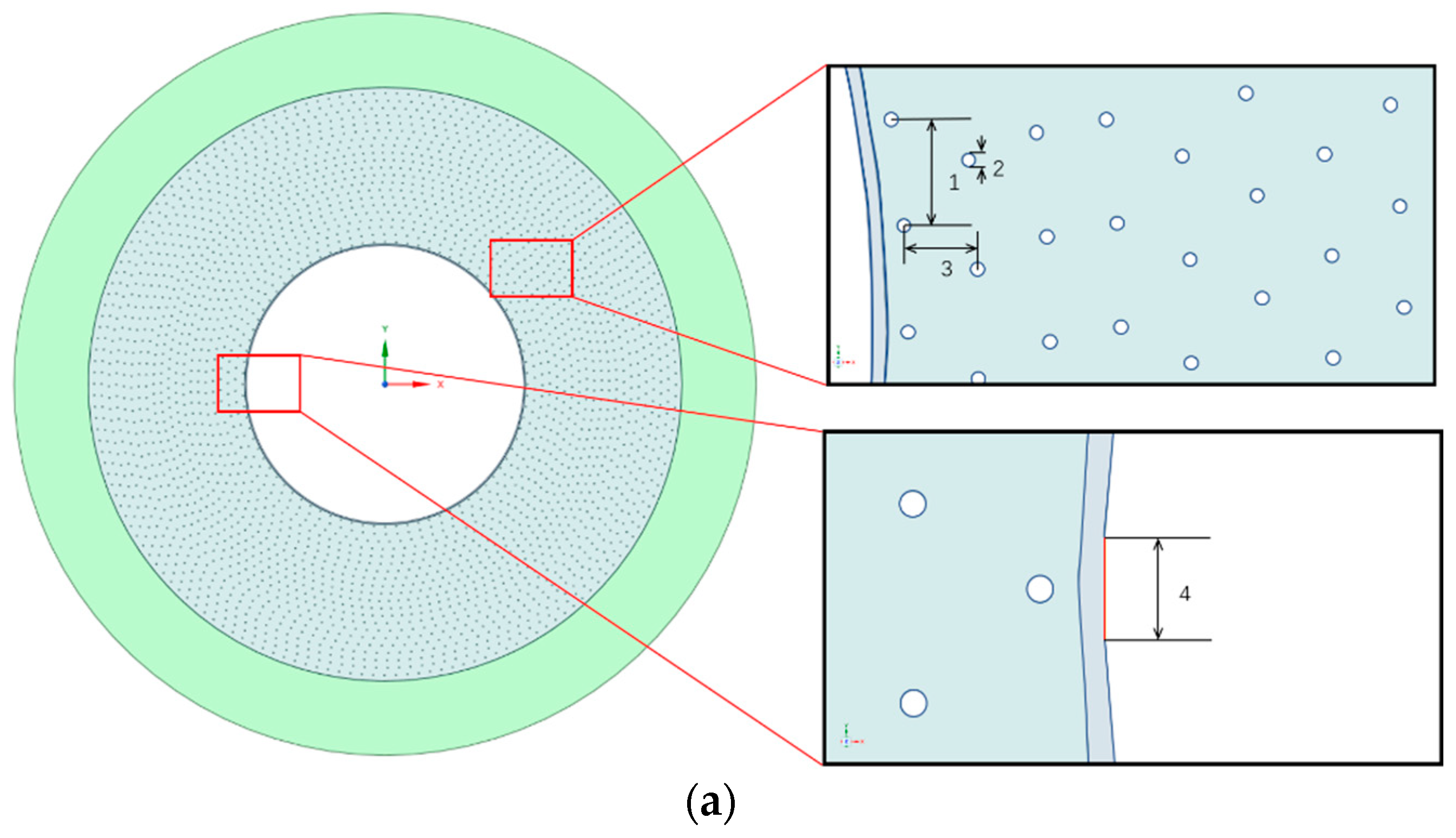
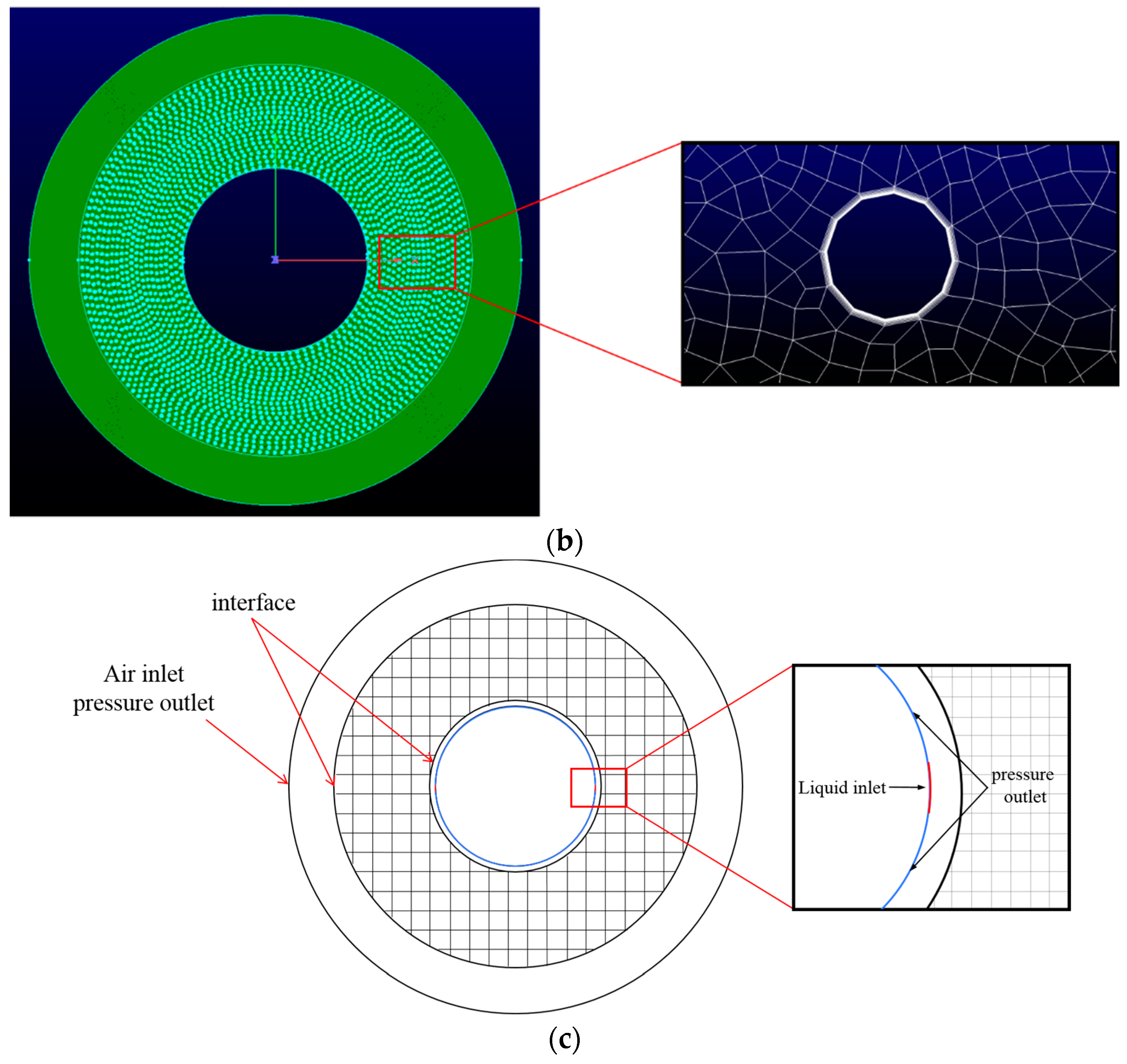
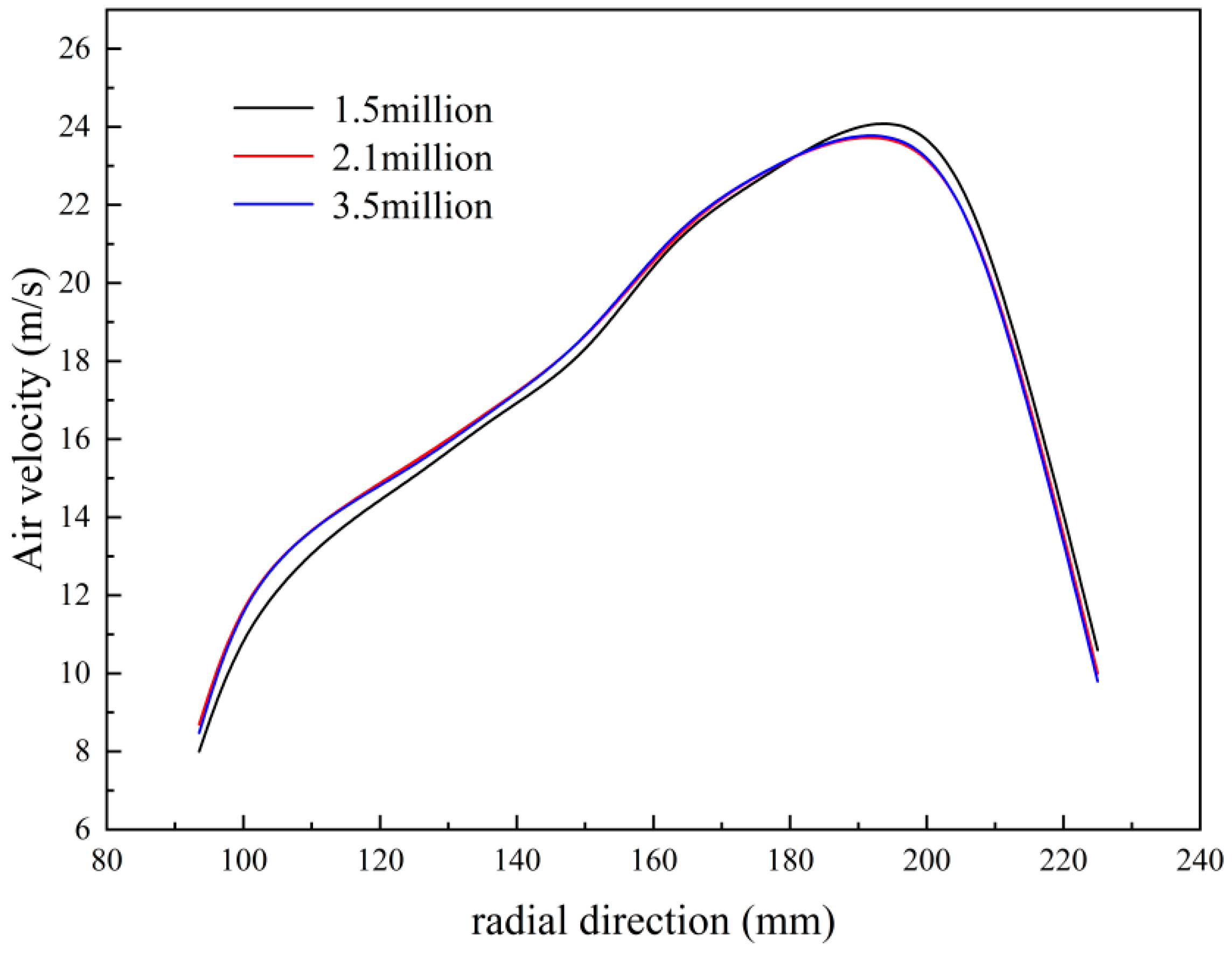
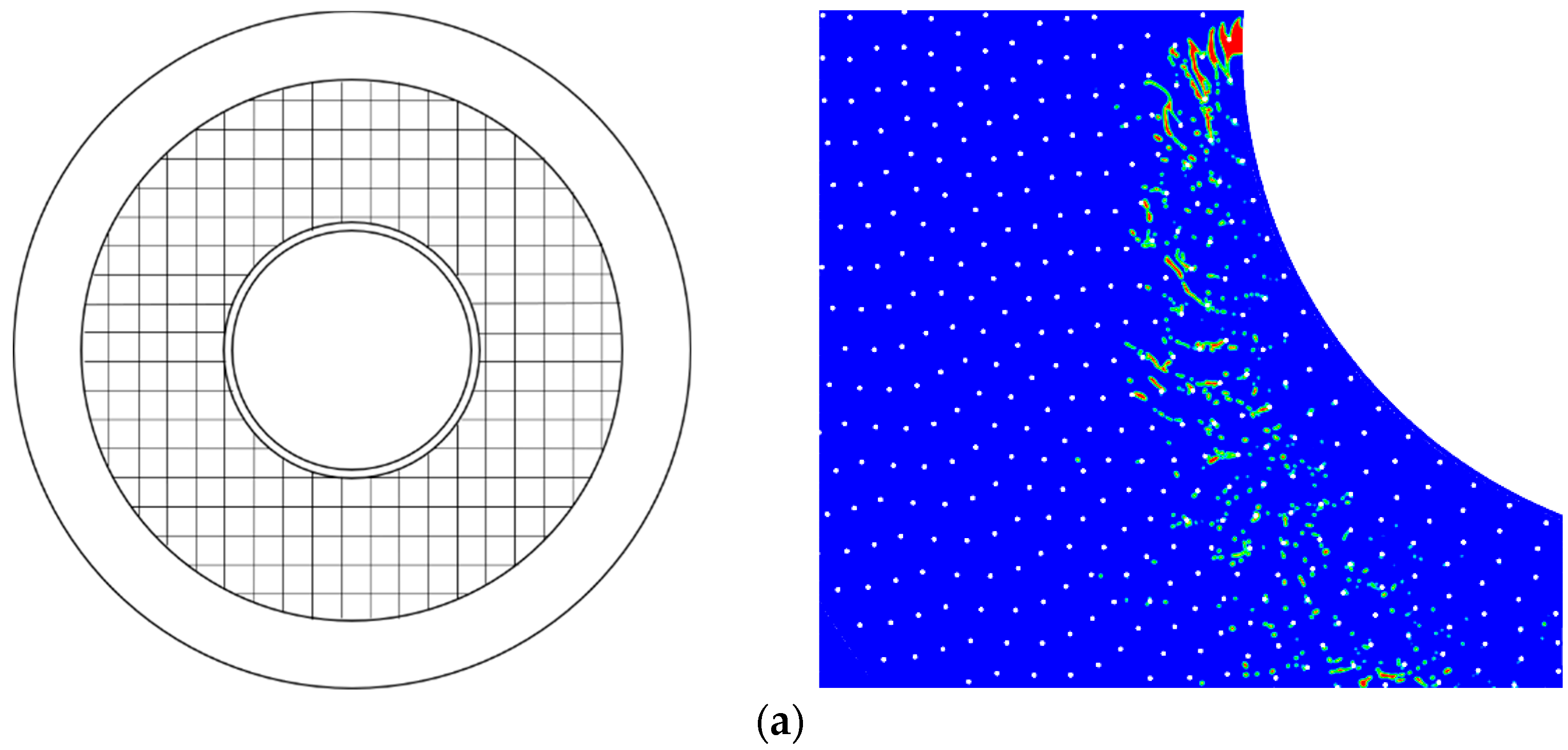
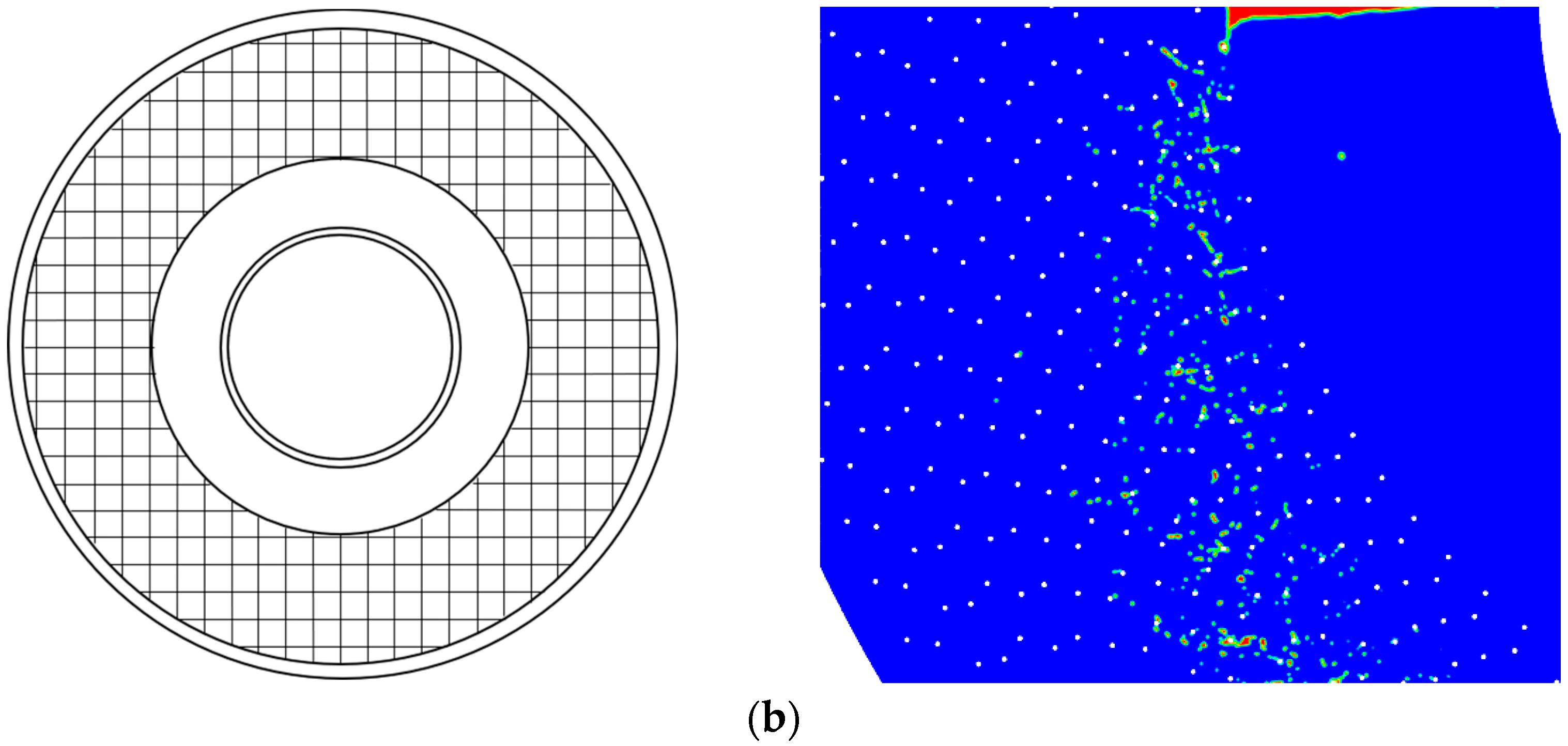
2.2. Computational Grid
2.3. Boundary Conditions
2.4. Mathematical Model
2.4.1. Multiphase Model
2.4.2. Turbulence Model
2.4.3. SM Model
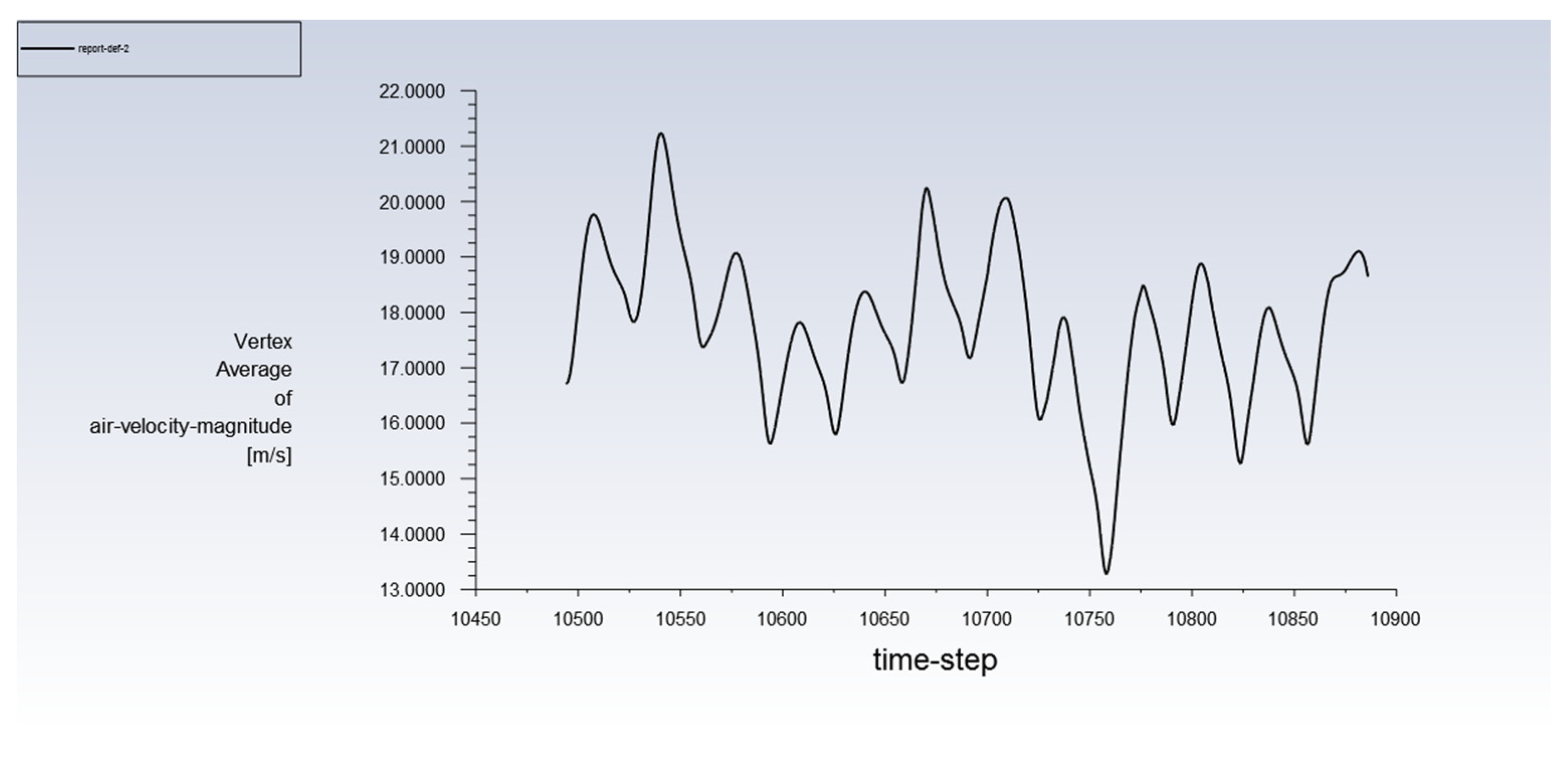
2.5. Calculation Method
3. Results and Discussion
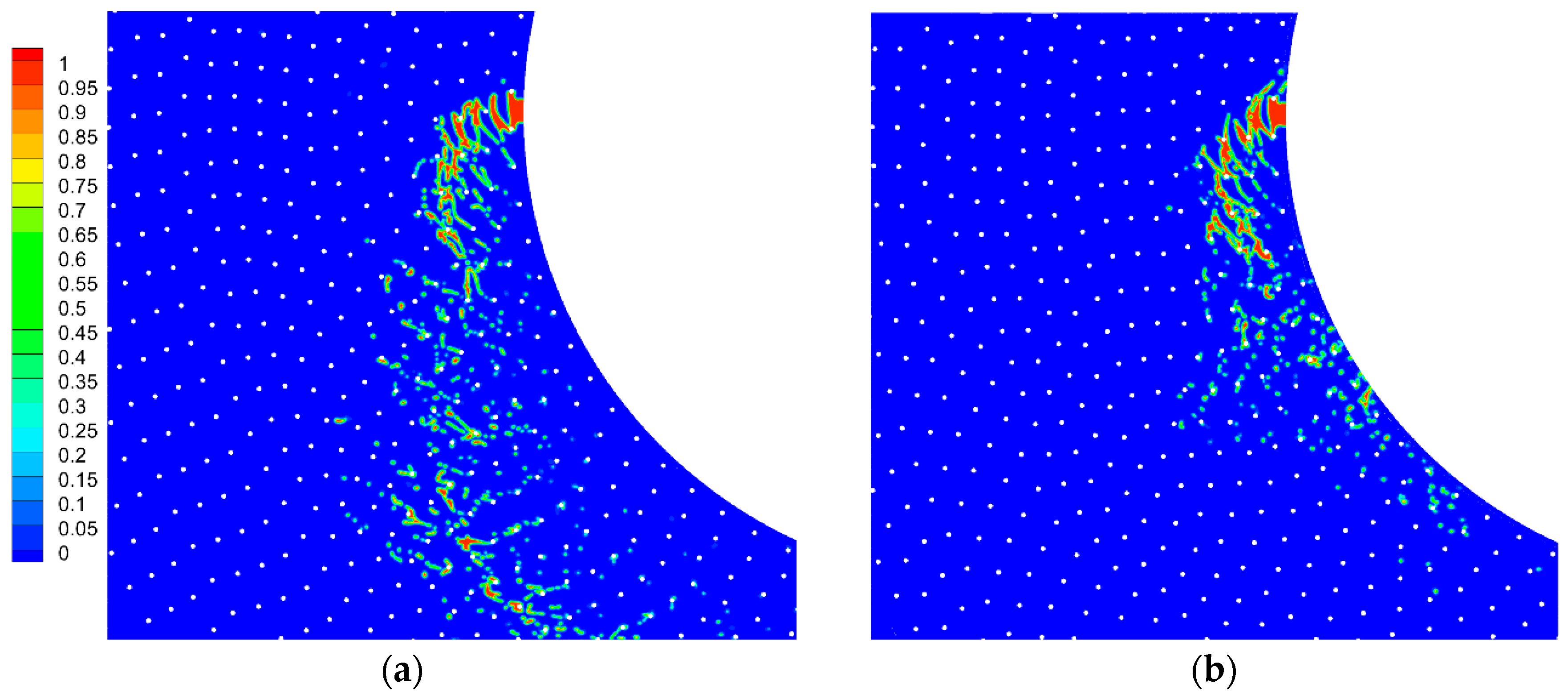
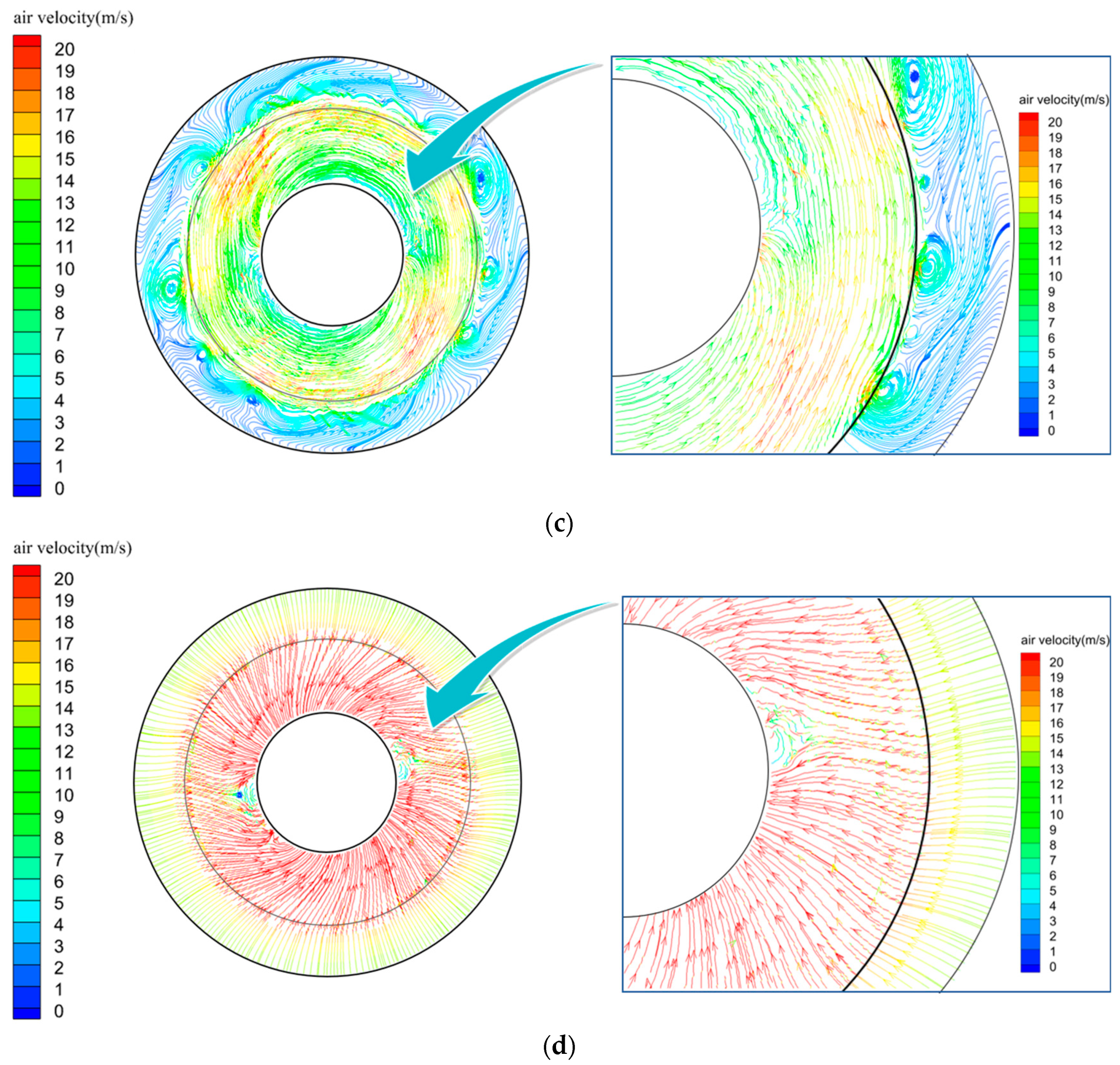
3.1. Gas–Liquid Flow Field
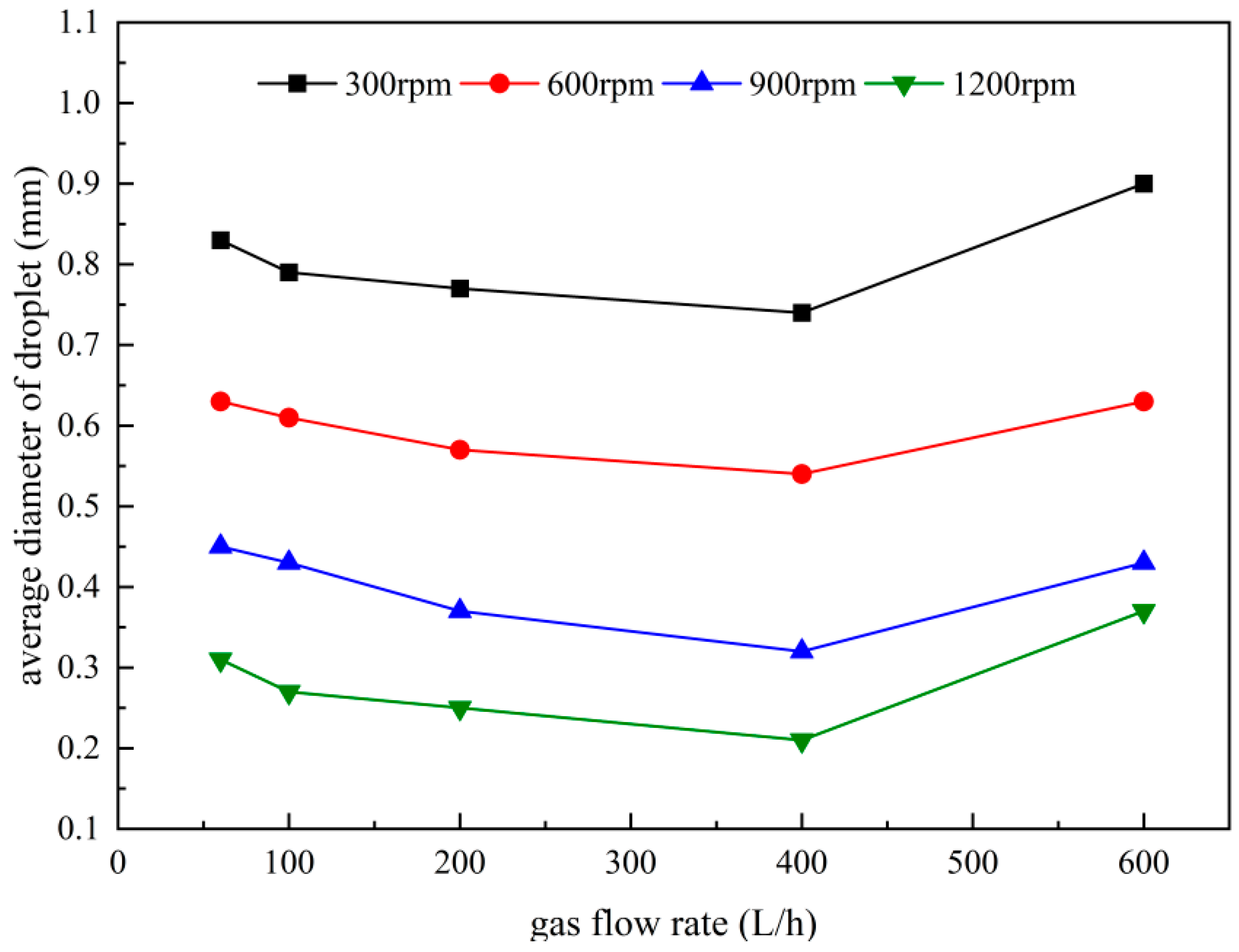
3.2. Liquid Droplet Size
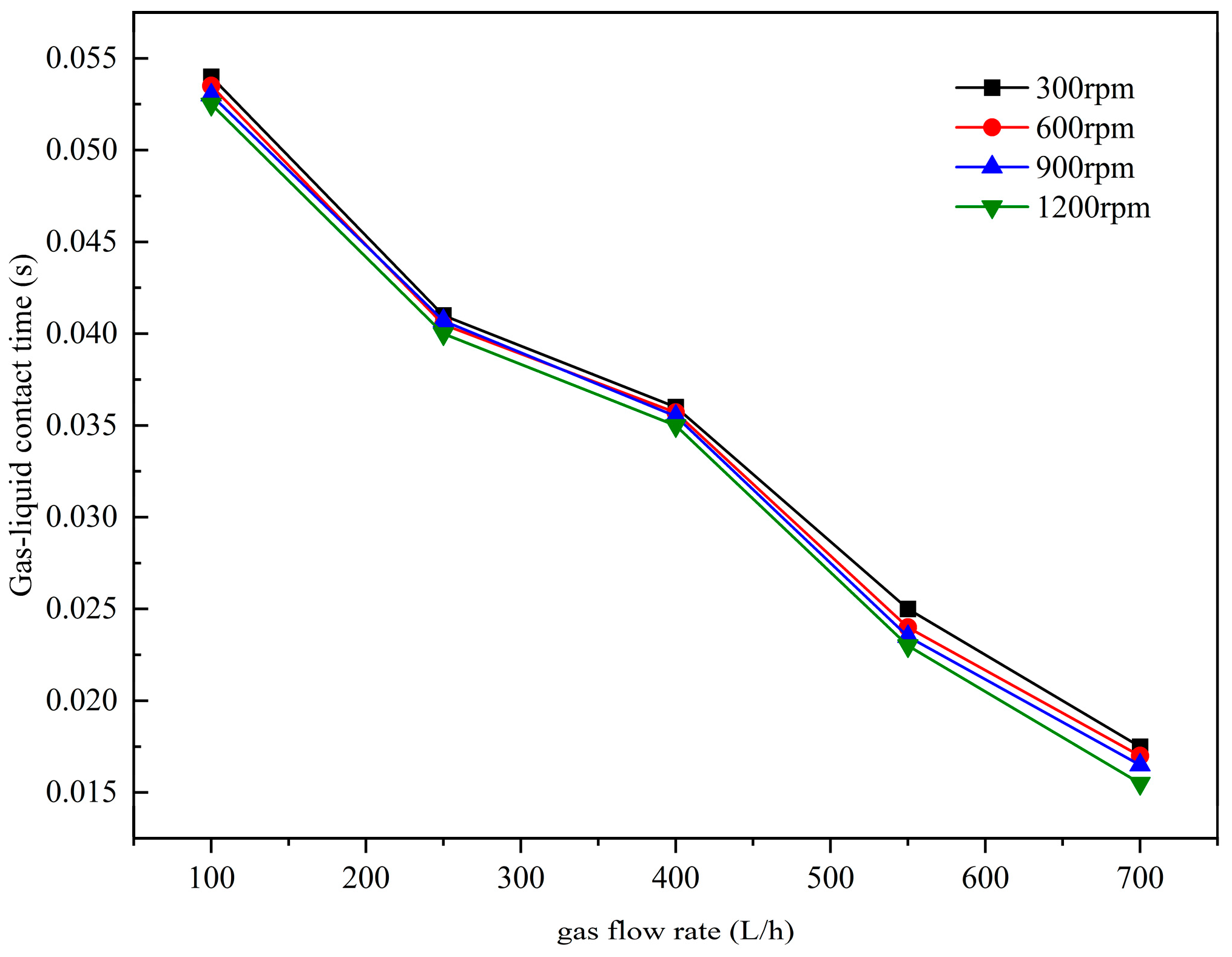
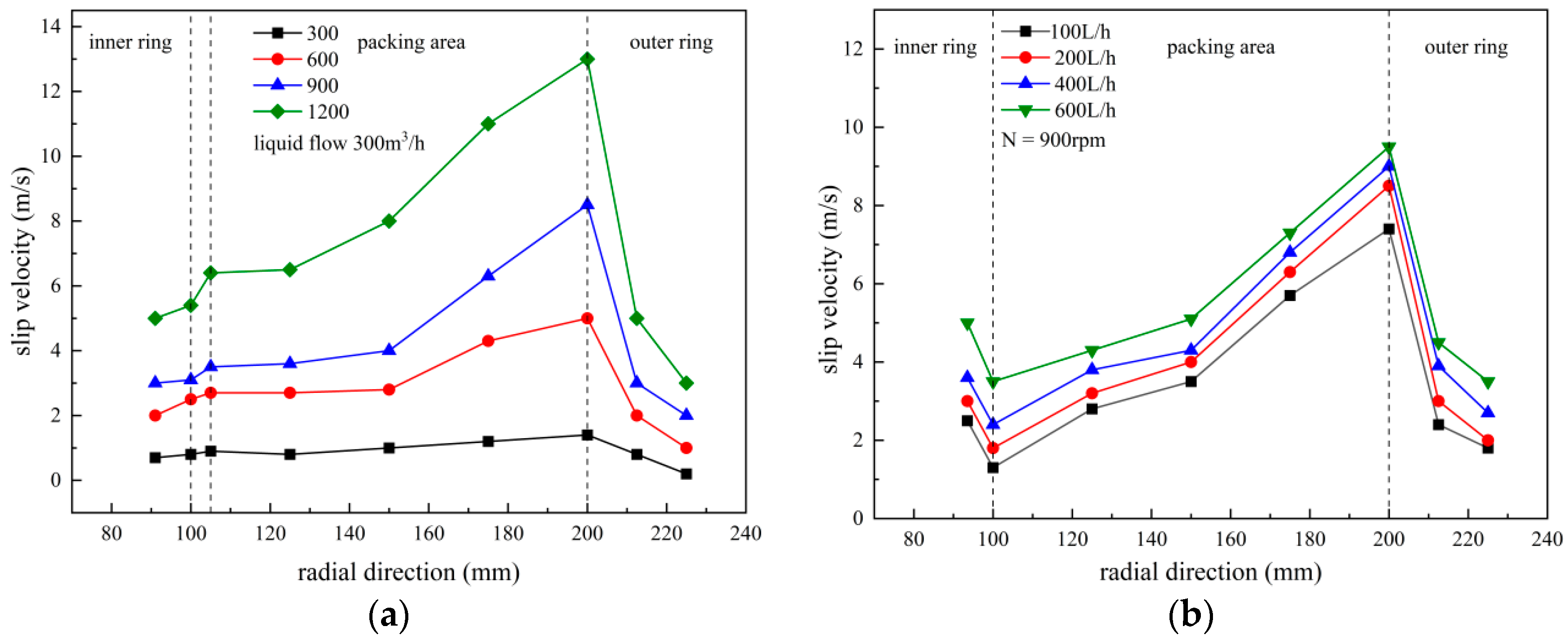
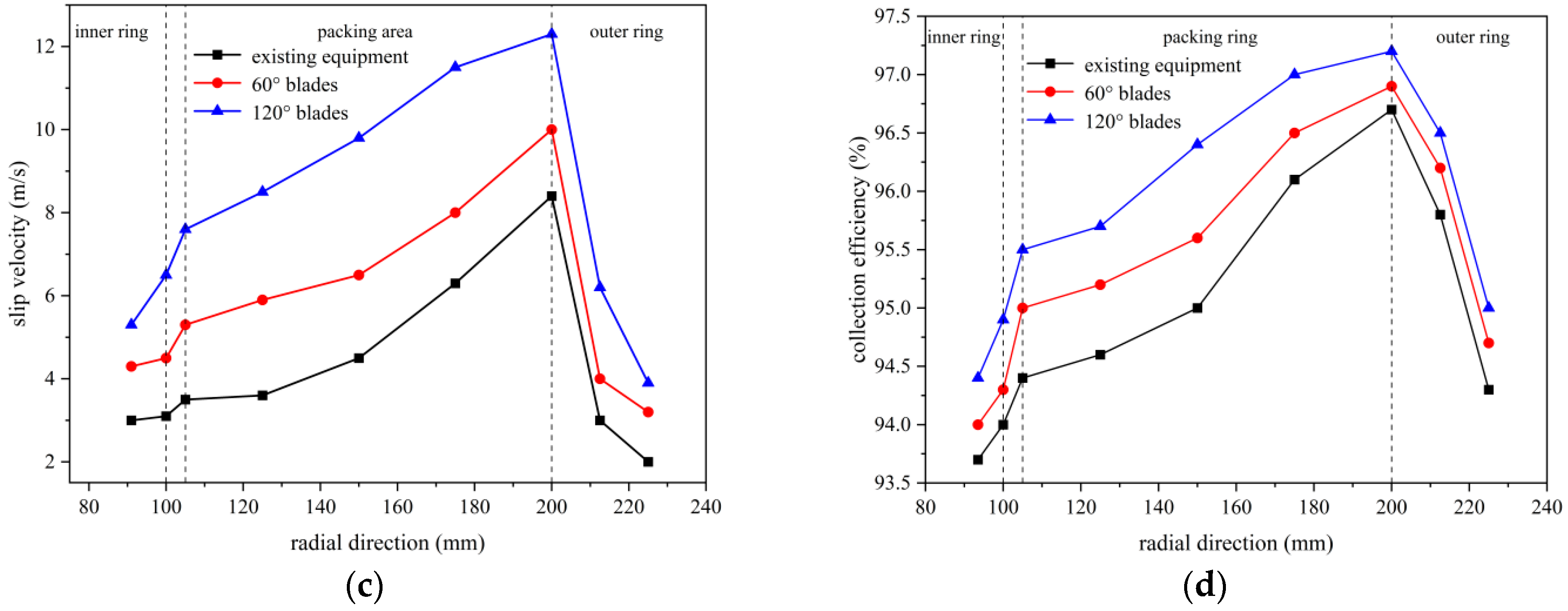
3.3. Gas–Liquid Slip Velocity
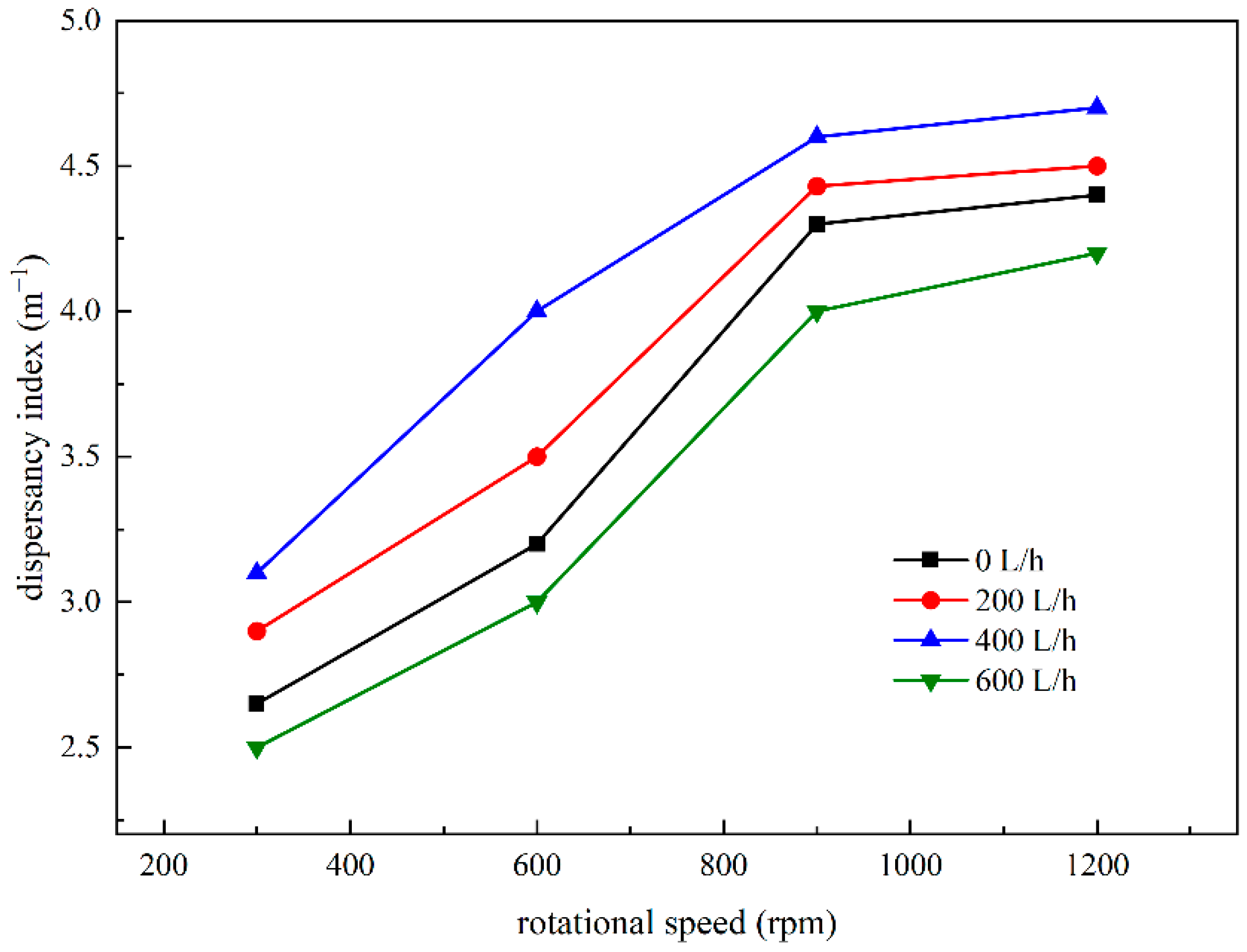
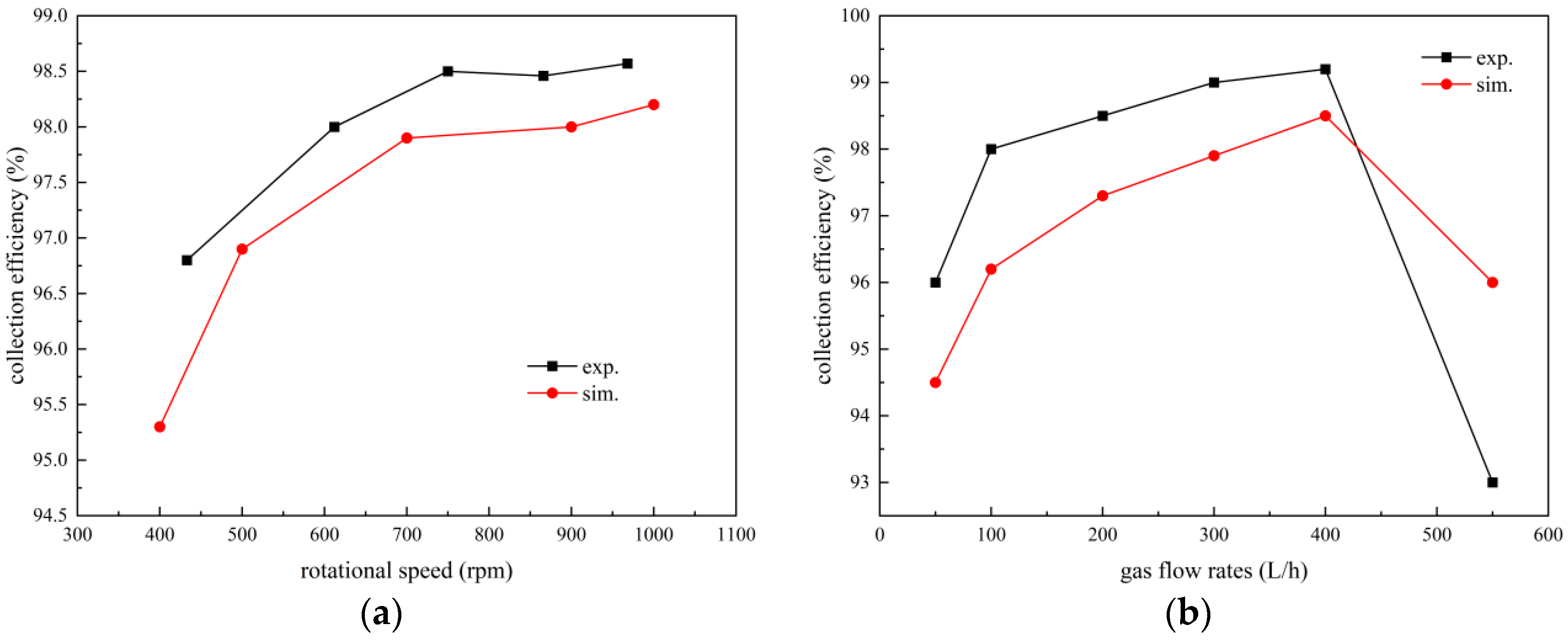
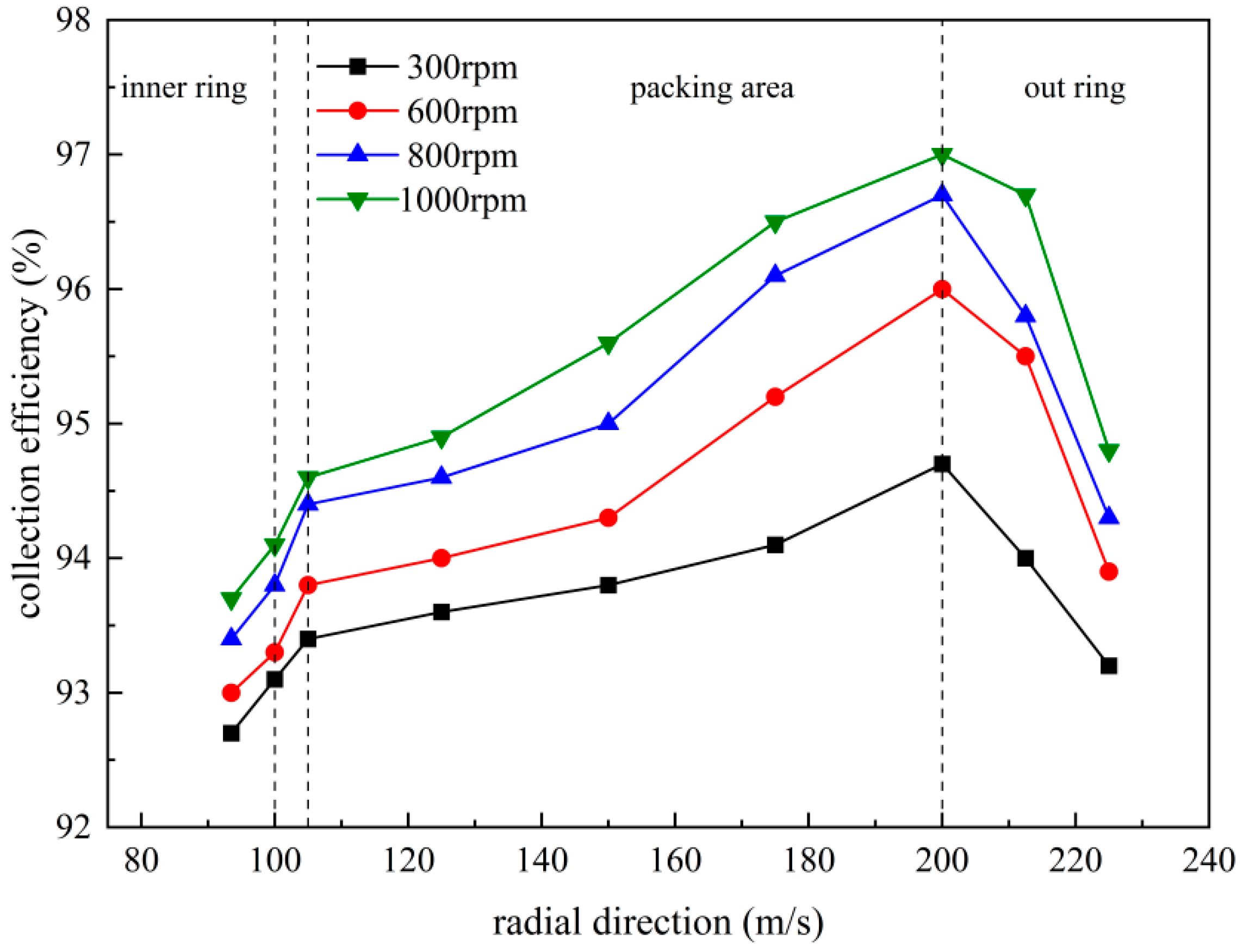
3.4. Dust Collection Efficiency
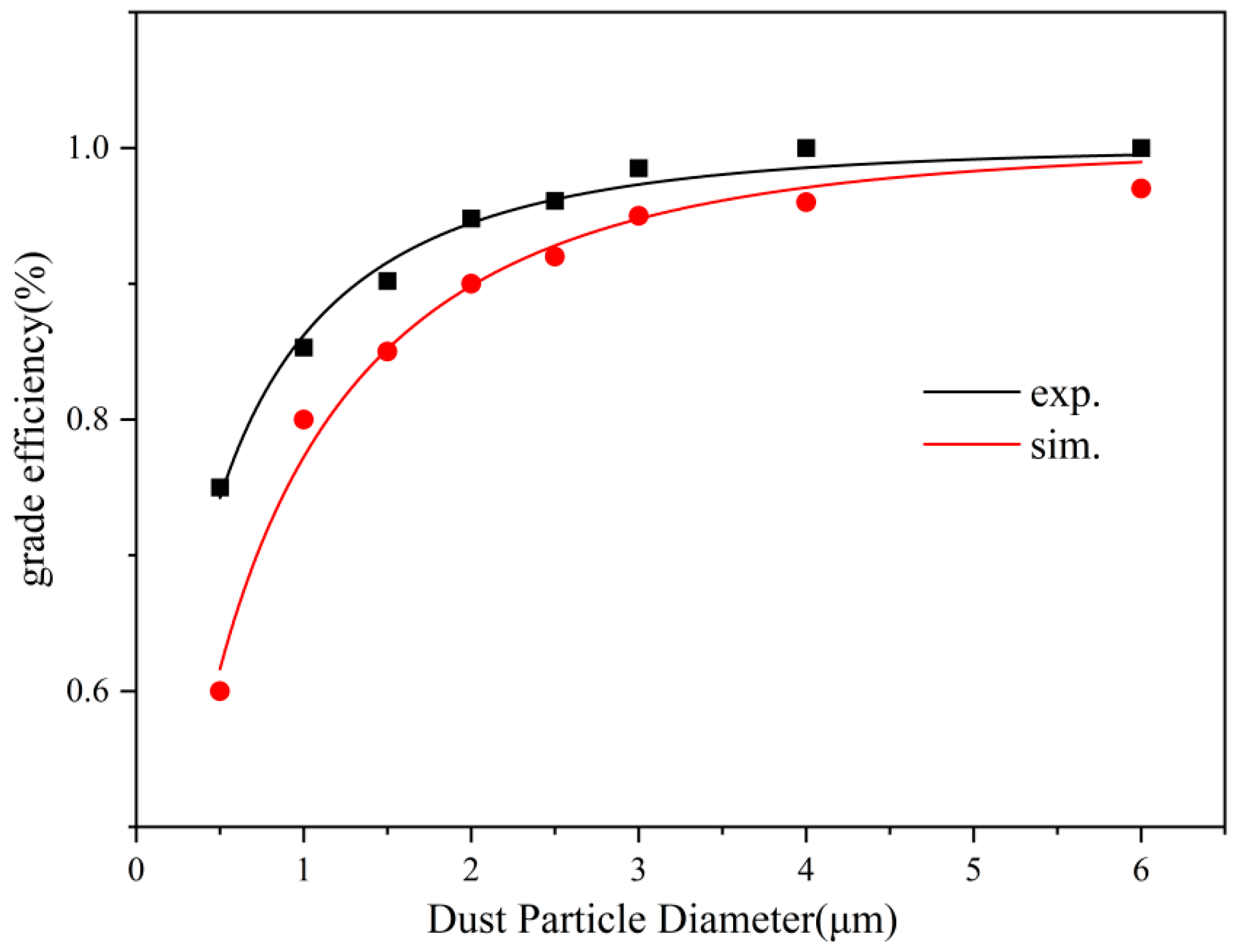
3.4.1. Classification Efficiency
3.4.2. Total Dust Removal Efficiency
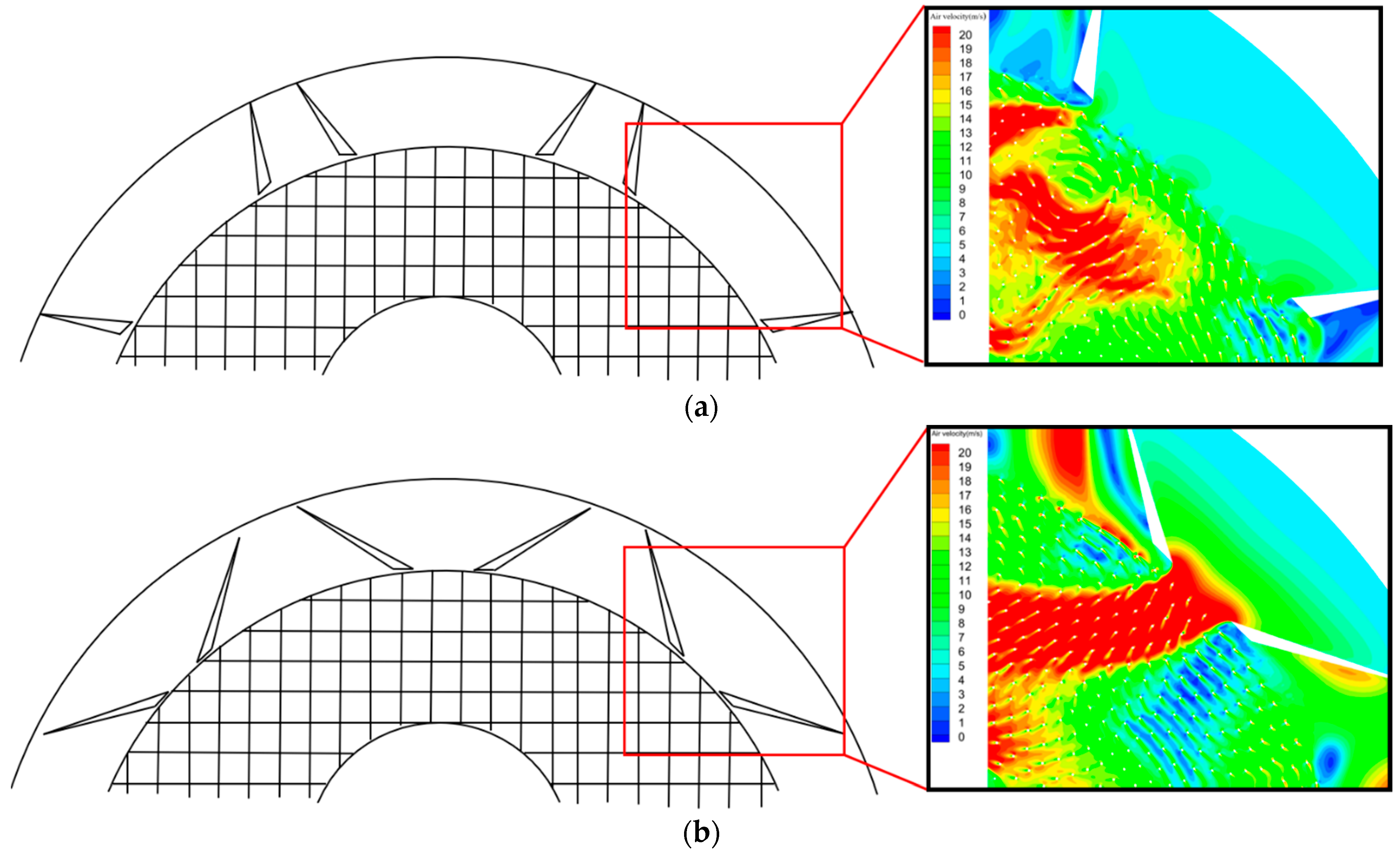
3.5. New Equipment Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pui, D.Y.H.; Chen, S.-C.; Zuo, Z. PM2.5 in China: Measurements, sources, visibility and health effects, and mitigation. Particuology 2014, 13, 1–26. [Google Scholar] [CrossRef]
- Cao, R.; Tan, H.; Xiong, Y.; Mikulčić, H.; Vujanović, M.; Wang, X.; Duić, N. Improving the removal of particles and trace elements from coal-fired power plants by combining a wet phase transition agglomerator with wet electrostatic precipitator. J. Clean. Prod. 2017, 161, 1459–1465. [Google Scholar] [CrossRef]
- Tian, S.-R.; Yang, G.-H.; Li, Z.; Shi, K.-Y.; Ding, G.-Z.; Hu, F.-X. Cascade filtration properties of a dual-layer granular bed filter. Powder Technol. 2016, 301, 545–556. [Google Scholar] [CrossRef]
- Li, W.; Wu, X.; Jiao, W.; Qi, G.; Liu, Y. Modelling of dust removal in rotating packed bed using artificial neural networks (ANN). Appl. Therm. Eng. 2017, 112, 208–213. [Google Scholar] [CrossRef]
- Fu, J.; Qi, G.; Liu, Y.; Tian, J.; Guo, Q.; Dong, M. Research on removal of fine particles by cross-flow rotating packed bed. Chem. Ind. Eng. Prog. 2015, 34, 680–694. [Google Scholar]
- Wang, A.; Song, Q.; Ji, B.; Yao, Q. Effect of droplet deformation on inertial and thermophoretic capture of particles. Atmos. Environ. 2016, 127, 187–195. [Google Scholar] [CrossRef]
- Mohan, B.R.; Meikap, B. Performance characteristics of the particulate removal in a novel spray-cum-bubble column scrubber. Chem. Eng. Res. Des. 2009, 87, 109–118. [Google Scholar] [CrossRef]
- Guo, F.; Zheng, C.; Guo, K.; Feng, Y.; Gardner, N.C. hydrodynamics and mass transfer in crossflow rotating packed bed. Chem. Eng. Sci. 1997, 52, 3853–3859. [Google Scholar] [CrossRef]
- Jamaat, S.S.; Abolhasani, M. Effect of blade packing structure and high-frequency ultrasound on micromixing efficiency enhancement in an RPB reactor. Chem. Eng. Res. Des. 2022, 188, 197–208. [Google Scholar] [CrossRef]
- Wu, W.; Luo, Y.; Chu, G.-W.; Su, M.-J.; Cai, Y.; Zou, H.-K.; Chen, J.-F. Liquid flow behavior in a multiliquid-inlet rotating packed bed reactor with three-dimensional printed packing. Chem. Eng. J. 2020, 386, 121537. [Google Scholar] [CrossRef]
- Carotenuto, C.; Di Natale, F.; Lancia, A. Wet electrostatic scrubbers for the abatement of submicronic particulate. Chem. Eng. J. 2010, 165, 35–45. [Google Scholar] [CrossRef]
- Li, Z.Y.; Dong, K.; Liang, Y.; Zhang, L.; Sun, B.; Chu, G.W.; Zou, H.K.; Chen, J.F. Study on the removal of fine particles by using water in a rotating packed bed. Canadian J. Chem. Eng. 2017, 95, 1063–1068. [Google Scholar] [CrossRef]
- Pak, S.I.; Chang, K.S. Performance estimation of a Venturi scrubber using a computational model for capturing dust particles with liquid spray. J. Hazard. Mater. 2006, 138, 560–573. [Google Scholar] [CrossRef]
- Ali, H.; Plaza, F.; Mann, A. Numerical Prediction of Dust Capture Efficiency of a Centrifugal Wet Scrubber. Aiche J. 2018, 64, 1001–1012. [Google Scholar] [CrossRef]
- Li, H.; Yuan, Z.; Liu, Y.; Liu, H. Characteristics of liquid flow in a countercurrent rotating bed. Chem. Eng. Process.-Process Intensif. 2019, 136, 72–81. [Google Scholar] [CrossRef]
- Shi, X.; Xiang, Y.; Wen, L.-X.; Chen, J.-F. CFD analysis of liquid phase flow in a rotating packed bed reactor. Chem. Eng. J. 2013, 228, 1040–1049. [Google Scholar] [CrossRef]
- Guo, T.-Y.; Cheng, K.-P.; Wen, L.-X.; Andersson, R.; Chen, J.-F. Three-Dimensional Simulation on Liquid Flow in a Rotating Packed Bed Reactor. Ind. Eng. Chem. Res. 2017, 56, 8169–8179. [Google Scholar] [CrossRef]
- Troshko, A.A.; Zdravistch, F. CFD modeling of slurry bubble column reactors for Fisher–Tropsch synthesis. Chem. Eng. Sci. 2009, 64, 892–903. [Google Scholar] [CrossRef]
- Harlow, F.H. Volume of fluid method for the dynamics of free boundary. Jcomputphys 1965, 201–225. [Google Scholar]
- INCA. ANSYS Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. Aiaa J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Yang, W.; Wang, Y.; Chen, J.; Fei, W. Computational fluid dynamic simulation of fluid flow in a rotating packed bed. Chem. Eng. J. 2010, 156, 582–587. [Google Scholar] [CrossRef]
- Lan, H.; Wegener, J.L.; Armaly, B.F.; Drallmeier, J.A. Developing Laminar Gravity-Driven Thin Liquid Film Flow Down an Inclined Plane. J. Fluids Eng. 2010, 132, 081301. [Google Scholar] [CrossRef]
- Chate, D.; Kamra, A. Collection efficiencies of large water drops collecting aerosol particles of various densities. Atmos. Environ. 1997, 31, 1631–1635. [Google Scholar] [CrossRef]
- Boll, R.H. Particle Collection and Pressure Drop in Venturi Scrubbers. Ind. Eng. Chem. Fundam. 1973, 12, 40–50. [Google Scholar] [CrossRef]
- Calvert, S. Venturi and other atomizing scrubbers efficiency and pressure drop. Aiche J. 1970, 16, 392–396. [Google Scholar] [CrossRef]
- Mohebbi, A.; Taheri, M.; Fathikaljahi, J.; Talaie, M. Simulation of an orifice scrubber performance based on Eulerian/Lagrangian method. J. Hazard. Mater. 2003, 99, 13–25. [Google Scholar] [CrossRef]
- Licht, W. Air Pollution Control Engineering: Basic Calculations for Particulate Collection; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Llerena-Chavez, H.; Larachi, F. Analysis of flow in rotating packed beds via CFD simulations—Dry pressure drop and gas flow maldistribution. Chem. Eng. Sci. 2009, 64, 2113–2126. [Google Scholar] [CrossRef]
- Yang, Y.C.; Xiang, Y.; Li, Y.; Chu, G.; Zou, H.; Arowo, M.; Chen, J. 3D CFD modelling and optimization of single-phase flow in rotating packed beds. Can. J. Chem. Eng. 2015, 93, 1138–1148. [Google Scholar] [CrossRef]


| Project | Value |
|---|---|
| Mesh Quantity | 2,102,140 |
| Boundary layer quantity | 12 |
| Growth rate | 1.2 |
| Minimum face area | 1.26 × 10−4 |
| Maximum face area | 4.95 × 10−4 |
| Minimum Orthogonal Quality | 0.631 |
| Maximum Aspect Ratio | 4.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Liu, Y.; Zhang, C.; Zhang, C.; Wang, S.; Li, Y.; Cheng, S. Computational Fluid Dynamics Analysis of Wet Dust Removal in High-Gravity Countercurrent Rotating Packed Bed. Atmosphere 2024, 15, 157. https://doi.org/10.3390/atmos15020157
Guo S, Liu Y, Zhang C, Zhang C, Wang S, Li Y, Cheng S. Computational Fluid Dynamics Analysis of Wet Dust Removal in High-Gravity Countercurrent Rotating Packed Bed. Atmosphere. 2024; 15(2):157. https://doi.org/10.3390/atmos15020157
Chicago/Turabian StyleGuo, Shuwei, Youzhi Liu, Chao Zhang, Chengqian Zhang, Shufei Wang, Yuliang Li, and Shangyuan Cheng. 2024. "Computational Fluid Dynamics Analysis of Wet Dust Removal in High-Gravity Countercurrent Rotating Packed Bed" Atmosphere 15, no. 2: 157. https://doi.org/10.3390/atmos15020157
APA StyleGuo, S., Liu, Y., Zhang, C., Zhang, C., Wang, S., Li, Y., & Cheng, S. (2024). Computational Fluid Dynamics Analysis of Wet Dust Removal in High-Gravity Countercurrent Rotating Packed Bed. Atmosphere, 15(2), 157. https://doi.org/10.3390/atmos15020157





