Detecting Indonesian Monsoon Signals and Related Features Using Space–Time Singular Value Decomposition (SVD)
Abstract
:1. Introduction
2. Materials and Methods
2.1. SVD Analysis
2.2. Correlation Map
2.3. The Fast Fourier Transform (FFT) Spectrum Algorithm
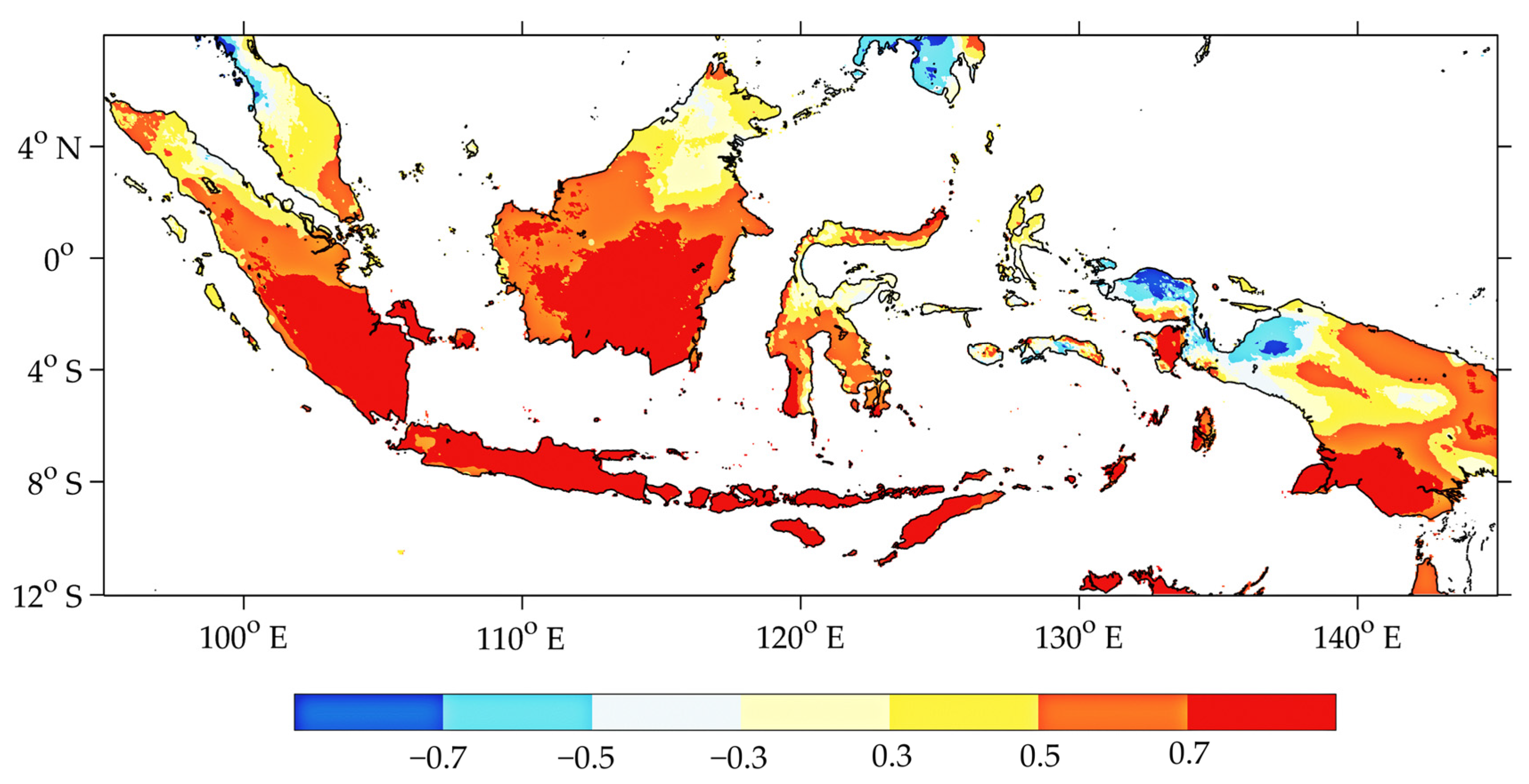
3. Results and Discussion
3.1. Detecting Indonesian Monsoon Signal
3.2. Phase of Indonesian Monsoon
3.3. Indonesian Monsoon Regimes
3.4. Related Features of Indonesian Monsoon Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Webster, P.; Fasullo, J. Tropical Meteorology and Climate: Monsoon: Dynamical Theory. In Encyclopedia of Atmospheric Sciences, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 151–164. [Google Scholar]
- Kirono, D.G.C.; Butler, J.R.A.; McGregor, J.L.; Ripaldi, A.; Katzfey, J.; Nguyen, K. Historical and Future Seasonal Rainfall Variability in Nusa Tenggara Barat Province, Indonesia: Implications for the Agriculture and Water Sectors. Clim. Risk Manag. 2016, 12, 45–58. [Google Scholar] [CrossRef]
- Naylor, R.L.; Battisti, D.S.; Vimont, D.J.; Falcon, W.P.; Burke, M.B. Assessing Risks of Climate Variability and Climate Change for Indonesian Rice Agriculture. Proc. Natl. Acad. Sci. USA 2007, 104, 7752–7757. [Google Scholar] [CrossRef]
- Dhishana, R.; Dubey, S.K. Characteristics of Spectral Energetics during Excess and Deficient Rainfall Years in India, Copernicus Meetings. In Proceedings of the EGU23, the 25th EGU General Assembly, Vienna, Austria, 23–28 April 2023. [Google Scholar]
- Kurniadi, A.; Weller, E.; Min, S.K.; Seong, M.G. Independent ENSO and IOD Impacts on Rainfall Extremes over Indonesia. Int. J. Climatol. 2021, 41, 3640–3656. [Google Scholar] [CrossRef]
- Wati, T.; Hadi, T.W.; Sopaheluwakan, A.; Hutasoit, L.M. The Study of Wind Field ERA-20C in Monsoon Domains for Rainfall Predictor in Indonesia (Java, Sumatra, and Borneo). Agromet 2023, 37, 34–43. [Google Scholar] [CrossRef]
- Schollaen, K.; Karamperidou, C.; Krusic, P.; Cook, E.; Helle, G. ENSO Flavors in a Tree-Ring δ18O Record of Tectona Grandis from Indonesia. Clim. Past 2015, 11, 1325–1333. [Google Scholar] [CrossRef]
- Supari; Tangang, F.; Juneng, L.; Cruz, F.; Chung, J.X.; Ngai, S.T.; Salimun, E.; Mohd, M.S.F.; Santisirisomboon, J.; Singhruck, P.; et al. Multi-Model Projections of Precipitation Extremes in Southeast Asia Based on CORDEX-Southeast Asia Simulations. Environ. Res. 2020, 184, 109350. [Google Scholar] [CrossRef]
- Supari; Tangang, F.; Juneng, L.; Aldrian, E. Observed Changes in Extreme Temperature and Precipitation over Indonesia. Int. J. Climatol. 2017, 37, 1979–1997. [Google Scholar] [CrossRef]
- Tangang, F.; Chung, J.X.; Juneng, L.; Supari; Salimun, E.; Ngai, S.T.; Jamaluddin, A.F.; Mohd, M.S.F.; Cruz, F.; Narisma, G.; et al. Projected Future Changes in Rainfall in Southeast Asia Based on CORDEX–SEA Multi-Model Simulations. Clim. Dyn. 2020, 55, 1247–1267. [Google Scholar] [CrossRef]
- Kurniadi, A.; Weller, E.; Kim, Y.-H.; Min, S.-K. Evaluation of Coupled Model Intercomparison Project Phase 6 Model-Simulated Extreme Precipitation over Indonesia. Int. J. Climatol. 2023, 43, 174–196. [Google Scholar] [CrossRef]
- Aldrian, E.; Dwi Susanto, R. Identification of Three Dominant Rainfall Regions within Indonesia and Their Relationship to Sea Surface Temperature. Int. J. Climatol. 2003, 23, 1435–1452. [Google Scholar] [CrossRef]
- Eguchi, T. Rainfall Distribution and Air Streams over Indonesia. Geogr. Rev. Jpn. 1983, 56, 151–170. [Google Scholar] [CrossRef]
- Xu, Z.; Fu, C.; Qian, Y. A New Index to Describe the Tropical Asian Summer Monsoon. Sci. China Ser. D Earth Sci. 2009, 52, 843–854. [Google Scholar] [CrossRef]
- Kajikawa, Y.; Wang, B.; Yang, J. A Multi-Time Scale Australian Monsoon Index. Int. J. Climatol. 2010, 30, 1114–1120. [Google Scholar] [CrossRef]
- Mulsandi, A.; Sopaheluwakan, A.; Faqih, A.; Hidayat, R.; Koesmaryono, Y. Evaluation of WNPMI and AUSMI Monsoon Index Performance Over Indonesian Region. J. Sains Teknol. Modif. Cuaca 2021, 22, 61–70. [Google Scholar] [CrossRef]
- Wang, P.X.; Wang, B.; Cheng, H.; Fasullo, J.; Guo, Z.; Kiefer, T.; Liu, Z. The Global Monsoon across Time Scales: Mechanisms and Outstanding Issues. Earth-Sci. Rev. 2017, 174, 84–121. [Google Scholar] [CrossRef]
- Xu, Q.; Guan, Z.; Jin, D.; Hu, D. Regional Characteristics of Interannual Variability of Summer Rainfall in the Maritime Continent and Their Related Anomalous Circulation Patterns. J. Clim. 2019, 32, 4179–4192. [Google Scholar] [CrossRef]
- Vera, C.; Higgins, W.; Amador, J.; Ambrizzi, T.; Garreaud, R.; Gochis, D.; Gutzler, D.; Lettenmaier, D.; Marengo, J.; Mechoso, C.R.; et al. Toward a Unified View of the American Monsoon Systems. J. Clim. 2006, 19, 4977–5000. [Google Scholar] [CrossRef]
- Kim, K.-Y.; Kullgren, K.; Lim, G.-H.; Boo, K.-O.; Kim, B.-M. Physical Mechanisms of the Australian Summer Monsoon: 2. Variability of Strength and Onset and Termination Times. J. Geophys. Res. Atmos. 2006, 111, 1–17. [Google Scholar] [CrossRef]
- Ramage, C.S. Monsoon Meteorology; Experimental Botany V. 10; Academic Press: Honolulu, HI, USA, 1971; ISBN 978-0-12-576650-0. [Google Scholar]
- Alapaty, K.; Raman, S.; Mohanty, U.C.; Madala, R.V. Sensitivity of Monsoon Circulations to Changes in Sea Surface Temperatures. Atmos. Environ. 1995, 29, 2139–2156. [Google Scholar] [CrossRef]
- Hamada, J.I.; Yamanaka, M.D.; Matsumoto, J.; Fukao, S.; Winarso, P.A.; Sribimawati, T. Spatial and Temporal Variations of the Rainy Season over Indonesia and Their Link to ENSO. J. Meteorol. Soc. Jpn. Ser. II 2002, 80, 285–310. [Google Scholar] [CrossRef]
- Haylock, M.; McBride, J. Spatial Coherence and Predictability of Indonesian Wet Season Rainfall. J. Clim. 2001, 14, 3882–3887. [Google Scholar] [CrossRef]
- Hendon, H.H. Indonesian Rainfall Variability: Impacts of ENSO and Local Air–Sea Interaction. J. Clim. 2003, 16, 1775–1790. [Google Scholar] [CrossRef]
- Setiawan, A.M.; Lee, W.-S.; Rhee, J. Spatio-Temporal Characteristics of Indonesian Drought Related to El Niño Events and Its Predictability Using the Multi-Model Ensemble. Int. J. Climatol. 2017, 37, 4700–4719. [Google Scholar] [CrossRef]
- Amirudin, A.A.; Salimun, E.; Tangang, F.; Juneng, L.; Zuhairi, M. Differential Influences of Teleconnections from the Indian and Pacific Oceans on Rainfall Variability in Southeast Asia. Atmosphere 2020, 11, 886. [Google Scholar] [CrossRef]
- Lestari, D.O.; Sutriyono, E.; Sabaruddin, S.; Iskandar, I. Respective Influences of Indian Ocean Dipole and El Niño-Southern Oscillation on Indonesian Precipitation. J. Math. Fundam. Sci. 2018, 50, 257–272. [Google Scholar] [CrossRef]
- Nur’utami, M.N.; Hidayat, R. Influences of IOD and ENSO to Indonesian Rainfall Variability: Role of Atmosphere-Ocean Interaction in the Indo-Pacific Sector. Procedia Environ. Sci. 2016, 33, 196–203. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Smith, C.; Wallace, J.M. An Intercomparison of Methods for Finding Coupled Patterns in Climate Data. J. Clim. 1992, 5, 541–560. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Firmansyah, A.J.; Nurjani, E.; Sekaranom, A.B. Effects of the El Niño-Southern Oscillation (ENSO) on Rainfall Anomalies in Central Java, Indonesia. Arab. J. Geosci. 2022, 15, 24. [Google Scholar] [CrossRef]
- Faisol, A.; Indarto, I.; Novita, E.; Budiyono, B. Assessment of Agricultural Drought Based on CHIRPS Data and SPI Method over West Papua–Indonesia. J. Water Land Dev. 2022, 52, 44–52. [Google Scholar] [CrossRef]
- Wiwoho, B.S.; Astuti, I.S.; Alfarizi, I.A.G.; Sucahyo, H.R. Validation of Three Daily Satellite Rainfall Products in a Humid Tropic Watershed, Brantas, Indonesia: Implications to Land Characteristics and Hydrological Modelling. Hydrology 2021, 8, 154. [Google Scholar] [CrossRef]
- Saragih, N.F.; Sitepu, S.; Simanungkalit, G.T.; Sinambela, M.; Rajagukguk, E.; Larosa, F.G.; Jaya, I.K. Validation of CHIRPS Estimation Rainfall Data Using Numerical Accuracy Test with Precitipation Observation Data. IOP Conf. Ser. Earth Environ. Sci. 2022, 1083, 012095. [Google Scholar] [CrossRef]
- Narulita, I.; Fajary, F.R.; Syahputra, M.R.; Kusratmoko, E.; Djuwansah, M.R. Spatio-Temporal Rainfall Variability of Equatorial Small Island: Case Study Bintan Island, Indonesia. Theor. Appl. Climatol. 2021, 144, 625–641. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.-M. Improvements of the Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Bjornsson, H.; Venegas, S.A. A Manual for EOF and SVD Analyses of Climate Data. CGCR Rep. 1997, 97, 112–134. Available online: https://www.geog.mcgill.ca/gec3/wp-content/uploads/2009/03/Report-no.-1997-1.pdf (accessed on 1 January 2023).
- Cochran, W.T.; Cooley, J.W.; Favin, D.L.; Helms, H.D.; Kaenel, R.A.; Lang, W.W.; Maling, G.C.; Nelson, D.E.; Rader, C.M.; Welch, P.D. What Is the Fast Fourier Transform? Proc. IEEE 1967, 55, 1664–1674. [Google Scholar] [CrossRef]
- Ferrett, S.; Yang, G.-Y.; Woolnough, S.J.; Methven, J.; Hodges, K.; Holloway, C.E. Linking Extreme Precipitation in Southeast Asia to Equatorial Waves. Q. J. R. Meteorol. Soc. 2020, 146, 665–684. [Google Scholar] [CrossRef]
- Latos, B.; Lefort, T.; Flatau, M.K.; Flatau, P.J.; Permana, D.S.; Baranowski, D.B.; Paski, J.A.I.; Makmur, E.; Sulystyo, E.; Peyrillé, P.; et al. Equatorial Waves Triggering Extreme Rainfall and Floods in Southwest Sulawesi, Indonesia. Mon. Weather Rev. 2021, 149, 1381–1401. [Google Scholar] [CrossRef]
- Robertson, A.W.; Moron, V.; Qian, J.-H.; Chang, C.-P.; Tangang, F.T.; Aldrian, E.; Koh, T.Y.; Liew, J. The Maritime Continent Monsoon. In The Global Monsoon System Research and Forecast; World Scientific Publication Company: New York, NY, USA, 2011; pp. 85–98. ISBN 978-981-4343-40-4. [Google Scholar]
- Xavier, P.; Lim, S.Y.; Ammar Bin Abdullah, M.F.; Bala, M.; Chenoli, S.N.; Handayani, A.S.; Marzin, C.; Permana, D.; Tangang, F.; Williams, K.D.; et al. Seasonal Dependence of Cold Surges and Their Interaction with the Madden–Julian Oscillation over Southeast Asia. J. Clim. 2020, 33, 2467–2482. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, S.; Jiang, X.; Zhao, P. Seasonal–Interannual Variation and Prediction of Wet and Dry Season Rainfall over the Maritime Continent: Roles of ENSO and Monsoon Circulation. J. Clim. 2016, 29, 3675–3695. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, S.; Jiang, X.; Huang, B. Roles of Remote and Local Forcings in the Variation and Prediction of Regional Maritime Continent Rainfall in Wet and Dry Seasons. J. Clim. 2016, 29, 8871–8879. [Google Scholar] [CrossRef]
- Chang, C.-P.; Harr, P.A.; McBride, J.L.; Hsu, H.H. Maritime Continent Monsoon: Annual Cycle and Boreal Winter. In East Asian Monsoon; World Scientific Series on Asia-Pacific Weather and Climate; World Scientific: New York, NY, USA, 2004; Volume 2, pp. 107–150. ISBN 978-981-238-769-1. [Google Scholar]
- Hung, C.; Liu, X.; Yanai, M. Symmetry and Asymmetry of the Asian and Australian Summer Monsoons. J. Clim. 2004, 17, 2413–2426. [Google Scholar] [CrossRef]
- Jo, S.; Ahn, J.-B. Improvement of CGCM Prediction for Wet Season Precipitation over Maritime Continent Using a Bias Correction Method. Int. J. Climatol. 2015, 35, 3721–3732. [Google Scholar] [CrossRef]
- McBride, J.L.; Haylock, M.R.; Nicholls, N. Relationships between the Maritime Continent Heat Source and the El Niño–Southern Oscillation Phenomenon. J. Clim. 2003, 16, 2905–2914. [Google Scholar] [CrossRef]
- Qian, W.; Deng, Y.; Zhu, Y.; Dong, W. Demarcating the Worldwide Monsoon. Theor. Appl. Climatol. 2002, 71, 1–16. [Google Scholar] [CrossRef]
- Wang, B.; Ding, Q. Changes in Global Monsoon Precipitation over the Past 56 Years. Geophys. Res. Lett. 2006, 33, L06711. [Google Scholar] [CrossRef]
- Ratri, D.N.; Whan, K.; Schmeits, M. Calibration of ECMWF Seasonal Ensemble Precipitation Reforecasts in Java (Indonesia) Using Bias-Corrected Precipitation and Climate Indices. Weather Forecast. 2021, 36, 1375–1386. [Google Scholar] [CrossRef]
- Li, S.; Robertson, A.W. Evaluation of Submonthly Precipitation Forecast Skill from Global Ensemble Prediction Systems. Mon. Weather Rev. 2015, 143, 2871–2889. [Google Scholar] [CrossRef]
- Gordon, A.L.; Susanto, R.D.; Vranes, K. Cool Indonesian Throughflow as a Consequence of Restricted Surface Layer Flow. Nature 2003, 425, 824–828. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Bassinot, F.; Guichard, F.; Fang, N.Q. Indonesian Throughflow and Monsoon Activity Records in the Timor Sea since the Last Glacial Maximum. Mar. Micropaleontol. 2013, 101, 115–126. [Google Scholar] [CrossRef]








| PC | The Square Covariance Fractions (SCFs) | |
|---|---|---|
| Individual | Cumulative | |
| PC1 | 33.1% | 33.1% |
| PC2 | 12.9% | 46% |
| PC3 | 11.2% | 57.2% |
| PC4 | 4.7% | 61.9% |
| PC5 | 2.9% | 64.8% |
| PC6 | 2.6% | 67.4% |
| PC7 | 2.4% | 69.8% |
| PC8 | 1.8% | 71.6% |
| PC9 | 1.8% | 73.4% |
| PC10 | 1.4% | 74.8% |
| PC | SCF | r | |
|---|---|---|---|
| Individual | Cumulative | ||
| PC1 | 70.4% | 70.4% | 0.86 |
| PC2 | 7.9% | 78.3% | 0.78 |
| PC3 | 5.0% | 83.3% | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulsandi, A.; Koesmaryono, Y.; Hidayat, R.; Faqih, A.; Sopaheluwakan, A. Detecting Indonesian Monsoon Signals and Related Features Using Space–Time Singular Value Decomposition (SVD). Atmosphere 2024, 15, 187. https://doi.org/10.3390/atmos15020187
Mulsandi A, Koesmaryono Y, Hidayat R, Faqih A, Sopaheluwakan A. Detecting Indonesian Monsoon Signals and Related Features Using Space–Time Singular Value Decomposition (SVD). Atmosphere. 2024; 15(2):187. https://doi.org/10.3390/atmos15020187
Chicago/Turabian StyleMulsandi, Adi, Yonny Koesmaryono, Rahmat Hidayat, Akhmad Faqih, and Ardhasena Sopaheluwakan. 2024. "Detecting Indonesian Monsoon Signals and Related Features Using Space–Time Singular Value Decomposition (SVD)" Atmosphere 15, no. 2: 187. https://doi.org/10.3390/atmos15020187
APA StyleMulsandi, A., Koesmaryono, Y., Hidayat, R., Faqih, A., & Sopaheluwakan, A. (2024). Detecting Indonesian Monsoon Signals and Related Features Using Space–Time Singular Value Decomposition (SVD). Atmosphere, 15(2), 187. https://doi.org/10.3390/atmos15020187








