CFD-DPM Simulation on the Atmospheric Pollutant Dispersion in Industrial Park
Abstract
:1. Introduction
| Reference | Research Object | Pollutant | Computational Model | Result |
|---|---|---|---|---|
| Liu et al., 2011 [11] | Wind field and pollutant dispersion in downtown Macao. | Gas (traffic exhaust) | Large Eddy Simulation (LES), a roughness element model of buildings. | The proposed model was an appropriate method for numerical prediction of urban atmospheric environment. |
| Wang and McNamara, 2006 [13] | Pollutant dispersion inside idealized building arrays. | Gas (Ethane) | Reynolds-Averaged Navier–Stokes equations (RANS). | The inadequate modeling of local flow patterns led to a deviation value compared with wind tunnel tests. |
| Steffens et al., 2013 [14] | Pollutant transport around roadside vegetation barriers. | Particulate matter | Continuous phase: RANS. Dispersed phase: Discrete Phase Model (DPM). | The model would be improved by using LES and the deposition effect of particles was significant in the simulation of pollutant dispersion. |
| Xie et al., 2005 [15] | Pollutant distribution inside idealized street canyon under the effect of solar radiation. | Gas (CO) | RANS and Boussinesq’s hypothesis. | The flow structure and contaminant distribution could be completely different under solar heating. |
| Punyisa Chaisri and Pimporn Ponpesh, 2022 [16] | Airflow fields and pollutant dispersion in Bangkok. | PM2.5 | RANS and DPM | The city configuration with the Skytrain structure located between the tall buildings results in higher concentration than the case without the Skytrain structure. |
| Meng et al., 2021 [17] | The spatial distributions of PM2.5 concentration due to road traffic emissions in building arrays. | PM2.5 | RNG and DPM | The PM2.5 concentration was decreased within 0 to 120 m distance from the road and was stabilized when the building height was above 60 m. |
2. Computational Methodology
2.1. Eulerian–Lagrangian Method
2.2. Governing Equations of Gas Phase
2.3. Particle Motion Equations
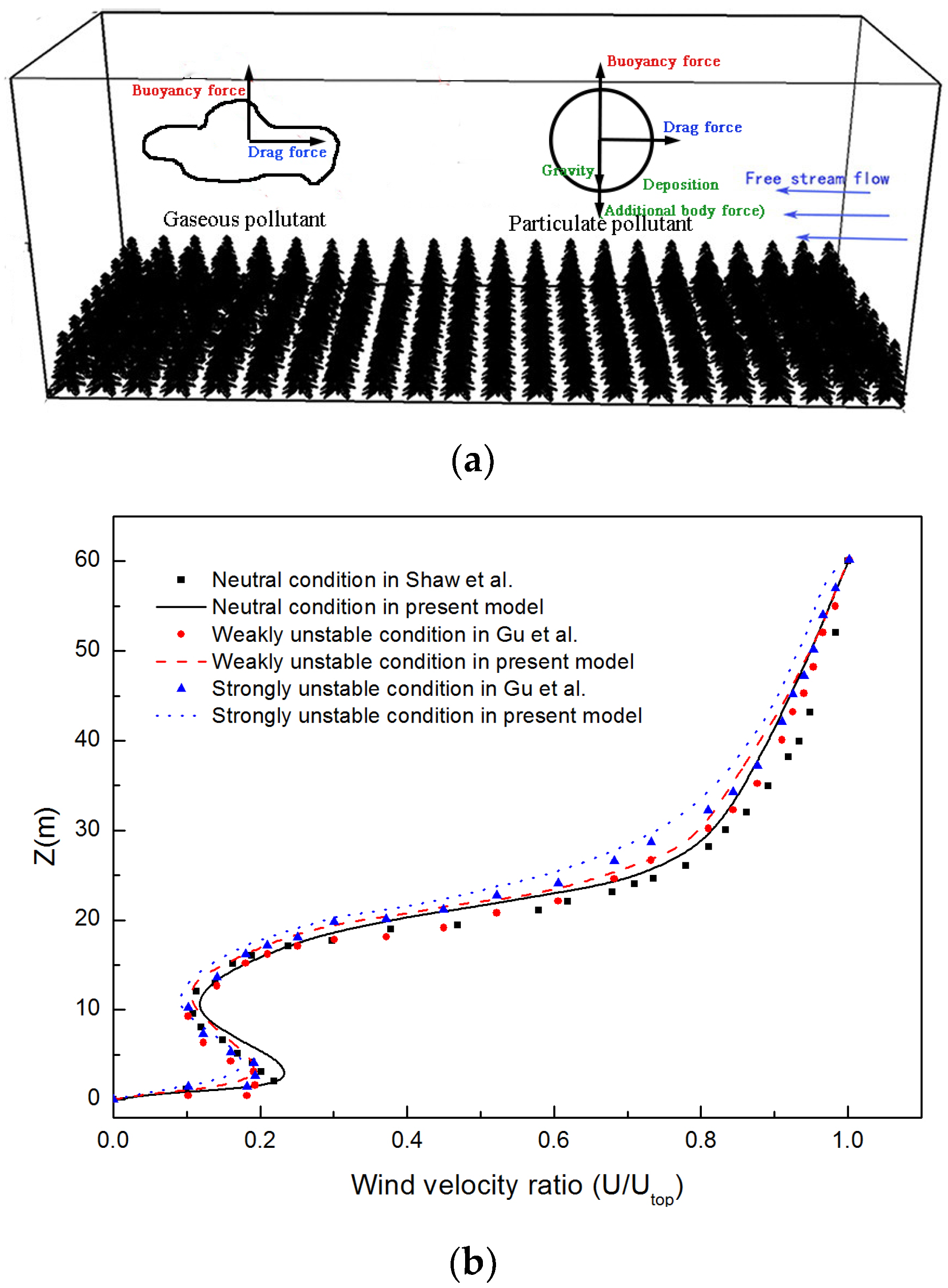
2.4. Vegetation Modeling Concept
2.4.1. Spatial Averaging Method
2.4.2. Drag Effect on Wind Flow
2.4.3. Effect of Buoyancy Force
2.4.4. Dry Deposition Inside Vegetation Area
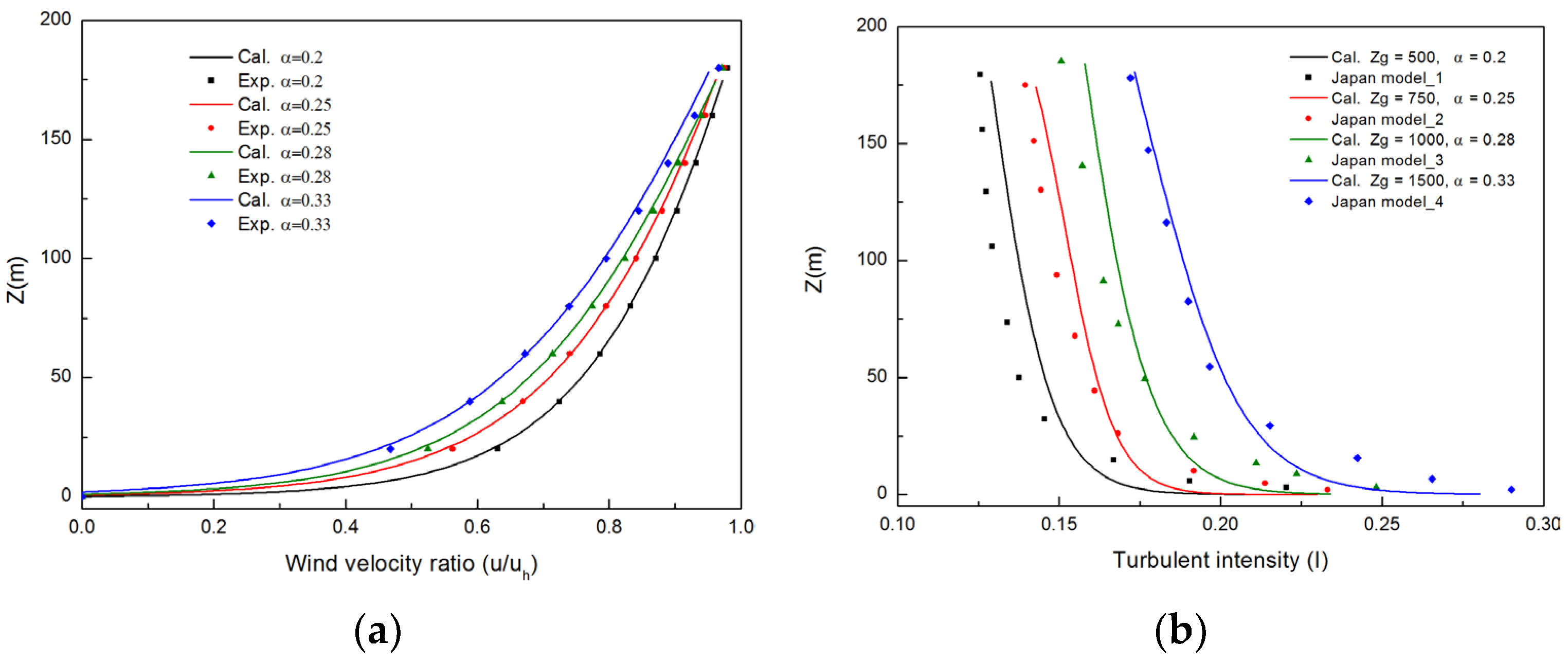
2.4.5. Model Validation
2.5. Numerical Setup and Simulations
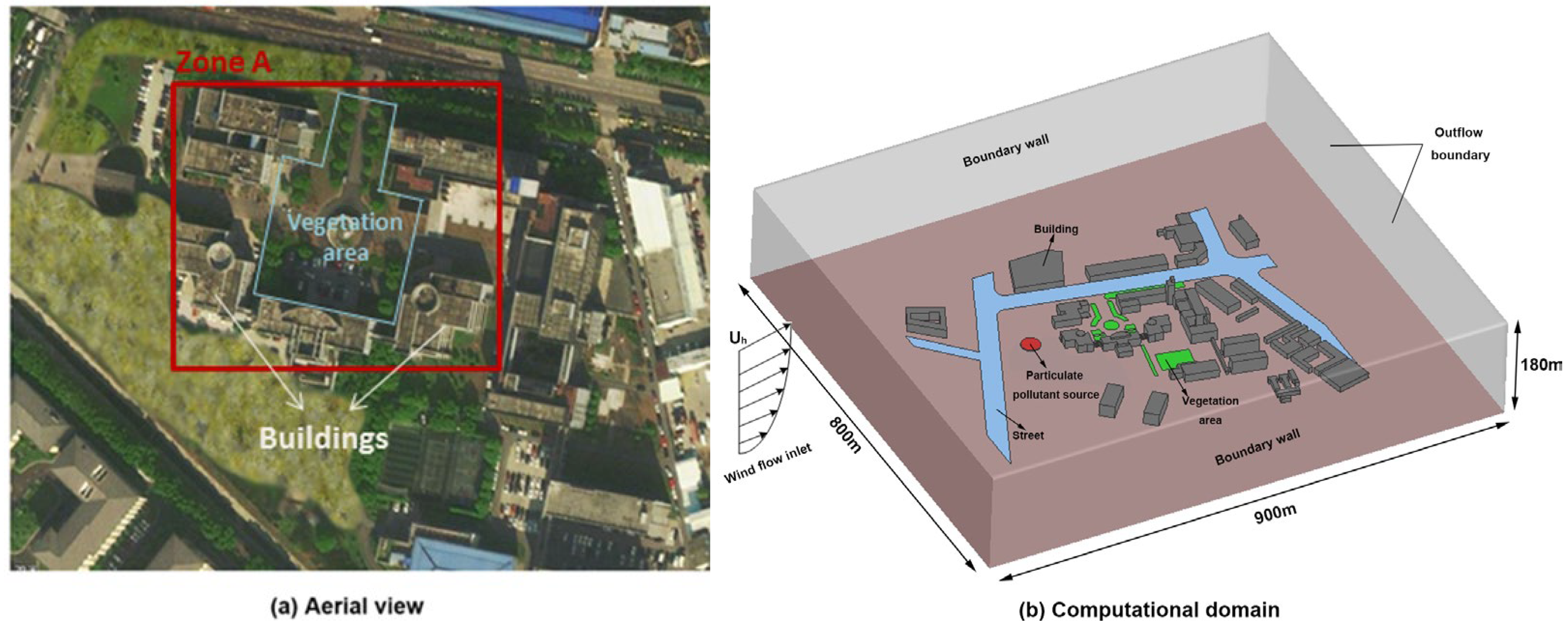
2.5.1. Computational Domain and Grid Generation
2.5.2. Boundary Conditions
- (1)
- Wind flow inlet boundary
- (2)
- Outflow boundaries
- (3)
- Building walls and ground
- (4)
- Pollutant source
2.5.3. Computational Settings and Numerical Method
3. Results and Discussion
3.1. Turbulent Characteristics of Atmospheric Boundary Layer
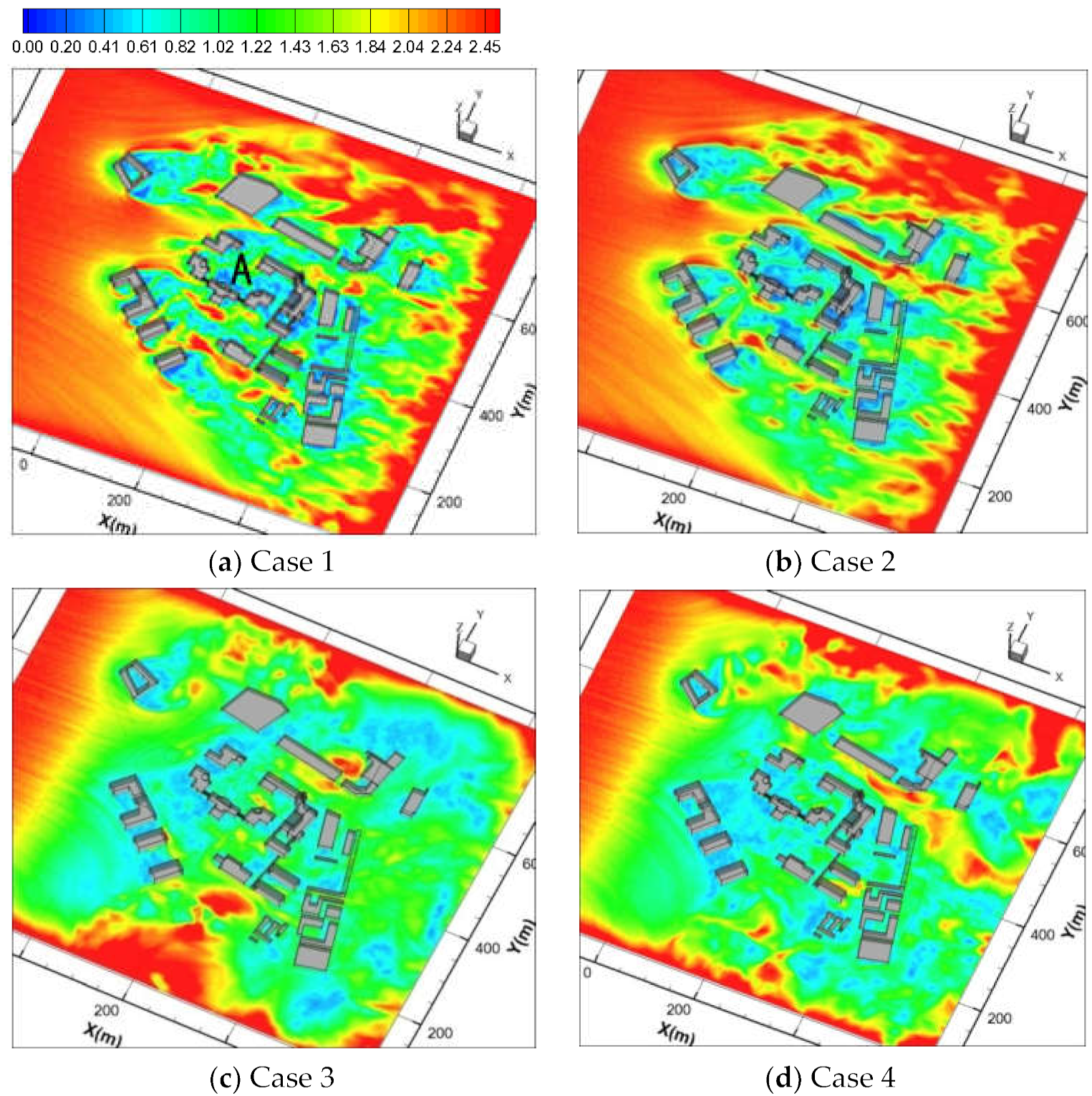
3.2. Effects of Meteorological Conditions on Wind Field
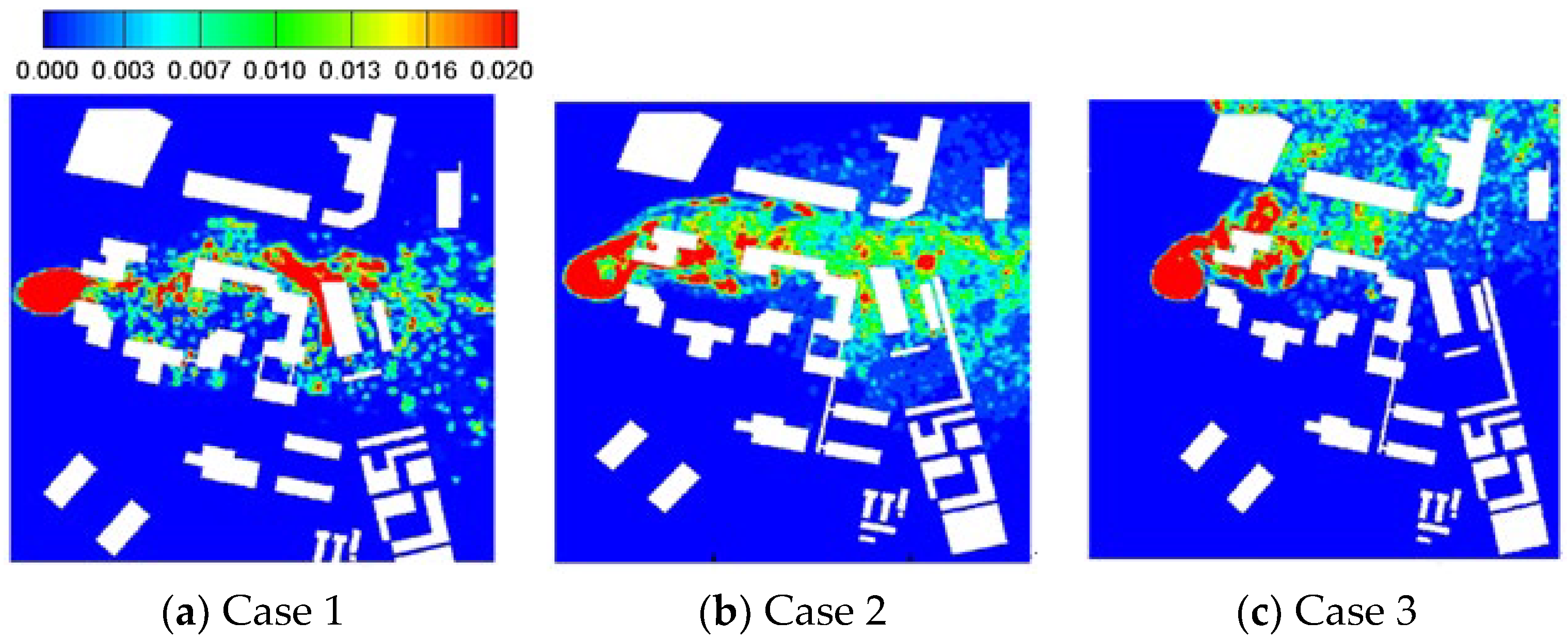
3.3. Effects of Meteorological Conditions on Particulate Pollutant Distribution
3.4. Sensitivity Analysis
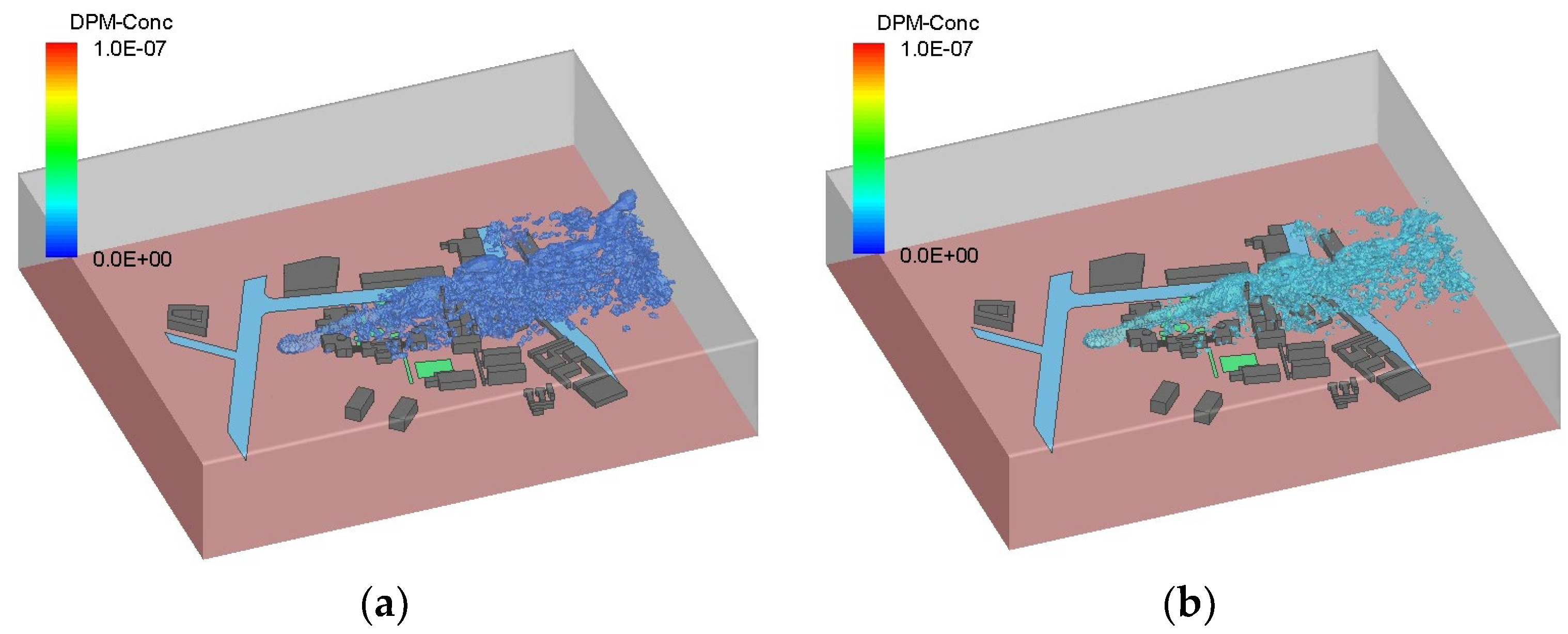
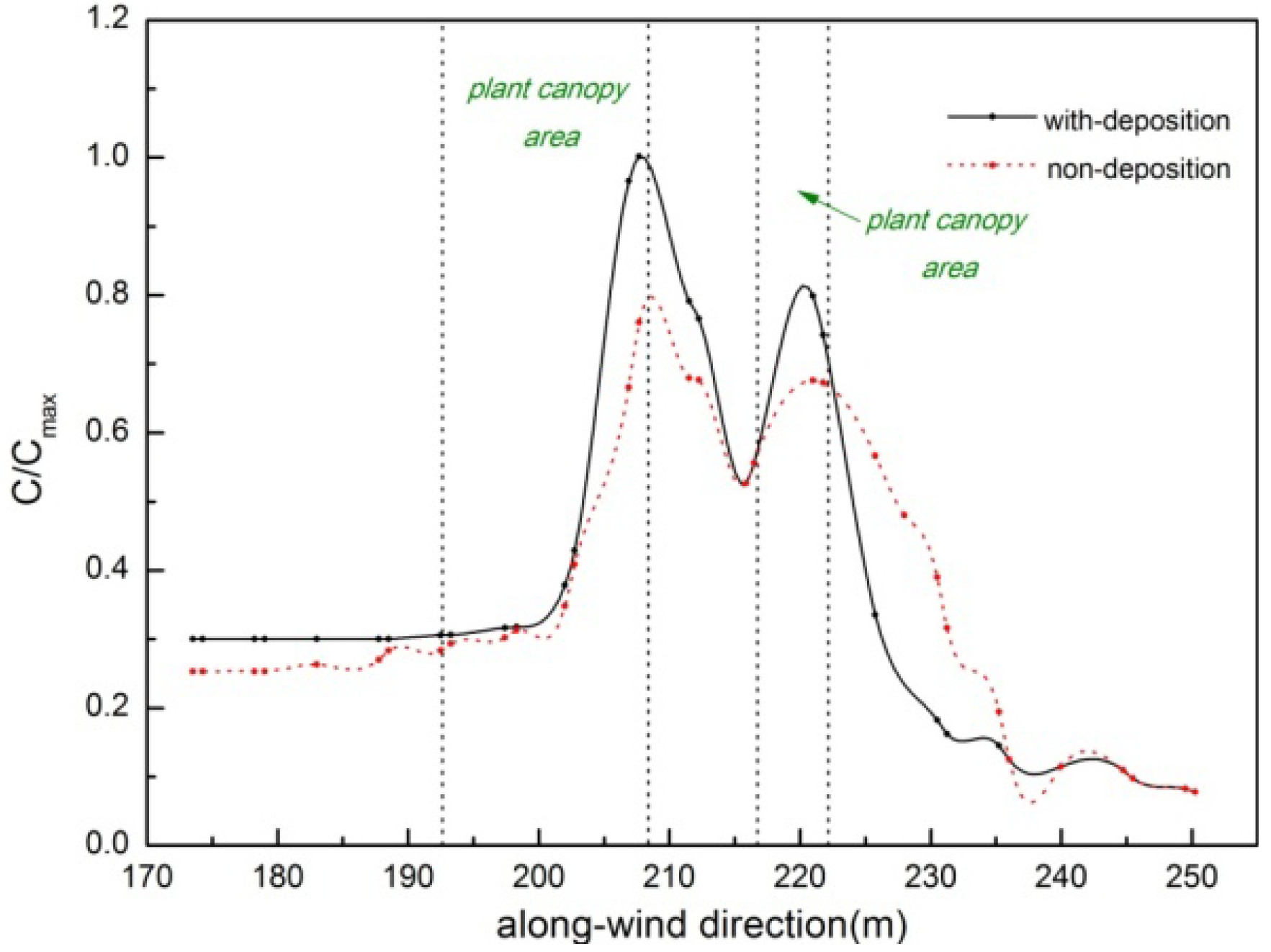
3.4.1. Deposition Effect
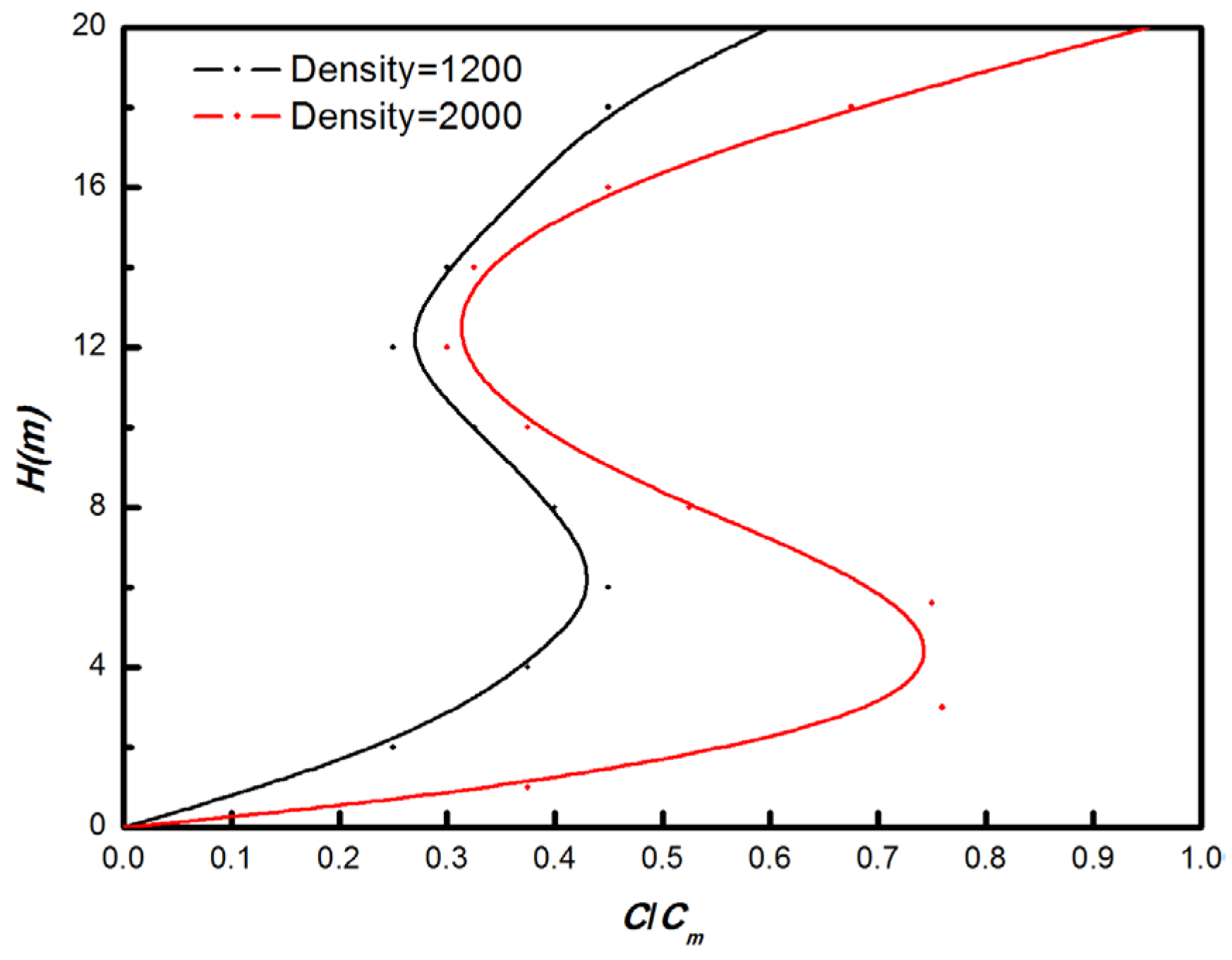
3.4.2. Particle Density and Diameter
4. Conclusions
- To accurately set the inlet boundary condition, it is necessary to calculate both wind velocity and turbulent intensity profiles based on meteorological conditions. The two parameters are validated with standard data before the calculation of wind flow in the park.
- Four cases are simulated to analyze the effects of meteorological conditions; the wind filed can be blocked by a plant canopy, and it is completely changed when the buoyancy force is taken into account in unstable weather conditions and the wind field near the ground becomes uniform.
- The dispersion of pollutants is also influenced by meteorological conditions. In the presence of weather instability, the direction of pollutant dispersion shifts toward the northeast due to turbulent streamlines surrounding canopy regions, resulting in higher concentrations on the windward side of the plant canopies.
- The deposition effect of a plant canopy on particles plays a crucial role in the analysis of pollutant distribution. Under stable weather conditions, approximately 50% of particulate pollutants entering the canopy regions can be effectively removed. However, it is imperative to investigate the relationship between buoyancy and the deposition effect.
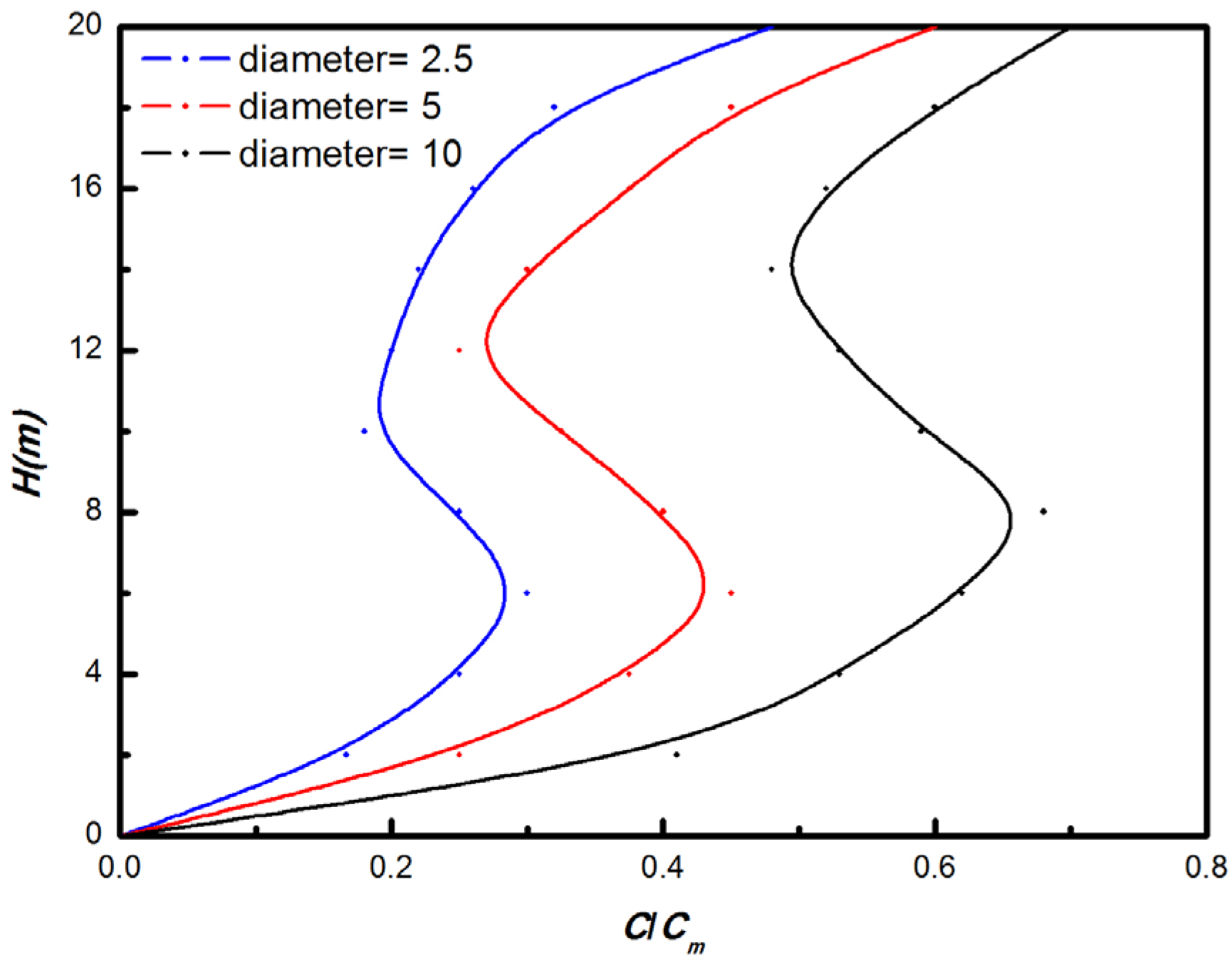
- The deposition effects are prominently observed on particles with high density and a large diameter. Additionally, the parameter LAD significantly influences the deposition process. In comparison to PM10, PM2.5 exhibits a lower deposition velocity, resulting in its wider dispersion both within and outside the industrial park.
- There are some approximate treatments and limitations in this research. For example, the leaf area index of different seasons in Nanjing Sample Industrial Park is processed approximately. The canopy regions are treated by the spatial averaging method, which is explained in Section 2.4.1. Weather conditions, wind velocities, and directions are not fully considered in this study. Some physical models need to be added for simulations under rainy or foggy conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Yu, Q.; Huang, Z.; Ma, W.; Zhang, Y. Identifying Key Potential Source Areas for Ambient Methyl Mercaptan Pollution Based on Long-Term Environmental Monitoring Data in an Industrial Park. Atmosphere 2018, 9, 501. [Google Scholar] [CrossRef]
- Dockery, D.W.; Pope, C.A., III; Xu, X.; Spengler, J.D.; Ware, J.H.; Fay, M.E.; Ferris, B.G., Jr.; Speizer, F.E. An Association between Air Pollution and Mortality in Six U.S. Cities. N. Engl. J. Med. 1993, 329, 1753–1759. [Google Scholar] [CrossRef]
- Hong, Y.-J.; Huang, Y.-C.; Lee, I.-L.; Chiang, C.-M.; Lin, C.; Jeng, H.A. Assessment of volatile organic compounds and particulate matter in a dental clinic and health risks to clinic personnel. J. Environ. Sci. Health Part A 2015, 50, 1205–1214. [Google Scholar] [CrossRef]
- Liu, Y.S.; Miao, S.G.; Zhang, C.L.; Cui, G.X.; Zhang, Z.S. Study on micro-atmospheric environment by coupling large eddy simulation with mesoscale model. J. Wind. Eng. Ind. Aerodyn. 2012, 107–108, 106–117. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Buccolieri, R.; Salim, S.M.; Leo, L.S.; Di Sabatino, S.; Chan, A.; Ielpo, P.; de Gennaro, G.; Gromke, C. Analysis of local scale tree–atmosphere interaction on pollutant concentration in idealized street canyons and application to a real urban junction. Atmos. Environ. 2011, 45, 1702–1713. [Google Scholar] [CrossRef]
- Bohrer, G.; Katul, G.G.; Walko, R.L.; Avissar, R. Exploring the effects of microscale structural heterogeneity of forest canopies using large-eddy simulations. Bound.-Layer Meteorol. 2009, 132, 351–382. [Google Scholar] [CrossRef]
- Boppana, V.B.L.; Xie, Z.-T.; Castro, I.P. Large-eddy simulation of dispersion from surface sources in arrays of obstacles. Bound.-Layer Meteorol. 2010, 135, 433–454. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Overney, J.; Rogers, B.D.; Parlange, M.B. The effects of building representation and clustering in large-eddy simulations of flows in urban canopies. Bound.-Layer Meteorol. 2009, 132, 415–436. [Google Scholar] [CrossRef]
- Huang, J.; Cassiani, M.; Albertson, J.D. The effects of vegetation density on coherent turbulent structures within the canopy sublayer: A large-eddy simulation study. Bound.-Layer Meteorol. 2009, 133, 253–275. [Google Scholar] [CrossRef]
- Liu, Y.S.; Cui, G.X.; Wang, Z.S.; Zhang, Z.S. Large eddy simulation of wind field and pollutant dispersion in downtown Macao. Atmos. Environ. 2011, 45, 2849–2859. [Google Scholar] [CrossRef]
- Hanna, S.R.; Tehranian, S.; Carissimo, B.; Macdonald, R.W.; Lohner, R. Comparisons of model simulations with observations of mean flow and turbulence within simple obstacle arrays. Atmos. Environ. 2002, 36, 5067–5079. [Google Scholar] [CrossRef]
- Wang, X.; McNamara, K.F. Evaluation of CFD simulation using RANS turbulence models for building effects on pollutant dispersion. Environ. Fluid Mech. 2006, 6, 181–202. [Google Scholar] [CrossRef]
- Steffens, J.T.; Heist, D.K.; Perry, S.G.; Zhang, K.M. Modeling the effects of a solid barrier on pollutant dispersion under various atmospheric stability conditions. Atmos. Environ. 2013, 69, 76–85. [Google Scholar] [CrossRef]
- Xie, X.; Huang, Z.; Wang, J.; Xie, Z. The impact of solar radiation and street layout on pollutant dispersion in street canyon. J. Affect. Disord. 2005, 40, 201–212. [Google Scholar] [CrossRef]
- Chaisri, P.; Ponpesh, P. Prediction of PM2.5 Dispersion in Bangkok Pathumwan District) Using CFD Modeling. Eng. J. 2022, 26, 1–13. [Google Scholar] [CrossRef]
- Meng, M.-R.; Cao, S.-J.; Kumar, P.; Tang, X.; Feng, Z. Spatial distribution characteristics of PM2.5 concentration around residential buildings in urban traffic-intensive areas: From the perspectives of health and safety. Saf. Sci. 2021, 141, 105318. [Google Scholar] [CrossRef]
- Zhang, K.M.; Wexler, A.S. Evolution of particle number distribution near roadways—Part I: Analysis of aerosol dynamics and its implications for engine emission measurement. Atmos. Environ. 2004, 38, 6643–6653. [Google Scholar] [CrossRef]
- Sagaut, P.; Lee, Y.-T. Large Eddy simulation for incompressible flows: An introduction. Scientific computation series. Appl. Mech. Rev. 2002, 55, B115–B116. [Google Scholar] [CrossRef]
- Reynolds, W.C. Computation of turbulent flows. Annu. Rev. Fluid Mech. 1976, 8, 183–208. [Google Scholar] [CrossRef]
- Erlebacher, G.; Hussaini, M.Y.; Speziale, C.G.; Zang, T.A. Toward the large-eddy simulation of compressible turbulent flows. J. Fluid Mech. 1992, 238, 155–185. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A: Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Steffens, J.T.; Wang, Y.J.; Zhang, K.M. Exploration of effects of a vegetation barrier on particle size distributions in a near-road environment. Atmos. Environ. 2012, 50, 120–128. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Gosman, A.D.; Loannides, E. Aspects of computer simulation of liquid-fueled combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- Wang, H.; Takle, E.S.; Shen, J. Shelterbelts and windbreaks: Mathematical modeling and computer simulations of turbulent flows. Annu. Rev. Fluid Mech. 2001, 33, 549–586. [Google Scholar] [CrossRef]
- Thom, A. Momentum, mass and heat exchange of vegetation. Q. J. R. Meteorol. Soc. 1972, 98, 124–134. [Google Scholar] [CrossRef]
- Yang, L.; Qian, F.; Song, D.-X.; Zheng, K.-J. Research on urban heat-island effect. Procedia Eng. 2016, 169, 11–18. [Google Scholar] [CrossRef]
- Gu, Z.; Zhang, Y.; Lei, K. Large eddy simulation of flow in a street canyon with tree planting under various atmospheric instability conditions. Sci. China Technol. Sci. 2010, 53, 1928–1937. [Google Scholar] [CrossRef]
- Piskunov, V. Parameterization of aerosol dry deposition velocities onto smooth and rough surfaces. J. Aerosol Sci. 2009, 40, 664–679. [Google Scholar] [CrossRef]
- Petroff, A.; Zhang, L. Development and validation of a size-resolved particle dry deposition scheme for application in aerosol transport models. Geosci. Model Dev. 2010, 3, 753–769. [Google Scholar] [CrossRef]
- Shaw, R.H.; Schumann, U. Large-eddy simulation of turbulent flow above and within a forest. Bound.-Layer Meteorol. 1992, 61, 47–64. [Google Scholar] [CrossRef]
- Ma, X.; Zhong, W.; Feng, W.; Li, G. Modelling of pollutant dispersion with atmospheric instabilities in an industrial park. Powder Technol. 2017, 314, 577–588. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Smirnov, A.; Shi, S.; Celik, I. Random flow generation technique for large eddy simulations and particle-dynamics modeling. J. Fluids Eng. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Uchida, T.; Ohya, Y. Large-eddy simulation of turbulent airflow over complex terrain. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 219–229. [Google Scholar] [CrossRef]






| Parameter | Value | Unit | |
|---|---|---|---|
| Meteorological conditions | The time of day | Daytime, night | / |
| Season | Summer, winter | / | |
| Weather | Sunny, cloudy | / | |
| Wind field | Wind velocity (Uh) | 10 | m/s |
| Height of atmospheric boundary layer (Zg) | 500, 750, 1000, 1500 | m | |
| Exponential coefficient | 0.2, 0.25, 0.28, 0.33 | / | |
| LAI | 2, 5 | / | |
| Solar radiation heat flux () | Calculated by solar calculator in Fluent (800, 200, 0) | W/m2 | |
| Air density () | 1.225 (288 K) | kg/m3 | |
| Particulate pollutant | Density () | 1200, 2000 | kg/m3 |
| Particle diameter (dp) | 2.5, 5, 10 | ||
| Particle mass flux () | 0.008 | kg·m−2·s−1 | |
| Discharge velocity () | 0.2 | m/s |
| Case | The Time of Day | Weather | The Height of Boundary Layer Zg (m) | α |
|---|---|---|---|---|
| A | Night | Cloudy | 500 | 0.2 |
| B | Daytime | Cloudy | 750 | 0.25 |
| C | Night | Clear | 1000 | 0.28 |
| D | Daytime | Clear | 1500 | 0.33 |
| Case | The Time of Day | Weather | Season | Atmospheric Instability | Solar Radiation Heat Flux | LAI |
|---|---|---|---|---|---|---|
| 1 | Night | Cloudy | Winter | Neutral | 0 | 2 |
| 2 | Night | Cloudy | Summer | Neutral | 0 | 5 |
| 3 | Daytime | Clear | Summer | Strongly | 800 | 5 |
| 4 | Daytime | Cloudy | Summer | Weakly | 200 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Zhong, W. CFD-DPM Simulation on the Atmospheric Pollutant Dispersion in Industrial Park. Atmosphere 2024, 15, 298. https://doi.org/10.3390/atmos15030298
Ma X, Zhong W. CFD-DPM Simulation on the Atmospheric Pollutant Dispersion in Industrial Park. Atmosphere. 2024; 15(3):298. https://doi.org/10.3390/atmos15030298
Chicago/Turabian StyleMa, Xiaofei, and Wenqi Zhong. 2024. "CFD-DPM Simulation on the Atmospheric Pollutant Dispersion in Industrial Park" Atmosphere 15, no. 3: 298. https://doi.org/10.3390/atmos15030298
APA StyleMa, X., & Zhong, W. (2024). CFD-DPM Simulation on the Atmospheric Pollutant Dispersion in Industrial Park. Atmosphere, 15(3), 298. https://doi.org/10.3390/atmos15030298





