Evaluation of Nine Planetary Boundary Layer Turbulence Parameterization Schemes of the Weather Research and Forecasting Model Applied to Simulate Planetary Boundary Layer Surface Properties in the Metropolitan Region of São Paulo Megacity, Brazil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Region of Study
2.2. Observation
2.2.1. Sensor’s Description
2.2.2. Vertical Turbulent Fluxes of Sensible and Latent Heat
2.3. Meteorological Conditions during the Field Campaigns
2.4. WRF Model Configuration
2.4.1. PBL Turbulence Parametrization Schemes
2.4.2. Local Closures of 1.5 Orders
Mellor-Yamada Janjic
Mellor-Yamada Nakanishi-Niino
Quasi-Normal Scale Elimination
University of Washington
Bougeault-Lacarrère
2.4.3. Nonlocal Closures of 1.0 Order
Yonsei University
Shin-Hong
2.4.4. Hybrid Local-Nonlocal Closures of Orders 1.0 and 1.5
Asymmetric Convective Model
Total Energy-Mass Flux
2.5. Statistical Parameters
3. Results
3.1. Summer Campaign (19–28 February 2013)
3.1.1. Conventional Meteorological Variables (T, RH, q, WSP, WDIR)
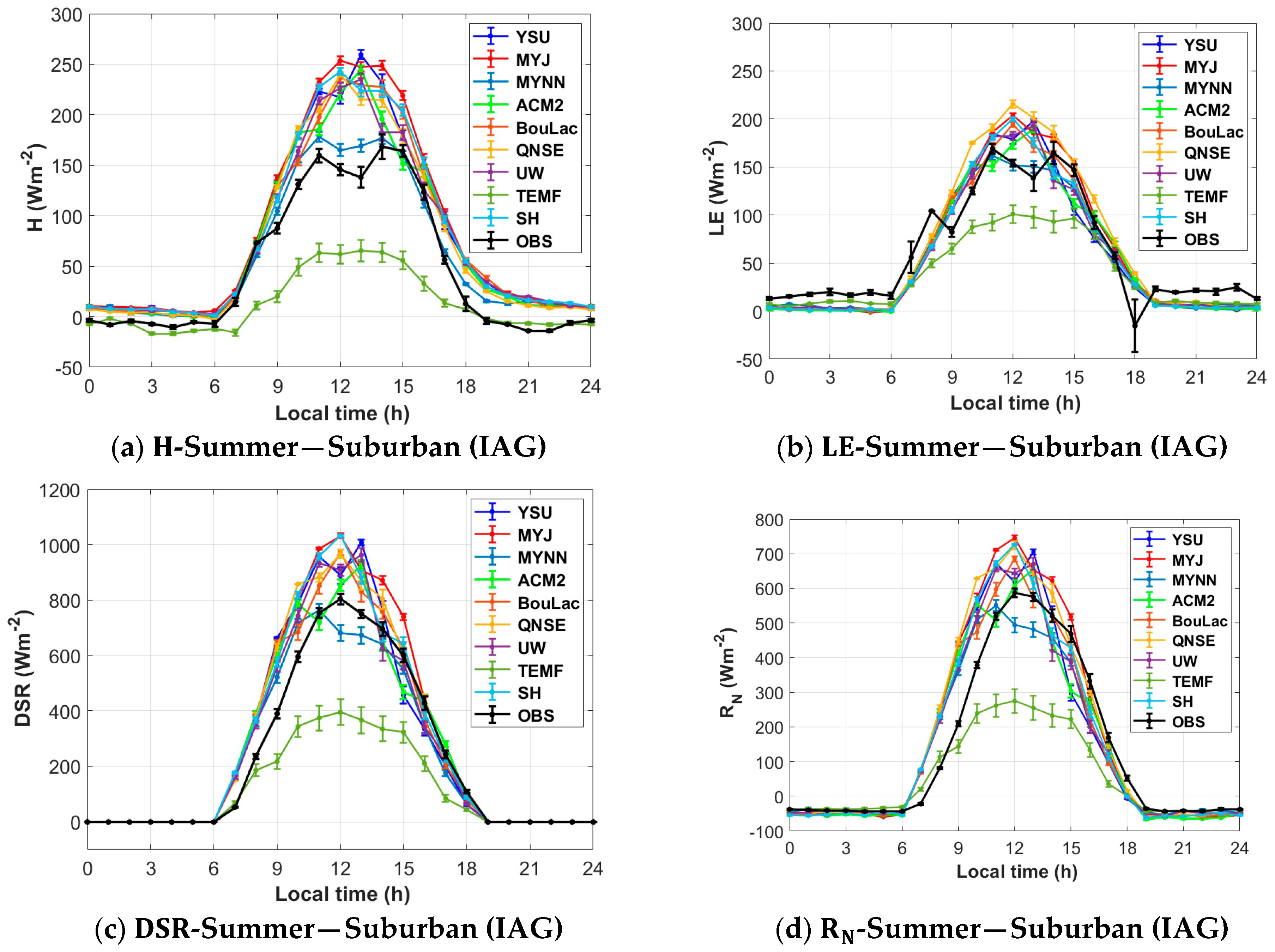
3.1.2. Unconventional Variables (H, LE, RN DSR)
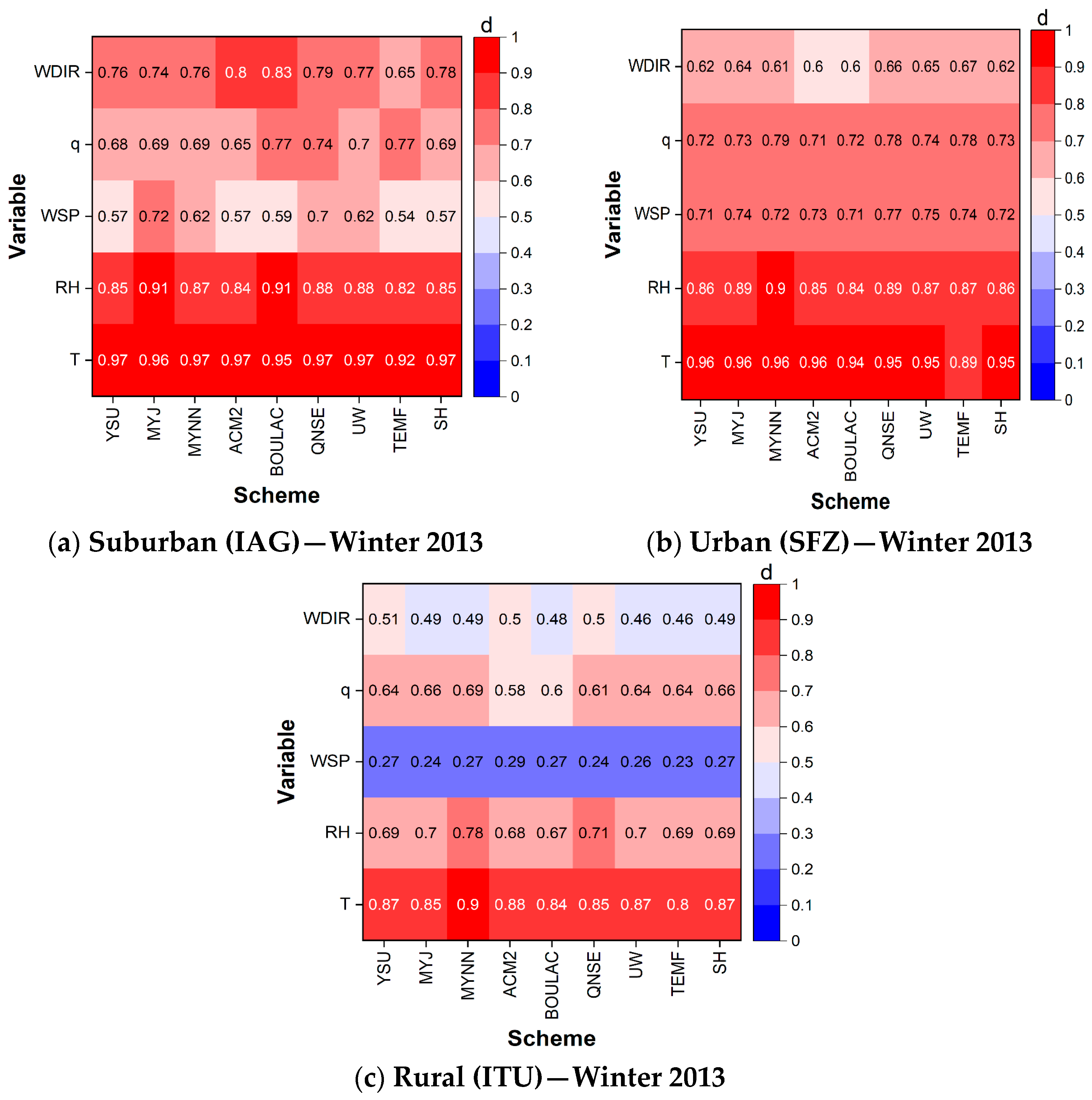
3.2. Winter Campaign (6–15 August 2013)
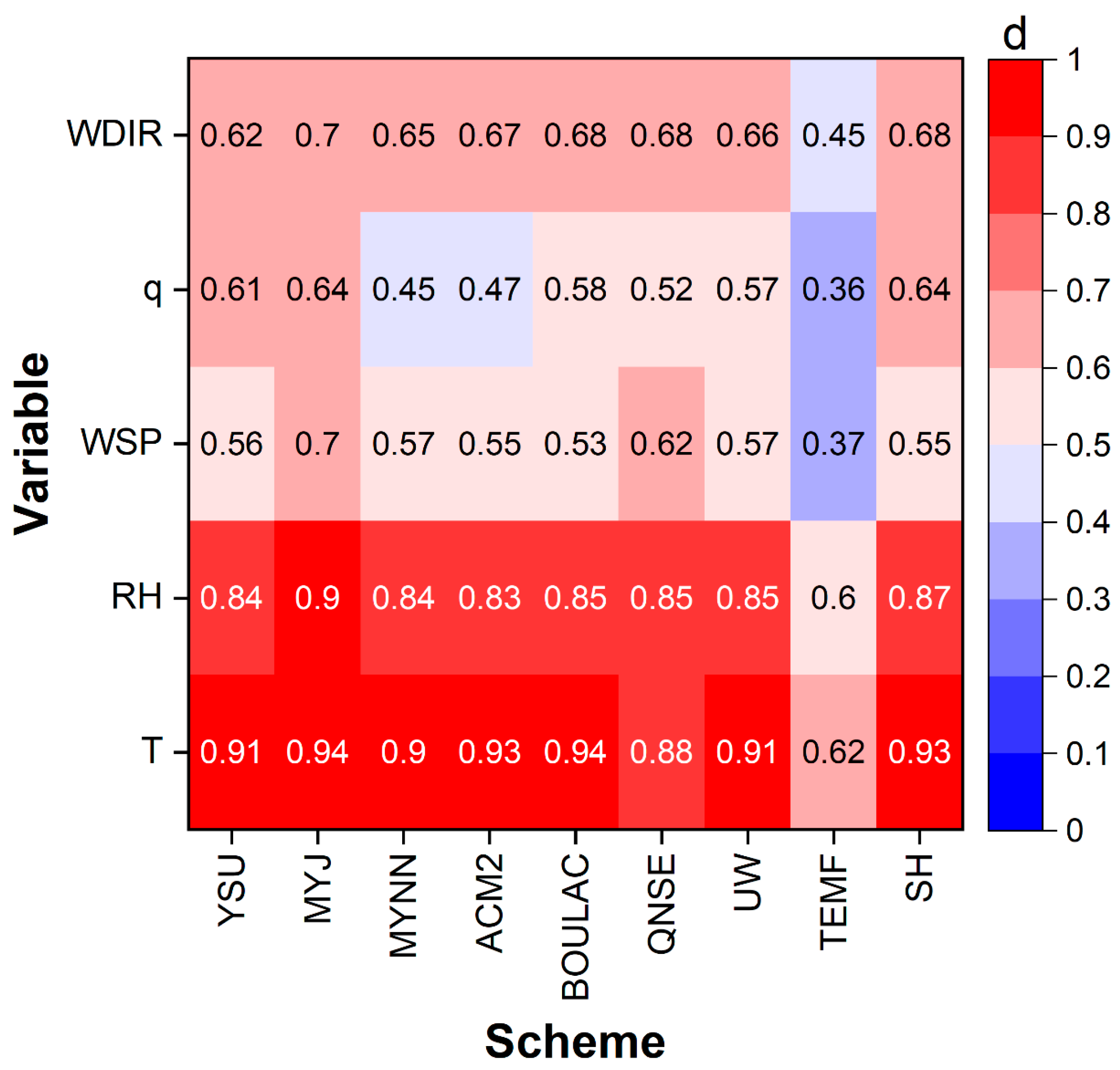
3.2.1. Conventional Meteorological Variables (T, RH, q, WSP, WDIR)
3.2.2. Unconventional Variables (H, LE, RN, DSR)
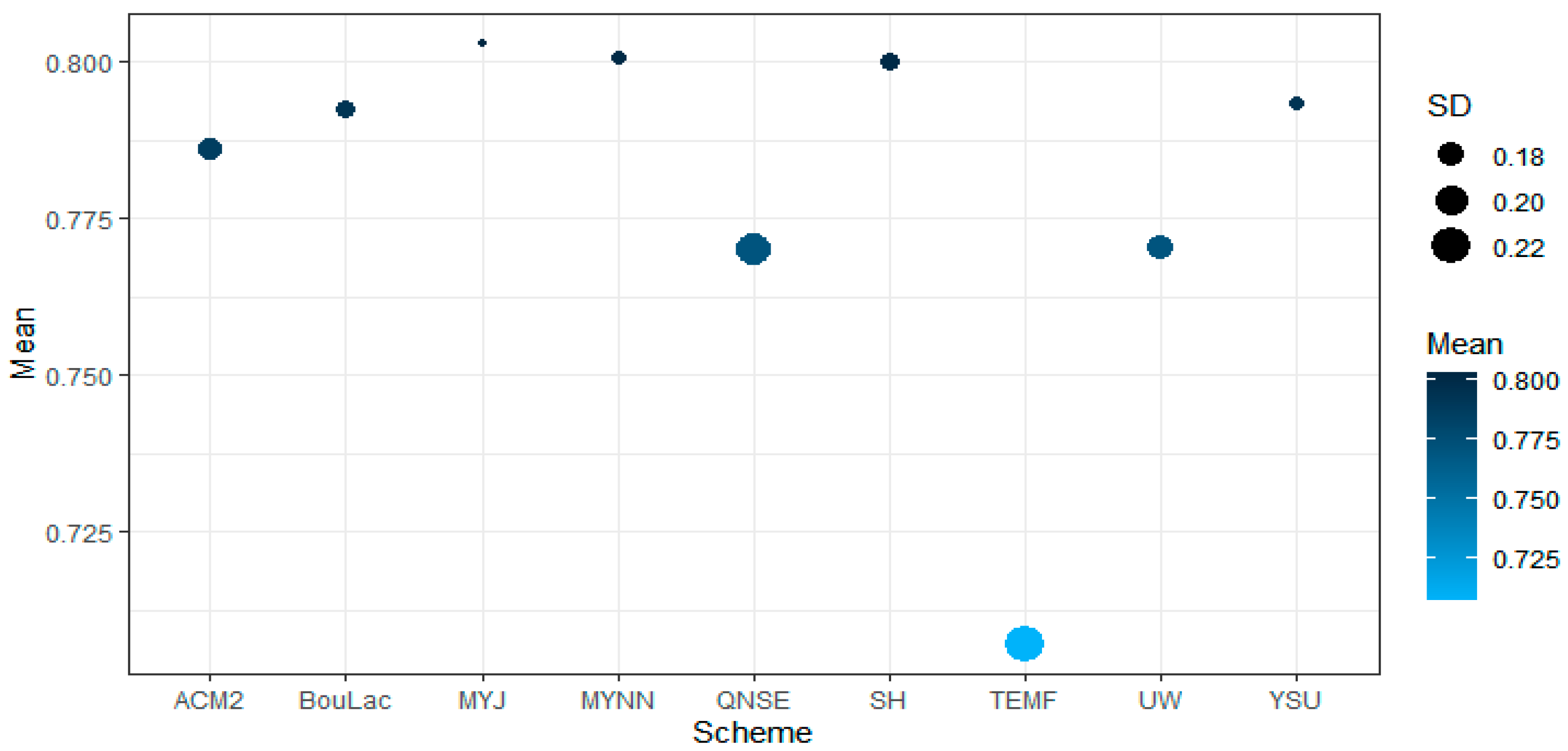
3.3. Summary of WRF Model Performance in the MRSP
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Statistical Parameters—Summer Field Campaign of 2013 (19–28 February) | |||||
|---|---|---|---|---|---|
| Conventional Variable | PBL Scheme | Suburban (IAG) | |||
| T (°C) | d | r | MBE (°C) | RMSE (°C) | |
| YSU | 0.91 | 0.87 | −0.65 | 1.91 | |
| MYJ | 0.94 | 0.89 | −0.27 | 1.68 | |
| MYNN | 0.90 | 0.87 | −0.83 | 2.00 | |
| ACM2 | 0.93 | 0.88 | 0.05 | 1.74 | |
| BouLac | 0.94 | 0.90 | 0.04 | 1.62 | |
| QNSE | 0.88 | 0.87 | −1.21 | 2.17 | |
| UW | 0.91 | 0.87 | −0.63 | 1.93 | |
| TEMF | 0.62 | 0.56 | −3.95 | 5.19 | |
| SH | 0.93 | 0.91 | −0.33 | 1.61 | |
| RH (%) | d | r | MBE (%) | RMSE (%) | |
| YSU | 0.84 | 0.75 | −2.25 | 10.57 | |
| MYJ | 0.90 | 0.85 | −3.75 | 9.11 | |
| MYNN | 0.84 | 0.76 | −6.30 | 12.24 | |
| ACM2 | 0.83 | 0.77 | −7.66 | 12.81 | |
| BouLac | 0.85 | 0.78 | −4.81 | 10.78 | |
| QNSE | 0.85 | 0.77 | −0.48 | 9.98 | |
| UW | 0.85 | 0.75 | −2.75 | 10.60 | |
| TEMF | 0.60 | 0.54 | −8.29 | 19.60 | |
| SH | 0.87 | 0.80 | −3.60 | 9.99 | |
| q (g kg−1) | d | r | MBE (g kg−1) | RMSE (g kg−1) | |
| YSU | 0.61 | 0.49 | −0.90 | 1.53 | |
| MYJ | 0.64 | 0.53 | −0.94 | 1.43 | |
| MYNN | 0.45 | 0.28 | −1.90 | 2.53 | |
| ACM2 | 0.47 | 0.24 | −1.48 | 2.13 | |
| BouLac | 0.58 | 0.37 | −0.82 | 1.53 | |
| QNSE | 0.52 | 0.31 | −1.00 | 1.69 | |
| UW | 0.57 | 0.42 | −1.01 | 1.58 | |
| TEMF | 0.36 | 0.31 | −1.88 | 2.59 | |
| SH | 0.64 | 0.53 | −0.91 | 1.46 | |
| WSP (m s−1) | d | r | MBE (m s−1) | RMSE (m s−1) | |
| YSU | 0.56 | 0.59 | 1.70 | 2.21 | |
| MYJ | 0.70 | 0.64 | 0.85 | 1.52 | |
| MYNN | 0.57 | 0.52 | 1.44 | 1.99 | |
| ACM2 | 0.55 | 0.59 | 1.82 | 2.28 | |
| BouLac | 0.53 | 0.51 | 1.70 | 2.26 | |
| QNSE | 0.62 | 0.61 | 1.30 | 1.83 | |
| UW | 0.57 | 0.56 | 1.49 | 2.18 | |
| TEMF | 0.37 | 0.35 | 1.66 | 2.70 | |
| SH | 0.55 | 0.52 | 1.63 | 2.14 | |
| WDIR (°) | d | r | MBE (°) | RMSE (°) | |
| YSU | 0.62 | 0.51 | −1.36 | 20.65 | |
| MYJ | 0.70 | 0.68 | 1.38 | 20.94 | |
| MYNN | 0.65 | 0.55 | −0.51 | 7.77 | |
| ACM2 | 0.67 | 0.57 | 10.59 | 160.27 | |
| BouLac | 0.68 | 0.62 | 8.11 | 122.79 | |
| QNSE | 0.68 | 0.63 | −0.13 | 2.04 | |
| UW | 0.66 | 0.60 | −2.66 | 40.25 | |
| TEMF | 0.45 | 0.23 | 11.54 | 174.61 | |
| SH | 0.68 | 0.65 | −1.94 | 29.38 | |
| Statistical Parameters—Summer Field Campaign of 2013 (19–28 February) | |||||
|---|---|---|---|---|---|
| Unconventional Variable | PBL Scheme | Suburban (IAG) | |||
| d | r | MBE (W m−2) | RMSE (W m−2) | ||
| H (W m−2) | YSU | 0.84 | 0.83 | 38.48 | 70.20 |
| MYJ | 0.86 | 0.87 | 42.63 | 66.54 | |
| MYNN | 0.93 | 0.83 | 12.80 | 40.07 | |
| ACM2 | 0.89 | 0.86 | 28.41 | 54.46 | |
| BouLac | 0.89 | 0.89 | 36.66 | 59.32 | |
| QNSE | 0.90 | 0.90 | 33.99 | 55.64 | |
| UW | 0.89 | 0.88 | 33.03 | 56.21 | |
| TEMF | 0.65 | 0.43 | −44.35 | 89.10 | |
| SH | 0.88 | 0.88 | 37.60 | 61.08 | |
| LE (W m−2) | YSU | 0.91 | 0.86 | −0.55 | 41.49 |
| MYJ | 0.91 | 0.85 | 1.94 | 42.57 | |
| MYNN | 0.89 | 0.81 | −6.40 | 42.68 | |
| ACM2 | 0.90 | 0.83 | −4.32 | 42.09 | |
| BouLac | 0.93 | 0.88 | 1.08 | 37.23 | |
| QNSE | 0.90 | 0.86 | 12.64 | 47.26 | |
| UW | 0.92 | 0.86 | −1.32 | 39.86 | |
| TEMF | 0.78 | 0.65 | −27.12 | 62.44 | |
| SH | 0.91 | 0.85 | −1.19 | 40.45 | |
| DSR (W m−2) | YSU | 0.92 | 0.86 | 42.55 | 198.75 |
| MYJ | 0.93 | 0.90 | 68.42 | 186.70 | |
| MYNN | 0.94 | 0.88 | −1.65 | 156.28 | |
| ACM2 | 0.94 | 0.88 | 30.55 | 166.70 | |
| BouLac | 0.94 | 0.89 | 38.28 | 171.90 | |
| QNSE | 0.94 | 0.90 | 53.60 | 174.85 | |
| UW | 0.94 | 0.89 | 34.57 | 173.69 | |
| TEMF | 0.84 | 0.57 | 88.37 | 205.19 | |
| SH | 0.94 | 0.91 | 51.06 | 165.77 | |
| RN (W m−2) | YSU | 0.91 | 0.84 | 18.09 | 156.55 |
| MYJ | 0.93 | 0.89 | 41.74 | 145.75 | |
| MYNN | 0.93 | 0.86 | −3.84 | 132.11 | |
| ACM2 | 0.93 | 0.86 | 6.63 | 136.97 | |
| BouLac | 0.93 | 0.87 | 14.11 | 136.85 | |
| QNSE | 0.93 | 0.89 | 39.56 | 144.38 | |
| UW | 0.93 | 0.87 | 14.10 | 139.57 | |
| TEMF | 0.75 | 0.59 | −83.81 | 229.26 | |
| SH | 0.94 | 0.89 | 21.42 | 133.54 | |
Appendix B
| Statistical Parameters—Winter Field Campaign of 2013 (6–15 August) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conventional Variable | PBL Scheme | ||||||||||||
| Suburban (IAG) | Urban (SFZ) | Rural (ITU) | |||||||||||
| T (°C) | d | r | MBE (°C) | RMSE (°C) | d | r | MBE (°C) | RMSE (°C) | d | r | MBE (°C) | RMSE (°C) | |
| YSU | 0.97 | 0.95 | 0.43 | 1.75 | 0.96 | 0.95 | 1.40 | 2.26 | 0.87 | 0.86 | 2.64 | 3.92 | |
| MYJ | 0.96 | 0.93 | −0.56 | 2.07 | 0.96 | 0.93 | 0.64 | 2.17 | 0.85 | 0.83 | 2.71 | 4.24 | |
| MYNN | 0.97 | 0.94 | −0.16 | 1.84 | 0.96 | 0.92 | 0.06 | 2.09 | 0.90 | 0.88 | 1.68 | 3.22 | |
| ACM2 | 0.97 | 0.95 | 0.35 | 1.73 | 0.96 | 0.95 | 1.33 | 2.21 | 0.88 | 0.88 | 2.67 | 3.83 | |
| BouLac | 0.95 | 0.94 | −0.86 | 2.13 | 0.94 | 0.94 | 1.97 | 2.69 | 0.84 | 0.83 | 3.13 | 4.47 | |
| QNSE | 0.97 | 0.95 | 0.20 | 1.83 | 0.95 | 0.93 | 1.09 | 2.25 | 0.85 | 0.85 | 2.96 | 4.19 | |
| UW | 0.97 | 0.95 | 0.33 | 1.73 | 0.95 | 0.94 | 1.37 | 2.28 | 0.87 | 0.85 | 2.71 | 4.05 | |
| TEMF | 0.92 | 0.89 | 1.43 | 2.95 | 0.89 | 0.88 | 2.41 | 3.57 | 0.80 | 0.82 | 3.94 | 5.19 | |
| SH | 0.97 | 0.95 | 0.46 | 1.82 | 0.95 | 0.94 | 1.42 | 2.29 | 0.87 | 0.85 | 2.53 | 3.93 | |
| RH (%) | d | r | MBE (%) | RMSE (%) | d | r | MBE (%) | RMSE (%) | d | r | MBE (%) | RMSE (%) | |
| YSU | 0.85 | 0.81 | −8.79 | 14.77 | 0.86 | 0.80 | −8.19 | 15.38 | 0.69 | 0.62 | −17.06 | 24.55 | |
| MYJ | 0.91 | 0.85 | −3.98 | 10.98 | 0.89 | 0.81 | −4.13 | 12.75 | 0.70 | 0.59 | −15.09 | 23.25 | |
| MYNN | 0.87 | 0.82 | −7.59 | 13.60 | 0.90 | 0.82 | −2.30 | 11.42 | 0.78 | 0.71 | −11.94 | 18.54 | |
| ACM2 | 0.84 | 0.83 | −10.63 | 15.62 | 0.85 | 0.82 | −9.67 | 15.76 | 0.68 | 0.65 | −19.39 | 26.04 | |
| BouLac | 0.91 | 0.84 | −2.70 | 10.05 | 0.84 | 0.80 | −9.70 | 15.97 | 0.67 | 0.57 | −17.71 | 26.16 | |
| QNSE | 0.88 | 0.83 | −6.50 | 12.48 | 0.89 | 0.82 | −5.63 | 13.14 | 0.71 | 0.65 | −16.45 | 23.45 | |
| UW | 0.88 | 0.84 | −7.95 | 13.39 | 0.87 | 0.81 | −7.33 | 14.31 | 0.70 | 0.62 | −15.77 | 23.69 | |
| TEMF | 0.82 | 0.73 | −7.66 | 15.62 | 0.87 | 0.78 | −4.63 | 13.85 | 0.69 | 0.57 | −13.93 | 23.59 | |
| SH | 0.85 | 0.82 | −9.41 | 14.84 | 0.86 | 0.81 | −8.60 | 15.17 | 0.69 | 0.60 | −16.67 | 24.66 | |
| q (g kg−1) | d | r | MBE (g kg−1) | RMSE (g kg−1) | d | r | MBE (g kg−1) | RMSE (g kg−1) | d | r | MBE (g kg−1) | RMSE (g kg−1) | |
| YSU | 0.68 | 0.57 | −1.13 | 1.81 | 0.72 | 0.54 | −0.62 | 1.53 | 0.64 | 0.43 | −0.70 | 1.96 | |
| MYJ | 0.69 | 0.54 | −0.95 | 1.74 | 0.73 | 0.55 | −0.37 | 1.45 | 0.66 | 0.48 | −0.37 | 1.77 | |
| MYNN | 0.69 | 0.59 | −1.22 | 1.83 | 0.79 | 0.63 | −0.33 | 1.31 | 0.69 | 0.52 | −0.47 | 1.74 | |
| ACM2 | 0.65 | 0.58 | −1.44 | 1.99 | 0.71 | 0.55 | −0.87 | 1.63 | 0.58 | 0.33 | −1.04 | 2.20 | |
| BouLac | 0.77 | 0.68 | −0.84 | 1.48 | 0.72 | 0.52 | −0.51 | 1.54 | 0.60 | 0.38 | −0.57 | 1.97 | |
| QNSE | 0.74 | 0.62 | −0.86 | 1.60 | 0.78 | 0.62 | −0.35 | 1.33 | 0.61 | 0.39 | −0.42 | 1.90 | |
| UW | 0.70 | 0.60 | −1.06 | 1.70 | 0.74 | 0.58 | −0.49 | 1.42 | 0.64 | 0.44 | −0.53 | 1.86 | |
| TEMF | 0.77 | 0.63 | −0.31 | 1.62 | 0.78 | 0.67 | 0.54 | 1.52 | 0.64 | 0.41 | 0.48 | 2.02 | |
| SH | 0.69 | 0.59 | −1.17 | 1.81 | 0.73 | 0.56 | −0.64 | 1.51 | 0.66 | 0.45 | −0.71 | 1.93 | |
| WSP (m s−1) | d | r | MBE (m s−1) | RMSE (m s−1) | d | r | MBE (m s−1) | RMSE (m s−1) | d | r | MBE (m s−1) | RMSE (m s−1) | |
| SU | 0.57 | 0.57 | 1.92 | 2.68 | 0.71 | 0.58 | 0.67 | 2.28 | 0.27 | 0.39 | 3.78 | 4.24 | |
| MYJ | 0.72 | 0.70 | 0.99 | 1.89 | 0.74 | 0.57 | −0.30 | 2.10 | 0.24 | 0.34 | 4.24 | 4.75 | |
| MYNN | 0.62 | 0.67 | 1.77 | 2.44 | 0.72 | 0.54 | 0.35 | 2.07 | 0.27 | 0.46 | 4.30 | 4.70 | |
| ACM2 | 0.57 | 0.60 | 2.08 | 2.71 | 0.73 | 0.59 | 0.71 | 2.17 | 0.29 | 0.52 | 3.99 | 4.38 | |
| BouLac | 0.59 | 0.57 | 1.81 | 2.47 | 0.71 | 0.58 | 0.84 | 2.28 | 0.27 | 0.39 | 3.76 | 4.25 | |
| QNSE | 0.70 | 0.70 | 1.22 | 1.99 | 0.77 | 0.63 | −0.04 | 1.90 | 0.24 | 0.38 | 4.54 | 5.00 | |
| UW | 0.62 | 0.65 | 1.70 | 2.42 | 0.75 | 0.64 | 0.52 | 2.12 | 0.26 | 0.34 | 3.72 | 4.24 | |
| TEMF | 0.54 | 0.53 | 1.64 | 2.72 | 0.74 | 0.58 | −0.20 | 1.89 | 0.23 | 0.28 | 4.43 | 5.06 | |
| SH | 0.57 | 0.57 | 1.94 | 2.68 | 0.72 | 0.58 | 0.65 | 2.23 | 0.27 | 0.39 | 3.74 | 4.22 | |
| WDIR (°) | d | r | MBE (°) | RMSE (°) | d | r | MBE (°) | RMSE (°) | d | r | MBE (°) | RMSE (°) | |
| YSU | 0.76 | 0.57 | −8.55 | 136.00 | 0.62 | 0.51 | −19.23 | 126.01 | 0.51 | 0.23 | −14.58 | 141.22 | |
| MYJ | 0.74 | 0.56 | −7.74 | 123.05 | 0.64 | 0.57 | −21.87 | 125.70 | 0.49 | 0.21 | −15.36 | 138.63 | |
| MYNN | 0.76 | 0.52 | −3.36 | 53.43 | 0.61 | 0.52 | −18.57 | 123.99 | 0.49 | 0.17 | −12.97 | 139.14 | |
| ACM2 | 0.80 | 0.74 | −6.91 | 109.92 | 0.60 | 0.45 | −19.89 | 125.58 | 0.50 | 0.18 | −14.06 | 138.07 | |
| BouLac | 0.83 | 0.65 | −7.45 | 118.42 | 0.60 | 0.51 | −16.64 | 126.98 | 0.48 | 0.16 | −14.17 | 144.85 | |
| QNSE | 0.79 | 0.73 | −10.48 | 166.77 | 0.66 | 0.56 | −23.53 | 124.25 | 0.50 | 0.21 | −20.49 | 136.75 | |
| UW | 0.77 | 0.71 | −6.28 | 99.91 | 0.65 | 0.55 | −19.42 | 125.19 | 0.46 | 0.10 | −10.07 | 144.88 | |
| TEMF | 0.65 | 0.49 | 3.80 | 60.42 | 0.67 | 0.56 | −17.41 | 128.81 | 0.46 | 0.22 | −3.61 | 152.73 | |
| SH | 0.78 | 0.66 | −7.33 | 116.67 | 0.62 | 0.53 | −19.03 | 126.89 | 0.49 | 0.19 | −13.36 | 140.56 | |
| Statistical Parameter—Winter Field Campaign of 2013 (6–15 August) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unconventional Variable | PBL Scheme | Suburban (IAG) | Urban (SFZ) | Rural (ITU) | |||||||||
| d | r | MBE (Wm−2) | RMSE (Wm−2) | d | r | MBE (Wm−2) | RMSE (Wm−2) | d | r | MBE (W m−2) | RMSE (W m−2) | ||
| c (W m−2) | YSU | 0.93 | 0.87 | 6.11 | 37.83 | 0.79 | 0.68 | 8.09 | 56.62 | 0.95 | 0.92 | 16.15 | 46.07 |
| MYJ | 0.93 | 0.87 | 9.65 | 38.66 | 0.79 | 0.67 | 9.33 | 56.29 | 0.94 | 0.91 | 26.25 | 55.86 | |
| MYNN | 0.93 | 0.88 | 1.20 | 36.15 | 0.76 | 0.65 | 8.64 | 60.26 | 0.94 | 0.92 | 28.22 | 54.69 | |
| ACM2 | 0.94 | 0.89 | 4.63 | 34.26 | 0.76 | 0.65 | 7.32 | 59.78 | 0.96 | 0.93 | 13.40 | 41.57 | |
| BouLac | 0.94 | 0.90 | 5.54 | 34.32 | 0.78 | 0.67 | 7.20 | 57.32 | 0.94 | 0.91 | 14.38 | 47.95 | |
| QNSE | 0.94 | 0.88 | −1.01 | 34.89 | 0.80 | 0.69 | 5.91 | 53.15 | 0.94 | 0.92 | 27.11 | 58.37 | |
| UW | 0.94 | 0.89 | 6.19 | 34.81 | 0.76 | 0.65 | 10.68 | 60.32 | 0.95 | 0.91 | 13.20 | 46.24 | |
| TEMF | 0.85 | 0.82 | −18.84 | 47.59 | 0.82 | 0.69 | −4.33 | 46.88 | 0.93 | 0.88 | 14.51 | 53.88 | |
| SH | 0.94 | 0.88 | 6.05 | 36.64 | 0.79 | 0.69 | 8.00 | 56.31 | 0.95 | 0.91 | 16.25 | 47.99 | |
| LE (W m−2) | YSU | 0.70 | 0.85 | 23.56 | 45.54 | 0.58 | 0.42 | 6.40 | 22.21 | 0.88 | 0.91 | −20.77 | 35.93 |
| MYJ | 0.68 | 0.85 | 26.50 | 50.03 | 0.58 | 0.44 | 7.64 | 23.57 | 0.88 | 0.90 | −18.97 | 35.51 | |
| MYNN | 0.65 | 0.84 | 29.47 | 54.15 | 0.59 | 0.45 | 6.80 | 22.31 | 0.88 | 0.92 | −19.77 | 35.18 | |
| ACM2 | 0.69 | 0.84 | 25.29 | 48.01 | 0.58 | 0.43 | 6.65 | 22.63 | 0.89 | 0.90 | −18.89 | 35.24 | |
| BouLac | 0.68 | 0.83 | 25.17 | 48.39 | 0.58 | 0.44 | 7.48 | 22.84 | 0.89 | 0.90 | −18.15 | 34.81 | |
| QNSE | 0.62 | 0.85 | 33.77 | 59.04 | 0.53 | 0.44 | 11.00 | 27.31 | 0.91 | 0.90 | −13.66 | 31.63 | |
| UW | 0.70 | 0.85 | 23.73 | 46.06 | 0.58 | 0.43 | 6.61 | 22.48 | 0.87 | 0.90 | −20.82 | 36.83 | |
| TEMF | 0.56 | 0.78 | 37.95 | 67.83 | 0.47 | 0.39 | 12.81 | 29.42 | 0.89 | 0.88 | −13.44 | 34.30 | |
| SH | 0.70 | 0.85 | 24.54 | 46.28 | 0.58 | 0.43 | 6.48 | 22.12 | 0.88 | 0.91 | −20.55 | 35.96 | |
| d | r | MBE (W m−2) | RMSE (W m−2) | d | r | MBE (W m−2) | RMSE (W m−2) | d | r | MBE (W m−2) | RMSE (W m−2) | ||
| DSR (W m−2) | YSU | 0.96 | 0.95 | 44.92 | 109.38 | 0.94 | 0.94 | 62.50 | 130.03 | 0.92 | 0.89 | 64.34 | 147.29 |
| MYJ | 0.96 | 0.95 | 47.95 | 111.33 | 0.94 | 0.94 | 61.82 | 130.89 | 0.92 | 0.89 | 63.03 | 149.32 | |
| MYNN | 0.97 | 0.95 | 35.53 | 98.80 | 0.95 | 0.95 | 42.49 | 109.26 | 0.96 | 0.94 | 43.35 | 103.49 | |
| ACM2 | 0.96 | 0.96 | 43.26 | 100.19 | 0.95 | 0.95 | 58.82 | 118.65 | 0.93 | 0.90 | 59.64 | 140.09 | |
| BouLac | 0.97 | 0.96 | 28.18 | 86.75 | 0.93 | 0.94 | 64.14 | 132.48 | 0.90 | 0.85 | 67.26 | 168.77 | |
| QNSE | 0.96 | 0.95 | 45.86 | 108.84 | 0.93 | 0.94 | 62.72 | 131.68 | 0.90 | 0.86 | 66.90 | 164.91 | |
| UW | 0.96 | 0.95 | 46.84 | 109.98 | 0.93 | 0.94 | 63.97 | 134.24 | 0.90 | - | 64.46 | 169.75 | |
| TEMF | 0.93 | 0.88 | 19.56 | 133.11 | 0.91 | 0.87 | 39.53 | 147.39 | 0.90 | 0.84 | 66.46 | 169.76 | |
| SH | 0.97 | 0.96 | 44.48 | 100.36 | 0.94 | 0.94 | 60.98 | 130.99 | 0.93 | 0.90 | 59.58 | 141.97 | |
| RN (W m−2) | YSU | 0.97 | 0.95 | 10.16 | 68.05 | 0.94 | 0.94 | 31.30 | 91.86 | 0.93 | 0.91 | −31.84 | 90.44 |
| MYJ | 0.97 | 0.95 | 21.14 | 73.06 | 0.93 | 0.94 | 39.96 | 99.94 | 0.94 | 0.90 | −28.35 | 90.17 | |
| MYNN | 0.97 | 0.96 | 7.11 | 66.44 | 0.94 | 0.94 | 28.71 | 87.45 | 0.95 | 0.95 | −39.09 | 81.38 | |
| ACM2 | 0.98 | 0.96 | 4.83 | 62.82 | 0.95 | 0.95 | 25.40 | 85.88 | 0.94 | 0.92 | −37.71 | 89.15 | |
| BouLac | 0.98 | 0.96 | 7.62 | 57.15 | 0.94 | 0.94 | 32.81 | 92.48 | 0.93 | 0.89 | −28.35 | 95.23 | |
| QNSE | 0.97 | 0.95 | 22.45 | 76.20 | 0.93 | 0.94 | 44.31 | 104.71 | 0.94 | 0.90 | −23.58 | 91.03 | |
| UW | 0.97 | 0.95 | 9.85 | 70.62 | 0.94 | 0.93 | 31.31 | 95.98 | 0.93 | - | −36.00 | 93.07 | |
| TEMF | 0.94 | 0.89 | 0.62 | 96.13 | 0.91 | 0.87 | 25.47 | 113.27 | 0.92 | 0.87 | −22.67 | 100.10 | |
| SH | 0.98 | 0.96 | 8.42 | 63.29 | 0.94 | 0.94 | 30.03 | 92.51 | 0.93 | 0.92 | −35.78 | 90.66 | |
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; 666p. [Google Scholar]
- Stensrud, D.J. Parameterization Schemes: Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2007; 459p. [Google Scholar]
- Braun, S.A.; Tao, W.-K. Sensitivity of High-Resolution Simulations of Hurricane Bob (1991) to Planetary Boundary Layer Parameterizations. Mon. Weather Rev. 2000, 128, 3941–3961. [Google Scholar] [CrossRef]
- Li, X.; Pu, Z. Sensitivity of Numerical Simulation of Early Rapid Intensification of Hurricane Emily (2005) to Cloud Microphysical and Planetary Boundary Layer Parameterizations. Mon. Weather Rev. 2008, 136, 4819–4838. [Google Scholar] [CrossRef]
- Cohen, A.E.; Cavallo, S.M.; Coniglio, M.C.; Brooks, H.E. A Review of Planetary Boundary Layer Parameterization Schemes and Their Sensitivity in Simulating Southeastern U.S. Cold Season Severe Weather Environments. Weather Forecast. 2015, 30, 591–612. [Google Scholar] [CrossRef]
- Seaman, N.L. Meteorological modeling for air-quality assessments. Atmos. Environ. 2000, 34, 2231–2259. [Google Scholar] [CrossRef]
- Bossioli, E.; Tombrou, M.; Dandou, A.; Athanasopoulou, E.; Varotsos, K.V. The Role of Planetary Boundary-Layer Parameterizations in the Air Quality of an Urban Area with Complex Topography. Bound.-Layer Meteorol. 2009, 131, 53–72. [Google Scholar] [CrossRef]
- Banks, R.F.; Tiana-Alsina, J.; Baldasano, J.M.; Rocadenbosch, F.; Papayannis, A.; Solomos, S.; Tzanis, C.G. Sensitivity of boundary-layer variables to PBL schemes in the WRF model based on surface meteorological observations, lidar, and radiosondes during the HygrA-CD campaign. Atmos. Res. 2016, 176–177, 185–201. [Google Scholar] [CrossRef]
- Avolio, E.; Federico, S.; Migliettac, M.; Lo Feudo, T.; Calidonnaa, C.R.; Semprevivad, A.M. Sensitivity analysis of WRF model PBL schemes in simulating boundary-layer variables in southern Italy: An experimental campaign. Atmos. Res. 2017, 192, 58–71. [Google Scholar] [CrossRef]
- Holton, J.R. Introduction to Dynamic Meteorology, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2004; p. 535. [Google Scholar]
- Cheng, F.; Chin, S.C.; Liu, T.H. The role of boundary layer schemes in meteorological and air quality simulations of the Taiwan area. Atmos. Environ. 2012, 54, 714–727. [Google Scholar] [CrossRef]
- Wang, W.; Shen, X.; Huang, W. A Comparison of Boundary-Layer Characteristics Simulated Using Different Parametrization Schemes. Bound.-Layer Meteorol. 2016, 161, 375–403. [Google Scholar] [CrossRef]
- Jia, W.; Zhang, X. The role of the planetary boundary layer parameterization schemes on the meteorological and aerosol pollution simulations: A review. Atmos. Res. 2020, 239, 104890. [Google Scholar] [CrossRef]
- Banks, R.F.; Tiana-Alsina, J.; Rocadenbosch, F.; Baldasano, J.M. Performance Evaluation of the Boundary-Layer Height from Lidar and the Weather Research and Forecasting Model at an Urban Coastal Site in the North-East Iberian Peninsula. Bound.-Layer Meteorol. 2015, 157, 265–292. [Google Scholar] [CrossRef]
- Boadh, R.; Satyanarayana, A.N.V.; Rama Krishna, T.V.B.P.S.; Madala, S. Sensitivity of PBL schemes of the WRF-ARW model in simulating the boundary layer flow parameters for its application to air pollution dispersion modeling over a tropical station. Atmosfera 2016, 29, 61–81. [Google Scholar]
- Sathyanadh, A.; Prabhab, T.V.; Balajib, B.; Resmib, E.A.; Karipot, A. Evaluation of WRF PBL parameterization schemes against direct observations during a dry event over the Ganges valley. Atmos. Res. 2017, 193, 125–141. [Google Scholar] [CrossRef]
- Imran, H.M.; Kala, J.; Ng, A.W.M.; Muthukumaran, S. An evaluation of the performance of a WRF multi-physics ensemble for heatwave events over the city of Melbourne in southeast Australia. Clim. Dyn. 2018, 50, 2553–2586. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.M. Evaluating the performance of WRF urban schemes and PBL schemes over Dallas Fort Worth during a dry summer and a wet summer. J. Appl. Meteorol. Clim. 2021, 60, 779–798. [Google Scholar] [CrossRef]
- Hu, X.M.; Nielsen-Gammon, J.W.; Zhang, F. Evaluation of Three Planetary Boundary Layer Schemes in the WRF Model. J. Appl. Meteorol. Clim. 2010, 49, 1831–1844. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.-Y. Intercomparison of Planetary Boundary-Layer Parametrizations in the WRF Model for a Single Day from CASES-99. Bound.-Layer Meteorol. 2011, 139, 261–281. [Google Scholar] [CrossRef]
- Coniglio, M.C.; Correia, J., Jr.; Marsh, P.T.; Kong, F. Verification of convection-allowing WRF Model forecasts of the planetary boundary layer using sounding observations. Weather Forecast. 2013, 28, 842–862. [Google Scholar] [CrossRef]
- Kim, Y.; Sartelet, K.; Raut, J.C.; Chazette, P. Evaluation of the Weather Research and Forecast/Urban Model Over Greater Paris. Bound.-Layer Meteorol. 2013, 149, 105–132. [Google Scholar] [CrossRef]
- Draxl, C.; Hahmann, A.N.; Peña, A.; Giebel, G. Evaluating winds and vertical wind shear from Weather Research and Forecasting model forecasts using seven planetary boundary layer schemes. Wind Energy 2014, 17, 39–55. [Google Scholar] [CrossRef]
- Ferrero, E.; Vandenberghe, F.; Alessandrini, S.; Mortarini, L. Comparison of WRF PBL models in low-wind speed conditions against measured data. In Air Pollution Modeling and Its Application XXV; Springer International Publishing: Cham, Switzerland, 2018; Volume 35, pp. 129–134. [Google Scholar]
- Tyagi, B.; Magliulo, V.; Finardi, S.; Gasbarra, D.; Carlucci, P.; Toscano, P.; Zaldei, A.; Riccio, A.; Calori, G.; D’allura, A.; et al. Performance Analysis of Planetary Boundary Layer Parameterization Schemes in WRF Modeling Set Up over Southern Italy. Atmosphere 2018, 9, 272. [Google Scholar] [CrossRef]
- Hu, X.-M.; Ma, Z.; Lin, W.; Zhang, H.; Hu, J.; Wang, Y.; Xu, X.; Fuentes, J.D.; Xue, M. Impact of the Loess Plateau on the atmospheric boundary layer structure and air quality in the North China Plain: A case study. Sci. Total. Environ. 2014, 499, 228–237. [Google Scholar] [CrossRef] [PubMed]
- Penchah, M.; Malakooti, H.; Satkin, M. Evaluation of planetary boundary layer simulations for wind resource study in east of Iran. Renew. Energy 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Tymvios, F.; Charalambous, D.; Michaelides, S.; Lelieveld, J. Intercomparison of boundary layer parameterizations for summer conditions in the eastern Mediterranean island of Cyprus using the WRF–ARW model. Atmos. Res. 2017, 208, 45–59. [Google Scholar] [CrossRef]
- Huang, M.; Gao, Z.; Miao, S.; Chen, F. Sensitivity of urban boundary layer simulation to urban canopy models and PBL schemes in Beijing. Meteorog. Atmos. Phys. 2019, 131, 1235–1248. [Google Scholar] [CrossRef]
- Oliveira, A.P.; Marques Filho, E.P.; Ferreira, M.J.; Codato, G.; Ribeiro, F.N.D.; Landulfo, E.; Moreira, G.A.; Pereira, M.M.R.; Mlakar, P.; Boznar, M.Z.; et al. Assessing urban effects on the climate of metropolitan regions of Brazil–Preliminary results of the MCITY BRAZIL project. Explor. Environ. Sci. Res. 2020, 1, 38–77. [Google Scholar] [CrossRef]
- IBGE. Demographics Censuses. Available online: http://www.ibge.gov.br/english/ (accessed on 20 April 2024).
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; De Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2014, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, M.P.; Oliveira, A.P.; Varona, R.P.; Tito, J.V.; Codato, G.; Ribeiro, F.N.D.; Marques Filho, E.P.; Silveira, L.C. Radiosonde based analysis of the urban boundary layer in the metropolitan region of São Paulo, Brazil. Earth Space Sci. 2020, 7, e2019EA000781. [Google Scholar] [CrossRef]
- Oliveira, A.P.; Bornstein, R.D.; Soares, J. Annual and Diurnal Wind Patterns in the City of São Paulo. Water Air Soil Pollut. Focus 2003, 3, 3–15. [Google Scholar] [CrossRef]
- Sánchez, M.P.; Oliveira, A.P.; Varona, R.P.; Tito, J.V.; Codato, G.; Ynoue, R.Y. Observational investigation of the low-level jets in the metropolitan region of São Paulo, Brazil. Earth and Space Science 2022, 9, e2021EA002190. [Google Scholar] [CrossRef]
- Silveira, L.C.; Oliveira, A.P.; Sánchez, M.P.; Codato, G.; Ferreira, M.J.; Marques Filho, E.P.; Božnar, M.Z.; Mlakar, P. Observational Investigation of the Statistical Properties of Surface-Layer Turbulence in a Suburban Area of São Paulo, Brazil: Objective Analysis of Scaling-Parameter Accuracy and Uncertainties. Bound. Layer Meteorol. 2022, 185, 161–195. [Google Scholar] [CrossRef]
- Ribeiro, F.N.D.; Oliveira, A.P.; Soares, J.; Miranda, R.M.; Barlage, M.; Chen, F. Effect of sea breeze propagation on the urban boundary layer of the metropolitan region of Sao Paulo, Brazil. Atmos. Res. 2018, 214, 174–188. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gil, D.A.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A description of the advanced research WRF version 3. NCAR Tech. Note 2008, 475, 113. [Google Scholar]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. Q. J. R. Meteorol. Soc. 2008, 113, D13. [Google Scholar] [CrossRef]
- Arakawa, A. The Cumulus Parameterization Problem: Past, Present, and Future. J. Clim. 2004, 17, 2493–2525. [Google Scholar] [CrossRef]
- Mukul Tewari, N.C.A.R.; Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; et al. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 10–15 January 2004; pp. 11–15. [Google Scholar]
- Kusaka, H.; Kimura, F. Coupling a Single-Layer Urban Canopy Model with a Simple Atmospheric Model: Impact on Urban Heat Island Simulation for an Idealized Case. J. Meteorol. Soc. Jpn. 2004, 82, 67–80. [Google Scholar] [CrossRef]
- Kusaka, H.; Kondo, H.; Kikegawa, Y.; Kimura, F. A simple single-layer urban canopy model for atmospheric models: Comparison with multi-layer and slab models. Bound.-Layer Meteorol. 2001, 101, 329–358. [Google Scholar] [CrossRef]
- Vahmani, P.; Hogue, T.S. Incorporating an Urban Irrigation Module into the Noah Land Surface Model Coupled with an Urban Canopy Model. J. Hydrometeorol. 2014, 15, 1440–1456. [Google Scholar] [CrossRef]
- Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar]
- Brousse, O.; Martilli, A.; Foley, M.; Mills, G.; Bechtel, B. WUDAPT, an efficient land use producing data tool for mesoscale models? Integration of urban LCZ in WRF over Madrid. Urban Clim. 2016, 17, 116–134. [Google Scholar] [CrossRef]
- Dzebre, D.F.; Adaramola, M.S. A preliminary sensitivity study of Planetary Boundary Layer parameterization schemes in the weather research and forecasting model to surface winds in coastal Ghana. Renew. Energy 2020, 146, 66–86. [Google Scholar] [CrossRef]
- Janjic, Z.I. Nonsingular implementation of the Mellor–Yamada level 2.5 scheme in the NCEP meso model. NCEP Off. Note 2002, 437, 61. [Google Scholar]
- Janjić, Z.I. The Step-Mountain Coordinate: Physical Package. Mon. Weather Rev. 1990, 118, 1429–1443. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An Improved Mellor-Yamada Level-3 Model: Its Numerical Stability and Application to a Regional Prediction of Advection Fog. Bound.-Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Sukoriansky, S.; Galperin, B.; Perov, V. ‘Application of a New Spectral Theory of Stably Stratified Turbulence to the Atmospheric Boundary Layer over Sea Ice’. Bound.-Layer Meteorol. 2005, 117, 231–257. [Google Scholar] [CrossRef]
- Kosović, B.; Curry, J.A. A Large Eddy Simulation Study of a Quasi-Steady, Stably Stratified Atmospheric Boundary Layer. J. Atmos. Sci. 2000, 57, 1052–1068. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Park, S. A New Moist Turbulence Parameterization in the Community Atmosphere Model. J. Clim. 2009, 22, 3422–3448. [Google Scholar] [CrossRef]
- Yang, Q.; Berg, L.K.; Pekour, M.; Fast, J.D.; Newsom, R.K.; Stoelinga, M.; Finley, C. Evaluation of WRF-Predicted Near-Hub-Height Winds and Ramp Events over a Pacific Northwest Site with Complex Terrain. J. Appl. Meteorol. Clim. 2013, 52, 1753–1763. [Google Scholar] [CrossRef]
- Chadee, X.T.; Seegobin, N.R.; Clarke, R.M. Optimizing the Weather Research and Forecasting (WRF) Model for Mapping the Near-Surface Wind Resources over the Southernmost Caribbean Islands of Trinidad and Tobago. Energies 2017, 10, 931. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of orography-induced turbulences in a mesobeta-scale model. Mon. Weather Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
- Martilli, A.; Clappier, A.; Rotach, M.W. An Urban Surface Exchange Parameterization for Mesoscale Models. Bound.-Layer Meteorol. 2002, 104, 261–304. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Hong, S.Y. A new stable boundary-layer mixing scheme and its impact on the simulated East Asian summer monsoon. Q. J. R. Meteorol. Soc. 2010, 136, 1481–1496. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.Y. Representation of the Subgrid-Scale Turbulent Transport in Convective Boundary Layers at Gray-Zone Resolutions. Mon. Weather Rev. 2015, 143, 250–271. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.-Y. Analysis of Resolved and Parameterized Vertical Transports in Convective Boundary Layers at Gray-Zone Resolutions. J. Atmos. Sci. 2013, 70, 3248–3261. [Google Scholar] [CrossRef]
- Fiori, E.; Parodi, A.; Siccardi, F. Turbulence Closure Parameterization and Grid Spacing Effects in Simulated Supercell Storms. J. Atmos. Sci. 2010, 67, 3870–3890. [Google Scholar] [CrossRef]
- Catalano, F.; Moeng, C. Large-Eddy Simulation of the Daytime Boundary Layer in an Idealized Valley Using the Weather Research and Forecasting Numerical Model. Bound.-Layer Meteorol. 2010, 137, 49–75. [Google Scholar] [CrossRef]
- Pleim, J.E. A Combined Local and Nonlocal Closure Model for the Atmospheric Boundary Layer. Part I: Model Description and Testing. J. Appl. Meteorol. Climatol. 2007, 46, 1383–1395. [Google Scholar] [CrossRef]
- Pleim, J.E. A Combined Local and Nonlocal Closure Model for the Atmospheric Boundary Layer. Part II: Application and Evaluation in a Mesoscale Meteorological Model. J. Appl. Meteorol. Clim. 2007, 46, 1396–1409. [Google Scholar] [CrossRef]
- Angevine, W.M.; Jiang, H.; Mauritsen, T. Performance of an Eddy Diffusivity–Mass Flux Scheme for Shallow Cumulus Boundary Layers. Mon. Weather Rev. 2010, 138, 2895–2912. [Google Scholar] [CrossRef]
- Mauritsen, T.; Svensson, G. Observations of Stably Stratified Shear-Driven Atmospheric Turbulence at Low and High Richardson Numbers. J. Atmos. Sci. 2007, 64, 645–655. [Google Scholar] [CrossRef]
- Ooi, M.C.G.; Chan, A.; Kumarenthiran, S.; Morris, K.I.; Oozeer, M.Y.; Slam, M.A.; Salleh, S.A. Comparison of WRF local and nonlocal boundary layer Physics in Greater Kuala Lumpur, Malaysia. IOP Conf. Ser. Earth Environ. Sci. 2018, 117, 012015. [Google Scholar] [CrossRef]
- Reames, L.J.; Stensrud, D.J. Sensitivity of Simulated Urban–Atmosphere Interactions in Oklahoma City to Urban Parameterization. J. Appl. Meteorol. Clim. 2017, 5, 1405–1430. [Google Scholar] [CrossRef]
- Hu, X.-M.; Xue, M. Influence of Synoptic Sea-Breeze Fronts on the Urban Heat Island Intensity in Dallas–Fort Worth, Texas. Mon. Weather Rev. 2016, 144, 1487–1507. [Google Scholar] [CrossRef]

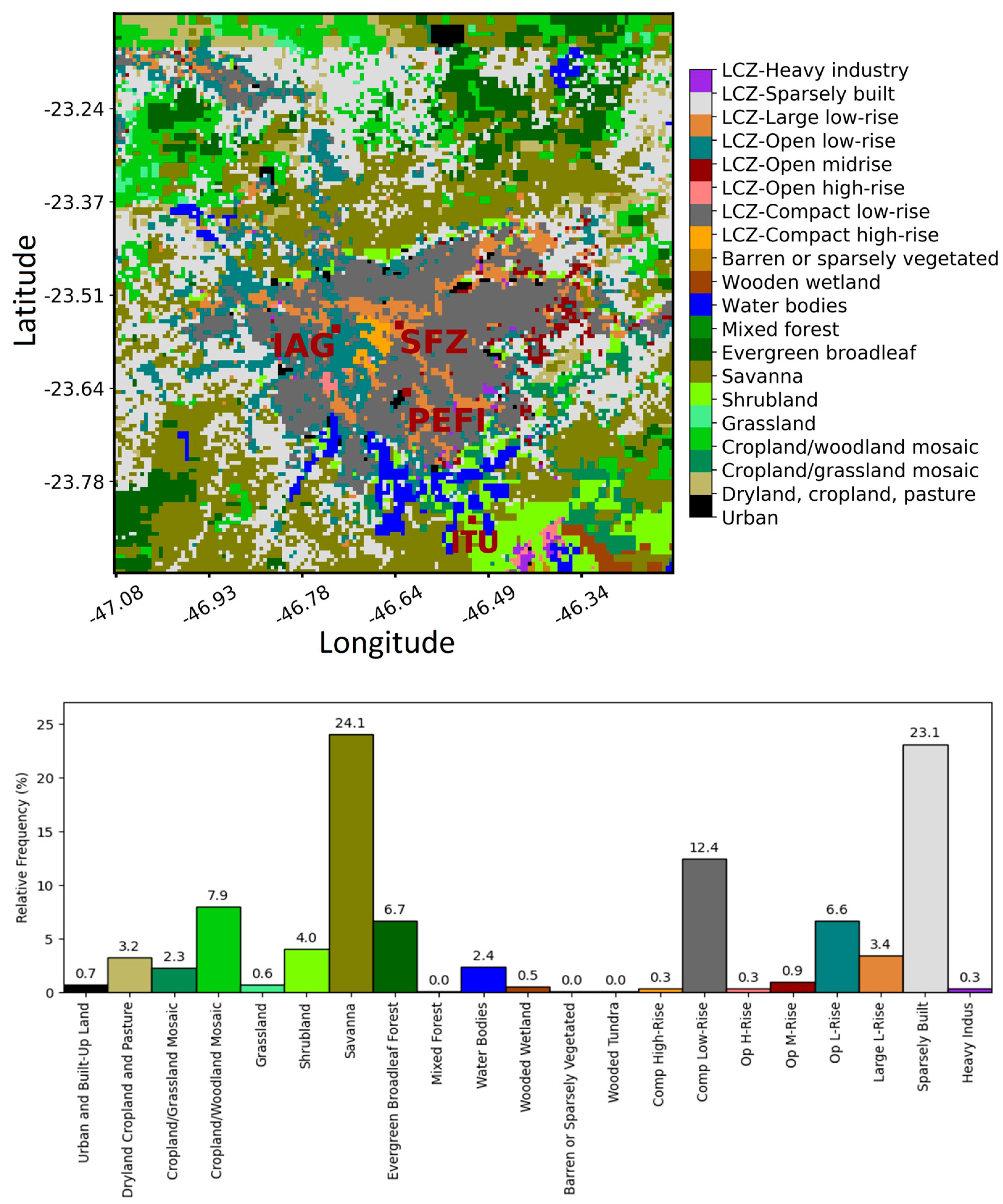


| Site | Geographic Position | Elevation (m asl) # | Period * | Sensor and Apparatus | Variable |
|---|---|---|---|---|---|
| IAG | 23°33′34″ S, 46°44′01″ W | 744 | 19–28 February (Summer) and 6–15 August (Winter) | 3D sonic anemometer and infrared gas analyzer, model IRGASON, CSI **, USA Temperature and relative humidity sensor, model CS215, CSI, USA. 3-cup anemometer and vane, model 034B, MetOne Instruments Inc., USA Net radiometer, model CNR4, Kipp-Zonen Inc., The Netherlands | Sensible (H) and latent (LE) heat fluxes Temperature (T) and relative humidity (RH) Wind speed (WSP) and direction (WDIR) Net radiation (RN) and Incoming downward solar radiation (DSR) |
| SFZ | 23°33′01″ S, 46°37′49″ W | 741 | 6–15 August (Winter) | ||
| ITU | 23°49′32″ S, 46°30′32″ W | 760 |
| Physical Process | Parametrization | Main Reference |
|---|---|---|
| Microphysics | Single-moment 5-class microphysics scheme (WSM5) | Hong et al. [41] |
| Radiation | Rapid Radiative Transfer Model (RRTMG) | Iacono et al. [42] |
| Cumulus | Grell-Freitas (GF) | Arakawa et al. [43] |
| Surface Energy Balance | Noah Land Surface Model (Noah LSM) | Tewari et al. [44] |
| Single Layer Urban Canopy Model (SLUCM) | Kusaka e Kimura [45] |
| Item | Scheme | Closure Order | Surface Layer Scheme |
|---|---|---|---|
| 1 | MYJ | 1.5 local | ETA |
| 2 | MYNN | 1.5 local | MYNN |
| 3 | QNSE | 1.5 local | QNSE |
| 4 | UW | 1.5 local | MM5 |
| 5 | BouLac | 1.5 local | MM5 |
| 6 | YSU | 1.0 nonlocal | MM5 |
| 7 | SH | 1.0 nonlocal | MM5 |
| 8 | ACM2 | 1.0 hybrid | MM5 |
| 9 | TEMF | 1.5 hybrid | TEMF |
| Variable | Summer (19–28 February 2013) | Winter (6–15 August 2013) | ||
|---|---|---|---|---|
| Suburban (IAG) | Suburban (IAG) | Urban (SFZ) | Rural (ITU) | |
| T (°C) | ||||
| RH (%) | ||||
| q (g Kg−1) | ||||
| WSP (ms−1) | ||||
| WDIR (°) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tito, J.V.; Oliveira, A.P.d.; Sánchez, M.P.; Fornaro, A. Evaluation of Nine Planetary Boundary Layer Turbulence Parameterization Schemes of the Weather Research and Forecasting Model Applied to Simulate Planetary Boundary Layer Surface Properties in the Metropolitan Region of São Paulo Megacity, Brazil. Atmosphere 2024, 15, 785. https://doi.org/10.3390/atmos15070785
Tito JV, Oliveira APd, Sánchez MP, Fornaro A. Evaluation of Nine Planetary Boundary Layer Turbulence Parameterization Schemes of the Weather Research and Forecasting Model Applied to Simulate Planetary Boundary Layer Surface Properties in the Metropolitan Region of São Paulo Megacity, Brazil. Atmosphere. 2024; 15(7):785. https://doi.org/10.3390/atmos15070785
Chicago/Turabian StyleTito, Janet Valdés, Amauri Pereira de Oliveira, Maciel Piñero Sánchez, and Adalgiza Fornaro. 2024. "Evaluation of Nine Planetary Boundary Layer Turbulence Parameterization Schemes of the Weather Research and Forecasting Model Applied to Simulate Planetary Boundary Layer Surface Properties in the Metropolitan Region of São Paulo Megacity, Brazil" Atmosphere 15, no. 7: 785. https://doi.org/10.3390/atmos15070785
APA StyleTito, J. V., Oliveira, A. P. d., Sánchez, M. P., & Fornaro, A. (2024). Evaluation of Nine Planetary Boundary Layer Turbulence Parameterization Schemes of the Weather Research and Forecasting Model Applied to Simulate Planetary Boundary Layer Surface Properties in the Metropolitan Region of São Paulo Megacity, Brazil. Atmosphere, 15(7), 785. https://doi.org/10.3390/atmos15070785







