Assessing the Impact of Lightning Data Assimilation in the WRF Model
Abstract
:1. Introduction
2. Background
3. Material and Methods
3.1. Data, Model Settings, and Experiment Design
3.2. Assimilation Algorithm
3.3. Adaptative Threshold
3.4. Performance Evaluation
- 30 km and 1 mm;
- 20 km and 5 mm;
- 20 km and 10 mm.
4. Results and Discussion
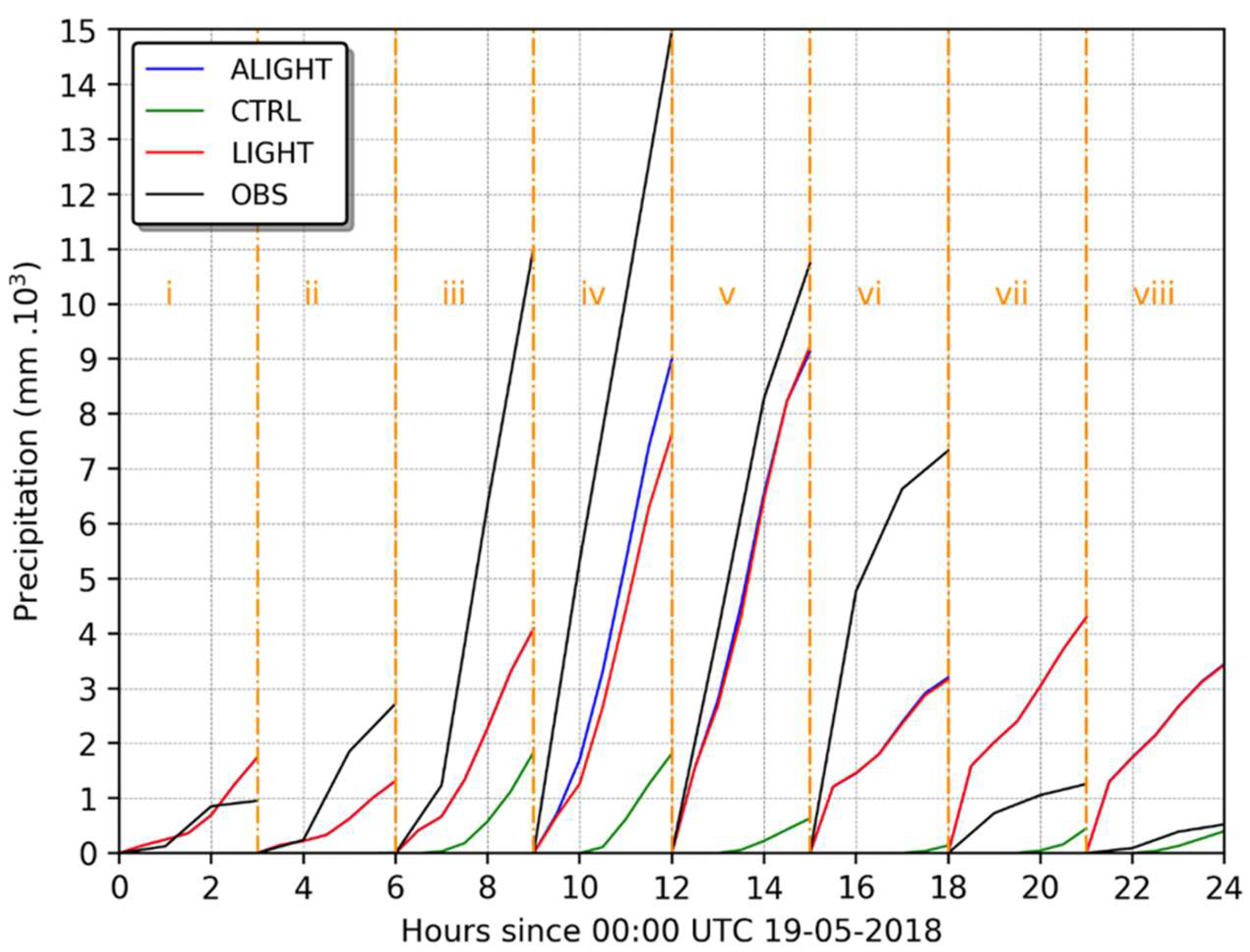
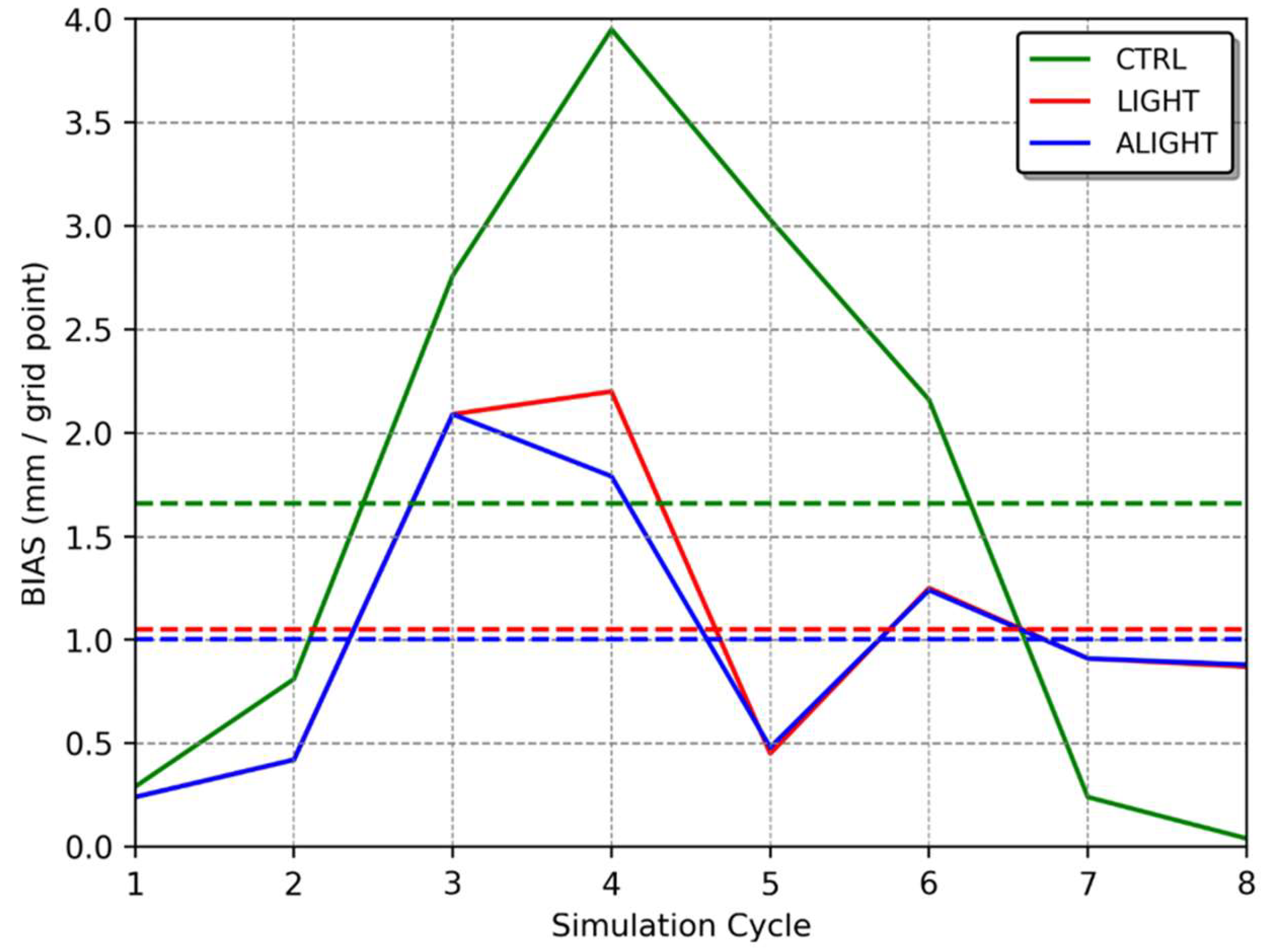
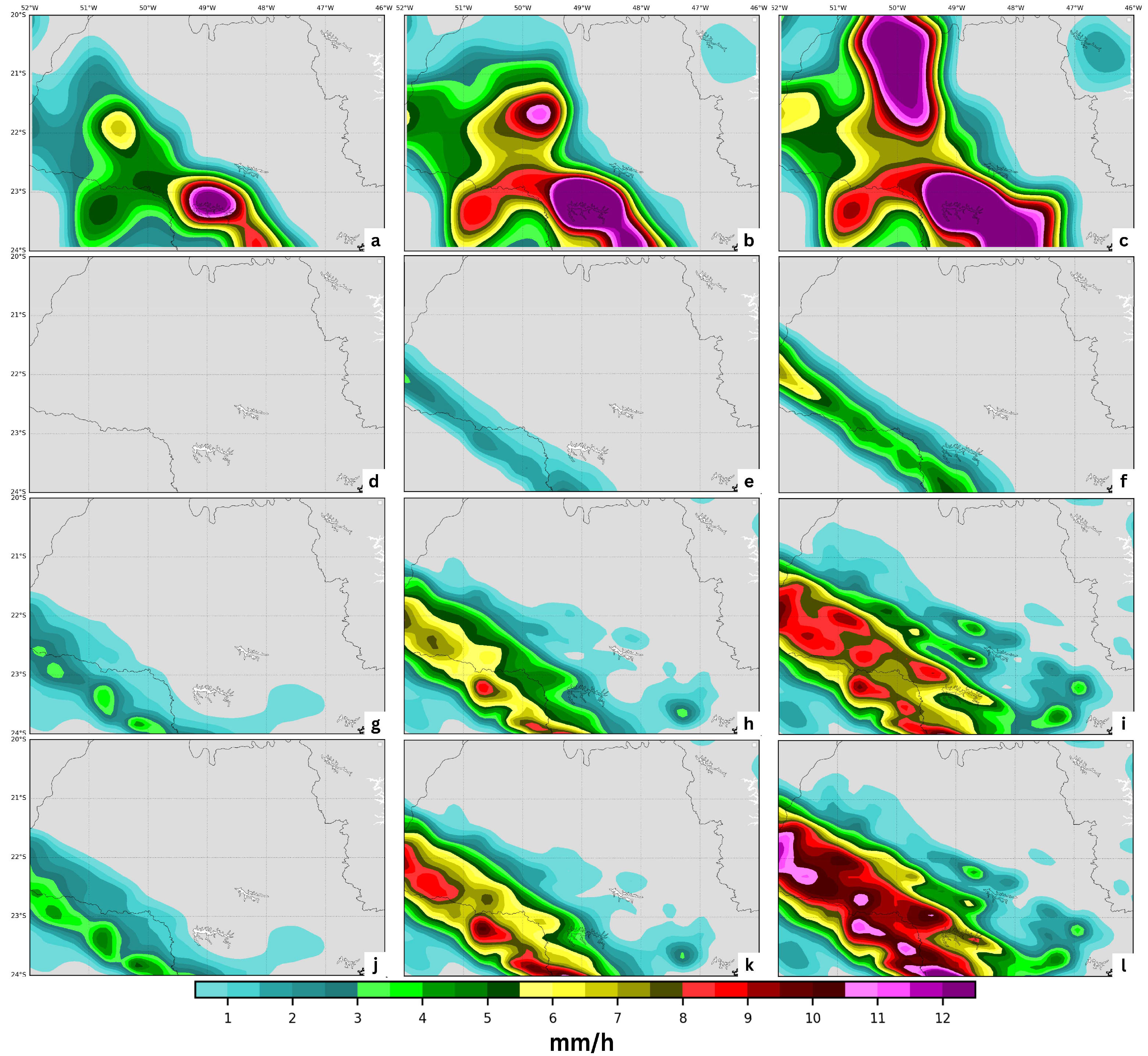
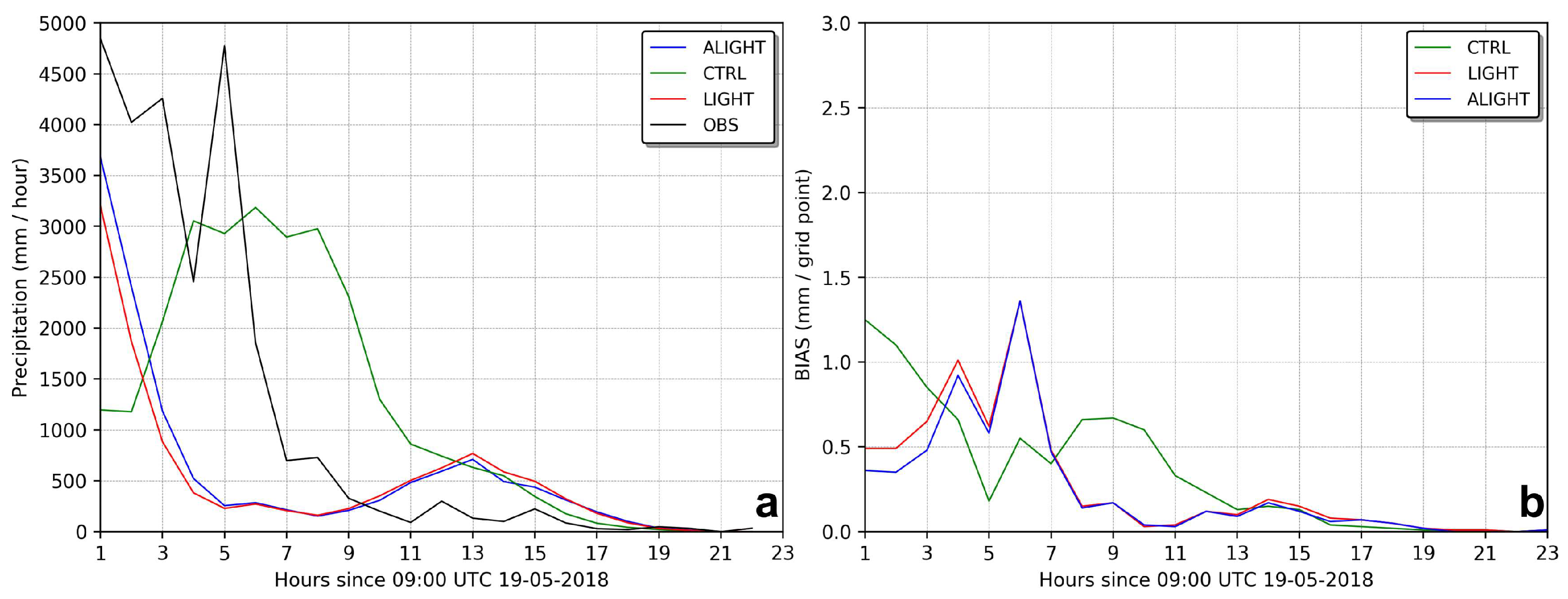
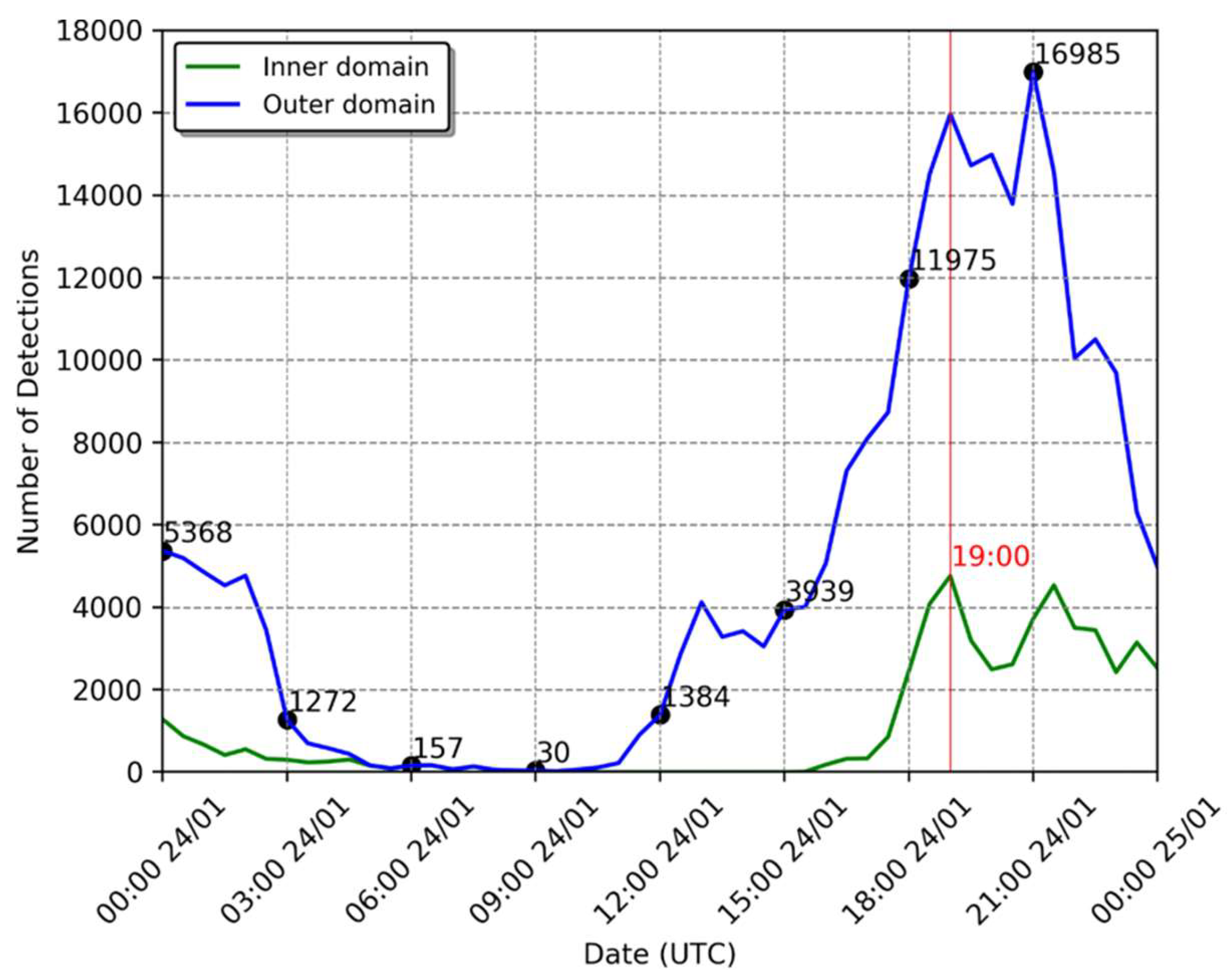
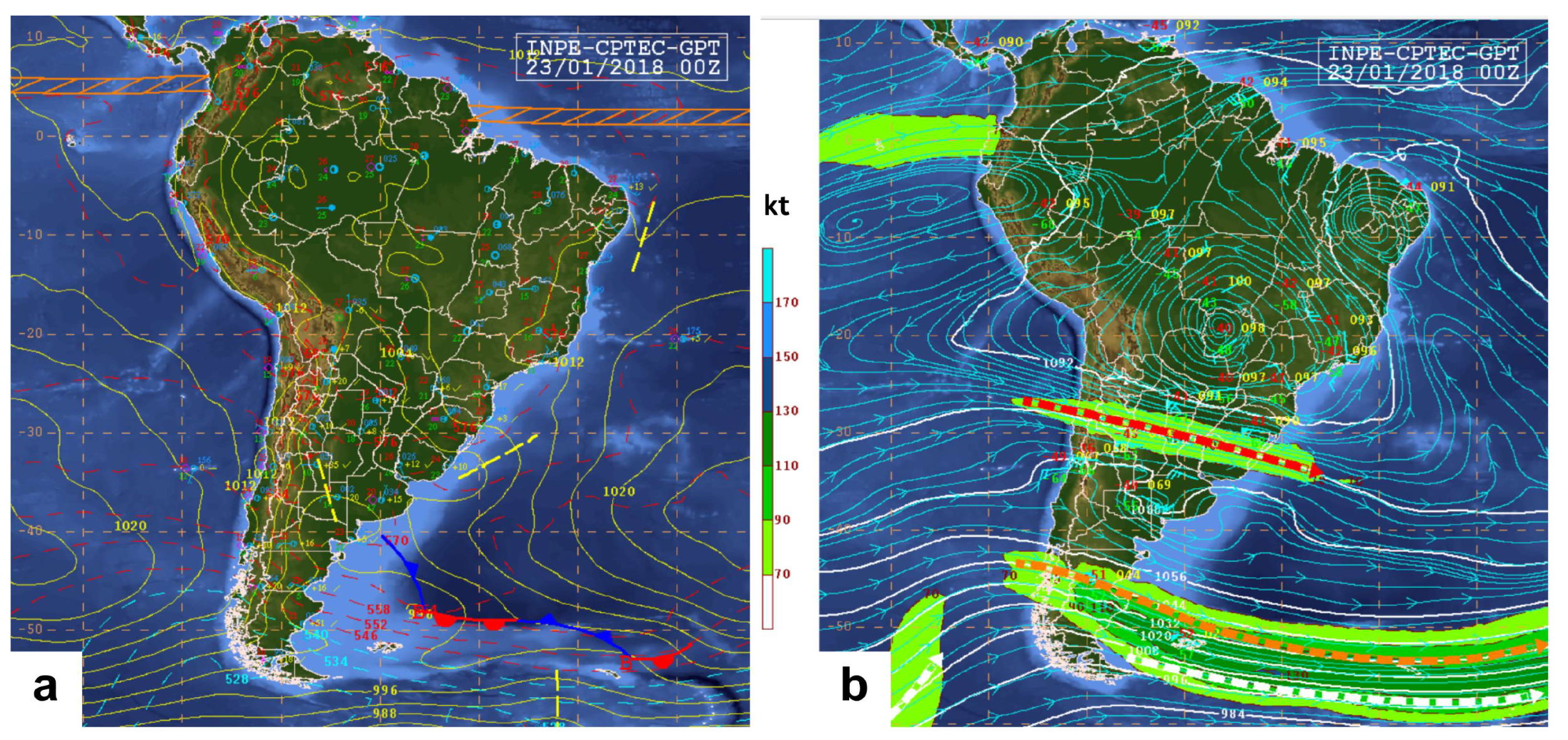
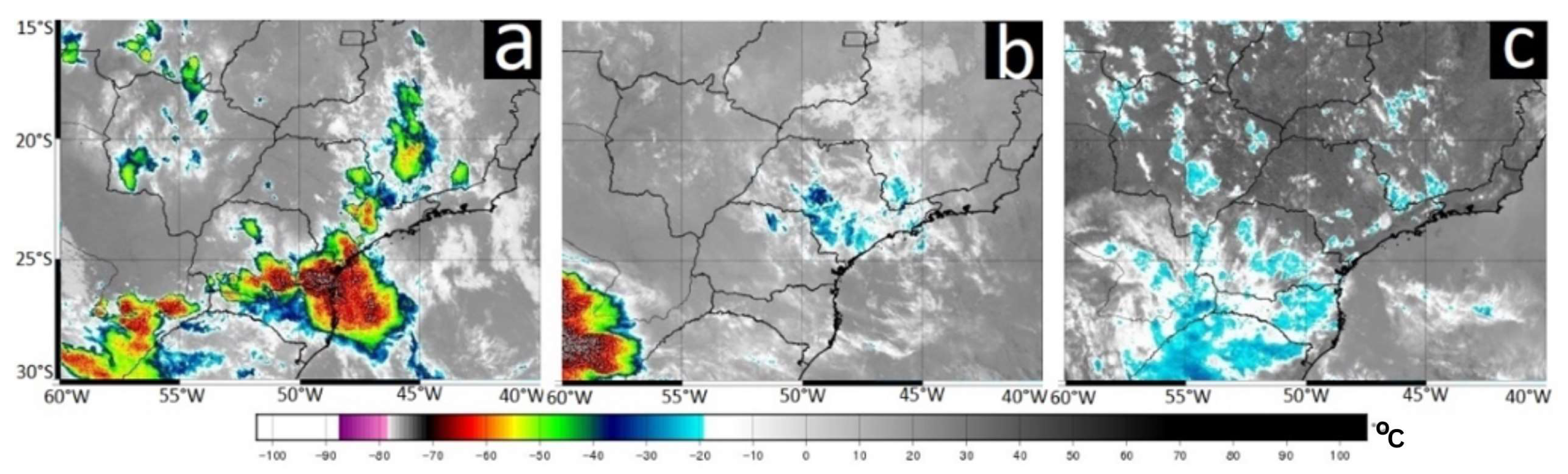
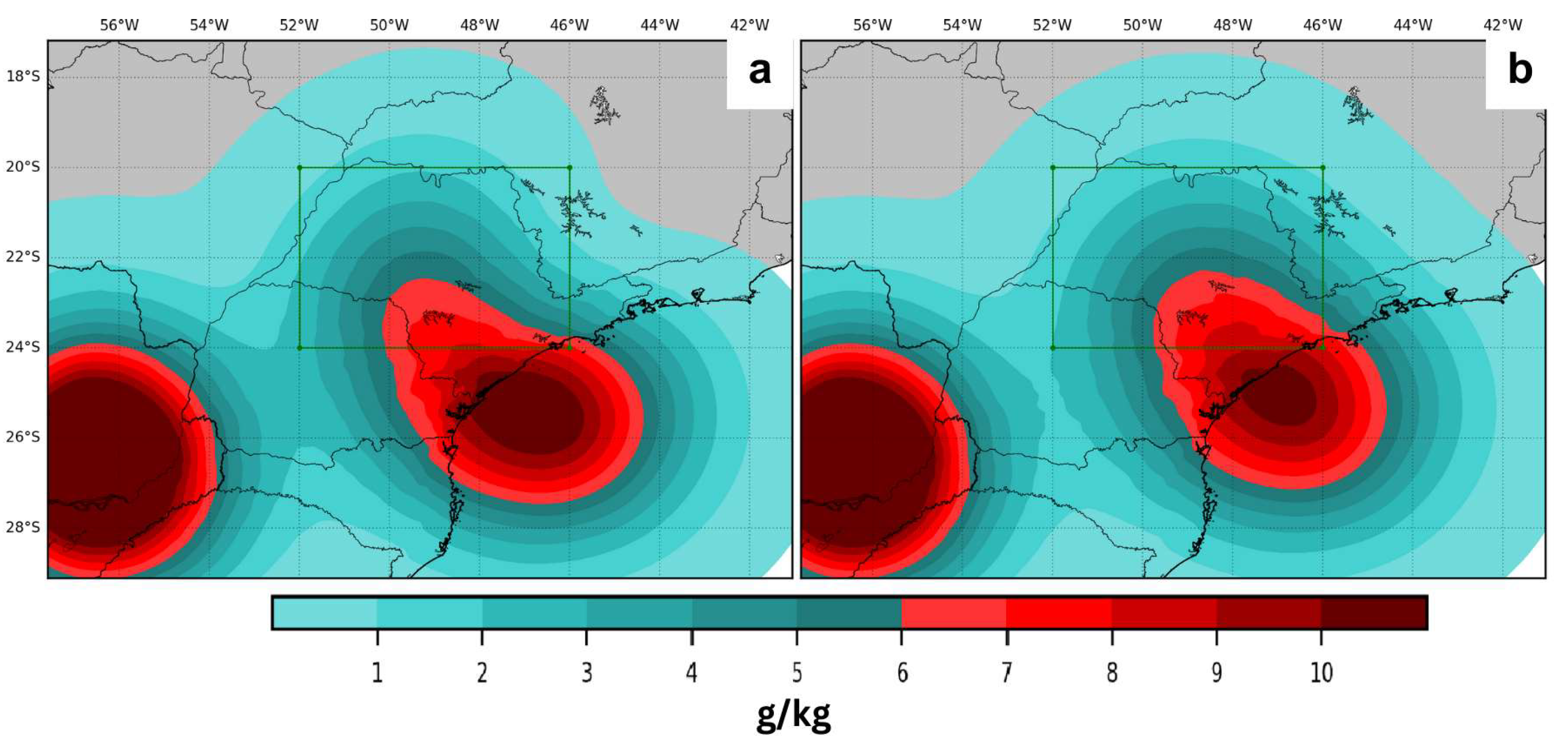
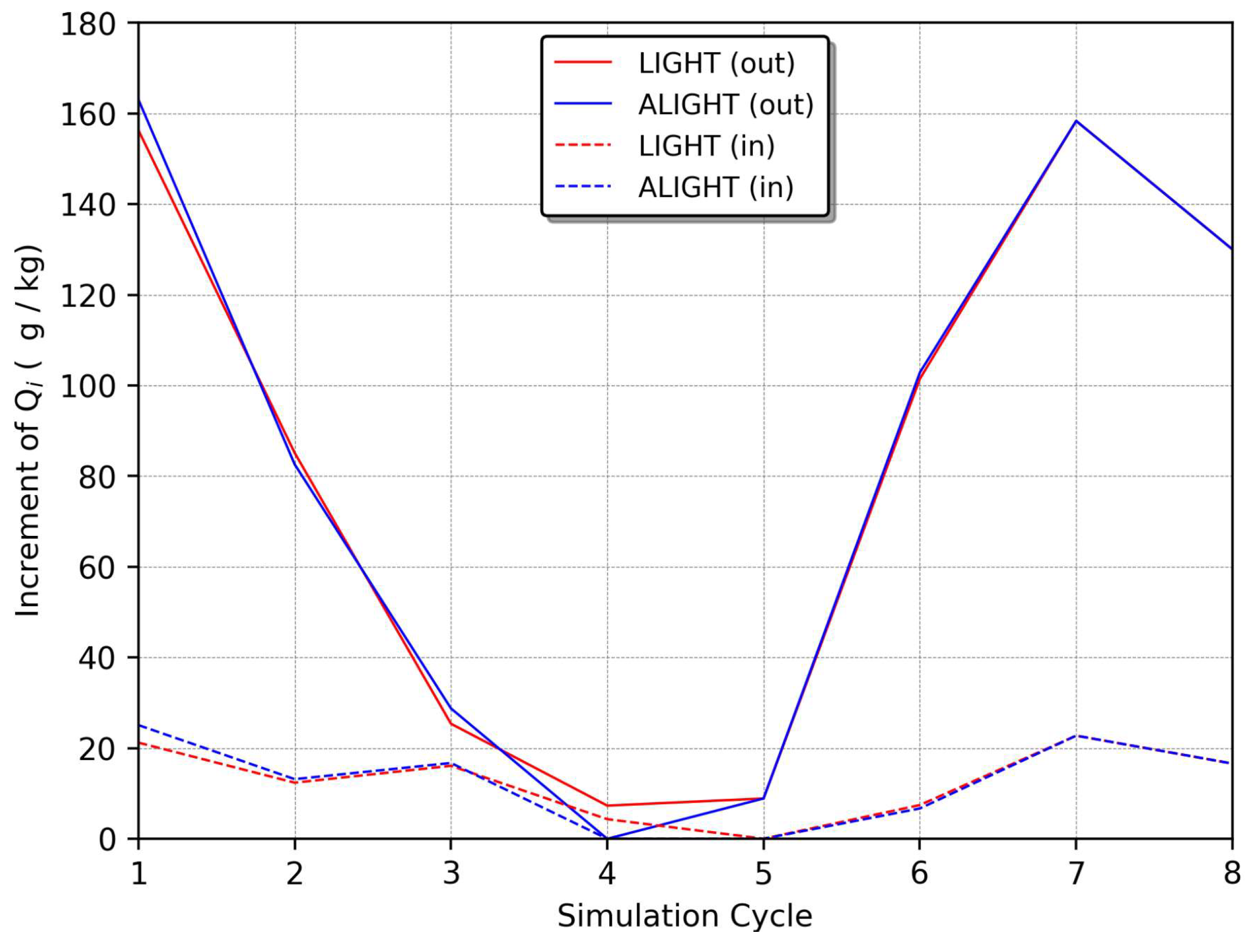
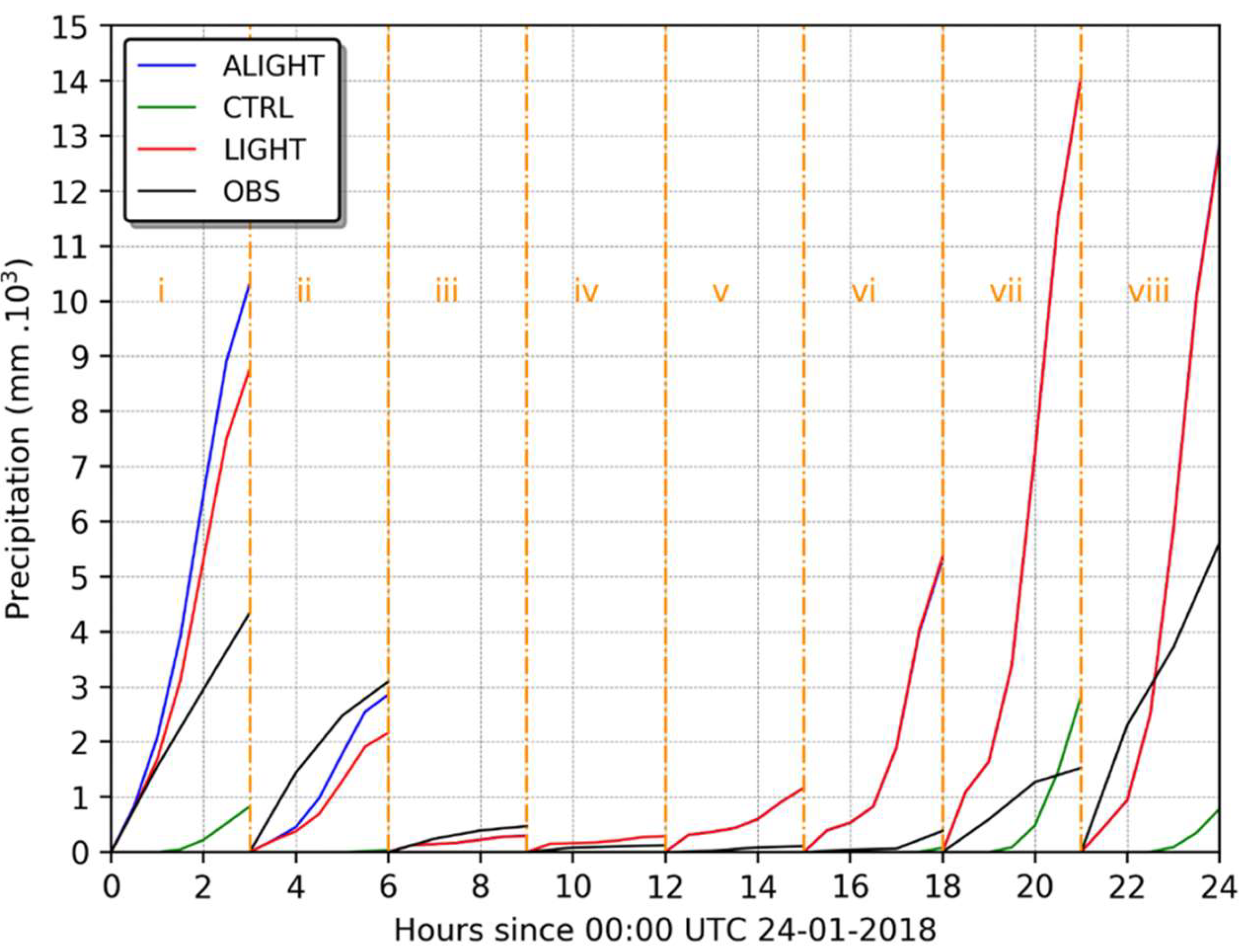
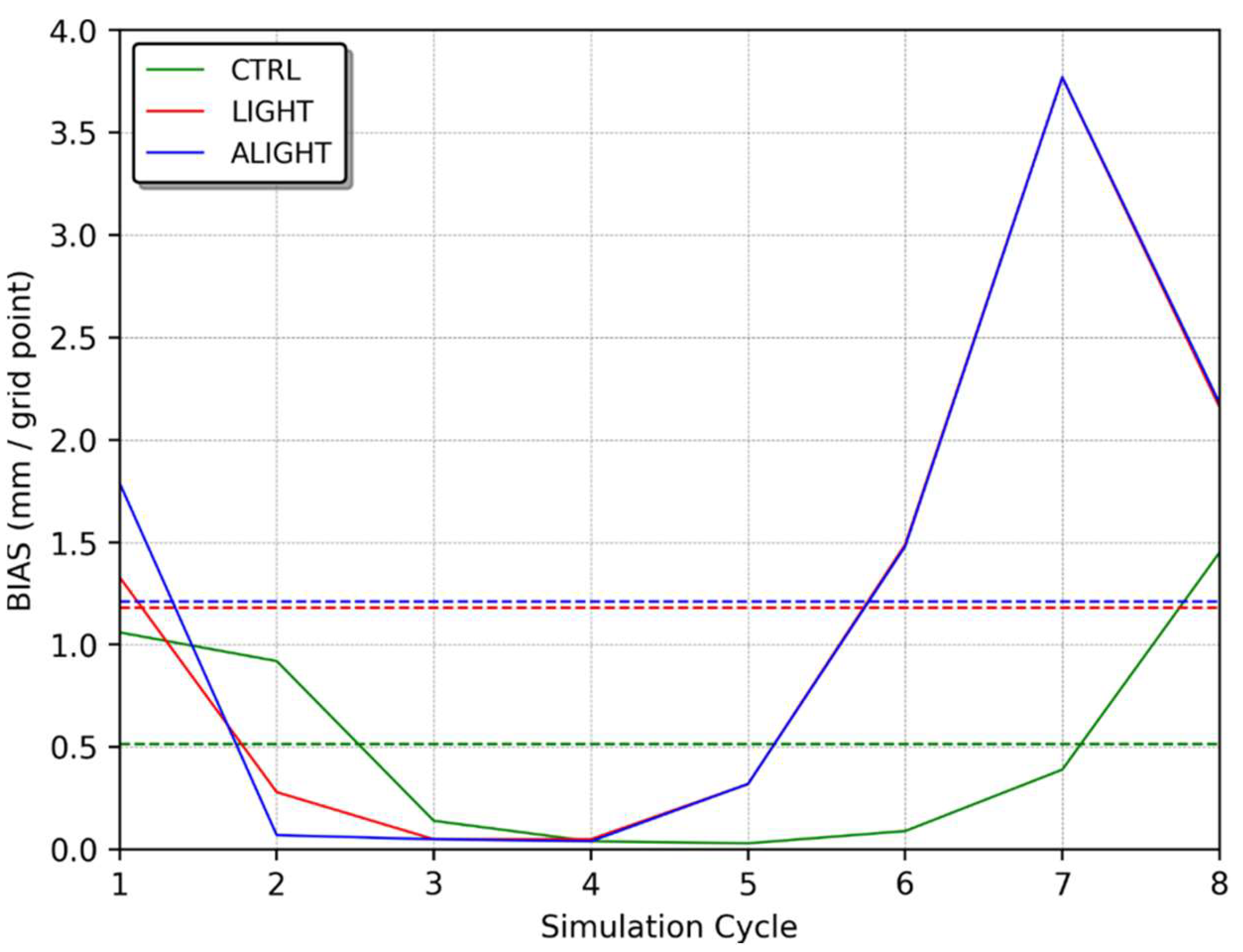
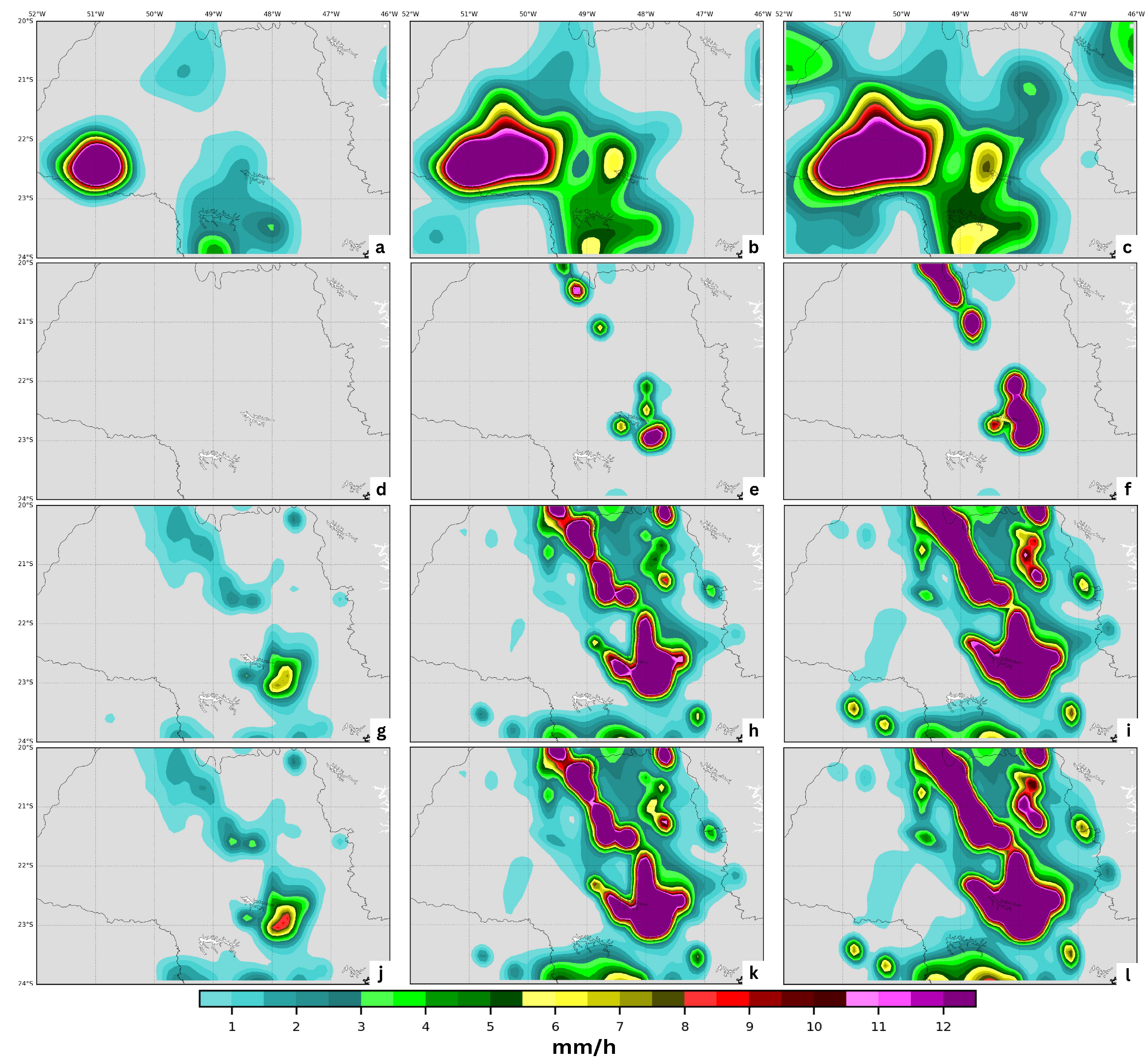
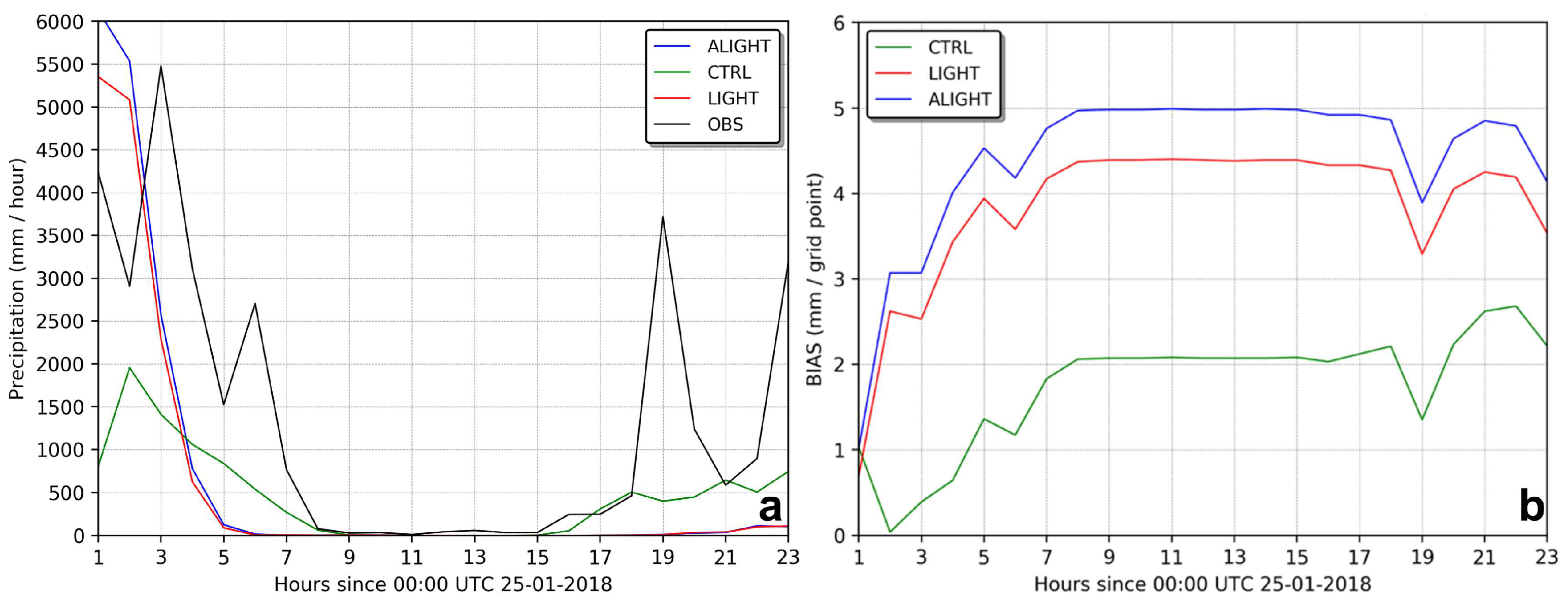
4.1. Case Study I
4.2. Case Study II
5. Conclusions
- Evaluating the assimilation algorithm’s performance in different seasonal and geographical contexts, particularly in mid-latitude regions during winter, where large-scale systems are predominant.
- Adjusting assimilation algorithm coefficients, potentially using machine learning to optimize settings and enhance performance across various atmospheric conditions.
- Exploring alternative parameterizations and/or spatial resolutions to improve model representation of graupel, which could in turn refine the assimilation process.
- Implementing multiple assimilation cycles to enhance initial model conditions while also incorporating filters to mitigate numerical instabilities from added mass.
- Comparing different assimilation approaches, such as 4DVAR, Kalman filtering, and hybrid methods, to further optimize the data assimilation framework.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Davidson, N.E.; Puri, K. Tropical prediction using dynamical nudging, satellite-defined convective heat sources, and a cyclone bogus. Mon. Weather Rev. 1992, 120, 2501–2522. [Google Scholar] [CrossRef]
- Manobianco, J.; Koch, S.; Karyampudi, V.M.; Negri, A.J. The impact of assimilating satellite-derived precipitation rates on numerical simulations of the ERICA IOP 4 cyclone. Mon. Weather Rev. 1994, 122, 341–365. [Google Scholar] [CrossRef]
- Skamarock, W.C. A Description of the Advanced Research WRF Version 2; No. NCAR/TN-468+STR; University Corporation for Atmospheric Research: Boulder, CO, USA, 2005. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A description of the Advanced Research WRF Version 3. NCAR Tech. Note 2008, 475, 10–5065. [Google Scholar]
- Bergthörsson, P.; Döös, B.R. Numerical weather map analysis. Tellus 1955, 7, 329–340. [Google Scholar] [CrossRef]
- Hoke, J.E.; Anthes, R.A. The initialization of numerical models by a dynamic-initialization technique. Mon. Weather Rev. 1976, 104, 1551–1556. [Google Scholar] [CrossRef]
- Kistler, R.E. A Study of Data Assimilation Techniques in an Autobarotropic, Primitive Equation, Channel Model. Ph.D. Thesis, Pennsylvania State University, University Park, PA, USA, 1974. [Google Scholar]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.-R.; Bourgeois, A.J.; Xiao, Q.N. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Hamill, T.M.; Snyder, C. A hybrid ensemble Kalman filter–3D variational analysis scheme. Mon. Weather Rev. 2000, 128, 2905–2919. [Google Scholar] [CrossRef]
- Wang, X.; Barker, D.M.; Snyder, C.; Hamill, T.M. A hybrid ETKF–3DVAR data assimilation scheme for the WRF model. Part I: Observing system simulation experiment. Mon. Weather Rev. 2008, 136, 5116–5131. [Google Scholar] [CrossRef]
- Fierro, A.O.; Mansell, E.R.; Ziegler, C.L.; MacGorman, D.R. Application of a lightning data assimilation technique in the WRF-ARW model at cloud-resolving scales for the tornado outbreak of 24 May 2011. Mon. Weather Rev. 2012, 140, 2609–2627. [Google Scholar] [CrossRef]
- MacGorman, D.R.; Burgess, D.W.; Mazur, V.; Rust, W.D.; Taylor, W.L.; Johnson, B.C. Lightning rates relative to tornadic storm evolution on 22 May 1981. J. Atmos. Sci. 1989, 46, 221–251. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Chronis, T.G.; Anagnostou, E.N. Improving convective precipitation forecasting through assimilation of regional lightning measurements in a mesoscale model. Mon. Weather Rev. 2005, 133, 1961–1977. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Zhu, K. Assimilation of Chinese Doppler radar and lightning data using WRF-GSI: A case study of mesoscale convective system. Adv. Meteorol. 2015, 2015, 1–17. [Google Scholar] [CrossRef]
- Apodaca, K.; Zupanski, M.; DeMaria, M.; Knaff, J.A.; Grasso, L.D. Development of a hybrid variational-ensemble data assimilation technique for observed lightning tested in a mesoscale model. Nonlinear Process. Geophys. 2014, 21, 1027–1041. [Google Scholar] [CrossRef]
- Stefanescu, R.; Navon, I.M.; Fuelberg, H.; Marchand, M. 1D+ 4D-VAR data assimilation of lightning with WRFDA system using nonlinear observation operators. arXiv 2013, arXiv:1306.1884. [Google Scholar]
- Stefanescu, R.; Navon, M.I.; Marchand, M.; Fuelberg, H. Data Assimilation of Lightning in WRF 3/4-D VAR Using Observation Operators. Mon. Weather Rev. 2012, 140, 2723–2741. [Google Scholar]
- Goodman, S.J.; Blakeslee, R.J.; Koshak, W.J.; Mach, D.; Bailey, J.; Buechler, D.; Carey, L.; Schultz, C.; Bateman, M.; McCaul, E.; et al. The GOES-R geostationary lightning mapper (GLM). Atmos. Res. 2013, 125, 34–49. [Google Scholar] [CrossRef]
- Grenet, G. Essai d’explication de la charge electrique des nuages d’orages. Ann. Geophys. 1947, 3, 306–307. [Google Scholar]
- Elster, J.; Geitel, H. Zur Influenztheorie der Niederschlagselektizität. Physik Z 1913, 14, 1287. [Google Scholar]
- Reynolds, S.E.; Brook, M.; Gourley, M.F. Thunderstorm charge separation. J. Atmos. Sci. 1957, 14, 426–436. [Google Scholar] [CrossRef]
- Baker, M.; Dash, J. Charge transfer in thunderstorms and the surface melting of ice. J. Cryst. Growth 1989, 97, 770–776. [Google Scholar] [CrossRef]
- Fletcher, N.H. Surface structure of water and ice. Philos. Mag. 1962, 7, 255–269. [Google Scholar] [CrossRef]
- Williams, E.R. The electrification of thunderstorms. Sci. Am. 1988, 259, 88–99. [Google Scholar] [CrossRef]
- Cooray, G.V. The Lightning Flash; The Institution of Electrical Engineers: London, UK, 2003. [Google Scholar]
- MacGorman, D.R.; Rust, W.D. The Electrical Nature of Storms; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Schultz, C.J.; Petersen, W.A.; Carey, L.D. Lightning and severe weather: A comparison between total and cloud-to-ground lightning trends. Weather. Forecast. 2011, 26, 744–755. [Google Scholar] [CrossRef]
- Cummins, K.L.; Murphy, M.J.; Tuel, J.V. Lightning detection methods and meteorological applications. In Proceedings of the IV International Symposium on Military Meteorology, Malbork, Poland, 26–28 September 2000; pp. 26–28. [Google Scholar]
- Naccarato, K.P.; Bourscheidt, V.; Pinto, O. The fourth generation of the Brazilian detection efficiency model for BrasilDAT network (RDEM4). In Proceedings of the 14th International Conference on Atmospheric Electricity, Rio de Janeiro, Brazil, 8–12 August 2011; pp. 1–3. [Google Scholar]
- Alexander, G.D.; Weinman, J.A.; Karyampudi, V.M.; Olson, W.S.; Lee, A.C.L. The effect of assimilating rain rates derived from satellites and lightning on forecasts of the 1993 superstorm. Mon. Weather Rev. 1999, 127, 1433–1457. [Google Scholar] [CrossRef]
- Chang, D.-E.; Weinman, J.A.; Morales, C.A.; Olson, W.S. The effect of spaceborne microwave and ground-based continuous lightning measurements on forecasts of the 1998 Groundhog Day storm. Mon. Weather Rev. 2001, 129, 1809–1833. [Google Scholar] [CrossRef]
- Mansell, E.R.; Ziegler, C.L.; MacGorman, D.R. A lightning data assimilation technique for mesoscale forecast models. Mon. Weather Rev. 2007, 135, 1732–1748. [Google Scholar] [CrossRef]
- Qie, X.; Zhu, R.; Yuan, T.; Wu, X.; Li, W.; Liu, D. Application of total-lightning data assimilation in a mesoscale convective system based on the WRF model. Atmos. Res. 2014, 145, 255–266. [Google Scholar] [CrossRef]
- Fierro, A.O.; Gao, J.; Ziegler, C.L.; Mansell, E.R.; MacGorman, D.R.; Dembek, S.R. Evaluation of a cloud-scale lightning data assimilation technique and a 3DVAR method for the analysis and short-term forecast of the 29 June 2012 derecho event. Mon. Weather Rev. 2014, 142, 183–202. [Google Scholar] [CrossRef]
- Dixon, K.; Mass, C.F.; Hakim, G.J.; Holzworth, R.H. The impact of lightning data assimilation on deterministic and ensemble forecasts of convective events. J. Atmos. Ocean. Technol. 2016, 33, 1801–1823. [Google Scholar] [CrossRef]
- Chen, Z.; Qie, X.; Liu, D.; Xiong, Y. Lightning data assimilation with comprehensively nudging water contents at cloud-resolving scale using WRF model. Atmos. Res. 2019, 221, 72–87. [Google Scholar] [CrossRef]
- Pessi, A.T.; Businger, S. The impact of lightning data assimilation on a winter storm simulation over the North Pacific Ocean. Mon. Weather Rev. 2009, 137, 3177–3195. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Kotroni, V.; Defer, E.; Bousquet, O. Study of a heavy precipitation event over southern France, in the frame of HYMEX project: Observational analysis and model results using assimilation of lightning. Atmos. Res. 2013, 134, 45–55. [Google Scholar] [CrossRef]
- Fierro, A.O.; Clark, A.J.; Mansell, E.R.; MacGorman, D.R.; Dembek, S.R.; Ziegler, C.L. Impact of storm-scale lightning data assimilation on WRF-ARW precipitation forecasts during the 2013 warm season over the contiguous United States. Mon. Weather Rev. 2015, 143, 757–777. [Google Scholar] [CrossRef]
- Lynn, B.H.; Kelman, G.; Ellrod, G. An evaluation of the efficacy of using observed lightning to improve convective lightning forecasts. Weather Forecast 2015, 30, 405–423. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Zhao, T.; Liu, Y.; Xu, M.; Shen, S.; Jiang, Y.; Yang, H.; Feng, S. Continuous assimilation of lightning data using time-lagged ensembles for a convection-allowing numerical weather prediction model. J. Geophys. Res. Atmos. 2018, 123, 9652–9673. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, S.; Liu, Y.; Li, Y. Comparison of the WRF-FDDA-Based Radar Reflectivity and Lightning Data Assimilation for Short-Term Precipitation and Lightning Forecasts of Severe Convection. Remote. Sens. 2022, 14, 5980. [Google Scholar] [CrossRef]
- Gonçalves, L.d.J.M.; Kaiser, J.; Palmeira, R.M.d.J.; Gallo, M.N.; Parente, C.E. Evaluation of a High Resolution WRF Model for Southeast Brazilian Coast: The Importance of Physical Parameterization to Wind Representation. Atmosphere 2024, 15, 533. [Google Scholar] [CrossRef]
- Computational and Information Systems Laboratory (CISL). Cheyenne: HPE/SGI ICE XA System (Climate Simulation Laboratory); Computational and Information Systems Laboratory (CISL): Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
- MMM/UCAR. WRF User Page. CO, USA. 2018. Available online: https://www2.mmm.ucar.edu/wrf/users/ (accessed on 29 June 2024).
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon Weather Rev 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Tewari, M. Implementation and Verification of the Unified NOAH Land Surface Model in the WRF Model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 12–16 January 2004. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Liu, D.; Zhang, D.; Yao, W.; Wang, C. A case study of assimilating lightning-proxy relative humidity with WRF-3DVAR. Atmosphere 2017, 8, 55. [Google Scholar] [CrossRef]
- Schultz, C.J.; Petersen, W.A.; Carey, L.D. Preliminary development and evaluation of lightning jump algorithms for the real-time detection of severe weather. J. Appl. Meteorol. Clim. 2009, 48, 2543–2563. [Google Scholar] [CrossRef]
- Williams, E.; Boldi, B.; Matlin, A.; Weber, M.; Hodanish, S.; Sharp, D.; Goodman, S.; Raghavan, R.; Buechler, D. The behavior of total lightning activity in severe Florida thunderstorms. Atmos. Res. 1999, 51, 245–265. [Google Scholar] [CrossRef]
- Barnes, S.L. A technique for maximizing details in numerical weather map analysis. J. Appl. Meteorol. 1964, 3, 396–409. [Google Scholar] [CrossRef]
- Stanski, H.R.; Laurence, J.W.; Burrows, W.R. Survey of Common Verification Methods in Meteorology. 1989. Available online: https://www.cawcr.gov.au/projects/verification/Stanski_et_al/Stanski_et_al.html (accessed on 1 March 1999).
- Browning, K.A.; Ludlam, F.H. Airflow in convective storms. Q. J. R. Meteorol. Soc. 1962, 88, 117–135. [Google Scholar] [CrossRef]
- Petty, G.W. A First Course in Atmospheric Thermodynamics; Sundog Publishing LLC: Danvers, MA, USA, 2023. [Google Scholar]
- Weisman, M.L.; Klemp, J.B. Characteristics of isolated convective storms. In Mesoscale Meteorology and Forecasting; American Meteorological Society: Boston, MA, USA, 1986; pp. 331–358. [Google Scholar]
- Bergeron, T. On the physics of fronts. Bull. Am. Meteorol. Soc. 1937, 18, 265–275. [Google Scholar] [CrossRef]
- Reboita, M.S.; Gan, M.A.; Rocha, R.P.D.; Ambrizzi, T. Regimes de precipitação na América do Sul: Uma revisão bibliográfica. Rev. Bras. Meteorol. 2010, 25, 185–204. [Google Scholar] [CrossRef]
- Brundidge, K.C. The wind and temperature structure of nocturnal cold fronts in the first 1,420 feet. Mon. Weather Rev. 1965, 93, 587–603. [Google Scholar] [CrossRef]
- CPTEC/INPE. Technical Report. 2019. Available online: http://tempo.cptec.inpe.br/boletimtecnico/pt (accessed on 4 April 2019).
- Bjerknes, V. On the Dynamics of the Circular Vortex: With Applications to the Atmosphere and Atmospheric Vortex and Wave Motions; Cammermeyers Bokhandel: Oslo, Norway; Volume 2, No. 4.
- Houze, R.A. Structure and dynamics of a tropical squall–line system. Mon. Weather Rev. 1977, 105, 1540–1567. [Google Scholar] [CrossRef]
- DSA/CPTEC. Technical Report; DSA/CPTEC: Cachoeira Paulista, SP, Brazil, 2019. [Google Scholar]
- Barker, D.M.; Huang, W.; Guo, Y.R.; Bourgeois, A. A Three-Dimensional Variational (3DVAR) Data Assimilation System for Use with MM5; No. NCAR/TN-453+STR; University Corporation for Atmospheric Research: Boulder, CO, USA, 2003. [Google Scholar] [CrossRef]
- Moya-Álvarez, A.S.; Gálvez, J.; Holguín, A.; Estevan, R.; Kumar, S.; Villalobos, E.; Martínez-Castro, D.; Silva, Y. Extreme rainfall forecast with the WRF-ARW model in the Central Andes of Peru. Atmosphere 2018, 9, 362. [Google Scholar] [CrossRef]
- Chen, F.; Manning, K.W.; LeMone, M.A.; Trier, S.B.; Alfieri, J.G.; Roberts, R.; Tewari, M.; Niyogi, D.; Horst, T.W.; Oncley, S.P.; et al. Description and evaluation of the characteristics of the NCAR high-resolution land data assimilation system. J. Appl. Meteorol. Clim. 2007, 46, 694–713. [Google Scholar] [CrossRef]
- Cosgrove, B.A.; Lohmann, D.; Mitchell, K.E.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. Land surface model spin-up behavior in the North American Land Data Assimilation System (NLDAS). J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Sokol, Z. Effects of an assimilation of radar and satellite data on a very-short range forecast of heavy convective rainfalls. Atmos. Res. 2009, 93, 188–206. [Google Scholar] [CrossRef]
- Oliveira Júnior, J.F.; Delgado, R.C.; Gois, G.; Lannes, A.; Dias, F.O.; Souza, J.C.; Souza, M. Análise da precipitação e sua relação com sistemas meteorológicos em Seropédica, Rio de Janeiro. Floresta Ambiente 2014, 21, 140–149. [Google Scholar] [CrossRef]
- Ahasan, M.N.; Debsarma, S.K. Impact of data assimilation in simulation of thunderstorm (squall line) event over Bangladesh using WRF model, during SAARC–STORM Pilot Field Experiment 2011. Nat. Hazards 2015, 75, 1009–1022. [Google Scholar] [CrossRef]
- Su, Y.; Ping, F.; Shen, X.-Y.; Miao, C.-S. Real-time simulation and mechanistic analysis of a squall line case in East China. Atmos. Ocean. Sci. Lett. 2016, 9, 394–400. [Google Scholar] [CrossRef]
- Peckham, S.E.; Smirnova, T.G.; Benjamin, S.G.; Brown, J.M.; Kenyon, J.S. Implementation of a digital filter initialization in the WRF Model and its application in the Rapid Refresh. Mon. Weather Rev. 2016, 144, 99–106. [Google Scholar] [CrossRef]
- Lynch, P.; Huang, X.-Y. Initialization of the HIRLAM model using a digital filter. Mon. Weather Rev. 1992, 120, 1019–1034. [Google Scholar] [CrossRef]
- Harter, F.P. Uso de Filtro Digital para Iniciar um Modelo de Área Limitada; Instituto Nacional de Pesquisas Espaciais: São José dos Campos, Brazil, 1999. [Google Scholar]
- Kousky, V.E.; Gan, M.A. Upper tropospheric cyclonic vortices in the tropical South Atlantic. Tellus 1981, 33, 538. [Google Scholar] [CrossRef]
- Nascimento, E.L. Influência dos bloqueios atmosféricos na propagação de Ondas de Rossby em escoamentos de inverno no Hemisfério Sul. Ph.D. Dissertation, University of Sao Paulo, São Paulo, SP, Brazil, 1998. [Google Scholar]
- Bringi, V.N.; Knupp, K.; Detwiler, A.; Liu, L.; Caylor, I.J.; Black, R.A. Evolution of a Florida thunderstorm during the Convection and Precipitation/Electrification Experiment: The case of 9 August 1991. Mon. Weather Rev. 1997, 125, 2131–2160. [Google Scholar] [CrossRef]
- Dye, J.E.; Jones, J.J.; Weinheimer, A.J.; Winn, W.P. Observations within two regions of charge during initial thunderstorm electrification. Q. J. R. Meteorol. Soc. 1988, 114, 1271–1290. [Google Scholar] [CrossRef]
- Ziegler, C.L.; MacGorman, D.R.; Dye, J.E.; Ray, P.S. A model evaluation of noninductive graupel-ice charging in the early electrification of a mountain thunderstorm. J. Geophys. Res. Atmos. 1991, 96, 12833–12855. [Google Scholar] [CrossRef]
- Tao, Y.; Li, H.Y.; Hong, Y.C. Numerical studies on cloud physics characteristic and influence of the graupel/hail category on cloud and precipitation during a heavy rainstorm over North China. Plateau Meteorol. 2013, 32, 166–178. [Google Scholar]
- Adams-Selin, R.D.; Heever, S.C.v.D.; Johnson, R.H. Impact of graupel parameterization schemes on idealized bow echo simulations. Mon. Weather Rev. 2013, 141, 1241–1262. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
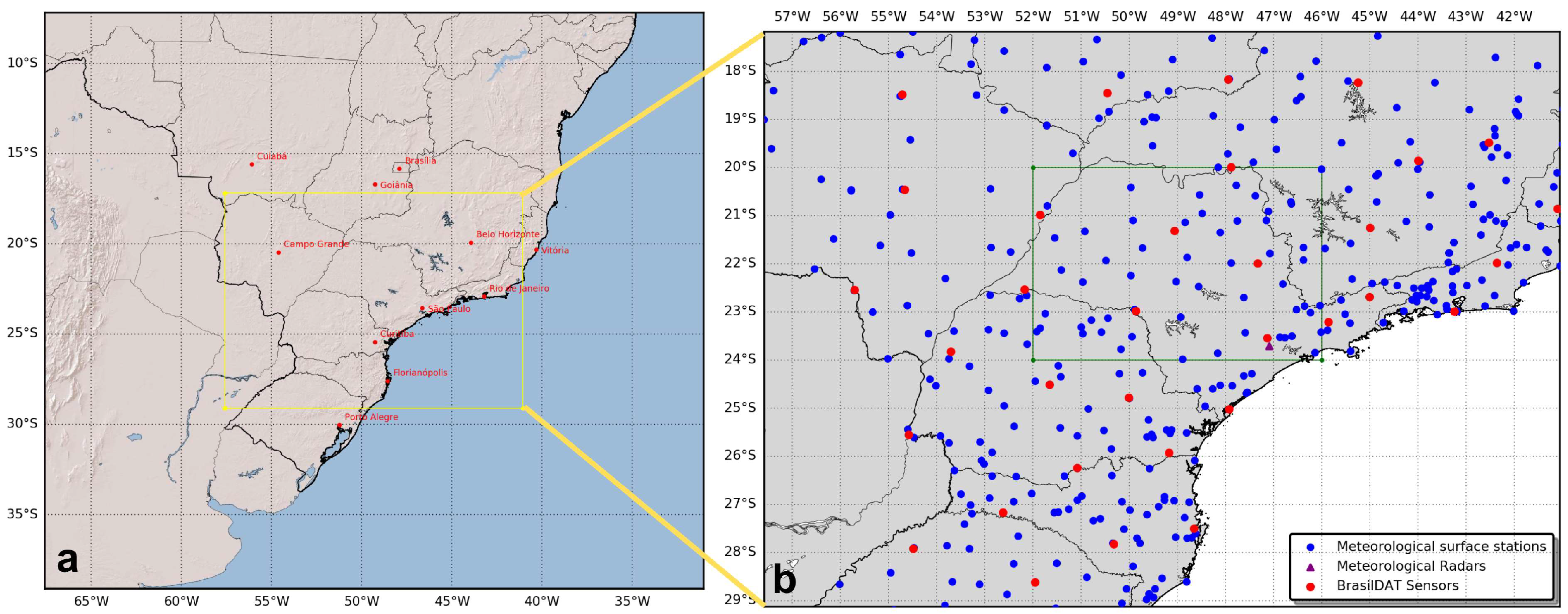
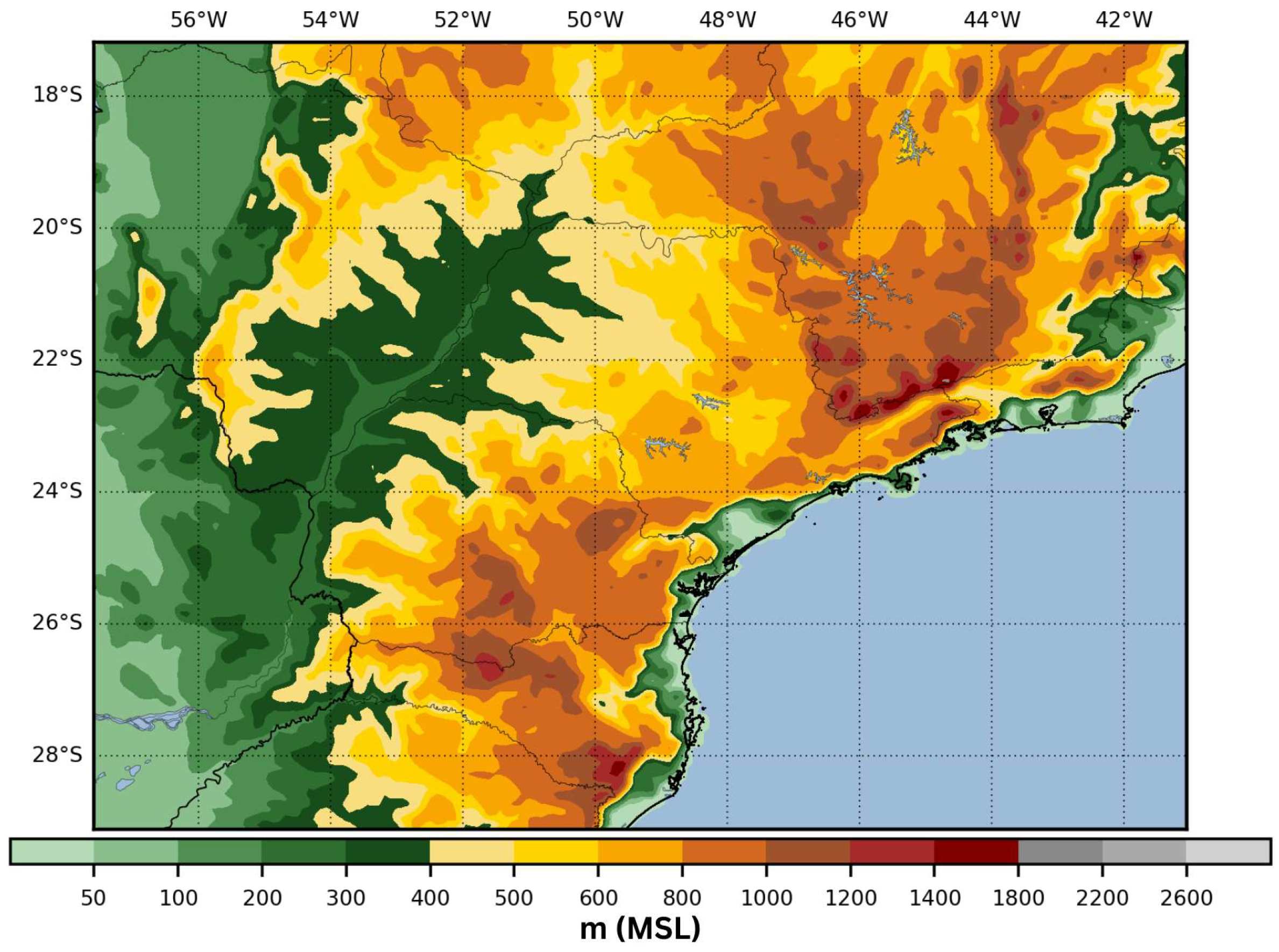

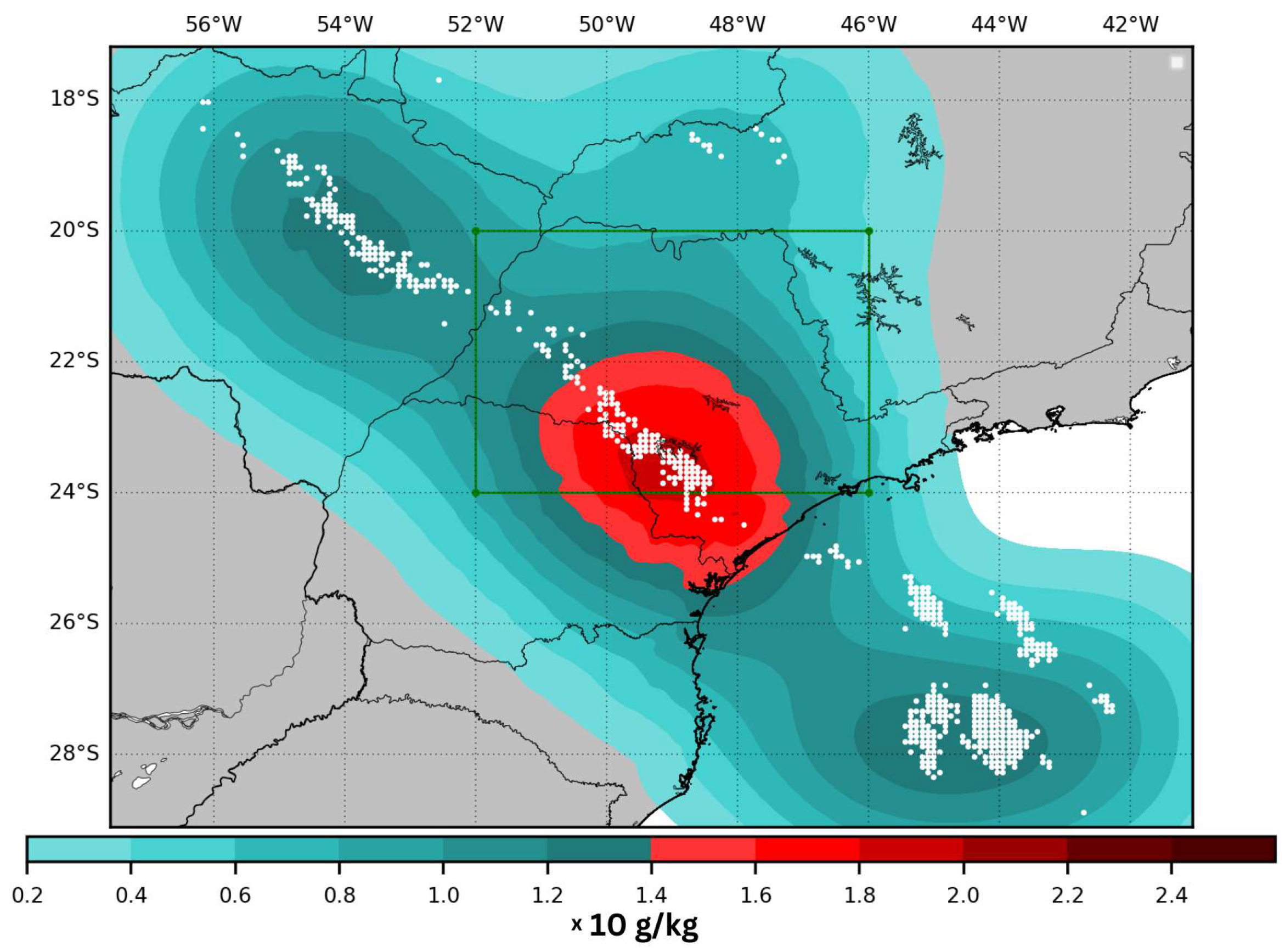


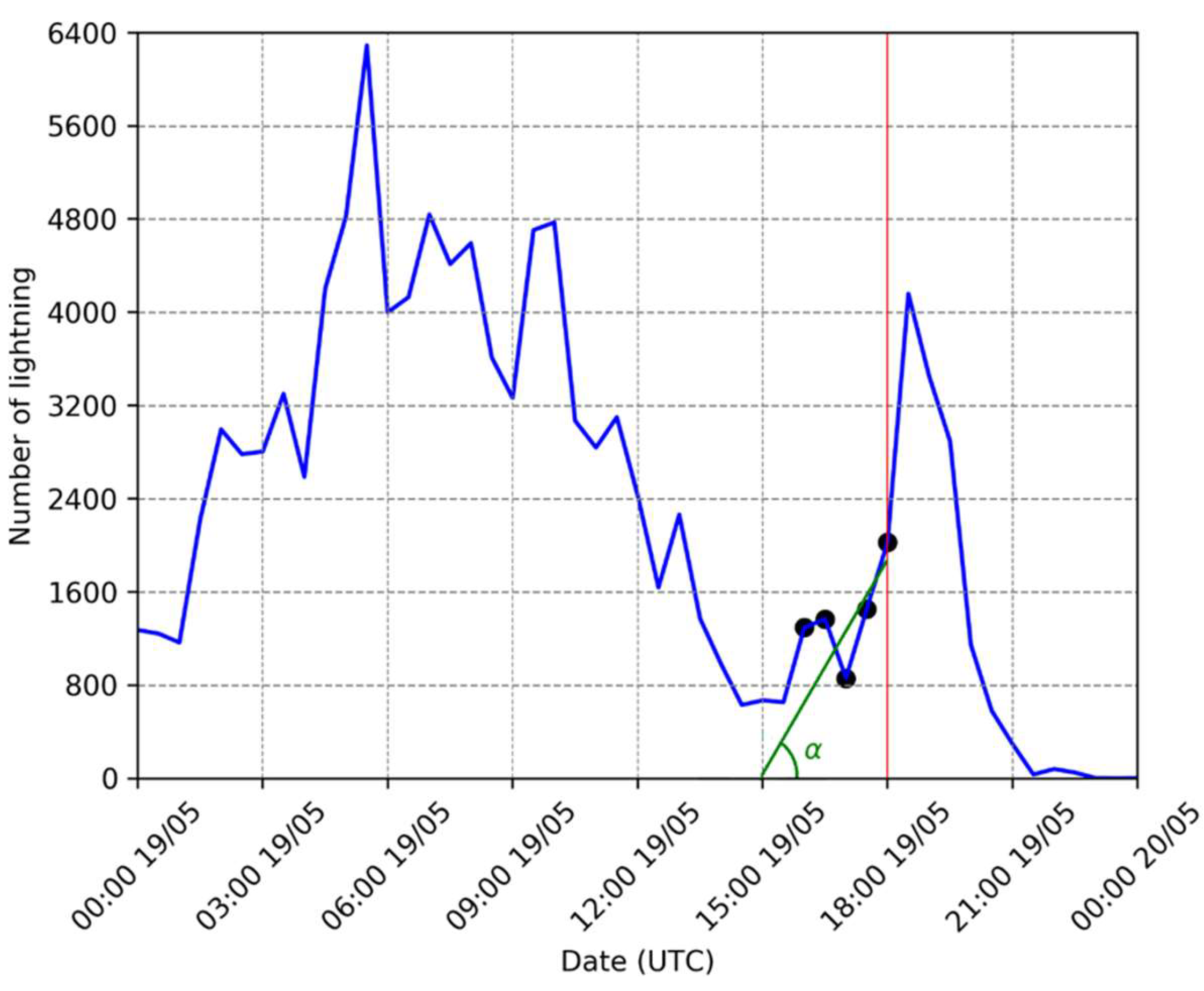


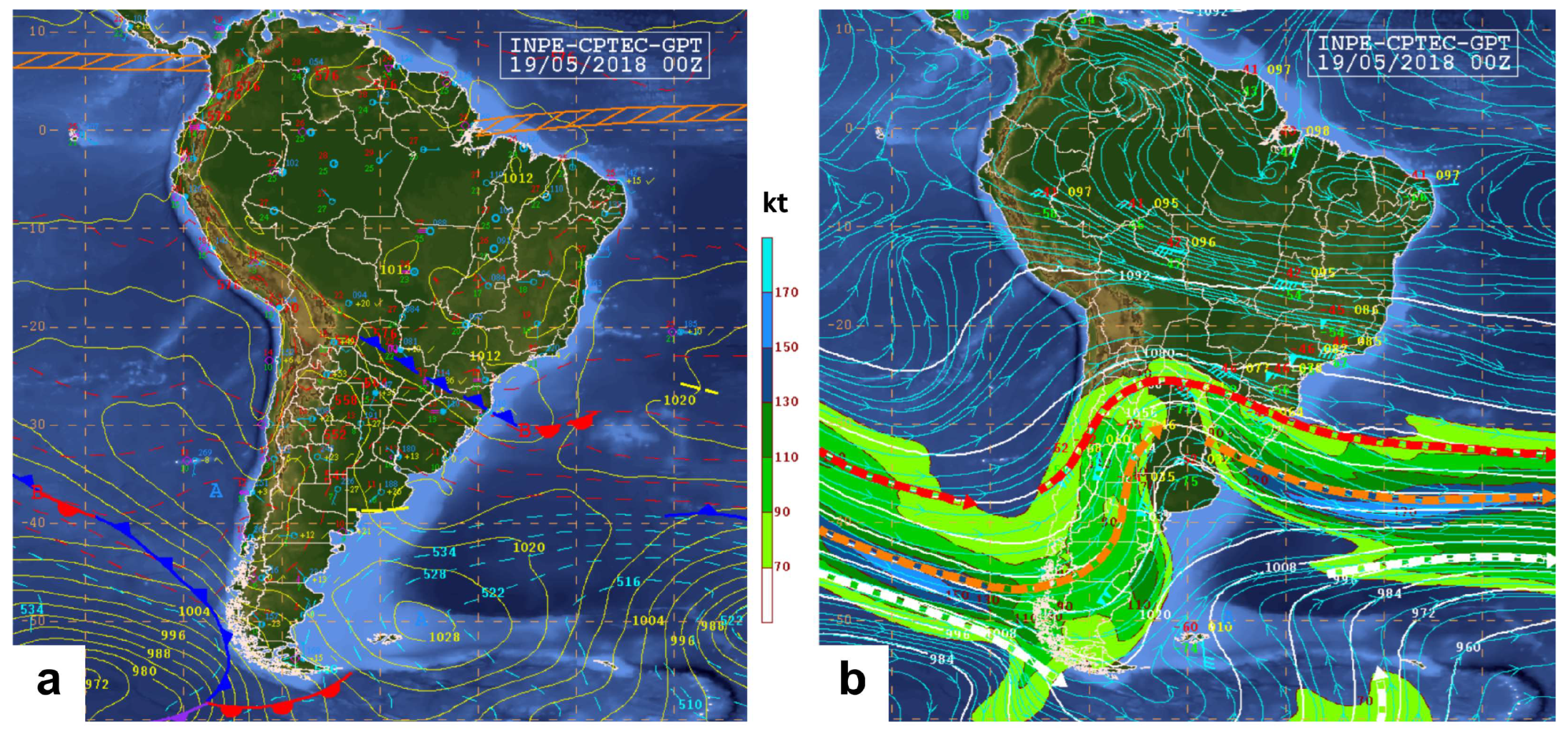
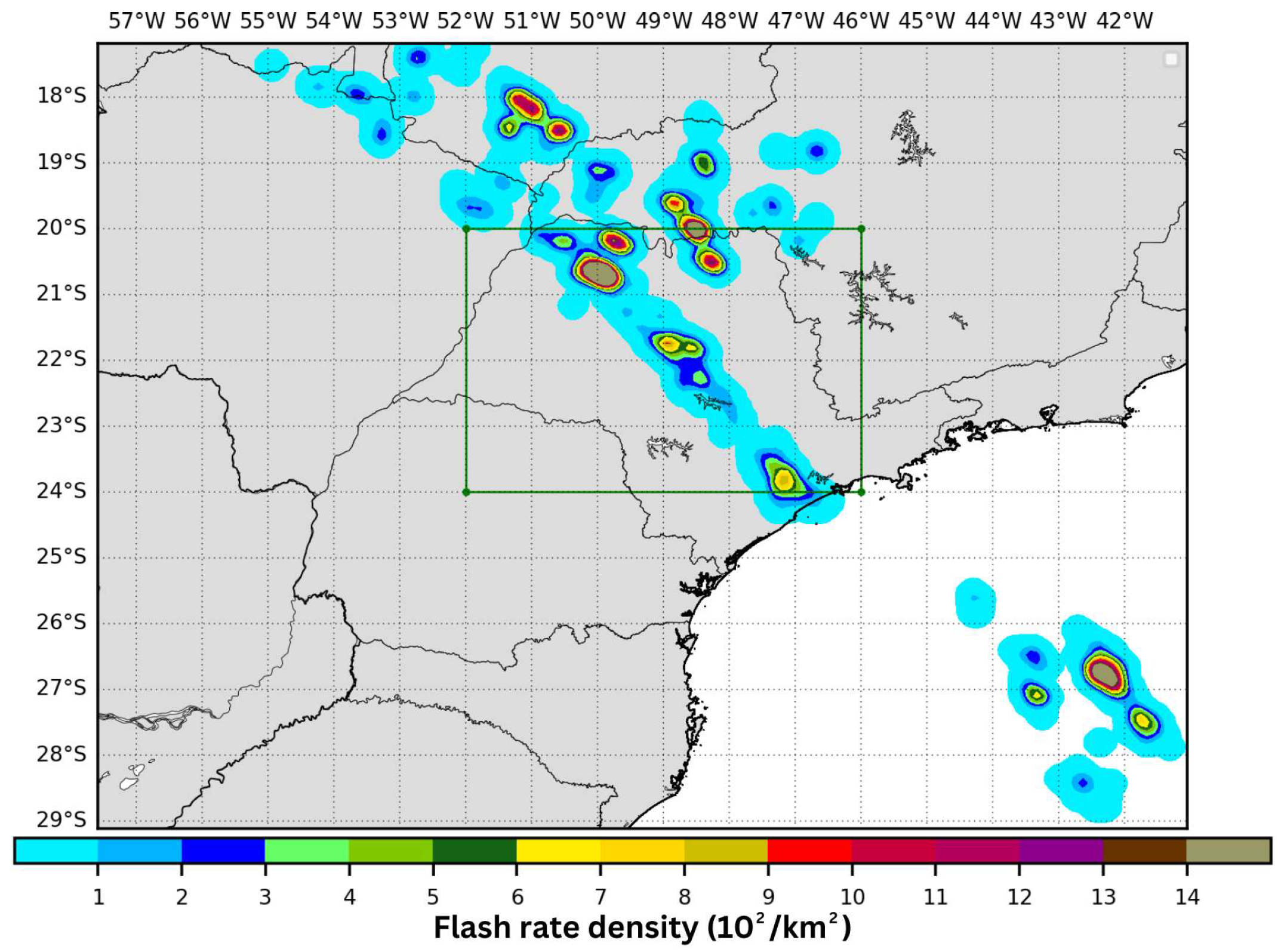

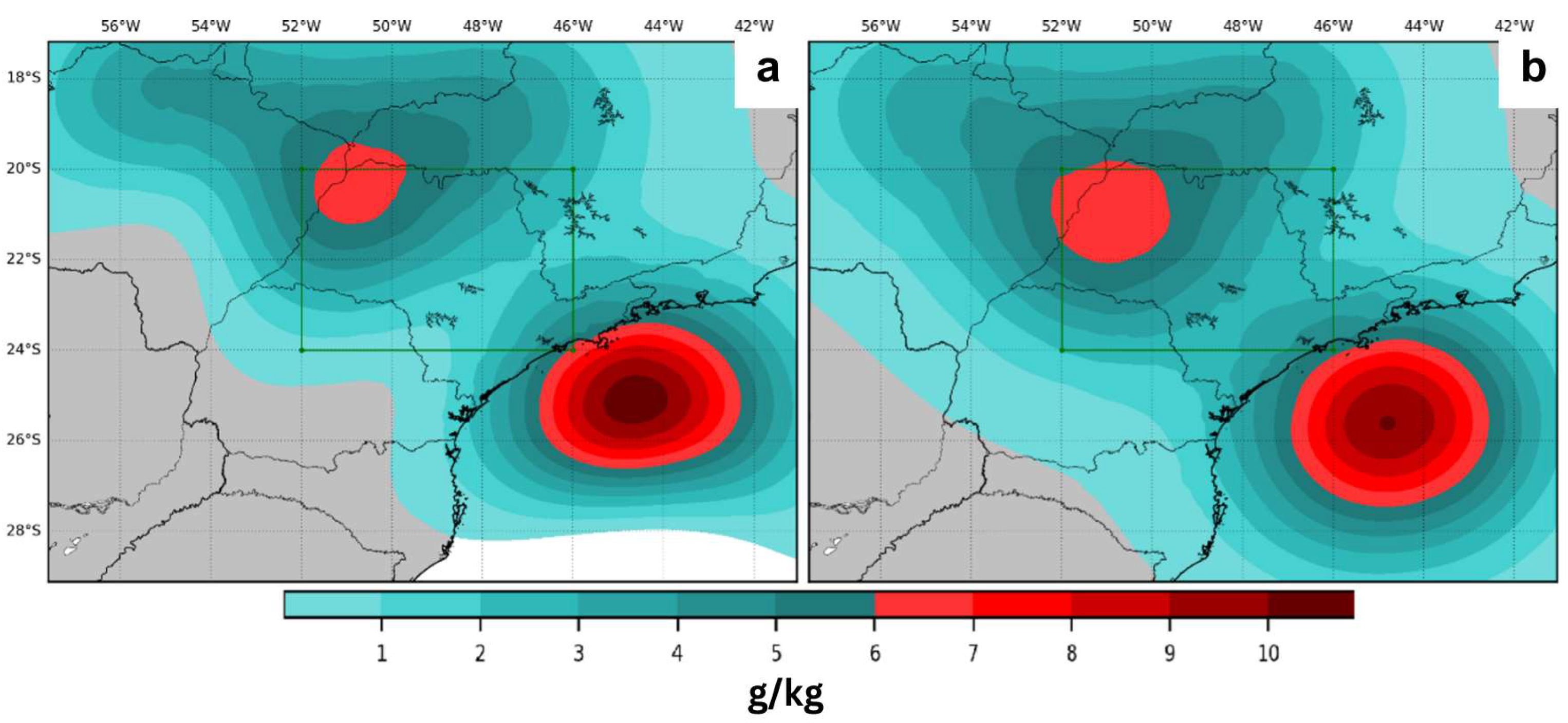
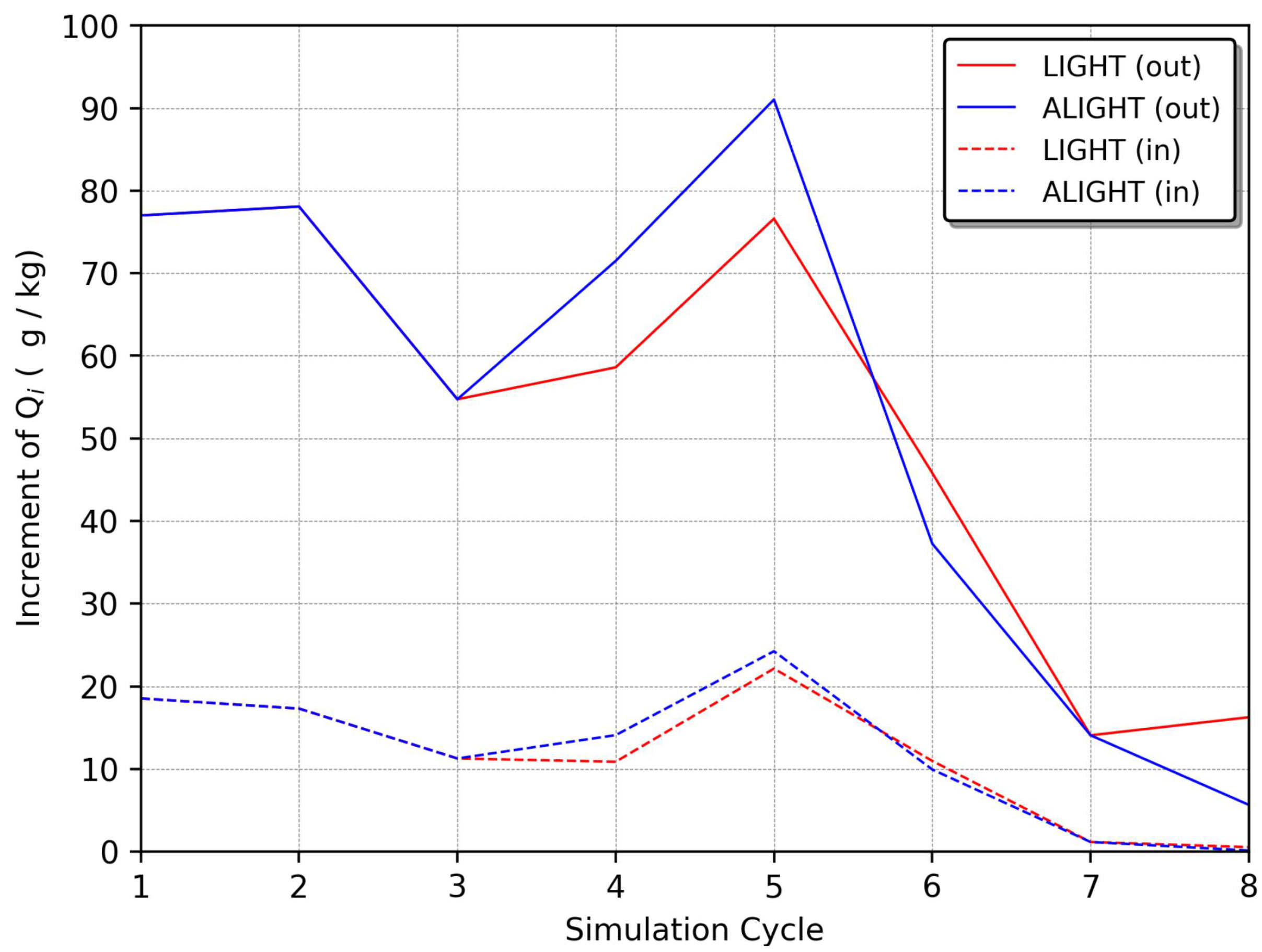



| Ref. | Year | Study Area | Data Source | Model | Assimilation Technique |
|---|---|---|---|---|---|
| [35] | 1999 | Mexican Gulf | NLDN | MM5 | Nudging (precipitation rate) |
| [36] | 2001 | Mexican Gulf | STARNET-1; LIS | MM5 | Nudging (precipitation rate) |
| [18] | 2005 | Europe and Africa | ZEUS | SKIRON/ETA | Nudging (humidity) |
| [37] | 2007 | Midwest USA | NLDN; LMA | COAMPS | Nudging (convective scheme) |
| [42] | 2009 | North Pacific Ocean | LIS; OTD | MM5 | Nudging (convective scheme) |
| [16] | 2012 | Midwest USA | ENTLN | WRF | Nudging (microphysics scheme) |
| [22] | 2012 | Alabama | WWLLN | WRF | Observation operator (CAPE) |
| [43] | 2013 | Southern France | LINET | MM5 | Nudging (convective scheme) |
| [21] | 2013 | USA | ENTLN | WRF | Observation operator (CAPE) |
| [38] | 2014 | North China | SAFIR | WRF | Nudging (microphysics scheme) |
| [39] | 2014 | Northeast USA | ENTLN | WRF | Nudging (microphysics scheme) |
| [20] | 2014 | East USA | WWLLN | WRF | Observation operator () |
| [44] | 2015 | USA | ENTLN | WRF | Nudging (humidity) |
| [45] | 2015 | East USA | ENTLN; USPLN | WRF | Nudging (humidity) |
| [40] | 2016 | Midwest and eastern of USA | WWLLN | WRF | Nudging (humidity) |
| [46] | 2018 | East China | SAFIR | WRF | Nudging (humidity) |
| [41] | 2019 | Northern China | BLNET | WRF | Nudging (microphysics scheme) |
| [47] | 2022 | Southern China | ENTLN | WRF | Nudging (humidity) |
| Simulated/Observed | Yes | No |
|---|---|---|
| Yes | Hits | False alarms |
| No | Misses | Correct negatives |
| Experiment | Simulation Cycle | 30 km and 1 mm | 20 km and 5 mm | 20 km and 10 mm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| POD | FAR | TS | POD | FAR | TS | POD | FAR | TS | ||
| CTRL | i | 0.00 | Null | 0.00 | 0.00 | Null | 0.00 | 0.00 | Null | 0.00 |
| ii | 0.00 | Null | 0.00 | 0.00 | Null | 0.00 | 0.00 | Null | 0.00 | |
| iii | 0.26 | 0.00 | 0.26 | 0.20 | 0.00 | 0.20 | 0.17 | 0.16 | 0.16 | |
| iv | 0.30 | 0.00 | 0.30 | 0.06 | 0.42 | 0.06 | 0.00 | Null | 0.00 | |
| v | 0.06 | 0.68 | 0.06 | 0.00 | Null | 0.00 | 0.00 | Null | 0.00 | |
| vi | 0.10 | 0.00 | 0.10 | 0.08 | 0.00 | 0.08 | 0.03 | 0.68 | 0.03 | |
| vii | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | Null | 0.00 | |
| viii | 0.17 | 0.94 | 0.04 | Null | Null | Null | Null | Null | Null | |
| Mean | 0.11 | 0.44 | 0.09 | 0.05 | 0.36 | 0.05 | 0.02 | 0.42 | 0.02 | |
| LIGHT | i | 0.49 | 0.89 | 0.10 | 0.22 | 0.91 | 0.07 | 0.00 | 1.00 | 0.00 |
| ii | 0.49 | 0.60 | 0.28 | 0.14 | 0.70 | 0.11 | 0.00 | 1.00 | 0.00 | |
| iii | 0.64 | 0.38 | 0.46 | 0.37 | 0.10 | 0.36 | 0.18 | 0.22 | 0.17 | |
| iv | 0.57 | 0.22 | 0.49 | 0.45 | 0.26 | 0.39 | 0.06 | 0.79 | 0.05 | |
| v | 0.55 | 0.45 | 0.38 | 0.21 | 0.76 | 0.13 | 0.07 | 0.94 | 0.04 | |
| vi | 0.44 | 0.74 | 0.20 | 0.22 | 0.17 | 0.21 | 0.03 | 0.44 | 0.03 | |
| vii | 0.46 | 0.93 | 0.06 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | |
| viii | 0.65 | 0.91 | 0.09 | Null | 1.00 | 0.00 | Null | 1.00 | 0.00 | |
| Mean | 0.54 | 0.64 | 0.26 | 0.23 | 0.61 | 0.16 | 0.05 | 0.80 | 0.04 | |
| ALIGHT | i | 0.49 | 0.89 | 0.10 | 0.22 | 0.91 | 0.07 | 0.00 | 1.00 | 0.00 |
| ii | 0.49 | 0.60 | 0.28 | 0.14 | 0.70 | 0.11 | 0.00 | 1.00 | 0.00 | |
| iii | 0.64 | 0.38 | 0.46 | 0.37 | 0.10 | 0.36 | 0.18 | 0.22 | 0.17 | |
| iv | 0.57 | 0.22 | 0.50 | 0.48 | 0.27 | 0.41 | 0.13 | 0.86 | 0.07 | |
| v | 0.56 | 0.45 | 0.38 | 0.20 | 0.78 | 0.12 | 0.01 | 0.99 | 0.01 | |
| vi | 0.44 | 0.75 | 0.19 | 0.22 | 0.16 | 0.21 | 0.03 | 0.72 | 0.03 | |
| vii | 0.46 | 0.93 | 0.06 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | |
| viii | 0.65 | 0.91 | 0.09 | Null | 1.00 | 0.00 | Null | 1.00 | 0.00 | |
| Mean | 0.54 | 0.64 | 0.26 | 0.23 | 0.62 | 0.15 | 0.05 | 0.85 | 0.04 | |
| Experiment | Simulation Cycle | 30 km and 1 mm | 20 km and 5 mm | 20 km and 10 mm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| POD | FAR | TS | POD | FAR | TS | POD | FAR | TS | ||
| CTRL | i | 0.24 | 0.67 | 0.16 | 0.05 | 0.82 | 0.04 | 0.03 | 0.97 | 0.02 |
| ii | 0.00 | Null | 0.00 | Null | 1.00 | Null | Null | Null | Null | |
| iii | 0.00 | Null | 0.00 | Null | Null | Null | Null | Null | Null | |
| iv | Null | Null | Null | Null | Null | Null | Null | Null | Null | |
| v | Null | 1.00 | 0.00 | Null | Null | Null | Null | Null | Null | |
| vi | 0.34 | 0.81 | 0.14 | Null | 1.00 | 0.00 | Null | 1.00 | 0.00 | |
| vii | 0.40 | 0.82 | 0.14 | 0.19 | 0.98 | 0.02 | Null | 1.00 | 0.00 | |
| viii | 0.16 | 0.53 | 0.14 | 0.09 | 0.66 | 0.08 | 0.07 | 0.90 | 0.04 | |
| Mean | 0.19 | 0.77 | 0.08 | 0.11 | 0.86 | 0.03 | 0.05 | 0.97 | 0.01 | |
| LIGHT | i | 0.44 | 0.77 | 0.18 | 0.29 | 0.88 | 0.09 | 0.27 | 0.96 | 0.04 |
| ii | 0.28 | 0.82 | 0.12 | 0.10 | 0.92 | 0.05 | Null | Null | Null | |
| iii | 0.00 | 1.00 | 0.00 | Null | Null | Null | Null | Null | Null | |
| iv | Null | 1.00 | 0.00 | Null | Null | Null | Null | Null | Null | |
| v | Null | 1.00 | 0.00 | Null | Null | Null | Null | Null | Null | |
| vi | 0.47 | 0.96 | 0.04 | Null | Null | Null | Null | 1.00 | 0.00 | |
| vii | 0.47 | 0.87 | 0.11 | 0.36 | 0.98 | 0.02 | Null | 1.00 | 0.00 | |
| viii | 0.49 | 0.71 | 0.22 | 0.30 | 0.88 | 0.10 | 0.35 | 0.94 | 0.06 | |
| Mean | 0.36 | 0.89 | 0.08 | 0.26 | 0.91 | 0.06 | 0.31 | 0.97 | 0.02 | |
| ALIGHT | i | 0.51 | 0.77 | 0.19 | 0.33 | 0.87 | 0.10 | 0.27 | 0.96 | 0.04 |
| ii | 0.37 | 0.79 | 0.15 | 0.11 | 0.92 | 0.05 | Null | Null | Null | |
| iii | 0.00 | 1.00 | 0.00 | Null | Null | Null | Null | Null | Null | |
| iv | Null | Null | Null | Null | Null | Null | Null | Null | Null | |
| v | Null | 1.00 | 0.00 | Null | Null | Null | Null | Null | Null | |
| vi | 0.47 | 0.96 | 0.04 | Null | Null | Null | Null | 1.00 | 0.00 | |
| vii | 0.47 | 0.87 | 0.11 | 0.36 | 0.98 | 0.02 | Null | 1.00 | 0.00 | |
| viii | 0.49 | 0.71 | 0.22 | 0.30 | 0.88 | 0.10 | 0.35 | 0.94 | 0.06 | |
| Mean | 0.39 | 0.87 | 0.10 | 0.27 | 0.91 | 0.06 | 0.31 | 0.97 | 0.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas, V., Jr.; Ferreira, R.C.; Pinto, O., Jr.; Herdies, D.L. Assessing the Impact of Lightning Data Assimilation in the WRF Model. Atmosphere 2024, 15, 826. https://doi.org/10.3390/atmos15070826
Vargas V Jr., Ferreira RC, Pinto O Jr., Herdies DL. Assessing the Impact of Lightning Data Assimilation in the WRF Model. Atmosphere. 2024; 15(7):826. https://doi.org/10.3390/atmos15070826
Chicago/Turabian StyleVargas, Vanderlei, Jr., Rute Costa Ferreira, Osmar Pinto, Jr., and Dirceu Luis Herdies. 2024. "Assessing the Impact of Lightning Data Assimilation in the WRF Model" Atmosphere 15, no. 7: 826. https://doi.org/10.3390/atmos15070826
APA StyleVargas, V., Jr., Ferreira, R. C., Pinto, O., Jr., & Herdies, D. L. (2024). Assessing the Impact of Lightning Data Assimilation in the WRF Model. Atmosphere, 15(7), 826. https://doi.org/10.3390/atmos15070826






