The Evaluation of Rainfall Forecasting in a Global Navigation Satellite System-Assisted Numerical Weather Prediction Model
Abstract
:1. Introduction
2. Data and Methods
2.1. Data Description
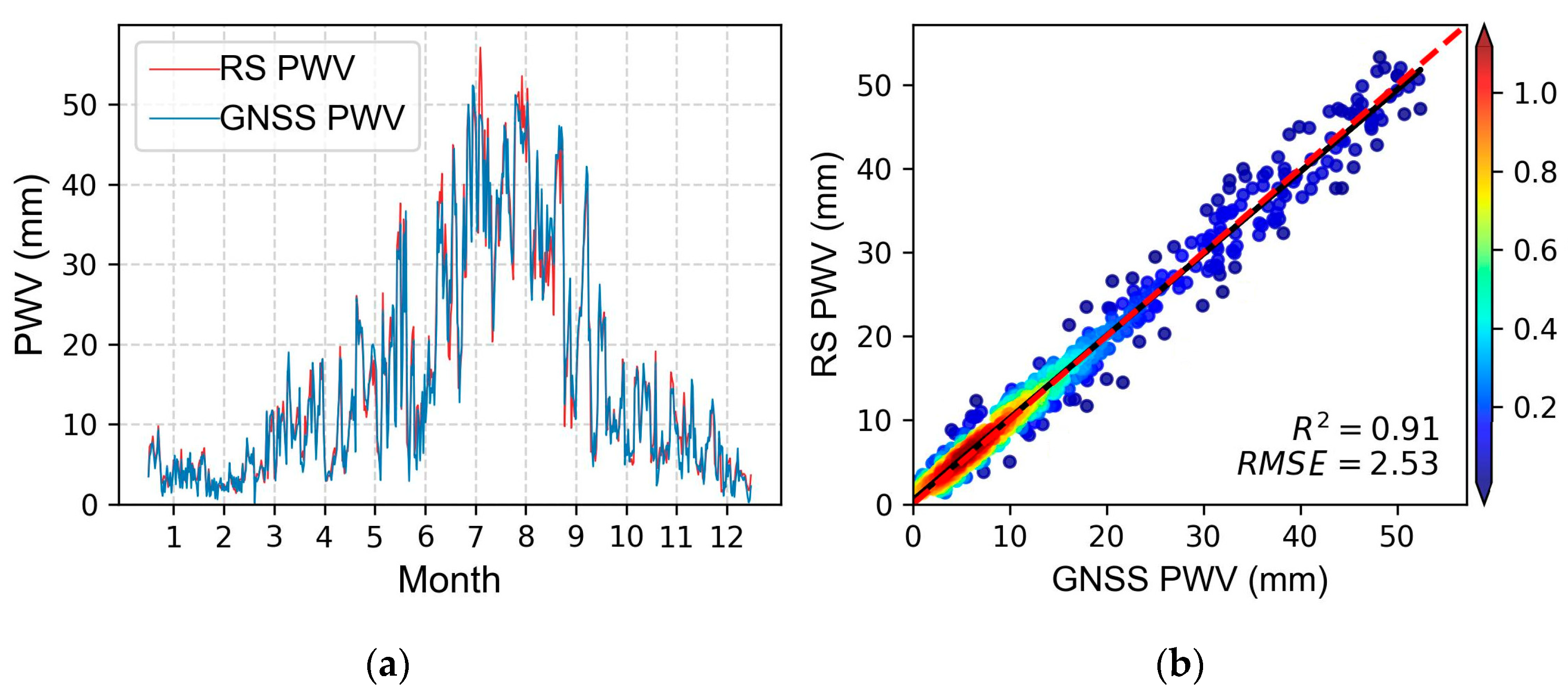
2.1.1. GNSS PWV Data
2.1.2. Meteorological Data
2.1.3. Radiosonde Data
2.1.4. ERA5 Reanalysis Data
2.2. WRF Model
3. Construction of a Rainfall Forecast Platform for GNSS-Assisted NWP Model
3.1. Platform Parameter Setting
3.2. Experimental Scheme and Process
3.3. Accuracy Validation Index
- (1)
- RMSE
- (2)
- RMSEIR
- (3)
- Bias
- (4)
- POD
- (5)
- FAR
- (6)
- TS
- (7)
- ETS
4. Results and Analysis
4.1. Validation of GNSS-Derived PWV
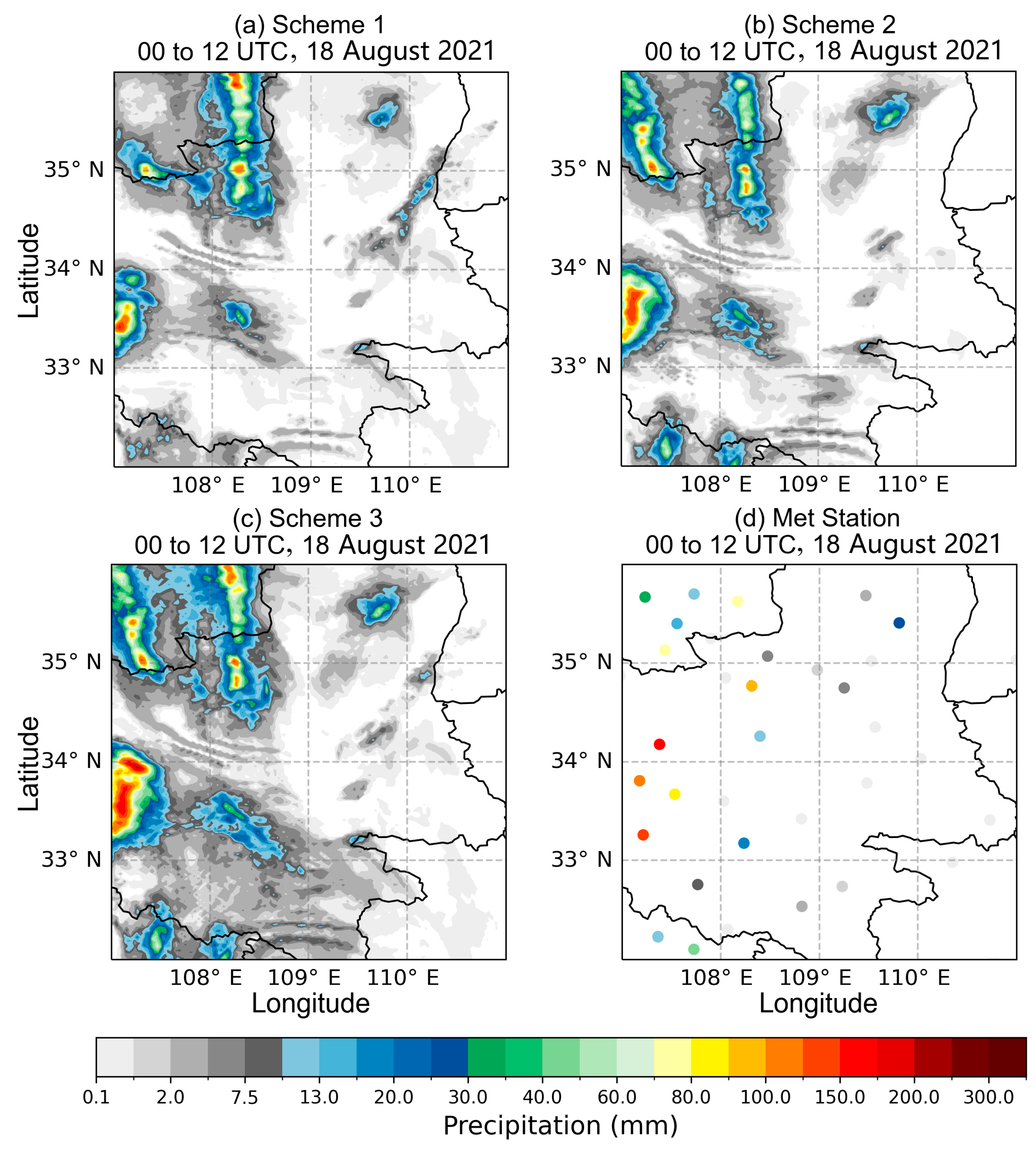
4.2. Accuracy Validation of Forecast Results
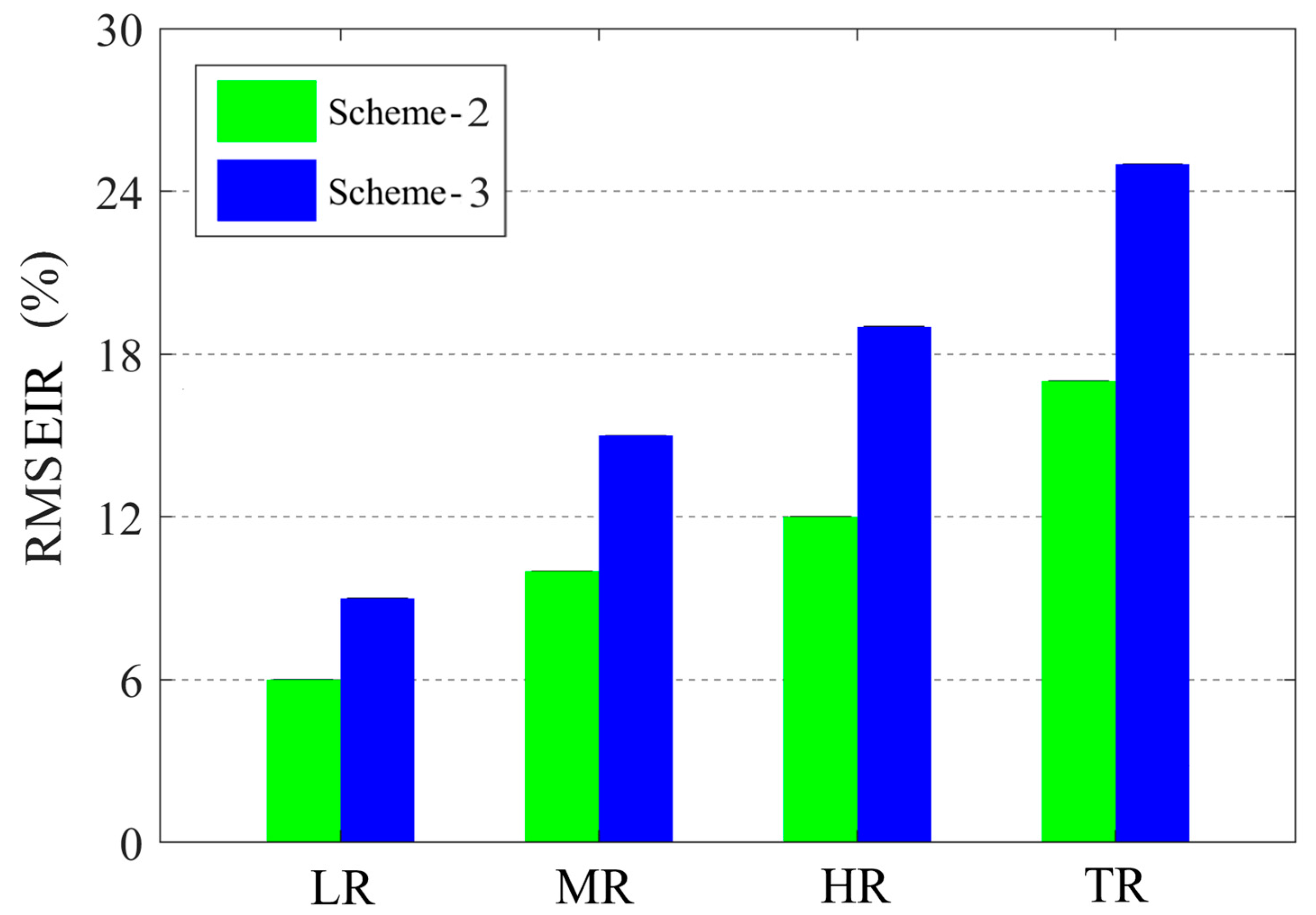
4.3. Analysis of the Impact of the PWV Magnitude on WRF Rainfall Forecast
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palmer, T. The primacy of doubt: Evolution of numerical weather prediction from determinism to probability. J. Adv. Model. Earth Syst. 2017, 9, 730–734. [Google Scholar] [CrossRef]
- Moya-Álvarez, A.S.; Gálvez, J.; Holguín, A.; Estevan, R.; Kumar, S.; Villalobos, E.; Martínez-Castro, D.; Silva, Y. Extreme rainfall forecast with the WRF-ARW model in the Central Andes of Peru. Atmosphere 2018, 9, 362. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M. Review on the role of GNSS meteorology in monitoring water vapor for atmospheric physics. Remote Sens. 2021, 13, 2287. [Google Scholar] [CrossRef]
- Khaniani, A.S.; Motieyan, H.; Mohammadi, A. Rainfall forecast based on GPS PWV together with meteorological parameters using neural network models. J. Atmos. Sol. Terr. Phys. 2021, 214, 105533. [Google Scholar] [CrossRef]
- Flamant, C.; Chazette, P.; Caumont, O.; Di Girolamo, P.; Behrendt, A.; Sicard, M.; Totems, J.; Lange, D.; Fourrié, N.; Brousseau, P.; et al. A network of water vapor Raman lidars for improving heavy precipitation forecasting in southern France: Introducing the WaLiNeAs initiative. Bull. Atmos. Sci. Technol. 2021, 2, 1–21. [Google Scholar] [CrossRef]
- Shrestha, D.L.; Robertson, D.E.; Wang, Q.J.; Pagano, T.C.; Hapuarachchi, H.A.P. Evaluation of numerical weather prediction model precipitation forecasts for short-term streamflow forecasting purpose. Hydrol. Earth Syst. Sci. 2013, 17, 1913–1931. [Google Scholar] [CrossRef]
- Cao, Y.; Kuznetsov, E.; Miao, C.; Chen, S.; Meng, T. The current situation of Russia’s GNSS continuous operating reference station network and thinking on future development. Adv. Space Res. 2024, 73, 3896–3908. [Google Scholar] [CrossRef]
- Zhang, K.; Li, H.; Wang, X.; Zhu, D.; He, Q.; Li, L.; Hu, A.H.A.; Zheng, N.; Li, H. Recent progresses and future prospectives of ground-based GNSS water vapor sounding. Acta Geod. Cartogr. Sin. 2022, 51, 1172–1191. [Google Scholar]
- Wu, Z.; Lu, C.; Zheng, Y.; Liu, Y.; Liu, Y.; Xu, W.; Jin, K.; Tang, Q. Evaluation of shipborne GNSS precipitable water vapor over global oceans from 2014 to 2018. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5802515. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Risanto, C.B.; Castro, C.L.; Moker, J.M., Jr.; Arellano, A.F., Jr.; Adams, D.K.; Fierro, L.M.; Minjarez Sosa, C.M. Evaluating forecast skills of moisture from convective-permitting WRF-ARW model during 2017 North American Monsoon season. Atmosphere 2019, 10, 694. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Guo, Y.R.; Westwater, E.R. Assimilation of precipitable water measurements into a mesoscale numerical model. Mon. Weather Rev. 1993, 121, 1215–1238. [Google Scholar] [CrossRef]
- Mateus, P.; Tomé, R.; Nico, G.; Catalão, J. Three-dimensional variational assimilation of InSAR PWV using the WRFDA model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7323–7330. [Google Scholar] [CrossRef]
- Yuan, Z.; Ding, J.; Chen, M. Preliminary study on applying GPS observations to mesoscale numerical weather prediction model. Acta Meteorol. Sin. 2004, 62, 200–212. [Google Scholar]
- Sharifi, M.A.; Azadi, M.; Khaniani, A.S. Numerical simulation of rainfall with assimilation of conventional and GPS observations over north of Iran. Ann. Geophys. 2016, 59, 0322. [Google Scholar]
- Risanto, C.B.; Castro, C.L.; Arellano, A.F.; Moker, J.M.; Adams, D.K. The impact of assimilating gps precipitable water vapor in convective-permitting wrf-arw on north american monsoon precipitation forecasts over northwest mexico. Mon. Weather Rev. 2021, 149, 3013–3035. [Google Scholar] [CrossRef]
- Rohm, W.; Guzikowski, J.; Wilgan, K.; Kryza, M. 4DVAR assimilation of GNSS zenith path delays and precipitable water into a numerical weather prediction model WRF. Atmos. Meas. Tech. 2019, 12, 345–361. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Liu, Y.; Cao, Y.; Liang, H.; Hu, H.; Liang, J.; Tu, M. Assimilation of GNSS PWV with NCAR-RTFDDA to Improve Prediction of a Landfall Typhoon. Remote Sens. 2022, 14, 178. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, Z.; Chan, P.W.; Hon, K.K. Assimilating GNSS PWV and radiosonde meteorological profiles to improve the PWV and rainfall forecasting performance from the Weather Research and Forecasting (WRF) model over the South China. Atmos. Res. 2023, 286, 106677. [Google Scholar] [CrossRef]
- Corrales, P.B.; Galligani, V.; Ruiz, J.; Sapucci, L.; Dillon, M.E.; García Skabar, Y.; Sacco, M.; Schwartz, C.S.; Nesbitt, S.W. Hourly assimilation of different sources of observations including satellite radiances in a mesoscale convective system case during RELAMPAGO campaign. Atmos. Res. 2023, 281, 106456. [Google Scholar] [CrossRef]
- Brotzge, J.A.; Berchoff, D.; Carlis, D.L.; Carr, F.H.; Carr, R.H.; Gerth, J.J.; Gross, B.D.; Hamill, T.M.; Haupt, S.E.; Jacobs, N.; et al. Challenges and opportunities in numerical weather prediction. Bull. Am. Meteorol. Soc. 2023, 104, E698–E705. [Google Scholar] [CrossRef]
- Imrišek, M.; Derková, M.; Janák, J. Estimation of GNSS tropospheric products and their meteorological exploitation in Slovakia. Contrib. Geophys. Geod. 2020, 50, 83–111. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Huva, R.; Verbois, H.; Walsh, W. Comparisons of next-day solar forecasting for Singapore using 3DVAR and 4DVAR data assimilation approaches with the WRF model. Renew. Energy 2020, 147, 663–671. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Yao, Y. A global model for estimating tropospheric delay and weighted mean temperature developed with atmospheric reanalysis data from 1979 to 2017. Remote Sens. 2019, 11, 1893. [Google Scholar] [CrossRef]
- Ding, J.; Chen, J.; Tang, W.; Song, Z. Spatial–Temporal Variability of Global GNSS-Derived Precipitable Water Vapor (1994–2020) and Climate Implications. Remote Sens. 2022, 14, 3493. [Google Scholar] [CrossRef]
- Meng, L.; Liu, J.; Tarasick, D.W.; Randel, W.J.; Steiner, A.K.; Wilhelmsen, H.; Wang, L.; Haimberger, L. Continuous rise of the tropopause in the Northern Hemisphere over 1980–2020. Sci. Adv. 2021, 7, eabi8065. [Google Scholar] [CrossRef]
- Huang, J.; Yin, J.; Wang, M.; He, Q.; Guo, J.; Zhang, J.; Liang, X.; Xie, Y. Evaluation of five reanalysis products with radiosonde observations over the Central Taklimakan Desert during summer. Earth Space Sci. 2021, 8, e2021EA001707. [Google Scholar] [CrossRef]
- Pryor, S.C.; Shepherd, T.J.; Barthelmie, R.J.; Hahmann, A.N.; Volker, P. Wind farm wakes simulated using WRF. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1256, p. 012025. [Google Scholar]
- Zhang, S.; Xu, S.; Fu, H.; Wu, L.; Liu, Z.; Gao, Y.; Zhao, C.; Wan, W.; Wan, L.; Lu, H.; et al. Toward Earth system modeling with resolved clouds and ocean submesoscales on heterogeneous many-core HPCs. Natl. Sci. Rev. 2023, 10, nwad069. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Liu, Z.; Chen, D.; Yan, P.; Zhang, Y.; Hu, H.; Liang, H.; Liang, X. GPS-ZTD data assimilation and its impact on wintertime haze prediction over North China Plain using WRF 3DVAR and CMAQ modeling system. Environ. Sci. Pollut. Res. 2021, 28, 68523–68538. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Li, C.; Yu, F.; Wang, W. Effect of the assimilation frequency of radar reflectivity on rain storm prediction by using WRF-3DVAR. Remote Sens. 2021, 13, 2103. [Google Scholar] [CrossRef]
- Gleiter, T. Improving Data Assimilation for MJO Prediction Based on Experiments with the Skeleton Model for Tropical Intraseasonal Variability. Master’s Thesis, Ludwig-Maximilians-Universität, München, Germany, 2021. [Google Scholar]
- Ye, X.; Zhu, H.; Wang, J.; Zheng, W.; Zhang, W.; Schenato, L.; Pastuto, A.; Catani, F. Towards hydrometeorological thresholds of reservoir-induced landslide from subsurface strain observations. Sci. China Technol. Sci. 2024, 67, 1907–1922. [Google Scholar] [CrossRef]






| Station | Location | |
|---|---|---|
| Latitude | Longitude | |
| 52495 | 40.8 | 104.5 |
| 52681 | 38.6 | 103.1 |
| 52983 | 35.9 | 104.2 |
| 53463 | 40.9 | 111.6 |
| 53513 | 40.7 | 107.4 |
| 53543 | 39.8 | 109.9 |
| 53614 | 38.5 | 106.2 |
| 53772 | 37.6 | 112.6 |
| 53845 | 36.6 | 109.5 |
| 53915 | 35.6 | 106.7 |
| 57127 | 33.1 | 107.0 |
| Configuration | Domains | ||
|---|---|---|---|
| D01 | D02 | D03 | |
| Projection | Lambert conformal conic | Lambert conformal conic | Lambert conformal conic |
| Number of grid points (North–South × East–West) | 136 × 99 | 259 × 148 | 278 × 222 |
| Grid spacing | 9 km | 3 km | 1 km |
| Number of WRF layers | 38 | 38 | 38 |
| Model top pressure | 1 hPa | 1 hPa | 1 hPa |
| Variable Type | Variable Name |
|---|---|
| Three-dimensional data | Temperature |
| Relative Humidity | |
| Geopotential height | |
| Wind field U and V components | |
| Two-dimensional data | Surface pressure |
| Mean sea level pressure | |
| Surface temperature | |
| 2 m temperature | |
| 2 m relative humidity or specific humidity | |
| 10 m wind field U and V components | |
| Soil temperature and moisture |
| Experimental Scheme | Assimilation Data | Forecast Parameters |
|---|---|---|
| scheme 1 | No assimilation | Precipitation |
| scheme 2 | RS + Met | Precipitation |
| scheme 3 | GNSS PWV + RS + Met | Precipitation |
| Parameter | Scheme | RMSE after Data Assimilation | ||
|---|---|---|---|---|
| 1 h | 6 h | 12 h | ||
| Rainfall (mm) | 2 | 2.17 | 3.87 | 5.12 |
| 3 | 1.39 | 3.56 | 4.93 | |
| Index | Scheme | LR | MR | HR | TR |
|---|---|---|---|---|---|
| POD | 1 | 0.89 | 0.75 | 0.68 | 0.61 |
| 2 | 0.91 | 0.77 | 0.70 | 0.63 | |
| 3 | 0.94 | 0.85 | 0.76 | 0.69 | |
| FAR | 1 | 0.07 | 0.16 | 0.22 | 0.28 |
| 2 | 0.06 | 0.14 | 0.21 | 0.27 | |
| 3 | 0.05 | 0.11 | 0.17 | 0.24 | |
| TS | 1 | 0.84 | 0.66 | 0.57 | 0.49 |
| 2 | 0.86 | 0.68 | 0.58 | 0.51 | |
| 3 | 0.91 | 0.75 | 0.64 | 0.57 | |
| ETS | 1 | 0.80 | 0.61 | 0.53 | 0.46 |
| 2 | 0.82 | 0.64 | 0.55 | 0.48 | |
| 3 | 0.87 | 0.69 | 0.60 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Ma, Y.; Li, Z.; Zhao, Q.; Zhai, Y. The Evaluation of Rainfall Forecasting in a Global Navigation Satellite System-Assisted Numerical Weather Prediction Model. Atmosphere 2024, 15, 992. https://doi.org/10.3390/atmos15080992
Guo H, Ma Y, Li Z, Zhao Q, Zhai Y. The Evaluation of Rainfall Forecasting in a Global Navigation Satellite System-Assisted Numerical Weather Prediction Model. Atmosphere. 2024; 15(8):992. https://doi.org/10.3390/atmos15080992
Chicago/Turabian StyleGuo, Hongwu, Yongjie Ma, Zufeng Li, Qingzhi Zhao, and Yuan Zhai. 2024. "The Evaluation of Rainfall Forecasting in a Global Navigation Satellite System-Assisted Numerical Weather Prediction Model" Atmosphere 15, no. 8: 992. https://doi.org/10.3390/atmos15080992
APA StyleGuo, H., Ma, Y., Li, Z., Zhao, Q., & Zhai, Y. (2024). The Evaluation of Rainfall Forecasting in a Global Navigation Satellite System-Assisted Numerical Weather Prediction Model. Atmosphere, 15(8), 992. https://doi.org/10.3390/atmos15080992






