Integrating Cost-Effective Measurements and CFD Modeling for Accurate Air Quality Assessment
Abstract
:1. Introduction
2. Methodology
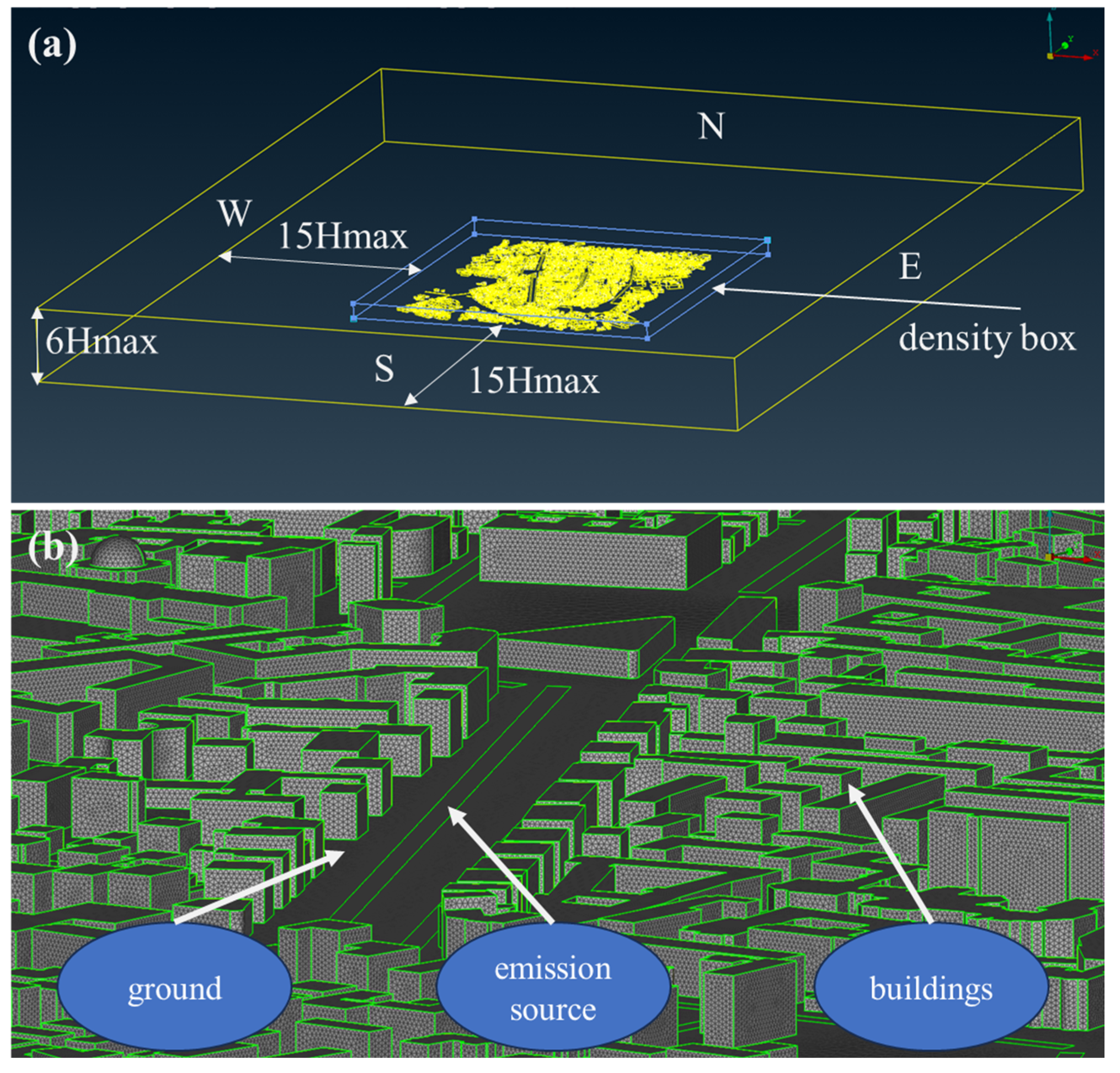
2.1. Test Case Area and Computational Grid
2.2. Description of smartAQnet
2.3. Calibration Methodology
2.4. Numerical Model
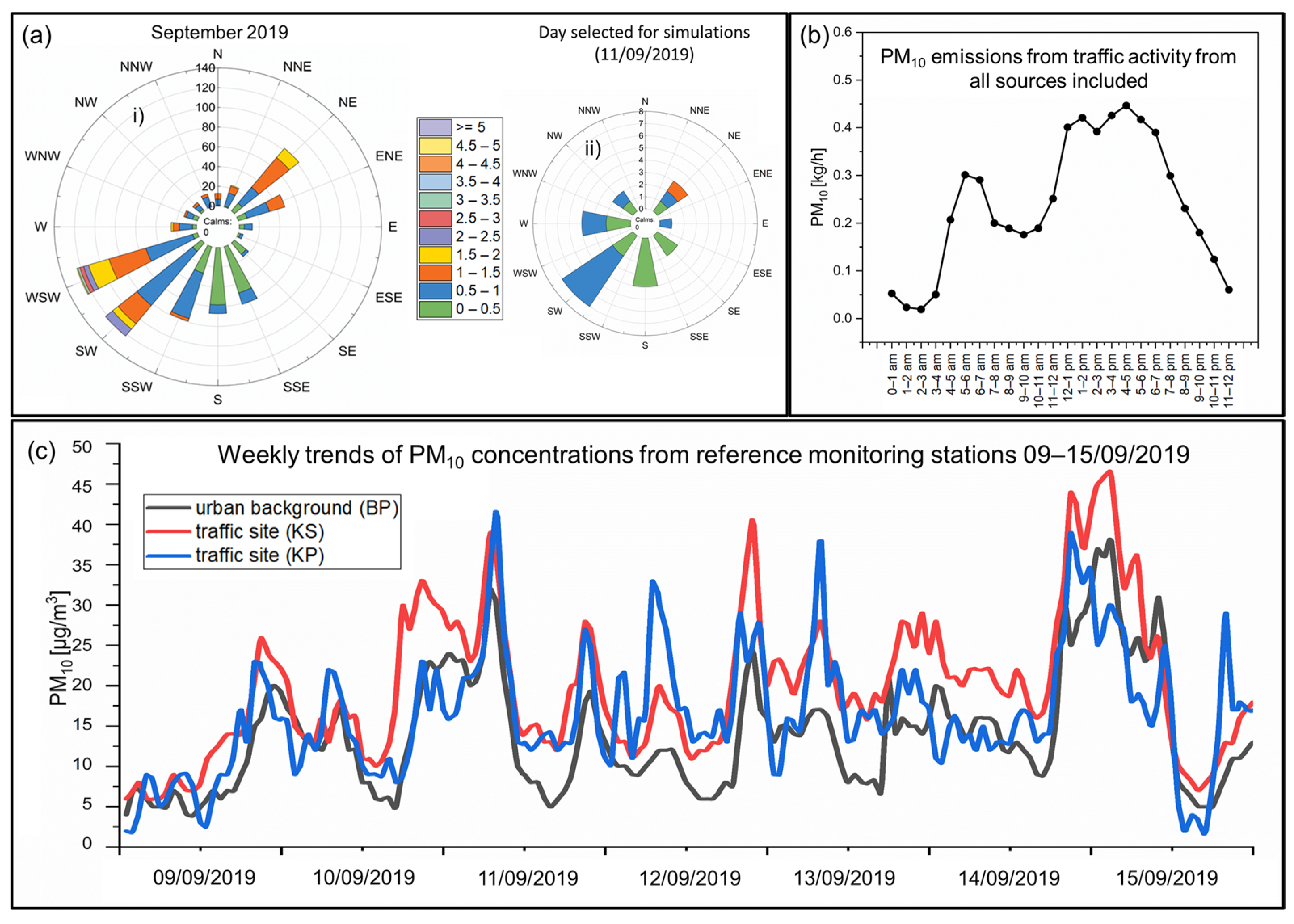
2.5. Traffic Emissions and Meteorological Data
3. Results and Discussion
3.1. Model Results
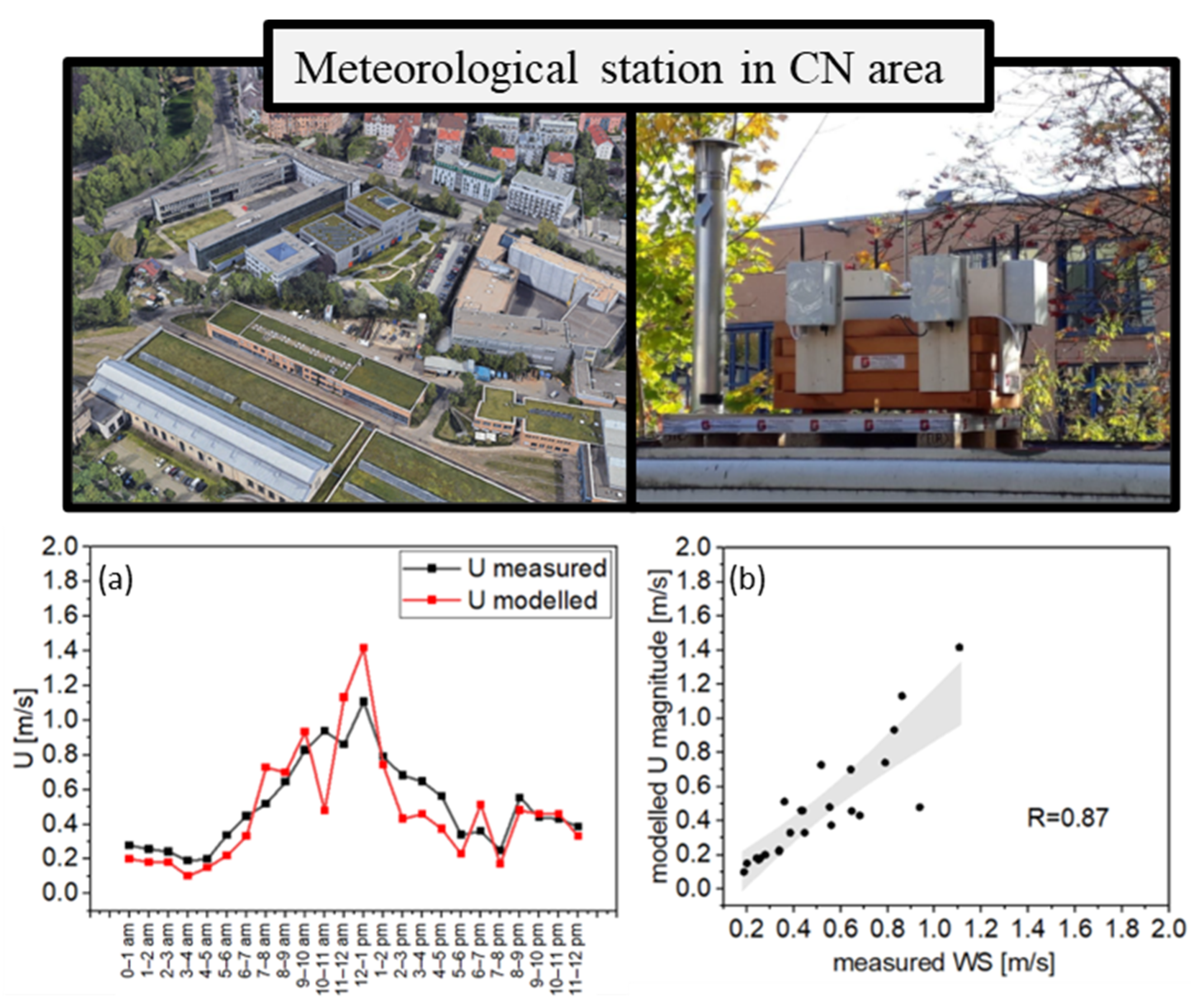
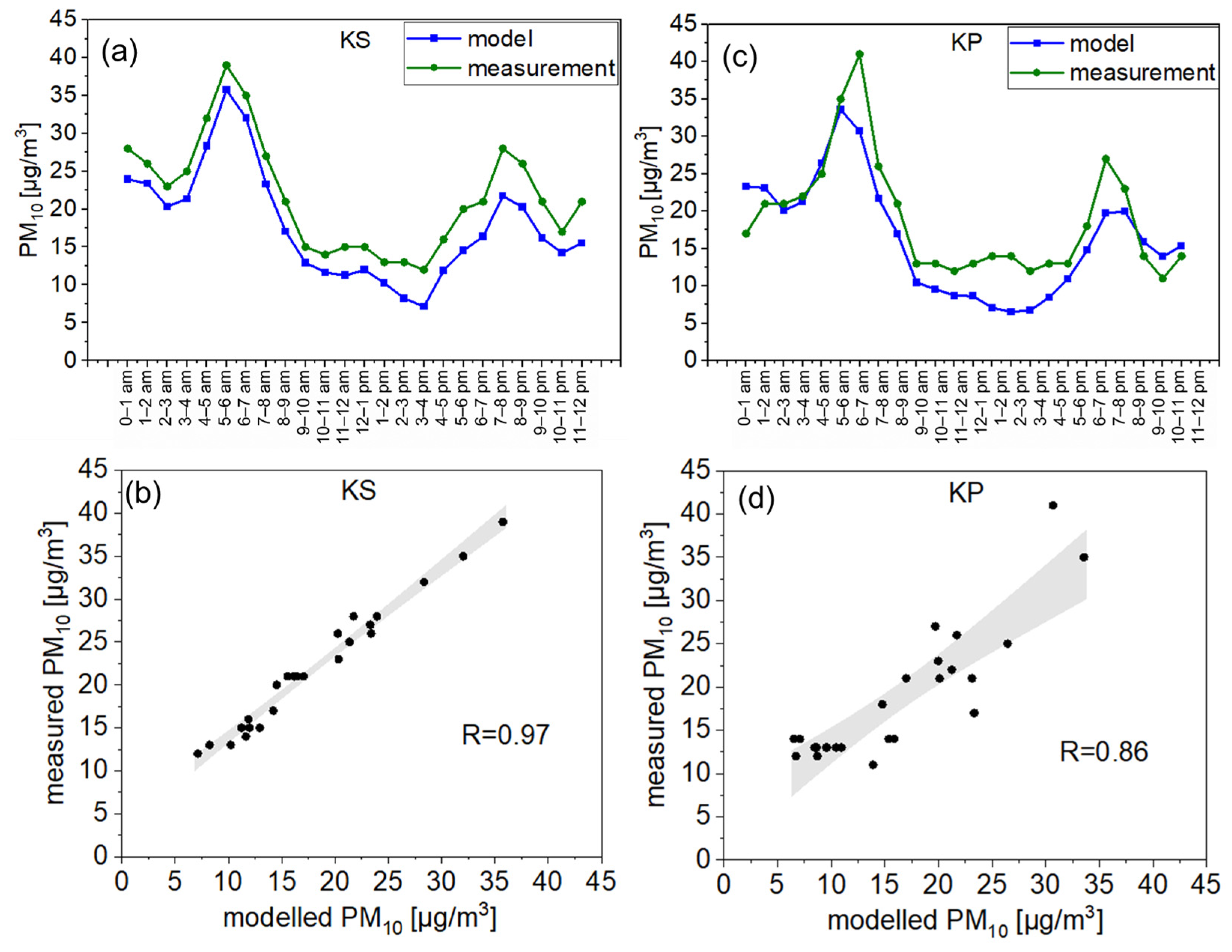
3.2. Model Validation
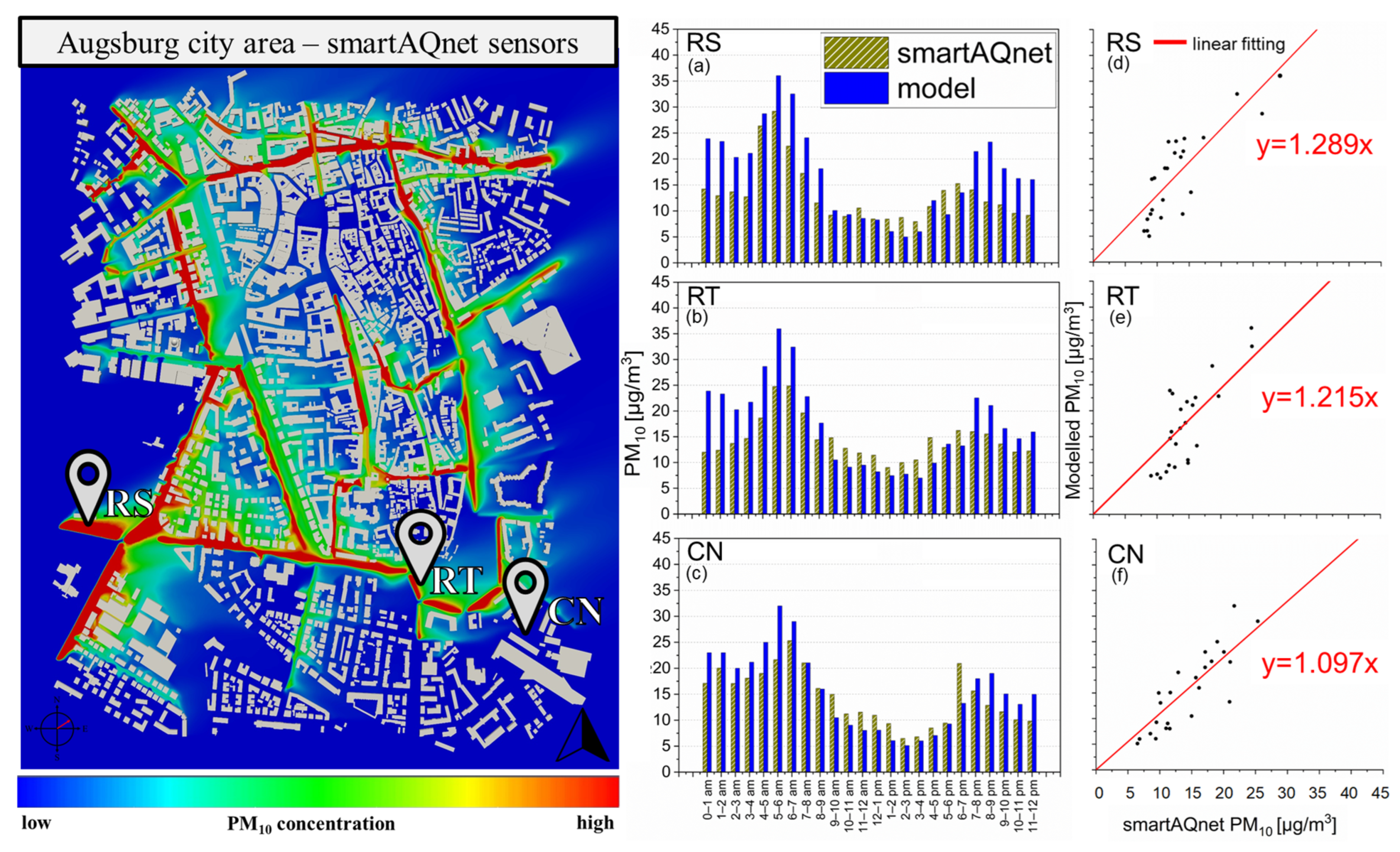
3.3. Comparison with smartAQnet Indications
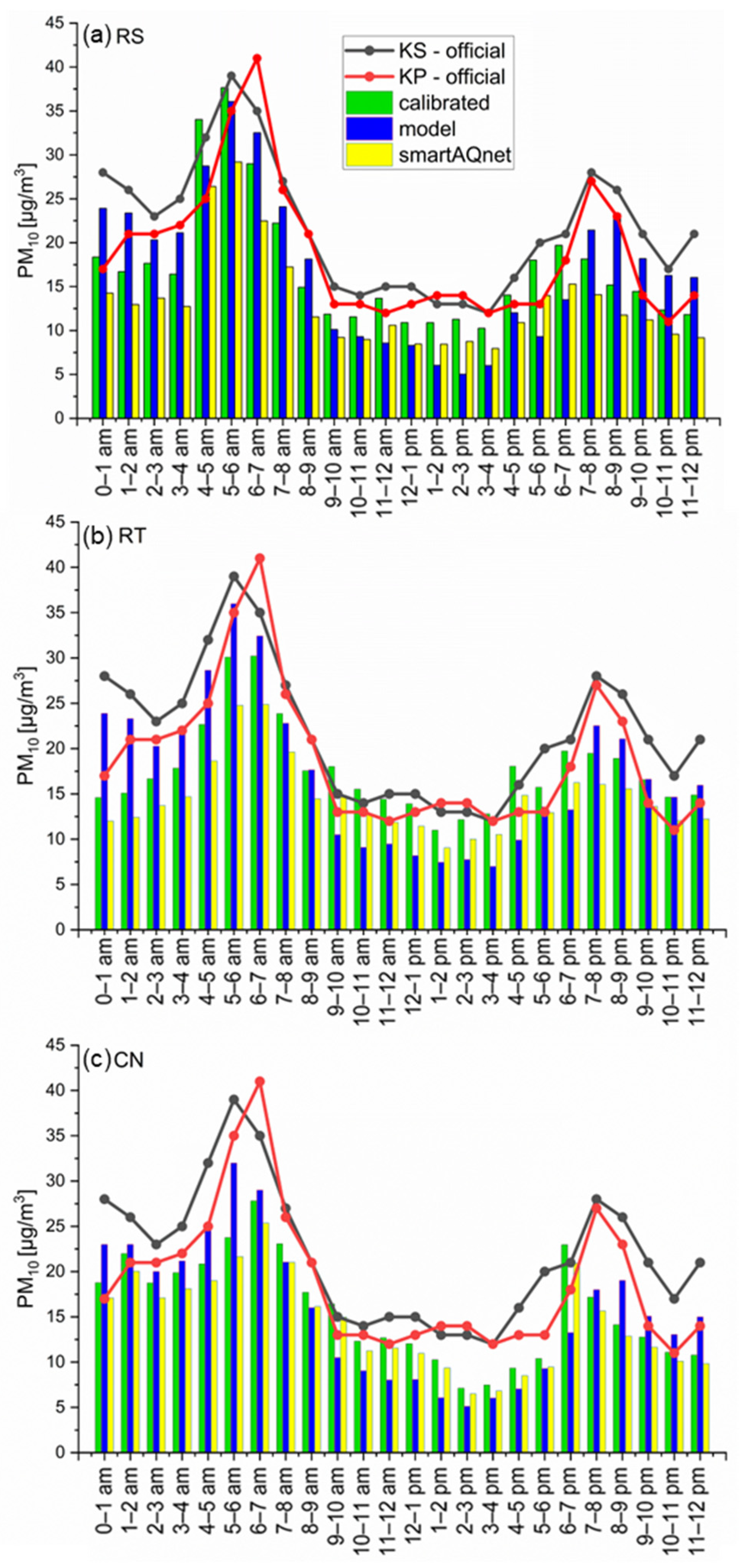
3.4. Calibration of SmartAQnet Indications
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Piracha, A.; Chaudhary, M.T. Urban Air Pollution, Urban Heat Island and Human Health: A Review of the Literature. Sustainability 2022, 14, 9234. [Google Scholar] [CrossRef]
- Schwela, D.H.; Haq, G. Strengths and Weaknesses of the WHO Urban Air Pollutant Database. Aerosol Air Qual. Res. 2020, 20, 1026–1037. [Google Scholar] [CrossRef]
- Munir, S.; Mayfield, M.; Coca, D.; Jubb, S.A.; Osammor, O. Analysing the Performance of Low-Cost Air Quality Sensors, Their Drivers, Relative Benefits and Calibration in Cities—A Case Study in Sheffield. Environ. Monit. Assess. 2019, 191, 94. [Google Scholar] [CrossRef] [PubMed]
- Giordano, M.R.; Malings, C.; Pandis, S.N.; Presto, A.A.; McNeill, V.F.; Westervelt, D.M.; Beekmann, M.; Subramanian, R. From Low-Cost Sensors to High-Quality Data: A Summary of Challenges and Best Practices for Effectively Calibrating Low-Cost Particulate Matter Mass Sensors. J. Aerosol Sci. 2021, 158, 105833. [Google Scholar] [CrossRef]
- Raysoni, A.U.; Pinakana, S.D.; Mendez, E.; Wladyka, D.; Sepielak, K.; Temby, O. A Review of Literature on the Usage of Low-Cost Sensors to Measure Particulate Matter. Earth 2023, 4, 168–186. [Google Scholar] [CrossRef]
- Schmitz, S.; Towers, S.; Villena, G.; Caseiro, A.; Wegener, R.; Klemp, D.; Langer, I.; Meier, F.; Von Schneidemesser, E. Unravelling a Black Box: An Open-Source Methodology for the Field Calibration of Small Air Quality Sensors. Atmos. Meas. Tech. 2021, 14, 7221–7241. [Google Scholar] [CrossRef]
- Liang, L. Calibrating Low-Cost Sensors for Ambient Air Monitoring: Techniques, Trends, and Challenges. Environ. Res. 2021, 197, 111163. [Google Scholar] [CrossRef]
- Stavroulas, I.; Grivas, G.; Michalopoulos, P.; Liakakou, E.; Bougiatioti, A.; Kalkavouras, P.; Fameli, K.M.; Hatzianastassiou, N.; Mihalopoulos, N.; Gerasopoulos, E. Field Evaluation of Low-Cost PM Sensors (Purple Air PA-II) Under Variable Urban Air Quality Conditions, in Greece. Atmosphere 2020, 11, 926. [Google Scholar] [CrossRef]
- Frederickson, L.B.; Sidaraviciute, R.; Schmidt, J.A.; Hertel, O.; Johnson, M.S. Are Dense Networks of Low-Cost Nodes Really Useful for Monitoring Air Pollution? A Case Study in Staffordshire. Atmos. Chem. Phys. 2022, 22, 13949–13965. [Google Scholar] [CrossRef]
- Bisignano, A.; Carotenuto, F.; Zaldei, A.; Giovannini, L. Field Calibration of a Low-Cost Sensors Network to Assess Traffic-Related Air Pollution along the Brenner Highway. Atmos. Environ. 2022, 275, 119008. [Google Scholar] [CrossRef]
- Bagkis, E.; Kassandros, T.; Karatzas, K. Learning Calibration Functions on the Fly: Hybrid Batch Online Stacking Ensembles for the Calibration of Low-Cost Air Quality Sensor Networks in the Presence of Concept Drift. Atmosphere 2022, 13, 416. [Google Scholar] [CrossRef]
- Liang, C.J.; Yu, P.R. Assessment and Improvement of Two Low-Cost Particulate Matter Sensor Systems by Using Spatial Interpolation Data from Air Quality Monitoring Stations. Atmosphere 2021, 12, 300. [Google Scholar] [CrossRef]
- Paul, T.; Riedel, T.; Matthias, B. Spatial Interpolation of Air Quality Data with 616 Multidimensional Gaussian Processes. In INFORMATIK 2021, Proceedings of the Workshop Künstliche Intelligenz 618 in der Umweltinformatik (KIUI-2021), Berlin, Germany, 27 September 2021–1 October 2021; Gesellschaft für Informatik: Bonn, Germany, 2021; pp. 269–286. PISSN: 1617-5468; ISBN 978-3-88579-708-1. [Google Scholar] [CrossRef]
- Santiago, J.L.; Martín, F.; Martilli, A. A Computational Fluid Dynamic Modelling Approach to Assess the Representativeness of Urban Monitoring Stations. Sci. Total Environ. 2013, 454–455, 61–72. [Google Scholar] [CrossRef]
- Du, Y.; Blocken, B.; Abbasi, S.; Pirker, S. Efficient and High-Resolution Simulation of Pollutant Dispersion in Complex Urban Environments by Island-Based Recurrence CFD. Environ. Model. Softw. 2021, 145, 105172. [Google Scholar] [CrossRef]
- Ioannidis, G.; Li, C.; Tremper, P.; Riedel, T.; Ntziachristos, L. Application of CFD Modelling for Pollutant Dispersion at an Urban Traffic Hotspot. Atmosphere 2024, 15, 113. [Google Scholar] [CrossRef]
- Antoniou, A.; Ioannidis, G.; Ntziachristos, L. Realistic Simulation of Air Pollution in an Urban Area to Promote Environmental Policies. Environ. Model. Softw. 2024, 172, 105918. [Google Scholar] [CrossRef]
- Boikos, C.; Rapkos, N.; Ioannidis, G.; Oppo, S.; Armengaud, A.; Siamidis, P.; Tsegas, G.; Ntziachristos, L. Factors Affecting Pedestrian-Level Ship Pollution in Port Areas: CFD in the Service of Policy-Making. Build. Environ. 2024, 258, 111594. [Google Scholar] [CrossRef]
- Schäfer, K.; Budde, M.; Cyrys, J.; Emeis, S.; Gratza, T.; Grimm, H.; Hank, M.; Hinterreiter, S.; Pesch, M.; Petersen, E.; et al. Smart Air Quality Network for Spatial High-Resolution Monitoring in Urban Area; SPIE-Intl Soc Optical Eng: St Bellingham, WA, USA, 2018; p. 10. [Google Scholar]
- Trindade da Silva, F.; Costa Reis, N.; Santos, J.M.; Valentim Goulart, E.; Simões Maciel, F.; Bragança, L.; Engel de Alvarez, C. Atmospheric Dispersion and Urban Planning: An Interdisciplinary Approach to City Modeling. Sustain. Cities Soc. 2021, 70, 102882. [Google Scholar] [CrossRef]
- Gkirmpas, P.; Tsegas, G.; Ioannidis, G.; Vlachokostas, C.; Moussiopoulos, N. Identification of an Unknown Stationary Emission Source in Urban Geometry Using Bayesian Inference. Atmosphere 2024, 15, 871. [Google Scholar] [CrossRef]
- Blocken, B. Computational Fluid Dynamics for Urban Physics: Importance, Scales, Possibilities, Limitations and Ten Tips and Tricks towards Accurate and Reliable Simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Ariff, M.; Salim, S.M.; Cheong, S. Wall Y + approach for dealing with turbulent flow over a surface mounted cube: Part 1—Low reynolds number. In Proceedings of the Seventh International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia, 9–11 December 2009. [Google Scholar]
- Pantusheva, M.; Mitkov, R.; Hristov, P.O.; Petrova-Antonova, D. Air Pollution Dispersion Modelling in Urban Environment Using CFD: A Systematic Review. Atmosphere 2022, 13, 1640. [Google Scholar] [CrossRef]
- Li, C.; Budde, M.; Tremper, P.; Schäfer, K.; Riesterer, J.; Redelstein, J.; Petersen, E.; Khedr, M.; Liu, X.; Köpke, M.; et al. SmartAQnet 2020: A New Open Urban Air Quality Dataset from Heterogeneous PM Sensors; Proscience: Culver City, CA, USA, 2021. [Google Scholar]
- Budde, M.; Riedel, T.; Schäfer, K. Mid-Term and 1st International Networking Workshop of the SmartAQnet Project December 4th and 5th 2018, Munich; Karlsruher Institut für Technologie (KIT): Karlsruhe, Germany, 2019. [Google Scholar] [CrossRef]
- Budde, M.; Schwarz, A.; Müller, T.; Schwarz, A.D.; Laquai, B.; Streibl, N.; Schindler, G.; Köpke, M.; Riedel, T.; Dittler, A.; et al. Potential and Limitations of the Low-Cost SDS011 Particle Sensor for Monitoring Urban Air Quality. ProScience 2018, 5, 6–12. [Google Scholar] [CrossRef]
- Peralta, C.; Nugusse, H.; Kokilavani, S.P.; Schmidt, J.; Stoevesandt, B. Validation of the SimpleFoam (RANS) Solver for the Atmospheric Boundary Layer in Complex Terrain. ITM Web Conf. 2014, 2, 01002. [Google Scholar] [CrossRef]
- Elfverson, D.; Lejon, C. Use and Scalability of Openfoam for Wind Fields and Pollution Dispersion with Building- and Ground-Resolving Topography. Atmosphere 2021, 12, 1124. [Google Scholar] [CrossRef]
- Bonifacio, H.F.; Maghirang, R.G.; Glasgow, L.A. Numerical Simulation of Transport of Particles Emitted from Ground-Level Area Source Using AERMOD and CFD. Eng. Appl. Comput. Fluid Mech. 2014, 8, 488–502. [Google Scholar] [CrossRef]
- Holmes, N.S.; Morawska, L. A Review of Dispersion Modelling and Its Application to the Dispersion of Particles: An Overview of Different Dispersion Models Available. Atmos. Environ. 2006, 40, 5902–5928. [Google Scholar] [CrossRef]
- Amorim, J.H.; Rodrigues, V.; Tavares, R.; Valente, J.; Borrego, C. CFD Modelling of the Aerodynamic Effect of Trees on Urban Air Pollution Dispersion. Sci. Total Environ. 2013, 461–462, 541–551. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Turbulent Schmidt Numbers for CFD Analysis with Various Types of Flowfield. Atmos. Environ. 2007, 41, 8091–8099. [Google Scholar] [CrossRef]
- Yang, Y.; Gu, M.; Chen, S.; Jin, X. New Inflow Boundary Conditions for Modelling the Neutral Equilibrium Atmospheric Boundary Layer in Computational Wind Engineering. J. Wind Eng. Ind. Aerodyn. 2009, 97, 88–95. [Google Scholar] [CrossRef]
- Irwan Ramli, N.; Idris Ali, M.; Saad, H. Estimation of the Roughness Length (zo) in Malaysia Using Satellite Image. In Proceedings of the Seventh Asia-Pacific Conference on Wind Engineering, Taipei, Taiwan, 8–12 November 2009. [Google Scholar]
- Boikos, C.; Siamidis, P.; Oppo, S.; Armengaud, A.; Tsegas, G.; Mellqvist, J.; Conde, V.; Ntziachristos, L. Validating CFD Modelling of Ship Plume Dispersion in an Urban Environment with Pollutant Concentration Measurements. Atmos. Environ. 2024, 319, 120261. [Google Scholar] [CrossRef]
- Toscano, D.; Marro, M.; Mele, B.; Murena, F.; Salizzoni, P. Assessment of the Impact of Gaseous Ship Emissions in Ports Using Physical and Numerical Models: The Case of Naples. Build. Environ. 2021, 196, 107812. [Google Scholar] [CrossRef]
- Ricci, A.; Janssen, W.D.; van Wijhe, H.J.; Blocken, B. CFD Simulation of Wind Forces on Ships in Ports: Case Study for the Rotterdam Cruise Terminal. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104315. [Google Scholar] [CrossRef]
- Murray, D.R.; Newman, M.B. Probability Analyses of Combining Background Concentrations with Model-Predicted Concentrations. J. Air Waste Manag. Assoc. 2014, 64, 248–254. [Google Scholar] [CrossRef] [PubMed]
- Jon, K.S.; Huang, Y.; Sin, C.H.; Cui, P.; Luo, Y. Influence of Wind Direction on the Ventilation and Pollutant Dispersion in Different 3D Street Canyon Configurations: Numerical Simulation and Wind-Tunnel Experiment. Environ. Sci. Pollut. Res. 2023, 30, 31647–31675. [Google Scholar] [CrossRef]
- Hang, J.; Liang, J.; Wang, X.; Zhang, X.; Wu, L.; Shao, M. Investigation of O3–NOx–VOCs Chemistry and Pollutant Dispersion in Street Canyons with Various Aspect Ratios by CFD Simulations. Build. Environ. 2022, 226, 109667. [Google Scholar] [CrossRef]
- Di Sabatino, S.; Buccolieri, R.; Olesen, H.R.; Ketzel, M.; Berkowicz, R.; Franke, J.; Schatzmann, M.; Schlünzen, K.H.; Leitl, B.; Britter, R.; et al. COST 732 in Practice: The MUST Model Evaluation Exercise. Int. J. Environ. Pollut. 2011, 44, 403–418. [Google Scholar] [CrossRef]
- Di Sabatino, S.; Buccolieri, R.; Pulvirenti, B.; Britter, R. Simulations of Pollutant Dispersion within Idealised Urban-Type Geometries with CFD and Integral Models. Atmos. Environ. 2007, 41, 8316–8329. [Google Scholar] [CrossRef]
- Goricsán, I.; Balczó, M.; Balogh, M.; Czáder, K.; Rákai, A.; Tonkó, C. Simulation of Flow in an Idealised City Using Various CFD Codes. Int. J. Environ. Pollut. 2011, 44, 359–367. [Google Scholar] [CrossRef]
- Gómez-suárez, J.; Arroyo, P.; Alfonso, R.; Suárez, J.I.; Pinilla-gil, E.; Lozano, J. A Novel Bike-Mounted Sensing Device with Cloud Connectivity for Dynamic Air-Quality Monitoring by Urban Cyclists. Sensors 2022, 22, 1272. [Google Scholar] [CrossRef] [PubMed]


| Elements | Boundary Condition Type in CFD Model | ||
|---|---|---|---|
| Velocity U | k | Epsilon | |
| inlets | atmBoundary | fixedValue | fixedValue |
| LayerInletVelocity | |||
| outlets | pressureInlet | inletOutlet | inletOutlet |
| OutletVelocity | |||
| buildings | noSlip | kqRWallFunction | epsilonWallFunction |
| emission sources | fixedValue | kqRWallFunction | epsilonWallFunction |
| ground | noSlip | kqRWallFunction | epsilonWallFunction |
| top | symmetry | symmetry | symmetry |
| RS smartAQnet | RS Calibrated | RT smartAQnet | RT Calibrated | CN smartAQnet | CN Calibrated | Ideal | Accepted | |
|---|---|---|---|---|---|---|---|---|
| HIT RATE | 0.38 | 0.68 | 0.38 | 0.66 | 0.63 | 0.67 | 1 | ≥0.66 |
| FB | 0.36 | 0.11 | 0.25 | 0.11 | 0.1 | 0.02 | 0 | −0.3 ≤ FB ≤ 0.3 |
| MG | 1.2 | 0.93 | 1.09 | 0.95 | 1.01 | 0.97 | 1 | 0.7 ≤ MG ≤ 1.3 |
| NMSE | 0.47 | 0.13 | 0.42 | 0.26 | 0.09 | 0.05 | 0 | ≤1.5 |
| VG | 1.17 | 1.14 | 1.13 | 1.1 | 1.08 | 1.07 | 1 | ≤1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ioannidis, G.; Tremper, P.; Li, C.; Riedel, T.; Rapkos, N.; Boikos, C.; Ntziachristos, L. Integrating Cost-Effective Measurements and CFD Modeling for Accurate Air Quality Assessment. Atmosphere 2024, 15, 1056. https://doi.org/10.3390/atmos15091056
Ioannidis G, Tremper P, Li C, Riedel T, Rapkos N, Boikos C, Ntziachristos L. Integrating Cost-Effective Measurements and CFD Modeling for Accurate Air Quality Assessment. Atmosphere. 2024; 15(9):1056. https://doi.org/10.3390/atmos15091056
Chicago/Turabian StyleIoannidis, Giannis, Paul Tremper, Chaofan Li, Till Riedel, Nikolaos Rapkos, Christos Boikos, and Leonidas Ntziachristos. 2024. "Integrating Cost-Effective Measurements and CFD Modeling for Accurate Air Quality Assessment" Atmosphere 15, no. 9: 1056. https://doi.org/10.3390/atmos15091056
APA StyleIoannidis, G., Tremper, P., Li, C., Riedel, T., Rapkos, N., Boikos, C., & Ntziachristos, L. (2024). Integrating Cost-Effective Measurements and CFD Modeling for Accurate Air Quality Assessment. Atmosphere, 15(9), 1056. https://doi.org/10.3390/atmos15091056







