Effects of Discretization of Smagorinsky–Lilly Subgrid Scale Model on Large-Eddy Simulation of Stable Boundary Layers
Abstract
:1. Introduction
2. Methodology
2.1. Homogeneous Isotropic Turbulence Direct Numerical Simulation
2.2. Large-Eddy Simulation
2.3. Subgrid-Scale Model Discretization
3. Results
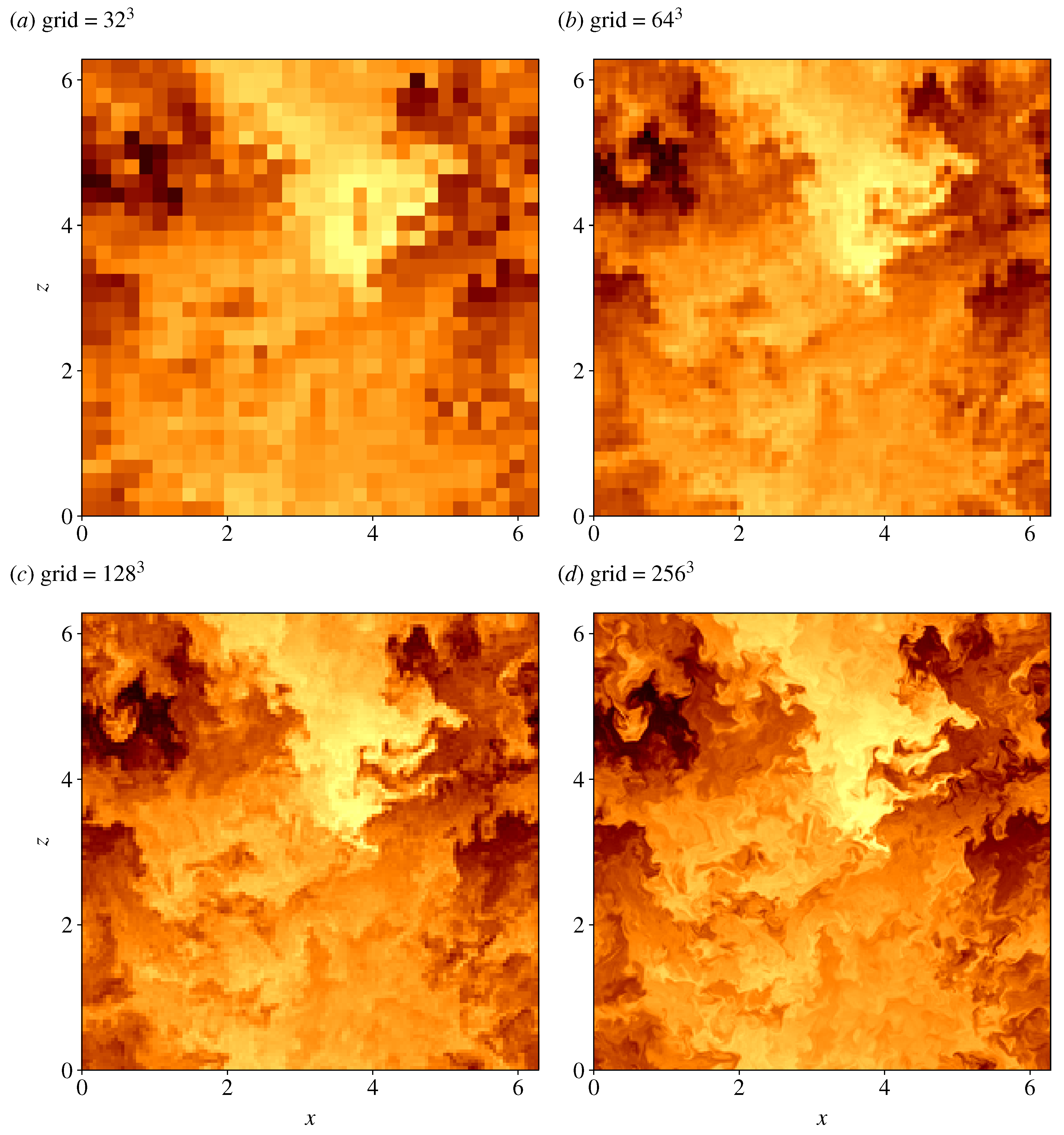
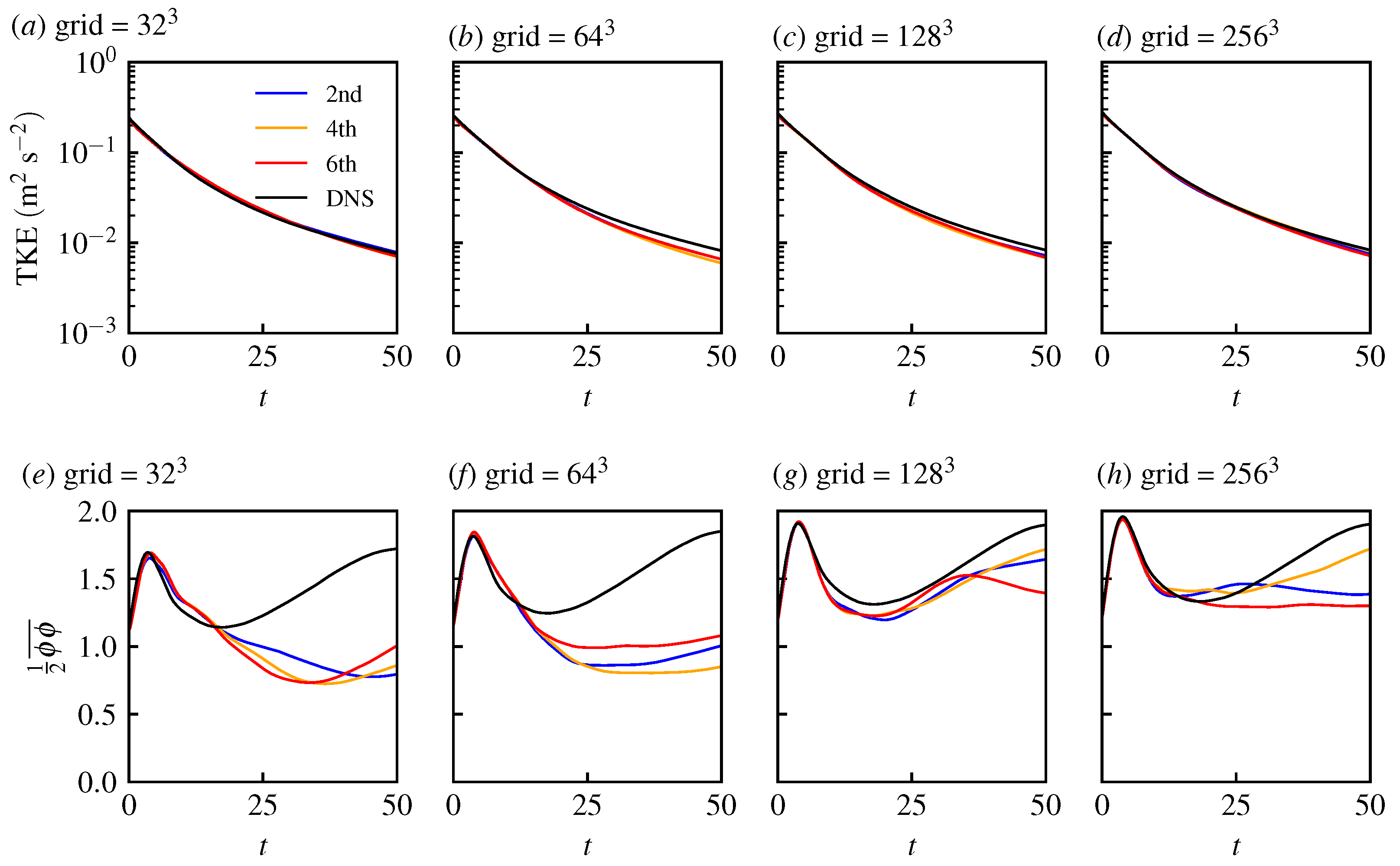
3.1. Homogeneous Isotropic Turbulence
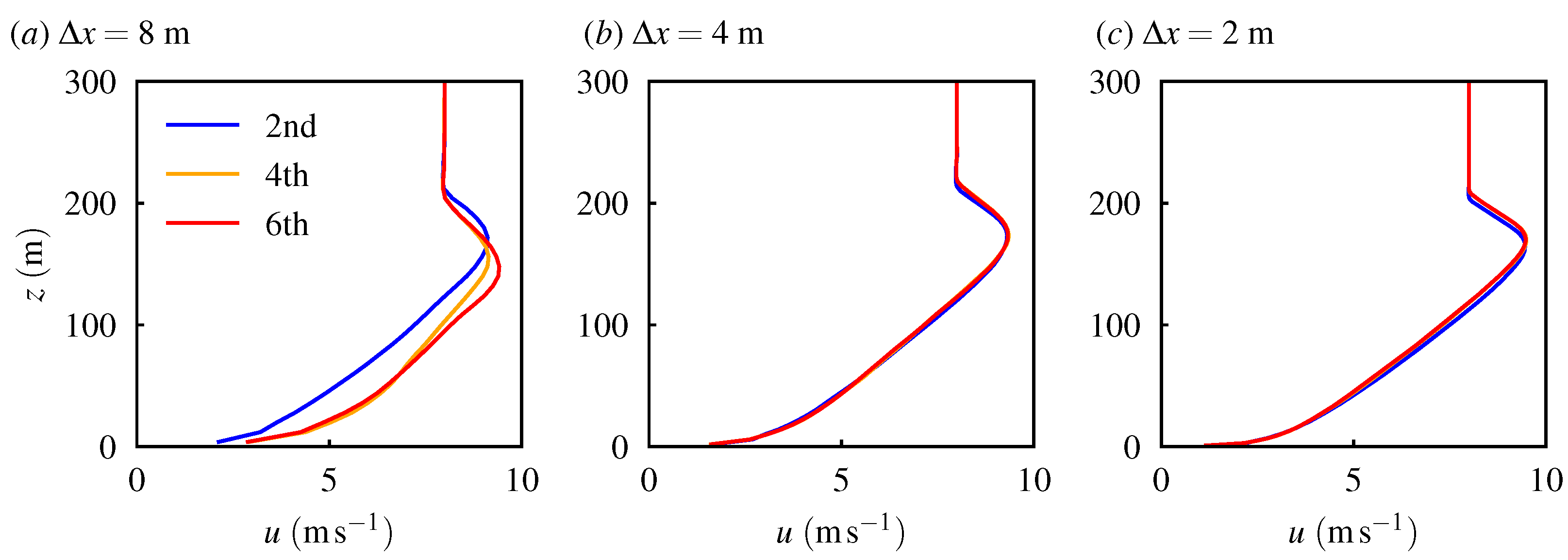
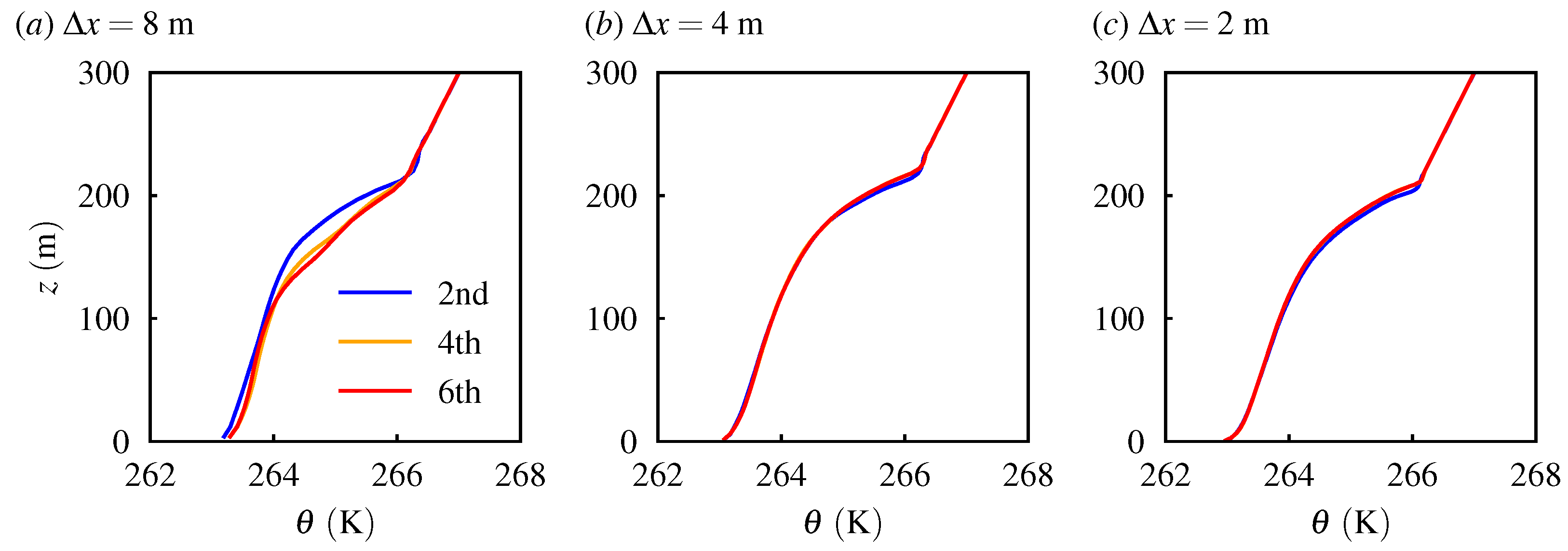
3.2. Stable Atmospheric Boundary Layer
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. N. J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sullivan, P.G.; Patton, E.G. The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. J. Atmos. Sci. 2011, 68, 2395–2415. [Google Scholar] [CrossRef]
- Matheou, G.; Chung, D. Large-eddy simulation of stratified turbulence. Part II: Application of the stretched-vortex model to the atmospheric boundary layer. J. Atmos. Sci. 2014, 71, 4439–4460. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. I. The Basic Experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Lilly, D.K. On the Application of the Eddy Viscosity Concept in the Inertial Sub-Range of Turbulence; National Center for Atmospheric Research: Boulder, CO, USA, 1966; Volume 123. [Google Scholar]
- Lilly, D.K. The representation of small-scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symposium on Environmental Sciences, Yorktown Heights, NY, USA, 14–15 November 1966; pp. 195–210. [Google Scholar]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Lomax, H.; Pulliam, T.H.; Zingg, D.W. Fundamentals of Computational Fluid Dynamics; Scientific Computation; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Matheou, G. Numerical discretization and subgrid-scale model effects on large-eddy simulations of a stable boundary layer. Q. J. R. Meteorol. Soc. 2016, 142, 3050–3062. [Google Scholar] [CrossRef]
- Leonard, A. Energy cascade in large-eddy simulations of turbulent fluid flows. Adv. Geophys. 1974, 18, 237–248. [Google Scholar]
- Ghosal, S. An analysis of numerical errors in large-eddy simulations of turbulence. J. Comput. Phys. 1996, 125, 187–206. [Google Scholar] [CrossRef]
- Vreman, B.; Geurts, B.; Kuerten, H. Comparison of numerical schemes in large-eddy simulation of the temporal mixing layer. Int. J. Numer. Methods Fluids 1996, 22, 297–311. [Google Scholar] [CrossRef]
- Chow, F.K.; Moin, P. A further study of numerical errors in large-eddy simulations. J. Comput. Phys. 2003, 184, 366–380. [Google Scholar] [CrossRef]
- Meyers, J.; Geurts, B.J.; Baelmans, M. Database analysis of errors in large-eddy simulation. Phys. Fluids 2003, 15, 2740–2755. [Google Scholar] [CrossRef]
- Hill, D.J.; Pullin, D.I. Hybrid tuned center-difference-WENO method for large eddy simulations in the presence of strong shocks. J. Comput. Phys. 2004, 194, 435–450. [Google Scholar] [CrossRef]
- Overholt, M.R.; Pope, S.B. Direct numerical simulation of a passive scalar with imposed mean gradient in isotropic turbulence. Phys. Fluids 1996, 8, 3128–3148. [Google Scholar] [CrossRef]
- Perlman, E.; Burns, R.; Li, Y.; Meneveau, C. Data exploration of turbulence simulations using a database cluster. In Proceedings of the 2007 ACM/IEEE Conference on Supercomputing, Reno, NV, USA, 10–16 November 2007; pp. 1–11. [Google Scholar]
- Li, Y.; Perlman, E.; Wan, M.; Yang, Y.; Meneveau, C.; Burns, R.; Chen, S.; Szalay, A.; Eyink, G. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 2008, 9, N31. [Google Scholar] [CrossRef]
- Chung, D.; Matheou, G. Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 2012, 696, 434–467. [Google Scholar] [CrossRef]
- Beare, R.J.; MacVean, M.K.; Holtslag, A.A.M.; Cuxart, J.; Esau, I.; Golaz, J.C.; Jimenez, M.A.; Khairoutdinov, M.; Kosovic, B.; Lewellen, D.; et al. An intercomparison of large-eddy simulations of the stable boundary layer. Bound.-Layer Meteorol. 2006, 118, 247–272. [Google Scholar] [CrossRef]
- Batchelor, G.K. The condition for dynamical similarity of motions of a frictionless perfect-gas atmosphere. Q. J. R. Meteorol. Soc. 1953, 79, 224–235. [Google Scholar] [CrossRef]
- Ogura, Y.; Phillips, N.A. Scale analysis of deep and shallow convection in the atmosphere. J. Atmos. Sci. 1962, 19, 173–179. [Google Scholar] [CrossRef]
- Morinishi, Y.; Lund, T.S.; Vasilyev, O.V.; Moin, P. Fully Conservative Higher Order Finite Difference Schemes for Incompressible Flow. J. Comput. Phys. 1998, 143, 90–124. [Google Scholar] [CrossRef]
- Spalart, P.R.; Moser, R.D.; Rogers, M.M. Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 1991, 96, 297–324. [Google Scholar] [CrossRef]
- Mason, P.J.; Callen, N.S. On the magnitude of the subgrid-scale eddy coefficient in large-eddy simulations of turbulent channel flow. J. Fluid Mech. 1986, 162, 439–462. [Google Scholar] [CrossRef]
- Lilly, D.K. On the numerical simulation of buoyant convection. Tellus 1962, 14, 148–172. [Google Scholar] [CrossRef]
- Canuto, V.M.; Cheng, Y. Determination of the Smagorinsky–Lilly constant CS. Phys. Fluids 1997, 9, 1368–1378. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational design of the basic dynamical processes of the UCLA general circulation model. In Methods of Computational Physics; Academic Press: Cambridge, MA, USA, 1977; Volume 17, pp. 173–265. [Google Scholar]
- Matheou, G.; Chung, D.; Nuijens, L.; Stevens, B.; Teixeira, J. On the fidelity of large-eddy simulation of shallow precipitating cumulus convection. Mon. Weather Rev. 2011, 139, 2918–2939. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar]
- Sullivan, P.P.; Weil, J.C.; Patton, E.G.; Jonker, H.J.; Mironov, D.V. Turbulent winds and temperature fronts in large-eddy simulations of the stable atmospheric boundary layer. J. Atmos. Sci. 2016, 73, 1815–1840. [Google Scholar] [CrossRef]


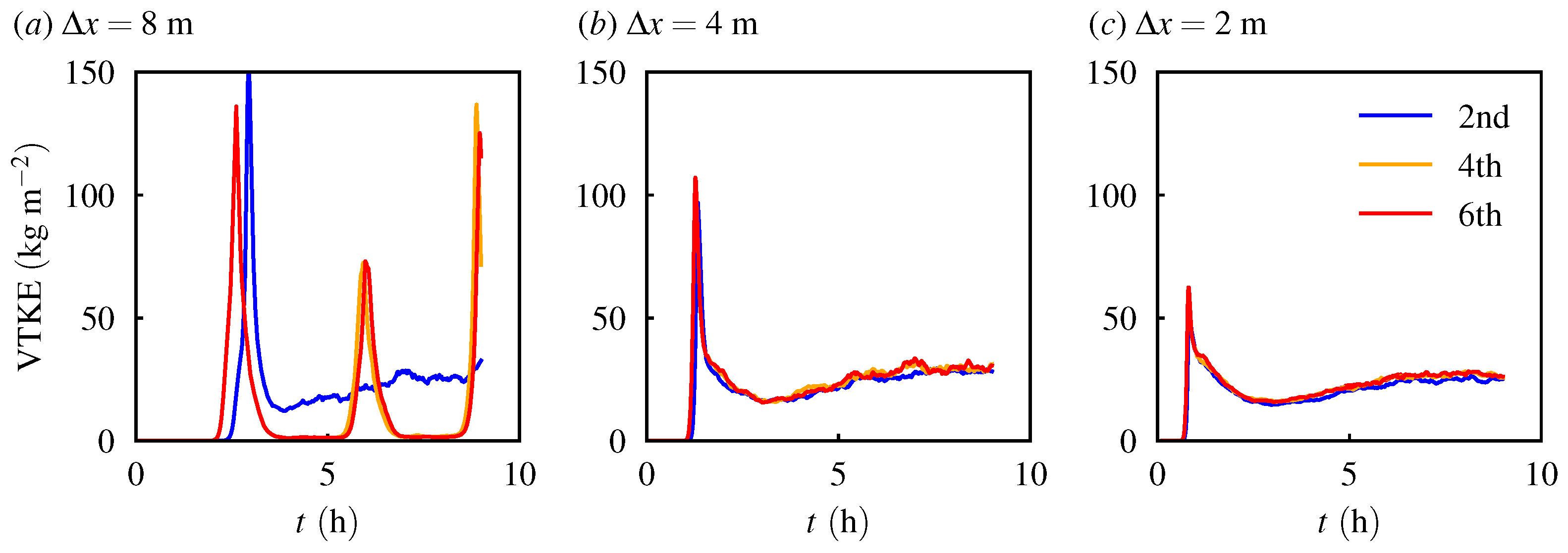
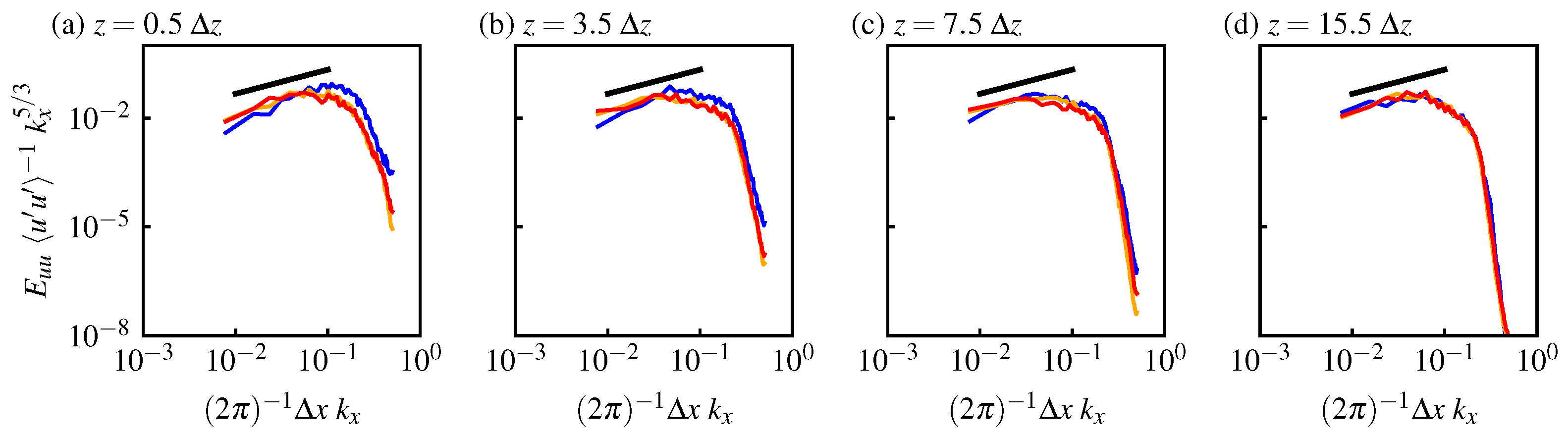
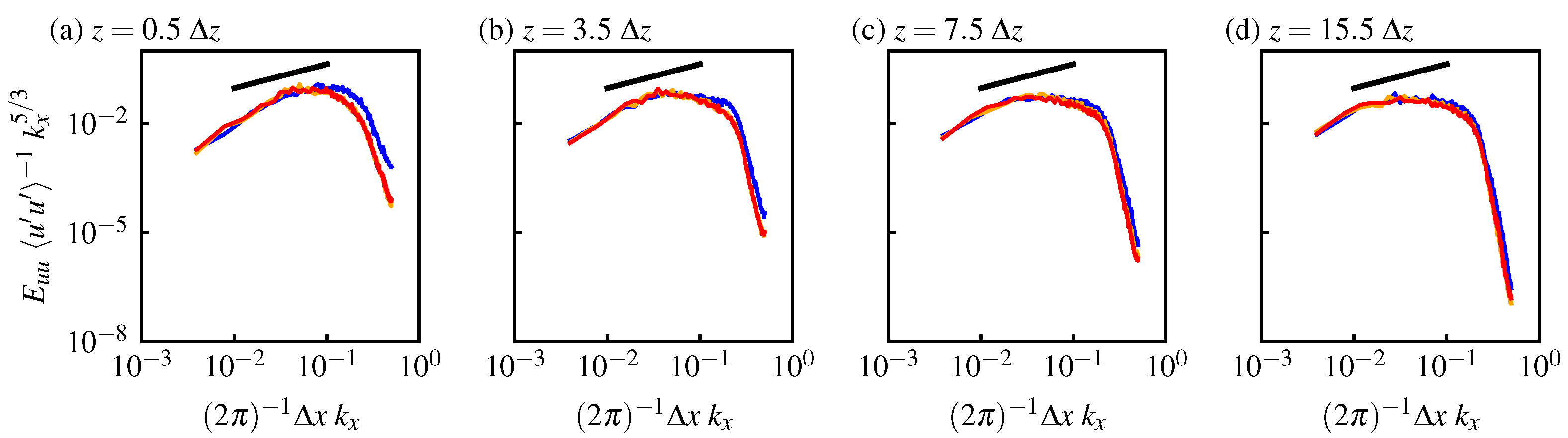
| Order | ||||||
|---|---|---|---|---|---|---|
| Second | 0 | 0 | 1 | 0 | 0 | |
| Fourth | 0 | 0 | ||||
| Sixth |
| Name | Type | Flow | Order | ||||
|---|---|---|---|---|---|---|---|
| D | DNS | HIT | 1024 | 1024 | – | – | |
| H2-32 | LES | HIT | 32 | 32 | 0.18 | Second | |
| H2-64 | LES | HIT | 64 | 32 | 0.18 | Second | |
| H2-128 | LES | HIT | 128 | 32 | 0.18 | Second | |
| H2-256 | LES | HIT | 256 | 32 | 0.18 | Second | |
| H4-32 | LES | HIT | 32 | 32 | 0.18 | Fourth | |
| H4-64 | LES | HIT | 64 | 64 | 0.18 | Fourth | |
| H4-128 | LES | HIT | 128 | 128 | 0.18 | Fourth | |
| H4-256 | LES | HIT | 256 | 256 | 0.18 | Fourth | |
| H6-32 | LES | HIT | 32 | 32 | 0.18 | Sixth | |
| H6-64 | LES | HIT | 64 | 64 | 0.18 | Sixth | |
| H6-128 | LES | HIT | 128 | 128 | 0.18 | Sixth | |
| H6-256 | LES | HIT | 256 | 256 | 0.18 | Sixth | |
| S2-128 | LES | ABL | 128 | 50 | 8 | 0.2 | Second |
| S2-256 | LES | ABL | 256 | 100 | 4 | 0.2 | Second |
| S2-512 | LES | ABL | 512 | 200 | 2 | 0.2 | Second |
| S4-128 | LES | ABL | 128 | 50 | 8 | 0.2 | Fourth |
| S4-256 | LES | ABL | 256 | 100 | 4 | 0.2 | Fourth |
| S4-512 | LES | ABL | 512 | 200 | 2 | 0.2 | Fourth |
| S6-128 | LES | ABL | 128 | 50 | 8 | 0.2 | Sixth |
| S6-256 | LES | ABL | 256 | 100 | 4 | 0.2 | Sixth |
| S6-512 | LES | ABL | 512 | 200 | 2 | 0.2 | Sixth |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banhos, J.; Matheou, G. Effects of Discretization of Smagorinsky–Lilly Subgrid Scale Model on Large-Eddy Simulation of Stable Boundary Layers. Atmosphere 2025, 16, 310. https://doi.org/10.3390/atmos16030310
Banhos J, Matheou G. Effects of Discretization of Smagorinsky–Lilly Subgrid Scale Model on Large-Eddy Simulation of Stable Boundary Layers. Atmosphere. 2025; 16(3):310. https://doi.org/10.3390/atmos16030310
Chicago/Turabian StyleBanhos, Jonas, and Georgios Matheou. 2025. "Effects of Discretization of Smagorinsky–Lilly Subgrid Scale Model on Large-Eddy Simulation of Stable Boundary Layers" Atmosphere 16, no. 3: 310. https://doi.org/10.3390/atmos16030310
APA StyleBanhos, J., & Matheou, G. (2025). Effects of Discretization of Smagorinsky–Lilly Subgrid Scale Model on Large-Eddy Simulation of Stable Boundary Layers. Atmosphere, 16(3), 310. https://doi.org/10.3390/atmos16030310






