Self-Organizing Map-Based Classification for Fire Weather Index in the Beijing–Tianjin–Hebei Region and Their Potential Causes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
2.2.1. Fire Weather Index Model
2.2.2. Self-Organizing Map Analysis
2.2.3. Derivation of Partial Differential Equations for Fire Weather Index
2.2.4. Contributions of the Fuel Available Index and Wildfire Spread Rate Index on the Fire Weather Index
3. Results
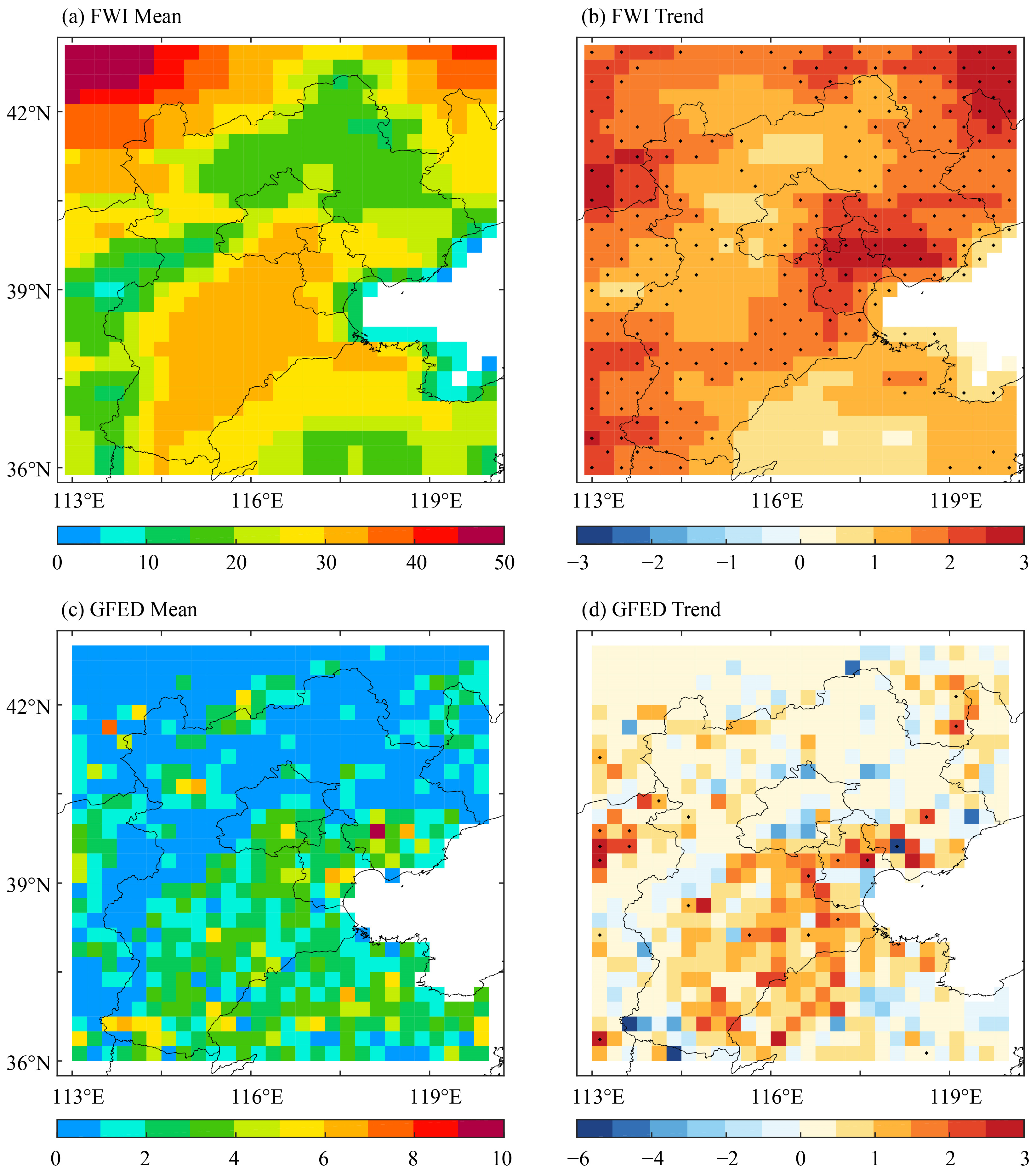
3.1. Spatial Characteristics of the Fire Weather Index and Wildfire Days
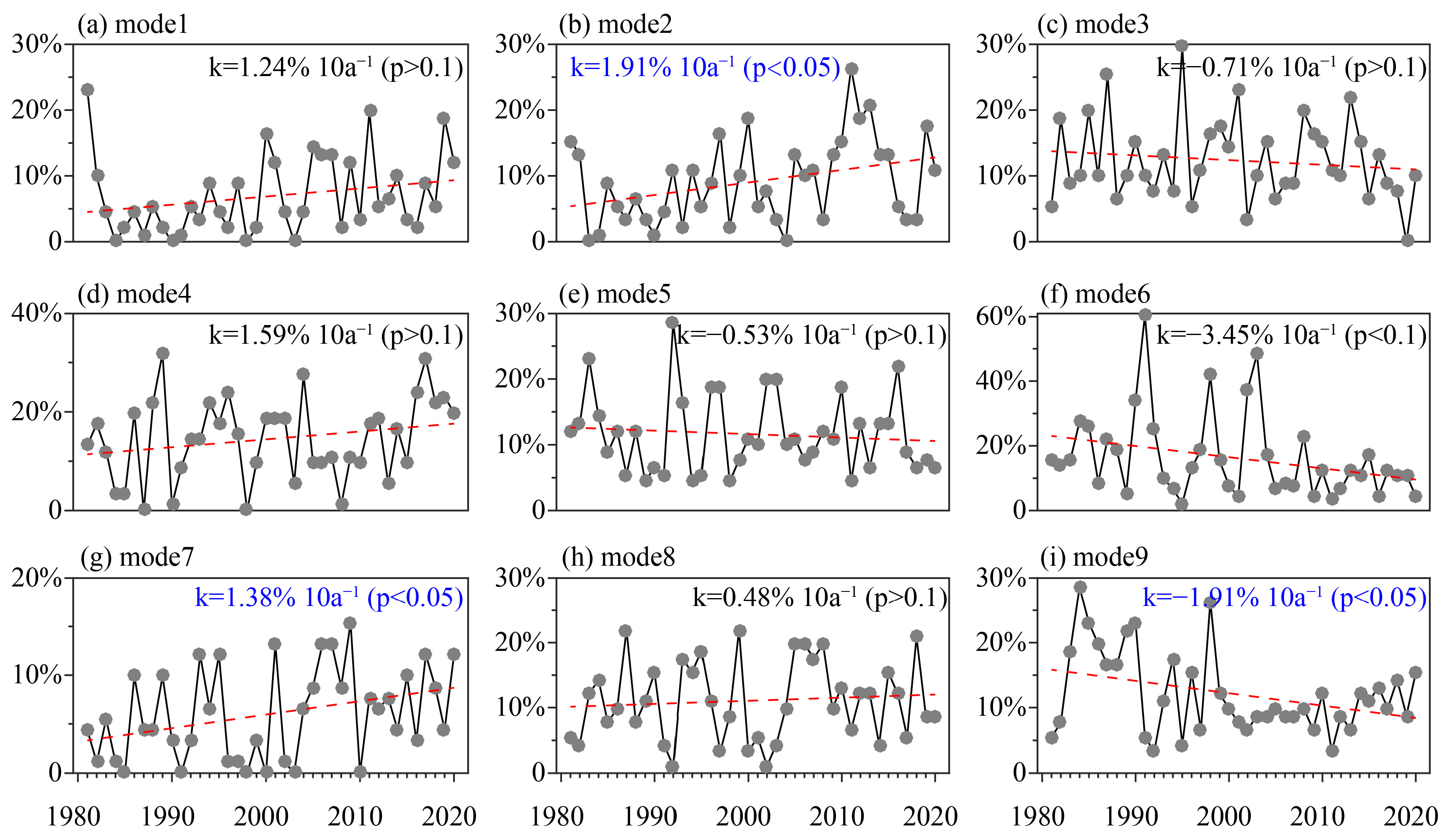
3.2. SOM Analysis of the Fire Weather Index Composites
3.3. Impact of Atmospheric Circulation Anomalies on the FWI
3.4. Contributions of the Fuel Available Index and Wildfire Spread Rate Index to the Fire Weather Index
4. Discussion
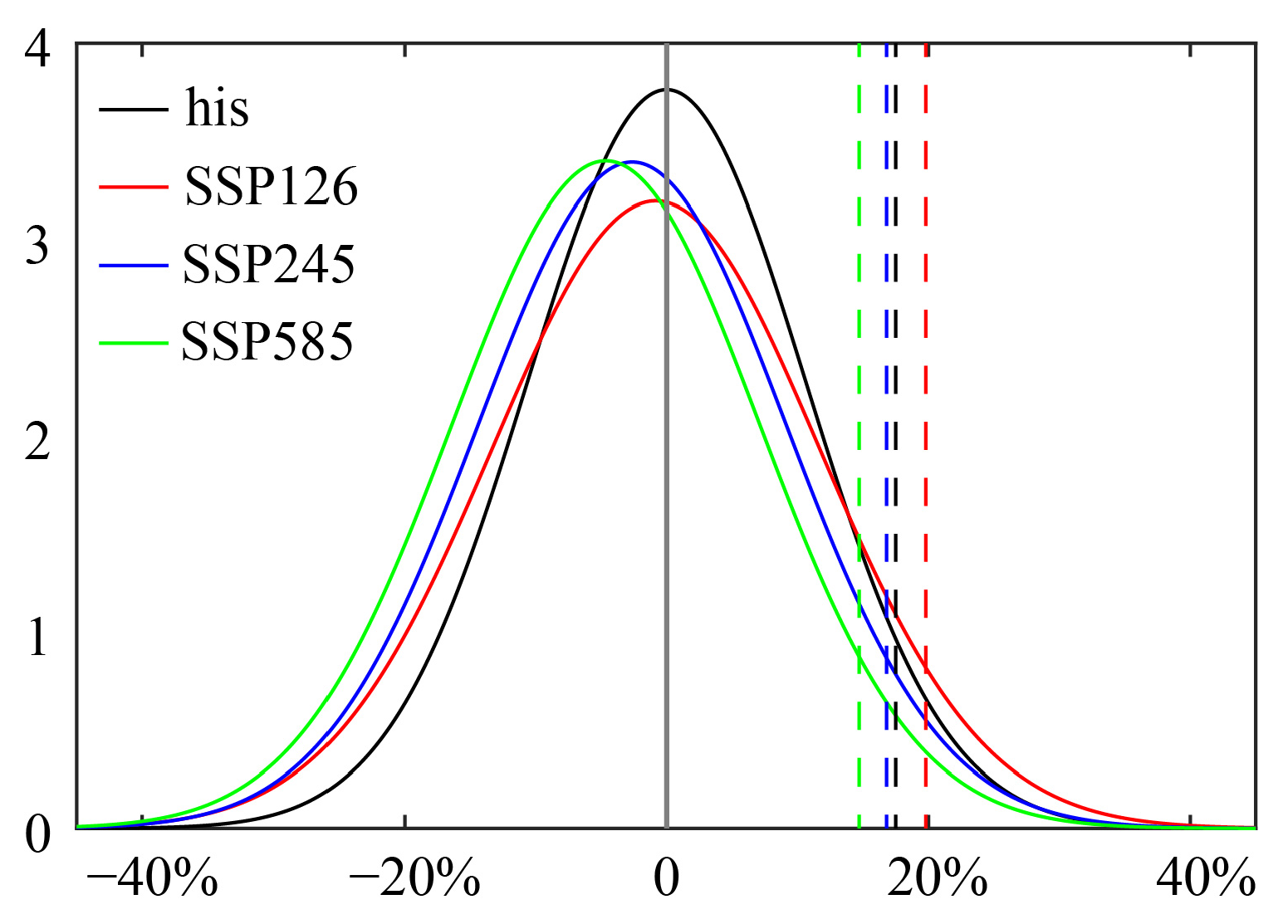
4.1. The Composites of Fire Weather Index Anomaly Under the Different SSP Scenarios
4.2. The Application of the SOM in Classifying Wildfire Patterns
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Knorr, W.; Arneth, A.; Jiang, L. Demographic controls of future global fire risk. Nat. Clim. Chang. 2016, 61, 781–787. [Google Scholar] [CrossRef]
- Hudiburg, T.; Mathias, J.; Bartowitz, K.; Berardi, D.M.; Bryant, K.; Graham, E.; Kolden, C.A.; Betts, R.A.; Lynch, L. Terrestrial carbon dynamics in an era of increasing wildfire. Nat. Clim. Chang. 2024, 13, 1306–1316. [Google Scholar] [CrossRef]
- Chinese Academy of Science. Blue Book of Forest Fire Carbon Emissions Research. 2023. Available online: http://www.iae.cas.cn/gb2019/xwzx_156509/ttxw_156510/202312/P020231212296936577850.pdf (accessed on 1 March 2024). (In Chinese).
- Williams, A.P.; Abatzoglou, J.T.; Gershunov, A.; Guzman-Morales, J.; Bishop, D.A.; Balch, J.K.; Lettenmaier, D.P. Observed Impacts of Anthropogenic Climate Change on Wildfire in California. Earths Future 2019, 7, 892–910. [Google Scholar] [CrossRef]
- Jain, P.; Castellanos-Acuna, D.; Coogan, S.C.P.; Abatzoglou, J.T.; Flannigan, M.D. Observed increases in extreme fire weather driven by atmospheric humidity and temperature. Nat. Clim. Chang. 2021, 12, 63–72. [Google Scholar] [CrossRef]
- McDowell, N.G.; Allen, C.D. Darcy’s law predicts widespread forest mortality under climate warming. Nat. Clim. Change 2015, 5, 669–672. [Google Scholar] [CrossRef]
- Touma, D.; Stevenson, S.; Lehner, F.; Coats, S. Human-driven greenhouse gas and aerosol emissions cause distinct regional impacts on extreme fire weather. Nat. Commun. 2021, 12, 212. [Google Scholar] [CrossRef]
- Tomasevic, I.C.; Vucetic, V.; Cheung, K.K.W.; Fox-Hughes, P.; Beggs, P.J.; Prtenjak, M.T.; Malecic, B. Comparison of Meteorological Drivers of Two Large Coastal Slope-Land Wildfire Events in Croatia and South-East Australia. Atmosphere 2023, 14, 1076. [Google Scholar] [CrossRef]
- Chaparro, D.; Piles, M.; Vall-Llossera, M.; Camps, A. Surface moisture and temperature trends anticipate drought conditions linked to wildfire activity in the Iberian Peninsula. Eur. J. Remote Sens. 2017, 49, 955–971. [Google Scholar] [CrossRef]
- Chen, L.F.; Dou, Q.; Zhang, Z.M.; Shen, Z.H. Moisture content variations in soil and plant of post-fire regenerating forests in central Yunnan Plateau, Southwest China. J. Geogr. Sci. 2019, 29, 1179–1192. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Williams, A.P. Impact of anthropogenic climate change on wildfire across western US forests. Proc. Natl. Acad. Sci. USA 2016, 113, 11770–11775. [Google Scholar] [CrossRef]
- Goss, M.; Swain, D.L.; Abatzoglou, J.T.; Sarhadi, A.; Kolden, C.A.; Williams, A.P.; Diffenbaugh, N.S. Climate change is increasing the likelihood of extreme autumn wildfire conditions across California. Environ. Res. Lett. 2020, 15, 094016. [Google Scholar] [CrossRef]
- Kirchmeier-Young, M.C.; Zwiers, F.W.; Gillett, N.P.; Cannon, A.J. Attributing extreme fire risk in Western Canada to human emissions. Clim. Chang. 2017, 144, 365–379. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.R.; Shu, L.F.; Zhao, F.J.; Wang, M.Y. Impacts of climate change on forest fire danger in China. Sci. Silvae Sin. 2017, 53, 159–169. [Google Scholar] [CrossRef]
- Bai, M.X.; Du, W.P.; Wu, M.W.; Zhang, C.P.; Xing, P.; Hao, Z.X. Variation in fire danger in the Beijing-Tianjin-Hebei region over the past 30 years and its linkage with atmospheric circulation. Clim. Chang. 2024, 177, 27. [Google Scholar] [CrossRef]
- Ding, Y.H.; Wang, Z.Y.; Sun, Y. Inter-decadal variation of the summer precipitation in East China and its association with decreasing Asian summer monsoon. Part I: Observed evidences. Int. J. Climatol. 2008, 28, 1139–1161. [Google Scholar] [CrossRef]
- Ding, Y.H.; Sun, Y.; Wang, Z.Y.; Zhu, Y.X.; Song, Y.F. Inter-decadal variation of the summer precipitation in China and its association with decreasing Asian summer monsoon Part II: Possible causes. Int. J. Climatol. 2009, 29, 1926–1944. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Wu, C.Q.; Jia, R.; Huang, J.P. An overview of the influence of atmospheric circulation on the climate in arid and semi-arid region of Central and East Asia. Sci. China Earth Sci. 2018, 61, 1183–1194. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, J.; Chen, B.Y.; Chen, Y.; Shu, Y. Similarities of Three Most Extreme Precipitation Events in North China. Atmosphere 2023, 14, 1149. [Google Scholar] [CrossRef]
- Yang, Q.R.; Jiang, C.; Ding, T. Impacts of Extreme-High-Temperature Events on Vegetation in North China. Remote Sens. 2023, 15, 4542. [Google Scholar] [CrossRef]
- Du, W.P.; Hao, Z.X.; Bai, M.X.; Zhang, L.; Zhang, C.P.; Wang, Z.R.; Xing, P. Spatiotemporal Variation in the Meteorological Drought Comprehensive Index in the Beijing-Tianjin-Hebei Region during 1961–2023. Water 2024, 15, 4230. [Google Scholar] [CrossRef]
- Bai, M.X.; Du, W.P.; Hao, Z.X.; Zhang, L.; Xing, P. The characteristics and future projections of fire danger in the areas around mega-city based on meteorological data–a case study of Beijing. Front. Earth Sci. 2024, 18, 637–648. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Development and Structure of the Canadian Forest Fire Weather Index System; Canadian Forest Search Technology Report; Petawawa National Forestry Institute, Canadian Forest Service: Chalk River, ON, Canada, 1987. [Google Scholar]
- Laneve, G.; Pampanoni, V.; Shaik, R.U. The Daily Fire Hazard Index: A Fire Danger Rating Method for Mediterranean Areas. Remote Sens. 2020, 12, 2356. [Google Scholar] [CrossRef]
- Field, R.D. Evaluation of Global Fire Weather Database reanalysis and short-term forecast products. Nat. Hazards Earth Syst. Sci. 2020, 20, 1123–1147. [Google Scholar] [CrossRef]
- McElhinny, M.; Beckers, J.F.; Hanes, C.; Flannigan, M.; Jain, P. A high-resolution reanalysis of global fire weather from 1979 to 2018-overwintering the Drought Code. Earth Syst. Sci. Data 2020, 12, 1823–1833. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Choudhury, D.; Ji, F.; Nishant, N.; Di Virgilio, G. Evaluation of ERA5-Simulated Temperature and Its Extremes for Australia. Atmosphere 2023, 14, 913. [Google Scholar] [CrossRef]
- Dhmane, L.A.; Moustadraf, J.; Rachdane, M.; Saidi, M.E.; Benjmel, K.; Amraoui, F.; Ezzaouini, M.A.; Sliman, A.A.; Hadri, A. Spatiotemporal Assessment and Correction of Gridded Precipitation Products in North Western Morocco. Atmosphere 2023, 14, 1239. [Google Scholar] [CrossRef]
- Ramon, J.; Lledo, L.; Torralba, V.; Soret, A.; Doblas-Reyes, F.J. What global reanalysis best represents near-surface winds? Q. J. R. Meteorol. Soc. 2019, 145, 3236–3251. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; van Dijk, A.I.J.M.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef]
- van der Werf, G.R.; Randerson, J.T.; Giglio, L.; van Leeuwen, T.T.; Chen, Y.; Rogers, B.M.; Mu, M.Q.; van Marle, M.J.E.; Morton, D.C.; Collatz, G.J.; et al. Global fire emissions estimate during 1997–2016. Earth Syst. Sci. Data 2017, 9, 697–720. [Google Scholar] [CrossRef]
- Zhang, T.R.; Wooster, M.J.; de Jong, M.C.; Xu, W.D. How Well Does the “Small Fire Boost” Methodology Used within the GFED4.1s Fire Emissions Database Represent the Timing, Location and Magnitude of Agricultural Burning? Remote Sens. 2018, 10, 823. [Google Scholar] [CrossRef]
- Andela, N.; Morton, D.C.; Giglio, L.; Paugam, R.; Chen, Y.; Hantson, S.; van der Werf, G.R.; Randerson, J.T. The Global Fire Atlas of individual fire size, duration, speed and direction. Earth Syst. Sci. Data 2019, 11, 529–552. [Google Scholar] [CrossRef]
- Pinto, G.A.S.J.; Rousseu, F.; Niklasson, M.; Drobyshev, I. Effects of human-related and biotic landscape features on the occurrence and size of modern forest fires in Sweden. Agric. For. Meteorol. 2020, 291, 108084. [Google Scholar] [CrossRef]
- Wastl, C.; Schunk, C.; Leuchner, M.; Pezzatti, G.B.; Menzel, A. Recent climate change: Long-term trends in meteorological forest fire danger in the Alps. Agric. For. Meteorol. 2012, 162, 1–13. [Google Scholar] [CrossRef]
- Grillakis, M.; Voulgarakis, A.; Rovithakis, A.; Seiradakis, K.D.; Koutroulis, A.; Field, R.D.; Kasoar, M.; Papadopoulos, A.; Lazaridis, M. Climate drivers of global wildfire burned area. Environ. Res. Lett. 2022, 17, 045021. [Google Scholar] [CrossRef]
- Johnson, N.C.; Feldstein, S.B.; Tremblay, B. The Continuum of Northern Hemisphere Teleconnection Patterns and a Description of the NAO Shift with the Use of Self-Organizing Maps. J. Clim. 2008, 21, 6354–6371. [Google Scholar] [CrossRef]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef]
- Dong, L.; Leung, L.R.; Qian, Y.; Zou, Y.F.; Song, F.F.; Chen, X.D. Meteorological Environments Associated with California Wildfires and Their Potential Roles in Wildfire Changes During 1984–2017. J. Geophys. Res. Atmos. 2021, 126, e2020JD033180. [Google Scholar] [CrossRef]
- Rodrigues, M.; González-Hidalgo, J.C.; Peña-Angulo, D.; Jiménez-Ruano, A. Identifying wildfire-prone atmospheric circulation weather types on mainland Spain. Agric. For. Meteorol. 2019, 264, 92–103. [Google Scholar] [CrossRef]
- Trouet, V.; Taylor, A.H.; Carleton, A.M.; Skinner, C.N. Fire-climate interactions in forests of the American Pacific coast. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Zhong, S.Y.; Yu, L.J.; Heilman, W.E.; Bian, X.D.; Fromm, H. Synoptic weather patterns for large wildfires in the northwestern United States-a climatological analysis using three classification methods. Theor. Appl. Climatol. 2020, 141, 1057–1073. [Google Scholar] [CrossRef]



| ID | Abbreviation of Model Name | Institution and Country | Resolution (Lon × Lat: Number of Grids, L: Vertical Levels) |
|---|---|---|---|
| 1 | ACCESS-CM2 | Commonwealth Scientific and Industrial Research Organization, Australian Research Council Centre of Excellence for Climate System Science, Australia | 192 × 145, L85 |
| 2 | ACCESS-ESM1-5 | Commonwealth Scientific and Industrial Research Organization, Australia | 192 × 145, L38 |
| 3 | CanESM5 | Canadian Centre for Climate Modelling and Analysis, Canada | 128 × 64, L49 |
| 4 | CMCC-ESM2 | Euro-Mediterranean Centre for Climate Change Foundation, Italy | 288 × 192, L30 |
| 5 | EC-Earth3 | EC-Earth Consortium, Europe | 512 × 256, L91 |
| 6 | FGOALS-g3 | Chinese Academy of Sciences, China | 180 × 80, L26 |
| 7 | GFDL-CM4 | National Oceanic and Atmospheric Administration, Geophysical FluidDynamics Laboratory, USA | 288 × 180, L49 |
| 8 | INM-CM4-8 | Institute for Numerical Mathematics, Russia | 180 × 120, L21 |
| 9 | INM-CM5-0 | Institute for Numerical Mathematics, Russia | 180 × 120, L73 |
| 10 | IPSL-CM6A-LR | Institute Pierre Simon Laplace, France | 144 × 143, L79 |
| 11 | MIROC6 | Atmosphere and Ocean Research Institute, The University of Tokyo, Japan | 256 × 128, L81 |
| 12 | MIROC-ES2L | National Institute for Environmental Studies, The University of Tokyo, Japan | 128 × 64, L40 |
| 13 | MPI-ESM1-2-HR | Max Planck Institute for Meteorology, Germany | 384 × 192, L95 |
| 14 | MPI-ESM1-2-LR | Max Planck Institute for Meteorology, Alfred Wegener Institute, Germany | 192 × 96, L47 |
| 15 | MRI-ESM2-0 | Meteorological Research Institute, Japan | 320 × 160, L80 |
| 16 | NorESM2-LM | NorESM Climate Modeling Consortium, Norway | 144 × 96, L32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Zhang, C.; Li, M.; Du, W.; Chen, J.; Zhao, C. Self-Organizing Map-Based Classification for Fire Weather Index in the Beijing–Tianjin–Hebei Region and Their Potential Causes. Atmosphere 2025, 16, 403. https://doi.org/10.3390/atmos16040403
Wu M, Zhang C, Li M, Du W, Chen J, Zhao C. Self-Organizing Map-Based Classification for Fire Weather Index in the Beijing–Tianjin–Hebei Region and Their Potential Causes. Atmosphere. 2025; 16(4):403. https://doi.org/10.3390/atmos16040403
Chicago/Turabian StyleWu, Maowei, Chengpeng Zhang, Meijiao Li, Wupeng Du, Jianming Chen, and Caishan Zhao. 2025. "Self-Organizing Map-Based Classification for Fire Weather Index in the Beijing–Tianjin–Hebei Region and Their Potential Causes" Atmosphere 16, no. 4: 403. https://doi.org/10.3390/atmos16040403
APA StyleWu, M., Zhang, C., Li, M., Du, W., Chen, J., & Zhao, C. (2025). Self-Organizing Map-Based Classification for Fire Weather Index in the Beijing–Tianjin–Hebei Region and Their Potential Causes. Atmosphere, 16(4), 403. https://doi.org/10.3390/atmos16040403






