Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models
Abstract
:1. Introduction
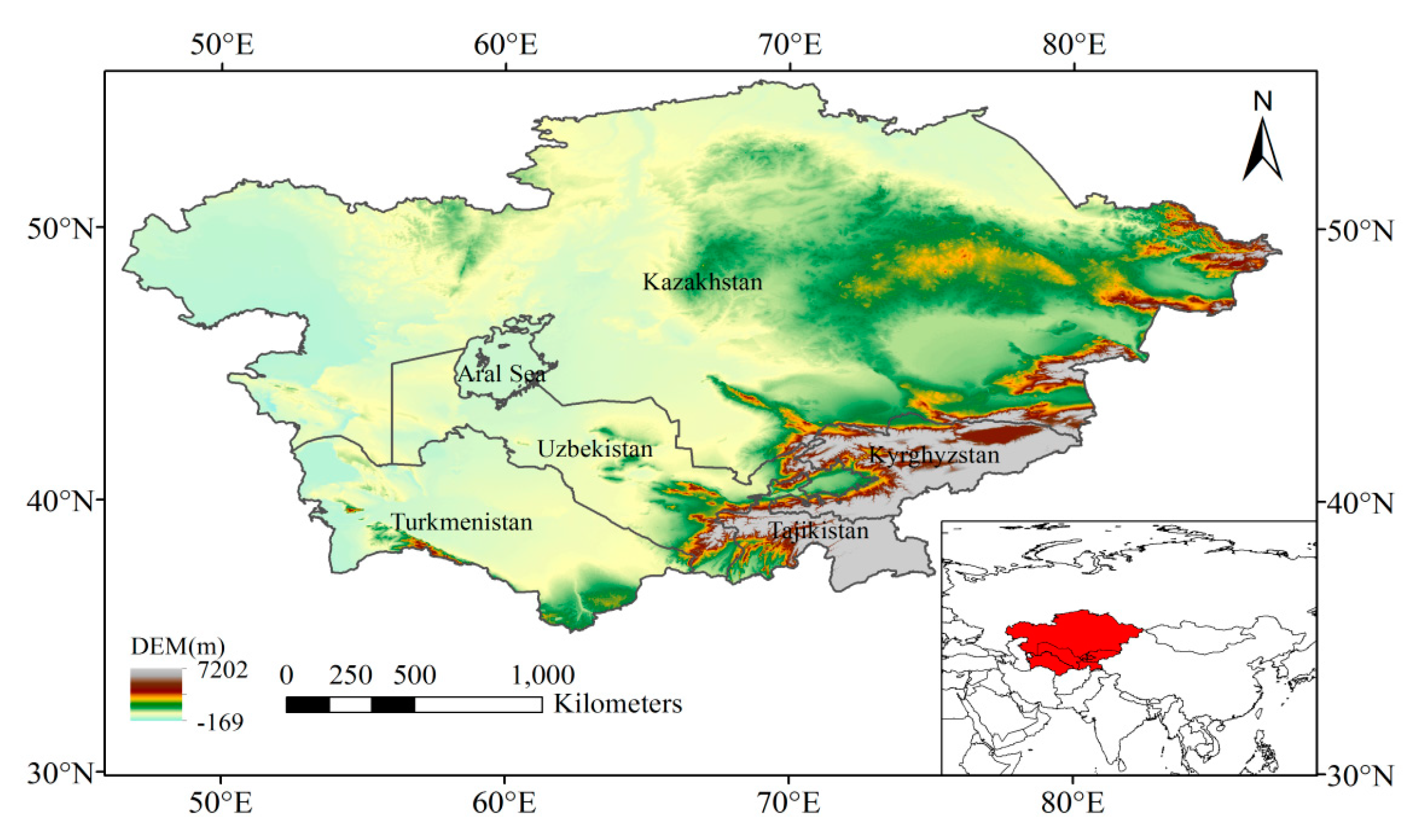
2. Data
3. Methods
4. Results
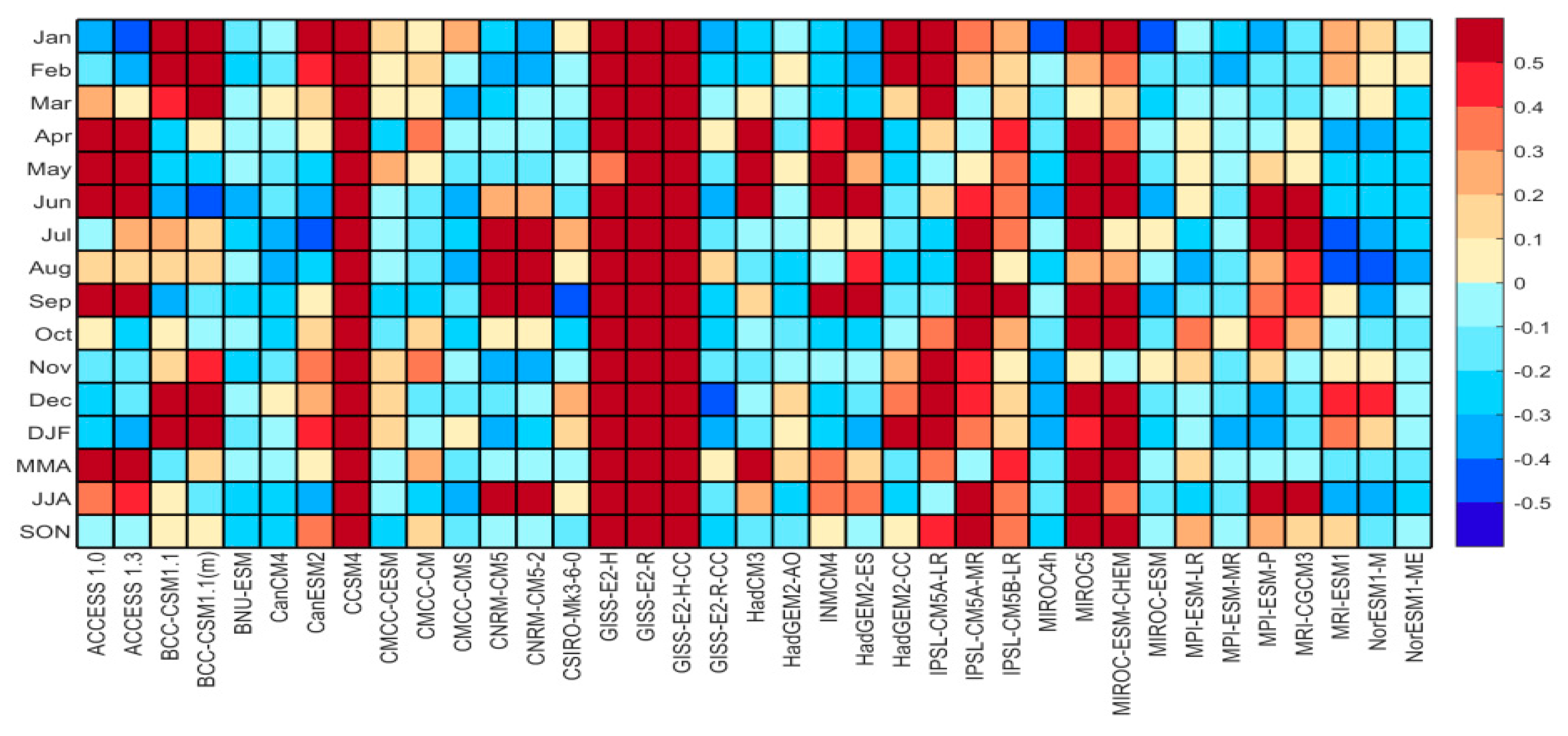
4.1. The Comparison of Observation and Simulation Using Conventional Statistics
4.2. The Simulation of Historical Precipitation from 1986 to 2005 in Central Asia
5. Discussion and Conclusions
- (1)
- Most GCMs models can capture the characteristics of annual mean, seasonal, monthly, and spatial variations of the precipitation in CA. The CMIP5 MME can reproduce the spatial distribution characteristics, and it has good agreement with observations. However, most of CMIP5 models have overestimated the interannual variability of precipitation in CA;
- (2)
- The CMIP5 MME has a good ability to simulate the seasonal variation of precipitation from winter to summer. However, there are some differences between simulation and observation, especially in February;
- (3)
- Assessing the precipitation of each CMIP5 model in different time scales, there are four models that lack basic simulation capability for the precipitation in climatological monthly and seasonal mean, such as CCSM4, GISS-E2-H, GISS-E2-H-CC, and GISS-E2-R;
- (4)
- The GCMs can simulate EOF1 of precipitation in Central Asia well, and have some simulation capabilities on the EOF2, but lacks simulation capability for EOF3, EOF4. Thirty-seven models can simulate the first two EOFs of precipitation in CA, but the models with a spatial correlation coefficient greater than 0.8, an RRMSE less than 0, and a KGE larger than 0.7 are MIROC5, MPI-ESM-LR, MPI-ESM-P, CMCC-CM, CMCC-CMS.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Immerzeel, W.W. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Seager, R.; Ting, M.; Held, I.; Kushnir, Y.; Lu, J.; Vecchi, G.; Huang, H.P.; Harnik, N.; Leetmaa, A.; Lau, N.C. Model projections of an imminent transition to a more arid climate in southwestern North America. Science 2007, 316, 1181–1184. [Google Scholar] [CrossRef] [PubMed]
- Sivakumar, B. Global climate change and its impacts on water resources planning and management: Assessment and challenges. Stoch. Environ. Res. Risk Assess. 2011, 25, 583–600. [Google Scholar] [CrossRef]
- Mehran, A.; AghaKouchak, A.; Phillips, T.J. Evaluation of CMIP5 continental precipitation simulations relative to satellite-based gauge-adjusted observations. J. Geophys. Res. Atmos. 2014, 119, 1695–1707. [Google Scholar] [CrossRef] [Green Version]
- Wehner, M. Methods of projecting future changes in extremes. Water Sci. Technol. Libr. 2013, 65, 223–237. [Google Scholar]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Moise, A.F.; Delage, F.P. New climate model metrics based on object-orientated pattern matching of rainfall. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Chen, L.; Frauenfeld, O.W. A comprehensive evaluation of precipitation simulations over China based on CMIP5 multimodel ensemble projections. J. Geophys. Res. Atmos. 2014, 119, 5767–5786. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Merwade, V.; Kinter, J.L.; Niyogi, D. Evaluation of temperature and precipitation trends and long-term persistence in CMIP5 twentieth-century climate simulations. J. Clim. 2013, 26, 4168–4185. [Google Scholar] [CrossRef]
- Aloysius, N.R.; Sheffield, J.; Saiers, J.E.; Li, H.B.; Wood, E.F. Evaluation of historical and future simulations of precipitation and temperature in central Africa from CMIP5 climate models. J. Geophys. Res. Atmos. 2016, 121, 130–152. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Wang, L.; Lin, Z. Characteristics, processes, and causes of the spatio-temporal variabilities of the East Asian monsoon system. Adv. Atmos. Sci. 2013, 29, 910–942. [Google Scholar] [CrossRef]
- Qu, X.; Huang, G.; Zhou, W. Consistent responses of East Asian summer mean rainfall to global warming in CMIP5 simulations. Theor. Appl. Clim. 2014, 117, 123–131. [Google Scholar] [CrossRef]
- Wei, K.; Xu, T.; Du, Z.; Gong, H.; Xie, B. How well do the current state-of-the-art CMIP5 models characterise the climatology of the East Asian winter monsoon? Clim. Dyn. 2014, 43, 1241–1255. [Google Scholar] [CrossRef]
- Dai, A. Precipitation characteristics in eighteen coupled climate models. J. Clim. 2006, 19, 4605–4630. [Google Scholar] [CrossRef]
- Fu, G.; Liu, Z.; Charles, S.P.; Xu, Z.; Yao, Z. A score-based method for assessing the performance of GCMs: A case study of southeastern Australia. J. Geophys. Res. Atmos. 2013, 118, 4154–4167. [Google Scholar] [CrossRef] [Green Version]
- Lioubimtseva, E.; Henebry, G.M. Climate and environmental change in arid Central Asia: Impacts, vulnerability, and adaptations. J. Arid Environ. 2009, 73, 963–977. [Google Scholar] [CrossRef]
- Yin, G.; Zengyun, H.U.; Chen, X.; Tashpolat, T. Vegetation dynamics and its response to climate change in Central Asia. J. Arid Land 2016, 8, 375–388. [Google Scholar] [CrossRef]
- Yoo, C.; Cho, E. Comparison of GCM precipitation predictions with their RMSEs and pattern correlation coefficients. Water 2018, 10, 28. [Google Scholar] [CrossRef]
- Conway, D.; Hanson, C.E.; Doherty, R.; Persechino, A. GCM simulations of the Indian Ocean dipole influence on East African rainfall: Present and future. Geophys. Res. Lett. 2007, 34, 116–142. [Google Scholar] [CrossRef]
- Singhrattna, N.; Babel, M.S. Changes in summer monsoon rainfall in the upper Chao Phraya river basin, Thailand. Clim. Res. 2011, 49, 155–168. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; Ge, M.; Rostkier-Edelstein, D.; Descombes, G.; Kunin, P.; Warner, T.; Swerdlin, S.; Givati, A.; Hopson, T. Statistical downscaling of climate forecast system seasonal predictions for the Southeastern Mediterranean. Atmos. Res. 2012, 118, 346–356. [Google Scholar] [CrossRef]
- Kioutsioukis, I.; Melas, D.; Zanis, P. Statistical downscaling of daily precipitation over Greece. Int. J. Clim. 2010, 28, 679–691. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Jackson, B.; Mcmillan, H.; Gupta, H. Use of an entropy-based metric in multiobjective calibration to improve model performance. Water Resour. Res. 2015, 50, 8066–8083. [Google Scholar] [CrossRef]
- Mitchell, T.D.; Jones, P.D. An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int. J. Clim. 2005, 25, 693–712. [Google Scholar] [CrossRef] [Green Version]
- Toddbrown, K.E.O.; Randerson, J.T.; Post, W.M.; Hoffman, F.M.; Tarnocai, C.; Schuur, E.A.G.; Allison, S.D. Causes of variation in soil carbon simulations from CMIP5 Earth system models and comparison with observations. Biogeosciences 2013, 10, 1717–1736. [Google Scholar] [CrossRef]
- Jones, G.S.; Stott, P.A.; Christidis, N. Attribution of observed historial near-surface temperature variations to anthropogenic and natural causes using CMIP5 simulations. J. Geophys. Res. Atmos. 2013, 118, 4001–4024. [Google Scholar] [CrossRef]
- Palazzi, E.; Hardenberg, J.V.; Terzago, S.; Provenzale, A. Precipitation in the karakoram-himalaya: A CMIP5 view. Clim. Dyn. 2015, 45, 21–45. [Google Scholar] [CrossRef]
- Colin, K.; Mingfang, T.; Richard, S.; Yochanan, K. Mediterranean precipitation climatology, seasonal cycle, and trend as simulated by CMIP5. Geophys. Res. Lett. 2012, 39, 21703. [Google Scholar] [CrossRef]
- Chen, F.H.; Huang, W.; Jin, L.Y.; Chen, J.H.; Wang, J.S. Spatiotemporal precipitation variations in the arid Central Asia in the context of global warming. Sci. China Earth Sci. 2011, 54, 1812–1821. [Google Scholar] [CrossRef]
- Kirkland, E.J. Bilinear interpolation. In Advanced Computing in Electron Microscopy; Springer: Boston, MA, USA, 2010; pp. 261–263. [Google Scholar]
- Dieppois, B.; Rouault, M.; New, M. The impact of ENSO on Southern African rainfall in CMIP5 ocean atmosphere coupled climate models. Clim. Dyn. 2015, 45, 2425–2442. [Google Scholar] [CrossRef] [Green Version]
- Miao, C.; Duan, Q.; Sun, Q.; Huang, Y.; Kong, D.; Yang, T.; Ye, A.; Di, Z.; Gong, W. Assessment of CMIP5 climate models and projected temperature changes over Northern Eurasia. Environ. Res. Lett. 2014, 9, 055007. [Google Scholar] [CrossRef] [Green Version]
- Qu, X.; Huang, G.; Hu, K.M.; Xie, S.P.; Du, Y.; Zheng, X.T.; Liu, L. Equatorward shift of the South Asian high in response to anthropogenic forcing. Theor. Appl. Clim. 2015, 119, 113–122. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef] [Green Version]
- Su, F.G.; Duan, X.L.; Chen, D.L.; Hao, Z.C.; Cuo, L. Evaluation of the global climate models in the CMIP5 over the Tibetan Plateau. J. Clim. 2013, 26, 3187–3208. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Dennison, P.E.; Roberts, D.A. Endmember selection for multiple endmember spectral mixture analysis using endmember average RMSE. Remote Sens. Environ. 2003, 87, 123–135. [Google Scholar] [CrossRef]
- Zhou, B.T.; Wen, Q.H.; Xu, Y.; Song, L.C.; Zhang, X.B. Projected changes in temperature and precipitation extremes in China by the CMIP5 multimodel ensembles. J. Clim. 2014, 27, 6591–6611. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, Y. An assessment on the performance of IPCC AR4 climate models in simulating interdecadal variations of the East Asian summer monsoon. Acta Meteorol. Sin. 2008, 22, 472–488. [Google Scholar]
- Kutzbach, J.E. Empirical eigenvectors of sea-level pressure, surface temperature and precipitation complexes over North America. J. Appl. Meterol. 1967, 6, 791–802. [Google Scholar] [CrossRef]
- Wallace, J.M.; Dickinson, R.E. Empirical orthogonal representation of time series in the frequency domain. Part I: Theoretical considerations. J. Appl. Meteorol. 1972, 11, 887–892. [Google Scholar] [CrossRef]
- Wypych, A.; Bochenek, B.; Różycki, M. Atmospheric moisture content over Europe and the Northern Atlantic. Atmosphere 2018, 9, 18. [Google Scholar] [CrossRef]
- Kou, X.; Huang, Z.; Liu, H.; Zhang, M.; Shen, S.; Peng, Z. Evaluating the role of the EOF analysis in 4DEnVar methods. Atmosphere 2017, 8, 146. [Google Scholar] [CrossRef]
- Sun, Z.; Chang, N.-B.; Huang, Q.; Opp, C. Precipitation patterns and associated hydrological extremes in the Yangtze River basin, China, using TRMM/PR data and EOF analysis. Int. Assoc. Sci. Hydrol. Bull. 2012, 57, 1315–1324. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.J.; Wang, B.; Ding, Q. The global monsoon variability simulated by CMIP3 coupled climate models. J. Clim. 2008, 21, 5271–5294. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling errors in the estimation of empirical orthogonal functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Campi, P.; Palumbo, A.D.; Mastrorilli, M. Evapotranspiration estimation of crops protected by windbreak in a Mediterranean region. Agric. Water Manag. 2012, 104, 153–162. [Google Scholar] [CrossRef]
- Genthon, C.; Krinner, G. Antarctic surface mass balance and systematic biases in general circulation models. J. Geophys. Res. Atmos. 2001, 106, 20653–20664. [Google Scholar] [CrossRef] [Green Version]
- Nahar, J.; Johnson, F.; Sharma, A. Assessing the extent of non-stationary biases in GCMs. J. Hydrol. 2017, 549, 148–162. [Google Scholar] [CrossRef]
- Giorgi, F.; Marinucci, M.R. A investigation of the sensitivity of simulated precipitation to model resolution and its implications for climate studies. Mon. Weather Rev. 1996, 124, 148–166. [Google Scholar] [CrossRef]



| Model | Modeling Center | Horizontal Resolution (Lat × Lon) |
|---|---|---|
| ACCESS 1.0 | CSIRO-BOM, Australia | 1.875° × 1.25° |
| ACCESS 1.3 | CSIRO-BOM, Australia | 1.875° × 1.25° |
| BCC-CSM1.1 | BCC, China | 2.8125° × 2.8125° |
| BCC-CSM1.1 (m) | BCC, China | 1.125° × 1.125° |
| BNU-ESM | GCESS, China | 2.8125° × 2.8125° |
| CanCM4 | CCCMA, Canada | 2.8125° × 2.8125° |
| CanESM2 | CCCMA, Canada | 2.8125° × 2.8125° |
| CCSM4 | NCAR, USA | 1.25° × 1° |
| CMCC-CESM | CMCC, Italy | 3.75° × 3.75° |
| CMCC-CM | CMCC, Italy | 0.75° × 0.75° |
| CMCC-CMS | CMCC, Italy | 1.875° × 1.875° |
| CNRM-CM5 | CNRM-CERFACS, France | ~1.4° × 1.4° |
| CNRM-CM5-2 | CNRM-CERFACS, France | ~1.4° × 1.4° |
| CSIRO-Mk3-6-0 | CSIRO-QCCCE, Australia | 1.875° × 1.875° |
| GISS-E2-H | NASA GISS, USA | 2.5° × 2.5° |
| GISS-E2-R | NASA GISS, USA | 2.5° × 2.5° |
| GISS-E2-H-CC | NASA GISS, USA | 2.5° × 2.5° |
| GISS-E2-R-CC | NASA GISS, USA | 2.5° × 2.5° |
| HadCM3 | MOHC, UK | ~3.75° × 2.5° |
| HadGEM2-AO | NIMR/KMA, Korea/UK | 1.875° × 1.25° |
| INMCM4 | UNM, Russia | 2° × 1.5° |
| HadGEM2-ES | MOHC, UK | 1.875° × 1.25° |
| HadGEM2-CC | MOHC, UK | 1.875° × 1.25° |
| IPSL-CM5A-LR | IPSL, France | 3.75° × 1.875° |
| IPSL-CM5A-MR | IPSL, France | 2.5° × 1.25° |
| IPSL-CM5B-LR | IPSL, France | 3.75° × 1.875° |
| MIROC4h | MIROC, Japan | 0.5625° × 0.5625° |
| MIROC5 | MIROC, Japan | ~1.4° × 1.4° |
| MIROCESM-CHEM | MIROC, Japan | 2.8125° × 2.8125° |
| MIROC-ESM | MIROC, Japan | 2.8125° × 2.8125° |
| MPI-ESM-LR | MPI-M, Germany | 1.875° × 1.875° |
| MPI-ESM-MR | MPI-M, Germany | 1.875° × 1.875° |
| MPI-ESM-P | MPI-M, Germany | 1.875° × 1.875° |
| MRI-CGCM3 | MRI, Japan | 1.125° × 1.125° |
| MRI-ESM1 | MRI, Japan | 1.125° × 1.125° |
| NorESM1-M | NCC, Norway | 2.5° × 1.875° |
| NorESM1-ME | NCC, Norway | 2.5° × 1.875° |
| Model Name | Variance Contribution Rate (EOF1) | Variance Contribution Rate (EOF2) | Correlation Coefficient (EOF1) | Correlation Coefficient (EOF2) | RRMSE | KGE |
|---|---|---|---|---|---|---|
| ACCESS 1.0 | 76.93% | 9.13% | 0.86 | −0.73 | 5.51% | 0.56 |
| ACCESS 1.3 | 75.08% | 9.68% | 0.81 | 0.81 | 6.35% | 0.57 |
| BCC-CSM1.1 | 84.92% | 5.17% | 0.55 | 0.11 | 3.22% | 0.53 |
| BCC-CSM1.1 (m) | 83.59% | 4.78% | 0.69 | 0.84 | 2.98% | 0.55 |
| BNU-ESM | 87.83% | 5.34% | 0.69 | 0.92 | 48.04% | 0.11 |
| CanCM4 | 78.94% | 8.75% | 0.67 | −0.92 | −13.71% | 0.68 |
| CanESM2 | 78.59% | 7.97% | 0.63 | −0.9 | −14.87% | 0.62 |
| CCSM4 | 79.38% | 7.65% | 0.58 | −0.9 | 0.59% | 0.61 |
| CMCC-CESM | 76.36% | 12.77% | 0.63 | 0.93 | −10.39% | 0.63 |
| CMCC-CM | 74.20% | 9.57% | 0.85 | −0.93 | −0.24% | 0.71 |
| CMCC-CMS | 74.56% | 11.27% | 0.87 | 0.96 | −5.56% | 0.7 |
| CNRM-CM5 | 74.11% | 8.79% | 0.76 | −0.77 | −6.29% | 0.66 |
| CNRM-CM5-2 | 74.09% | 8.70% | −0.78 | 0.71 | −7.94% | 0.68 |
| CSIRO-Mk3-6-0 | 75.76% | 8.75% | 0.67 | 0.02 | −10.19% | 0.66 |
| GISS-E2-H | 84.02% | 5.37% | 0.75 | 0.61 | 48.50% | 0.13 |
| GISS-E2-R | 86.47% | 4.38% | 0.69 | −0.85 | 65.84% | −0.06 |
| GISS-E2-H-CC | 85.42% | 4.76% | 0.72 | −0.07 | 53.76% | 0.09 |
| GISS-E2-R-CC | 85.90% | 4.80% | 0.71 | −0.85 | 70.30% | −0.12 |
| HadCM3 | 80.32% | 9.43% | 0.84 | 0.95 | −15.64% | 0.79 |
| HadGEM2-AO | 75.24% | 9.29% | 0.89 | −0.81 | 8.24% | 0.52 |
| INMCM4 | 80.64% | 6.75% | 0.67 | 0.9 | −5.36% | 0.64 |
| HadGEM2-ES | 75.21% | 8.72% | 0.88 | −0.75 | 1.48% | 0.61 |
| HadGEM2-CC | 74.00% | 9.79% | 0.87 | −0.69 | −1.11% | 0.64 |
| IPSL-CM5A-LR | 78.79% | 8.92% | 0.78 | 0.9 | 0.24% | 0.65 |
| IPSL-CM5A-MR | 79.71% | 8.96% | 0.7 | 0.9 | 10.94% | 0.59 |
| IPSL-CM5B-LR | 75.72% | 10.41% | 0.79 | −0.86 | 8.96% | 0.63 |
| MIROC4h | 78.79% | 7.01% | 0.82 | −0.82 | 6.84% | 0.56 |
| MIROC5 | 77.98% | 10.65% | 0.83 | 0.93 | −16.81% | 0.75 |
| MIROC-ESM-CHEM | 82.99% | 7.30% | 0.83 | 0.96 | 18.89% | 0.38 |
| MIROC-ESM | 77.98% | 10.65% | 0.79 | 0.93 | 12.24% | 0.45 |
| MPI-ESM-LR | 75.06% | 11.38% | 0.85 | −0.94 | −8.77% | 0.74 |
| MPI-ESM-MR | 74.85% | 11.16% | 0.84 | 0.94 | −1.05% | 0.69 |
| MPI-ESM-P | 72.81% | 12.15% | 0.8 | −0.92 | −11.14% | 0.73 |
| MRI-CGCM3 | 77.22% | 7.92% | −0.82 | −0.18 | −3.16% | 0.69 |
| MRI-ESM1 | 75.98% | 8.12% | 0.84 | −0.04 | 0.64% | 0.65 |
| NorESM1-M | 81.34% | 7.66% | 0.85 | −0.94 | −0.87% | 0.64 |
| NorESM1-ME | 80.24% | 8.25% | 0.54 | 0.91 | −11.57% | 0.66 |
| Model Name | PC1 | PC2 | ||
|---|---|---|---|---|
| NAO | PDO | NAO | PDO | |
| CMCC-CESM | 0.0678 ** | −0.0179 | −0.1675 ** | −0.0126 ** |
| CMCC-CMS | 0.0944 ** | −0.0116 | 0.1905 ** | 0.0219 ** |
| HadCM3 | 0.0358 ** | 0.0118 | 0.1867 ** | 0.0153 ** |
| MIROC5 | 0.1104 ** | 0.1189 ** | 0.2378 ** | 0.0522 ** |
| MPI-ESM-LR | 0.5552 ** | 0.0075 | −0.1667 ** | −0.0560 ** |
| MPI-ESM-P | −0.0263 ** | −0.0774 ** | −0.1298 | −0.0446 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ta, Z.; Yu, Y.; Sun, L.; Chen, X.; Mu, G.; Yu, R. Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models. Water 2018, 10, 1516. https://doi.org/10.3390/w10111516
Ta Z, Yu Y, Sun L, Chen X, Mu G, Yu R. Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models. Water. 2018; 10(11):1516. https://doi.org/10.3390/w10111516
Chicago/Turabian StyleTa, Zhijie, Yang Yu, Lingxiao Sun, Xi Chen, Guijin Mu, and Ruide Yu. 2018. "Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models" Water 10, no. 11: 1516. https://doi.org/10.3390/w10111516
APA StyleTa, Z., Yu, Y., Sun, L., Chen, X., Mu, G., & Yu, R. (2018). Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models. Water, 10(11), 1516. https://doi.org/10.3390/w10111516






