3D Numerical Study of the Flow Properties in a Double-Spur Dikes Field during a Flood Process
Abstract
:1. Introduction
2. Numerical Methodology
2.1. Mathematical Formula
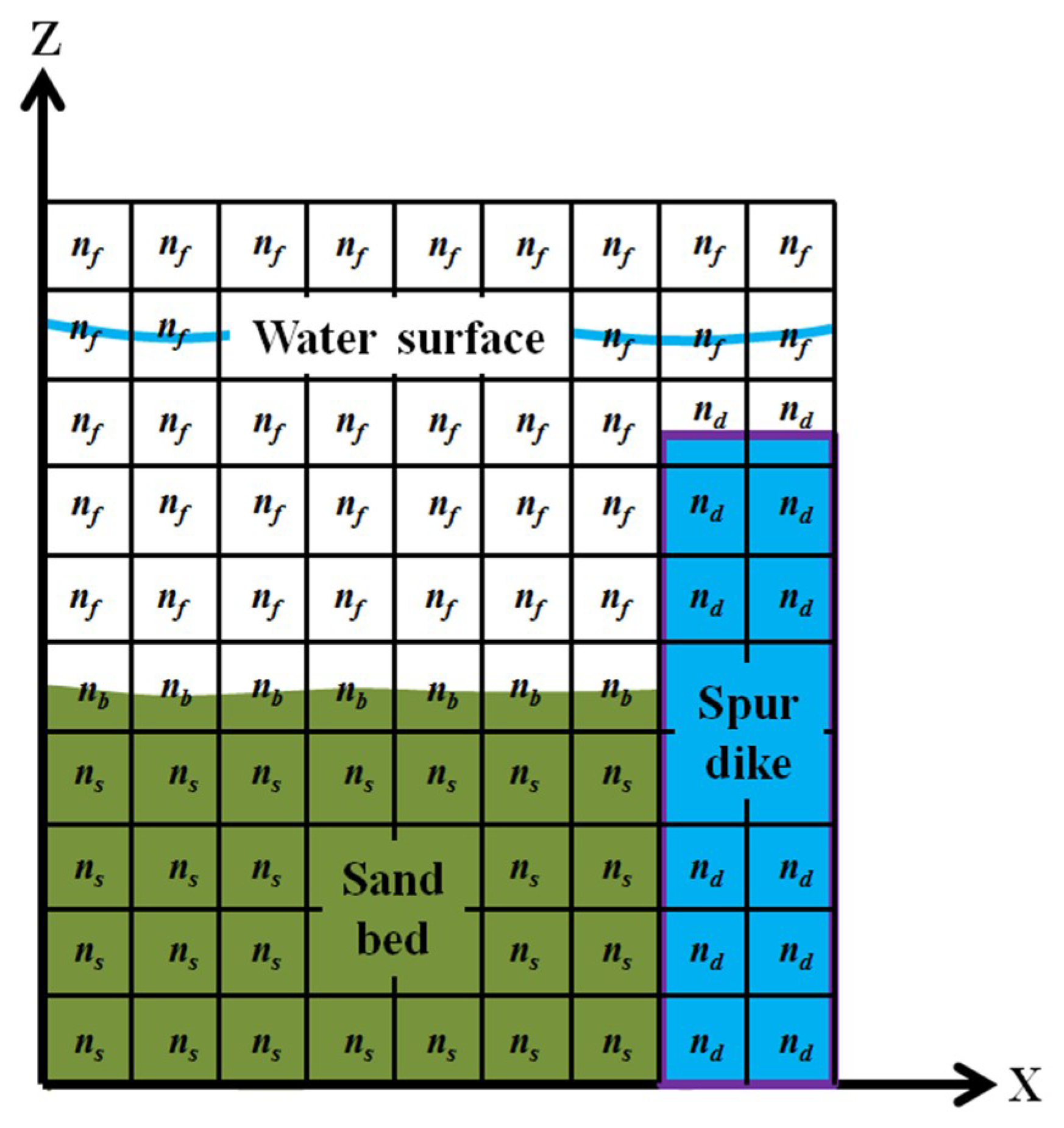
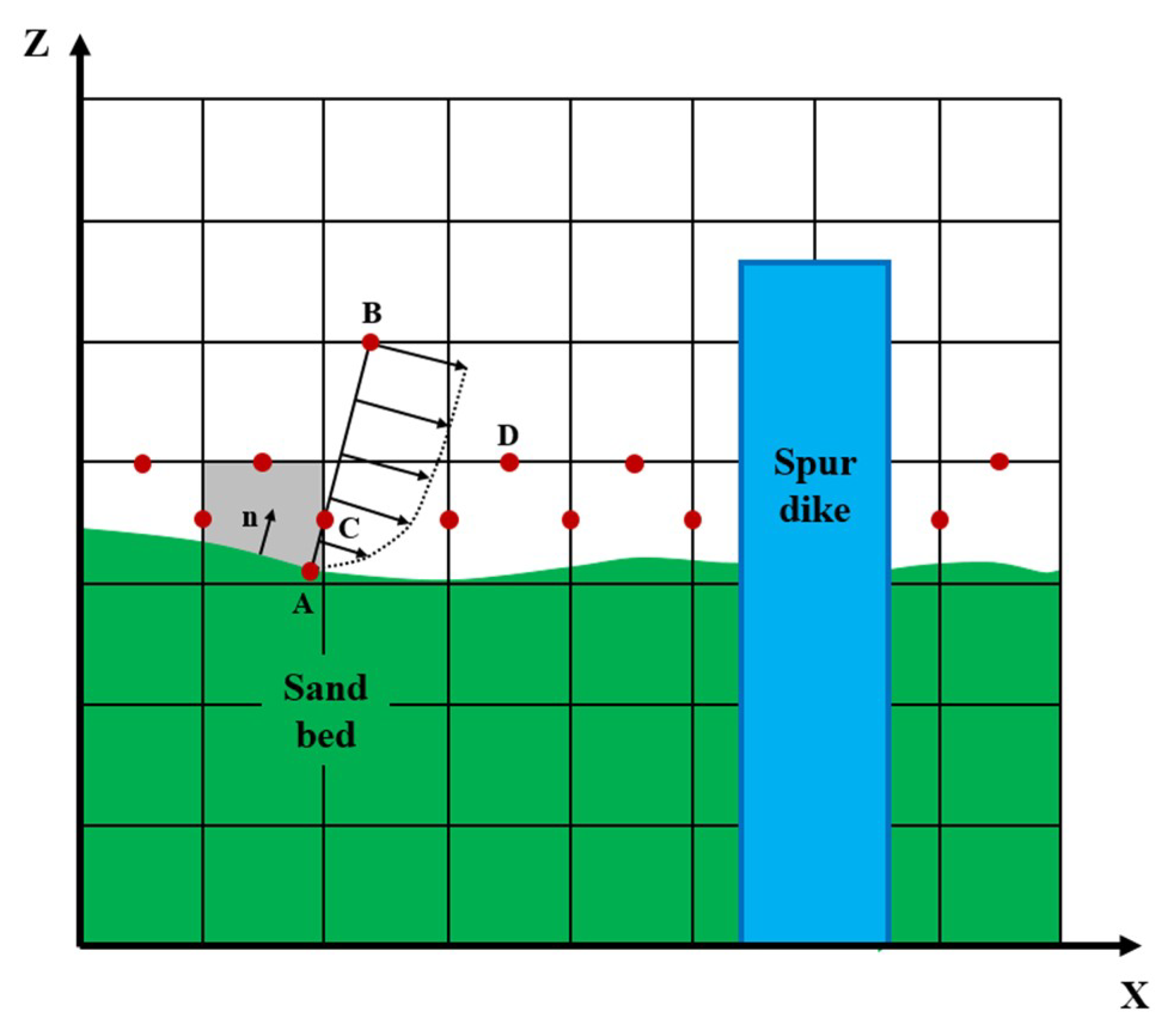
2.2. Numerical Implementation
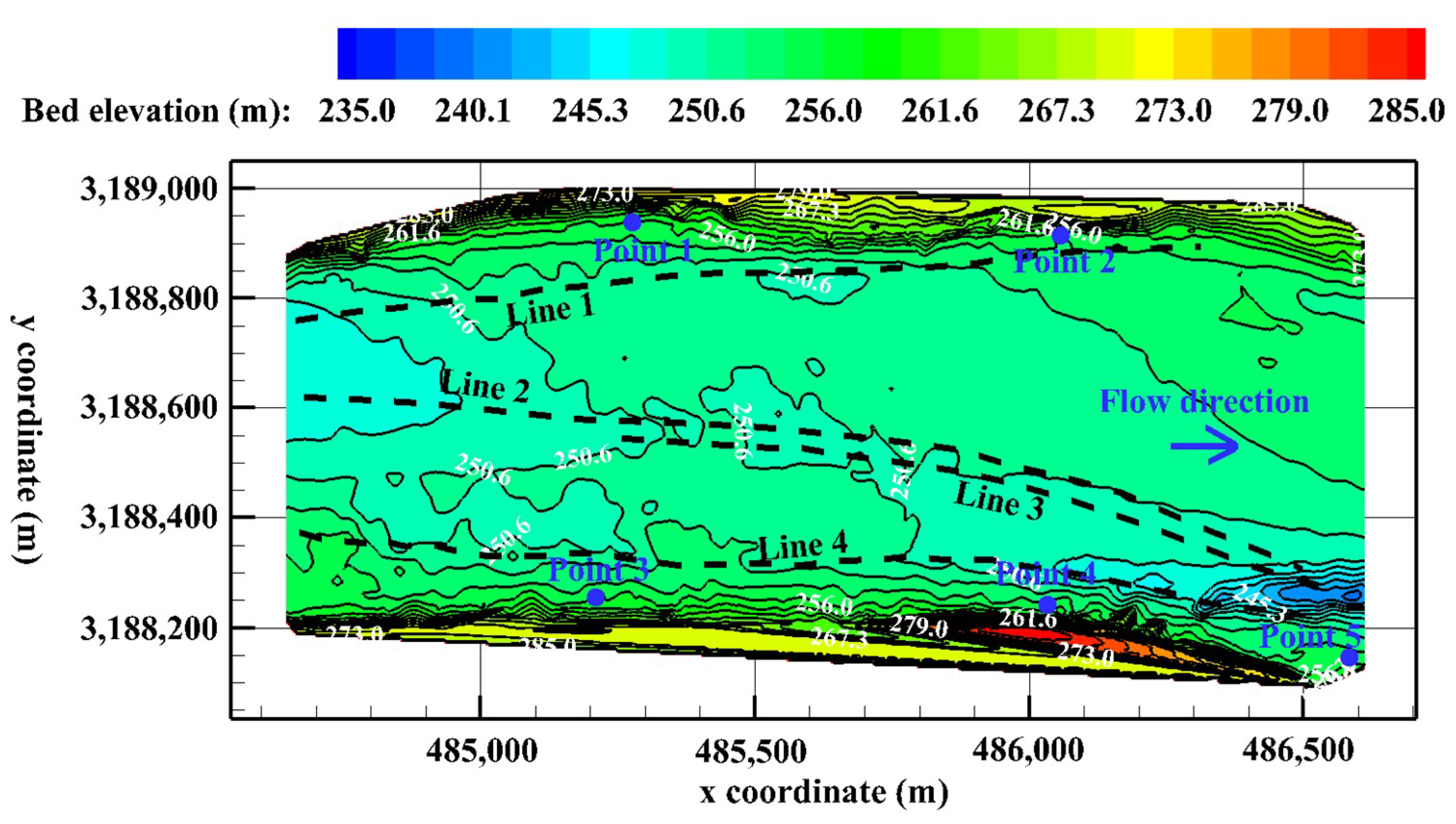
3. Field Measurement
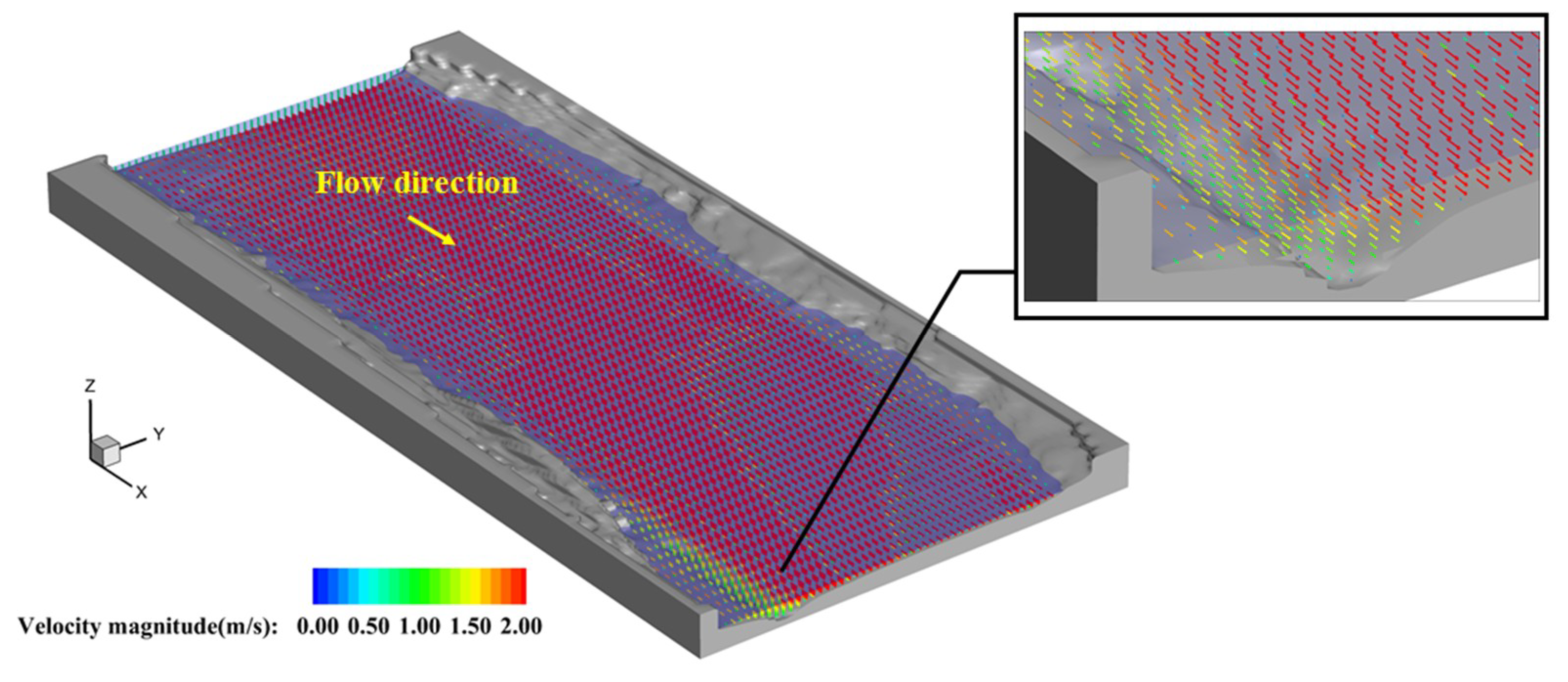
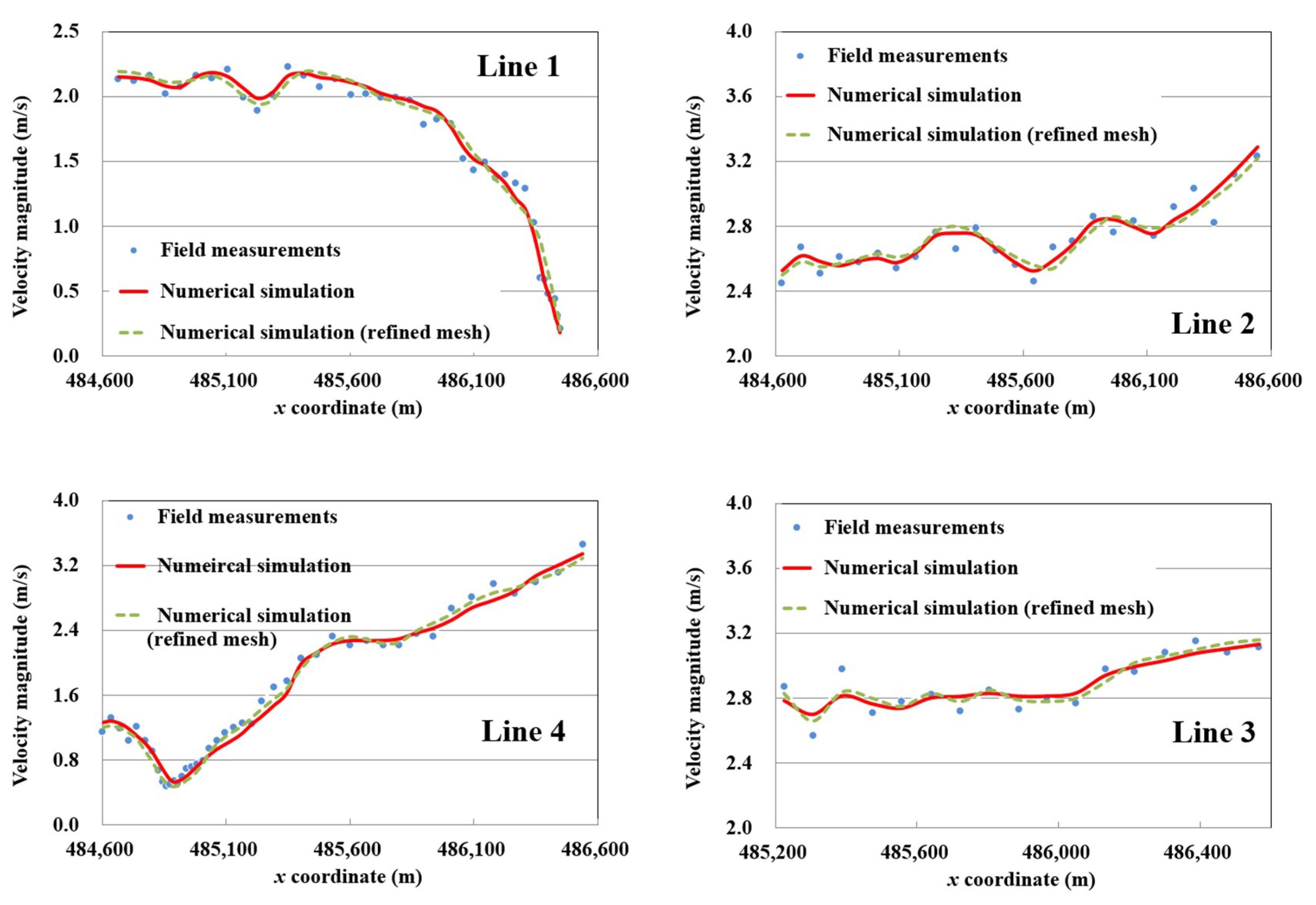
4. Model Verification
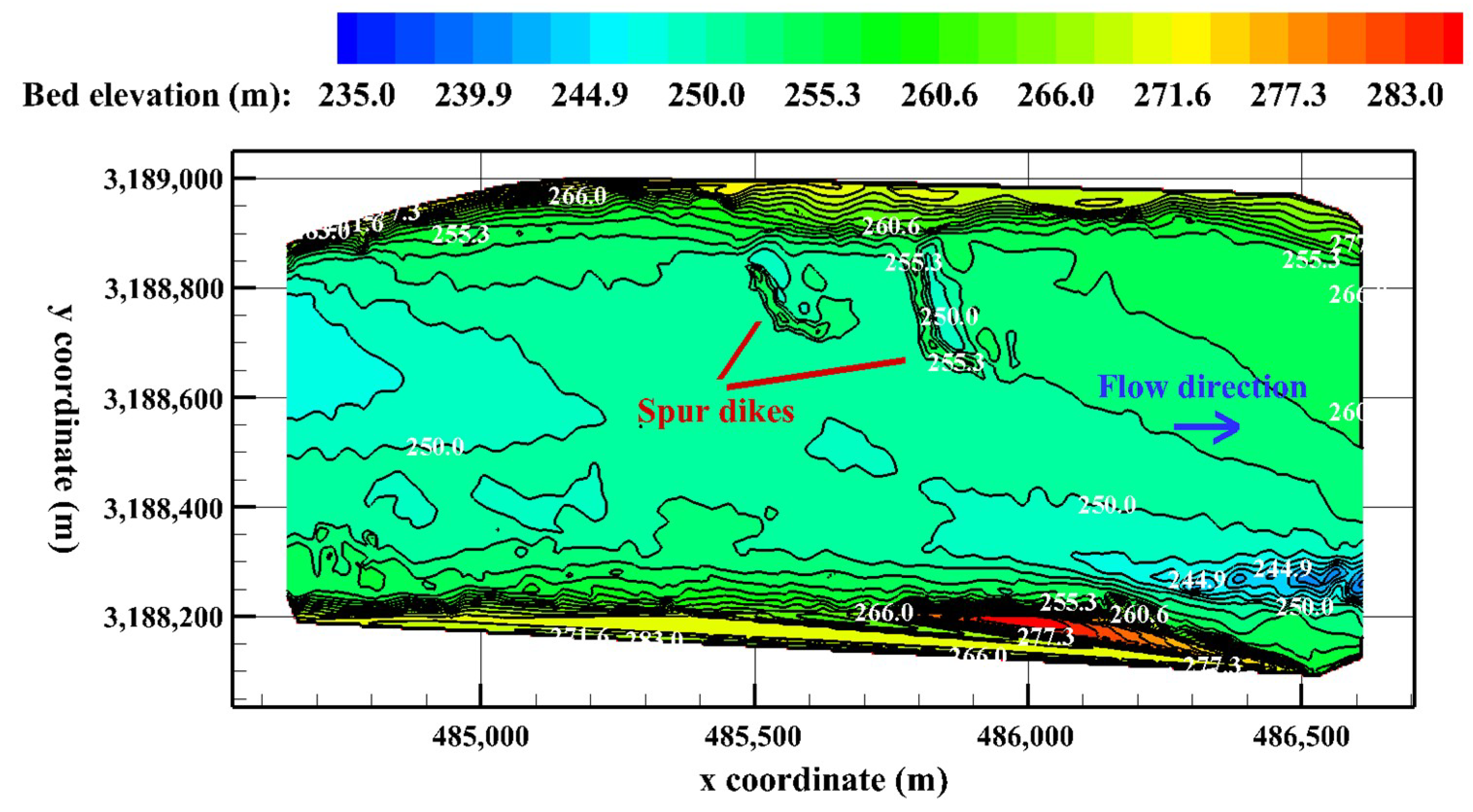
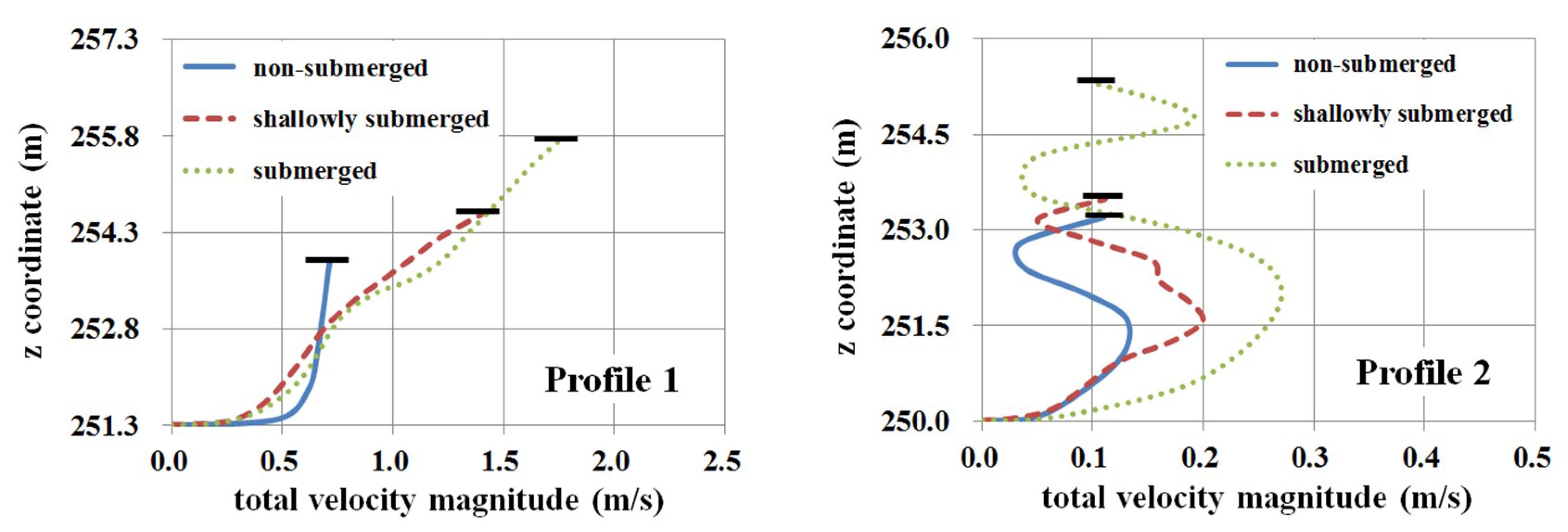
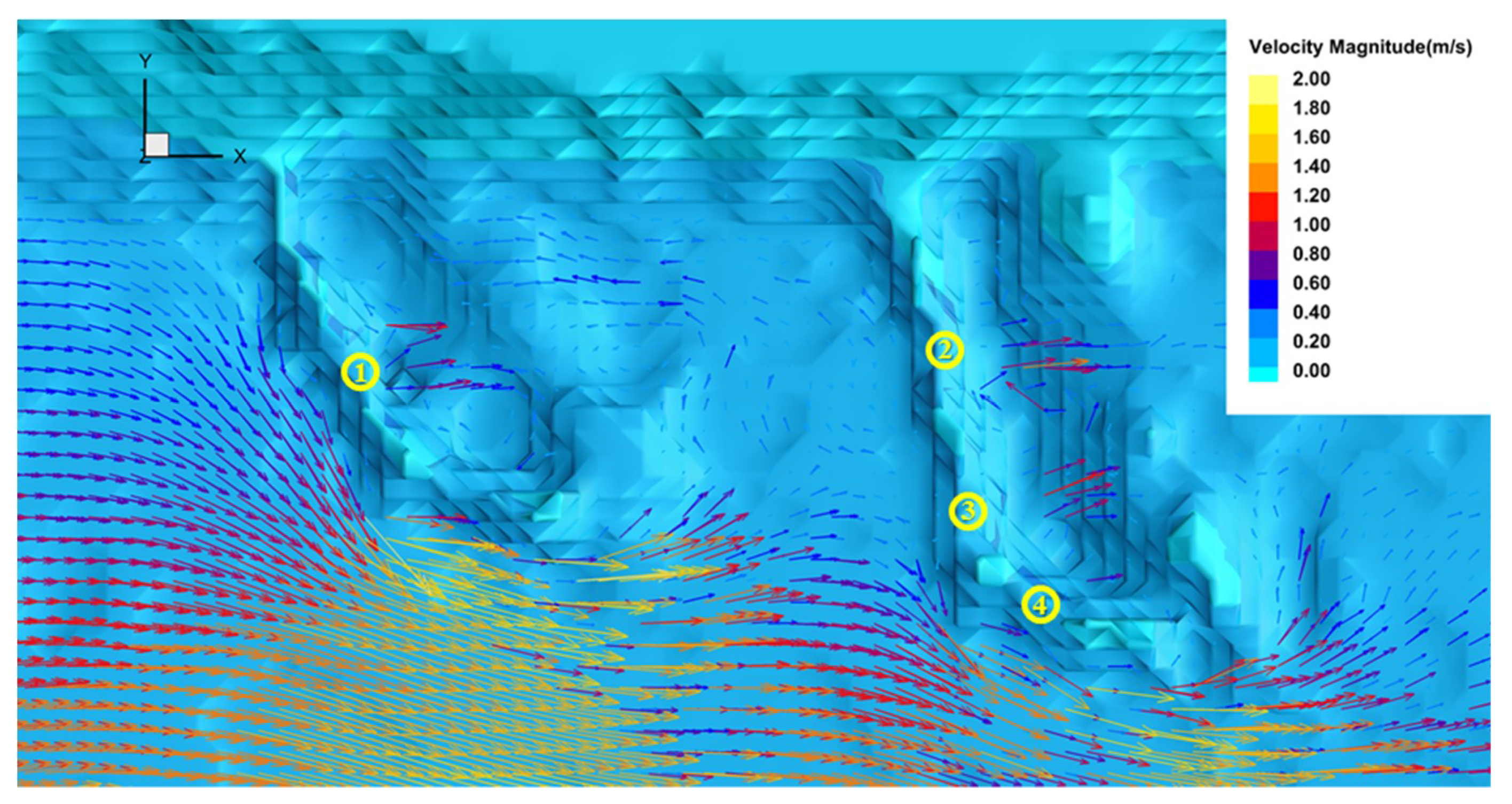
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bowles, R.E.; Pennington, C.H.; Howell, F.G. Macroinvertebrate drift associated with a dike field in the lower Mississippi River. Am. Zool. 1983, 23, 1003. [Google Scholar]
- Shields, F.D. Fate of lower Mississippi River habitats associated with river training dikes. Aquat. Conserv. 1995, 5, 97–108. [Google Scholar] [CrossRef]
- Ten Brinke, W.B.M.; Schulze, F.H.; van der Veer, P. Sand exchange between groyne-field beaches and the navigation channel of the Dutch Rhine: The impact of navigation versus river flow. River Res. Appl. 2004, 20, 899–928. [Google Scholar] [CrossRef]
- Dong, N.H.; Zhao, X.J.; Liu, Y. Experimental study on characteristics of sediment scouring and deposition in dike-narrowed river channel of Lower Yellow River. J. Hydraul. Eng. 2009, 40, 688–695. (In Chinese) [Google Scholar]
- Jamieson, E.C.; Rennie, C.D. 3-D flow and scour near a submerged wing dike: ADCP measurements on the Missouri River. Water Resour. Res. 2011, 47, W07544. [Google Scholar] [CrossRef]
- Schloesser, J.T.; Paukert, C.P.; Doyle, W.J. Fish assemblages at engineered and natural channel structures in the lower Missouri River: Implications for modified dike structures. River Res. Appl. 2012, 28, 1695–1707. [Google Scholar] [CrossRef]
- Braun, A.P.; Sobotka, M.J.; Phelps, Q.E. Fish Associations among Un-notched, Notched and L-head Dikes in the Middle Mississippi River. River Res. Appl. 2016, 32, 804–811. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Nwachukwu, B.A. Flow near groin-like structures. J. Hydraul. Eng. 1983, 109, 463–480. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Alonso, C.V.; Shields, F.D., Jr. Geometry of scour holes associated with 90° spur dikes. J. Hydraul. Eng. 1999, 125, 972–978. [Google Scholar] [CrossRef]
- Kuhnle, R.; Jia, Y.; Shields, F.D., Jr. Local Scour Associated with Angled Spur Dikes. J. Hydraul. Eng. 2002, 128, 1087–1093. [Google Scholar] [CrossRef]
- Duan, J.G. Mean flow and turbulence around a laboratory spur dike. J. Hydraul. Eng. 2009, 135, 803–811. [Google Scholar] [CrossRef]
- Duan, J.G.; He, L.; Wang, G.Q.; Fu, X.D. Mean flow and turbulence around experimental spur dike. Adv. Water Resour. 2009, 32, 1717–1725. [Google Scholar] [CrossRef]
- Kang, J.G.; Yeo, H.K.; Kim, S.J.; Ji, U. Permeability effects of single groin on flow characteristics. J. Hydraul. Res. 2011, 49, 728–735. [Google Scholar] [CrossRef]
- Kang, J.G.; Yeo, H.K. Experimental study on the flow characteristics of L-type groyne. Engineering 2011, 3, 1002–1011. [Google Scholar] [CrossRef]
- Zhang, H. Study on Flow and Bed Evolution in Channels with Spur Dykes. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 2005. [Google Scholar]
- Zhang, H.; Nakagawa, H.; Mizutani, H. Bed morphology and grain size characteristics around a spur dyke. Int. J. Sediment Res. 2012, 27, 141–157. [Google Scholar] [CrossRef]
- Uijttewaal, W.S.J. Effects of groyne layout on the flow in groyne fields: Laboratory experiments. J. Hydraul. Eng. 2005, 131, 782–791. [Google Scholar] [CrossRef]
- Tingsanchali, T.; Maheswaran, S. 2-D depth-average flow computation near groyne. J. Hydraul. Eng. 1990, 116, 71–86. [Google Scholar] [CrossRef]
- Mayerle, R.; Toro, F.M.; Wang, S.S.Y. Verification of a three-dimensional numerical model simulation of the flow in the vicinity of spur dikes. J. Hydraul. Res. 1995, 33, 243–256. [Google Scholar] [CrossRef]
- Molls, T.; Chaudhry, M.H.; Khan, K.W. Numerical simulation of two–dimensional flow near a spur dike. Adv. Water Resour. 1995, 118, 227–236. [Google Scholar] [CrossRef]
- Ouillon, S.; Dartus, D. Three-dimensional computation of flow around groyne. J. Hydraul. Eng. 1997, 123, 962–970. [Google Scholar] [CrossRef]
- Nagata, N.; Hosoda, T.; Nakato, T.; Muramoto, Y. Three-dimensional numerical model for flow and bed deformation around river hydraulic structures. J. Hydraul. Eng. 2005, 131, 1074–1087. [Google Scholar] [CrossRef]
- Peng, J. Three-Dimensional Flow Structure and Local Scour Around Spur Dikes. Ph.D. Thesis, University of Tokyo, Tokyo, Japan, 1998. [Google Scholar]
- Yu, X.; Tang, X.L.; Wang, W.C.; Wang, F.J.; Chen, Z.C.; Shi, X.Y. A lattice Boltzmann model coupled with a Large Eddy Simulation model for flows around a groyne. Int. J. Sediment Res. 2010, 25, 271–282. [Google Scholar] [CrossRef]
- McCoy, A.; Constantinescu, S.G.; Weber, L. A numerical investigation of the dynamics of coherent structures and mass exchange processes in a channel flow with two lateral submerged groynes. Water Resour. Res. 2007, 43, W05445. [Google Scholar] [CrossRef]
- McCoy, A.; Constantinescu, S.G.; Weber, L. Numerical investigation of flow hydrodynamics in a channel with series of groynes. J. Hydraul. Eng. 2008, 134, 157–172. [Google Scholar] [CrossRef]
- Koken, M.; Constantinescu, G. An investigation of the flow and scour mechanisms around isolated spur dikes in a shallow open channel: 1. Conditions corresponding to the initiation of the erosion and deposition process. Water Resour. Res. 2008, 44, W08406. [Google Scholar] [CrossRef]
- Koken, M.; Constantinescu, G. An investigation of the flow and scour mechanisms around isolated spur dikes in a shallow open channel: 2. Conditions corresponding to the final stages of the erosion and deposition process. Water Resour. Res. 2008, 44, W08407. [Google Scholar] [CrossRef]
- Koken, M.; Constantinescu, G. Flow and turbulence structure around a spur dike in a channel with a large scour hole. Water Resour. Res. 2011, 47, W12511. [Google Scholar] [CrossRef]
- Khosronejad, A.; Hill, C.; Kang, S.; Sotiropoulos, F. Computational and experimental investigation of scour past laboratory models of stream restoration rock structures. Adv. Water Resour. 2013, 1, 191–207. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kozarek, J.L.; Palmsten, M.L.; Sotiropoulos, F. Numerical simulation of large dunes in meandering streams and rivers with in-stream rock structures. Adv. Water Resour. 2014, 9, 309–332. [Google Scholar] [CrossRef]
- Lin, P.; Li, C.W. Wave-current interaction with a vertical square cylinder. Ocean. Eng. 2003, 30, 55–76. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. A numerical study of three-dimensional liquid sloshing in tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. Three-dimensional liquid sloshing in a tank with baffles. Ocean. Eng. 2009, 36, 202–212. [Google Scholar] [CrossRef]
- Lin, P. Numerical Modeling of Water Waves, 1st ed.; Taylor &Francis: London, UK; New York, NY, USA, 2008. [Google Scholar]
- Xue, M.; Lin, P. Numerical study of ring baffle effects on reducing violent liquid sloshing. Comput. Fluids 2011, 52, 116–129. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, L.; Liu, D. A two-phase flow model for wave–structure interaction using a virtual boundary force method. Comput. Fluids 2016, 129, 101–110. [Google Scholar] [CrossRef]
- Karunarathna, S.A.S.A.; Lin, P. Numerical simulation of wave damping over porous Seabeds. Coast. Eng. 2006, 53, 845–855. [Google Scholar] [CrossRef]
- Lin, P.; Karunarathna, S.A.S.A. Numerical study of solitary wave interaction with porous breakwaters. J. Waterw. Port C 2007, 133, 352–363. [Google Scholar] [CrossRef]
- Gueyffier, D.; Li, J.; Nadim, A.; Scardovelli, R.; Zaleski, S. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows. J. Comput. Phys. 1999, 152, 423–456. [Google Scholar] [CrossRef]
- Youngs, D.L. Time-dependent multi-material flow with large fluid distortion. Numer. Methods Fluid Dyn. 1982, 24, 273–285. [Google Scholar]
- Smagorinsky, J.S. General circulation experiments with the primitive equations—1, the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Jia, G.; She, J.; Wang, T.; Zhang, G. PIV measurement of flow structure behind submerged spur dike. Int. J. Hydroelectr. Energy 2012, 30, 84–86. (In Chinese) [Google Scholar]




| Case No. | Total Flow Discharge (m3/s) | Mean Water Elevation of Reach Outlet (m) |
|---|---|---|
| No.1 | 6270 | 256.2 |
| No.2 | 3120 | 253.6 |
| Point No. | Field Measurement (m) | Numerical Results with Coarse Mesh (m) | Numerical Results with Fine Mesh (m) | Bed Elevation (m) | Relative Error with Coarse Mesh | Relative Error with Refined Mesh |
|---|---|---|---|---|---|---|
| 1 | 256.76 | 256.88 | 256.82 | 255.50 | 9.5% | 4.8% |
| 2 | 256.48 | 256.54 | 256.55 | 255.60 | 6.8% | 8.0% |
| 3 | 256.80 | 256.72 | 256.70 | 255.80 | 8.0% | 10.0% |
| 4 | 256.31 | 256.20 | 256.18 | 255.20 | 9.9% | 11.7% |
| 5 | 255.86 | 255.95 | 255.91 | 254.80 | 8.5% | 4.7% |
| Location No. | Depth-Averaged Flow Velocity (m/s) | Positions (x, y) |
|---|---|---|
| 1 | 0.85 | 485,531 m, 3,188,792 m |
| 2 | 0.96 | 485,808 m, 3,188,806 m |
| 3 | 0.92 | 485,820 m, 3,188,733 m |
| 4 | 0.73 | 485,853 m, 3,188,681 m |
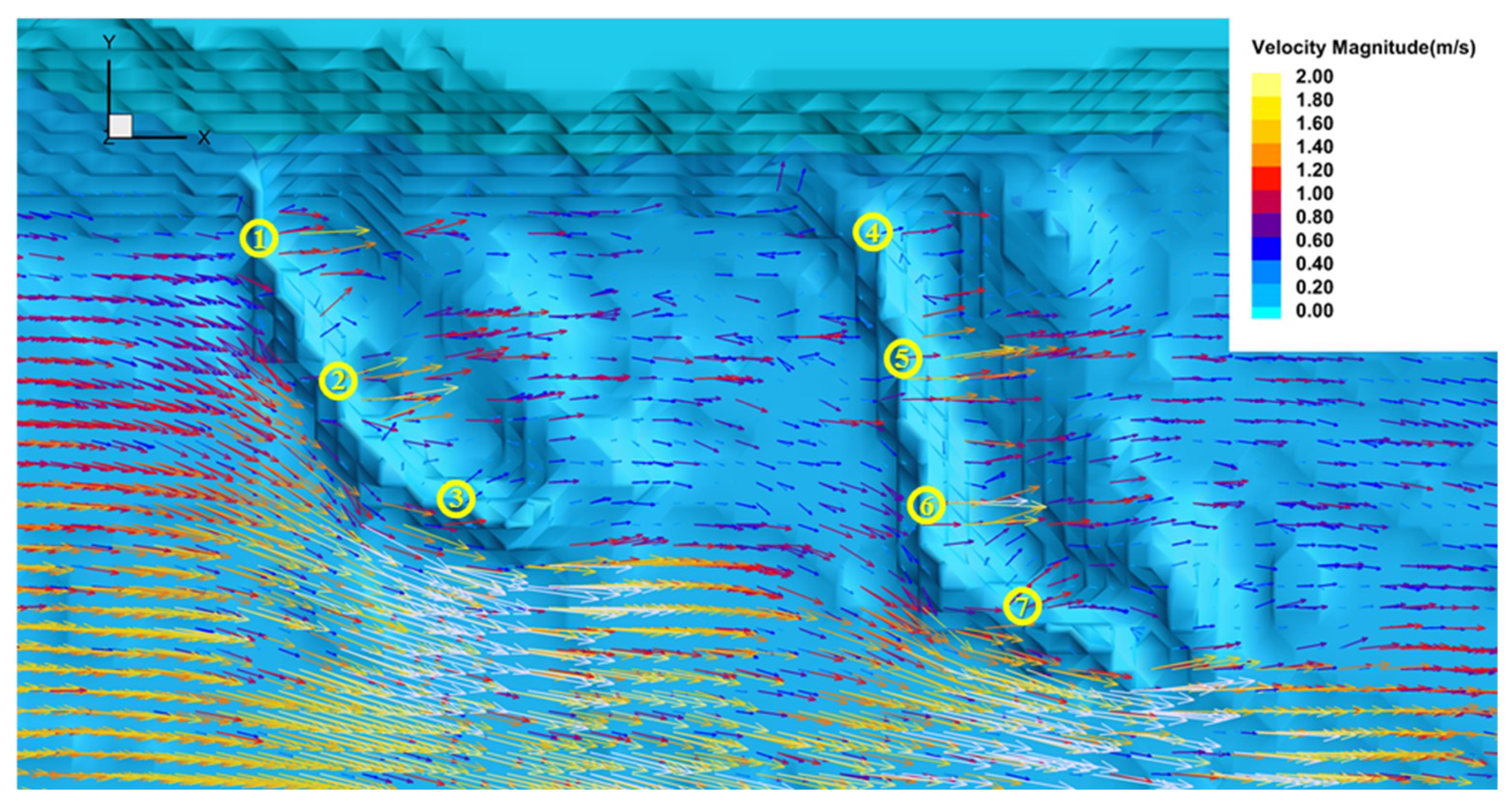
| Location No. | Depth-Averaged Flow Velocity (m/s) | Positions (x, y) |
|---|---|---|
| 1 | 1.42 | 485,496 m, 3,188,865 m |
| 2 | 1.23 | 485,534 m, 3,188,796 m |
| 3 | 0.78 | 485,587 m, 3,188,743 m |
| 4 | 1.09 | 485,792 m, 3,188,864 m |
| 5 | 1.65 | 485,807 m, 3,188,804 m |
| 6 | 1.82 | 485,817 m, 3,188,731 m |
| 7 | 1.12 | 485,859 m, 3,188,697 m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Lin, P. 3D Numerical Study of the Flow Properties in a Double-Spur Dikes Field during a Flood Process. Water 2018, 10, 1574. https://doi.org/10.3390/w10111574
Han X, Lin P. 3D Numerical Study of the Flow Properties in a Double-Spur Dikes Field during a Flood Process. Water. 2018; 10(11):1574. https://doi.org/10.3390/w10111574
Chicago/Turabian StyleHan, Xun, and Pengzhi Lin. 2018. "3D Numerical Study of the Flow Properties in a Double-Spur Dikes Field during a Flood Process" Water 10, no. 11: 1574. https://doi.org/10.3390/w10111574
APA StyleHan, X., & Lin, P. (2018). 3D Numerical Study of the Flow Properties in a Double-Spur Dikes Field during a Flood Process. Water, 10(11), 1574. https://doi.org/10.3390/w10111574




