Quantifying the Relationship between Drought and Water Scarcity Using Copulas: Case Study of Beijing–Tianjin–Hebei Metropolitan Areas in China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. SPEI
2.3. WEI+
2.4. Copula Model and Conditional Probability Distribution
2.4.1. Copula Model
2.4.2. Conditional Probability Distribution
3. Results and Discussion
3.1. SPEI Calculation Results
3.2. WEI+ Calculation Results
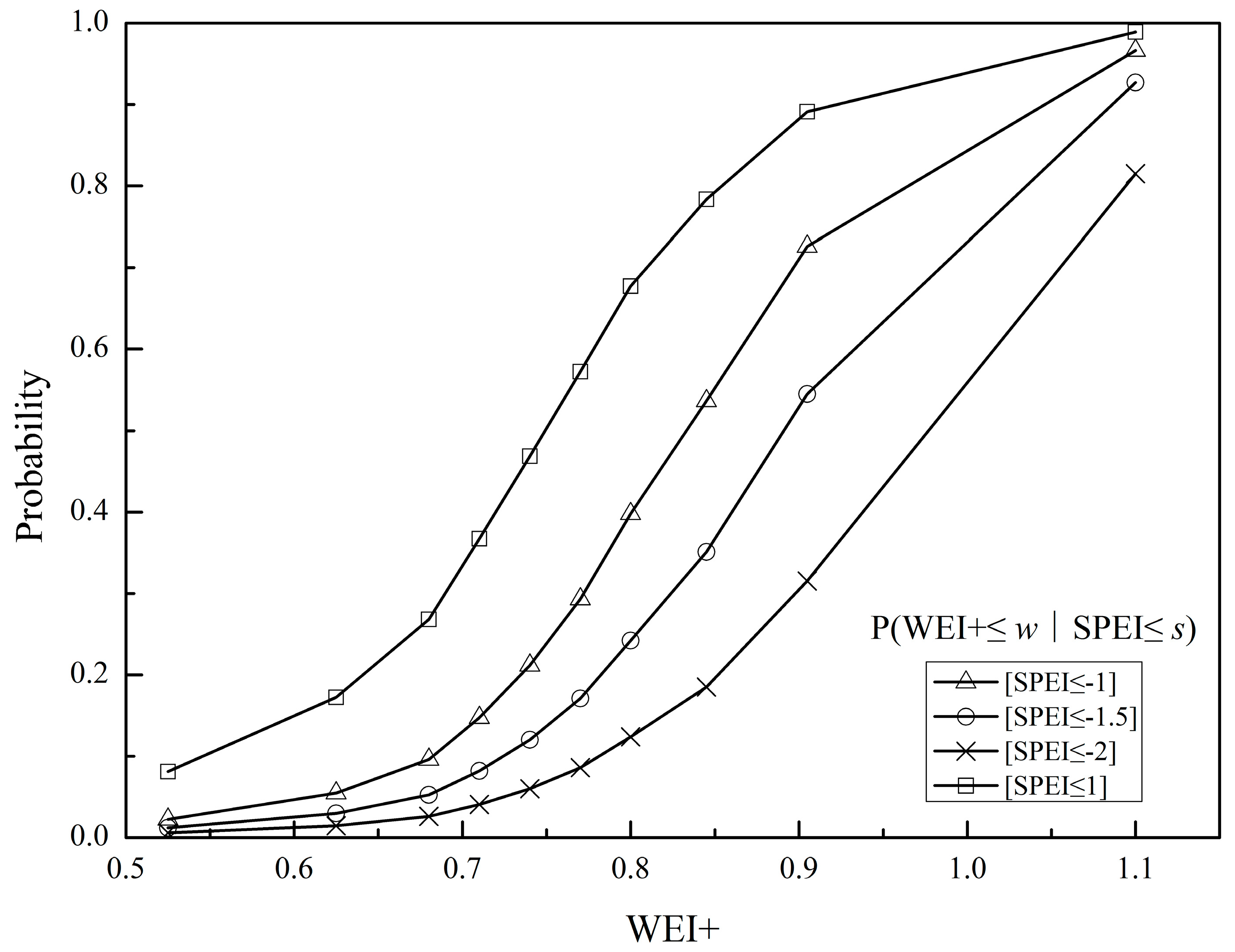
3.3. Conditional Probability Distribution between SPEI and WEI+
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A review of water scarcity and drought indexes in water resources planning and management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Wang, H.; Wang, C.; Lai, W.; Zhao, Y. Exploration of use of copulas in analysing the relationship between precipitation and meteorological drought in Beijing, China. Adv. Meteorol. 2017, 43, 1–11. [Google Scholar] [CrossRef]
- UN-WATER. Coping with Water Scarcity: A Strategic Issue and Priority for System-Wide Action. Available online: www.unwater.org/downloads/waterscarcity.pdf (accessed on 16 July 2012).
- FAO. Coping with Water Scarcity. Challenge of the Twenty-First Century. Available online: http://www.fao.org/nr/water/docs/escarcity.pdf (accessed on 1 March 2007).
- Van Loon, A.F.; Van Lanen, H.A.J. Making the distinction between water scarcity and drought using an observation-modeling framework. Water Resour. Res. 2013, 49, 1–20. [Google Scholar] [CrossRef]
- EU. Report on the Review of the European Water Scarcity and Droughts Policy, Communication from the Commission to the European Parliament and the Council, The European Economic and Social Committee and the Committee of the Regions. 2012. Available online: https://climate-adapt.eea.europa.eu/metadata/publications/report-on-the-review-of-the-european-water-scarcity-and-drought-policy/11309505 (accessed on 7 November 2018).
- Strosser, P.; Dworak, T.; Garzon, P.A.; Berglund, M.; Schmidt, G. Gap analysis of the Water Scarcity and Droughts Policy in the EU. Final report. European Commission Tender ENV.D.1/SER/2010/0049/Acteon 2012. Available online: http://ec.europa.eu/environment/water/quantity/pdf/WSDGapAnalysis.pdf (accessed on 7 November 2018).
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; Lópezmoreno, J.I. A multi-scalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W. Meteorological Drought. U.S. Department of Commerce Weather Bureau Research Paper. 1965. Available online: https://www.fws.gov/southwest/es/documents/R2ES/LitCited/LPC_2012/Palmer_1965.pdf (accessed on 7 November 2018).
- Faergemann, H. Update on Water Scarcity and Droughts Indicator Development; EC Expert Group on Water Scarcity & Droughts: Denmark, 2012. [Google Scholar]
- Falkenmark, M.; Widstrand, C. Population and water resources: A delicate balance. Potul. Bull. 1992, 47, 1–36. [Google Scholar]
- Estrela, T.; Vargas, E. Drought management plans in the European Union. The case of Spain. Water Resour. Manag. 2012, 26, 1537–1553. [Google Scholar] [CrossRef]
- Mortazavi, M.; Kuczera, G.; Cui, L. Multiobjective optimization of urban water resources: Moving toward more practical solutions. Water Resour. Res. 2012, 48, 3514. [Google Scholar] [CrossRef]
- Mazzanti, B.; Checcucci, G.; Monacelli, G.; Puma, F.; Vezzani, C. Drought and Water Scarcity Indicators: Experience and Operational Applications in Italian Basins. In Geophysical Research Abstracts; EGU General Assembly: Vienna, Austria, 2013; EGU2013-10311. [Google Scholar]
- Kossida, M.; Mimikou, M. An indicators’ based approach to Drought and Water Scarcity Risk Mapping in Pinios River Basin, Greece. In Geophysical Research Abstracts; EGU General Assembly: Vienna, Austria, 2013; EGU2013-6349, 2013. [Google Scholar]
- Van Lanen, H.A.J.; Tallaksen, L.M.; Stahl, K.; Van Loon, A.F.; Van Huijgevoort, M.H.J.; Corzo Perez, G.A. Drought, Water Scarcity and Climate Change. In Geophysical Research Abstracts; EGU General Assembly: Vienna, Austria, 2012; EGU2012-2143-2. [Google Scholar]
- Chen, F.; Li, J. Quantifying drought and water scarcity: A case study in the luanhe river basin. Nat. Hazards. 2016, 81, 1913–1927. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, Y.; Chen, Q.; Yao, Y. Spatial patterns and temporal variability of drought in Beijing-Tianjin-Hebei metropolitan areas in China. Adv. Meteorol. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Tan, C.; Yang, J.; Li, M. Temporal-spatial variation of drought indicated by SPI and SPEI in Ningxia hui autonomous region, china. Atmosphere 2015, 6, 1399–1421. [Google Scholar] [CrossRef]
- Raskin, P.; Gleick, P.; Kirshen, P.; Pontius, G.; Strzepek, K. Comprehensive Assessment of the Freshwater Resources of the World. Water Futures: Assessment of Long-Range Patterns and Problems; Stockholm Sweden Stockholm Environment Institute: Stockholm, Sweden, 1997. [Google Scholar]
- Lane, M.E.; Kirshen, P.H.; Vogel, R.M. Indicators of impacts of global climate change on US water resources. J. Water. Res. Plan. Mang. 1999, 125, 194–204. [Google Scholar] [CrossRef]
- Alcamo, J.; Thomas, H.T.; Rösch, T. World Water in 2025-Global Modeling Scenarios for the World Commission on Water for the 21st Century; Report A0002; Center for Environmental Systems Research: University of Kassel, Kassel, Germany, 2000. [Google Scholar]
- Sklar, A. N-Dimensional Distribution Functions and their Margins; L’Institut de statistique de l’universite de Paris: Paris, France, 1959; pp. 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Qian, L.; Wang, H.; Dang, S.; Wang, C.; Jiao, Z.; Zhao, Y. Modelling bivariate extreme precipitation distribution for data-scarce regions using Gumbel-Hougaard copula with maximum entropy estimation. Hydrol. Process. 2017, 32. [Google Scholar] [CrossRef]
- Moazami, S.; Golian, S.; Kavianpour, M.R.; Hong, Y. Uncertainty analysis of bias from satellite rainfall estimates using copula method. Atmos. Res. 2014, 137, 145–166. [Google Scholar] [CrossRef]
- Jordanger, L.A.; Tjøstheim, D. Model selection of copulas: AIC versus a cross validation copula information criterion. Stat. Prpbabil. Lett. 2014, 92, 249–255. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 15–18. [Google Scholar] [CrossRef]
- Brunner, M.I.; Favre, A.C.; Seibert, J. Bivariate return periods and their importance for flood peak and volume estimation. Wiley Interdiscip. Rev. Water 2016, 3, 819–833. [Google Scholar] [CrossRef]
- Stamatatou, N.; Vasiliades, L.; Loukas, A. Bivariate Flood Frequency Analysis Using Copulas. Proceedings 2018, 2, 635. [Google Scholar] [CrossRef]
- Azam, M.; Maeng, S.J.; Kim, H.S.; Murtazaev, A. Copula-Based Stochastic Simulation for Regional Drought Risk Assessment in South Korea. Water 2018, 10, 359. [Google Scholar] [CrossRef]
- Hesami Afshar, M.; Sorman, A.U.; Yilmaz, M.T. Conditional Copula-Based Spatial–Temporal Drought Characteristics Analysis—A Case Study over Turkey. Water 2016, 8, 426. [Google Scholar] [CrossRef]
- Yuan, F.; Ma, M.; Ren, L.; Shen, H.; Li, Y.; Jiang, S. Possible future climate change impacts on the hydrological drought events in the Weihe river basin, China. Adv. Meteorol. 2015, 2016, 1–14. [Google Scholar] [CrossRef]
- Shiau, J.T.; Modarres, R. Copula-based drought severity-duration-frequency analysis in Iran. Meteorol. Appl. 2009, 16, 481–489. [Google Scholar] [CrossRef] [Green Version]






| Aspects | Drought | Water Scarcity |
|---|---|---|
| Causes | Natural, due to a deficient of precipitation over a certain time period. | Man-made, due to the increasing water consumption over natural renewable water resources. |
| Occurrence | Drought is a normal, recurrent feature of all climates and can happen anywhere. | Water scarcity usually happens in places where population is larger while natural water resources are not enough. |
| Timescale | Drought can last from a few weeks to several years. | Usually, water scarcity may cause permanent damage to water ecosystems. |
| Impacts | The impacts cause by drought may be variable, according to its duration, severity, and also the vulnerability of society. It is more likely to influence the natural water cycle. | The impacts cause by water scarcity is more social. It will directly influence agricultural, industrial and domestic water consumption. |
| Spatial distribution | Usually evaluated by river basins, and can happen in both small and large scales. | Usually evaluated by administrative regions, and can happen in both small and large scales. |
| Interaction | When droughts occur in an area characterized by water scarcity, their impact will be more severe, as they are more vulnerable. Heat waves can aggravate droughts and water scarcity situations. Water scarcity can also be an effect of overexploitation due to (concurrent) drought events, but this does not apply vice versa (drought is not an effect of water scarcity) | |
| Risk | The risk of drought depends on the hazard, and the vulnerability and exposure of hazard-affected bodies. | The risk of water scarcity not only depends on the hazard, the vulnerability and exposure of hazard-affected bodies, but also depends on the reliability and resistance of hazard-affected bodies. The vulnerability and exposure may increase the risk, while the reliability and resistance can decrease the risk. |
| Indicators | SPI [8], SPEI [9], Palmer Index [10] | WEI+ [11], the Falkenmark indicator [12] |
| Station Name | Latitude (N) | Longitude (E) | Duration |
|---|---|---|---|
| Beijing | 39.80 | 116.47 | January 1951—December 2015 |
| Tianjin | 39.08 | 117.07 | January 1954—December 2015 |
| Tanggu | 39.05 | 117.72 | January 1954—December 2015 |
| Bohai | 38.45 | 118.42 | January 2004—December 2015 |
| Shijiazhuang | 38.03 | 114.42 | January 1955—December 2015 |
| Baoding | 38.85 | 115.52 | January 1955—December 2015 |
| Chengde | 40.98 | 117.95 | January 1951—December 2015 |
| Langfang | 39.12 | 116.38 | January 1957—December 2015 |
| Qinhuangdao | 39.85 | 119.52 | January 1954—December 2015 |
| Tangshan | 39.67 | 118.15 | January 1957—December 2015 |
| Xingtai | 37.07 | 114.50 | January 1954—December 2015 |
| Zhangjiakou | 40.78 | 114.88 | January 1956—December 2015 |
| Botou | 38.08 | 116.55 | January 1996—December 2015 |
| Huailai | 40.40 | 115.5 | January 1954—December 2015 |
| Huanghua | 38.37 | 117.35 | January 1960—December 2015 |
| Laoting | 39.43 | 118.88 | January 1957—December 2015 |
| Miyun | 40.38 | 116.87 | January 1989—December 2015 |
| Nangong | 37.37 | 115.38 | January 1958—December 2015 |
| Qinglong | 40.40 | 118.95 | January 1957—December 2015 |
| Raoyang | 38.23 | 115.73 | January 1957—December 2015 |
| Weichang | 41.93 | 117.75 | January 1951—December 2015 |
| Weixian | 39.83 | 114.57 | January 1954—December 2015 |
| Zhangbei | 41.15 | 114.70 | January 1956—December 2015 |
| Zunhua | 40.20 | 117.95 | January 1956—December 2015 |
| Class | SPEI Value | Description | Class | SPEI value | Description |
|---|---|---|---|---|---|
| 1 | SPEI ≥ 2.00 | Extremely wet | 5 | −1.50 ≤ SPEI < −1.00 | Moderate drought |
| 2 | 1.50 ≤ SPEI < 2.00 | Very wet | 6 | −2.00 ≤ SPEI < −1.50 | Severe drought |
| 3 | 1.00 ≤ SPEI < 1.50 | Moderately wet | 7 | SPEI < −2.00 | Extreme drought |
| 4 | −1.00 ≤ SPEI < 1.00 | Near normal |
| Year | Water Consumption (×108 m3) | RWR (×108 m3) | WEI+ |
|---|---|---|---|
| 2001 | 269.31 | 282.41 | 91.83% |
| 2002 | 265.97 | 287.90 | 88.87% |
| 2003 | 256.15 | 267.64 | 91.20% |
| 2004 | 250.97 | 256.45 | 92.44% |
| 2005 | 258.07 | 274.76 | 88.42% |
| 2006 | 261.30 | 278.80 | 87.55% |
| 2007 | 260.00 | 268.31 | 89.65% |
| 2008 | 261.47 | 284.25 | 83.85% |
| 2009 | 252.59 | 262.99 | 84.23% |
| 2010 | 251.59 | 255.69 | 86.42% |
| 2011 | 255.07 | 265.67 | 83.52% |
| 2012 | 254.36 | 294.70 | 73.40% |
| 2013 | 252.86 | 275.90 | 75.70% |
| 2014 | 256.49 | 277.05 | 79.01% |
| 2015 | 251.08 | 248.37 | 79.21% |
| Items | Gumbel | Frank | Clayton |
|---|---|---|---|
| Parameter estimation θ | 1.5905 | 3.7628 | 0.7679 |
| OLS | 0.0245 | 0.0250 | 0.1065 |
| MSE | 0.0006 | 0.00062 | 0.0114 |
| AIC | −361.55 | −359.65 | −217.45 |
| BIC | −356.92 | −355.02 | −212.82 |
| Water Scarcity Situation | SPEI ≤ −1 | SPEI ≤ −1.5 | SPEI ≤ −2 | SPEI ≤ 1 |
|---|---|---|---|---|
| WEI+ ≥ 0.5 | 97.76% | 98.80% | 99.41% | 91.89% |
| WEI+ ≥ 0.6 | 94.53% | 97.03% | 98.54% | 82.77% |
| WEI+ ≥ 0.7 | 85.25% | 91.80% | 95.93% | 63.27% |
| WEI+ ≥ 0.8 | 60.22% | 75.79% | 87.63% | 32.28% |
| WEI+ ≥ 0.9 | 27.40% | 45.52% | 68.47% | 10.89% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Wang, H.; Liu, Z.; Li, N. Quantifying the Relationship between Drought and Water Scarcity Using Copulas: Case Study of Beijing–Tianjin–Hebei Metropolitan Areas in China. Water 2018, 10, 1622. https://doi.org/10.3390/w10111622
Fan L, Wang H, Liu Z, Li N. Quantifying the Relationship between Drought and Water Scarcity Using Copulas: Case Study of Beijing–Tianjin–Hebei Metropolitan Areas in China. Water. 2018; 10(11):1622. https://doi.org/10.3390/w10111622
Chicago/Turabian StyleFan, Linlin, Hongrui Wang, Zhiping Liu, and Na Li. 2018. "Quantifying the Relationship between Drought and Water Scarcity Using Copulas: Case Study of Beijing–Tianjin–Hebei Metropolitan Areas in China" Water 10, no. 11: 1622. https://doi.org/10.3390/w10111622
APA StyleFan, L., Wang, H., Liu, Z., & Li, N. (2018). Quantifying the Relationship between Drought and Water Scarcity Using Copulas: Case Study of Beijing–Tianjin–Hebei Metropolitan Areas in China. Water, 10(11), 1622. https://doi.org/10.3390/w10111622






