Studying Inertia Effects in Open Channel Flow Using Saint-Venant Equations
Abstract
:1. Introduction
2. Theoretical and Numerical Approximations
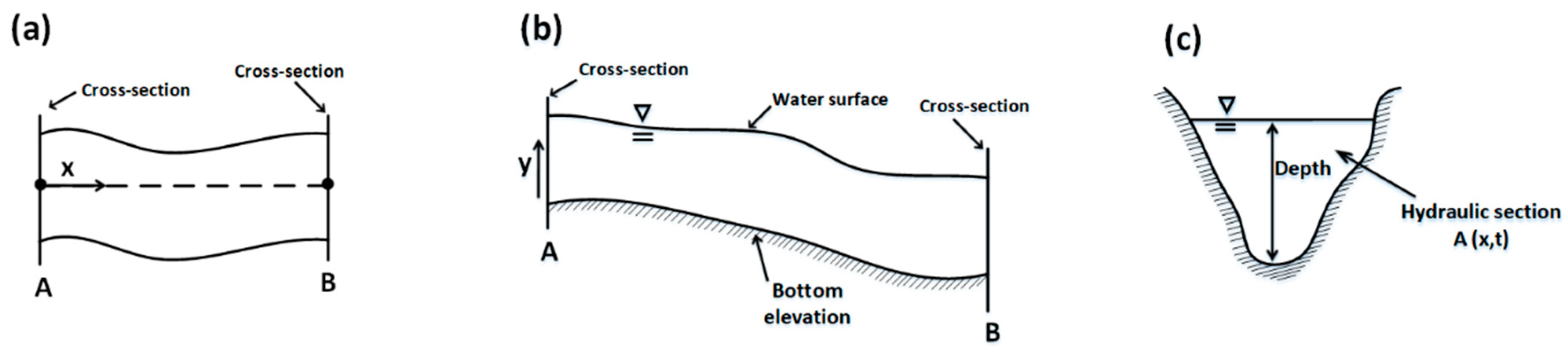
2.1. Theoretical Basis
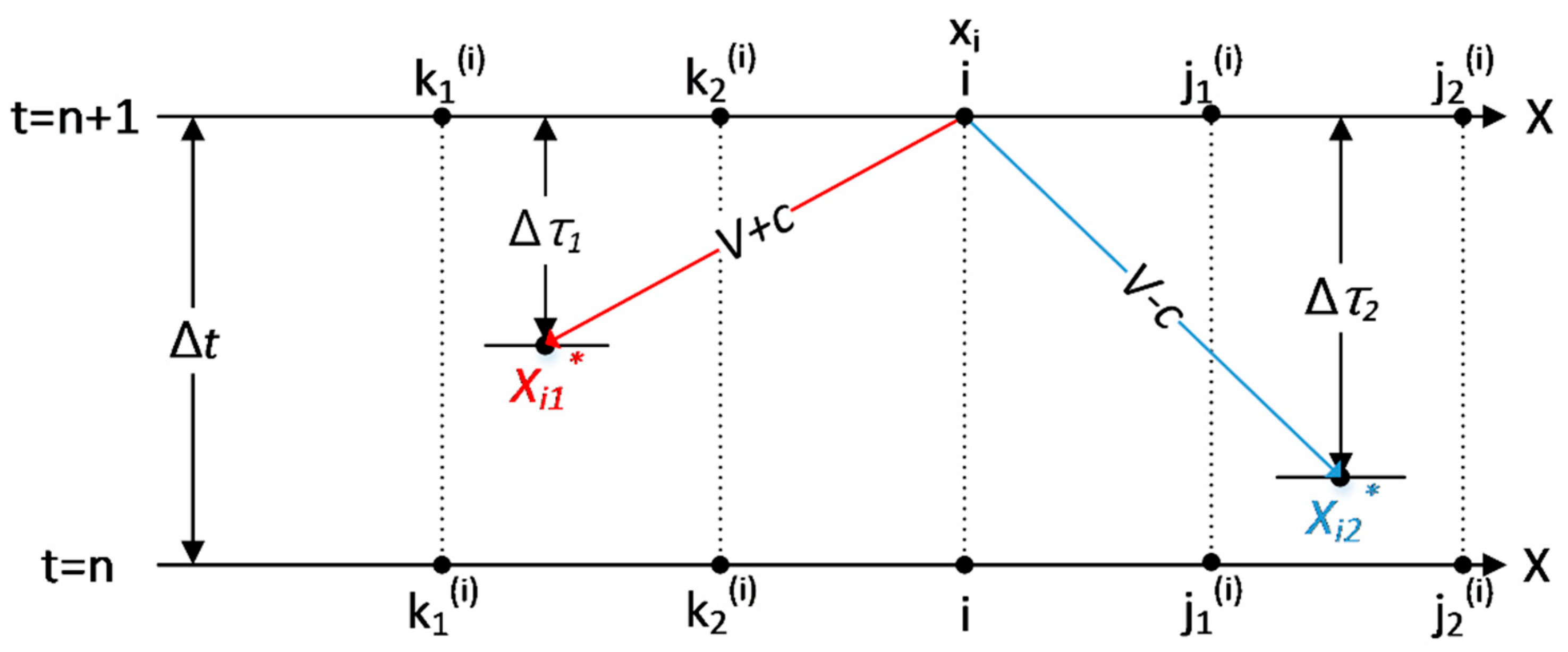
2.2. Numerical Approximations
3. Model Calibrations
3.1. Calibration of the Fully Dynamic Wave Module
3.2. Calibration of Diffusion Wave Module
3.3. Calibration of Kinematic Wave Module
4. Result and Discussions
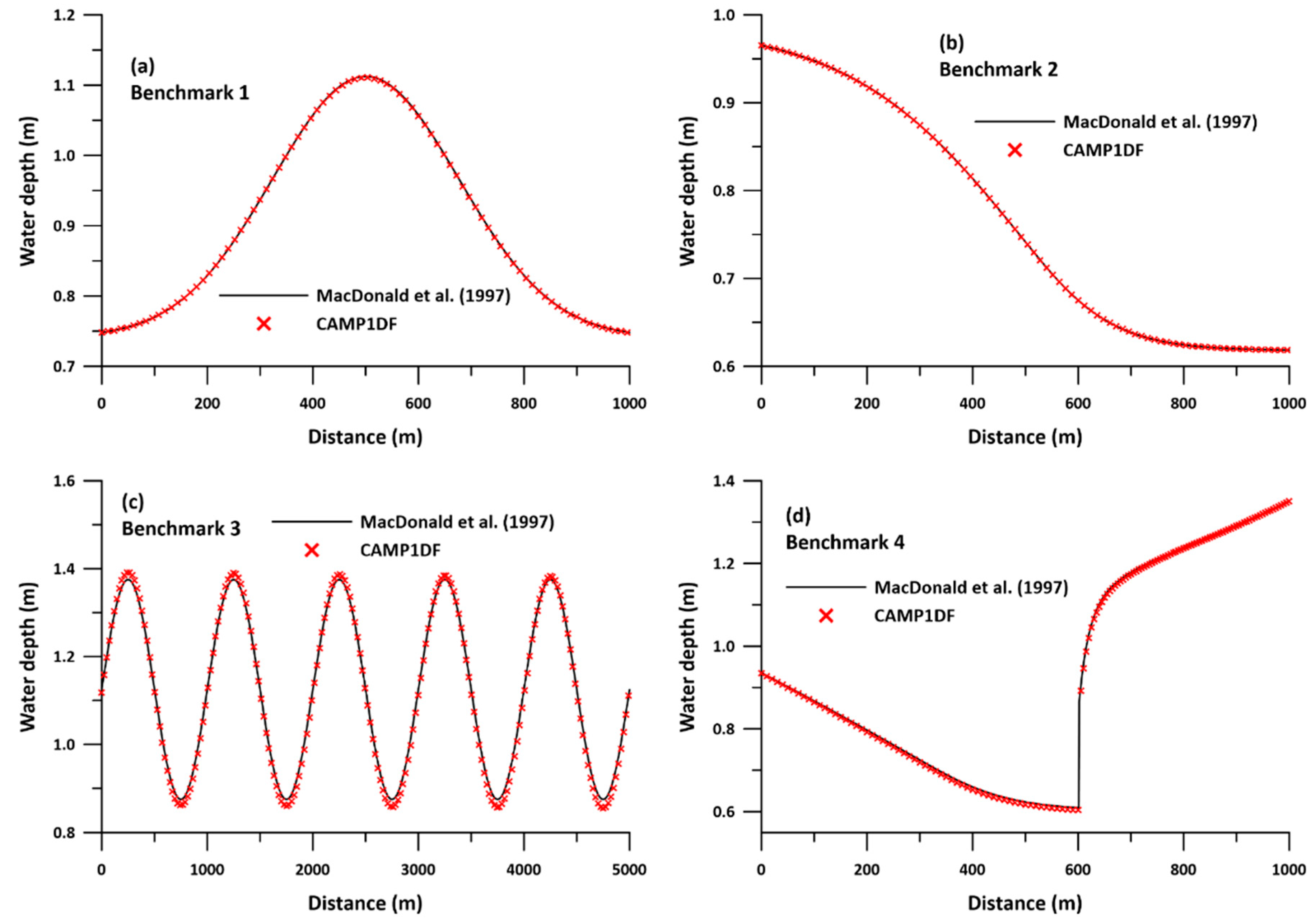
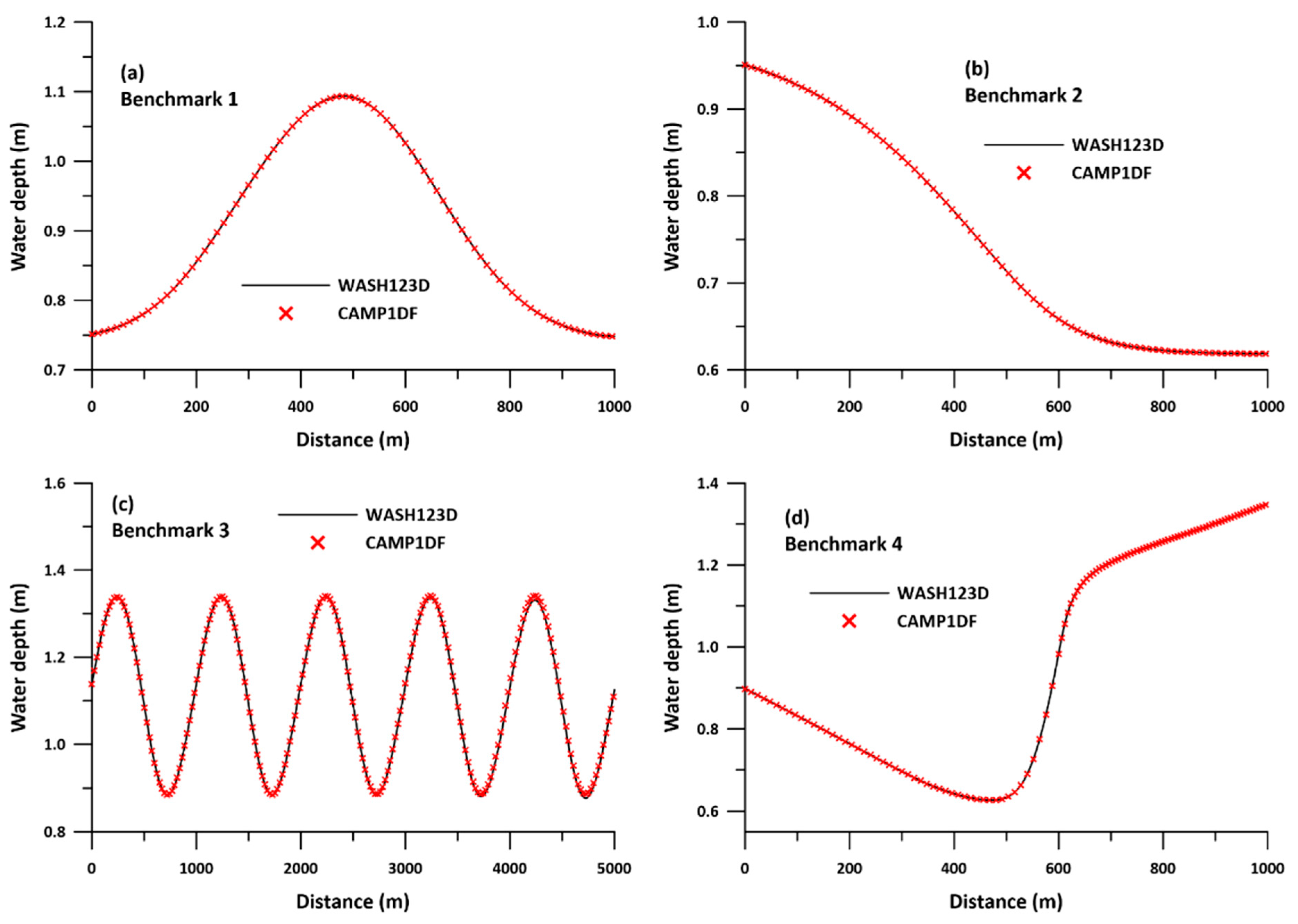
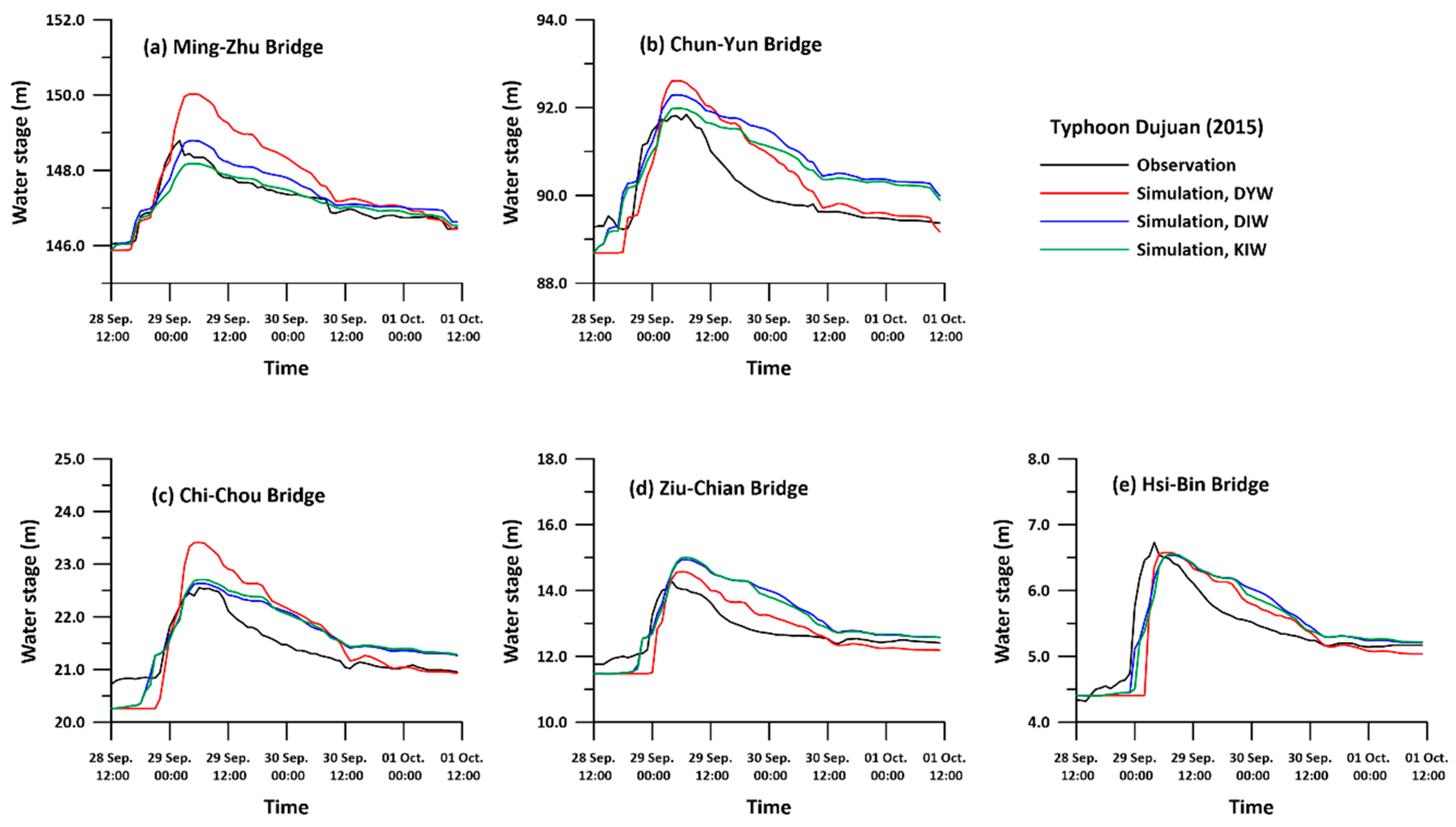
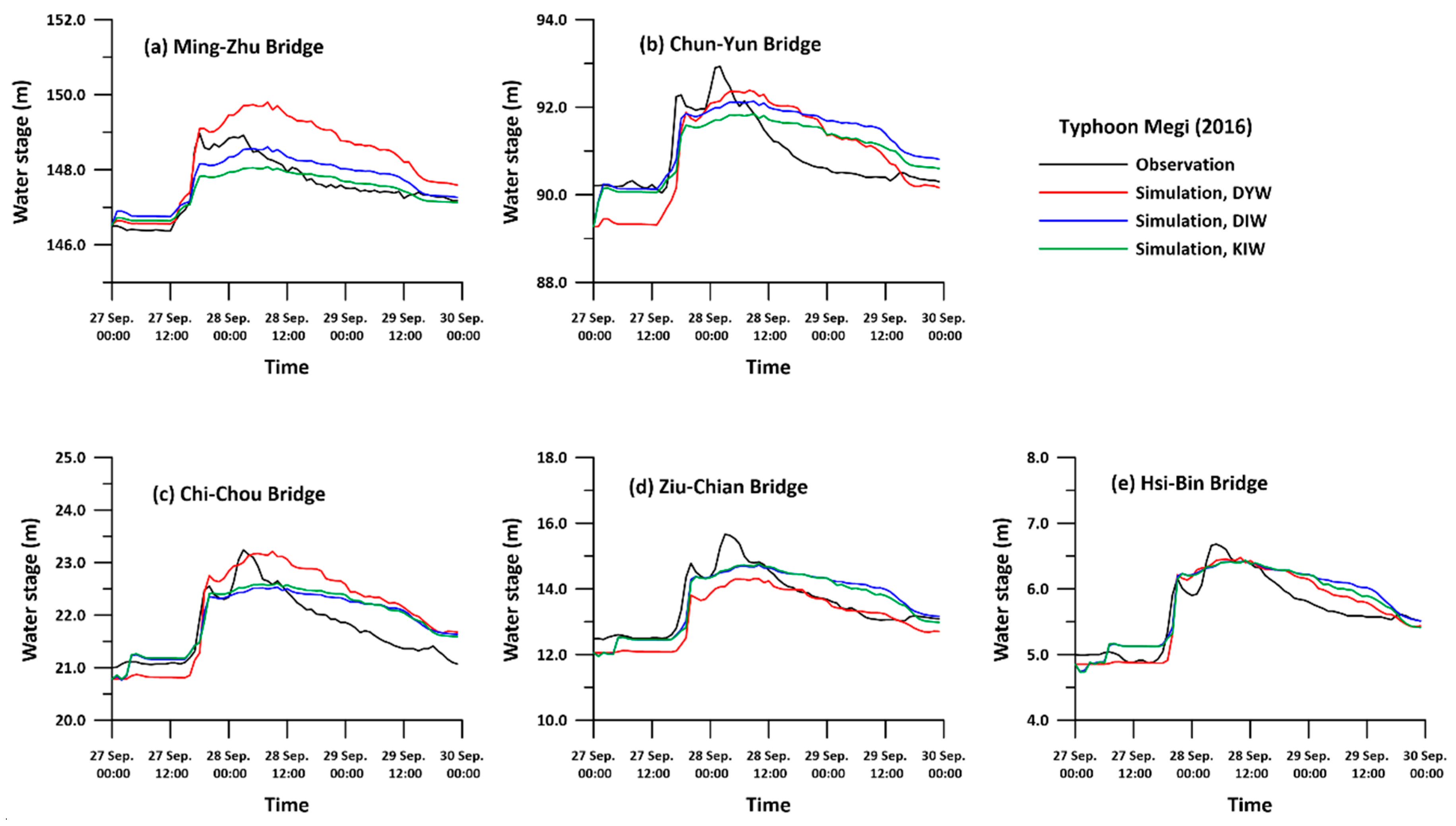
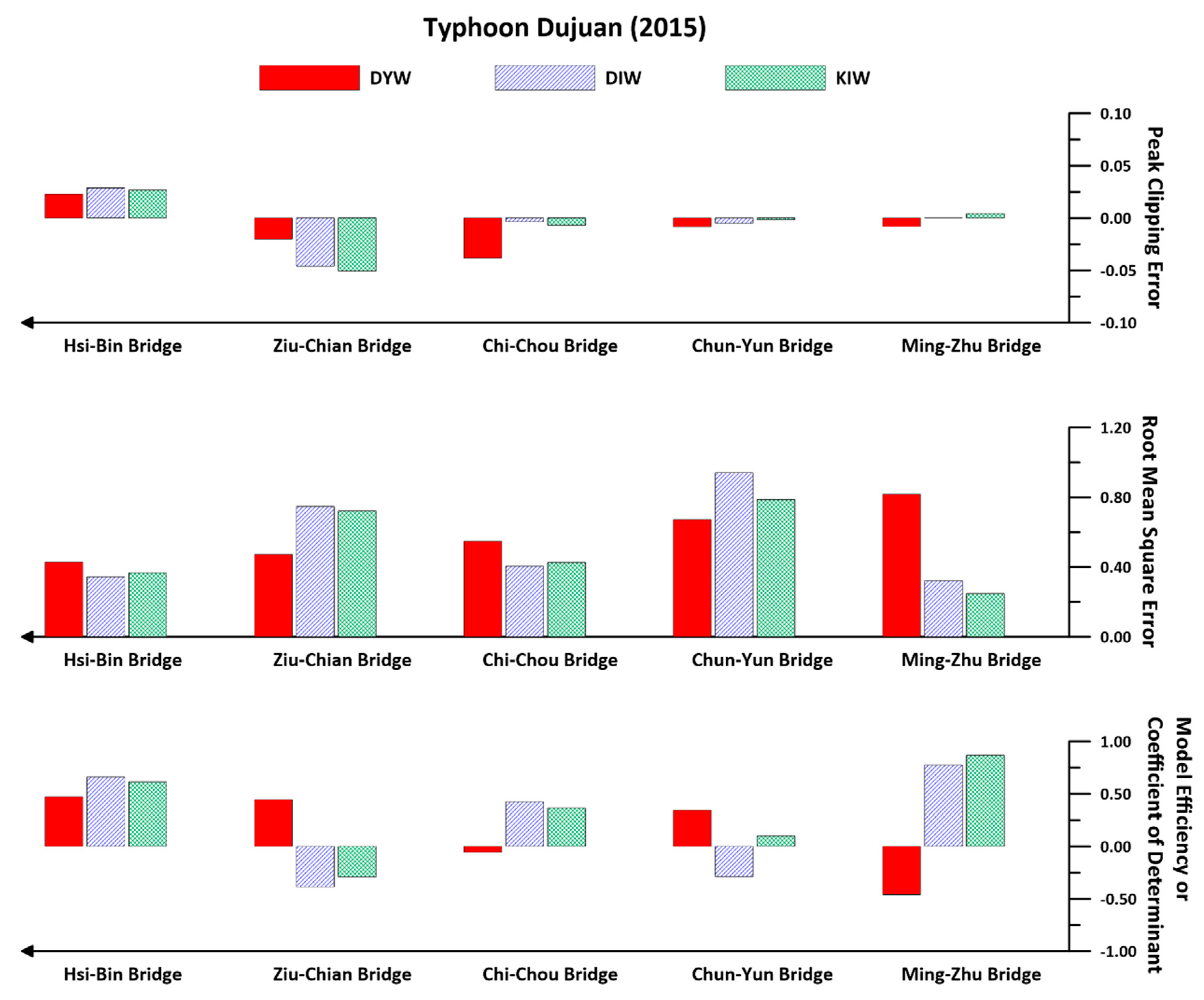
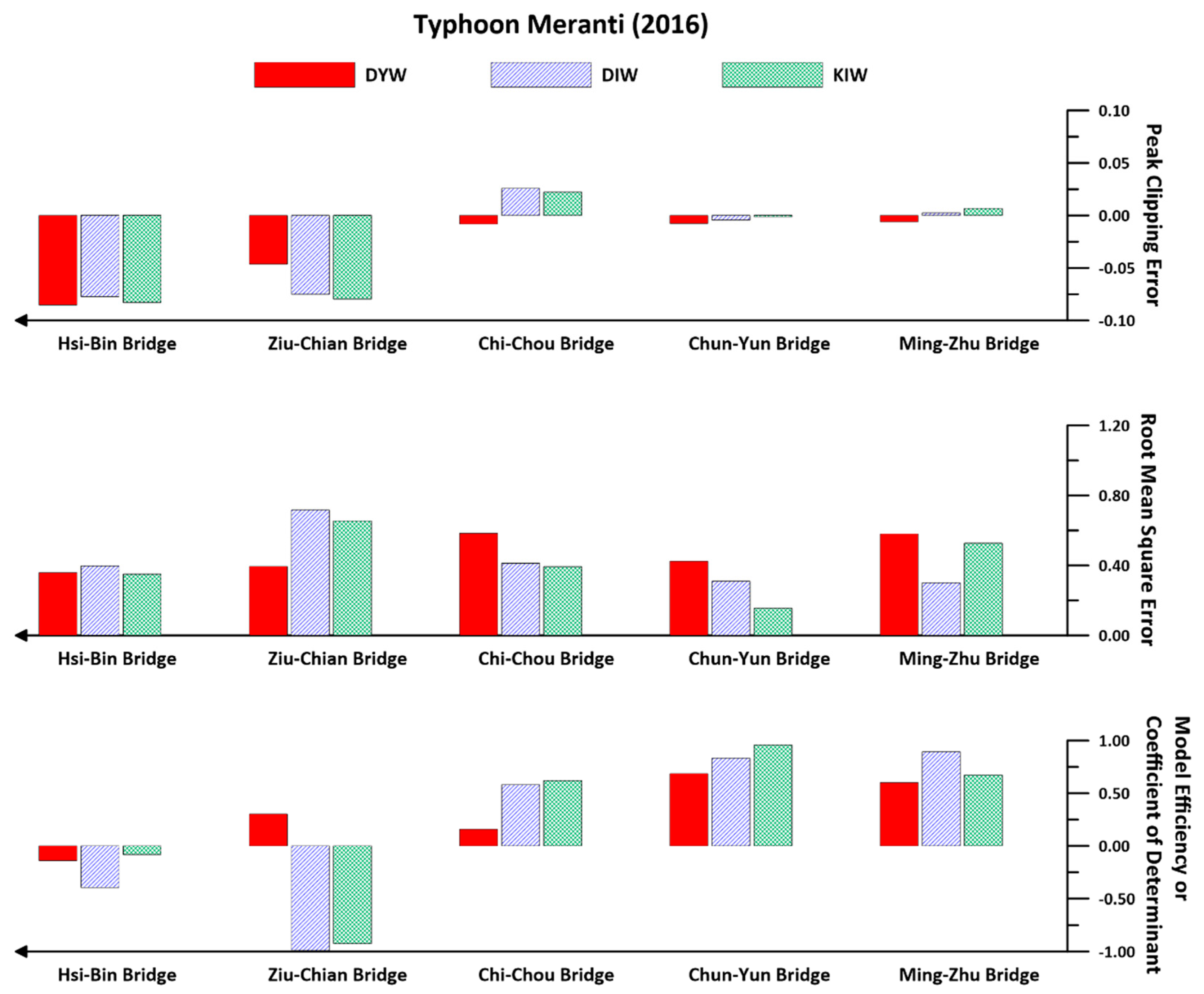
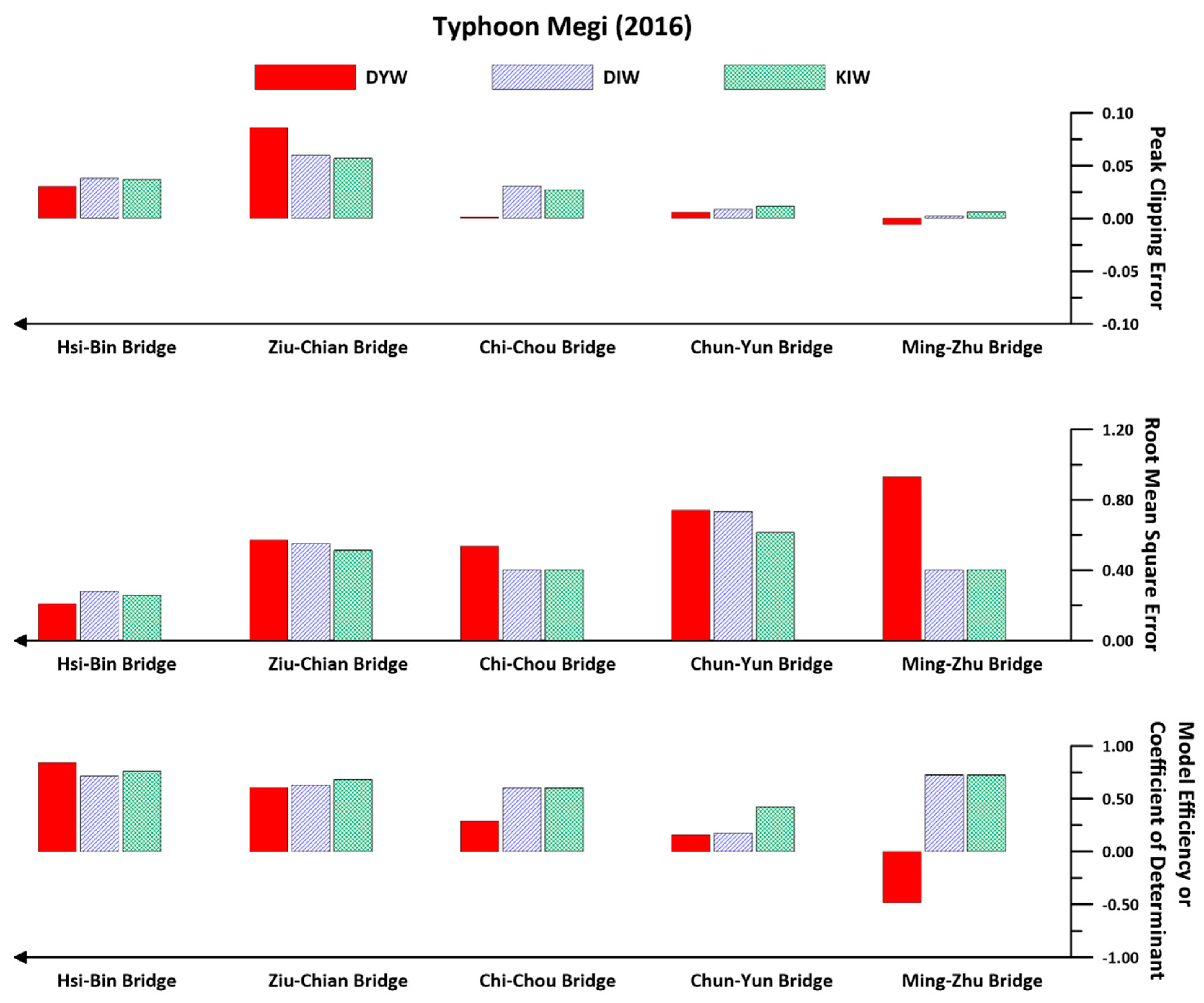
4.1. Discussion on Prismatic Cases
4.2. Discussion of Nonprismatic Cases
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chow, V.T. Open Channel Hydraulics; McGraw Hill: New York, NY, USA, 1959. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Yen, B.C.; Tsai, C.W.-S. On noninertia wave versus diffusion wave in flood routing. J. Hydrol. 2001, 244, 97–104. [Google Scholar] [CrossRef]
- García-Navarro, P.; Alcrudo, F.; Savirón, J.M. 1-D Open-Channel Flow Simulation Using TVD-McCormack Scheme. J. Hydraul. Eng. 1992, 118, 1359–1372. [Google Scholar] [CrossRef]
- Aral, M.M.; Zhang, Y.; Jin, S. Application of Relaxation Scheme to Wave-Propagation Simulation in Open-Channel Networks. J. Hydraul. Eng. 1998, 124, 1125–1133. [Google Scholar] [CrossRef]
- Vukovic, S.; Soptab, L. ENO and WENO Schemes with the Exact Conservation Property for One-Dimensional Shallow Water Equations. J. Comp. Phys. 2002, 179, 593–621. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, Y.; Wang, Z.; Liu, Z. Simple, Robust, and Efficient Algorithm for Gradually Varied Subcritical Flow Simulation in General Channel Networks. J. Hydraul. Eng. 2011, 137, 766–774. [Google Scholar] [CrossRef]
- Ponce, V.M.; Theurer, F.D. Accuracy Criteria in Diffusion Routing. J. Hydraul. Div. 1982, 108, 747–757. [Google Scholar]
- Sivaloganathan, K. Channel Flow Computations Using Characteristics. J. Hydraul. Div. 1979, 105, 899–910. [Google Scholar]
- Shih, D.S.; Yeh, G.T. Using a characteristic-based particle tracking method to solve one-dimensional fully dynamic wave flow. Comput. Geosci. 2018, 22, 439–449. [Google Scholar] [CrossRef]
- Suk, H.; Yeh, G.T. A multi-dimensional finite element particle tracking method for solving complex transient flow problems. J. Hydrol. Eng. 2009, 14, 759–766. [Google Scholar] [CrossRef]
- Williamson, D.L.; Rasch, P.J. Two-dimensional semi-Lagrangian transport with shape-preserving interpolation. Mon. Weather Rev. 1989, 117, 102–129. [Google Scholar] [CrossRef]
- Yen, B.C. Open-Channel Flow Equations Revised. J. Eng. Mech. Div. ASCE 1973, 99, 979–1009. [Google Scholar]
- Ponce, V.M.; Simons, D.B.; Li, R.M. Applicability of Kinematic and Diffusion Models. J. Hydraul. Div. 1978, 104, 353–360. [Google Scholar]
- Cozzolino, L.; Pepe, P.; Morlando, F.; Cimorelli, L.; D’Aniello, A.; Morte, R.D.; Pianese, D. Exact Solution of the Dam-Break Problem for Constrictions and Obstructions in Constant Width Rectangular Channels. J. Hydrol. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Channel Bed Slope Effect on the Height of Gravity Waves Produced by a Sudden Downstream Discharge Stoppage. J. Hydrol. Eng. 2010, 135. [Google Scholar] [CrossRef]
- Sridharan, V.K.; Monismith, S.G.; Fong, D.A.; Hench, J.L. One-Dimensional Particle Tracking with Streamline Preserving Junctions for Flows in Channel Networks. J. Hydrol. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Price, R.K.; Samuels, P.G. A computational hydraulic model for rivers. Proc. Inst. Civ. Engrs. 1980, 69, 87–96. [Google Scholar] [CrossRef]
- Samuels, P.G.; Gary, M.P. The Flucomp River Model Package—An Engineers Guide; Report No EX 999; HR Wallingford Ltd.: Swindon, UK, 1982. [Google Scholar]
- Bates, P.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Knight, D.W. Conveyance in 1D Models. Annex of Scoping Study on Reducing Uncertainty in River Flood Conveyance; Rand&D Technical Report to DEFRA/Environment Agency; HR Wallingford Ltd.: Swindon, UK, 2001. [Google Scholar]
- Lin, B.; Wicks, J.M.; Falconer, R.A.; Adams, K. Integrating 1D and 2D hydrodynamic models for flood simulation. Proc. Inst. Civ. Eng. Water Manag. 2006, 159, 19–25. [Google Scholar] [CrossRef]
- Goutal, N.; Maurel, F. A finite volume solver for 1D shallow-water equations applied to an actual river. Int. J. Numer. Meth. Fluids 2002, 38, 1–19. [Google Scholar] [CrossRef]
- Yeh, G.T.; Huang, G.B.; Zhang, F.; Cheng, H.P.; Lin, H.C. WASH123D: A Numerical Model of Flow, Thermal Transport, and Salinity, Sediment, and Water Quality Transport in WAterSHed Systems of 1-D Streamriver Network, 2-D Overland Regime, and 3-D Subsurface Media; Technical Report Submitted To EPA; Department of Civil and Environmental Engineering, University of Central Florida: Orlando, FL, USA, 2006. [Google Scholar]
- Brunner, G.W. HECRAS-River Analysis System, Hydraulic Reference Manual Version 4.0, U.S; Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2008.
- Huthoff, F.; Roos, P.C.; Augustijn, D.C.M.; Hulscher, S.J. Interacting divided channel method for compound channel flow. J. Hydraul. Eng. 2008, 134, 1158–1165. [Google Scholar] [CrossRef]
- Deltares: SOBEK Suite. 2011. Available online: https://www.deltares.nl/en/softwaresolutions/ (accessed on 15 June 2013).
- Danish Hydraulic Institute. 2016. Available online: http://www.mikepoweredbydhi.com/products/mike-she (accessed on 18 May 2018).
- Innovyze. 2016. Available online: http://www.innovyze.com/about/ (accessed on 15 May 2018).
- MacDonald, I.; Baines, M.J.; Nichols, N.K.; Samuels, P.G. Analytic benchmark solution for open-channel flows. J. Hydrol. Eng. 1997, 123, 1041–1045. [Google Scholar] [CrossRef]
- Singh, V.P. Kinematic Wave Modeling in Water Resources—Surface Water Hydrology; Wiley-Interscience: New York, NY, USA, 1996. [Google Scholar]
- Yeh, G.T.; Shih, D.S.; Cheng, J.R.C. An integrated media, integrated processes watershed model. Comput. Fluids 2011, 45, 2–13. [Google Scholar] [CrossRef]
- Hergarten, P.S.G.; Neugebauer, H.J. An integrated model for the surface runoff and the infiltration of water, EOS, transc. Am. Geophys. Union. 1995, 76, F320. [Google Scholar]
- Suk, H.; Yeh, G.T. 3D, three-phase flow simulations using the Lagrangian-Eulerian approach with adaptively zooming and peak/valley capturing scheme (LEZOOMPC). J. Hydrol. Eng. 2007, 12, 14–32. [Google Scholar] [CrossRef]
- Hsu, T.W.; Shih, D.S.; Chen, W.J. Destructive Flooding Induced by Broken Embankments along Linbian Creek, Taiwan, during Typhoon Morakot. J. Hydrol. Eng. 2015, 20, 05014025. [Google Scholar] [CrossRef]
- Hsu, T.W.; Shih, D.S.; Li, C.Y.; Lan, Y.J.; Lin, Y.C. A Study on Coastal Flooding and Risk Assessment under Climate Change in the Mid-Western Coast of Taiwan. Water 2017, 9, 390. [Google Scholar] [CrossRef]
- Shih, D.S.; Chen, C.H.; Yeh, G.T. Improving our understanding of flood forecasting using earlier hydro-meteorological intelligence. J. Hydrol. 2014, 512, 470–481. [Google Scholar] [CrossRef]
- Shih, D.S.; Hsu, T.W.; Chang, K.C.; Juan, H.L. Implementing Coastal Inundation Data with an Integrated Wind Wave Model and Hydrological Watershed Simulations. Terr. Atmos. Ocean. Sci. 2012, 23, 513–525. [Google Scholar] [CrossRef]
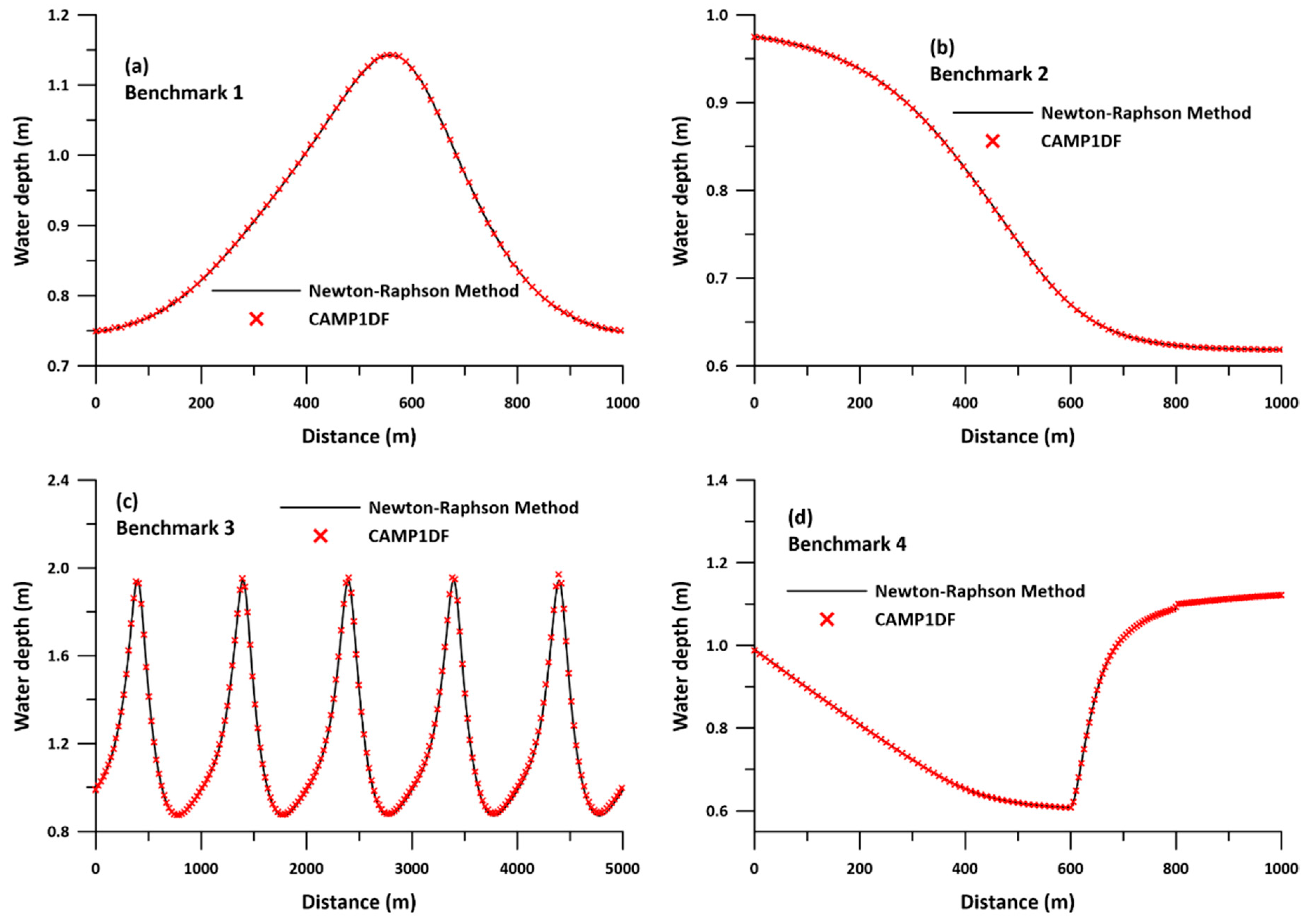
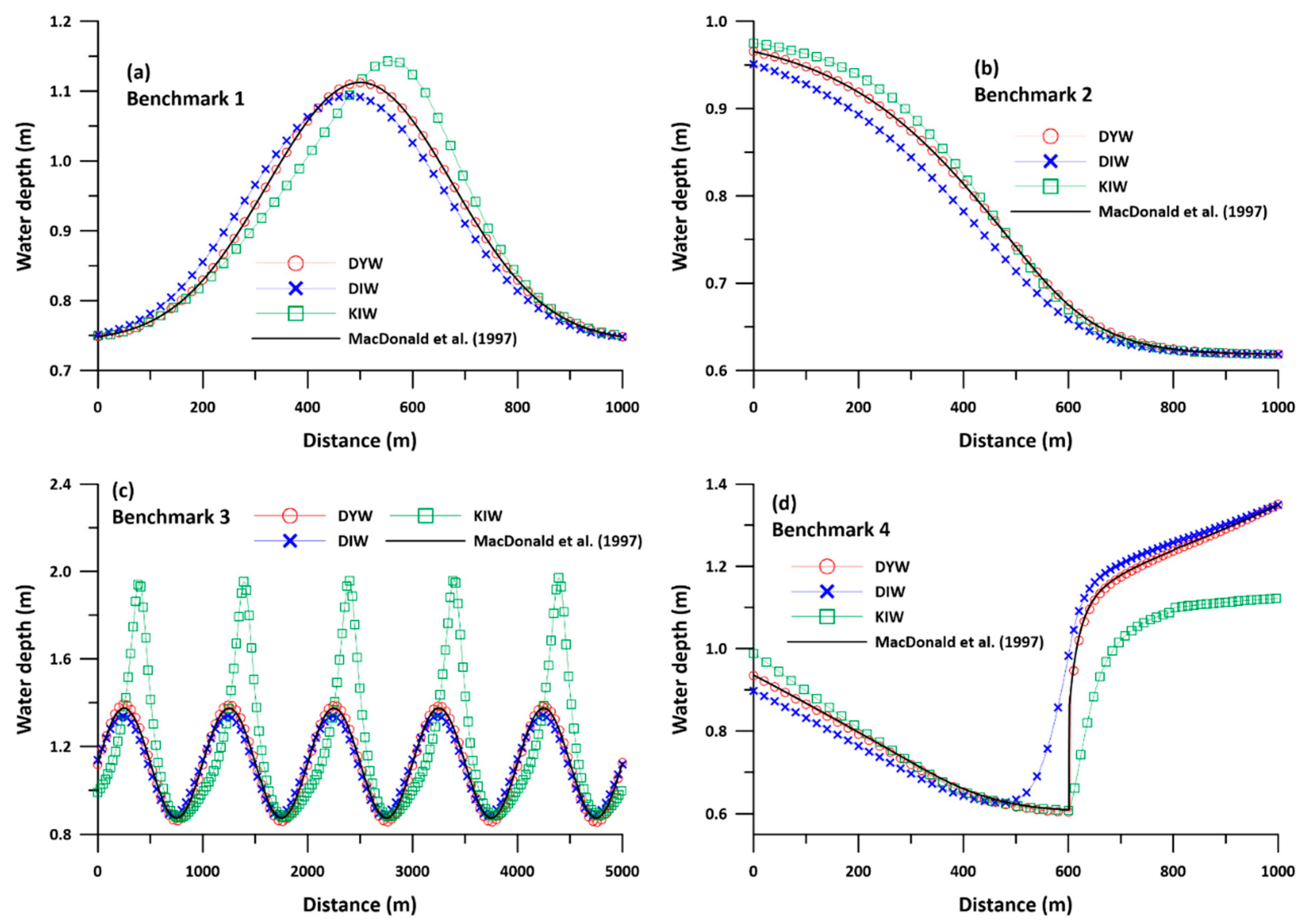
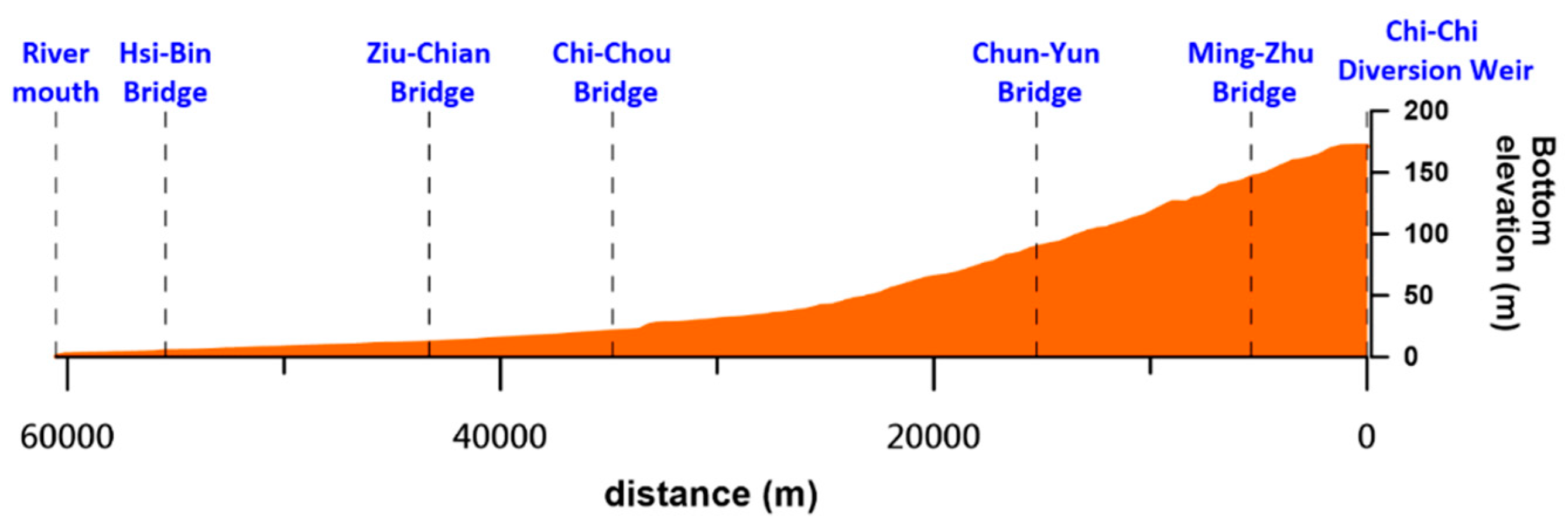
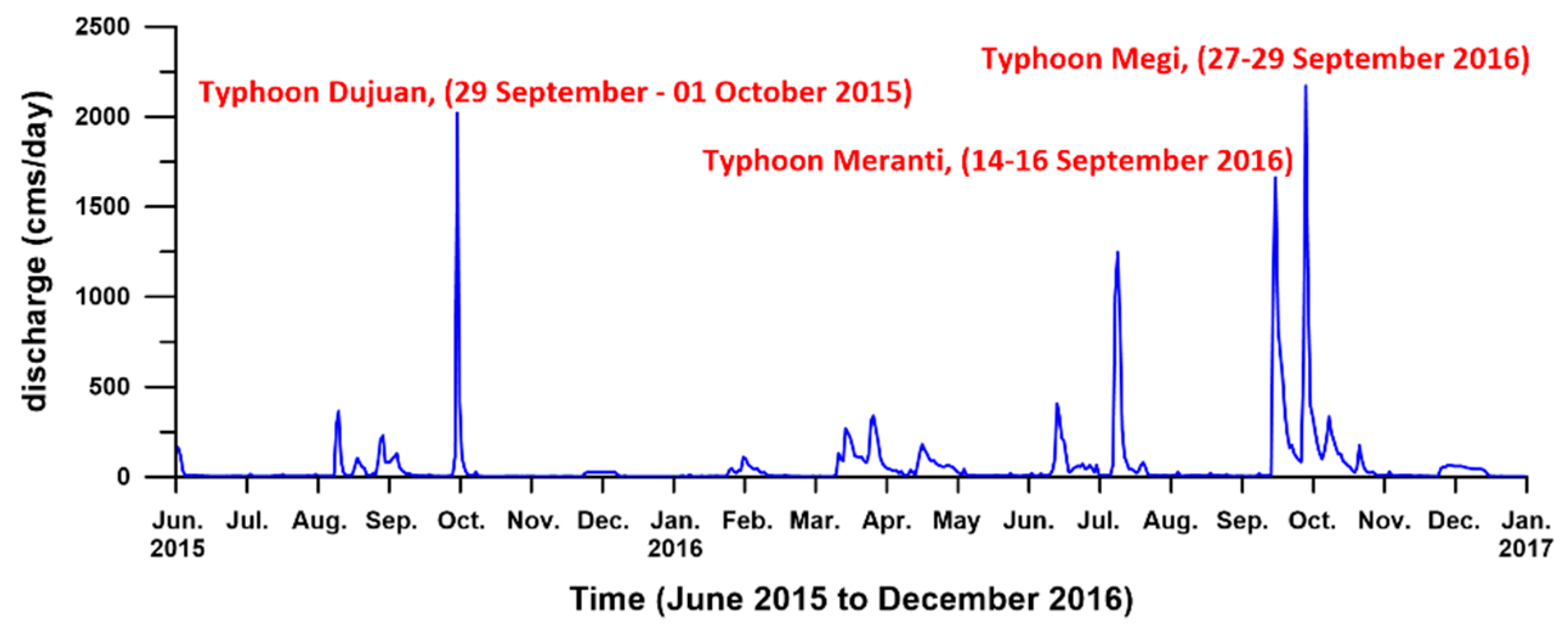

| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| εmean | −0.0006 | 0.0000 | −0.0046 | −0.0052 |
| εp | 0.0012 | 0.0001 | −0.0125 | −0.0004 |
| RMSE | 0.0009 | 0.0001 | 0.0123 | 0.0185 |
| C2 | 1.0000 | 1.0000 | 0.9995 | 0.9955 |
| R2 | 1.0000 | 1.0000 | 0.9952 | 0.9949 |
| U2 | 0.0000 | 0.0000 | 0.0001 | 0.0003 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| εmean | 0.0000 | 0.0000 | 0.0033 | −0.0009 |
| εp | 0.0000 | 0.0000 | −0.0018 | 0.0004 |
| RMSE | 0.0000 | 0.0001 | 0.0051 | 0.0011 |
| C2 | 1.0000 | 1.0000 | 0.9994 | 1.0000 |
| R2 | 1.0000 | 1.0000 | 0.9990 | 1.0000 |
| U2 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| εmean | 0.0006 | −0.0003 | 0.0098 | 0.0003 |
| εp | −0.0005 | 0.0004 | −0.0136 | −0.0008 |
| RMSE | 0.0008 | 0.0004 | 0.0115 | 0.0011 |
| C2 | 1.0000 | 1.0000 | 0.9997 | 1.0000 |
| R2 | 1.0000 | 1.0000 | 0.9988 | 1.0000 |
| U2 | 0.0000 | 0.0000 | 0.0001 | 0.0000 |
| Case 1 | Case 2 | Case 3 | Case 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DYW | DIW | KIW | DYW | DIW | KIW | DYW | DIW | KIW | DYW | DIW | KIW | |
| εmean | −0.0006 | −0.0028 | 0.0025 | 0.0000 | −0.0168 | 0.0059 | −0.0046 | −0.0102 | 0.0837 | −0.0052 | 0.0135 | −0.1023 |
| εp | 0.0012 | 0.0168 | −0.0279 | 0.0001 | 0.0151 | −0.0099 | −0.0125 | 0.0243 | 0.4328 | −0.0004 | 0.0000 | 0.1686 |
| RMSE | 0.0009 | 0.0202 | 0.0306 | 0.0001 | 0.0203 | 0.0108 | 0.0123 | 0.0275 | 0.2580 | 0.0185 | 0.0569 | 0.1449 |
| C2 | 1.0000 | 0.9770 | 0.9478 | 1.0000 | 0.9956 | 0.9991 | 0.9995 | 0.9873 | 0.4689 | 0.9955 | 0.9558 | 0.8912 |
| R2 | 1.0000 | 0.9751 | 0.9426 | 1.0000 | 0.9753 | 0.9930 | 0.9952 | 0.9758 | −1.1311 | 0.9949 | 0.9518 | 0.6870 |
| U2 | 0.0000 | 0.0005 | 0.0011 | 0.0000 | 0.0007 | 0.0002 | 0.0001 | 0.0006 | 0.0424 | 0.0003 | 0.0029 | 0.0242 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shih, D.-S.; Yeh, G.-T. Studying Inertia Effects in Open Channel Flow Using Saint-Venant Equations. Water 2018, 10, 1652. https://doi.org/10.3390/w10111652
Shih D-S, Yeh G-T. Studying Inertia Effects in Open Channel Flow Using Saint-Venant Equations. Water. 2018; 10(11):1652. https://doi.org/10.3390/w10111652
Chicago/Turabian StyleShih, Dong-Sin, and Gour-Tsyh Yeh. 2018. "Studying Inertia Effects in Open Channel Flow Using Saint-Venant Equations" Water 10, no. 11: 1652. https://doi.org/10.3390/w10111652
APA StyleShih, D.-S., & Yeh, G.-T. (2018). Studying Inertia Effects in Open Channel Flow Using Saint-Venant Equations. Water, 10(11), 1652. https://doi.org/10.3390/w10111652






