Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland
Abstract
1. Introduction
2. Materials and Methods
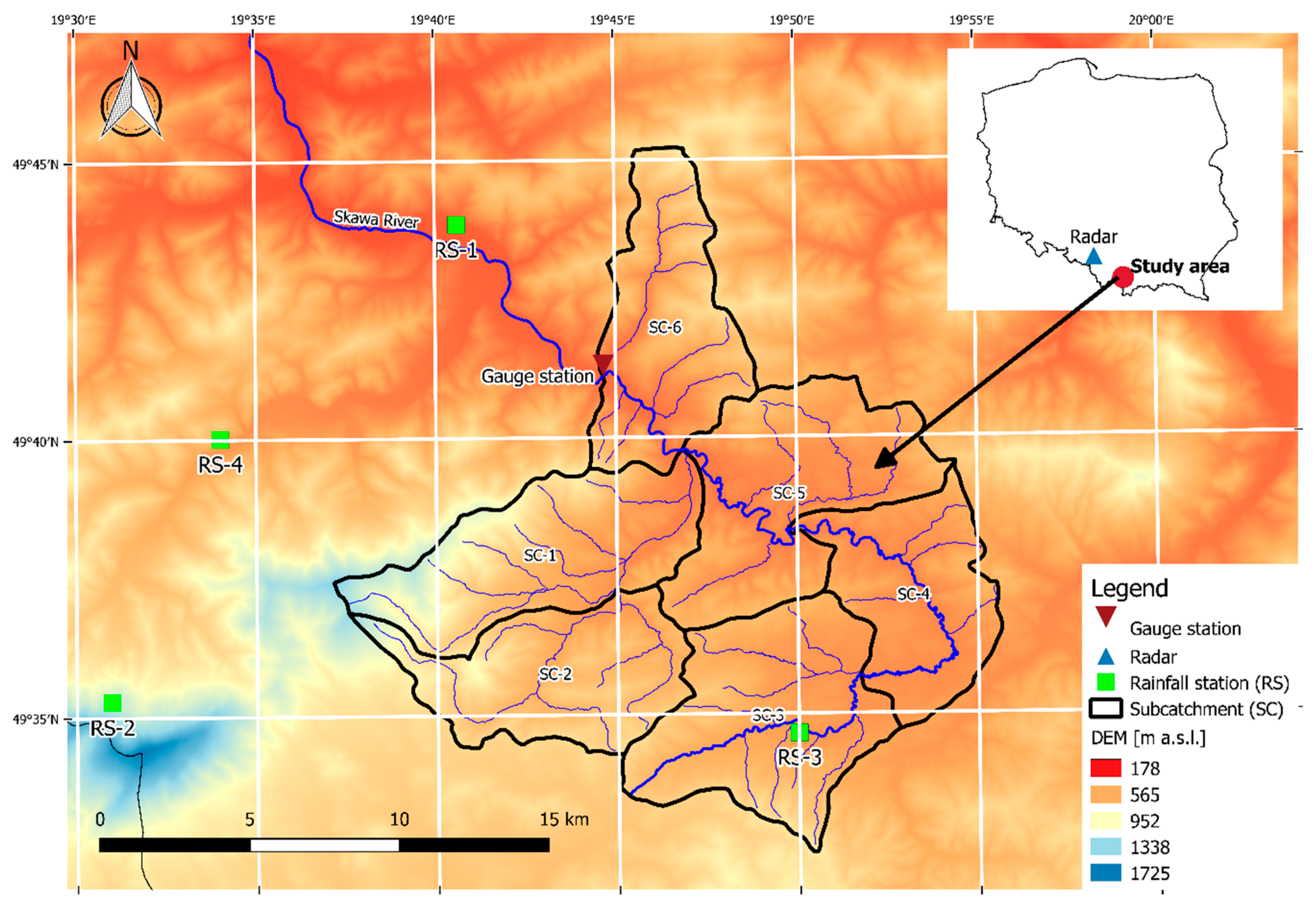
2.1. The Study Area
2.2. Data Collection and Processing
2.2.1. Discharge Data
2.2.2. Rain Gauges
2.2.3. Radar Rainfall Estimates
2.2.4. Adjustment of Radar Rainfall Estimates Using Weighted Multiple Regression (WMR) Method
- The spatial distribution of radar rainfall estimates corresponds to the rain gauge-based point measurements.
- Radar and rain gauge instruments perform the measurements at different heights, but the estimated rainfall from these instruments is assumed to be measured at the same level.
- The data analysis in each year is limited to the period from April to October to minimize the risk that radar would measure solid hydrometeors instead of liquid particles.
- Only simultaneous rainfall observations of rain gauge and radar are taken into further consideration; cases where only rain gauge or only radar registered rainfall were available are neglected.
- A semi-distributed hydrological model for each sub-catchment is assumed; mean value from all the radar estimates over the sub-catchment is assigned to its area. This mean value is accordingly adjusted and applied in the hydrological model.
2.2.5. IMERG GPM Satellite Rainfall Estimates
2.2.6. Digital Elevation Model and Land-Cover
2.3. HEC-HMS Hydrological Model
2.3.1. Model Set-up
2.3.2. Calibration and Validation
2.3.3. Simulation Time-Step Analysis
3. Results and Discussion
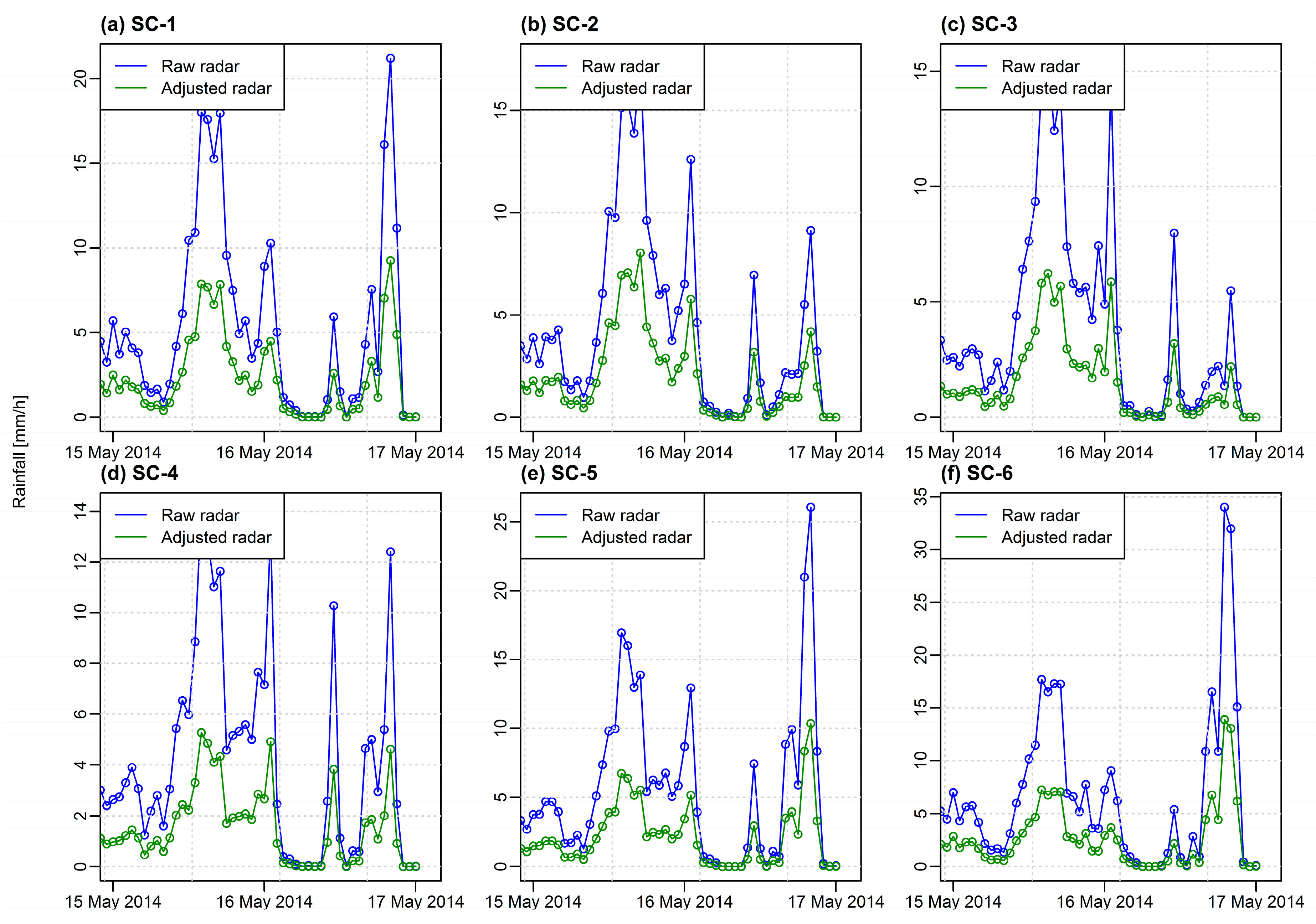
3.1. Adjustment of Radar Rainfall Estimates
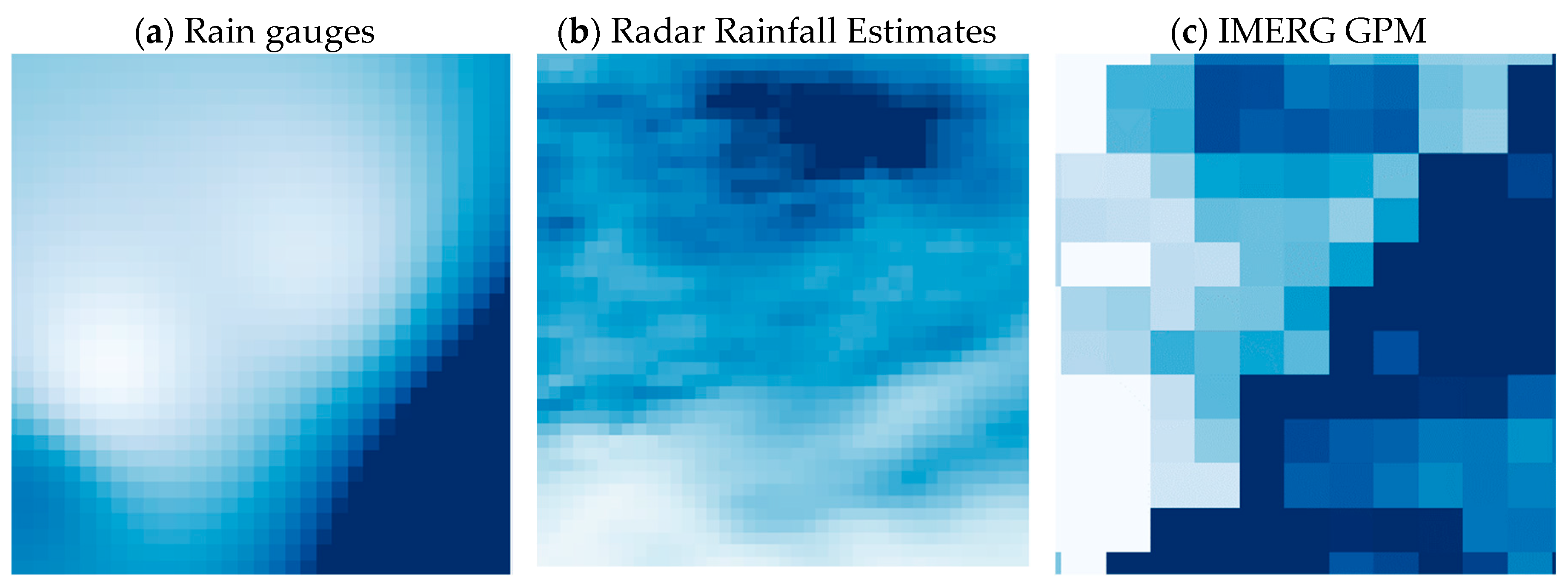
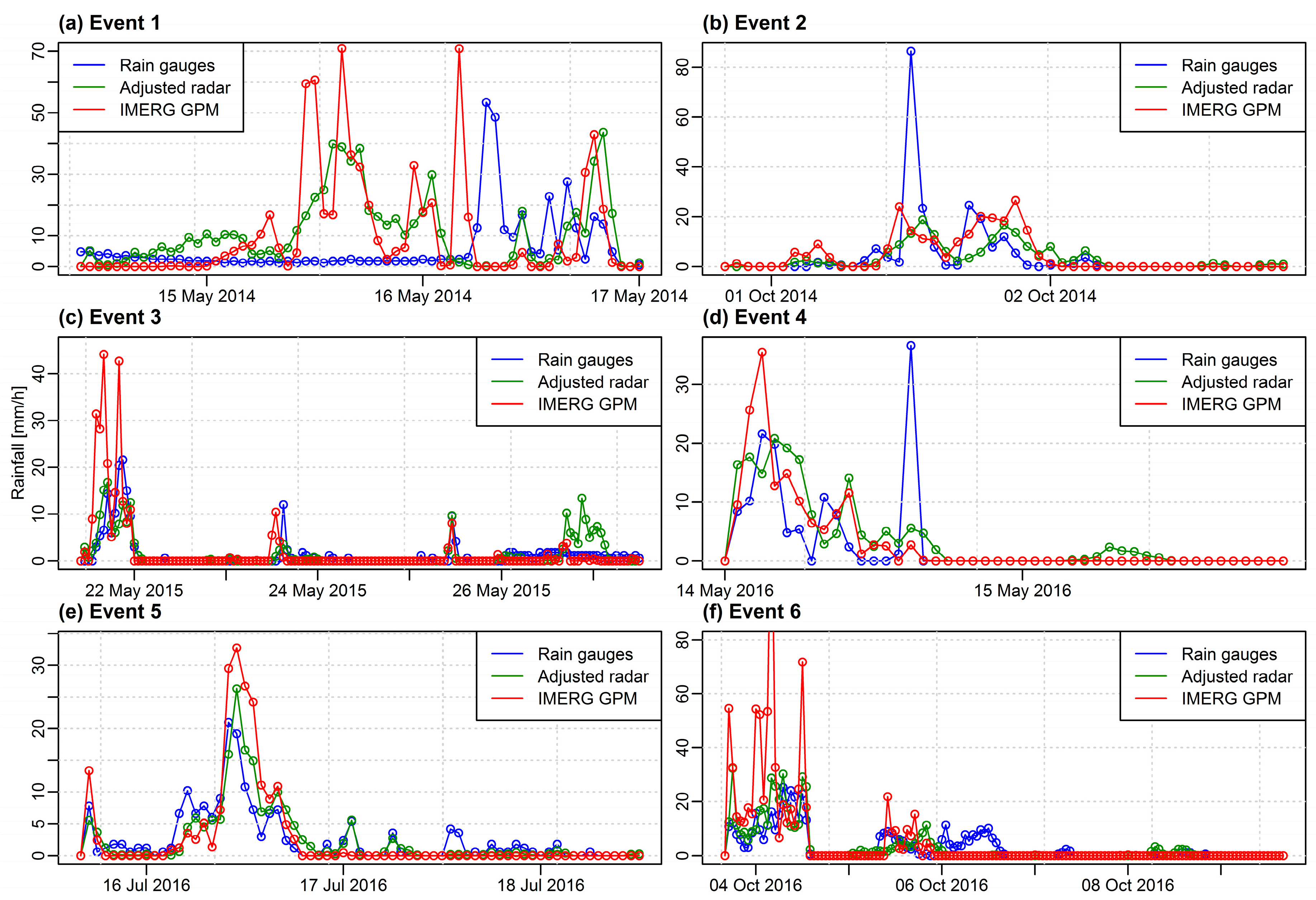
3.2. Intercomparison of Precipitation Products
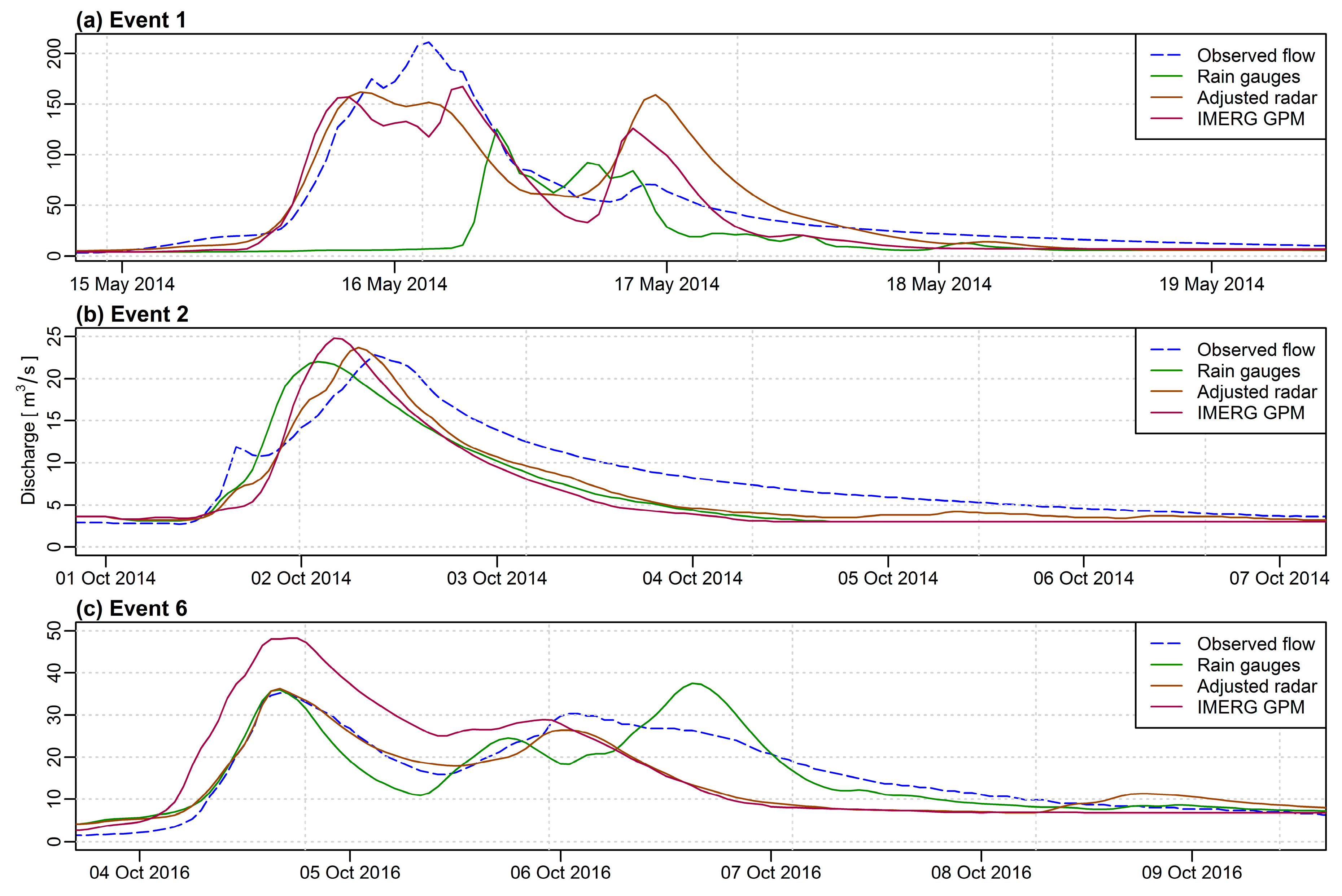
3.3. Simulation Results
3.3.1. Calibration and Validation of the Model
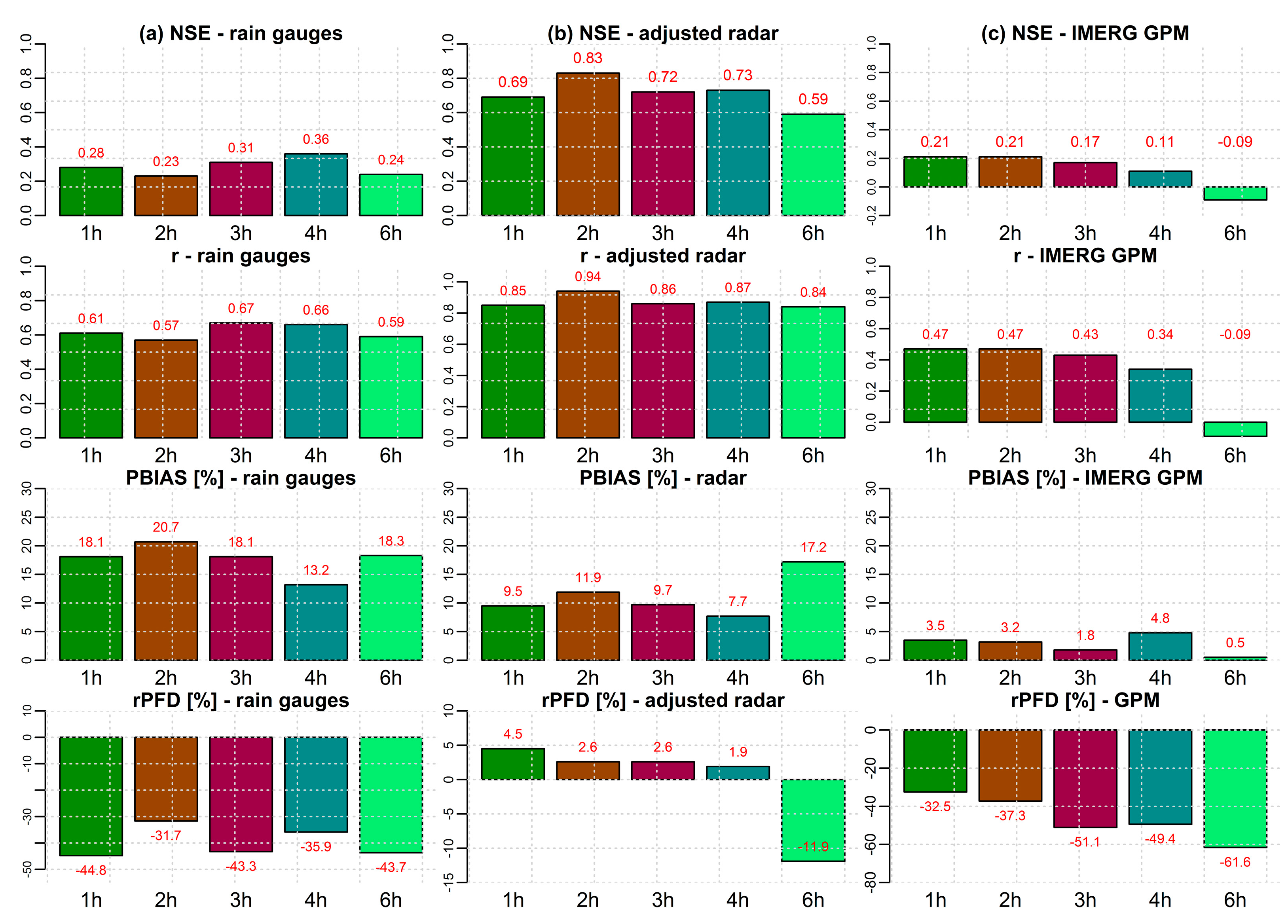
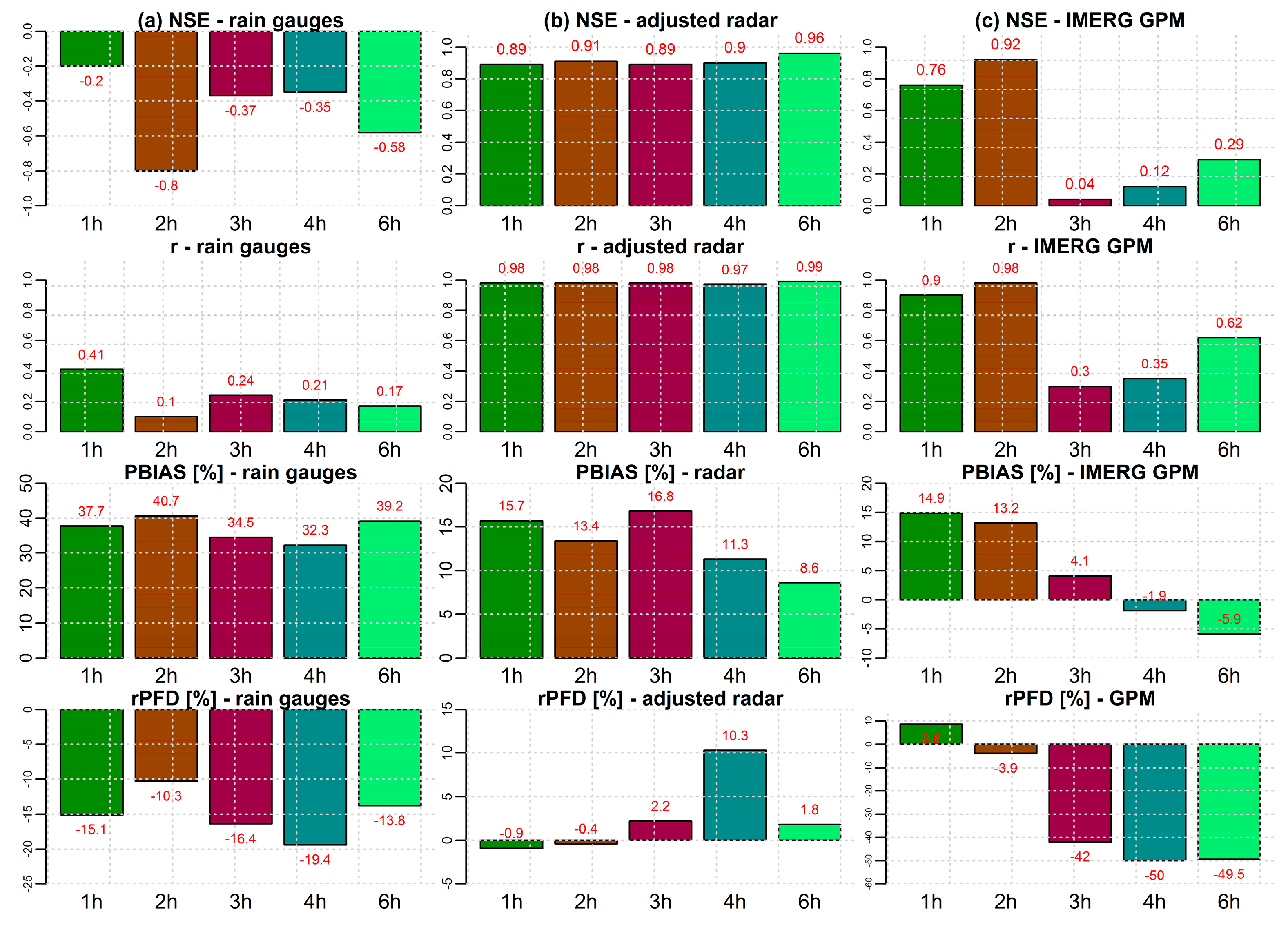
3.3.2. Simulation Time-Step Analysis
4. Conclusions
- (1)
- A good or very good model performance was obtained for most of the simulations during the calibration phase, but for the validation period, best results were obtained using the adjusted radar rainfall estimates and IMERG GPM data as precipitation data source.
- (2)
- Spatial and temporal distributions of rainfall estimated from different data sources vary significantly. As rainfall distribution in both time and space has a substantial impact on estimated values of model parameters a separate hydrological model should be applied for each source of the precipitation data.
- (3)
- Radar-estimated precipitation seems to be the most reliable source of information on the ‘real’ precipitation field. Precipitation interpolated from the rain gauge data seems to have a high degree of uncertainty, whereas IMERG GPM provides precipitation estimates of low spatial resolution.
- (4)
- Raw radar rainfall estimates seem to overestimate the observed rainfall significantly. Therefore, the radar data should be adjusted to minimize the bias between rain gauge measurement and radar estimation. When applied, the adjustment method for the radar rainfall estimates performed very well for event-based rainfall-runoff simulations in the mountainous area and can be easily adapted to other areas as it requires a relatively few data.
- (5)
- Short time of latency of IMERG GPM rainfall estimates makes it a valuable data source for near-real-time flood monitoring, but a rather sparse spatial resolution offsets this. Application of IMERG GPM rainfall estimates is challenging for small catchments as the satellite grids may cover the areas outside the sub-catchment or be partially common for several sub-catchment. If this is the case a weighting of rainfall should be done to account for the area of each sub-catchment covered by each grid.
- (6)
- Adequate choice of performance metrics is essential to evaluate the simulation results thoroughly. The evaluation criteria should allow judging the performance of the flow model regarding various flow characteristics (for the event-based modeling, these are predictive power of the model, timing of simulated and observed time series, tendency of over- or under-estimation of simulated flow, and accuracy in peak flow estimation). The applied evaluation metrics (Nash-Sutcliffe efficiency coefficient, Pearson’s correlation coefficient, percent bias, and relative peak flow difference) allowed to make a comprehensive assessment of simulation results regarding these characteristics.
- (7)
- Regardless of the values of the performance metrics, a visual analysis of the observed and simulated hydrographs should be performed. Sometimes the metrics can give satisfactory results even though the overall simulation results don’t fit the observed hydrograph.
- (8)
- Aggregation of simulation time-step up to 2 h improves the simulation results for radar- and satellite rainfall-based flow simulations. Further aggregation in time, up to 4 h, is valuable for simulations based on rain gauge precipitation data. The simulation results show that the time-step of simulations in a small catchment which have a short concentration time (like mountainous environments) should not exceed the response time of the catchment.
- (9)
- SCS Curve Number loss method applied in HEC-HMS is more adequate for simulations of flood events of unimodal distribution rather than of bimodal distribution. The method does not allow the regeneration of rainfall losses during the flood event and may lead to over- or underestimation of one of the flood event peaks.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E.; Knightes, C.D. Comparison of radar and gauge precipitation data in watershed models across varying spatial and temporal scales. Hydrol. Process. 2014, 28, 3505–3520. [Google Scholar] [CrossRef]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado, W. Impacts of satellite-based precipitation datasets on rainfall-runoff modeling of the Western Amazon basin of Peru and Ecuador. J. Hydrol. 2015, 528, 599–612. [Google Scholar] [CrossRef]
- McKee, J.L.; Binns, A.D. A review of gauge–radar merging methods for quantitative precipitation estimation in hydrology. Can. Water Resour. J. 2016, 41, 186–203. [Google Scholar] [CrossRef]
- Panthi, J.; Dahal, P.; Shrestha, M.; Aryal, S.; Krakauer, N.; Pradhanang, S.; Lakhankar, T.; Jha, A.; Sharma, M.; Karki, R. Spatial and temporal variability of rainfall in the Gandaki River Basin of Nepal Himalaya. Climate 2015, 3, 210–226. [Google Scholar] [CrossRef]
- Barry, R.G. Changes in mountain climate and glacio-hydrological responses. Mt. Res. Dev. 1990, 10, 161–170. [Google Scholar] [CrossRef]
- Gabella, M.; Speirs, P.; Hamann, U.; Germann, U.; Berne, A. Measurement of precipitation in the alps using dual-polarization C-Band ground-based radars, the GPM Spaceborne Ku-Band Radar, and rain gauges. Remote Sens. 2017, 9, 1147. [Google Scholar] [CrossRef]
- Khalki, E.M.E.; Tramblay, Y.; Saidi, M.E.M.; Bouvier, C.; Hanich, L.; Benrhanem, M.; Alaouri, M. Comparison of modeling approaches for flood forecasting in the High Atlas Mountains of Morocco. Arab. J. Geosci. 2018, 11, 410. [Google Scholar] [CrossRef]
- Sikorska, A.E.; Seibert, J. Value of different precipitation data for flood prediction in an alpine catchment: A Bayesian approach. J. Hydrol. 2018, 556, 961–971. [Google Scholar] [CrossRef]
- Sikorska, A.E.; Seibert, J. Appropriate temporal resolution of precipitation data for discharge modelling in pre-alpine catchments. Hydrol. Sci. J. 2018, 63, 1–16. [Google Scholar] [CrossRef]
- Looper, J.P.; Vieux, B.E. An assessment of distributed flash flood forecasting accuracy using radar and rain gauge input for a physics-based distributed hydrologic model. J. Hydrol. 2012, 412–413, 114–132. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of global precipitation measurement satellite products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Review of the different sources of uncertainty in single polarization radar-based estimates of rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Szturc, J. Niepewność w Radarowych Pomiarach Opadu z Punktu Widzenia Hydrologii; Instytut Meteorologii i Gospodarki Wodnej: Warszawa, Poland, 2010. [Google Scholar]
- Berne, A.; Krajewski, W.F. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Gabella, M.; Amitai, E. Radar rainfall estimates in an alpine environment using different gage-adjustment techniques. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2000, 25, 927–931. [Google Scholar] [CrossRef]
- Keblouti, M.; Ouerdachi, L.; Berhail, S. The use of weather radar for rainfall-runoff modeling, case of Seybouse watershed (Algeria). Arab. J. Geosci. 2015, 8. [Google Scholar] [CrossRef]
- Cecinati, F.; Rico-Ramirez, M.A.; Heuvelink, G.B.M.; Han, D. Representing radar rainfall uncertainty with ensembles based on a time-variant geostatistical error modelling approach. J. Hydrol. 2017, 548, 391–405. [Google Scholar] [CrossRef]
- Sungmin, O.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar] [CrossRef]
- Zubieta, R.; Geofísico, I.; Getirana, A. Hydrological modeling of the Peruvian–Ecuadorian Amazon Basin using GPM-IMERG satellite-based precipitation dataset. Hydrol. Earth Syst. Sci. 2017, 21, 3543–3555. [Google Scholar] [CrossRef]
- Gosset, M.; Alcoba, M.; Roca, R.; Cloché, S.; Urbani, G. Evaluation of TAPEER daily estimates and other GPM era products against dense gauge networks in West Africa, analyzing ground reference uncertainty. Q. J. R. Meteorol. Soc. 2018. [Google Scholar] [CrossRef]
- Mohsan, M.; Acierto, R.A.; Kawasaki, A.; Zin, W.W. Preliminary assessment of GPM satellite rainfall over Myanmar. J. Disaster Res. 2018, 13, 22–30. [Google Scholar] [CrossRef]
- Knebl, M.R.; Yang, Z.L.; Hutchison, K.; Maidment, D.R. Regional scale flood modeling using NEXRAD rainfall, GIS, and HEC-HMS/RAS: A case study for the San Antonio River Basin Summer 2002 storm event. J. Environ. Manag. 2005, 75, 325–336. [Google Scholar] [CrossRef] [PubMed]
- Halwatura, D.; Najim, M.M.M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Bhuiyan, H.A.K.M.; McNairn, H.; Powers, J.; Merzouki, A. Application of HEC-HMS in a cold region watershed and use of RADARSAT-2 soil moisture in initializing the model. Hydrology 2017, 4, 9. [Google Scholar] [CrossRef]
- Ren, J.; Zheng, X.; Chen, P.; Zhao, X.; Chen, Y.; Shen, Y. An investigation into sub-basin rainfall losses in different underlying surface conditions using HEC-HMS: A case study of a loess hilly region in Gedong basin in the western Shanxi Province of China. Water 2017, 9, 870. [Google Scholar] [CrossRef]
- Rauf, A.; Ghumman, A.R. Impact assessment of rainfall-runoff simulations on the flow duration curve of the Upper Indus River—A comparison of data-driven and hydrologic models. Water 2018, 10, 876. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Y.; Yin, Y. Impacts of land use change scenarios on storm-runoff generation in Xitiaoxi basin, China. Quat. Int. 2009, 208, 121–128. [Google Scholar] [CrossRef]
- Ali, M.; Khan, S.J.; Aslam, I.; Khan, Z. Simulation of the impacts of land-use change on surface runoff of Lai Nullah Basin in Islamabad, Pakistan. Landsc. Urban Plan. 2011, 102, 271–279. [Google Scholar] [CrossRef]
- Zope, P.E.; Eldho, T.I.; Jothiprakash, V. Impacts of land use-land cover change and urbanization on flooding: A case study of Oshiwara River Basin in Mumbai, India. Catena 2016, 145, 142–154. [Google Scholar] [CrossRef]
- Gilewski, P.; Węglarz, A. Impact of land-cover change related urbanization on surface runoff estimation. EDP Sci. 2018, 196. [Google Scholar] [CrossRef]
- Szturc, J.; Jurczyk, A.; Ośródka, K.; Wyszogrodzki, A.; Giszterowicz, M. Precipitation estimation and nowcasting at IMGW-PIB (SEiNO system). Meteorol. Hydrol. Water Manag. Res. Oper. Appl. 2018, 6. [Google Scholar] [CrossRef]
- Luo, X.; Xu, Y.; Xu, J. Application of radial basis function network for spatial precipitation interpolation. In Proceedings of the 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–5. [Google Scholar]
- Mair, A.; Fares, A. Comparison of rainfall interpolation methods in a mountainous region of a tropical island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Drogue, G.; Humbert, J.; Deraisme, J.; Mahr, N.; Freslon, N. A statistical-topographic model using an omnidirectional parameterization of the relief for mapping orographic rainfall. Int. J. Climatol. 2002, 22, 599–613. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P.; Bièvre, B.D.; Wyseure, G. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Kong, Y.F.; Tong, W.W. Spatial exploration and interpolation of the surface precipitation data. Geogr. Res. 2008, 27, 1097–1108. [Google Scholar] [CrossRef]
- Kurtzman, D.; Navon, S.; Morin, E. Improving interpolation of daily precipitation for hydrologic modelling: Spatial patterns of preferred interpolators. Hydrol. Process. 2009, 23, 3281–3291. [Google Scholar] [CrossRef]
- Chen, F.-W.; Liu, C.-W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Tuszyńska, I. Charakterystyka Produktów Radarowych; Instytut Meteorologii i Gospodarki Wodnej: Warszawa, Poland, 2011. [Google Scholar]
- Atlas, D. Radar calibration: Some simple approaches. Bull. Am. Meteorol. Soc. 2002, 83, 1313–1316. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Berne, A. Stochastic simulation experiment to assess radar rainfall retrieval uncertainties associated with attenuation and its correction. Hydrol. Earth Syst. Sci. 2008, 12, 587–601. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zrnic, D.S. Precipitation and attenuation measurements at a 10-cm Wavelength. J. Appl. Meteorol. 1995, 34, 2121–2134. [Google Scholar] [CrossRef]
- Tokay, A.; Kruger, A.; Krajewski, W.F. Comparison of drop size distribution measurements by impact and optical disdrometers. J. Appl. Meteorol. 2001, 40, 2083–2097. [Google Scholar] [CrossRef]
- Smith, J.A.; Hui, E.; Steiner, M.; Baeck, M.L.; Krajewski, W.F.; Ntelekos, A.A. Variability of rainfall rate and raindrop size distributions in heavy rain. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Harrold, T.W.; English, E.J.; Nicholass, C.A. The accuracy of radar-derived rainfall measurements in hilly terrain. Q. J. R. Meteorol. Soc. 1974, 100, 331–350. [Google Scholar] [CrossRef]
- Seo, D.-J.; Breidenbach, J.P. Real-time correction of spatially nonuniform bias in radar rainfall data using rain gauge measurements. J. Hydrometeorol. 2002, 3, 93–111. [Google Scholar] [CrossRef]
- Steiner, M.; Smith, J.A.; Burges, S.J.; Alonso, C.V.; Darden, R.W. Effect of bias adjustment and rain gauge data quality control on radar rainfall estimation. Water Resour. Res. 1999, 35, 2487–2503. [Google Scholar] [CrossRef]
- Szturc, J.; Ośródka, K.; Jurczyk, A.; Jelonek, L. Concept of dealing with uncertainty in radar-based data for hydrological purpose. Nat. Hazards Earth Syst. Sci. 2008, 8, 267–279. [Google Scholar] [CrossRef]
- Kawka, M.; Przyborowski, Ł.; Nawalany, M. Możliwości wykorzystania produktów radarowych w celu poprawy jakości prognozy modelu opad-odpływ. In Monografie Komitetu Inżynierii Środowiska Polskiej Akademii Nauk; Komitet Inżynierii Środowiska PAN: Warszawa, Poland, 2014; ISBN 978-83-63714-18-5. [Google Scholar]
- Niemi, T.J.; Warsta, L.; Taka, M.; Hickman, B.; Pulkkinen, S.; Krebs, G.; Moisseev, D.N.; Koivusalo, H.; Kokkonen, T. Applicability of open rainfall data to event-scale urban rainfall-runoff modelling. J. Hydrol. 2017, 547, 143–155. [Google Scholar] [CrossRef]
- Gabella, M.; Joss, J.; Perona, G.; Galli, G. Accuracy of rainfall estimates by two radars in the same Alpine environment using gage adjustment. J. Geophys. Res. 2001, 106, 5139–5150. [Google Scholar] [CrossRef]
- Blocken, B.; Poesen, J.; Carmeliet, J. Impact of wind on the spatial distribution of rain over micro-scale topography: Numerical modelling and experimental verification. Hydrol. Process. 2006, 20, 345–368. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, T.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG)—Algorithm Theoretical Basis Document (ATBD) Version 5.2; National Aeronautics and Space Administration: Washington, DC, USA, 2018. [Google Scholar]
- Tang, G.; Hui, Y.; Strobl, J.; Liu, W. The impact of resolution on the accuracy of hydrologic data derived from DEMs. J. Geogr. Sci. 2001, 11, 393–401. [Google Scholar] [CrossRef]
- Kenward, T.; Lettenmaier, D.P.; Wood, E.F.; Fielding, E. Effects of digital elevation model accuracy on hydrologic predictions. Remote Sens. Environ. 2000, 74, 432–444. [Google Scholar] [CrossRef]
- US Army Corps of Engineers (USACE). Hydrologic Modeling System HEC-HMS: Technical Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2000. [Google Scholar]
- Kibler, D.F. Urban Stormwater Hydrology; American Geophysical Union: Washington, DC, USA, 1982. [Google Scholar]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Zelelew, D.; Melesse, A. Applicability of a spatially semi-distributed hydrological model for watershed scale runoff estimation in Northwest Ethiopia. Water 2018, 10, 923. [Google Scholar] [CrossRef]
- Fang, G.; Yuan, Y.; Gao, Y.; Huang, X.; Guo, Y. Assessing the effects of urbanization on flood events with urban agglomeration polders type of flood control pattern using the HEC-HMS model in the Qinhuai River Basin, China. Water 2018, 10, 1003. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical contributions to the theory of evolution—On a form of spurious correlation which may arise when indices are used in the measurement of organs. Proc. R. Soc. Lond. 1896, 60, 489–498. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASAB 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Omranian, E.; Sharif, H.O.; Tavakoly, A.A. How well can Global Precipitation Measurement (GPM) capture hurricanes? Case study: Hurricane harvey. Remote Sens. 2018, 10, 1150. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef]
- Schoups, G.; Vrugt, J.A.; Fenicia, F.; van de Giesen, N.C. Corruption of accuracy and efficiency of Markov chain Monte Carlo simulation by inaccurate numerical implementation of conceptual hydrologic models. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Mishra, S.K.; Suresh Babu, P.; Singh, V.P. SCS-CN method revisited. In Advances in Hydraulics and Hydrology; Water Resources Publications: Littleton, CO, USA, 2007. [Google Scholar]



| Event | Start | End | Maximum Discharge (m3/s) |
|---|---|---|---|
| Event 1 | 14 May 2014 | 23 May 2014 | 211.1 |
| Event 2 | 3 October 2014 | 7 October 2014 | 22.8 |
| Event 3 | 21 May 2015 | 30 May 2015 | 26.8 |
| Event 4 | 14 May 2016 | 17 May 2016 | 19.9 |
| Event 5 | 17 July 2016 | 19 July 2016 | 23.2 |
| Event 6 | 3 October 2016 | 9 October 2016 | 35.2 |
| Rainfall Station | Acronym | Longitude | Latitude |
|---|---|---|---|
| Maków Podhalański | RS-1 | 19°40′ | 49°43′ |
| Markowe Szczawiny | RS-2 | 19°30′ | 49°35′ |
| Spytkowice Górne | RS-3 | 19°50′ | 49°34′ |
| Zawoja | RS-4 | 19°34′ | 49°40′ |
| Basin Model | Meteorological Model | ||
|---|---|---|---|
| Parameter Method | Selected Method | Parameter Method | Selected Method |
| Loss | SCS Curve Number | Precipitation | Inverse Distance (for rain gauges) |
| Transform | Snyder Unit Hydrograph | Specified Hyetograph (for radar and GPM) | |
| Baseflow | Recession | ||
| Routing | Muskingum-Cunge | ||
| Performance Metrics | Value | Classification | Reference |
|---|---|---|---|
| Nash-Sutcliffe efficiency coefficient (NSE) | NSE ≤ 0.4 | Unsatisfactory | [66] |
| 0.40–0.50 | Acceptable | ||
| 0.50–0.65 | Satisfactory | ||
| 0.65–0.75 | Good | ||
| 0.75–1.00 | Very Good | ||
| Pearson’s correlation coefficient (r) | r ≤ 0.4 | Unsatisfactory | [29] |
| 0.40–0.60 | Acceptable | ||
| 0.60–0.70 | Satisfactory | ||
| 0.70–0.85 | Good | ||
| 0.85–1.00 | Very Good | ||
| Percent bias (PBias) Relative peak flow difference (rPFD) | >20% | Unacceptable | [63] |
| ≤20% | Acceptable |
| Parameter | Rain Gauges 1 | Sub-Catchments 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GS-1 | GS-2 | GS-3 | GS-4 | SC-1 | SC-2 | SC-3 | SC-4 | SC-5 | SC-6 | |
| DR (km) | 82.8 | 84.9 | 101.7 | 80.8 | 91.6 | 94.5 | 100.8 | 102.4 | 96.9 | 90.4 |
| HG (m a.s.l.) | 367 | 1184 | 525 | 604 | 713.4 | 684.7 | 588.2 | 509.8 | 524.9 | 578.8 |
| MH (m) | 981.5 | 1434.1 | 1431.2 | 1011 | 1252.1 | 1482.4 | 1472.3 | 1384.8 | 1301.4 | 1067.1 |
| Event | Total Precipitation Accumulation (mm) | |||
|---|---|---|---|---|
| Rain Gauges | Raw Radar | Adjusted Radar | IMERG GPM | |
| Event 1 | 397 | 1680 | 692 | 678 |
| Event 2 | 212 | 437 | 179 | 223 |
| Event 3 | 227 | 577 | 236 | 293 |
| Event 4 | 129 | 452 | 184 | 149 |
| Event 5 | 175 | 424 | 175 | 190 |
| Event 6 | 448 | 1108 | 456 | 783 |
| Event | NSE | r | PBias (%) | rPFD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | |
| Event 1 | −0.46 | 0.79 | 0.81 | 0.17 | 0.89 | 0.90 | −61.20 | −0.60 | −6.00 | −40.6 | −23.2 | −20.7 |
| Event 2 | 0.75 | 0.91 | 0.74 | 0.87 | 0.95 | 0.88 | −2.30 | −4.50 | −4.50 | −3.5 | 3.9 | 8.7 |
| Event 6 | 0.78 | 0.66 | 0.20 | 0.89 | 0.84 | 0.76 | −3.70 | −13.50 | 0.50 | 6.5 | 3.1 | 36.9 |
| Sub-Catchment | Initial Abstraction (MM) | Curve Number (-) | ||||||
|---|---|---|---|---|---|---|---|---|
| Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | |||
| Initial | Optimized | Initial | Optimized | |||||
| SC-1 | 25.23 | 19.42 | 26.57 | 21.83 | 43.02 | 48.63 | 70.68 | 54.27 |
| SC-2 | 27.21 | 17.03 | 21.24 | 23.55 | 41.18 | 58.70 | 77.20 | 71.42 |
| SC-3 | 17.77 | 13.73 | 15.23 | 15.38 | 51.73 | 86.64 | 87.11 | 75.52 |
| SC-4 | 17.39 | 11.25 | 19.47 | 27.12 | 51.51 | 84.58 | 76.75 | 73.68 |
| SC-5 | 17.01 | 16.48 | 12.92 | 21.83 | 52.82 | 63.07 | 81.71 | 73.49 |
| SC-6 | 18.39 | 14.16 | 17.46 | 20.30 | 50.88 | 78.99 | 54.07 | 65.38 |
| Sub-Catchment | Standard Lag (HR) | Peaking Coefficient (-) | ||||||
|---|---|---|---|---|---|---|---|---|
| Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | |||
| Initial | Optimized | Initial | Optimized | |||||
| SC-1 | 1.74 | 1.54 | 2.75 | 2.07 | 0.4 | 0.49 | 0.36 | 0.19 |
| SC-2 | 2.82 | 2.59 | 3.09 | 2.44 | 0.4 | 0.37 | 0.51 | 0.21 |
| SC-3 | 2.82 | 2.61 | 2.96 | 2.86 | 0.4 | 0.40 | 0.26 | 0.20 |
| SC-4 | 1.99 | 2.06 | 2.44 | 2.81 | 0.4 | 0.42 | 0.24 | 0.21 |
| SC-5 | 1.77 | 2.31 | 2.16 | 2.58 | 0.4 | 0.37 | 0.32 | 0.22 |
| SC-6 | 2.35 | 2.31 | 1.80 | 2.58 | 0.4 | 0.55 | 0.42 | 0.37 |
| Sub-Catchment | Initial Discharge | Recession Constant | Threshold Discharge | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | ||||
| Initial | Optimized | Initial | Optimized | Initial | Optimized | |||||||
| SC-1 | 0.5 | 0.66 | 0.80 | 0.53 | 0.9 | 0.97 | 0.97 | 1.00 | 0.7 | 1.23 | 0.82 | 1.12 |
| SC-2 | 0.5 | 0.59 | 0.67 | 0.66 | 0.9 | 1.00 | 1.00 | 1.00 | 0.7 | 1.23 | 0.70 | 1.00 |
| SC-3 | 0.5 | 0.59 | 0.67 | 0.50 | 0.9 | 0.97 | 1.00 | 1.00 | 0.7 | 1.86 | 0.92 | 1.29 |
| SC-4 | 0.5 | 0.51 | 0.59 | 0.66 | 0.9 | 0.97 | 1.00 | 0.97 | 0.7 | 1.00 | 0.94 | 0.82 |
| SC-5 | 0.5 | 0.51 | 0.50 | 0.58 | 0.9 | 0.97 | 1.00 | 0.97 | 0.7 | 0.82 | 1.41 | 1.41 |
| SC-6 | 0.5 | 0.93 | 0.80 | 0.58 | 0.9 | 0.97 | 0.97 | 1.00 | 0.7 | 0.93 | 1.00 | 1.12 |
| Event | NSE | r | PBias (%) | rPFD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | Rain Gauges | Radar | IMERG | |
| Event 3 | 0.28 | 0.69 | 0.21 | 0.61 | 0.85 | 0.47 | 18.10 | 9.50 | 3.50 | −44.9 | 4.5 | −32.5 |
| Event 4 | 0.71 | 0.88 | 0.74 | 0.85 | 0.97 | 0.92 | 1.50 | 10.40 | 10.80 | 8.7 | −5.4 | −17.5 |
| Event 5 | −0.20 | 0.89 | 0.76 | 0.17 | 0.98 | 0.90 | 37.70 | 15.60 | 14.90 | −15.1 | −0.9 | 8.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilewski, P.; Nawalany, M. Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water 2018, 10, 1665. https://doi.org/10.3390/w10111665
Gilewski P, Nawalany M. Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water. 2018; 10(11):1665. https://doi.org/10.3390/w10111665
Chicago/Turabian StyleGilewski, Paweł, and Marek Nawalany. 2018. "Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland" Water 10, no. 11: 1665. https://doi.org/10.3390/w10111665
APA StyleGilewski, P., & Nawalany, M. (2018). Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water, 10(11), 1665. https://doi.org/10.3390/w10111665






