Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation
Abstract
:1. Introduction
2. Numerical Model
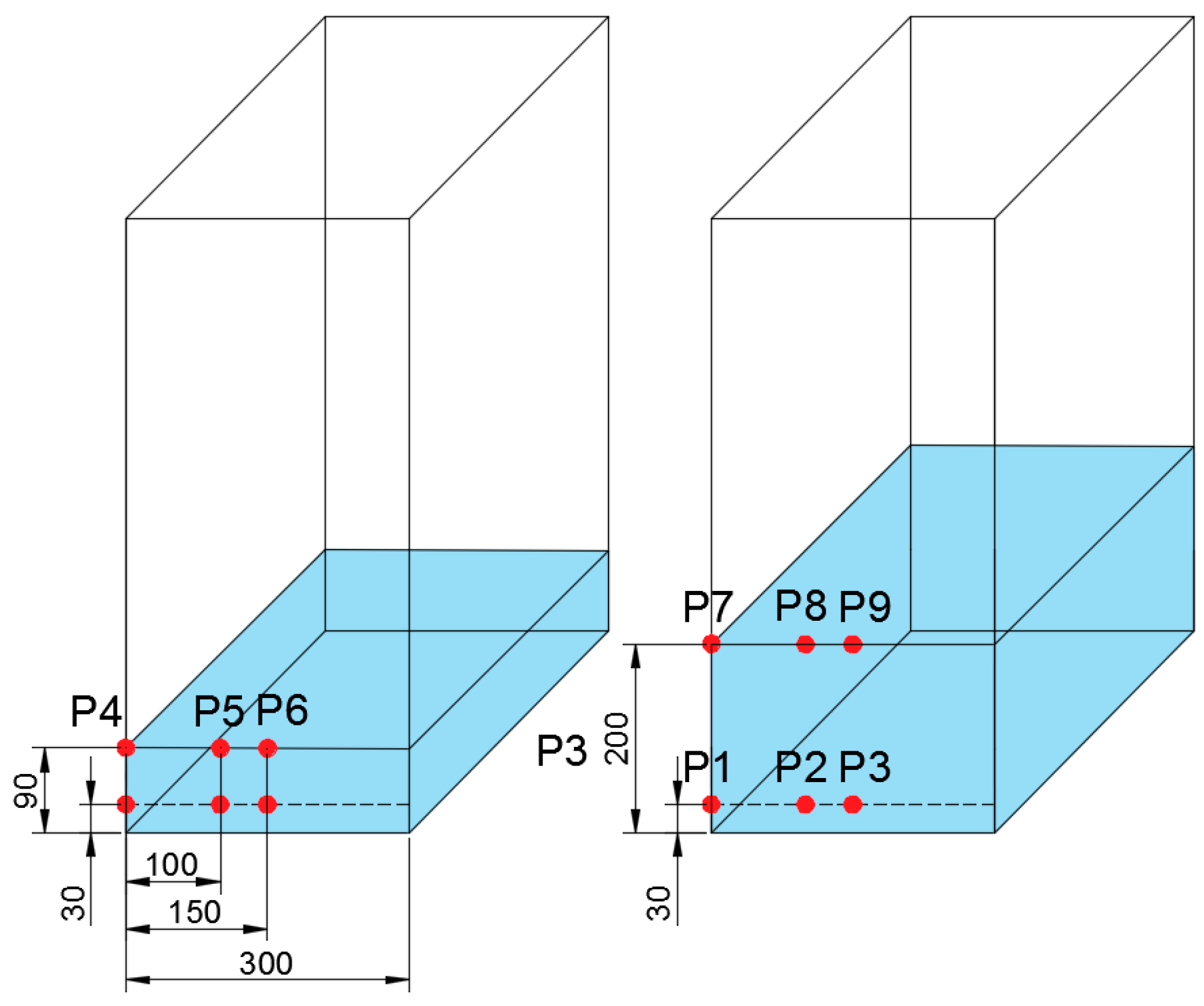
3. Experimental Setup
4. Model Validation
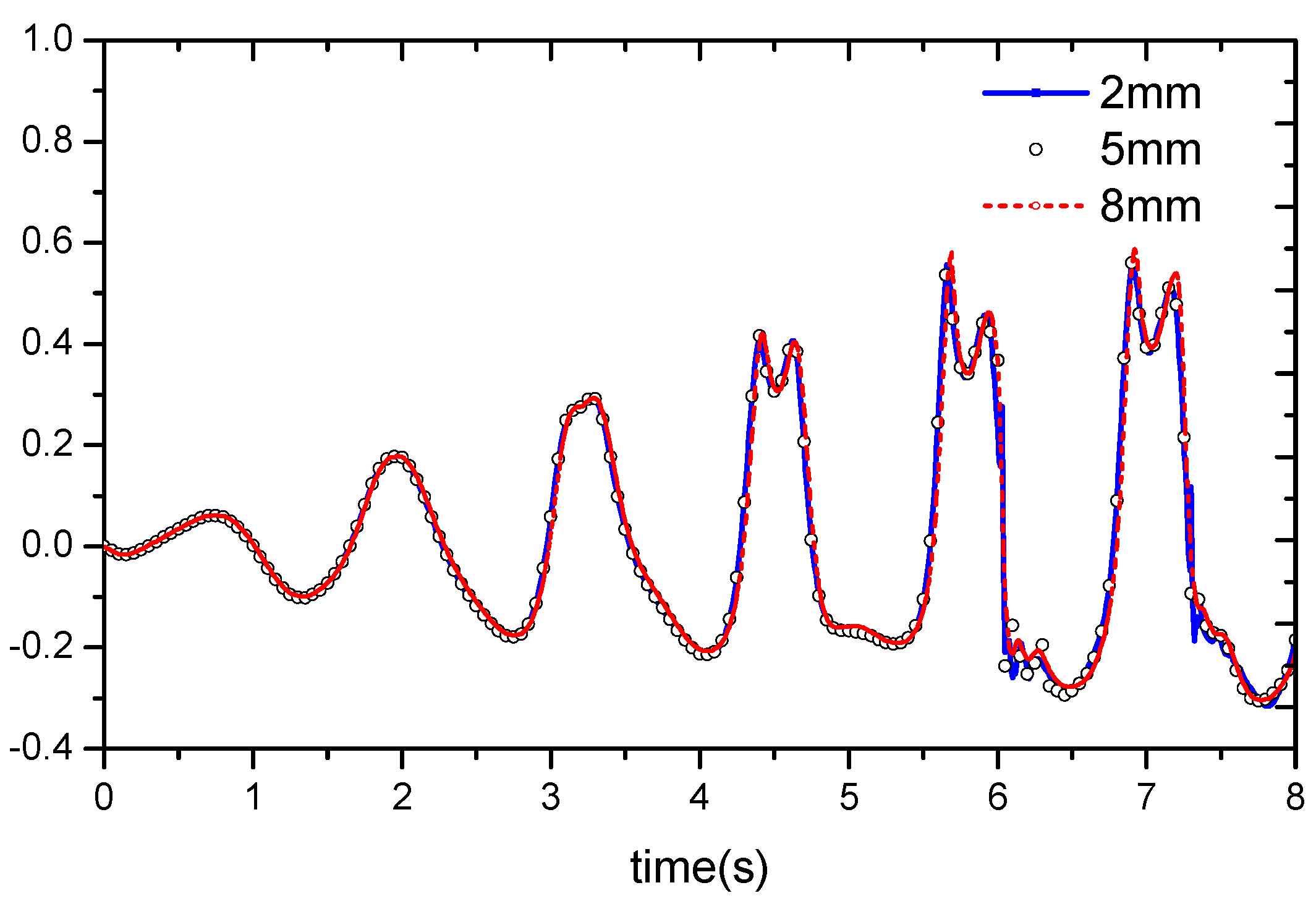
4.1. Mesh Convergence Test
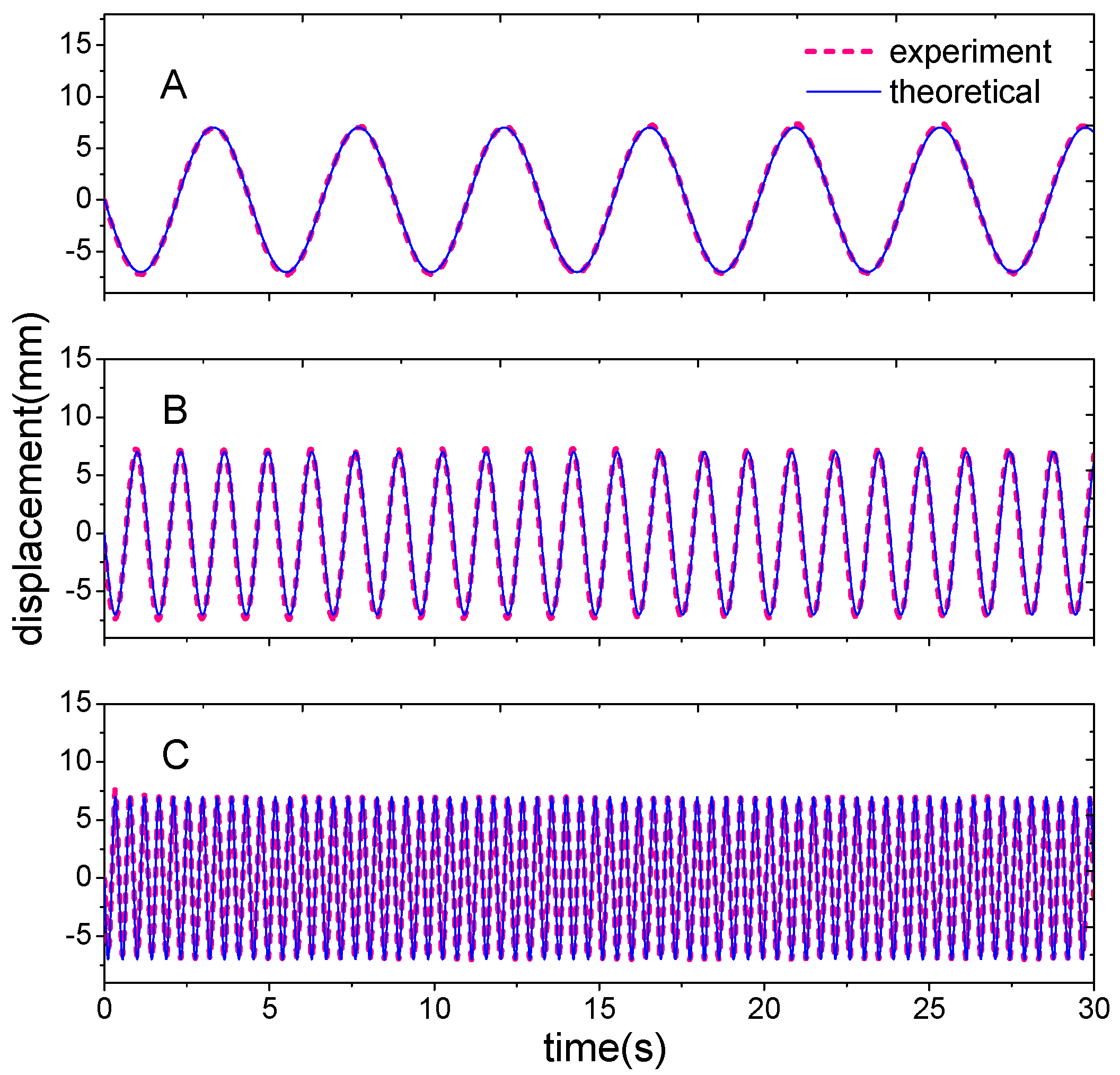
4.2. Experimental Validation
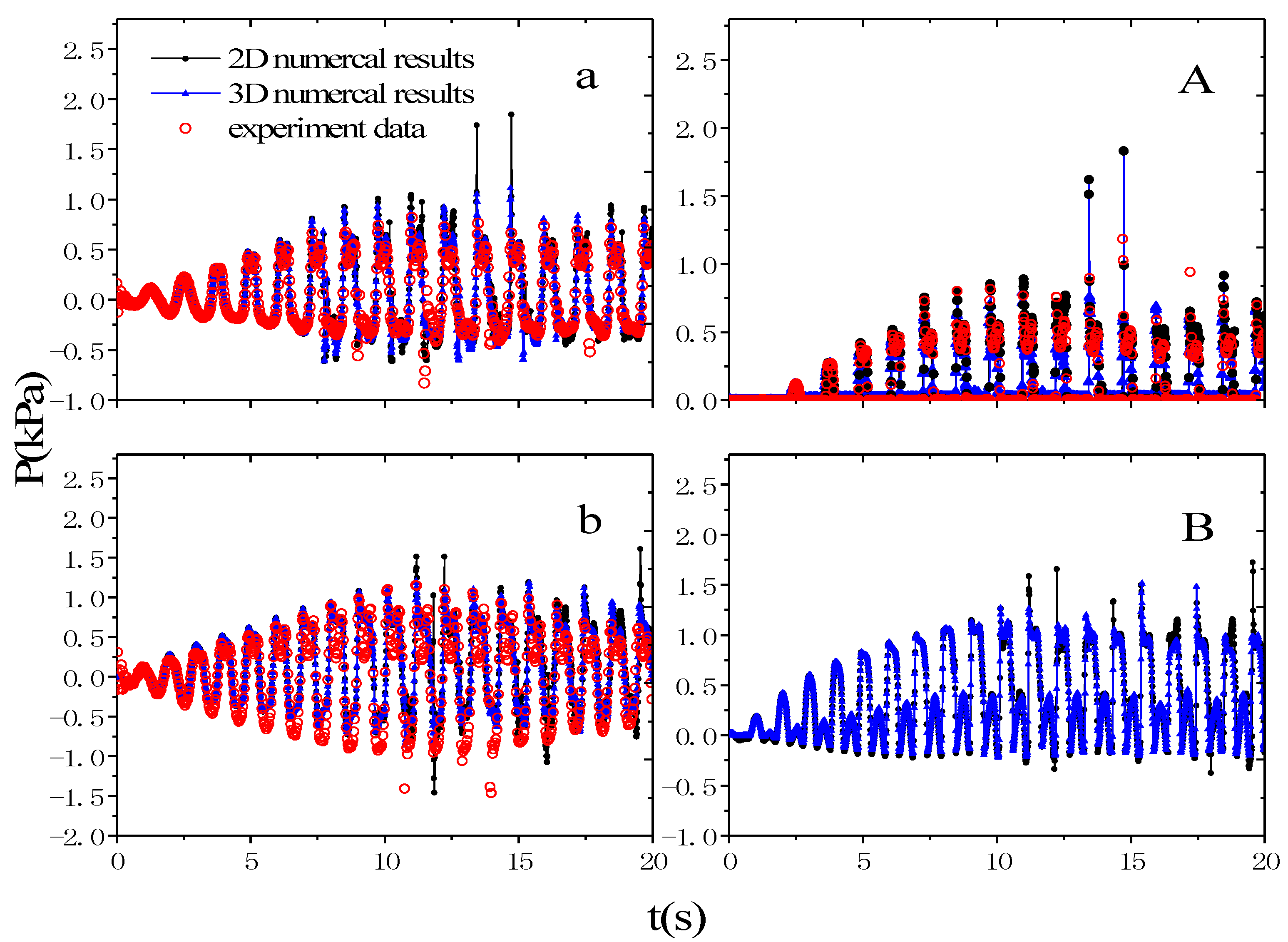
4.3. Three-Dimensional Results
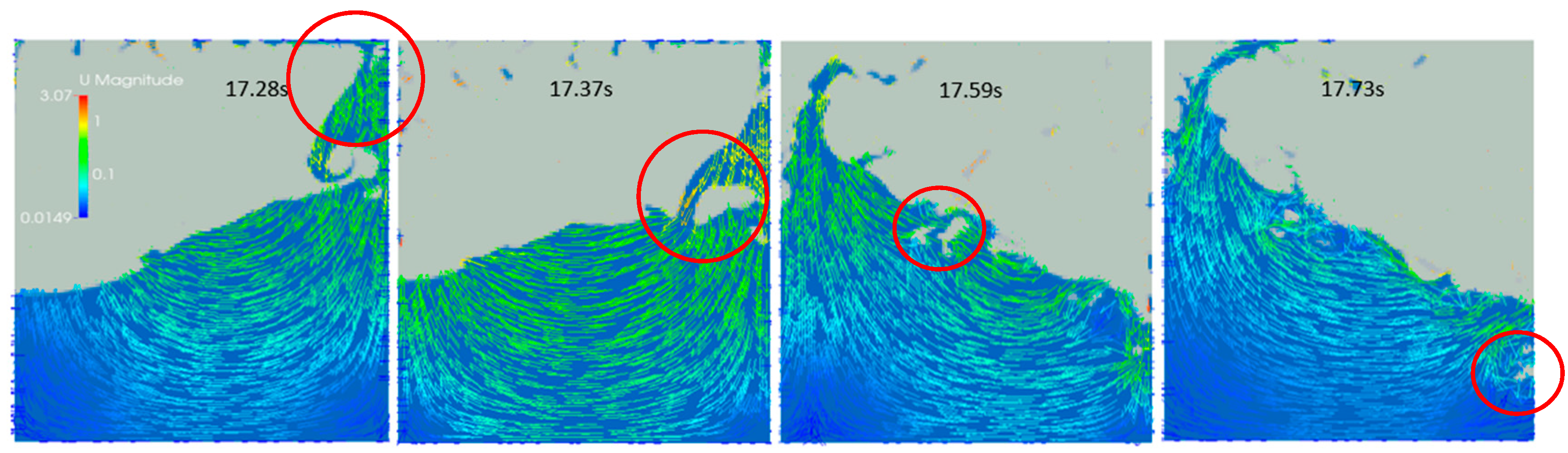
5. Results and Discussions
5.1. Effects of External Excitation Amplitudes
5.2. Resonant Hysteresis and Resonance in Advance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moiseev, N.N. On the theory of nonlinear vibrations of a liquid of finite volume. J. Appl. Math. Mech. 1958, 22, 860–872. [Google Scholar] [CrossRef]
- Faltinsen, O.M. A nonlinear theory of sloshing in rectangular tanks. J. Ship Res. 1974, 18, 224–241. [Google Scholar]
- Faltinsen, O.M.; Rognebakke, O.F.; Lukovsky, I.A.; Timokha, A.N. Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth. J. Fluid Mech. 2000, 407, 201–234. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. An adaptive multimodal approach to nonlinear sloshing in a rectangular tank. J. Fluid Mech. 2001, 432, 167–200. [Google Scholar]
- Ikeda, T.; Nakagawa, N. Non-linear vibrations of a structure caused by water sloshing in a rectangular tank. J. Sound Vib. 1997, 201, 23–41. [Google Scholar] [CrossRef]
- Pistani, F.; Thiagarajan, K. Experimental measurements and data analysis of the impact pressures in a sloshing experiment. Ocean Eng. 2012, 52, 60–74. [Google Scholar] [CrossRef]
- Xue, M.-A.; Zheng, J.; Lin, P.; Yuan, X. Experimental study on vertical baffles of different configurations in suppressing sloshing pressure. Ocean Eng. 2017, 136, 178–189. [Google Scholar] [CrossRef]
- Kalinichenko, V.A.; Sekerzh-Zen’kovich, S.Y. Experimental investigation of Faraday waves of maximum height. Fluid Dyn. 2007, 42, 959–965. [Google Scholar] [CrossRef]
- Xue, M.-A.; Lin, P.; Zheng, J.H.; Ma, Y.; Yuan, X.; Nguyen, V.T. Effects of perforated baffle on reducing sloshing in rectangular tank: experimental and numerical study. China Ocean Eng. 2013, 27, 615–628. [Google Scholar] [CrossRef]
- Cai, Z.H.; Wang, D.Y.; Li, Z. Influence of excitation frequency on slosh-induced impact pressures of liquefied natural gas tanks. J. Shanghai Jiaotong Univ. 2011, 16, 124–128. [Google Scholar] [CrossRef]
- Xue, M.-A.; Zheng, J.H.; Lin, P.; Xiao, Z. Violent transient sloshing-wave interaction with a baffle in a three-dimensional numerical tank. J. Ocean Univ. China 2017, 16, 661–673. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. A numerical study of three-dimensional liquid sloshing in tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Buldakov, E. Lagrangian modelling of fluid sloshing in moving tanks. J. Fluids Struct. 2014, 45, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Xue, M.-A.; Zheng, J.H.; Lin, P. Numerical simulation of sloshing phenomena in cubic tank with multiple baffles. J. Appl. Math. 2012, 2012, 1–21. [Google Scholar] [CrossRef]
- Kim, Y. Numerical simulation of sloshing flows with impact load. Appl. Ocean Res. 2001, 23, 53–62. [Google Scholar] [CrossRef]
- Ramaswamy, B.; Kawahara, M.; Nakayama, T. Lagrangian finite element method for the analysis of two-dimensional sloshing problems. Int. J. Numer. Methods Fluids 1986, 6, 659–670. [Google Scholar] [CrossRef]
- Oxtoby, O.F.; Malan, A.G.; Heyns, J.A. A computationally efficient 3D finite-volume scheme for violent liquid–gas sloshing. Int. J. Numer. Methods Fluids 2015, 79, 306–321. [Google Scholar] [CrossRef]
- Kishev, Z.R.; Hu, C.; Kashiwagi, M. Numerical simulation of violent sloshing by a CIP-based method. J. Mar. Sci. Technol. 2006, 11, 111–122. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Li, H.T.; Li, J. An investigation into the pressure on solid walls in 2D sloshing using SPH method. Ocean Eng. 2013, 59, 129–141. [Google Scholar] [CrossRef]
- Xue, M.-A.; Lin, P. Numerical study of ring baffle effects on reducing violent liquid sloshing. Comput. Fluids. 2011, 52, 116–129. [Google Scholar] [CrossRef]
- Kim, Y. Experimental and numerical analyses of sloshing flows. J. Eng. Math. 2007, 58, 191–210. [Google Scholar] [CrossRef]
- Jin, X.; Lin, P.Z. Viscous effects on liquid sloshing under external excitations. Ocean Eng. 2018, in press. [Google Scholar] [CrossRef]
- Ma, Z.H.; Causon, D.M.; Qian, L.; Mingham, C.G.; Martinez, F.P. Numerical investigation of air enclosed wave impacts in a depressurised tank. Ocean Eng. 2016, 123, 15–27. [Google Scholar] [CrossRef]
- Jiang, S.C.; Teng, B.; Bai, W.; Ying, G. Numerical simulation of coupling effect between ship motion and liquid sloshing under wave action. Ocean Eng. 2015, 108, 140–154. [Google Scholar] [CrossRef]
- Wang, Y.-S.; Politano, M.; Laughery, R. Towards full predictions of temperature dynamics in McNary Dam forebay using OpenFOAM. Water Sci. Eng. 2013, 6, 317–330. [Google Scholar]
- Faltinsen, O.M.; Timokha, A.N. Sloshing; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Liu, D.; Tang, W.; Wang, J.; Xue, H.; Wang, K. Comparison of laminar model, RANS, LES and VLES for simulation of liquid sloshing. Appl. Ocean Res. 2016, 59, 638–649. [Google Scholar] [CrossRef]
- Waterhouse, D.D. Resonant sloshing near a critical depth. J. Fluid Mech. 2006, 281, 313–318. [Google Scholar] [CrossRef]
- Kobine, J.J. Nonlinear resonant characteristics of shallow fluid layers. Philos. Trans. 2008, 366, 1331–1346. [Google Scholar] [CrossRef] [PubMed] [Green Version]









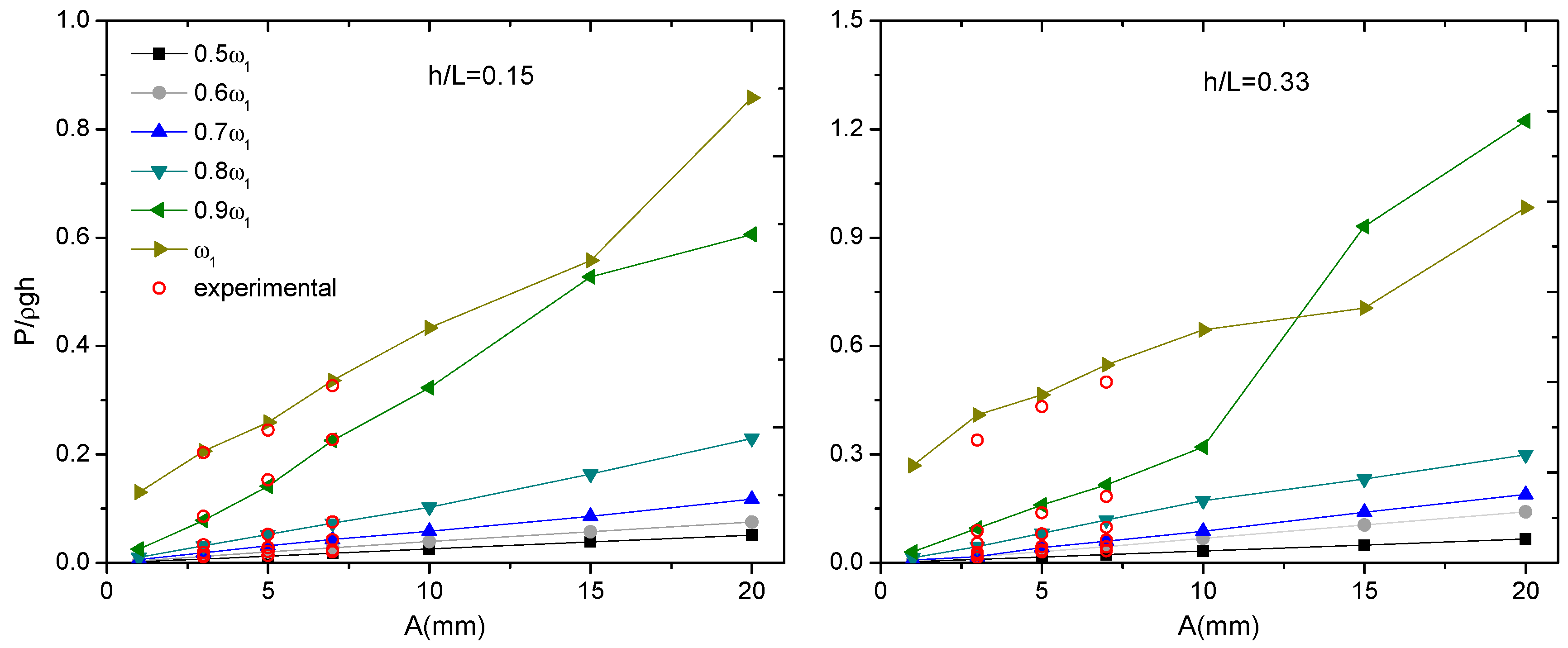
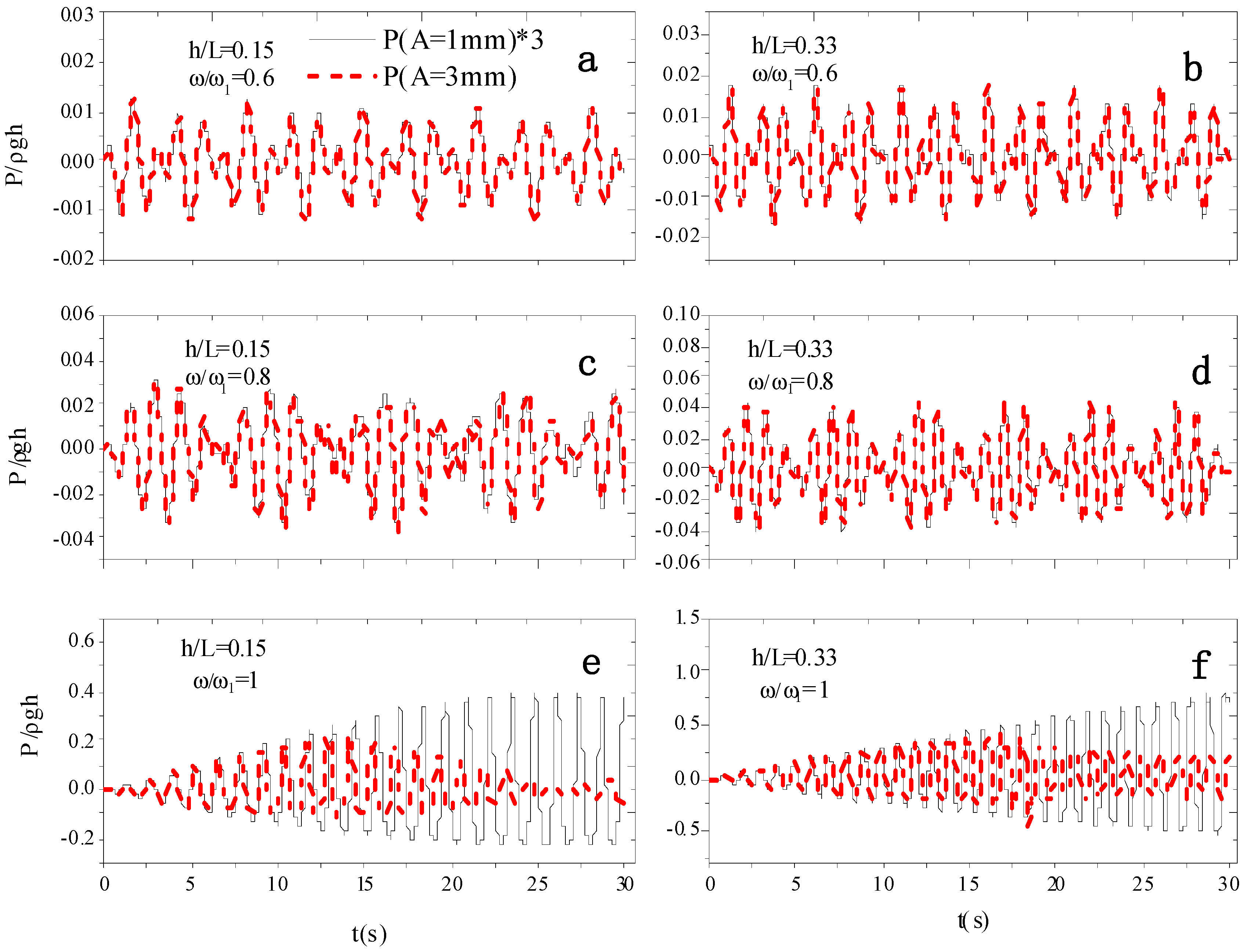
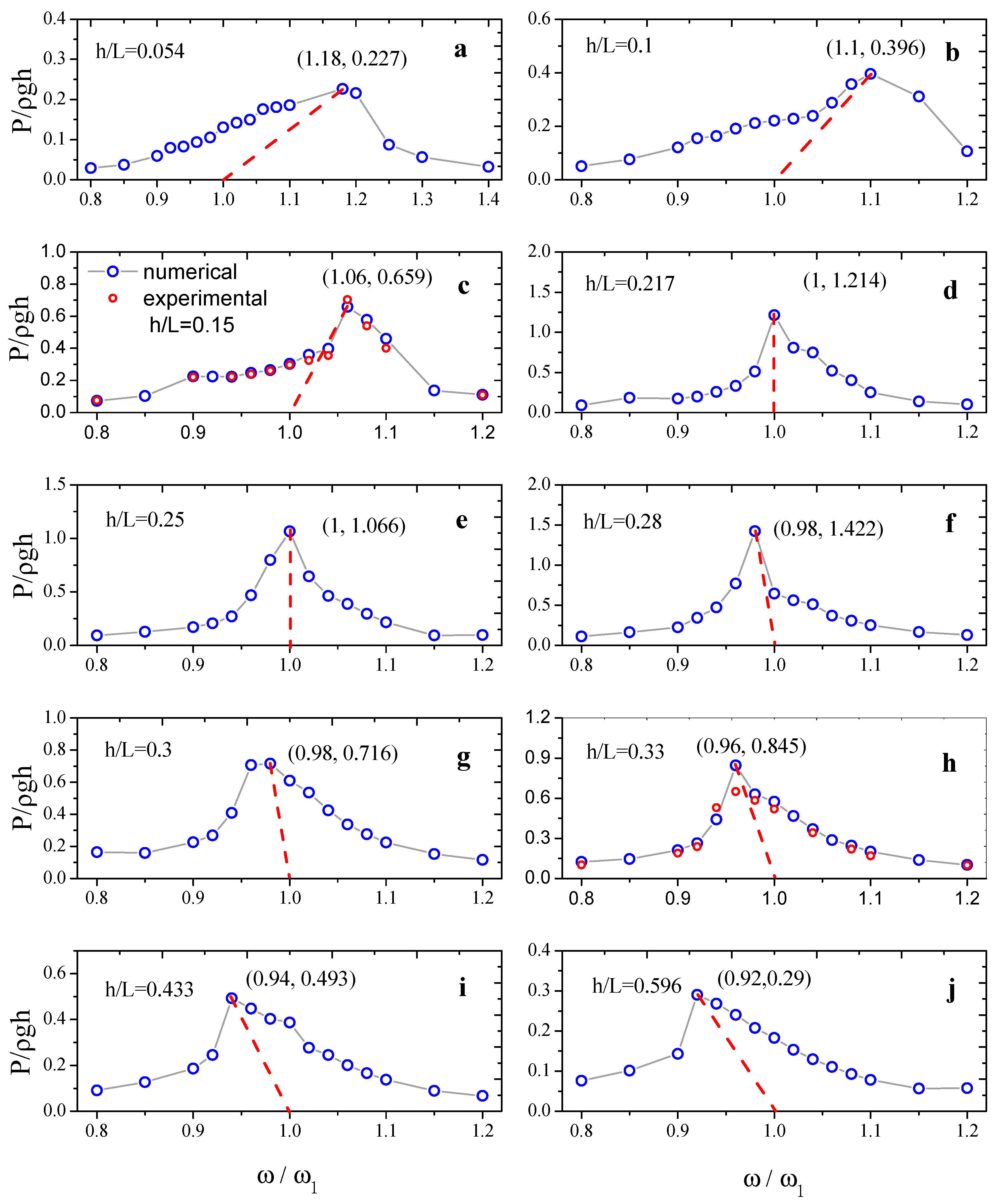
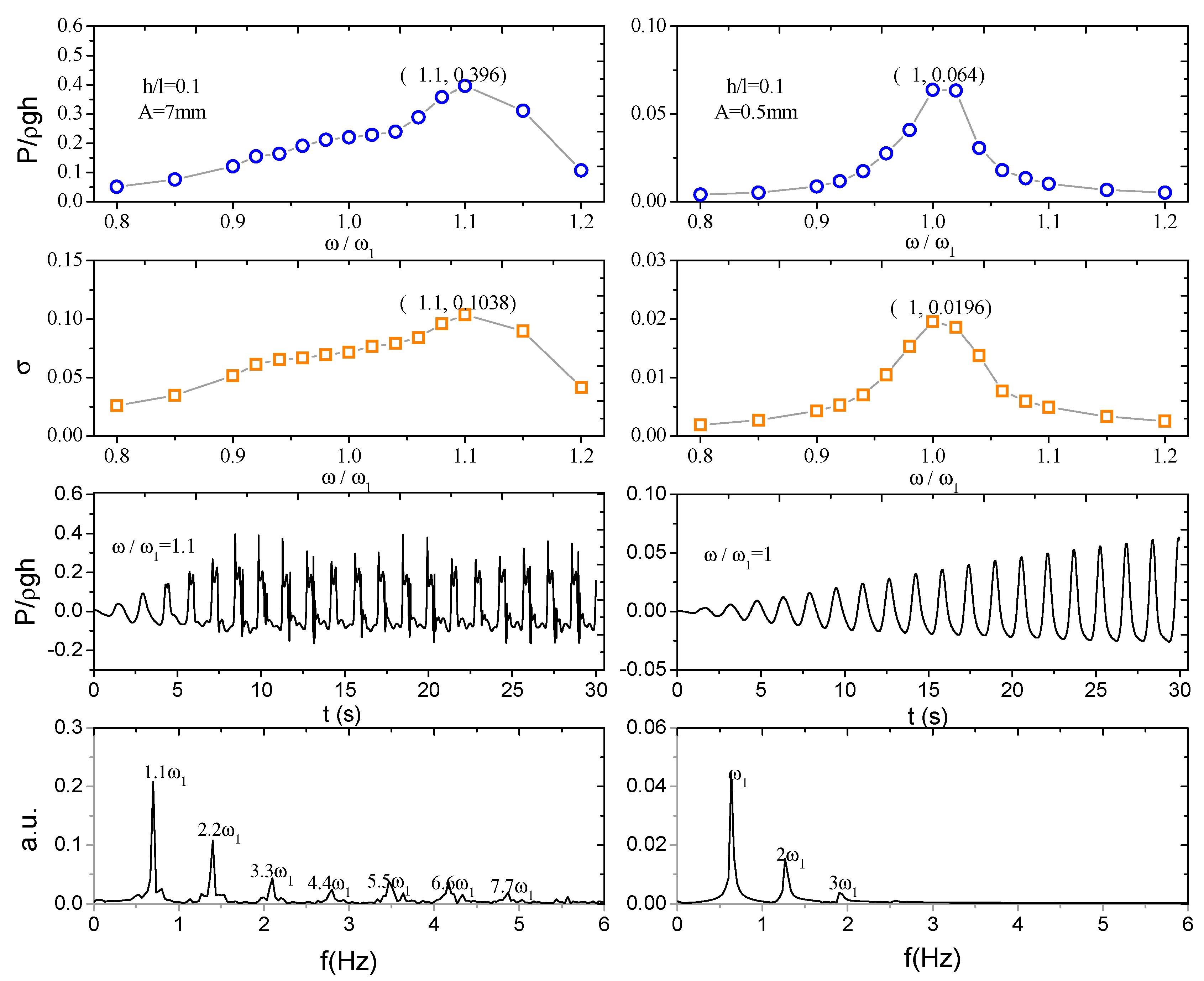



| Two-dimensional Model | Three-dimensional Model | |
|---|---|---|
| Mesh Size | 5 × 5 mm | 5 × 5 × 5 mm |
| Mesh Number | 15,600 | 936,000 |
| Computing | CPU:AMD Ryzen 7 1700X Eight-Core Processor 3.40 GHz no parallel | |
| Times | 1962 s | 394,971 s |
| Analysis of Result | In agreement with the experimental data; Sometimes there are large pressure peaks. | Match well with the experimental value |
| Case | h/L | ω1 (rad/s) | ω/ω1 | ω | A(m) |
|---|---|---|---|---|---|
| Case 1 | 0.15 | 4.749 | 0.5 | 2.3745 | 0.001 0.003 0.005 0.007 0.01 0.02 |
| Case 2 | 0.6 | 2.8494 | |||
| Case 3 | 0.7 | 3.3243 | |||
| Case 4 | 0.8 | 3.7992 | |||
| Case 5 | 0.9 | 4.2741 | |||
| Case 6 | 1 | 4.749 | |||
| Case 7 | 0.33 | 6.333 | 0.5 | 3.1665 | |
| Case 8 | 0.6 | 3.7998 | |||
| Case 9 | 0.7 | 4.4331 | |||
| Case 10 | 0.8 | 5.0664 | |||
| Case 11 | 0.9 | 5.6997 | |||
| Case 12 | 1 | 6.333 |
| Case | h/L | L(m) | h(m) | A(m) | ω1 (rad/s) | ω (rad/s) |
|---|---|---|---|---|---|---|
| Case 13 | 0.054 | 0.6 | 0.0324 | 0.007 | 2.942 | 0.8 ω1–1.2 ω1 |
| Case 14 | 0.1 | 0.06 | 3.953 | |||
| Case 15 | 0.15 | 0.09 | 4.749 | |||
| Case 16 | 0.217 | 0.1302 | 5.514 | |||
| Case 17 | 0.25 | 0.15 | 5.804 | |||
| Case 18 | 0.28 | 0.168 | 6.023 | |||
| Case 19 | 0.3 | 0.18 | 6.15 | |||
| Case 20 | 0.33 | 0.198 | 6.316 | |||
| Case 21 | 0.433 | 0.2598 | 6.711 | |||
| Case 22 | 0.596 | 0.3576 | 6.999 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Xue, M.-A. Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation. Water 2018, 10, 1752. https://doi.org/10.3390/w10121752
Chen Y, Xue M-A. Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation. Water. 2018; 10(12):1752. https://doi.org/10.3390/w10121752
Chicago/Turabian StyleChen, Yichao, and Mi-An Xue. 2018. "Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation" Water 10, no. 12: 1752. https://doi.org/10.3390/w10121752
APA StyleChen, Y., & Xue, M.-A. (2018). Numerical Simulation of Liquid Sloshing with Different Filling Levels Using OpenFOAM and Experimental Validation. Water, 10(12), 1752. https://doi.org/10.3390/w10121752






