A Critical Evaluation on the Role of Aerodynamic and Canopy–Surface Conductance Parameterization in SEB and SVAT Models for Simulating Evapotranspiration: A Case Study in the Upper Biebrza National Park Wetland in Poland
Abstract
:1. Introduction
- What is the performance of the three structurally different SEB/SVAT models in the UBNP wetland when simulated with high temporal frequency measurements?
- What are the effects of aerodynamic and surface conductances parameterizations and associated state variables in determining the model errors with respect to ET?
- To what extent the ET modelling errors and conductance parameterizations are impacted by a range of environmental and ecohydrological conditions?
2. Materials and Methods
2.1. Model Description
2.2. Uncertainties in gA and gS Parameterizations in SEB and SVAT
2.3. Eddy Covariance Estimation of gA and gS for Model Evaluation
2.4. Study Site: Ecological and Hydrological Significance of UBNP Wetland
2.5. Datasets
2.6. Model Evaluation and Comparison
2.7. Relationship between ET Modeling Errors, Conductances, and Ecohydrological Factors
3. Results
3.1. Statistical Intercomparison of the Conductances and λE (ET) Estimates from SCOPE1.7, STIC1.2 and SEBS Models
3.1.1. Evaluation of gA and gS Estimates from Models
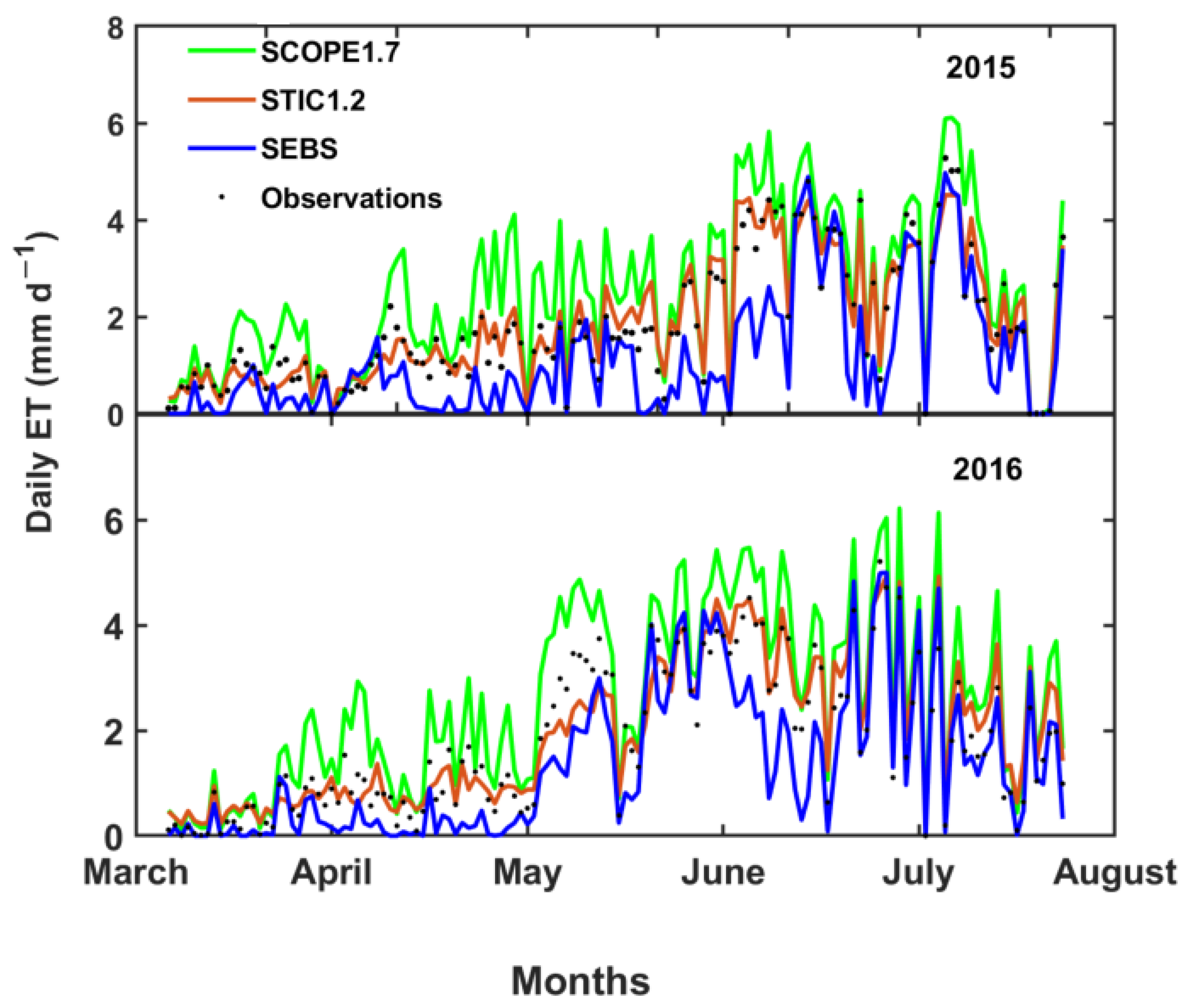
3.1.2. Evaluation of λE (ET) Estimates from Models
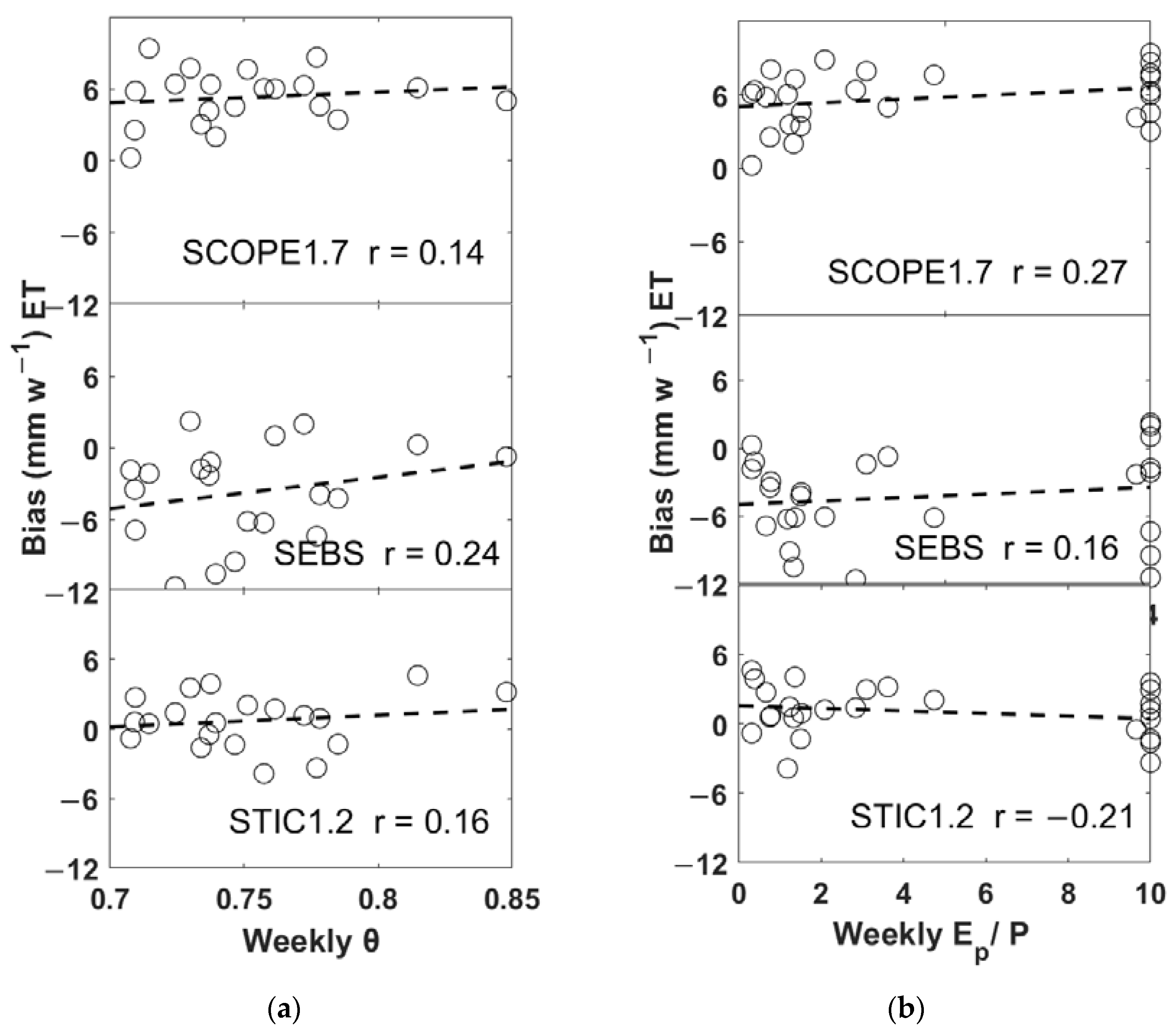
3.2. Effects of Biophysical Conductance Parameterization on Residual Error of the Models
3.3. Effects of Environmental and Ecohydrological Factors on the Model Performances
4. Discussion
4.1. Effects of Model Structure and Biophysical Parameterizations on Residual λE or ET Errors
4.2. Effects of Ecohydrological Conditions on Conductance Estimation and Implication on Model Performances
5. Conclusions
- (a)
- Notable differences were found out in the gA and gS estimates from the three models. While SCOPE1.7 revealed substantial overestimation of both gA and gS with respect to the EC tower estimates, STIC1.2 derived gA and gS were within the range of EC tower estimates. SEBS revealed a consistent overestimation of gA during the start of the growing season in spring, and gA estimates were is good agreement with the EC tower during the active vegetative phase in summer.
- (b)
- All the models explained significant variability in the observed ET with a root mean square error (RMSE) of 0.4–1 mm day−1 and mean absolute percent error (MAPE) of 16–44%. Model intercomparison showed STIC1.2 to produce the least bias and good agreement with the observations, whereas SEBS and SCOPE1.7 revealed consistent underestimation and overestimation, respectively, in both years.
- (c)
- Underestimation of λE (and ET) in SEBS was mainly attributed to the underestimation in the roughness lengths of momentum and heat transfers (z0M and z0H). While the underestimation of z0M is associated with the empirical modeling structure, the underestimation of z0H was associated with the overestimation of ‘kB−1-term’ under high soil moisture and low atmospheric aridity conditions. Underestimation of both z0M and z0H led to an overestimation of the aerodynamic conductance (gA) and sensible heat flux (H), which was consequently reflected in the underestimation of ET.
- (d)
- Although both SEBS and SCOPE1.7 had similar empirical parameterization of gA, a consistent overestimation of λE (and ET) in SCOPE1.7 was associated with the overestimation of the canopy–surface conductance (gS) under high atmospheric aridity and also presumably due to the gS-photosynthesis modeling uncertainty in SCOPE1.7 under high atmospheric vapor pressure deficit.
- (e)
- Despite all the three model captured substantial variability in λE (and ET), the principal difference between the models appear to be associated with the differences in gA and gS. Different magnitude gA and gS from all the models indicate the critical role of ambiguous parameterizations of these two important conductances for a broad spectrum of ecohydrological conditions. While SEBS require improved roughness length representation for enhancing the performance of gA sub-models under low fractional vegetation cover conditions; SCOPE1.7 requires robust parameterizations for both gA and gS, and default calibration parameters prior to large-scale ET monitoring in the wetlands.
- (f)
- The models showed promise as a quick and simple monitoring tool for wetland evapotranspiration. The simplified analytical model STIC1.2, requiring only surface-air temperature, humidity, and radiation data, can produce comparable results to more complex methods like SEBS under fully vegetated conditions and relatively better results under low fractional vegetation cover. Furthermore, this study demonstrated the model’s potential for large scale ET mapping in the wetlands to capture the spatio-temporal ET dynamics. A dense network of radiation, temperature and humidity monitoring stations would also help create near-real time ET maps for the eco-hydrological studies in the Upper Biebrza National Park region.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sanderson, J.S.; Cooper, D.J. Ground Water Discharge by Evapotranspiration in Wetlands of an Arid Intermountain Basin. J. Hydrol. 2008, 351, 344–359. [Google Scholar] [CrossRef]
- Oberg, W.J.; Melesse, M.A. Evapotranspiration Dynamics at an Ecohydrological Restoration Site: An Energy Balance and Remote Sensing Approach. J. Am. Water Resour. Assoc. 2007, 42, 565–582. [Google Scholar] [CrossRef]
- Ceron, N.C.; Melesse, M.A.; Price, R.; Dessu, B.S.; Kandel, P.H. Operational Actual Wetland Evapotranspiration Estimation for South Florida Using MODIS Imagery. Remote Sens. 2015, 7, 3615–3632. [Google Scholar] [CrossRef]
- Middleton, B.A.; Souter, J.N. Functional Integrity of Freshwater Forested Wetlands, Hydrologic Alteration, and Climate Change. Ecosyst. Heal. Sustain. 2016, 2, e01200. [Google Scholar] [CrossRef]
- Middleton, B.A. Climate and Land-Use Change in Wetlands: A Dedication. Ecosyst. Heal. Sustain. 2017, 3, 1–2. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Ahmad, M.; Chemin, Y. Satellite Surveillance of Evaporative Depletion across the Indus Basin. Water Resour. Res. 2002, 38, 1273. [Google Scholar] [CrossRef]
- Siedlecki, M.; Pawlak, W.; Fortuniak, K.; Zieliński, M. Wetland Evapotranspiration: Eddy Covariance Measurement in the Biebrza Valley, Poland. Wetlands 2016, 36, 1055–1067. [Google Scholar] [CrossRef] [Green Version]
- Sumner, D.; Clark, K. Measurement and Simulation of Evapotranspiration at a Wetland Site in the New Jersey Pinelands; U.S. Geological Survey: Reston, VA, USA, 2012.
- Stannard, D.I.; Gannett, M.W.; Polette, D.; Cameron, J.; Waibel, M.S.; Spears, J.M. Evapotranspiration from Marsh and Open-Water Sites at Upper Klamath Lake, Oregon, 2008–2010; U.S. Geological Survey: Reston, VA, USA, 2013.
- Jacobs, J.M.; Mergelsberg, S.L.; Lopera, A.F.; Myers, D.A. Evapotranspiration from a Wet Prairie Wetland under Drought Conditions: Paynes Prairie Preserve, Florida, USA. Wetlands 2002, 22, 374–385. [Google Scholar] [CrossRef]
- Whitfield, B.; Jacobs, J.M.; Judge, J. Intercomparison Study of the Land Surface Process Model and the Common Land Model for a Prairie Wetland in Florida. J. Hydrometeorol. 2006, 7, 1247–1258. [Google Scholar] [CrossRef]
- Kalma, J.; McVicar, T.; McCabe, M. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Kar, S.K. Evapotranspiration Estimation with Remote Sensing and Various Surface Energy Balance Algorithms—A Review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef] [Green Version]
- Anderson, W.B.; Zaitchik, B.F.; Hain, C.R.; Anderson, M.C.; Yilmaz, M.T.; Mecikalski, J.; Schultz, L. Towards an Integrated Soil Moisture Drought Monitor for East Africa. Hydrol. Earth Syst. Sci. 2012, 16, 2893–2913. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A Two-Source Approach for Estimating Turbulent Fluxes Using Multiple Angle Thermal Infrared Observations. Water Resour. Res. 1997, 33, 1495–1508. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C. Advances in Thermal Infrared Remote Sensing for Land Surface Modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source Approach for Estimating Soil and Vegetation Energy Fluxes in Observations of Directional Radiometric Surface Temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Liu, S.; Lu, L.; Mao, D.; Jia, L. Evaluating Parameterizations of Aerodynamic Resistance to Heat Transfer Using Field Measurements. Hydrol. Earth Syst. Sci. 2007, 11, 769–783. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Troufleau, D.; Lhomme, J.P.; Monteny, B.; Vidal, A. Sensible Heat Flux and Radiometric Surface Temperature over Sparse Sahelian Vegetation. I. An Experimental Analysis of the KB-1 Parameter. J. Hydrol. 1997, 188–189, 815–838. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Kustas, W.P.; Anderson, M.C.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A. Two-Source Energy Balance Model Estimates of Evapotranspiration Using Component and Composite Surface Temperatures. Adv. Water Resour. 2012, 50, 134–151. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Thomsen, A. Evaluating Evapotranspiration Rates and Surface Conditions Using Landsat TM to Estimate Atmospheric Resistance and Surface Resistance. Remote Sens. Environ. 2002, 79, 329–343. [Google Scholar] [CrossRef]
- Wallace, J.S.; Verhoef, A. Modelling Interactions in Mixed-Plant Communities: Light, Water and Carbon Dioxide. In Leaf developmentr and Canopy Growth; Sheffield Academic Press: Sheffield, UK, 2000; p. 250. [Google Scholar]
- Gökmen, M.; Vekerdy, Z.; Verhoef, A.; Verhoef, W.; Batelaan, O.; van der Tol, C. Integration of Soil Moisture in SEBS for Improving Evapotranspiration Estimation under Water Stress Conditions. Remote Sens. Environ. 2012, 121, 261–274. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional Evaporation Estimates from Flux Tower and MODIS Satellite Data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE Model for the Prediction of Water Stress and Evapotranspiration Components from Thermal Infra-Red Data and Its Evaluation over Irrigated and Rainfed Wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A Two-Source Time-Integrated Model for Estimating Surface Fluxes Using Thermal Infrared Remote Sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; González-Dugo, M.P.; Cammalleri, C.; D’Urso, G.; Pimstein, A.; et al. Mapping Daily Evapotranspiration at Field to Continental Scales Using Geostationary and Polar Orbiting Satellite Imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef] [Green Version]
- Kiptala, K.J.; Mohamed, Y.; Mul, M.M.; Zaag, P. Mapping Evapotranspiration Trends Using MODIS and SEBAL Model in a Data Scarce and Heterogeneous Landscape in Eastern Africa. Water Resour. Res. 2013, 49, 8495–8510. [Google Scholar] [CrossRef]
- Olioso, A.; Taconet, O.; Mehrez, B.; Nivoit, D.; Promayon, F.; Rahmoune, L. Estimation of Evapotranspiration Using SVAT Models and Surface IR Temperature. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, “Quantitative Remote Sensing for Science and Applications”, IGARSS ’95, Firenze, Italy, 10–14 July 1995; Volume 1, pp. 516–518. [Google Scholar]
- Su, Z.; McCabe, M.F.; Wood, E.F.; Su, Z.; Prueger, J.H. Modeling Evapotranspiration during SMACEX: Comparing Two Approaches for Local- and Regional-Scale Prediction. J. Hydrometeorol. 2005, 6, 910–922. [Google Scholar] [CrossRef]
- Singh, R.; Kilic, A.; Irmak, S.; Martin, D. Application of SEBAL Model for Mapping Evapotranspiration and Estimating Surface Energy Fluxes in South-Central Nebraska. J. Irrig. Drain. Eng. 2008, 134, 273–285. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Gosselink, J.J. Wetlands, 4th ed.; Van Nostrand, R., Ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Verhoeven, J.T.A. Wetlands in Europe: Perspectives for Restoration of a Lost Paradise. Ecol. Eng. 2014, 66, 6–9. [Google Scholar] [CrossRef]
- Bullock, A.; Acreman, M. The Role of Wetlands in the Hydrological Cycle. Hydrol. Earth Syst. Sci. 2003, 7, 358–389. [Google Scholar] [CrossRef]
- Fossey, M.; Rousseau, A.N.; Bullock, A.; Acreman, M. Assessing the Long-Term Hydrological Services Provided by Wetlands under Changing Climate Conditions: A Case Study Approach of a Canadian Watershed. J. Hydrol. 2016, 541, 1287–1302. [Google Scholar] [CrossRef]
- Mao, X.F.; Cui, L.J. Reflecting the Importance of Wetland Hydrologic Connectedness: A Network Perspective. Procedia Environ. Sci. 2012, 13, 1315–1326. [Google Scholar] [CrossRef]
- Acreman, M.C.; José, P. The Hydrology of the UK—A Study of Change. In Wetlands; Routledge: London, UK, 2000. [Google Scholar]
- Acreman, M.C.; Harding, R.J.; Lloyd, C.R.; McNeil, D.D. Evaporation Characteristics of Wetlands: Experience from a Wetgrassland and a Reedbed Using Eddy Correlation Measurements. Hydrol. Earth Syst. Sci. 2003, 7, 11–21. [Google Scholar] [CrossRef]
- Kossowska-Cezak, U.; Olszewski, K.; Przybylska, G. Klimat Kotliny Biebrzańskiej (Climate of the Biebrza Valley). Adv. Agric. Sci. Probl. 1991, 58, 119–160. [Google Scholar]
- Burkett, V.; Kusler, J. Climate Change: Potential Impacts and Interactions in Wetlands of the United States. J. Am. Water Resour. Assoc. 2000, 36, 313–320. [Google Scholar] [CrossRef]
- Erwin, K. Wetlands and Global Climate Change: The Role of Wetland Restoration in a Changing World. Wetl. Ecol. Manag. 2009, 17, 71–84. [Google Scholar] [CrossRef]
- Grygoruk, M.; Batelaan, O.; Okruszko, T.; Mirosław-Świątek, D.; Chormański, J.; Rycharski, M. Groundwater Modelling and Hydrological System Analysis of Wetlands in the Middle Biebrza Basin BT—Modelling of Hydrological Processes in the Narew Catchment; Świątek, D., Okruszko, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 89–109. [Google Scholar]
- Wassen, M.J.; Okruszko, T.; Kardel, I.; Chormanski, J.; Swiatek, D.; Mioduszewski, W.; Bleuten, W.; Querner, E.P.; El Kahloun, M.; Batelaan, O.; et al. Eco-Hydrological Functioning of the Biebrza Wetlands. In Wetlands: Functioning, Biodiversity Conservation, and Restoration SE—13; Bobbink, R., Beltman, B., Verhoeven, J.A., Whigham, D., Eds.; Ecological Studies; Springer: Berlin/Heidelberg, Germany, 2006; Volume 191, pp. 285–310. [Google Scholar]
- Chormański, J.; Batelaan, O. Application of the WetSpa Distributed Hydrological Model for Catchment with Significant Contribution of Organic Soil. Upper Biebrza Case Study. Ann. Wars. Univ. Life Sci. SGGW 2011, 43, 25–35. [Google Scholar]
- Chormański, J.; Berezowski, T.; Okruszko, T.; Ignar, S. Hydrography and Hydrology of the Upper Biebrza Basin. Contemp. Probl. Manag. Environ. Prot. 2011, 7, 175–203. [Google Scholar]
- Swiatek, D.; Chormanski, J. The Verification of the Numerical River Flow Model by Use of Remote Sensing. In Conference for Wetlands: Monitoring, Modelling and Management; CRC Press: Boca Raton, FL, USA, 2007; p. 173. [Google Scholar]
- De Doncker, L.; Troch, P.; Verhoeven, R.; Bal, K.; Meire, P.; Quintelier, J. Determination of the Manning Roughness Coefficient Influenced by Vegetation in the River Aa and Biebrza River. Environ. Fluid Mech. 2009, 9, 549–567. [Google Scholar] [CrossRef]
- Van Loon, A.H.; Schot, P.P.; Griffioen, J.; Bierkens, M.F.P.; Batelaan, O.; Wassen, M.J. Throughflow as a Determining Factor for Habitat Contiguity in a Near-Natural Fen. J. Hydrol. 2009, 379, 30–40. [Google Scholar] [CrossRef]
- Batelaan, O.; De Smedt, F. GIS-Based Recharge Estimation by Coupling Surface-Subsurface Water Balances. J. Hydrol. 2007, 337, 337–355. [Google Scholar] [CrossRef]
- Anibas, C.; Fleckenstein, J.H.; Volze, N.; Buis, K.; Verhoeven, R.; Meire, P.; Batelaan, O. Transient or Steady-State? Using Vertical Temperature Profiles to Quantify Groundwater-Surface Water Exchange. Hydrol. Process. 2009, 23, 2165–2177. [Google Scholar] [CrossRef]
- Turc, L. Estimation of Irrigation Water Requirements, Potential Evapotranspiration: A Simple Climatic Formula Evolved up to Date. Ann. Agron 1961, 12, 13–49. [Google Scholar]
- Christiansen, J.E. Pan Evaporation and Evapotranspiration from Climatic Data. J. Irrig. Drain. Div. 1968, 94, 243–266. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef] [Green Version]
- Campbell, D.I.; Williamson, J.L. Evaporation from a Raised Peat Bog. J. Hydrol. 1997, 193, 142–160. [Google Scholar] [CrossRef]
- Mallick, K.; Toivonen, E.; Trebs, I.; Boegh, E.; Cleverly, J.; Eamus, D.; Koivusalo, H.; Drewry, D.; Arndt, K.; Griebel, A.; et al. Bridging Thermal Infrared Sensing and Physically-Based Evapotranspiration Modeling: From Theoretical Implementation to Validation Across an Aridity Gradient in Australian Ecosystems. Water Resour. Res. 2018, 54, 3409–3435. [Google Scholar] [CrossRef] [Green Version]
- Mallick, K.; Trebs, I.; Boegh, E.; Giustarini, L.; Schlerf, M.; Drewry, D.; Hoffmann, L.; von Randow, C.; Kruijt, B.; Araùjo, A.; et al. Canopy-Scale Biophysical Controls of Transpiration and Evaporation in the Amazon Basin. Hydrol. Earth Syst. Sci. 2016, 20, 4237–4264. [Google Scholar] [CrossRef]
- Van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An Integrated Model of Soil-Canopy Spectral Radiances, Photosynthesis, Fluorescence, Temperature and Energy Balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Verhoef, W. Light Scattering by Leaf Layers with Application to Canopy Reflectance Modeling: The SAIL Model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the Leaf Optical Properties Model Separating Photosynthetic Pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Verhoef, W. Bayesian Optimisation Approach for Model Inversion of Hyperspectral—Multidirectional Observations: The Balance with A Priori Information. In Proceedings of the ISPRS 2007 10th International Symposium on Physical Measurements and Signatures Remote Sensing, Davos, Switzerland, 12–14 March 2017. [Google Scholar]
- Su, Z.; Schmugge, T.; Kustas, W.P.; Massman, W.J. An Evaluation of Two Models for Estimation of the Roughness Height for Heat Transfer between the Land Surface and the Atmosphere. J. Appl. Meteorol. 2001, 40, 1933–1951. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat Thermal Imagery in Monitoring Evapotranspiration and Managing Water Resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Verhoef, A.; McNaughton, K.G.; Jacobs, A.F.G. A Parameterization of Momentum Roughness Length and Displacement Height for a Wide Range of Canopy Densities. Hydrol. Earth Syst. Sci. 1997, 1, 81–91. [Google Scholar] [CrossRef]
- Faivre, R.; Colin, J.; Menenti, M. Evaluation of Methods for Aerodynamic Roughness Length Retrieval from Very High-Resolution Imaging LIDAR Observations over the Heihe Basin in China. Remote Sens. 2017, 9, 63. [Google Scholar] [CrossRef]
- Kanda, M.; Kanega, M.; Kawai, T.; Moriwaki, R.; Sugawara, H. Roughness Lengths for Momentum and Heat Derived from Outdoor Urban Scale Models. J. Appl. Meteorol. Clim. 2007, 46, 1067–1079. [Google Scholar] [CrossRef]
- Paul, G.; Gowda, P.; Prasad, P.V.V.; Howell, T.; Aiken, R.; Neale, C. Investigating the Influence of Roughness Length for Heat Transport (Zoh) on the Performance of SEBAL in Semi-Arid Irrigated and Dryland Agricultural Systems. J. Hydrol. 2013, 509, 231–244. [Google Scholar] [CrossRef]
- Rigden, A.; Li, D.; Salvucci, G. Dependence of Thermal Roughness Length on Friction Velocity across Land Cover Types: A Synthesis Analysis Using AmeriFlux Data. Agric. For. Meteorol. 2018, 249, 512–519. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Wood, E.F. Impact of Model Structure and Parameterization on Penman-Monteith Type Evaporation Models. J. Hydrol. 2015, 525, 521–535. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-Site Evaluation of Terrestrial Evaporation Models Using FLUXNET Data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.-L. How Sensitive Is SEBAL to Changes in Input Variables, Domain Size and Satellite Sensor? J. Geophys. Res. Atmos. 2011, 116, D21107. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. A Two-Source Trapezoid Model for Evapotranspiration (TTME) from Satellite Imagery. Remote Sens. Environ. 2012, 121, 370–388. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J. An Overview of the Use of the SimSphere Soil Vegetation Atmosphere Transfer (SVAT) Model for the Study of Land-Atmosphere Interactions. Sensors 2009, 9, 4286–4308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matheny, A.M.; Bohrer, G.; Stoy, P.C.; Baker, I.T.; Black, A.T.; Desai, A.R.; Dietze, M.C.; Gough, C.M.; Ivanov, V.Y.; Jassal, R.S.; et al. Characterizing the Diurnal Patterns of Errors in the Prediction of Evapotranspiration by Several Land-Surface Models: An NACP Analysis. J. Geophys. Res. Biogeosci. 2014, 119, 1458–1473. [Google Scholar] [CrossRef]
- Baldocchi, D.; Ma, S. How Will Land Use Affect Air Temperature in the Surface Boundary Layer? Lessons Learned from a Comparative Study on the Energy Balance of an Oak Savanna and Annual Grassland in California, USA. Tellus B Chem. Phys. Meteorol. 2013, 65, 19994. [Google Scholar] [CrossRef]
- Monteith, J.L. Accommodation between Transpiring Vegetation and the Convective Boundary Layer. J. Hydrol. 1995, 166, 251–263. [Google Scholar] [CrossRef]
- Bhattarai, N.; Mallick, K.; Brunsell, N.A.; Sun, G.; Jain, M. Regional Evapotranspiration from an Image-Based Implementation of the Surface Temperature Initiated Closure~(STIC1.2) Model and Its Validation across an Aridity Gradient in the Conterminous US. Hydrol. Earth Syst. Sci. 2018, 22, 2311–2341. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113 (Suppl. 1), S56–S66. [Google Scholar] [CrossRef]
- Wassen, M.J.; Barendregt, A.; Palczynski, A.; De Smidt, J.T.; De Mars, H. Hydro-Ecological Analysis of the Biebrza Mire (Poland). Wetl. Ecol. Manag. 1992, 2, 119–134. [Google Scholar] [CrossRef]
- Bootsma, M.C.; Wassen, M.J.; Jansen, A.J.M. The Biebrza-Valley as an Ecological Reference for Dutch Stream Valleys. Landscape 2000, 17, 113–117. [Google Scholar]
- Aber, J.D.; Melillo, J.M. Nitrogen Immobilization in Decaying Hardwood Leaf Litter as a Function of Initial Nitrogen and Lignin Content. Can. J. Bot. 1982, 60, 2263–2269. [Google Scholar] [CrossRef]
- Dawson, T.E.; Burgess, S.S.O.; Tu, K.P.; Oliveira, R.S.; Santiago, L.S.; Fisher, J.B.; Simonin, K.A.; Ambrose, A.R. Nighttime Transpiration in Woody Plants from Contrasting Ecosystems. Tree Physiol. 2007, 27, 561–575. [Google Scholar] [CrossRef] [PubMed]
- Chávez, J.L.; Neale, C.M.U.; Prueger, J.H.; Kustas, W.P. Daily Evapotranspiration Estimates from Extrapolating Instantaneous Airborne Remote Sensing ET Values. Irrig. Sci. 2008, 27, 67–81. [Google Scholar] [CrossRef]
- Donohue, R.J.; McVicar, T.R.; Roderick, M.L. Assessing the Ability of Potential Evaporation Formulations to Capture the Dynamics in Evaporative Demand within a Changing Climate. J. Hydrol. 2010, 386, 186–197. [Google Scholar] [CrossRef]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and Its Contribution to the Control of Photosynthesis under Different Environmental Conditions BT—Progress in Photosynthesis Research: Volume 4 Proceedings of the VIIth International Congress on Photosynthesis Providence; Biggins, J., Ed.; Springer: Dordrecht, The Netherlands, 1987; pp. 221–224. [Google Scholar]
- Bonan, G.; Williams, M.; Fisher, R.; Oleson, K. Modeling Stomatal Conductance in the Earth System: Linking Leaf Water-Use Efficiency and Water Transport along the Soil-plant-atmosphere Continuum. Geosci. Model Dev. 2014, 7, 2193. [Google Scholar] [CrossRef]
- Rogers, A.; Medlyn, B.E.; Dukes, J.S. Improving Representation of Photosynthesis in Earth System Models. New Phytol. 2014, 204, 12–14. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Anderegg, W.R.L.; Pacala, S.W. Optimal Stomatal Behavior with Competition for Water and Risk of Hydraulic Impairment. Proc. Natl. Acad. Sci. USA 2016, 113, E7222–E7230. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Domec, J.; Ward, E.J.; Duman, T.; Manoli, G.; Parolari, A.J.; Katul, G.G. The Effect of Plant Water Storage on Water Fluxes within the Coupled Soil-plant System. New Phytol. 2017, 213, 1093–1106. [Google Scholar] [CrossRef] [PubMed]
- Nikinmaa, E.; Hölttä, T.; Hari, P.; Kolari, P.; Mäkelä, A.; Sevanto, S.; Vesala, T. Assimilate Transport in Phloem Sets Conditions for Leaf Gas Exchange. Plant. Cell Environ. 2012, 36, 655–669. [Google Scholar] [CrossRef] [PubMed]
- Sperry, J.S.; Venturas, M.D.; Anderegg, W.R.L.; Mencuccini, M.; Mackay, D.S.; Wang, Y.; Love, D.M. Predicting Stomatal Responses to the Environment from the Optimization of Photosynthetic Gain and Hydraulic Cost. Plant. Cell Environ. 2016, 40, 816–830. [Google Scholar] [CrossRef] [PubMed]
- Timmermans, J.; Su, Z.; van der Tol, C.; Verhoef, A.; Verhoef, W. Quantifying the Uncertainty in Estimates of Surface-atmosphere Fluxes through Joint Evaluation of the SEBS and SCOPE Models. Hydrol. Earth Syst. Sci. 2013, 17, 1561–1573. [Google Scholar] [CrossRef]
- Prihodko, L.; Denning, A.S.; Hanan, N.P.; Baker, I.; Davis, K. Sensitivity, Uncertainty and Time Dependence of Parameters in a Complex Land Surface Model. Agric. For. Meteorol. 2008, 148, 268–287. [Google Scholar] [CrossRef]
- Meinzer, F.C.; Andrade, J.L.; Goldstein, G.; Holbrook, N.M.; Cavelier, J.; Jackson, P. Control of Transpiration from the Upper Canopy of a Tropical Forest: The Role of Stomatal, Boundary Layer and Hydraulic Architecture Components. Plant. Cell Environ. 2008, 20, 1242–1252. [Google Scholar] [CrossRef]
- Meinzer, F.C.; Hinckley, T.M.; Ceulemans, R. Apparent Responses of Stomata to Transpiration and Humidity in a Hybrid Poplar Canopy. Plant. Cell Environ. 2008, 20, 1301–1308. [Google Scholar] [CrossRef]
- Jarvis, P.G.; Mcnaughton, K. Stomatal Control of Transpiration: Scaling up from Leaf to Region. Adv. Ecol. Res. 1986, 15, 1–49. [Google Scholar]
- Van Dijk, A.I.J.M.; Gash, J.H.; van Gorsel, E.; Blanken, P.D.; Cescatti, A.; Emmel, C.; Gielen, B.; Harman, I.N.; Kiely, G.; Merbold, L.; et al. Rainfall Interception and the Coupled Surface Water and Energy Balance. Agric. For. Meteorol. 2015, 214–215, 402–415. [Google Scholar] [CrossRef]
- Holwerda, F.; Bruijnzeel, L.A.; Scatena, F.N.; Vugts, H.F.; Meesters, A.G.C.A. Wet Canopy Evaporation from a Puerto Rican Lower Montane Rain Forest: The Importance of Realistically Estimated Aerodynamic Conductance. J. Hydrol. 2012, 414–415, 1–15. [Google Scholar] [CrossRef]
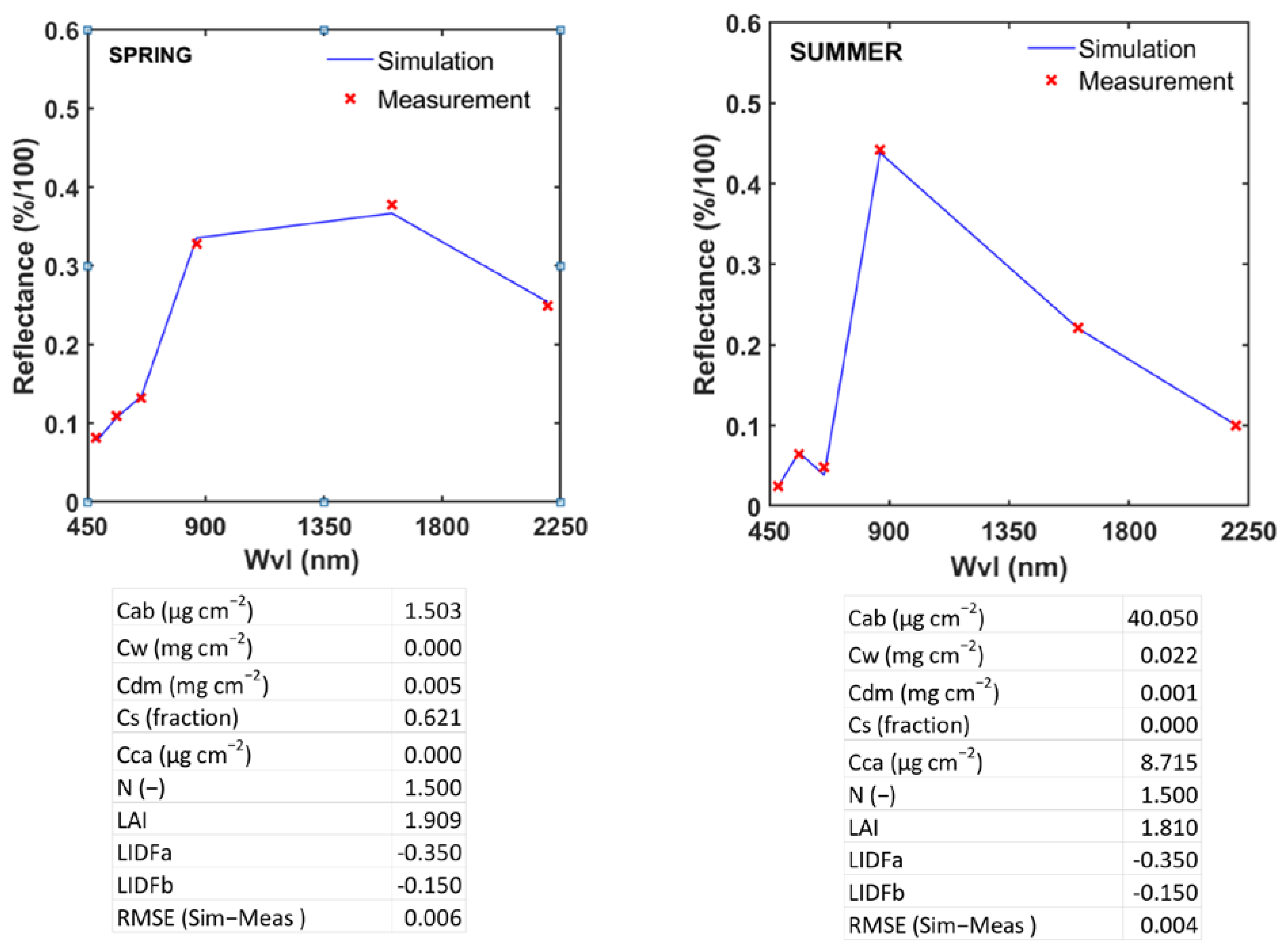








| SEB Model | Feature | Inputs | Outputs | Surface Parameterization | |
|---|---|---|---|---|---|
| Meteo | Leaf/Canopy | ||||
| STIC 1.2 [57,77] | Single source | TA, TD, RSin, RSout | gA, gS, T0, λr, M, H, λE | Analytically computes gA and gS | |
| Derivative of PM-WS | G, φ, Ts | Calibration free estimates of conductances | |||
| Integrates Ts into PM | |||||
| λE directly estimated from SEB | |||||
| SEBS [19] | Single source | TA, TD, RSin, RSout, | h, fc, z0H, z0M, d0 | gA, λr, kB−1, H, λE | Assumes Ts and T0 are equal |
| Uses MOST to solve for H | G, φ, TS | NDVI, LAI | Assumes kB−1 adjusts the inequality between the | ||
| Scales H between hypothetical | pa, u | roughness lengths of momentum and heat transfers | |||
| wet and dry limit | |||||
| Estimates λE as a residual component of SEB | |||||
| SCOPE 1.7 [58] | Multi source | TA, eA, RSin, RLin | PROSPECT [78] inputs | gA, gS(leaf), H, G, λE | Computes gA at (inertial, roughness and canopy) |
| Computes gS at leaf level | |||||
| Applies SVAT principle | pa, u | Vcmo, m, | RN, RSout, u* | ||
| Flux transfer based on K-theory | hc, LAI, LDFa, LIDFb, LW | ||||
| [23] | Soil thermal properties, SMC | ||||
| z0H, z0M, d0 | |||||
| rbs, rss, rwc | |||||
| VZA, RAA, SZA |
| Full Season | Spring | Summer | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Model | R2 | Slope | Intercept | RMSE, W m−2 | MAPD, % | MB W m−2 | R2 | Slope | Intercept | RMSE, W m−2 | MAPD, % | MB, W m−2 | R2 | Slope | Intercept | RMSE, W m−2 | MAPD, % | MB, W m−2 |
| 2015 | SCOPE1.7 | 0.8 | 1.06 | 16 | 52 | 32 | 23 | 0.81 | 1.05 | 16 | 49 | 32 | 22 | 0.74 | 1.07 | 15 | 64 | 32 | 25 |
| SEBS | 0.67 | 0.84 | −3 | 75 | 40 | −51 | 0.62 | 0.73 | −21 | 80 | 46 | −57 | 0.8 | 1.06 | −43 | 55 | 24 | −33 | |
| STIC1.2 | 0.91 | 0.91 | −2 | 29 | 18 | −13 | 0.92 | 0.89 | −1 | 28 | 19 | −13 | 0.9 | 0.96 | −3 | 30 | 15 | −10 | |
| 2016 | SCOPE1.7 | 0.91 | 1.08 | 5 | 37 | 22 | 14 | 0.9 | 1.09 | 6 | 38 | 23 | 15 | 0.96 | 1.08 | −11 | 21 | 12 | −0 |
| SEBS | 0.8 | 0.91 | −30 | 62 | 33 | −43 | 0.79 | 0.91 | −30 | 62 | 33 | −42 | 0.83 | 0.87 | −28 | 61 | 32 | −50 | |
| STIC1.2 | 0.92 | 0.88 | 1 | 31 | 19 | −13 | 0.92 | 0.89 | 1 | 30 | 19 | −12 | 0.94 | 0.84 | 0 | 34 | 19 | −23 | |
| Year | Model | R2 | RMSE (mm day−1) | MAPD (%) | MB (mm day−1) |
|---|---|---|---|---|---|
| 2015 | SCOPE1.7 | 0.87 | 0.89 | 38 | 0.67 |
| SEBS | 0.75 | 0.95 | 40 | −0.68 | |
| STIC1.2 | 0.92 | 0.37 | 16 | −0.05 | |
| 2016 | SCOPE1.7 | 0.95 | 0.92 | 44 | 0.79 |
| SEBS | 0.80 | 0.74 | 33 | −0.46 | |
| STIC1.2 | 0.89 | 0.46 | 21 | −0.14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallick, K.; Wandera, L.; Bhattarai, N.; Hostache, R.; Kleniewska, M.; Chormanski, J. A Critical Evaluation on the Role of Aerodynamic and Canopy–Surface Conductance Parameterization in SEB and SVAT Models for Simulating Evapotranspiration: A Case Study in the Upper Biebrza National Park Wetland in Poland. Water 2018, 10, 1753. https://doi.org/10.3390/w10121753
Mallick K, Wandera L, Bhattarai N, Hostache R, Kleniewska M, Chormanski J. A Critical Evaluation on the Role of Aerodynamic and Canopy–Surface Conductance Parameterization in SEB and SVAT Models for Simulating Evapotranspiration: A Case Study in the Upper Biebrza National Park Wetland in Poland. Water. 2018; 10(12):1753. https://doi.org/10.3390/w10121753
Chicago/Turabian StyleMallick, Kaniska, Loise Wandera, Nishan Bhattarai, Renaud Hostache, Malgorzata Kleniewska, and Jaroslaw Chormanski. 2018. "A Critical Evaluation on the Role of Aerodynamic and Canopy–Surface Conductance Parameterization in SEB and SVAT Models for Simulating Evapotranspiration: A Case Study in the Upper Biebrza National Park Wetland in Poland" Water 10, no. 12: 1753. https://doi.org/10.3390/w10121753
APA StyleMallick, K., Wandera, L., Bhattarai, N., Hostache, R., Kleniewska, M., & Chormanski, J. (2018). A Critical Evaluation on the Role of Aerodynamic and Canopy–Surface Conductance Parameterization in SEB and SVAT Models for Simulating Evapotranspiration: A Case Study in the Upper Biebrza National Park Wetland in Poland. Water, 10(12), 1753. https://doi.org/10.3390/w10121753






