Flume Test Simulation and Study of Salt and Fresh Water Mixing Influenced by Tidal Reciprocating Flow
Abstract
:1. Introduction
2. Materials and Methods
2.1. Flume Layout and Brine Treatment
2.2. Data Acquisition
2.2.1. Flow Velocity Data Acquisition
2.2.2. Salinity Data Acquisition
2.2.3. Other Data Acquisition
2.3. Test Repeatability
- Velocity repeatability test: 12 min was taken as a tidal cycle and the velocity repeatability under the conditions of several cycles on the same day, the same input conditions on different dates and different flow measurement equipment at the same measuring points were verified.
- Buoy displacement test: A buoy was placed on the water surface at a certain interval to record the limit position that the buoy reached in each tidal cycle. The results showed that the drift range of the buoy tended to be stable.
- Salty boundary repeatability test: The position of the salt boundary was recorded at set intervals. The results showed that the change of the salt boundary at the quasi-steady state tended to be within a certain range.
- Wedge thickness repeatability: Near the upstream, the brine intruded in a wedge shape. The video records showed that the wedge thickness and water depth at any time were almost constant after a tidal cycle.
- Salinity repeatability: The salinity of the same section in each layer was measured for two consecutive cycles. The repeatability of both the salinity of each layer and the depth averaged salinity must meet the test requirements.
2.4. Test Conditions
3. Results
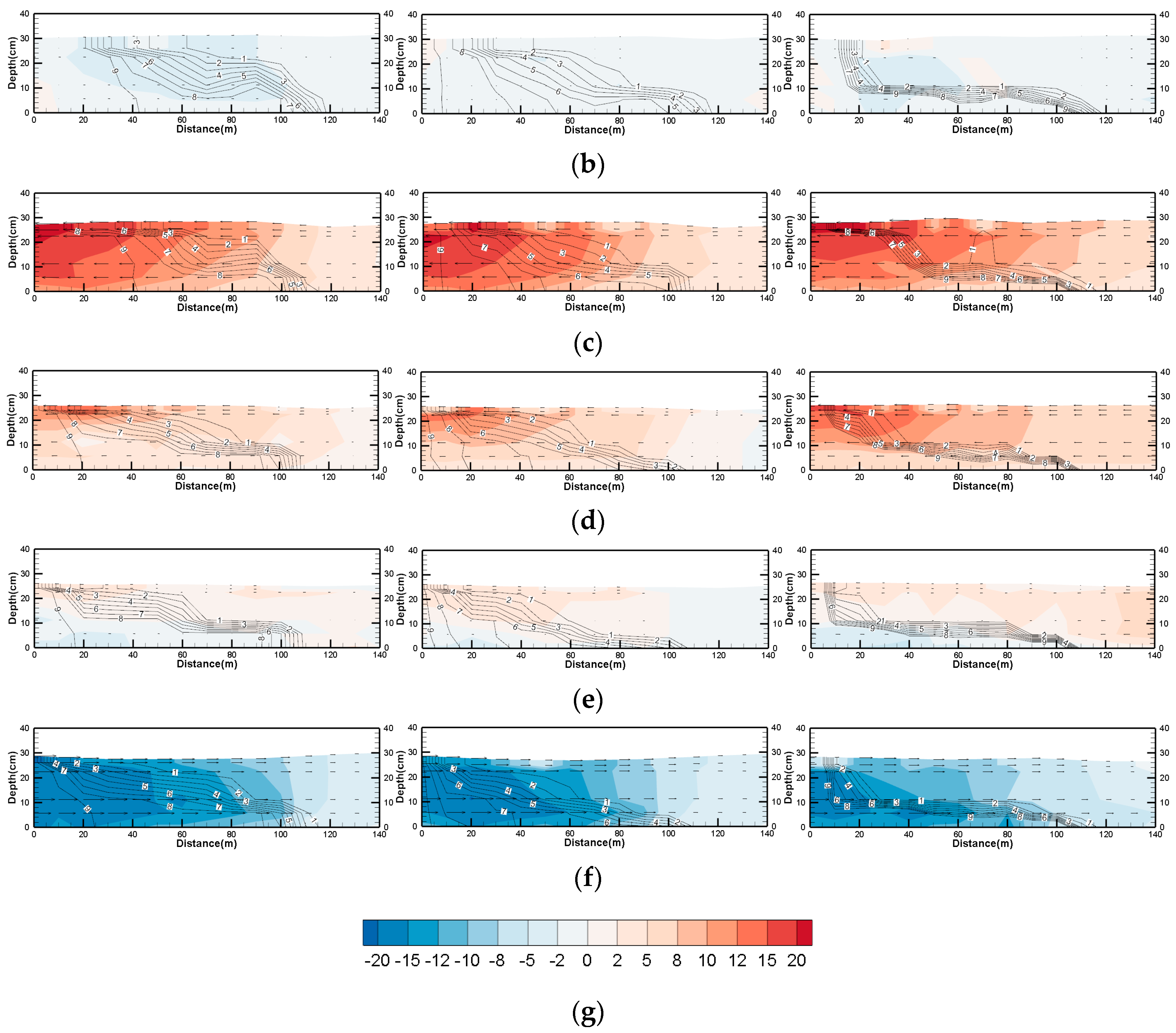
3.1. Influence of Tidal Range on the Mixed Type of Salt-Fresh Water
3.2. Influence of Runoff on the Mixed Type of Salt-Fresh Water
3.3. Change of Salt-Fresh Water Interface in the Condition of Tidal Reciprocating Flow
4. Discussion
4.1. Improvement of Flume Test Technology
4.2. Characteristics of Gravitational Circulation and Residual Circulation
4.2.1. Circulation Characteristics under Tidal Range Change
4.2.2. Circulation Characteristics under Runoff Change
4.3. Analysis of Salt-fresh Water Interface Stability
5. Conclusions
- The salt-fresh water mixing under the reciprocating tidal flow was successfully reproduced through the tide and runoff control systems at both ends of the flume, which realized the simulation of the partially mixed type and highly stratified type of salt-fresh water in estuaries. The research scope of the current flume test was expanded by improving the length of the straight segment of the flume. The laboratory pollution problem was effectively solved by developing the preparation, recycling and recovery system of experimental water. The simulation technique was improved by developing the synchronous, multi-section, multi-layer sampling system.
- The flume experiment was carried out by using the control variable method. Under the combined action of runoff and tidal current, the characteristics of salt-fresh water mixing showed obvious differences in different segments. It is roughly divided into three segments upstream from the entrance. The salt-fresh water mixing in the first segment reflected the obvious characteristics of fully mixed type. The second segment presented the remarkable characteristics of partial mixed type. In addition, the salt-fresh water was significantly stratified in the third segment where the saltwater wedge intruded. The distribution range of these three segments varied greatly with the flood and ebb tide, but was consistent in terms of the order.
- Based on the dynamic-state and steady-state, the influence of tidal range and runoff volume on the velocity and salinity distribution in the area of salt-fresh water mixing has been analyzed dialectically. And the contradictory effect of tide and runoff on changing mixing type has been considered respectively.The contradictory effect of tide: tidal stirring and tidal straining. The longitudinal dispersion of salinity caused by tidal straining will lead to the uneven vertical distribution of salinity, thus inhibiting the mixing, which is the opposite effect caused by tidal stirring. During the period of flood tide, the tidal stirring effect is more dominant than the tidal straining effect, while they lead to the fully mixed trend of salt and fresh water jointly. During the period of ebb tide, the tidal straining effect plays a more important role and the tidal stirring effect is inhibited, while the salt-fresh water shows the trend of stratification.The contradictory effect of runoff: stabilizing the stratification and breaking the stratification. The increase of runoff volume can not only stabilize the stratification by strengthening the gravitational circulation and maintaining the vertical density gradient of salt-fresh water interface, but also break the stratification by enhancing the ebb current and weakening the flood current in the upper layer to increase the velocity shear near the interface until it exceeds the critical value. The balance of these two contradictory effects is not only the balance of vertical density gradient and velocity shear, but also the balance of longitudinal convection transport and vertical diffusion.
- The stability of salt-fresh water interface under the condition of tidal reciprocating flow has been studied experimentally, and the periodic transition between stability and instability of the interface has been investigated. The interface stability is closely related to the vertical gradient of the density and velocity near the interface. The Keulegan number (Θ) has been employed in the quantitative analysis on the stability of interface. The experimental results show that, under the condition of turbulent flow, when Θ ≥ 0.152, the interface is stable; when 0.112 ≤ Θ < 0.152, the interface is instable and shows the K-H instability; When Θ < 0.112, the interface is broken. As a result, the critical value Θc of interface stabilization is 0.152.
6. Patents
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Hoang, L.P.; van Vliet, M.T.H.; Kummu, M.; Lauri, H.; Koponen, J.; Supit, I.; Leemans, R.; Kabat, P.; Ludwig, F. The Mekong’s future flows under multiple drivers: How climate change, hydropower developments and irrigation expansions drive hydrological changes. Sci. Total Environ. 2019, 649, 601–609. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Zhang, J.; Yu, X.; Chen, S.; Luo, J. Effect of Runoff Variability and Sea Level on Saltwater Intrusion: A Case Study of Nandu River Estuary, China. Water Resour. Res. 2018, 54, 9919–9934. [Google Scholar] [CrossRef]
- Thomson, D.M.; Shaffer, G.P.; McCorquodale, J.A. A potential interaction between sea-level rise and global warming: Implications for coastal stability on the Mississippi River Deltaic Plain. Glob. Planet. Chang. 2001, 32, 49–59. [Google Scholar] [CrossRef]
- Prasad, K.V.S.R.; Sridevi, T.; Sadhuram, Y. Influence of Dam-Controlled River Discharge and Tides on Salinity Intrusion in the Godavari Estuary, East Coast of India. J. Waterw. Port Coast. Ocean Eng. 2018, 144, 04017049. [Google Scholar] [CrossRef]
- He, W.; Zhu, L.; Hu, J. Impact of Lingding Navigation Channel on Fresh Salt-Water Mixing in Dry Season. J. South China Univ. Technol. Nat. Sci. Ed. 2017, 45, 138–144. [Google Scholar]
- Dang, C.; Morrissey, E.M.; Neubauer, S.C.; Franklin, R.B. Novel microbial community composition and carbon biogeochemistry emerge over time following saltwater intrusion in wetlands. Glob. Chang. Boil. 2019, 25, 549–561. [Google Scholar] [CrossRef]
- Wilson, B.J.; Servais, S.; Mazzei, V.; Kominoski, J.S.; Hu, M.; Davis, S.E.; Gaiser, E.; Sklar, F.; Bauman, L.; Kelly, S.; et al. Salinity pulses interact with seasonal dry-down to increase ecosystem carbon loss in marshes of the Florida Everglades. Ecol. Appl. 2018, 28, 2092–2108. [Google Scholar] [CrossRef]
- Van Ael, E.; Covaci, A.; Das, K.; Lepoint, G.; Blust, R.; Bervoets, L. Factors Influencing the Bioaccumulation of Persistent Organic Pollutants in Food Webs of the Scheldt Estuary. Environ. Sci. Technol. 2013, 47, 11221–11231. [Google Scholar] [CrossRef]
- Camilo Restrepo, J.; Schrottke, K.; Traini, C.; Bartholomae, A.; Ospino, S.; Carlos Ortiz, J.; Otero, L.; Orejarena, A. Estuarine and sediment dynamics in a microtidal tropical estuary of high fluvial discharge: Magdalena River (Colombia, South America). Mar. Geol. 2018, 398, 86–98. [Google Scholar] [CrossRef]
- Dyer, K.R. Estuaries: A Physical Introduction; John Wiley & Sons: London, UK, 1973. [Google Scholar]
- Maccready, P.; Geyer, W.R. Advances in estuarine physics. Ann. Rev. Mar. Sci. 2010, 2, 35–58. [Google Scholar] [CrossRef]
- Fan, J.H.; Chen, S.Q. Estuarine saltwater wedge and sediment deposition. Pearl River 1995, 25–29. [Google Scholar]
- Keulegan, G.H. Interfacial instability and mixing in stratified flows. J. Res. Natl. Bur. Stand. 1949, 43, 487–500. [Google Scholar] [CrossRef]
- Schijf, J.B.; Schönfled, J.C. Theoretical considerations on the motion of salt and fresh water. In Proceedings of the Minnesota International Hydraulic Convention, Minneapolis, MN, USA, 1–4 September 1953; pp. 321–333. [Google Scholar]
- Tan, W.Y. Review on investigation into laws of motion for saline wedges. Adv. Water Sci. 1994, 5, 149–159. [Google Scholar]
- Ippen, A.T.; Harleman, D.R.F. One-Dimensional Analysis of Salinity Intrusion in Estuaries; Committee on Tidal Hydraulics: Vicksburg, MS, USA, 1961. [Google Scholar]
- Arons, A.B.; Stommel, H. A mixing-length theory of tidal flushing. Trans. Am. Geophys. Union 1951, 32, 419–421. [Google Scholar] [CrossRef]
- Hansen, D.V.; Rattray, M. New Dimensions in Estuary Classification. Limnol. Oceanogr. 1966, 11, 319–326. [Google Scholar] [CrossRef]
- Pritchard, D.W. The dynamic structure of a coastal plain estuary. J. Mar. Res. 1956, 15, 33–42. [Google Scholar]
- Lerczak, J.A.; Geyer, W.R.; Chant, R.J. Mechanisms driving the time-dependent salt flux in a partially stratified estuary. J. Phys. Oceanogr. 2006, 36, 2296–2311. [Google Scholar] [CrossRef]
- Prandle, D. Saline intrusion in partially mixed estuaries. Estuar. Coast. Shelf Sci. 2004, 59, 385–397. [Google Scholar] [CrossRef]
- Harleman, D.R.F.; Ippen, A.T.; Han, N.B. Effects of saltwater intrusion on estuary deposition. Hydro-Sci. Eng. 1973, 8–23. [Google Scholar]
- Van Rees, A.J. Flume Study on Salinity Intrusion in Estuaries (X): Systematic Investigation Variations in Boundary Conditions and Flow Regime; Delft Hydraulics Laboratory: Delft, The Netherlands, 1970. [Google Scholar]
- Dermissis, V.; Partheniades, E. Dominant Shear Stresses in Arrested Saline Wedges. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 733–752. [Google Scholar] [CrossRef]
- Dermissis, V.; Partheniades, E. Interfacial Resistance in Stratified Flows. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 231–250. [Google Scholar] [CrossRef]
- Sargent, F.E.; Jirka, G.H. Experiments on Saline Wedge. J. Hydraul. Eng. 1987, 113, 1307–1323. [Google Scholar] [CrossRef]
- Lu, X.X. Model experiment on saltwater intrusion of the qiantang river estuary. Hydro-Sci. Eng. 1991, 3, 403–410. [Google Scholar]
- Su, B. Saltwater Intrusion and Salt-Suppression Technique in Modaomen Waterway; China Water & Power Press: Beijing, China, 2013. [Google Scholar]
- Lu, C.; Yuan, L.; Gao, S.; Chen, R.; Su, B. Experimental study on the relationship between tide strength and salt intrusion length. Adv. Water Sci. 2013, 24, 251–257. [Google Scholar]
- Zhang, Z.K. The Experimental Study and Numerical Simulation of the Salt-Water Intrusion in Estuary; Taiyuan University of Technology: Taiyuan, China, 2011. [Google Scholar]
- He, Z.; Lin, T.; Zhao, L.; Lin, Y.; Hu, P.; Ran, Q.; He, H. Experiments on gravity currents down a ramp in unstratified and linearly stratified salt water environments. Sci. Sin. Technol. 2016, 46, 570–578. [Google Scholar]
- Shen, H.T.; Zhu, J.R.; Wu, H.L. The Interaction Interface between Land and Sea in the Yangtze River Estuary; China Ocean Press: Beijing, China, 2008. [Google Scholar]
- Zhao, J.S. Coastal and Estuary Dynamics; China Ocean Press: Beijing, China, 1993. [Google Scholar]
- Simpson, J.H.; Brown, J.; Matthews, J.; Allen, G. Tidal straining, density currents, and stirring in the control of estuarine stratification. Estuaries 1990, 13, 125–132. [Google Scholar] [CrossRef]
- McCutcheon, S.C.; Liu, Z.G.; Wang, J.J. Vertical velocity distribution of stratified flow. Water Resour. Hydropower Northeast. China 1987, 51–55. [Google Scholar]
- Pritchard, D.W. Estuarine Hydrography. Adv. Geophys. 1952, 1, 243–280. [Google Scholar] [CrossRef]
- Blumberg, A.F. The influence of density variations on estuarine tides and circulations. Estuar. Coast. Mar. Sci. 1978, 6, 209–215. [Google Scholar] [CrossRef]
- MacCready, P. Estuarine adjustment to changes in river flow and tidal mixing. J. Phys. Oceanogr. 1999, 29, 708–726. [Google Scholar] [CrossRef]
- Ellison, T.H.; Turner, J.S. Turbulent entrainment in stratified flows. J. Fluid Mech. 1959, 6, 423–448. [Google Scholar] [CrossRef]
- Cotel, A.J. A review of recent developments on turbulent entrainment in stratified flows. Phys. Scr. 2010, T142, 014044. [Google Scholar] [CrossRef]
- Samothrakis, P.; Cotel, A.J. Propagation of a gravity current in a two-layer stratified environment. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- He, Z.; Zhao, L.; Lin, T.; Hu, P.; Lv, Y.; Ho, H.-C.; Lin, Y.-T. Hydrodynamics of Gravity Currents down a Ramp in Linearly Stratified Environments. J. Hydraul. Eng. 2016, 143, 04016085. [Google Scholar] [CrossRef]
- Yih, C.S. Solitary waves in stratified fluids and their interaction. Acta Mech. Sin. 1993, 9, 193–209. [Google Scholar] [CrossRef]
- Yu, C.Z. Introduction to Environmental Fluid Mechanics; Tsinghua University Press: Beijing, China, 1992. [Google Scholar]














| Case | Tidal Range (cm) | Runoff (m3/h) | Average Depth (cm) | Initial Salinity | Water Temperature (°C) |
|---|---|---|---|---|---|
| 1 | 4 | 3 | 35 | 10.1 | 9.9 |
| 2 | 2 | 3 | 35 | 9.5 | 9.7 |
| Case | Tidal Range (cm) | Runoff (m3/h) | Average Depth (cm) | Initial Salinity | Water Temperature (°C) |
|---|---|---|---|---|---|
| 3 | 4 | 0 | 28 | 10.1 | 10.4 |
| 4 | 4 | 3 | 28 | 9.4 | 9.6 |
| 5 | 4 | 11 | 28 | 18.8 | 10.8 |
| Time Sequence (s) | Depth (cm) | Thickness of Upper Layer (cm) | Interface State | Quantity of Wave Peaks within 50 cm Length | Wave Speed (cm/s) | Riw | Re | Frw | Θ |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 29.4 | 6.1 | Steady | \ | \ | 9.47 | 666 | 0.32 | 0.243 |
| 57 | 29.7 | 5.5 | Steady | \ | \ | 12.31 | 691 | 0.29 | 0.262 |
| 90 | 30.0 | 6.8 | K-H wave | 4.5 | 8.80 | 2.92 | 1056 | 0.59 | 0.140 |
| 134 | 29.0 | 7.0 | K-H wave | 5 | 11.63 | 2.55 | 1352 | 0.63 | 0.124 |
| 181 | 28.8 | 8.3 | K-H wave | 5 | 14.08 | 4.50 | 1826 | 0.47 | 0.135 |
| 193 | 28.8 | 8.3 | Broken | A large number | 14.97 | 2.82 | 2307 | 0.60 | 0.107 |
| 242 | 27.5 | 9.5 | Broken | A large number | 10.94 | 3.20 | 2492 | 0.56 | 0.109 |
| 447 | 25.5 | 13.0 | K-H wave | 3 | 4.11 | 6.56 | 2530 | 0.39 | 0.138 |
| 550 | 26.5 | 12.0 | K-H wave | 6 | 8.33 | 5.11 | 2438 | 0.44 | 0.128 |
| 577 | 27.0 | 12.0 | K-H wave | 5 | 9.67 | 5.36 | 2533 | 0.43 | 0.129 |
| 687 | 28.8 | 6.8 | Steady | \ | \ | 10.30 | 948 | 0.31 | 0.222 |
| 691 | 28.8 | 6.6 | Steady | \ | \ | 4.98 | 1305 | 0.45 | 0.157 |
| Time Sequence (s) | Depth (cm) | Thickness of Upper Layer (cm) | Interface State | Quantity of Wave Peaks within 50 cm Length | Wave Speed (cm/s) | Riw | Re | Frw | Θ |
|---|---|---|---|---|---|---|---|---|---|
| 40 | 30.5 | 9.5 | Steady | \ | \ | 6.78 | 1813 | 0.38 | 0.155 |
| 62 | 30.5 | 8.5 | Steady | \ | \ | 9.56 | 1336 | 0.32 | 0.193 |
| 95 | 29.9 | 7.9 | Steady | \ | \ | 5.66 | 1635 | 0.42 | 0.152 |
| 114 | 29.5 | 8.0 | K-H wave | 4 | 9.16 | 2.75 | 1812 | 0.60 | 0.115 |
| 135 | 29.5 | 8.5 | K-H wave | 4 | 10.75 | 3.06 | 2006 | 0.57 | 0.115 |
| 173 | 29.3 | 9.3 | K-H wave | 4 | 10.94 | 3.27 | 2345 | 0.55 | 0.112 |
| 185 | 29.1 | 10.1 | Broken | A large number | 10.71 | 1.58 | 3695 | 0.79 | 0.076 |
| 216 | 28.6 | 16.6 | Broken | A large number | 9.65 | 3.89 | 3941 | 0.51 | 0.100 |
| 263 | 27.5 | 15.5 | Broken | A large number | 8.91 | 4.12 | 3165 | 0.49 | 0.109 |
| 353 | 26.2 | 14.2 | Broken | A large number | 7.60 | 3.55 | 3814 | 0.53 | 0.098 |
| 377 | 26.0 | 14.0 | K-H wave | 7 | 7.40 | 7.22 | 2597 | 0.37 | 0.141 |
| 412 | 25.9 | 13.9 | K-H wave | 6 | 5.86 | 5.92 | 2654 | 0.41 | 0.131 |
| 466 | 26.0 | 14.0 | Standing wave | A large number | \ | 1.74 | 4205 | 0.76 | 0.075 |
| 485 | 26.0 | 14.0 | Broken | A large number | 4.67 | 1.72 | 4023 | 0.76 | 0.075 |
| 515 | 26.3 | 14.3 | K-H wave | 7.5 | 8.28 | 4.60 | 2522 | 0.47 | 0.122 |
| 552 | 27.0 | 15.0 | Broken | A large number | 12.79 | 1.58 | 4792 | 0.80 | 0.069 |
| 591 | 27.3 | 15.3 | Broken | A large number | 14.25 | 3.21 | 3990 | 0.56 | 0.093 |
| 618 | 28.0 | 16.0 | Broken | A large number | 10.62 | 4.05 | 3877 | 0.50 | 0.102 |
| 704 | 29.6 | 14.6 | Steady | \ | \ | 9.27 | 1867 | 0.33 | 0.171 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, W.; Zhao, X.; Zhao, R.; Zhang, X. Flume Test Simulation and Study of Salt and Fresh Water Mixing Influenced by Tidal Reciprocating Flow. Water 2019, 11, 584. https://doi.org/10.3390/w11030584
Xia W, Zhao X, Zhao R, Zhang X. Flume Test Simulation and Study of Salt and Fresh Water Mixing Influenced by Tidal Reciprocating Flow. Water. 2019; 11(3):584. https://doi.org/10.3390/w11030584
Chicago/Turabian StyleXia, Weiyi, Xiaodong Zhao, Riming Zhao, and Xinzhou Zhang. 2019. "Flume Test Simulation and Study of Salt and Fresh Water Mixing Influenced by Tidal Reciprocating Flow" Water 11, no. 3: 584. https://doi.org/10.3390/w11030584
APA StyleXia, W., Zhao, X., Zhao, R., & Zhang, X. (2019). Flume Test Simulation and Study of Salt and Fresh Water Mixing Influenced by Tidal Reciprocating Flow. Water, 11(3), 584. https://doi.org/10.3390/w11030584




