Sensitivity Analysis on the Rising Relation between Short-Term Rainfall and Groundwater Table Adjacent to an Artificial Recharge Lake
Abstract
:1. Introduction
2. Materials and Methods
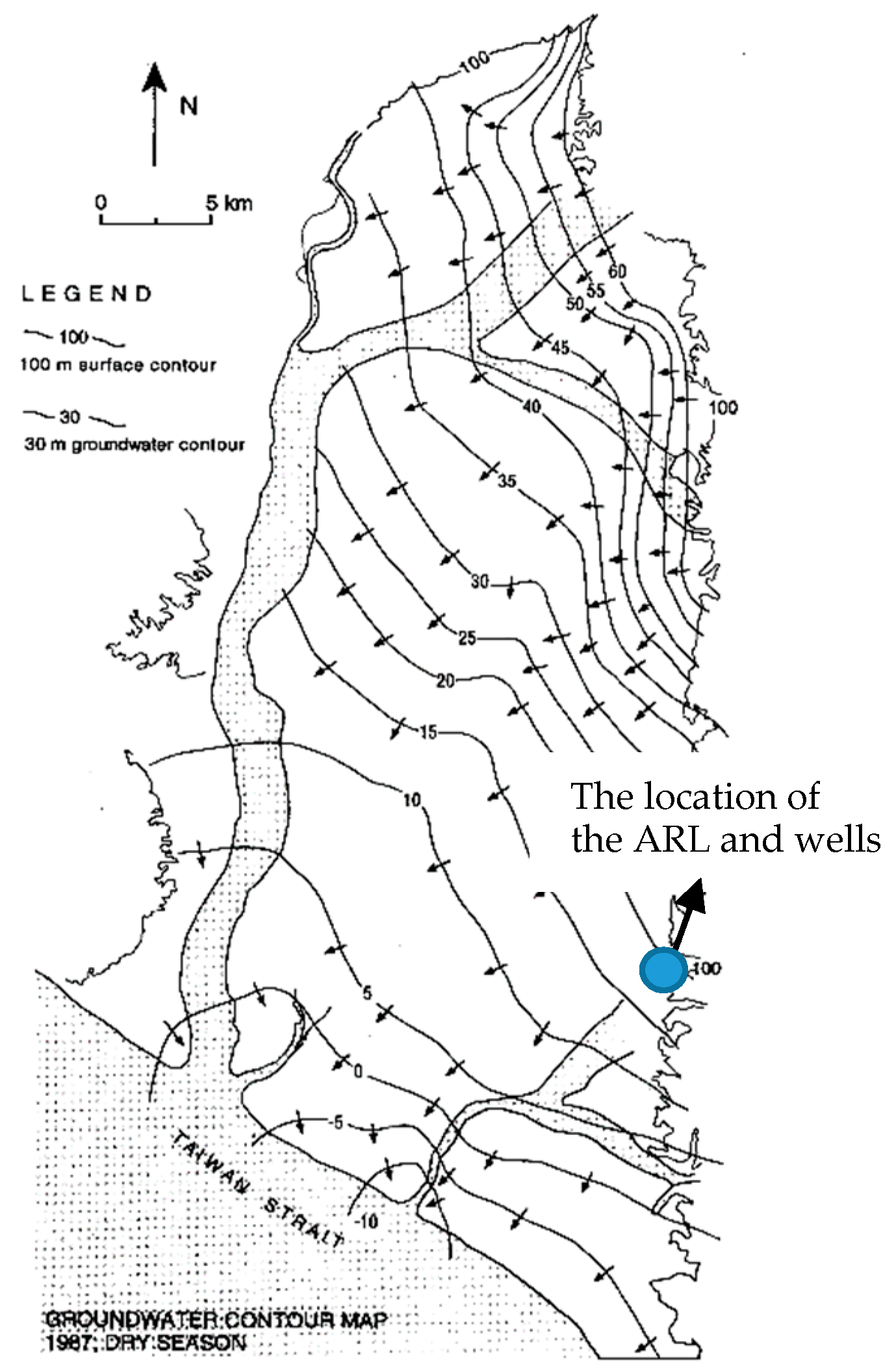
2.1. Study Area
2.2. Data Collection and Process
2.2.1. Rainfall Data
2.2.2. Groundwater Data
2.2.3. Data Normalization
2.3. Artificial Neural Network (ANN)
2.4. Sensitivity Analysis (SA)
3. Results
3.1. ANN Results
3.2. SA Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peng, T.R.; Lu, W.C.; Chen, K.Y.; Zhan, W.J.; Liu, T.K. Groundwater-recharge connectivity between a hills-and-plains’ area of western Taiwan using water isotopes and electrical conductivity. J. Hydrol. 2014, 517, 226–235. [Google Scholar] [CrossRef]
- Wang, C.H.; Kuo, C.H.; Chang, F.C. The Changing Face of the Groundwater Environment in Taiwan. Bull. Cent. Geol. Surv. 2004, 17, 1–22. [Google Scholar]
- T.W.R.A. Taiwan Water Usage Annual Report; Taiwan Water Resources Agency, Ministry of Economic Affairs: Taipei, Taiwan, 2017; p. A-14.
- T.W.R.A. Taiwan Groundwater Withdrawal and Pumping. Available online: https://www.wra.gov.tw/6950/7170/7356/7488/13319 (accessed on 14 July 2019).
- Liao, F.L. Using Artificial Neural Network for Estimating the Effects on Groundwater from Artificial Recharge or Rainfall. National Pingtung University of Science and Technology: Pingtung County, Taiwan, 2017. [Google Scholar]
- T.P.W.C.B. Compilation and Analysis of Existing Groundwater and Subsidence Data of Taiwan II–the Pingtung Plain; Ministry of Economic Affairs: Taipei, Taiwan, 1994.
- T.P.W.C.B. Study on the Improvement of the Groundwater Monitoring System in the Pingtung Plain; Ministry of Economic Affairs: Taipei, Taiwan, 1998.
- Ineson, J. Hydrogeological and Groundwater Aspects of Artificial Recharge. In Proceedings of the Artificial Groundwater Recharge Conference, England, UK, 21–24 September 1970; pp. 1–14. [Google Scholar]
- Muckel, D. Artificial Recharge in Relation to Groundwater Storage. In Proceedings of the Annual Conference on Water for Texas, College Station, TX, USA, 16–18 September 1958; pp. 85–94. [Google Scholar]
- Walton, W.C. Groundwater Resource Evaluation. In McGraw-Hill Series in Water Resources and Environmental Engineering (USA) eng; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Govindaraju, R. Laboratory investigation on the role of slope on infiltration over grassy soils. J. Hydrol. 2016, 543, 542–547. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R. A New Conceptual Model for Slope-Infiltration. Water 2019, 11, 678. [Google Scholar] [CrossRef]
- Chen, C.T.; Chen, L.S.; Huang, J.Y.; Huang, S.J. A Study on Ground Water Level Forecasting by Combining Neural Networks and Semi-variogram Model. J. Taiwan Agric. Eng. 2015, 61, 14–28. [Google Scholar] [CrossRef]
- Coppola, E.A., Jr.; Rana, A.J.; Poulton, M.M.; Szidarovszky, F.; Uhl, V.W. A neural network model for predicting aquifer water level elevations. Groundwater 2005, 43, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.-L.; Lin, Y.-C. Analysis of space–time non-stationary patterns of rainfall–groundwater interactions by integrating empirical orthogonal function and cross wavelet transform methods. J.Hydrol. 2015, 525, 585–597. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Nayak, P.C.; Rao, Y.S.; Sudheer, K. Groundwater level forecasting in a shallow aquifer using artificial neural network approach. Water Resour. Manag. 2006, 20, 77–90. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Liu, L.W.; Hsieh, S.H.; Chung, W.G.; Wang, Y.M. Sensitivity Analysis on the Rising Relation of Short-term Rainfall and Unconfined Aquifer Groundwater Table. In Proceedings of the 2017 4th International Conference on Coastal and Ocean Engineering (ICCOE 2017), Osaka, Japan, 29 March 2017; p. 64. [Google Scholar]
- Jha, M.K.; Sahoo, S. Efficacy of neural network and genetic algorithm techniques in simulating spatio-temporal fluctuations of groundwater. Hydrol. Process. 2015, 29, 671–691. [Google Scholar] [CrossRef]
- Ahlawat, R. Hydrological Data Network Modelling Using Artificial Neural Network in Betwa Catchment. Int. J. Soft Comput. Eng. (IJSCE) 2014, 3, 132–134. [Google Scholar]
- Ting, C.S.; Kerh, T.; Liao, C.J. Estimation of groundwater recharge using the chloride mass-balance method, Pingtung Plain, Taiwan. Hydrogeol. J. 1998, 6, 282–292. [Google Scholar] [CrossRef]
- Ting, C.S.; Zhou, Y.; Vries, J.D.; Simmers, I. Development of a Preliminary Ground Water Flow Model for Water Resources Management in the Pingtung Plain, Taiwan. Groundwater 1998, 36, 20–36. [Google Scholar] [CrossRef]
- T.P.W.C.B. Investigation Report on Ground Water Resources of the Pingtung Plain; Ministry of Economic Affairs: Taichung, Taiwan, 1961.
- Ministry of Economic Affairs. Geological Sensitive Groundwater Recharge Area Delineation Plan-G0002 Pingtung Plain; Ministry of Economic Affairs: Taipei, Taiwan, 2014.
- Ting, C.S. Groundwater Resources Evaluation and Management for Pingtung Plain, Taiwan. Ph.D. Thesis, Vrije Universiteit, Amsterdam, The Netherlands, 1997. [Google Scholar]
- C.T.C.I. Pingtung County Water Resources Development and Conservation of The Overall Planning and Lin-Bien River Upstream Artificial Lake Engineering Project Settings–Groundwater Recharge Field Test Report; Pingtung County Government: Pingtung, Taiwan, 2000; pp. 3–23.
- Tu, Y.-C.; Ting, C.-S.; Tsai, H.-T.; Chen, J.-W.; Lee, C.-H. Dynamic analysis of the infiltration rate of artificial recharge of groundwater: A case study of Wanglong Lake, Pingtung, Taiwan. Environ. Earth Sci. 2011, 63, 77–85. [Google Scholar] [CrossRef]
- Hida, N.; Ishikawa, E.; Ohta, Y. Experimental Study of Basin Artificial Recharge of Ground Water in Rokugo Alluvial Fan, Northern Japan. J. Groundw. Hydrol. 1999, 41, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.X.; Cai, Q.S. Research on the Groundwater Reservoir in the West Suburb of Beijing; Geological Publishing Company: Beijing, China, 1988. [Google Scholar]
- Abo-Monasar, A.; Al-Zahrani, M.A. Estimation of rainfall distribution for the southwestern region of Saudi Arabia. Hydrol. Sci. J. 2014, 59, 420–431. [Google Scholar] [CrossRef] [Green Version]
- Ewea, H.A.; Elfeki, A.M.M.; Bahrawi, J.A.; Al-Amri, N.S. Sensitivity analysis of runoff hydrographs due to temporal rainfall patterns in Makkah Al-Mukkramah region, Saudi Arabia. Arab. J. Geosci. 2016, 9, 424. [Google Scholar] [CrossRef]
- Tsou, I.; Chen, C.N.; Wang, Y.M.; Kuo, Y.C. A Simulation Study for Flood Disaster Reduction by Detention Pond in Lin-Bian River Basin. In Proceedings of the International Conference on Disaster Management, Kumamoto, Japan, 25 August 2012; pp. 399–406. [Google Scholar]
- Bogaard, T.A. Analysis of Hydrological Processes in Unstable Clayey Slopes. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2001. [Google Scholar]
- Jasmin, I.; Murali, T.; Mallikarjuna, P. Statistical analysis of groundwater table depths in upper Swarnamukhi River basin. J. Water Resour. Prot. 2010, 2, 577. [Google Scholar] [CrossRef]
- Apps, J.A.; Zheng, L.; Spycher, N.; Birkholzer, J.T.; Kharaka, Y.; Thordsen, J.; Kakouros, E.; Trautz, R. Transient changes in shallow groundwater chemistry during the MSU ZERT CO2 injection experiment. Energy Procedia 2011, 4, 3231–3238. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Elhag, T.M. An adaptive neuro-fuzzy inference system for bridge risk assessment. Expert Syst. Appl. 2008, 34, 3099–3106. [Google Scholar] [CrossRef]
- Talebizadeh, M.; Morid, S.; Ayyoubzadeh, S.A.; Ghasemzadeh, M. Uncertainty analysis in sediment load modeling using ANN and SWAT model. Water Resour. Manag. 2010, 24, 1747–1761. [Google Scholar] [CrossRef]
- Traore, S.; Wang, Y.M.; Chung, W.G. Predictive accuracy of backpropagation neural network methodology in evapotranspiration forecasting in Dédougou region, western Burkina Faso. J. Earth Syst. Sci. 2014, 123, 307–318. [Google Scholar] [CrossRef]
- Hsieh, S.H.; Chung, W.G.; Wang, Y.M. Using Artificial Neural Networks for Groundwater Table in Unconfined Aquifer Forecasting. In Proceedings of the 2017 4th International Conference on Coastal and Ocean Engineering (ICCOE 2017), Osaka, Japan, 29 March 2017; p. 63. [Google Scholar]
- Liao, F.L.; Liu, L.W.; Chung, W.G.; Wang, Y.M. Using ANN for modeling the unconfined groundwater table variation induced by artificial recharge lake in dry season. In Proceedings of the 2017 4th International Conference on Coastal and Ocean Engineering (ICCOE 2017), Osaka, Japan, 29 March 2017; p. 98. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Lippmann, R.P. An introduction to computing with neural nets. IEEE Assp Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesús, O. Neural Network Design; Pws Pub.: Boston, MA, USA, 1996; Volume 20. [Google Scholar]
- Memarian, H.; Balasundram, S.K.; Tajbakhsh, M. An expert integrative approach for sediment load simulation in a tropical watershed. J. Integr. Environ. Sci. 2013, 10, 161–178. [Google Scholar] [CrossRef] [Green Version]
- Memarian, H.; Bilondi, M.P.; Rezaei, M. Drought prediction using co-active neuro-fuzzy inference system, validation, and uncertainty analysis (case study: Birjand, Iran). Theor. Appl. Climatol. 2016, 125, 541–554. [Google Scholar] [CrossRef]
- Principe, J.C.; Euliano, N.R.; Lefebvre, W.C. Neural and Adaptive Systems: Fundamentals through Simulations; Wiley: New York, NY, USA, 2000; Volume 672. [Google Scholar]
- Tayfur, G.; Singh, V.P. ANN and fuzzy logic models for simulating event-based rainfall-runoff. J. Hydraul. Eng. 2006, 132, 1321–1330. [Google Scholar] [CrossRef]
- Yang, C.T.; Marsooli, R.; Aalami, M.T. Evaluation of total load sediment transport formulas using ANN. Int. J. Sediment Res. 2009, 24, 274–286. [Google Scholar] [CrossRef]
- Cheung, S.O.; Wong, P.S.P.; Fung, A.S.; Coffey, W. Predicting project performance through neural networks. Int. J. Proj. Manag. 2006, 24, 207–215. [Google Scholar] [CrossRef] [Green Version]








| Rainfall Station (Period) | Annual Rainfall (mm) | Coordinate | Control Area | ||
|---|---|---|---|---|---|
| (TWD97-X) | (TWD97-Y) | (km2) | (%) | ||
| Taiwu-1 (1955–2018) | 4366.2 | 217,853.20 | 2,500,983.30 | 50.76 | 15 |
| Xinlaiyi (1972–2018) | 3646.9 | 216,084.71 | 2,492,152.60 | 141.13 | 40 |
| Nanhan (1965–2018) | 2506.0 | 211,948.60 | 2,481,928.20 | 156.97 | 45 |
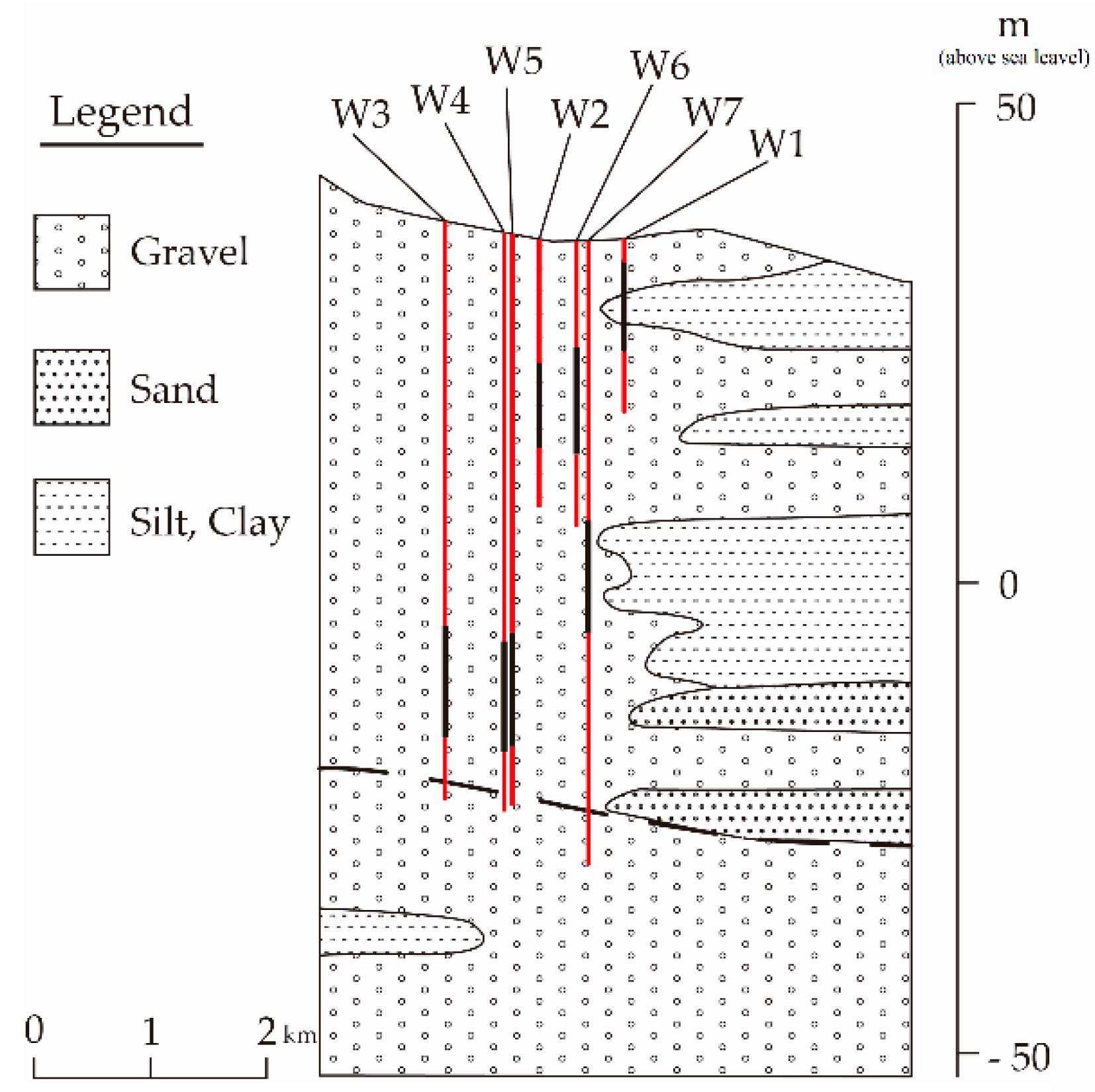
| Groundwater Monitoring Wells (Recording Period from 2010/05 to 2015/12) | Coordinate | Well Screen (Above Sea Level) | |
|---|---|---|---|
| (TWD97-X) | (TWD97-Y) | ||
| Well 1 | 211,320.61 | 2,491,816.04 | 24 to 33 |
| Well 2 | 211,084.75 | 2,490,990.15 | 14 to 23 |
| Well 3 | 210,331.36 | 2,490,524.91 | −17 to 5 |
| Well 4 | 210,031.63 | 2,491,209.14 | −18 to 6 |
| Well 5 | 209,115.70 | 2,491,773.84 | −17 to 5 |
| Well 6 | 209,097.66 | 2,492,587.59 | 13 to 25 |
| Well 7 | 210,184.92 | 2,492,093.04 | −5 to 7 |
| Groundwater Monitoring Wells | R2 |
|---|---|
| Well 1 | 0.848 |
| Well 2 | 0.854 |
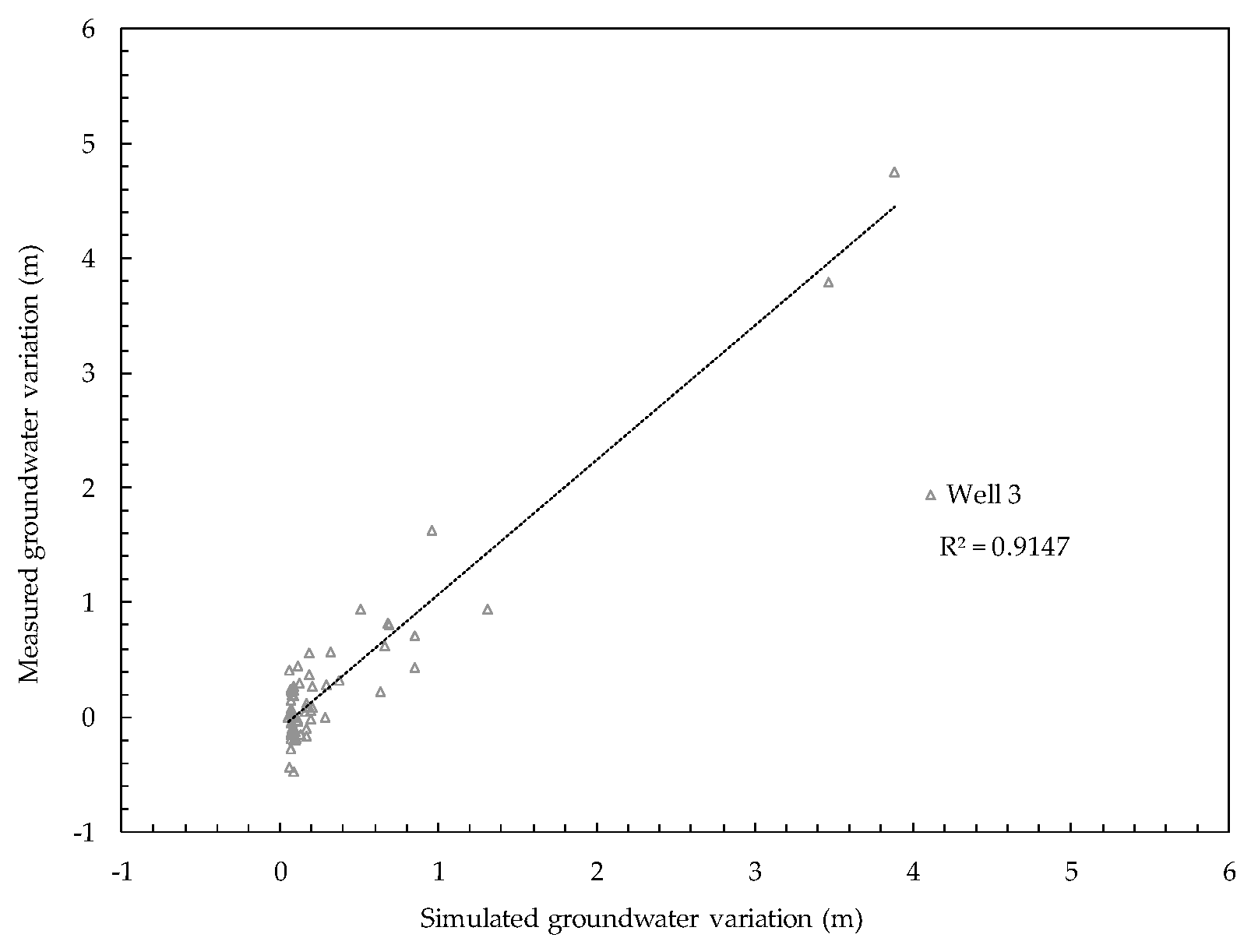
| Well 3 | 0.914 |
| Well 4 | 0.897 |
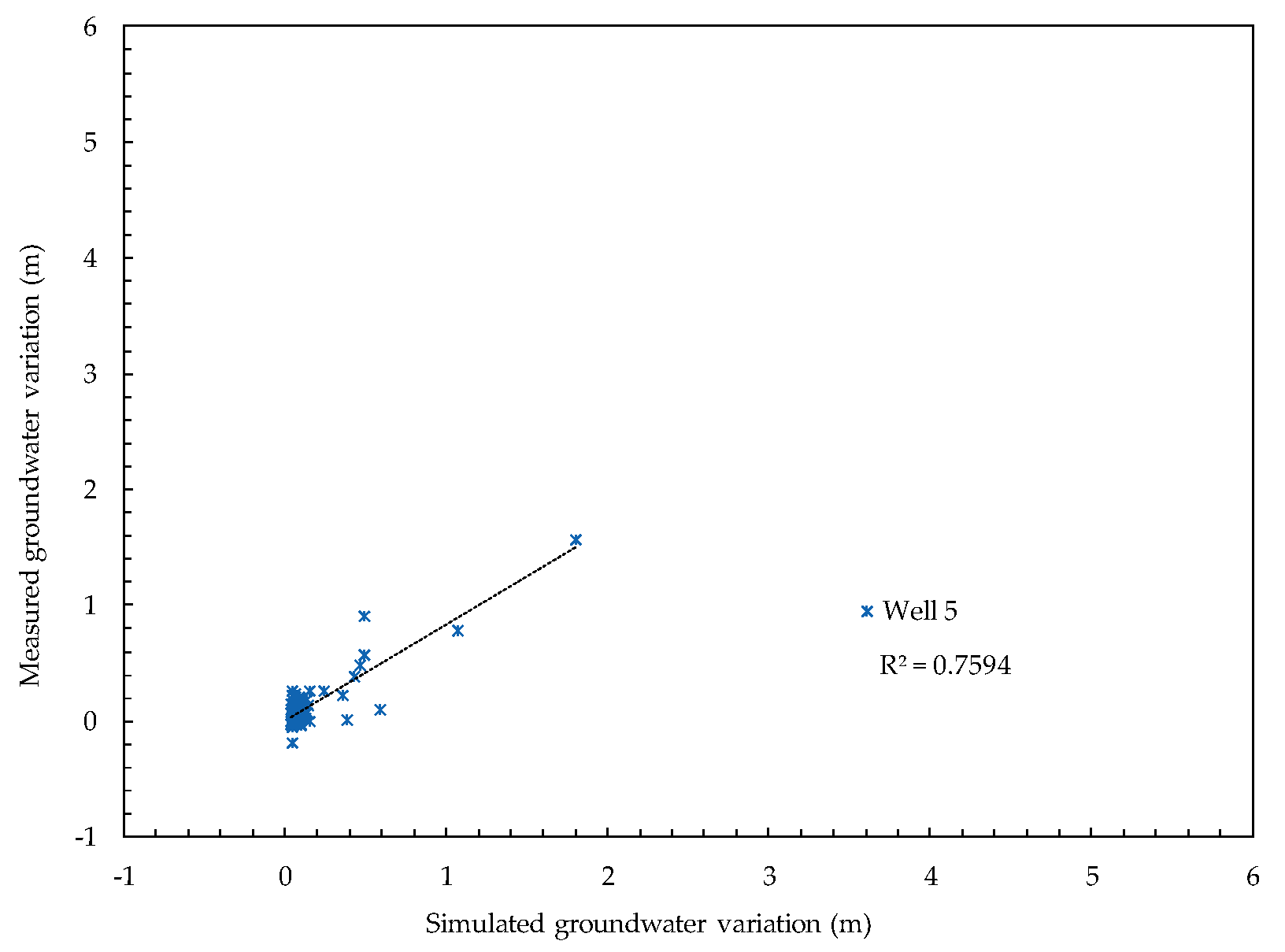
| Well 5 | 0.759 |
| Well 6 | 0.841 |
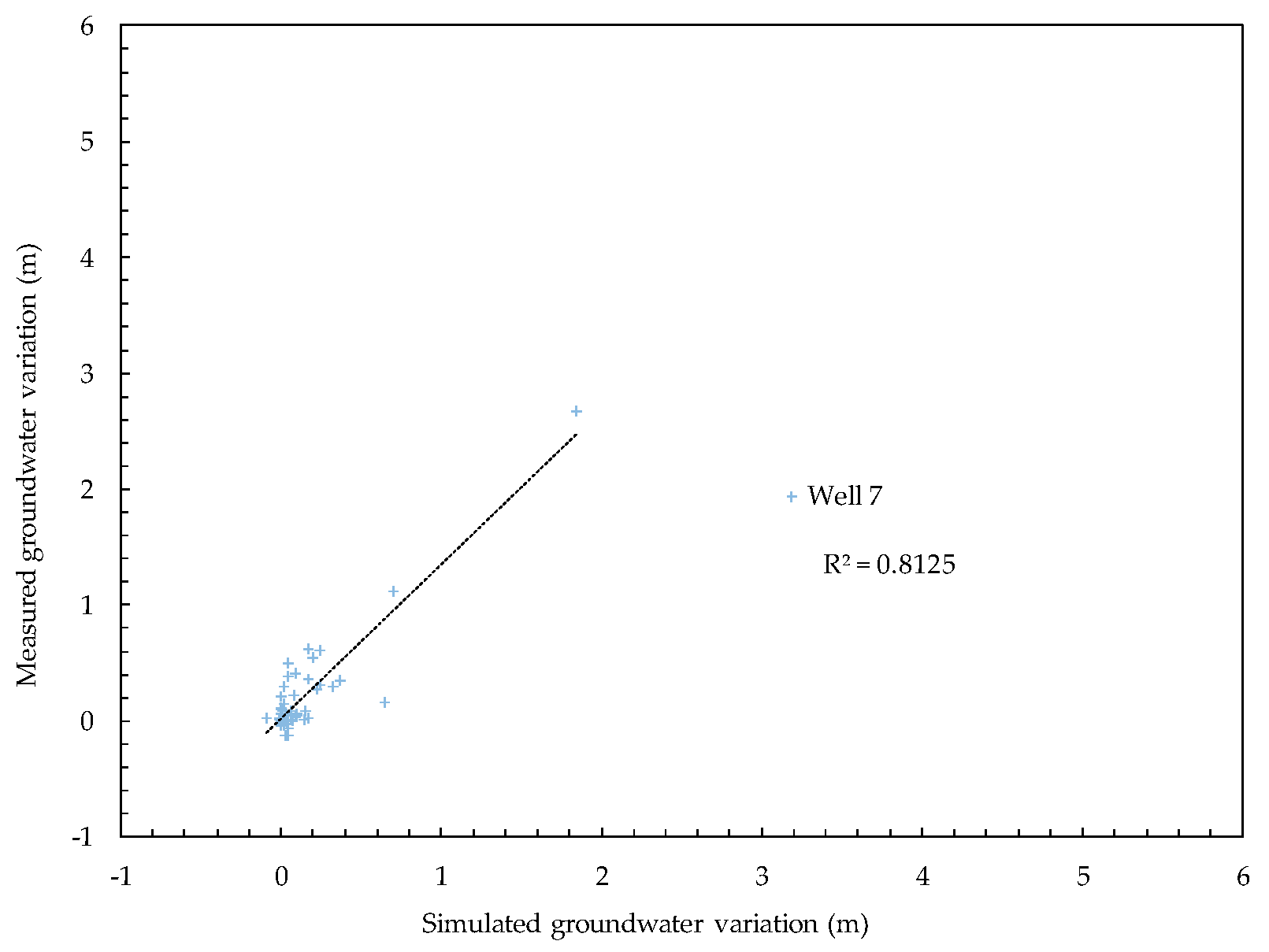
| Well 7 | 0.812 |
| Inputs | Well 1 | Well 2 | Well 3 | Well 4 | Well 5 | Well 6 | Well 7 |
|---|---|---|---|---|---|---|---|
| RI5 | 0.0216 | 0.0207 | 0.0163 | 0.0064 | 0.0096 | 0.0049 | 0.0145 |
| RI4 | 0.0045 | 0.0025 | 0.0035 | 0.0028 | 0.0047 | 0.0133 | 0.0033 |
| RI3 | 0.0223 | 0.0220 | 0.0156 | 0.0101 | 0.0076 | 0.0002 | 0.0164 |
| RI2 | 0.0040 | 0.0157 | 0.0231 | 0.0650 | 0.0044 | 0.0102 | 0.0037 |
| RI1 | 0.0017 | 0.0163 | 0.0130 | 0.0212 | 0.0051 | 0.0021 | 0.0200 |
| R5 | 0.0053 | 0.0132 | 0.0181 | 0.0035 | 0.0238 | 0.0084 | 0.0498 |
| R4 | 0.0203 | 0.0324 | 0.0639 | 0.0029 | 0.0181 | 0.0069 | 0.1489 |
| R3 | 0.0136 | 0.0594 | 0.0343 | 0.0036 | 0.0048 | 0.0036 | 0.0443 |
| R2 | 0.0849 | 0.1095 | 0.0362 | 0.0108 | 0.0030 | 0.0127 | 0.0092 |
| R1 | 0.0102 | 0.0027 | 0.0048 | 0.0173 | 0.0060 | 0.0042 | 0.0372 |
| Category of Sensitivity | Value of Sensitivity Index | Rank |
|---|---|---|
| 1. Very high sensitivity | >0.1 | 1 |
| 2. High sensitivity | 0.05 to 0.1 | 2 |
| 3. Moderate sensitivity | 0.01 to 0.05 | 3 |
| 4. Low sensitivity | 0.005 to 0.01 | 4 |
| 5. Very low sensitivity | ≤0.005 | 5 |
| Inputs | Well 1 | Well 2 | Well 3 | Well 4 | Well 5 | Well 6 | Well 7 |
|---|---|---|---|---|---|---|---|
| RI5 | 3 | 3 | 3 | 4 | 4 | 5 | 3 |
| RI4 | 5 | 5 | 5 | 5 | 5 | 3 | 5 |
| RI3 | 3 | 3 | 3 | 3 | 4 | 5 | 3 |
| RI2 | 5 | 3 | 3 | 2 | 5 | 3 | 5 |
| RI1 | 5 | 3 | 3 | 3 | 4 | 5 | 3 |
| R5 | 4 | 3 | 3 | 5 | 3 | 4 | 3 |
| R4 | 3 | 3 | 2 | 5 | 3 | 4 | 1 |
| R3 | 3 | 2 | 3 | 5 | 5 | 5 | 3 |
| R2 | 2 | 1 | 3 | 3 | 5 | 3 | 4 |
| R1 | 3 | 5 | 5 | 3 | 4 | 5 | 3 |
| Groundwater Monitoring Wells | Highest Sensitivity | 2nd Highest Sensitivity | ||
|---|---|---|---|---|
| Index | Variable | Index | Variable | |
| Well 1 | 2 | R2 | 3 | RI3 |
| Well 2 | 1 | R2 | 2 | R3 |
| Well 3 | 2 | R4 | 3 | R2 |
| Well 4 | 2 | RI2 | 3 | RI1 |
| Well 5 | 3 | R5 | 3 | R4 |
| Well 6 | 3 | RI4 | 3 | R2 |
| Well 7 | 1 | R4 | 3 | R5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, S.-H.; Liu, L.-W.; Chung, W.-G.; Wang, Y.-M. Sensitivity Analysis on the Rising Relation between Short-Term Rainfall and Groundwater Table Adjacent to an Artificial Recharge Lake. Water 2019, 11, 1704. https://doi.org/10.3390/w11081704
Hsieh S-H, Liu L-W, Chung W-G, Wang Y-M. Sensitivity Analysis on the Rising Relation between Short-Term Rainfall and Groundwater Table Adjacent to an Artificial Recharge Lake. Water. 2019; 11(8):1704. https://doi.org/10.3390/w11081704
Chicago/Turabian StyleHsieh, Sheng-Hsin, Li-Wei Liu, Wen-Guey Chung, and Yu-Min Wang. 2019. "Sensitivity Analysis on the Rising Relation between Short-Term Rainfall and Groundwater Table Adjacent to an Artificial Recharge Lake" Water 11, no. 8: 1704. https://doi.org/10.3390/w11081704
APA StyleHsieh, S.-H., Liu, L.-W., Chung, W.-G., & Wang, Y.-M. (2019). Sensitivity Analysis on the Rising Relation between Short-Term Rainfall and Groundwater Table Adjacent to an Artificial Recharge Lake. Water, 11(8), 1704. https://doi.org/10.3390/w11081704







