Water-Energy Nexus for an Italian Storage Hydropower Plant under Multiple Drivers
Abstract
:1. Introduction
2. Italian Hydropower: Current Situation and Climate Change Impact Projections
3. Methodology and Case Study
3.1. Study Area and Data
3.2. The Hydrological Model
- Alagna (1347 m.a.s.l.) and Bocchetta delle Pisse (2410 m.a.s.l.);
- Balme (1410 m.a.s.l) and Rifugio Gastaldi (2659 m.a.s.l);
- Macugnaga Pecetto (1360 m.a.s.l) and Rifugio Zamboni (2075 m.a.s.l);
- Noasca (1055 m.a.s.l) and Lago Agnel (2304 m.a.s.l);
- Prerichard (1353 m.a.s.l) and Rochemolles (1965 m.a.s.l).
3.3. Future Climate Scenarios
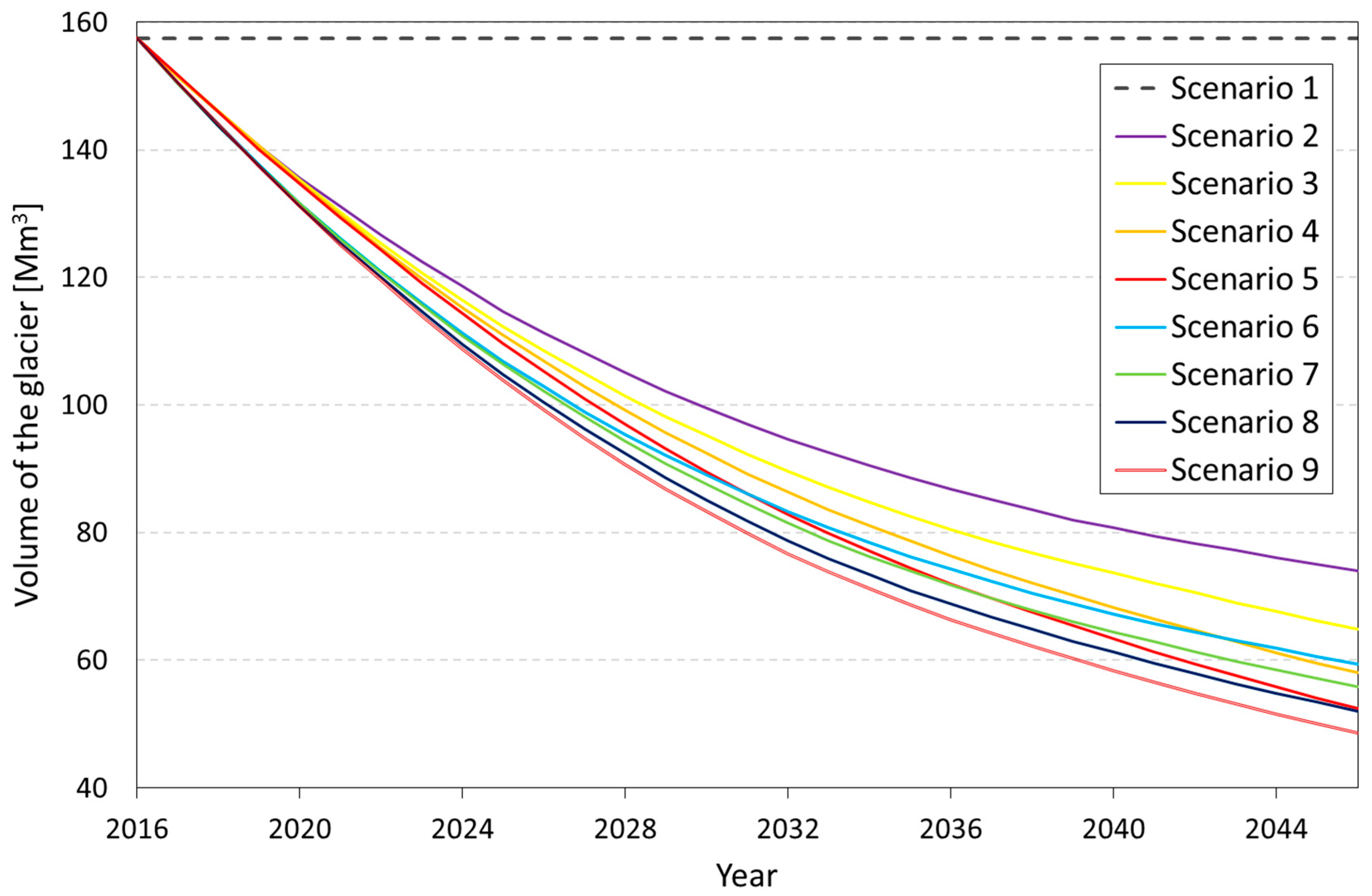
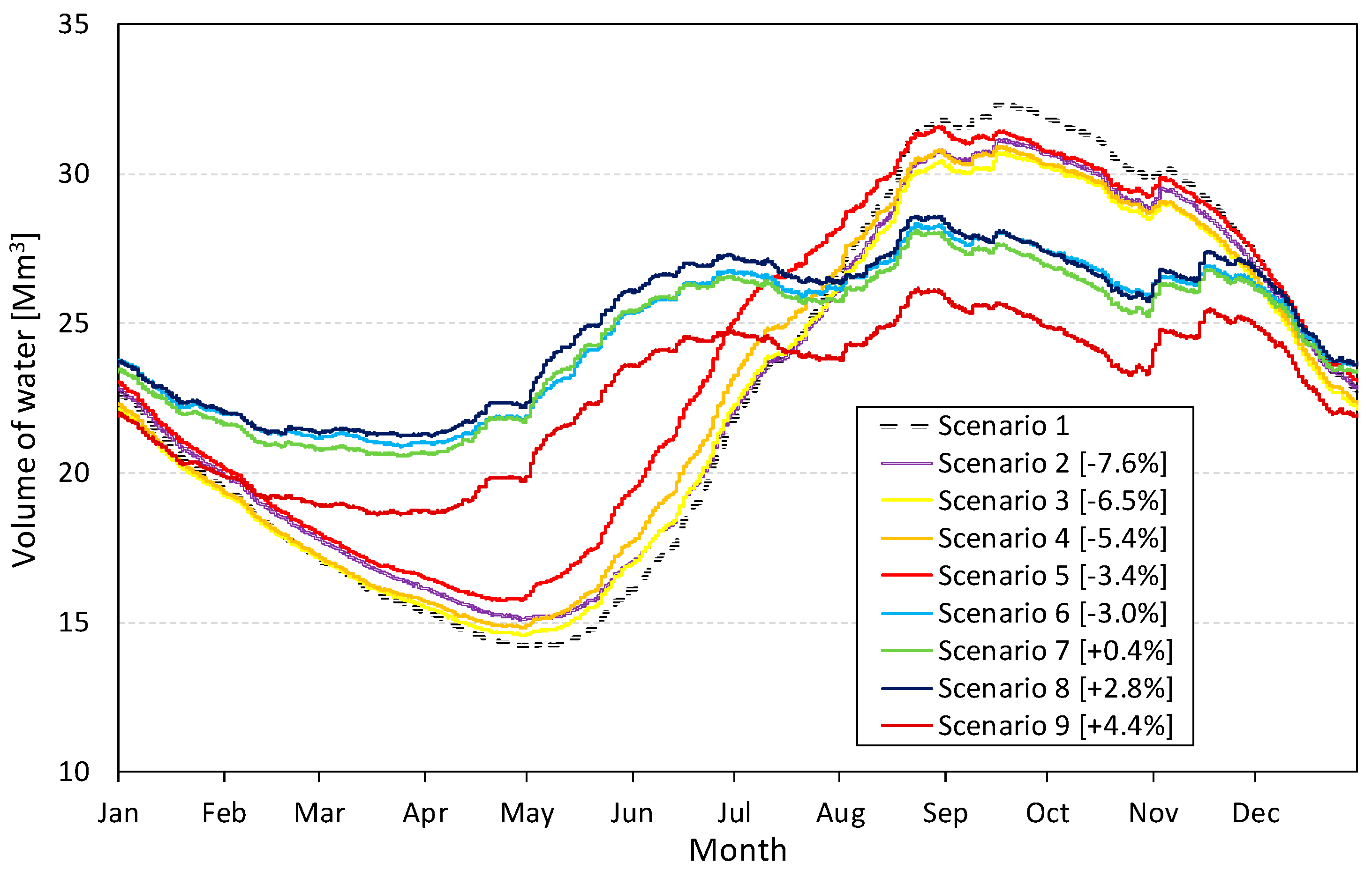
- Future-like-present scenarios (scenarios 1 and 2): They evaluate the future evolution of the glaciers at present conditions. Temperature and precipitation assume presents patterns, alternatively considering or neglecting the computation of the mass balance of the glaciers in the basin.
- Warmer future scenarios (scenarios 3–5): They evaluate the effects of positive trends in temperatures (+0.03 °C/y, +0.06 °C/y, and +0.09 °C/y) neglecting any modification of the precipitation pattern on the hydrological regime of the basin. These temperature trends are in line with the scientific literature [8,84,95].
- Liquid-precipitation scenario (scenario 6). This extreme scenario assumes liquid-only precipitation and neglects temperature warming.
- The mixed scenarios (scenarios 7–9): These complex scenarios built random series combining liquid-only precipitation and the three above-mentioned trends of temperature.
3.4. The Hydropower Management Model
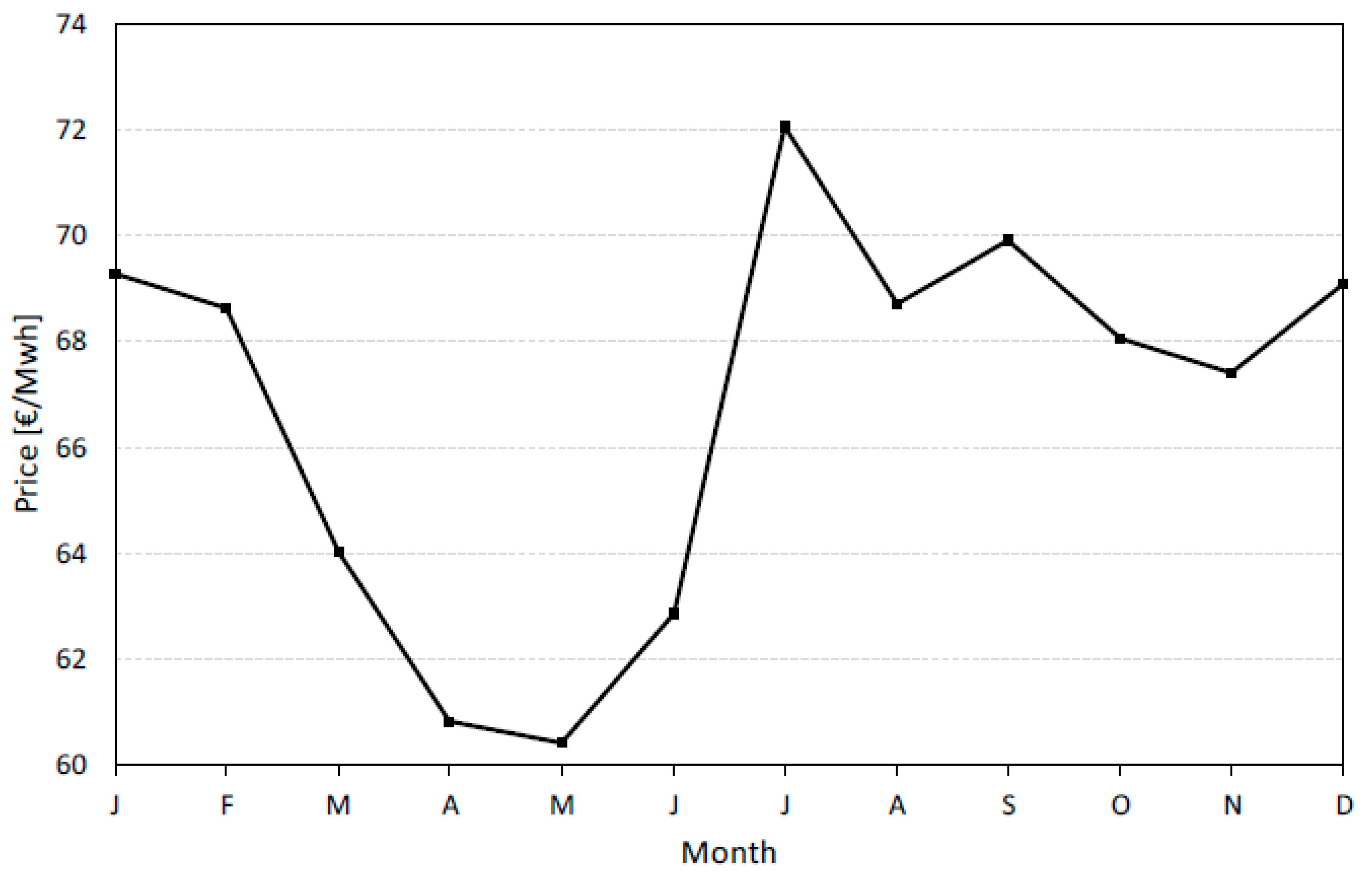
3.5. Electricity Price Scenarios
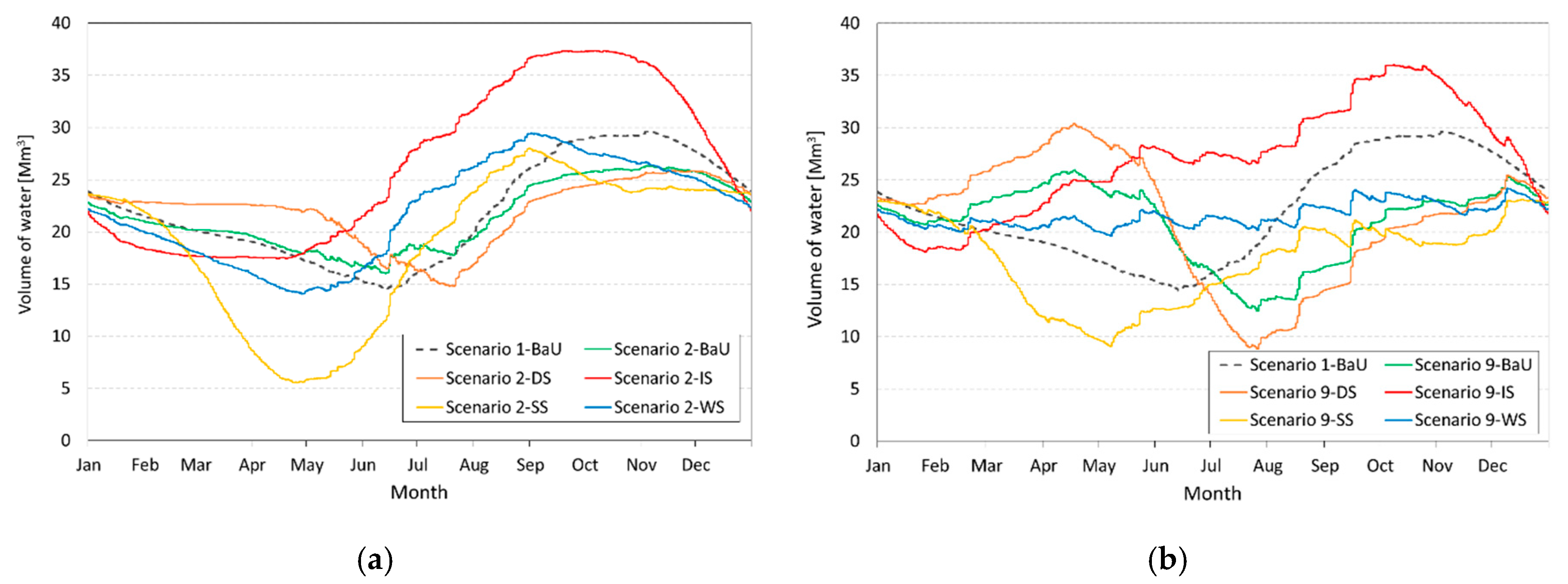
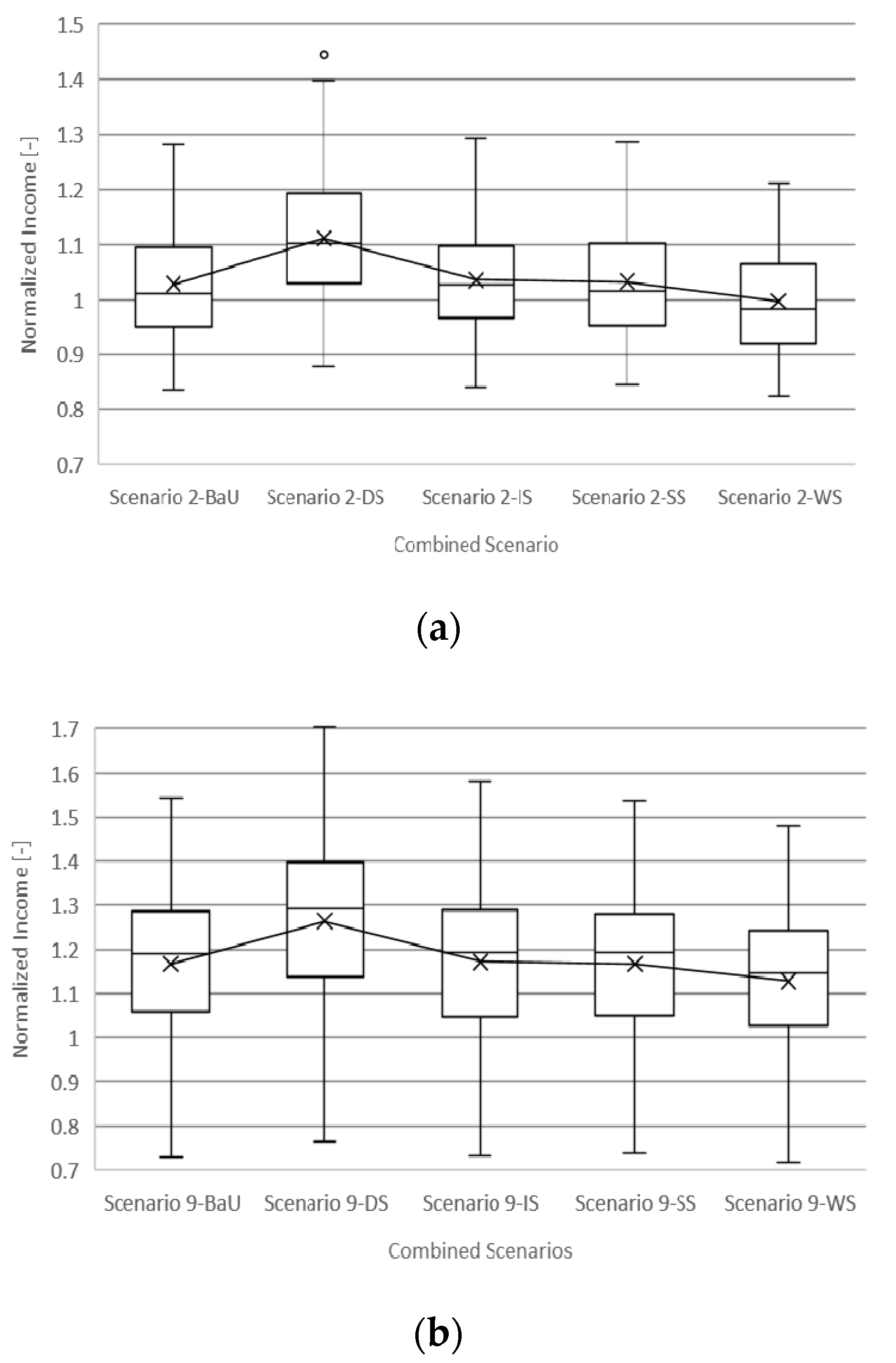
4. Results and Discussion
4.1. Climate Change Effects on Glacier and Flow Regimes
4.2. Climate Change Impact on Reservoir Volumes and Revenue
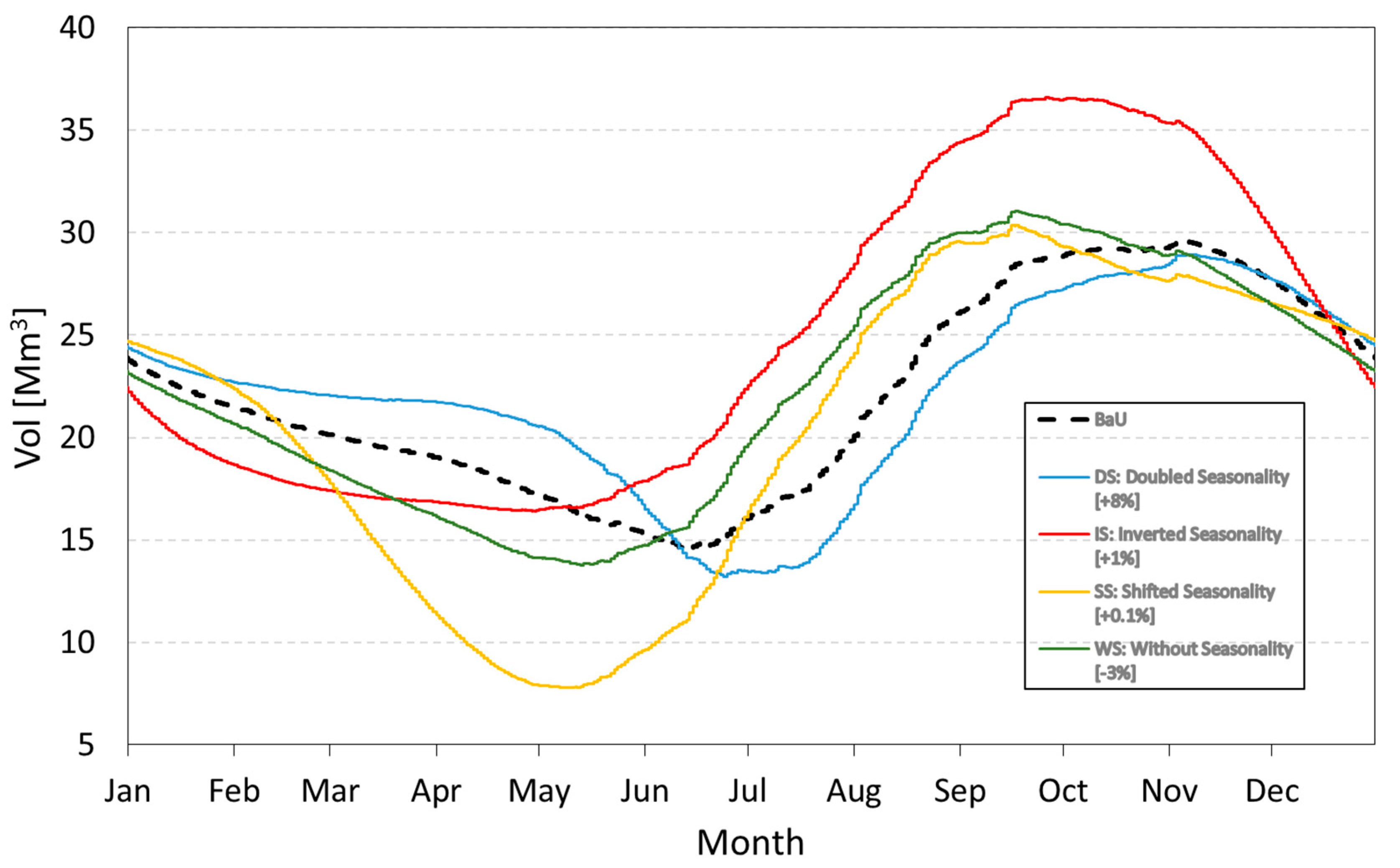
4.3. Impact of Electricity Price Scenarios
4.4. Impact of Mixed Scenarios
4.5. What If the Reservoir Configuration Becomes a Run of River Model?
if QF < QP, Qt = QF.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Renewable Energy Agency (IRENA). Global Energy Transformation: A Roadmap to 2050; IRENA: New York, NY, USA, 2018. [Google Scholar]
- IEA. WEO-2015 Special Report: Energy and Climate Change; IEA: Paris, France, 2015. [Google Scholar]
- Gebretsadik, Y.; Fant, C.; Strzepek, K.; Arndt, C. Optimized reservoir operation model of regional wind and hydro power integration case study: Zambezi basin and South Africa. Appl. Energy 2016, 161. [Google Scholar] [CrossRef]
- Hirth, L. The benefits of flexibility: The value of wind energy with hydropower. Appl. Energy 2016, 181. [Google Scholar] [CrossRef]
- Li, F.F.; Qiu, J. Multi-objective optimization for integrated hydro-photovoltaic power system. Appl. Energy 2016, 167, 377–384. [Google Scholar] [CrossRef]
- Rose, A.; Stoner, R.; Pérez-Arriaga, I. Prospects for grid-connected solar PV in Kenya: A systems approach. Appl. Energy 2016, 161, 583–590. [Google Scholar] [CrossRef] [Green Version]
- Schaefli, B. Projecting hydropower production under future climates: A guide for decision-makers and modelers to interpret and design climate change impact assessments. Wiley Interdiscip. Rev. Water 2015, 2, 271–289. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis; IPCC: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Blackshear, B.; Crocker, T.; Drucker, E.; Filoon, J. Hydropower Vulnerability and Climate Change—A Framework for Modeling the Future of Global Hydroelectric Resources; Middlebury College Environmental Studies Senior Seminar: Middlebury, VT, USA, 2011; 82p. [Google Scholar]
- Rothstein, B.; Schroedter-Homscheidt, M.; Häfner, C.; Bernhardt, S.; Mimler, S. Impacts of Climate Change on the Electricity Sector and Possible Adaptation Measures BT—Economics and Management of Climate Change: Risks, Mitigation and Adaptation; Hansjürgens, B., Antes, R., Eds.; Springer: New York, NY, USA, 2008; pp. 231–241. ISBN 978-0-387-77353-7. [Google Scholar]
- Ravazzani, G.; Dalla Valle, F.; Gaudard, L.; Mendlik, T.; Gobiet, A.; Mancini, M. Assessing Climate Impacts on Hydropower Production: The Case of the Toce River Basin. Climate 2016, 4, 16. [Google Scholar] [CrossRef]
- Laternser, M.; Schneebeli, M. Long-term snow climate trends of the Swiss Alps (1931-99). Int. J. Climatol. 2003, 23, 733–750. [Google Scholar] [CrossRef]
- Beniston, M.; Farinotti, D.; Stoffel, M.; Andreassen, L.M.; Coppola, E.; Eckert, N.; Fantini, A.; Giacona, F.; Hauck, C.; Huss, M.; et al. The European mountain cryosphere: A review of its current state, trends, and future challenges. Cryosphere 2018, 12, 759–794. [Google Scholar] [CrossRef]
- Wagner, T.; Themeßl, M.; Schüppel, A.; Gobiet, A.; Stigler, H.; Birk, S. Impacts of climate change on stream flow and hydro power generation in the Alpine region. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- Hughes, M.G.; Robinson, D.A. Historical snow cover variability in the great plains region of the USA: 1910 through to 1993. Int. J. Climatol. 1996, 16, 1005–1018. [Google Scholar] [CrossRef]
- Brown, R.D.; Goodison, B.E. Interannual variability in reconstructed Canadian snow cover, 1915-1992. J. Clim. 1996, 9, 1299–1318. [Google Scholar] [CrossRef]
- Frei, A.; Robinson, D.A. Northern Hemisphere snow extent: Regional variability 1972-1994. Int. J. Climatol. 1999, 19, 1535–1560. [Google Scholar] [CrossRef]
- Patro, E.R.; De Michele, C.; Avanzi, F. Future perspectives of run-of-the-river hydropower and the impact of glaciers’ shrinkage: The case of Italian Alps. Appl. Energy 2018, 231, 699–713. [Google Scholar] [CrossRef]
- Huss, M.; Jouvet, G.; Farinotti, D.; Bauder, A. Future high-mountain hydrology: A new parameterization of glacier retreat. Hydrol. Earth Syst. Sci. 2010, 14, 815–829. [Google Scholar] [CrossRef]
- Schaefli, B.; Manso, P.; Fischer, M.; Huss, M.; Farinotti, D. The role of glacier retreat for Swiss hydropower production. Renew. Energy 2019, 132, 615–627. [Google Scholar] [CrossRef]
- Cat Berro, D.; Acordon, V.; Di Napoli, G. Cambiamenti Climatici Sulla Montagna Piemontese; Società Meteorologica Subalpina: Bussoleno, Italy, 2008; 142p. [Google Scholar]
- Cannone, N.; Diolaiuti, G.; Guglielmin, M.; Smiraglia, C. Accelerating climate change impacts on alpine glacier forefield ecosystems in the European Alps. Ecol. Appl. 2008, 18, 637–648. [Google Scholar] [CrossRef] [PubMed]
- Diolaiuti, G.A.; Maragno, D.; D’Agata, C.; Smiraglia, C.; Bocchiola, D. Glacier retreat and climate change: Documenting the last 50 years of Alpine glacier history from area and geometry changes of Dosdè Piazzi glaciers (Lombardy Alps, Italy). Prog. Phys. Geogr. 2011, 35, 161–182. [Google Scholar] [CrossRef]
- Beniston, M. Impacts of climatic change on water and associated economic activities in the Swiss Alps. J. Hydrol. 2012, 412–413, 291–296. [Google Scholar] [CrossRef]
- Bongio, M.; Avanzi, F.; De Michele, C. Hydroelectric power generation in an Alpine basin: Future water-energy scenarios in a run-of-the-river plant. Adv. Water Resour. 2016, 94, 318–331. [Google Scholar] [CrossRef]
- Gaudard, L.; Avanzi, F.; De Michele, C. Seasonal aspects of the energy-water nexus: The case of a run-of-the-river hydropower plant. Appl. Energy 2018, 210, 604–612. [Google Scholar] [CrossRef]
- Etter, S.; Addor, N.; Huss, M.; Finger, D. Climate change impacts on future snow, ice and rain runoff in a Swiss mountain catchment using multi-dataset calibration. J. Hydrol. Reg. Stud. 2017, 13, 222–239. [Google Scholar] [CrossRef]
- Finger, D.; Heinrich, G.; Gobiet, A.; Bauder, A. Projections of future water resources and their uncertainty in a glacierized catchment in the Swiss Alps and the subsequent effects on hydropower production during the 21st century. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Ceppi, A.; Ravazzani, G.; Salandin, A.; Rabuffetti, D.; Montani, A.; Borgonovo, E.; Mancini, M. Effects of temperature on flood forecasting: Analysis of an operative case study in Alpine basins. Nat. Hazards Earth Syst. Sci. 2013, 13, 1051–1062. [Google Scholar] [CrossRef]
- Montaldo, N.; Ravazzani, G.; Mancini, M. On the prediction of the Toce alpine basin floods with distributed hydrologic models. Hydrol. Process. 2007. [Google Scholar] [CrossRef]
- Ravazzani, G.; Barbero, S.; Salandin, A.; Senatore, A.; Mancini, M. An integrated Hydrological Model for Assessing Climate Change Impacts on Water Resources of the Upper Po River Basin. Water Resour. Manag. 2014. [Google Scholar] [CrossRef]
- Ravazzani, G.; Ghilardi, M.; Mendlik, T.; Gobiet, A.; Corbari, C.; Mancini, M. Investigation of climate change impact on water resources for an alpine basin in northern Italy: Implications for evapotranspiration modeling complexity. PLoS ONE 2014. [Google Scholar] [CrossRef] [PubMed]
- Gaudard, L.; Romerio, F. Reprint of “The future of hydropower in Europe: Interconnecting climate, markets and policies”. Environ. Sci. Policy 2014, 43, 5–14. [Google Scholar] [CrossRef]
- Apadula, F.; Bassini, A.; Elli, A.; Scapin, S. Relationships between meteorological variables and monthly electricity demand. Appl. Energy 2012, 98, 346–356. [Google Scholar] [CrossRef]
- Bartos, M.; Chester, M.; Johnson, N.; Gorman, B.; Eisenberg, D.; Linkov, I.; Bates, M. Impacts of rising air temperatures on electric transmission ampacity and peak electricity load in the United States. Environ. Res. Lett. 2016, 11. [Google Scholar] [CrossRef]
- Kern, F.; Smith, A. Restructuring energy systems for sustainability? Energy transition policy in the Netherlands. Energy Policy 2008, 36, 4093–4103. [Google Scholar] [CrossRef]
- Scott, C.A.; Pierce, S.A.; Pasqualetti, M.J.; Jones, A.L.; Montz, B.E.; Hoover, J.H. Policy and institutional dimensions of the water-energy nexus. Energy Policy 2011, 39, 6622–6630. [Google Scholar] [CrossRef]
- Golombek, R.; Kittelsen, S.A.C.; Haddeland, I. Climate change: Impacts on electricity markets in Western Europe. Clim. Chang. 2012, 113, 357–370. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, T.; Muttaqi, K.M.; Agalgaonkar, A.P. Climate change impacts on electricity demand in the State of New South Wales, Australia. Appl. Energy 2012, 98, 376–383. [Google Scholar] [CrossRef]
- Christenson, M.; Manz, H.; Gyalistras, D. Climate warming impact on degree-days and building energy demand in Switzerland. Energy Convers. Manag. 2006, 47, 671–686. [Google Scholar] [CrossRef]
- Schaefli, B.; Hingray, B.; Musy, A. Climate change and hydropower production in the Swiss Alps: Quantification of potential impacts and related modelling uncertainties. Hydrol. Earth Syst. Sci. 2007, 11, 1191–1205. [Google Scholar] [CrossRef]
- Guegan, M.; Madani, K.; Uvo, C.B. Climate Change Effects on the High Elevation Hydropower System with Consideration of Warming Impacts on Electricity Demand and Pricing; California Energy Commission: Sacramento, CA, USA, 2012.
- Malik, R.P.S. Water-energy nexus in resource-poor economies: The Indian experience. Int. J. Water Resour. Dev. 2002. [Google Scholar] [CrossRef]
- Siddiqi, A.; Anadon, L.D. The water-energy nexus in Middle East and North Africa. Energy Policy 2011, 39, 4529–4540. [Google Scholar] [CrossRef]
- Madani, K.; Guégan, M.; Uvo, C.B. Climate change impacts on high-elevation hydroelectricity in California. J. Hydrol. 2014, 510, 153–163. [Google Scholar] [CrossRef]
- Gaudard, L.; Gilli, M.; Romerio, F. Climate Change Impacts on Hydropower Management. Water Resour. Manag. 2013, 27, 5143–5156. [Google Scholar] [CrossRef] [Green Version]
- Maran, S.; Volonterio, M.; Gaudard, L. Climate change impacts on hydropower in an alpine catchment. Environ. Sci. Policy 2014, 43, 15–25. [Google Scholar] [CrossRef]
- International Hydropower Association. Hydropower Status Report (2018); International Hydropower Association: London, UK, 2018; Available online: https://www.hydropower.org/sites/default/files/publications-docs/2018_hydropower_status_report_0.pdf (accessed on 24 June 2019).
- Agrillo, A.; Dal Verme, M.; Liberatore, P.; Lipari, D.; Maio, V.; Surace, V.; Benedetti, L. Rapporto Statistico 2017 Fonti Rinnovabili; Gestore dei Servizi Energetici S.p.A: Rome, Italy, 2018. [Google Scholar]
- Terna. Dati Statistici Sull’energia Elettrica in Italia. Available online: https://www.terna.it/it-it/%0Asistemaelettrico/statisticheeprevisioni/datistatistici.aspx (accessed on 24 June 2019).
- Miglietta, P.P.; Morrone, D.; De Leo, F. The water footprint assessment of electricity production: An overview of the economic-water-energy nexus in Italy. Sustainability 2018, 10, 228. [Google Scholar] [CrossRef]
- Unione Petrolifera. Available online: http://www.unionepetrolifera.it/?page_id=6419 (accessed on 21 June 2019).
- Italy’s National Energy Strategy. 2017. Available online: https://www.mise.gov.it/images/stories/documenti/BROCHURE_ENG_SEN.PDF (accessed on 24 June 2019).
- Proposta Di Piano Nazionale Integrato Per L’energia E Il Clima. 2018. Available online: https://www.mise.gov.it/images/stories/documenti/Proposta_di_Piano_Nazionale_Integrato_per_Energia_e_il_Clima_Italiano.pdf (accessed on 26 Jun 2019).
- International Energy Agency (IEA). Energy Policies of IEA Countries: Italy 2016 Review; IEA: Paris, France, 2016. [Google Scholar]
- Gaudard, L.; Madani, K. Energy storage race: Has the monopoly of pumped-storage in Europe come to an end? Energy Policy 2019. [Google Scholar] [CrossRef]
- Autorità Di Regolazione Per Energia Reti E Ambiente (ARERA)—Relazioni Annuali Sullo Stato Dei Servizi e Sull’attività Svolta. Presidenza del Consiglio dei Ministri, Dipartimento per L’informazione e L’editoria. Available online: https://www.arera.it/it/index.htm (accessed on 26 June 2019).
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Ranzani, A.; Bonato, M.; Patro, E.; Gaudard, L.; De Michele, C. Hydropower Future: Between Climate Change, Renewable Deployment, Carbon and Fuel Prices. Water 2018, 10, 1197. [Google Scholar] [CrossRef]
- Farinotti, D.; Usselmann, S.; Huss, M.; Bauder, A.; Funk, M. Runoff evolution in the Swiss Alps: Projections for selected high-alpine catchments based on ENSEMBLES scenarios. Hydrol. Process. 2012, 26, 1909–1924. [Google Scholar] [CrossRef]
- Horton, P.; Schaefli, B.; Mezghani, A.; Hingray, B.; Musy, A. Assessment of climate-change impacts on alpine discharge regimes with climate model uncertainty. Hydrol. Process. 2006, 20, 2091–2109. [Google Scholar] [CrossRef]
- Addor, N.; Rössler, O.; Köplin, N.; Huss, M.; Weingartner, R.; Seibert, J. Robust changes and sources of uncertainty in the projected hydrological regimes of Swiss catchments. Water Resour. Res. 2014, 50, 7541–7562. [Google Scholar] [CrossRef] [Green Version]
- Smiraglia, C.; Azzoni, R.S.; D’agata, C.; Maragno, D.; Fugazza, D.; Diolaiuti, G.A. The evolution of the Italian glaciers from the previous data base to the new Italian inventory. Preliminary considerations and results. Geogr. Fis. Din. Quat. 2015, 38, 79–87. [Google Scholar] [CrossRef]
- Smiraglia, C.; Diolaiuti, G. The New Italian Glacier Inventory; Ev-K2-CNR Publish: Bergamo, Italy, 2015; 400p, ISBN 9788894090802. [Google Scholar]
- Comitato Glaciologico Italiano; Consiglio Nazionale delle Ricerche. Catasto dei Ghiacciai Italiani, Anno Geofisico Internazionale 1957–1958; Elenco generale e bibliografia dei ghiacciai italiani; CGI, CNR; Comitato Glaciologico Italiano: Torino, Italy, 1959; Volume 1, 172p. [Google Scholar]
- Berga, L. The Role of Hydropower in Climate Change Mitigation and Adaptation: A Review. Engineering 2016, 2, 313–318. [Google Scholar] [CrossRef] [Green Version]
- D’Agata, C.; Bocchiola, D.; Soncini, A.; Maragno, D.; Smiraglia, C.; Diolaiuti, G.A. Recent area and volume loss of Alpine glaciers in the Adda River of Italy and their contribution to hydropower production. Cold Reg. Sci. Technol. 2018, 148, 172–184. [Google Scholar] [CrossRef]
- Gaudard, L.; Romerio, F.; Dalla Valle, F.; Gorret, R.; Maran, S.; Ravazzani, G.; Stoffel, M.; Volonterio, M. Climate change impacts on hydropower in the Swiss and Italian Alps. Sci. Total Environ. 2014, 493, 1211–1221. [Google Scholar] [CrossRef] [PubMed]
- Jacob, D. A note to the simulation of the annual and inter-annual variability of the water budget over the Baltic Sea drainage basin. Meteorol. Atmos. Phys. 2001, 77, 61–73. [Google Scholar] [CrossRef]
- Pal, J.S.; Giorgi, F.; Bi, X.; Elguindi, N.; Solmon, F.; Gao, X.; Rauscher, S.A.; Francisco, R.; Zakey, A.; Winter, J.; et al. Regional climate modeling for the developing world: The ICTP RegCM3 and RegCNET. Bull. Am. Meteorol. Soc. 2007. [Google Scholar] [CrossRef]
- Ciarapica, L.; Todini, E. TOPKAPI: A model for the representation of the rainfall-runoff process at different scales. Hydrol. Process. 2002. [Google Scholar] [CrossRef]
- Boscarello, L.; Ravazzani, G.; Rabuffetti, D.; Mancini, M. Integrating glaciers raster-based modelling in large catchments hydrological balance: The Rhone case study. Hydrol. Process. 2014, 28, 496–508. [Google Scholar] [CrossRef]
- Majone, B.; Villa, F.; Deidda, R.; Bellin, A. Impact of climate change and water use policies on hydropower potential in the south-eastern Alpine region. Sci. Total Environ. 2016, 543, 965–980. [Google Scholar] [CrossRef]
- Bellin, A.; Majone, B.; Cainelli, O.; Alberici, D.; Villa, F. A continuous coupled hydrological and water resources management model. Environ. Model. Softw. 2016, 75, 176–192. [Google Scholar] [CrossRef]
- Mereu, S.; Sušnik, J.; Trabucco, A.; Daccache, A.; Vamvakeridou-Lyroudia, L.; Renoldi, S.; Virdis, A.; Savić, D.; Assimacopoulos, D. Operational resilience of reservoirs to climate change, agricultural demand, and tourism: A case study from Sardinia. Sci. Total Environ. 2016, 543, 1028–1038. [Google Scholar] [CrossRef] [Green Version]
- Ranzi, R.; Barontini, S.; Grossi, G.; Faggian, P.; Kouwen, N.; Maran, S. Impact of climate change scenarios on water resources management in the Italian Alps. In Proceedings of the IAHR Congress, Vancouver, BC, Canada, 9–14 August 2009; p. 8. [Google Scholar]
- Aronica, G.T.; Bonaccorso, B. Climate change effects on hydropower potential in the Alcantara River basin in Sicily (Italy). Earth Interact. 2013, 17. [Google Scholar] [CrossRef]
- Bombelli, G.M.; Soncini, A.; Bianchi, A.; Bocchiola, D. Potentially modified hydropower production under climate change in the Italian Alps. Hydrol. Process. 2019. [Google Scholar] [CrossRef]
- Hamududu, B.; Killingtveit, A. Assessing climate change impacts on global hydropower. Energies 2012, 5, 305–322. [Google Scholar] [CrossRef]
- François, B.; Hingray, B.; Borga, M.; Zoccatelli, D.; Brown, C.; Creutin, J.-D. Impact of Climate Change on Combined Solar and Run-of-River Power in Northern Italy. Energies 2018, 11, 290. [Google Scholar] [CrossRef]
- Tobin, I.; Greuell, W.; Jerez, S.; Ludwig, F.; Vautard, R.; van Vliet, M.T.H.; Bréon, F.-M. Vulnerabilities and resilience of European power generation to 1.5 °C, 2 °C and 3 °C warming. Environ. Res. Lett. 2018, 13, 044024. [Google Scholar] [CrossRef]
- Van Vliet, M.T.H.; Vögele, S.; Rübbelke, D. Water constraints on European power supply under climate change: Impacts on electricity prices. Environ. Res. Lett. 2013, 8. [Google Scholar] [CrossRef]
- Lehner, B.; Czisch, G.; Vassolo, S. The impact of global change on the hydropower potential of Europe: A model-based analysis. Energy Policy 2005, 33, 839–855. [Google Scholar] [CrossRef]
- Giaccone, E.; Colombo, N.; Acquaotta, F.; Paro, L.; Fratianni, S. Climate variations in a high altitude alpine basin and their effects on a glacial environment (Italian Western Alps). Atmosfera 2015, 28, 117–128. [Google Scholar] [CrossRef]
- Avanzi, F.; Yamaguchi, S.; Hirashima, H.; De Michele, C. Bulk volumetric liquid water content in a seasonal snowpack: Modeling its dynamics in different climatic conditions. Adv. Water Resour. 2015, 86, 1–13. [Google Scholar] [CrossRef]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Singh, P. Snow and Glacier Hydrology, 1st ed.; Springer: Dordrecht, The Netherlands, 2011; ISBN 9789048156351. [Google Scholar]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Bartolini, E.; Allamano, P.; Laio, F.; Claps, P. Runoff regime estimation at high-elevation sites: A parsimonious water balance approach. Hydrol. Earth Syst. Sci. 2011, 15, 1661–1673. [Google Scholar] [CrossRef]
- U.S. Department of Agriculture. Mockus Victor Design Hydrographs. In National Engineering Handbook; U.S. Department of Agriculture: Washington, DC, USA, 1972; p. 127. [Google Scholar]
- Nash, J.E. The form of the instantaneous unit hydrograph. Int. Assoc. Hydrol. Sci. 1957, 45, 114–121. [Google Scholar]
- Rosso, R. Nash Model Relation to Horton Order Ratios. Water Resour. Res. 1984, 20, 914–920. [Google Scholar] [CrossRef]
- Avanzi, F.; De Michele, C.; Ghezzi, A.; Jommi, C.; Pepe, M. A processing-modeling routine to use SNOTEL hourly data in snowpack dynamic models. Adv. Water Resour. 2014, 73, 16–29. [Google Scholar] [CrossRef]
- Rolland, C. Spatial and seasonal variations of air temperature lapse rates in alpine regions. J. Clim. 2003, 16, 1032–1046. [Google Scholar] [CrossRef]
- Toreti, A.; Desiato, F. Temperature trend over Italy from 1961 to 2004. Theor. Appl. Climatol. 2008, 91, 51–58. [Google Scholar] [CrossRef]
- Dueck, G.; Scheuer, T. Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing. J. Comput. Phys. 1990, 90, 161–175. [Google Scholar] [CrossRef]
- Moscato, P.; Fontanari, J.F. Stochastic versus deterministic update in simulated annealing. Phys. Lett. A 1990, 146, 204–208. [Google Scholar] [CrossRef]
- Winker, P. Optimization Heuristics in Econometrics: Application of Threshold Accepting; Wiley: Hoboken, NJ, USA, 2001; ISBN 978-0-471-85631-3. [Google Scholar]
- Peizhen, Z.; Molnar, P.; Downs, W.R. Increased sedimentation rates and grain sizes 2-4 Myr ago due to the influence of climate change on erosion rates. Nature 2001, 410, 891–897. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Canossi, M.; Petaccia, A.; Rosso, R. Bivariate Statistical Approach to Check Adequacy of Dam Spillway. J. Hydrol. Eng. 2005, 10, 50–57. [Google Scholar] [CrossRef]




| Region | Number of Hydropower Plants | Hydropower Potential (MW) |
|---|---|---|
| Piemonte | 905 | 2738.6 |
| Valle d’Aosta | 173 | 974.9 |
| Lombardia | 652 | 5141.4 |
| Trentino Alto Adige | 811 | 3348.4 |
| Veneto | 393 | 1170.6 |
| Friuli Venezia Giulia | 233 | 520.9 |
| Liguria | 88 | 90.4 |
| Emilia Romagna | 194 | 344.7 |
| Toscana | 212 | 372.9 |
| Umbria | 45 | 529.6 |
| Marche | 181 | 250.5 |
| Lazio | 99 | 410.3 |
| Abruzzo | 71 | 1013.3 |
| Molise | 34 | 87.9 |
| Campania | 58 | 342.4 |
| Puglia | 8 | 3.3 |
| Basilicata | 14 | 133.3 |
| Calabria | 54 | 772.5 |
| Sicilia | 25 | 150.7 |
| Sardegna | 18 | 466.4 |
| Study | Location | Climate Projections/Models | Hydrological Model | Other Associated Models | Input of the Model | Evaluation Period | Simulation and Optimization Approach | Main Results |
| [67] | Adda river basin | - | Glacier evolution runoff model neglecting hydrological losses | Glacier area and volume changes using geographic information system (GIS) and digital terrain model (DTM) | Aerial photos, orthophotos, glacier area records, DTM and digital surface model (DSM) products, precipitation | 1981–2007 | - |
|
| [68] | Val d’Aosta and Toce basin | Two RCMs, the REMO [69] and the RegCM3 [70] model | TOPKAPI [71] and FEST-WB [72] model | Electricity demand scenarios and electricity prices models | Temperature, precipitation and electricity prices | 2001–2050 | Deterministic optimization (SOLARIS and BPMPD solver) for the management of hydropower |
|
| [73] | Noce river basin | Ensemble of four climate models (CM) under the SRES A1B emission scenario | GEOTRANSF model [74] | - | Precipitation, temperature and streamflow | 2040–2070 | Particle Swarming Optimizer (PSO) |
|
| [25] | Anza basin at Ceppo Morelli dam | Deterministic climate scenario (temperature increase and liquid only precipitation) and RCP 4.5 and RCP 8.5 | HyM runoff model | Solid-liquid temperature thresholding | Precipitation, temperature streamflow, snow depth, and glacier inventory | 2015–2050 | - |
|
| [75] | Pedra ’e Othoni reservoir in Sardinia | RCPs 4.5 and 8.5 | STELLA Reservoir storage balance model | Precipitation, temperature, agricultural data, and four socio-economic development scenarios | 2035–2065 | - |
| |
| [18] | Italian Alpine-scale (42 basins) | Deterministic climate scenario (combination of temperature increase and liquid only precipitation) | HyM runoff model | Solid-liquid temperature thresholding | Precipitation, temperature and streamflow | 2016–2065 | - |
|
| [47] | Valle d’Aosta | RCM–REMO (25 × 25 km) | TOPKAPI model and SOLARIS model | Electricity demand model | Precipitation, temperature and energy prices | 2011–2050 | - |
|
| [76] | Oglio river basin and Lys river basin | PCM IPCC-SRES A2-scenario | WATFLOOD hydrological model | - | Precipitation, temperature | 2000–2099 | - |
|
| [77] | Alcantara river basin | HadCM3 with A2 and B2 scenarios | IHACRES model | First-order Markov chain and an autoregressive moving average (ARMA) model | Precipitation, temperature, and streamflow | 2013–2037 | - |
|
| [78] | Adda river basin | ECHAM6, CCSM4, EC-EARTH with RCP 2.6, RCP4 and RCP 8.5 scenarios | Poly-Hydro model | Poly-Power model | Precipitation, temperature, and streamflow | 2006–2100 | Mixed Integer Quadratic Programming |
|
| [11] | Toce Alpine river basin | REMO and RegCM3 | FEST-WB model | Model of the hydropower system for maximizing revenue | Temperature, precipitation, and streamflow | 2001–2050 | - |
|
| [79] | National scale derived from worldwide results | 12 GCM models | GIS based model | GRDC dataset for streamflow | 2050 | - |
| |
| [80] | Catchments of Aurino and Posina | CMIP5 with RCP 8.5 | ICHYMOD model | Energy model | Temperature, precipitation, solar irradiance, and streamflow | 1990–2099 | - |
|
| [81] | National scale derived from European-wide results | Five RCM from EUROCORDEX | VIC hydrological model | - | Temperature and precipitation | 1971–2084 | - |
|
| [82] | National scale derived from European-wide results | GCM with IPCC SRES A2 and B1 scenarios. | VIC hydrological model | - | Temperature, precipitation, and daily river flow | 1971–2060 | - |
|
| [83] | National scale derived from European-wide results | HadCM3 model and the ECHAM4/OPYC3 model | WaterGAP model | - | Temperature, precipitation, GRDC dataset for streamflow, and UCTE data tables for hydropower stations | 2070 | - |
|
| [26] | Anza river basin at Ceppo Morelli dam | Deterministic climate scenario (temperature increase and liquid only precipitation) | HyM runoff model | Solid-liquid temperature thresholdingElectricity price and scenarios | Precipitation, temperature, streamflow, snow depth, glacier inventory, and electricity price | 2015–2065 | - |
|
| Sabbione Basin and Morasco Power Plant | |
|---|---|
| Catchment area (km2) | ~16.59 |
| Maximum elevation (m.a.s.l.) | 3358 |
| Minimum elevation (m.a.s.l.) | 2399 |
| Average elevation (m.a.s.l.) | 2740 |
| Glacier coverage (%) | 30 |
| Glacier elevation range (m.a.s.l.) | ~2610–3230 |
| Maximum reservoir elevation (m.a.s.l.) | 2460 |
| Minimum reservoir elevation (m.a.s.l.) | 2412 |
| Reservoir Volume available (Mm3) | 44 |
| Maximum discharge (m3/s) | 10.1 |
| Maximum gross jump (m) | 640 |
| Type of turbine | Pelton |
| Power installed (MW) | 45.6 |
| Average production (GWh/year) | 45.4 |
| Efficiency (-) | 0.725 |
| Order | N. of Streams | Mean Length Stream (km) | RB | RL | RA | V (m/s) | LΩ (km) | nLIQ | kLIQ (hours) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 20 | 0.38 | 4.472 | 3.638 | 5.619 | 2.5 | 5.03 | 3.014 | 0.235 |
| 2 | 5 | 0.90 | |||||||
| 3 | 1 | 5.03 |
| Scenario | Code Name | Description |
|---|---|---|
| Business as Usual | BaU | In the future the periodicity will remain the same as the historical seasonality (2005–2016) |
| Doubled Seasonality | DS | Seasonality remains but the amplitude is doubled |
| Without Seasonality | WS | Seasonality is discarded, so the prices stay stable all over the year |
| Inverted Seasonality | IS | The seasonality is shifted by six months |
| Shifted Seasonality | SS | Seasonality is shifted onward by three months. This means that the prices will peak in spring and autumn instead of winter and summer. |
| Scenario | Variation Income (-) | |
|---|---|---|
| Reservoir | Run of River | |
| 1 | − | − |
| 2 | −7.6% | −9.4% |
| 3 | −6.5% | −8.1% |
| 4 | −5.4% | −7.3% |
| 5 | −3.4% | −5.8% |
| 6 | −3.0% | −7.2% |
| 7 | +0.4% | −3.7% |
| 8 | +2.8% | −2.3% |
| 9 | +4.4% | −0.4% |
| Scenario | Variation Income (-) | ||
|---|---|---|---|
| Sabbione | Ceppo Morelli [26] | ||
| Reservoir | Run of River | Run of River | |
| BaU | − | − | − |
| DS | +8.0% | +6.3% | +5% |
| IS | +0.8% | −6.6% | −7% |
| SS | +0.5% | −18.3% | −11% |
| WS | −3.0% | −6.2% | −5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonato, M.; Ranzani, A.; Patro, E.R.; Gaudard, L.; De Michele, C. Water-Energy Nexus for an Italian Storage Hydropower Plant under Multiple Drivers. Water 2019, 11, 1838. https://doi.org/10.3390/w11091838
Bonato M, Ranzani A, Patro ER, Gaudard L, De Michele C. Water-Energy Nexus for an Italian Storage Hydropower Plant under Multiple Drivers. Water. 2019; 11(9):1838. https://doi.org/10.3390/w11091838
Chicago/Turabian StyleBonato, Mattia, Alessandro Ranzani, Epari Ritesh Patro, Ludovic Gaudard, and Carlo De Michele. 2019. "Water-Energy Nexus for an Italian Storage Hydropower Plant under Multiple Drivers" Water 11, no. 9: 1838. https://doi.org/10.3390/w11091838
APA StyleBonato, M., Ranzani, A., Patro, E. R., Gaudard, L., & De Michele, C. (2019). Water-Energy Nexus for an Italian Storage Hydropower Plant under Multiple Drivers. Water, 11(9), 1838. https://doi.org/10.3390/w11091838







