Sediment Morphology and the Flow Velocity Field in a Gully Pot: An Experimental Study
Abstract
1. Introduction
2. Materials and Methods
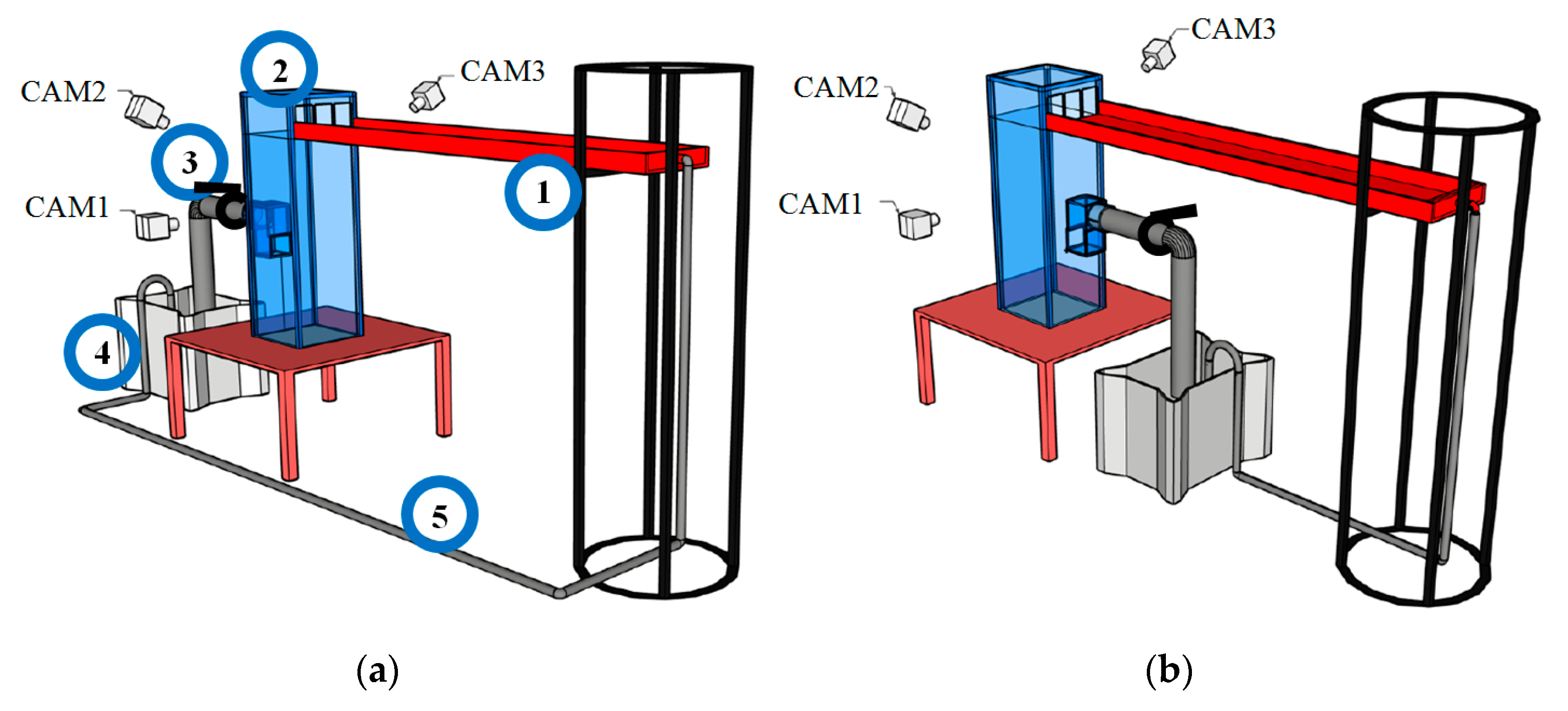
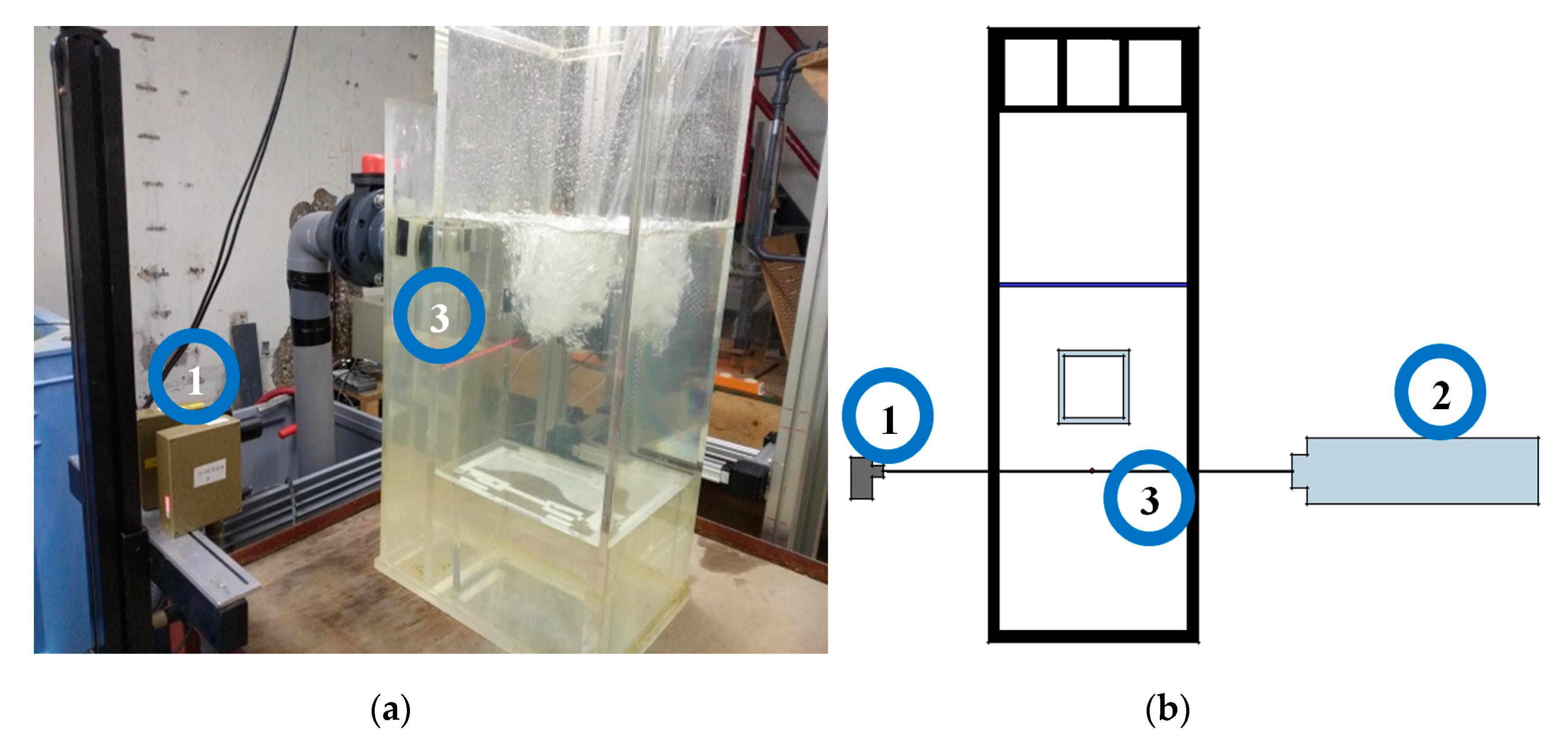
2.1. Experimental Setup
2.2. PIV
2.2.1. Tracer Particles
2.2.2. Laser
2.2.3. Imaging
2.2.4. Camera Calibration
2.3. LDA
2.3.1. LDA Equipment
2.3.2. LDA Post-Processing
2.4. Measurement Devices
2.4.1. Flowmeter
2.4.2. Thermometer
2.5. Test Conditions
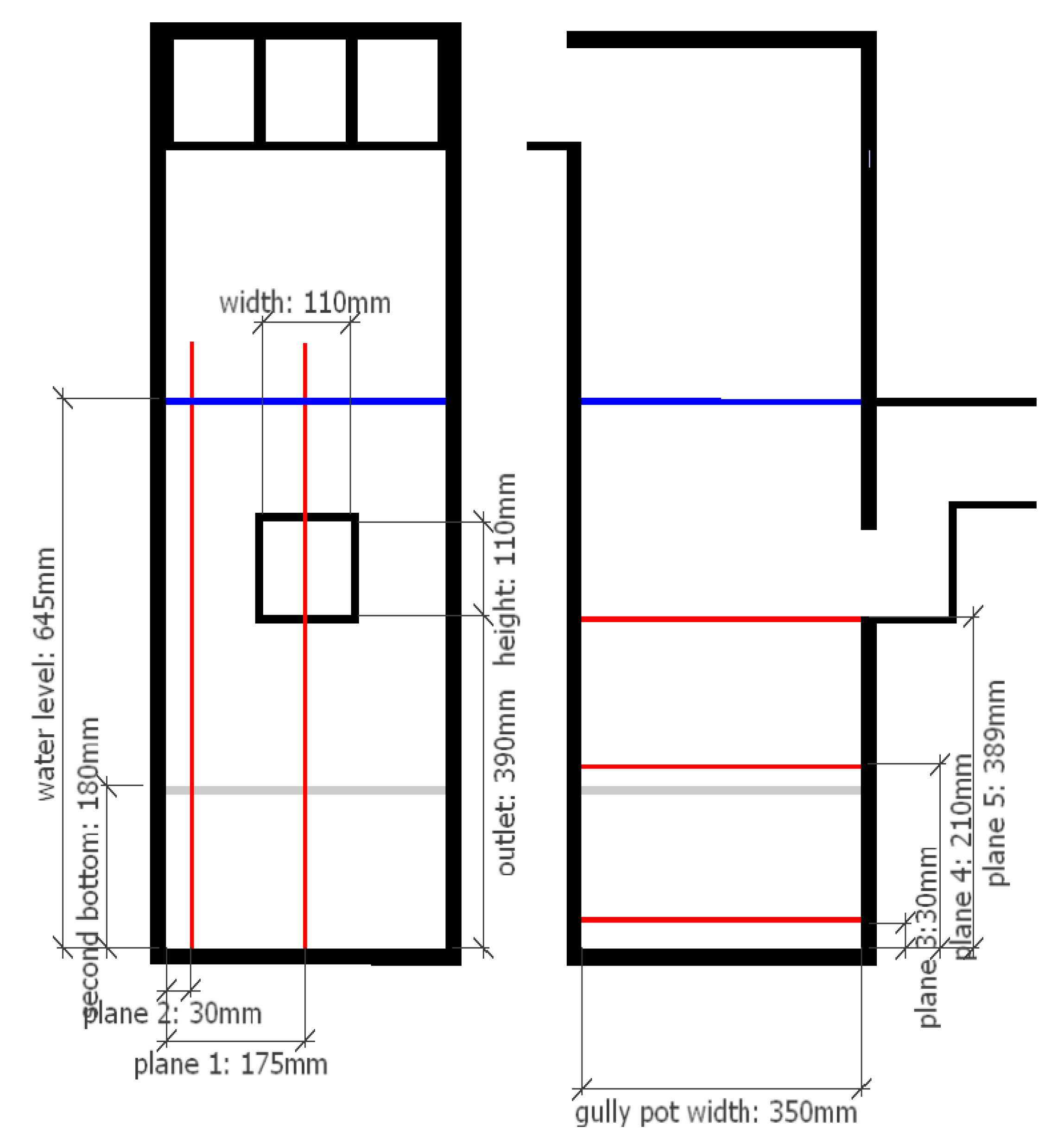
2.5.1. Planes of Interest
2.5.2. Discharge
2.5.3. Sand Trap Depth
2.5.4. Outlet Position
2.5.5. The Presence of a Sediment Bed
2.6. Stereo Photography
3. Results and Discussion
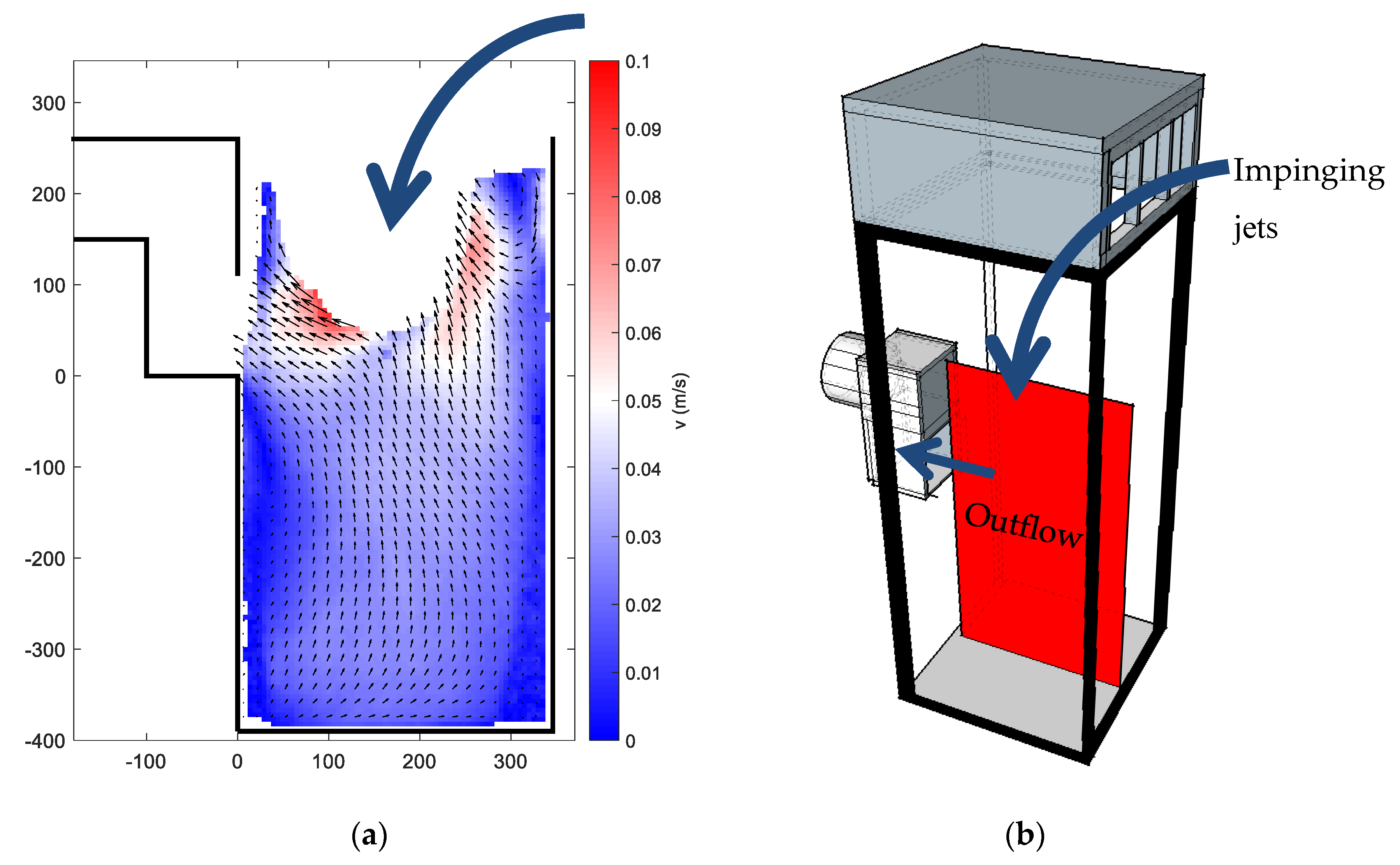
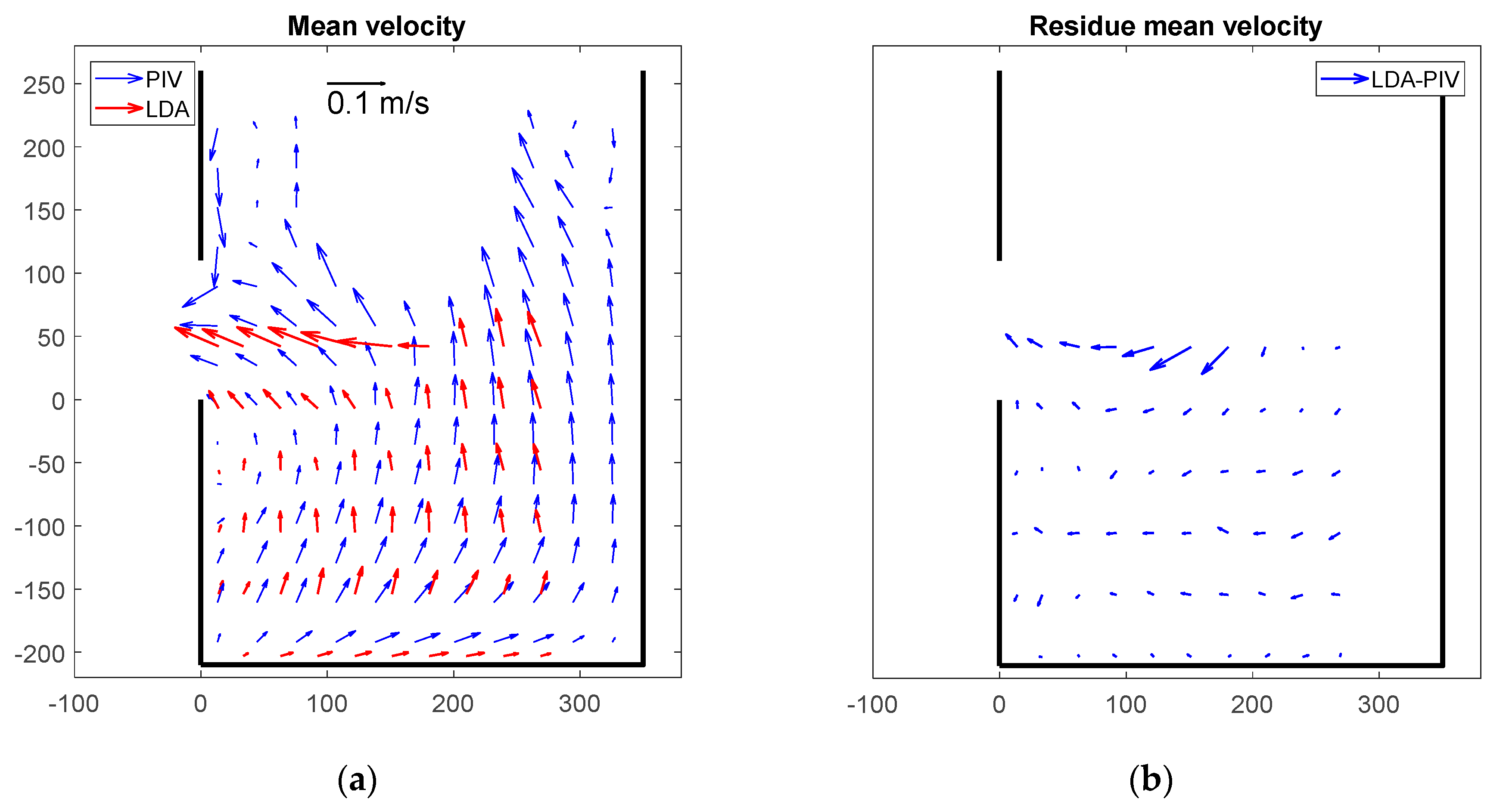
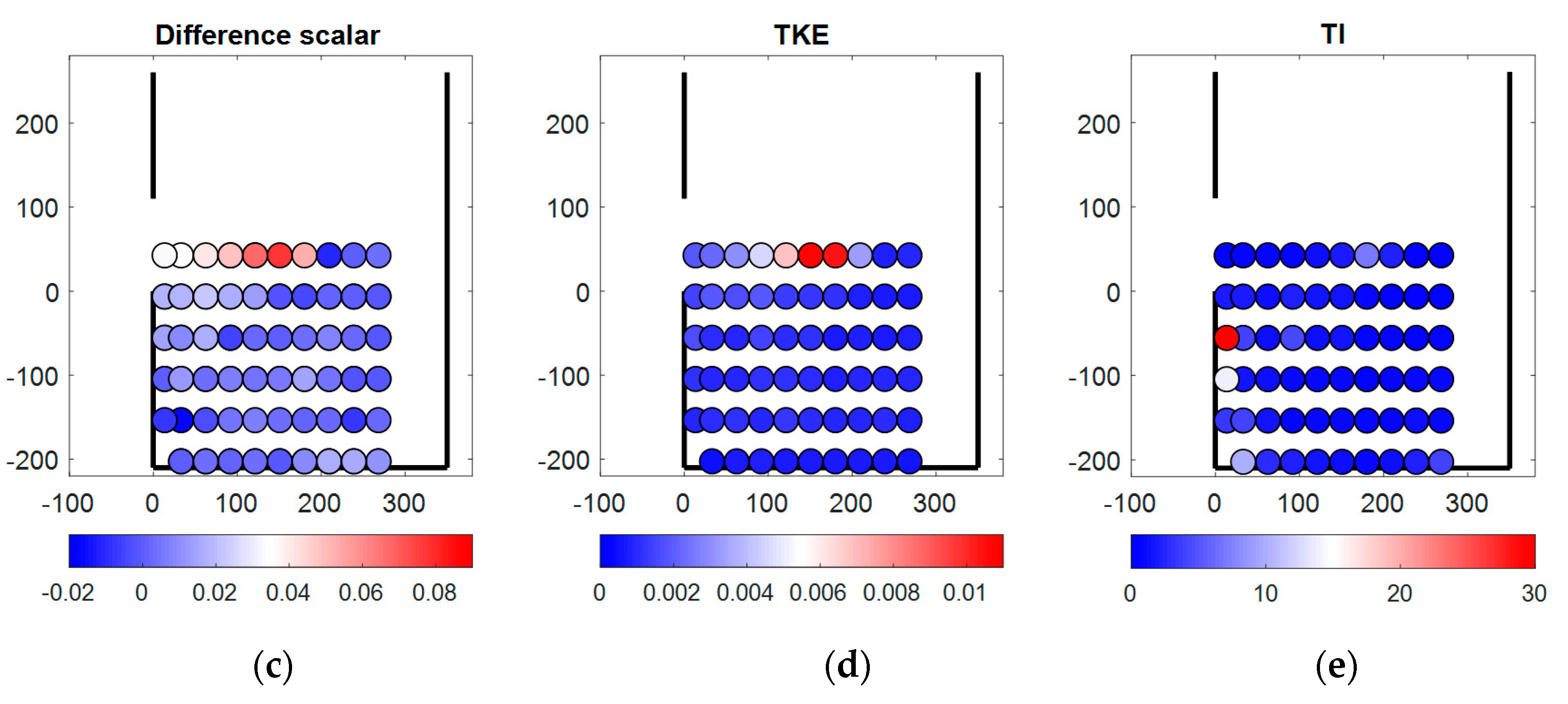
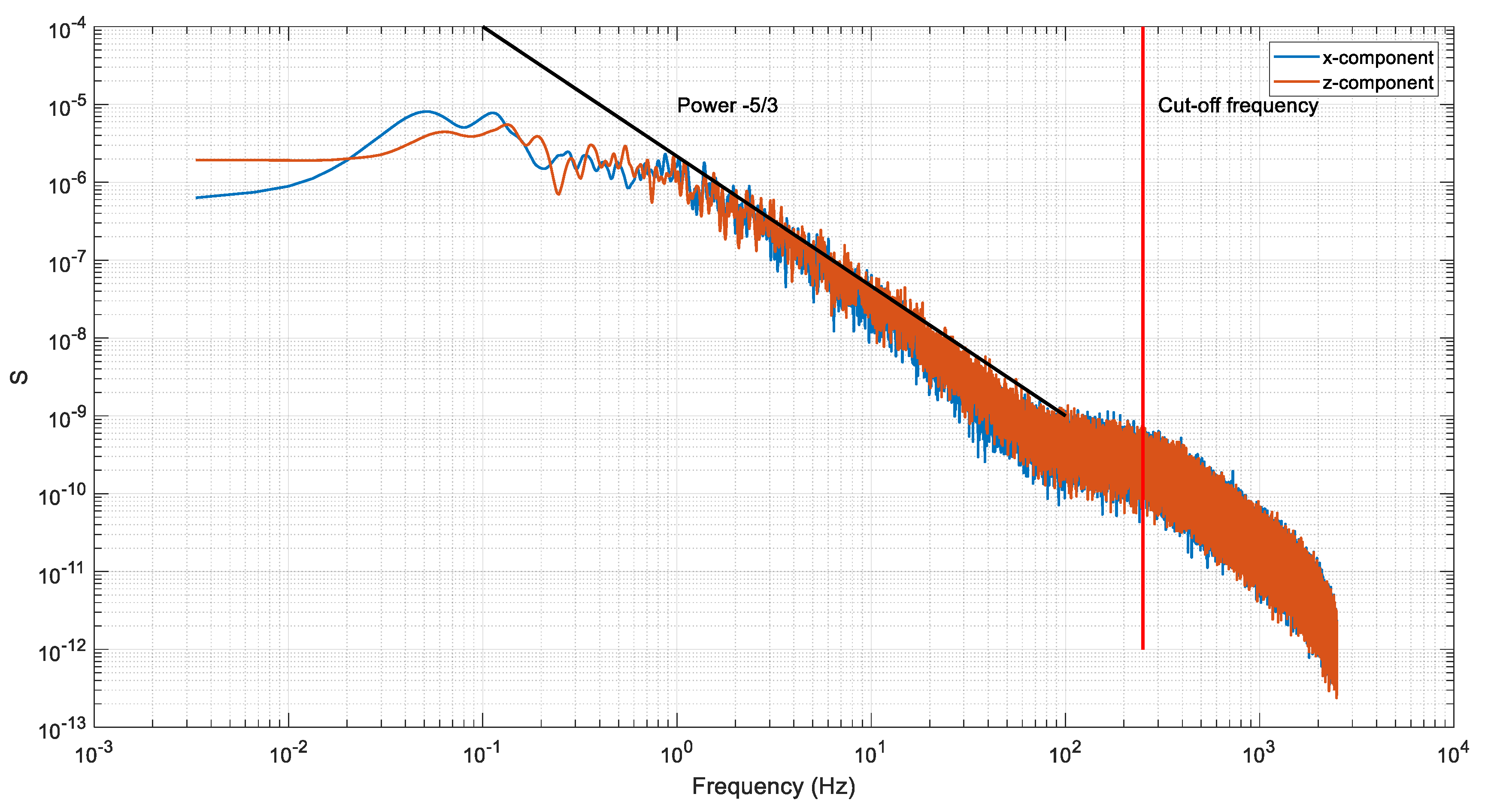
3.1. Preliminary Observations in PIV and LDA Measurements
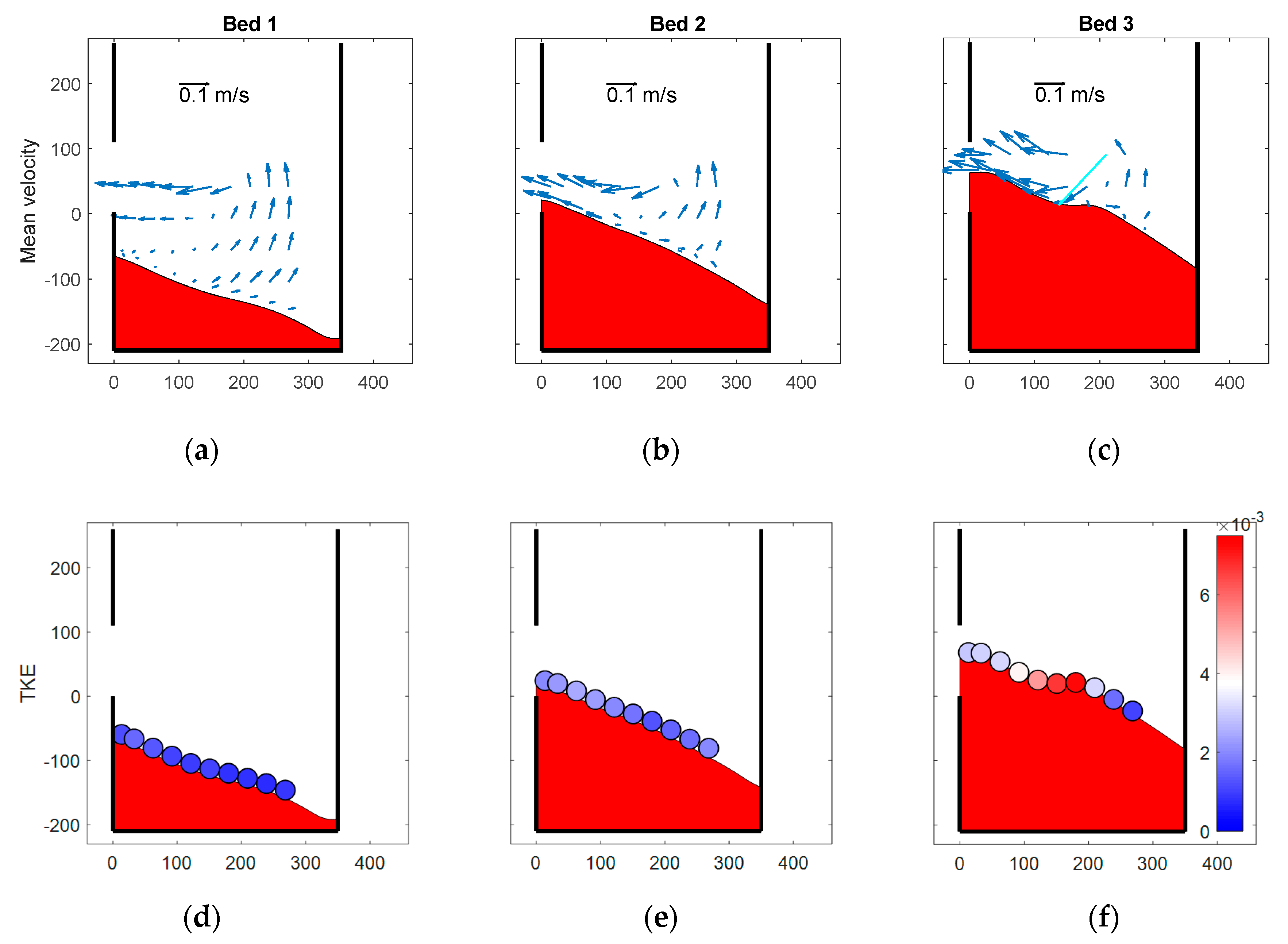
3.2. The Effect of the Sediment Bed
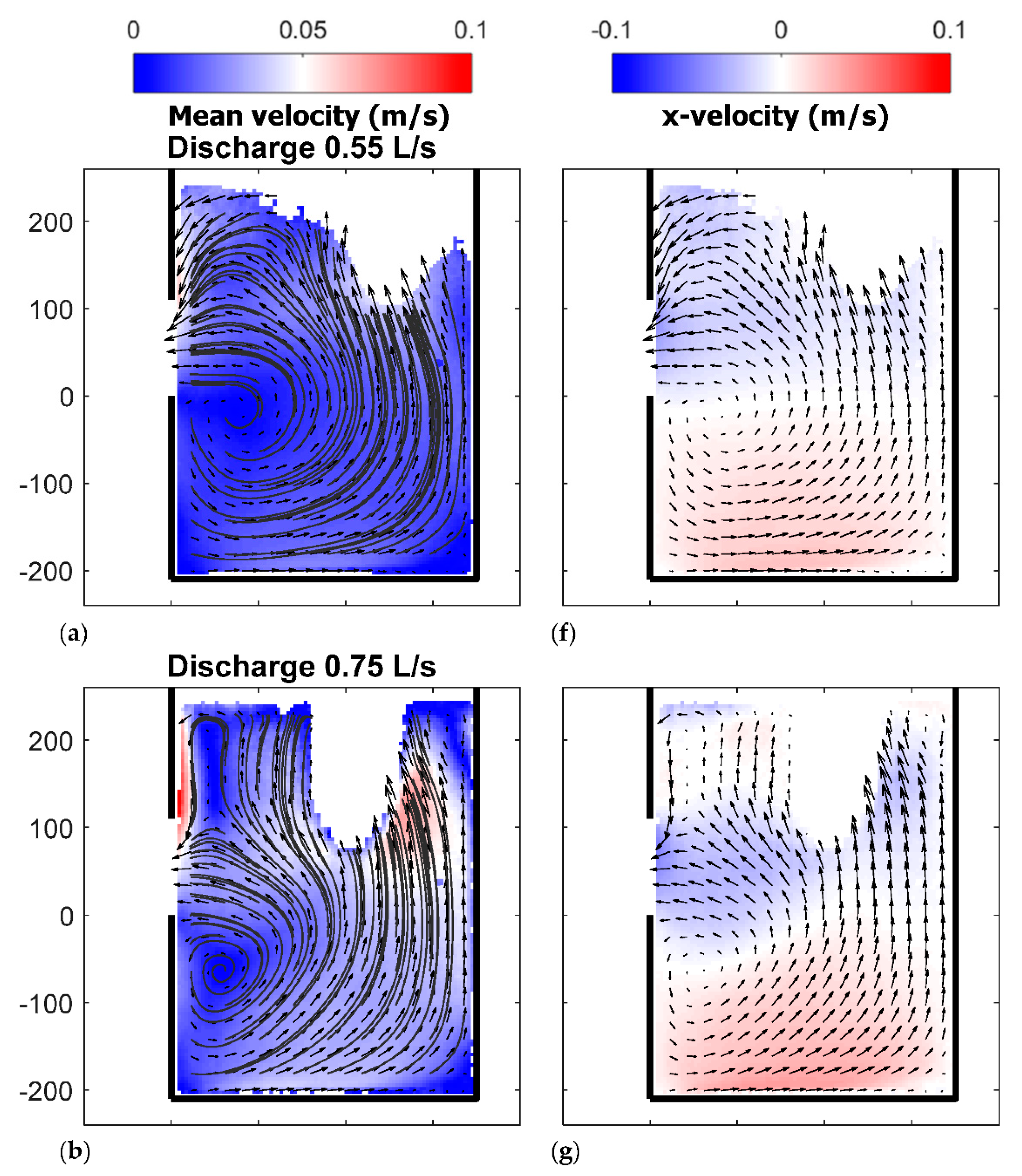
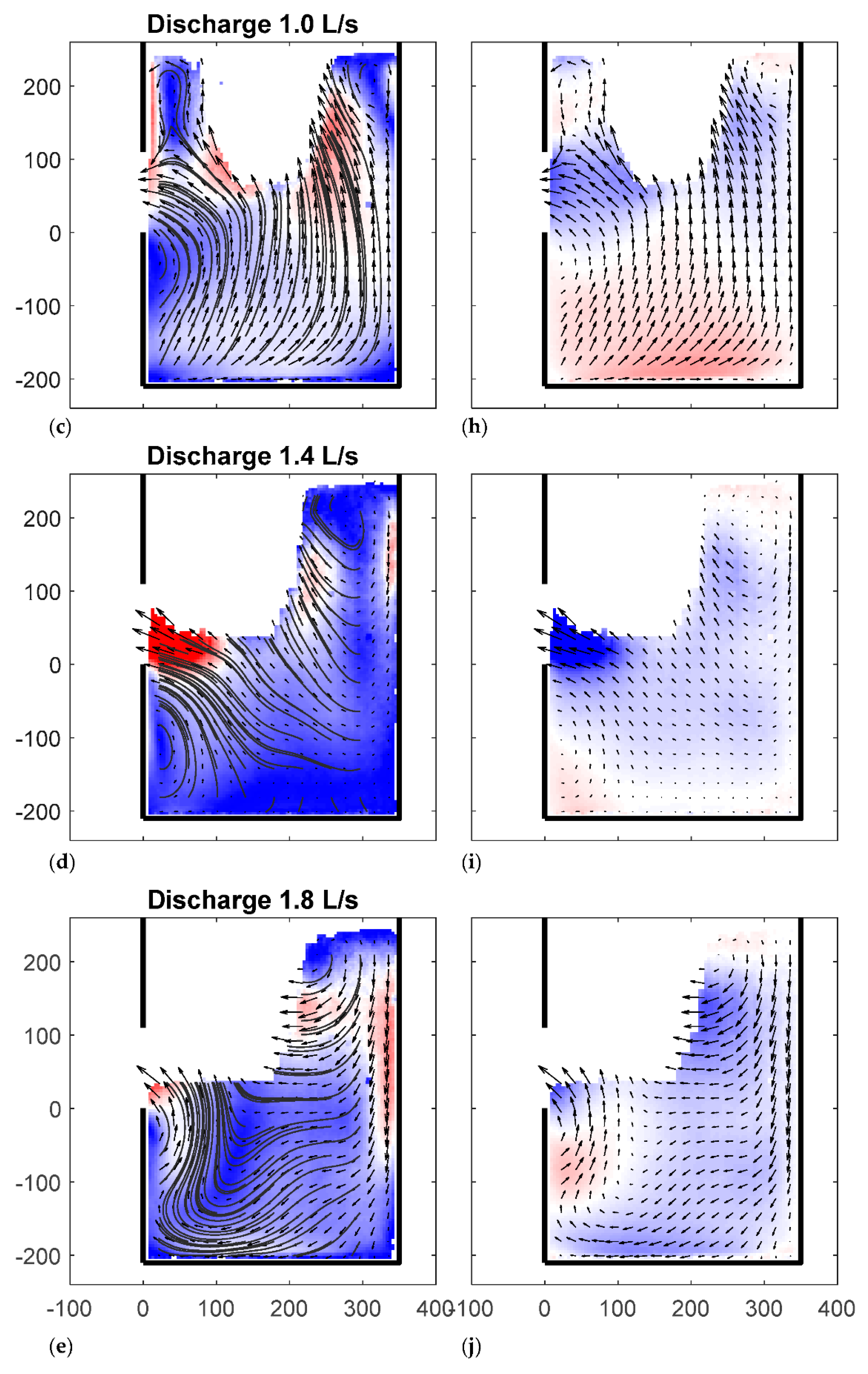
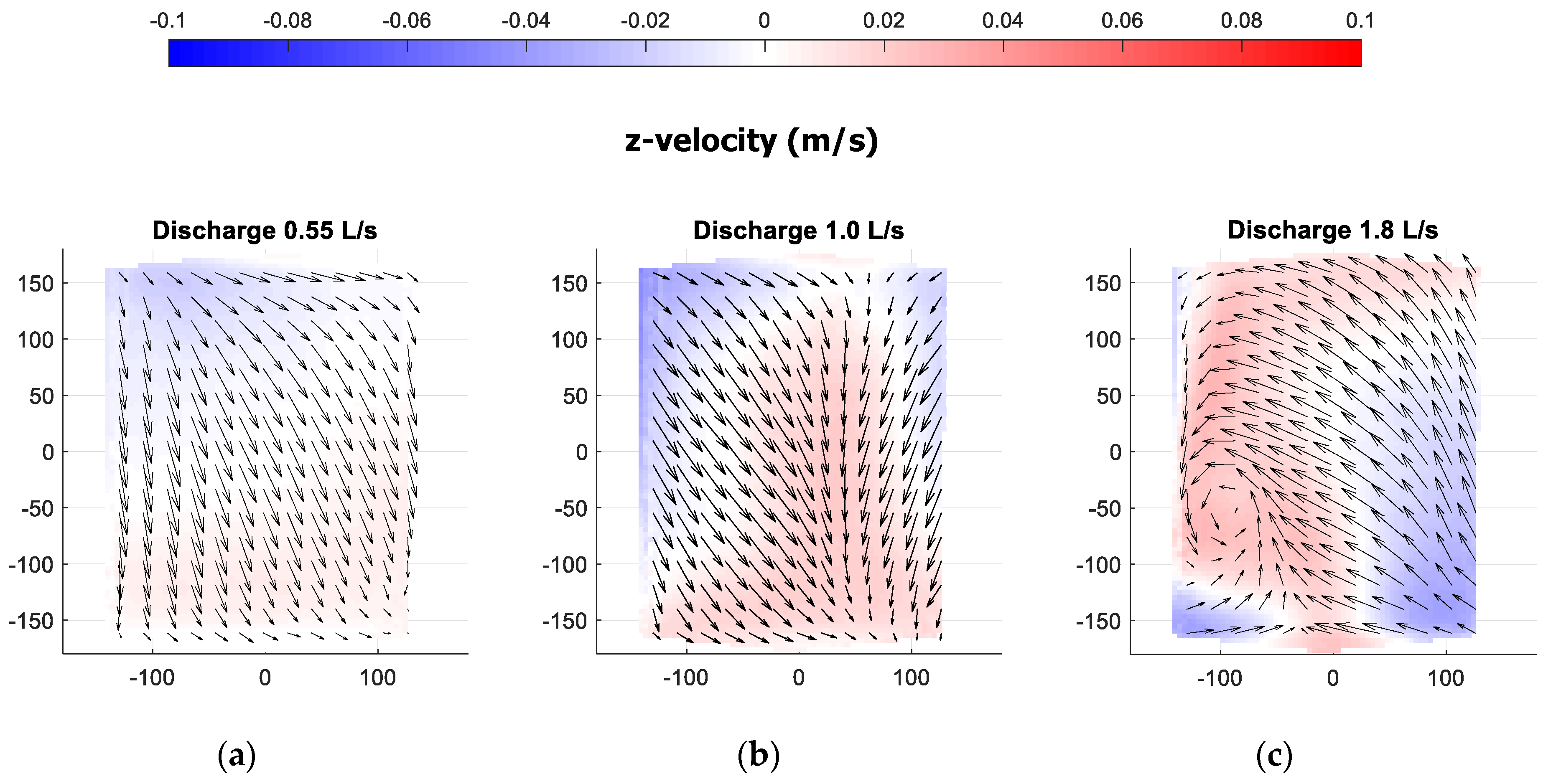
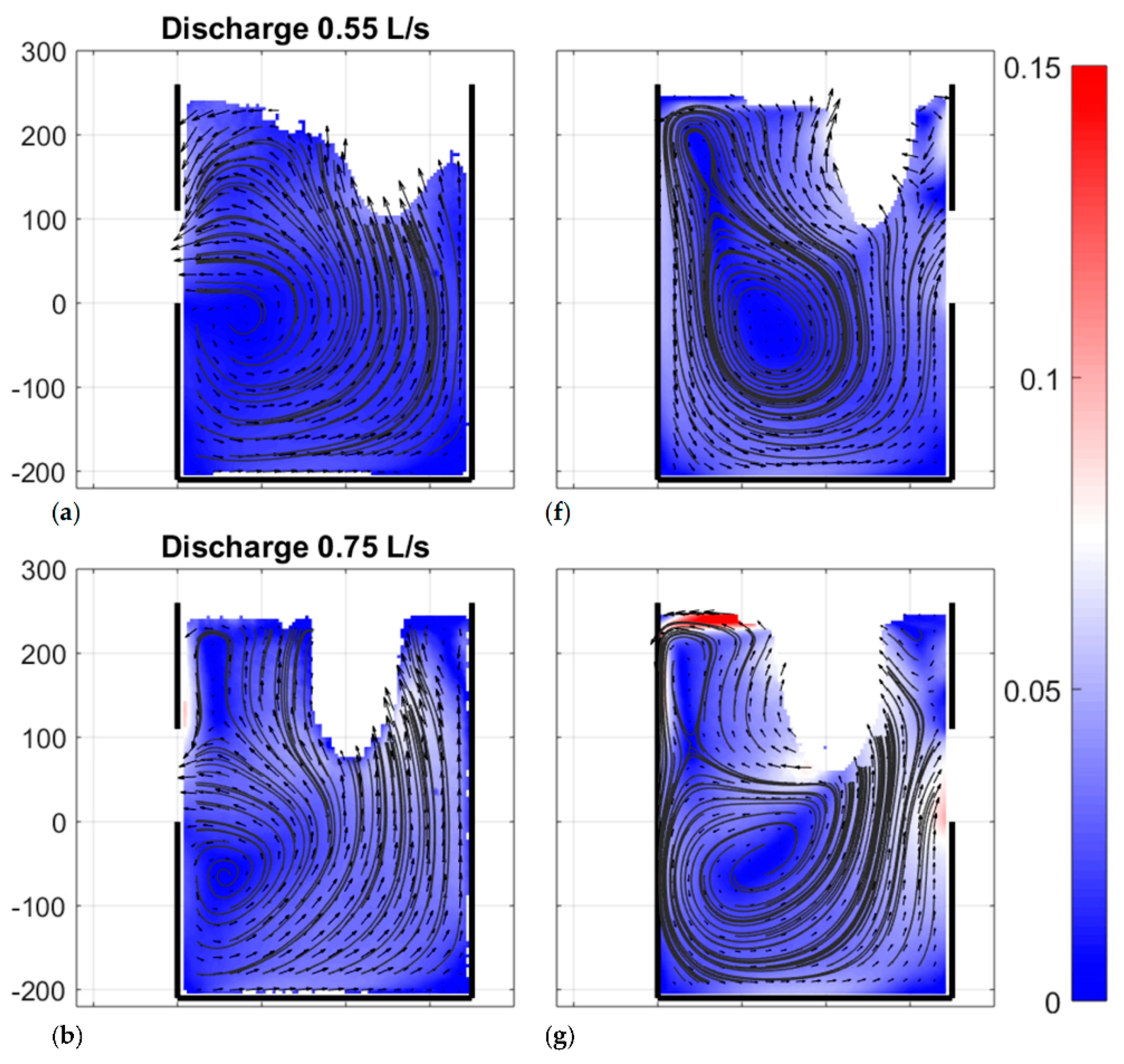
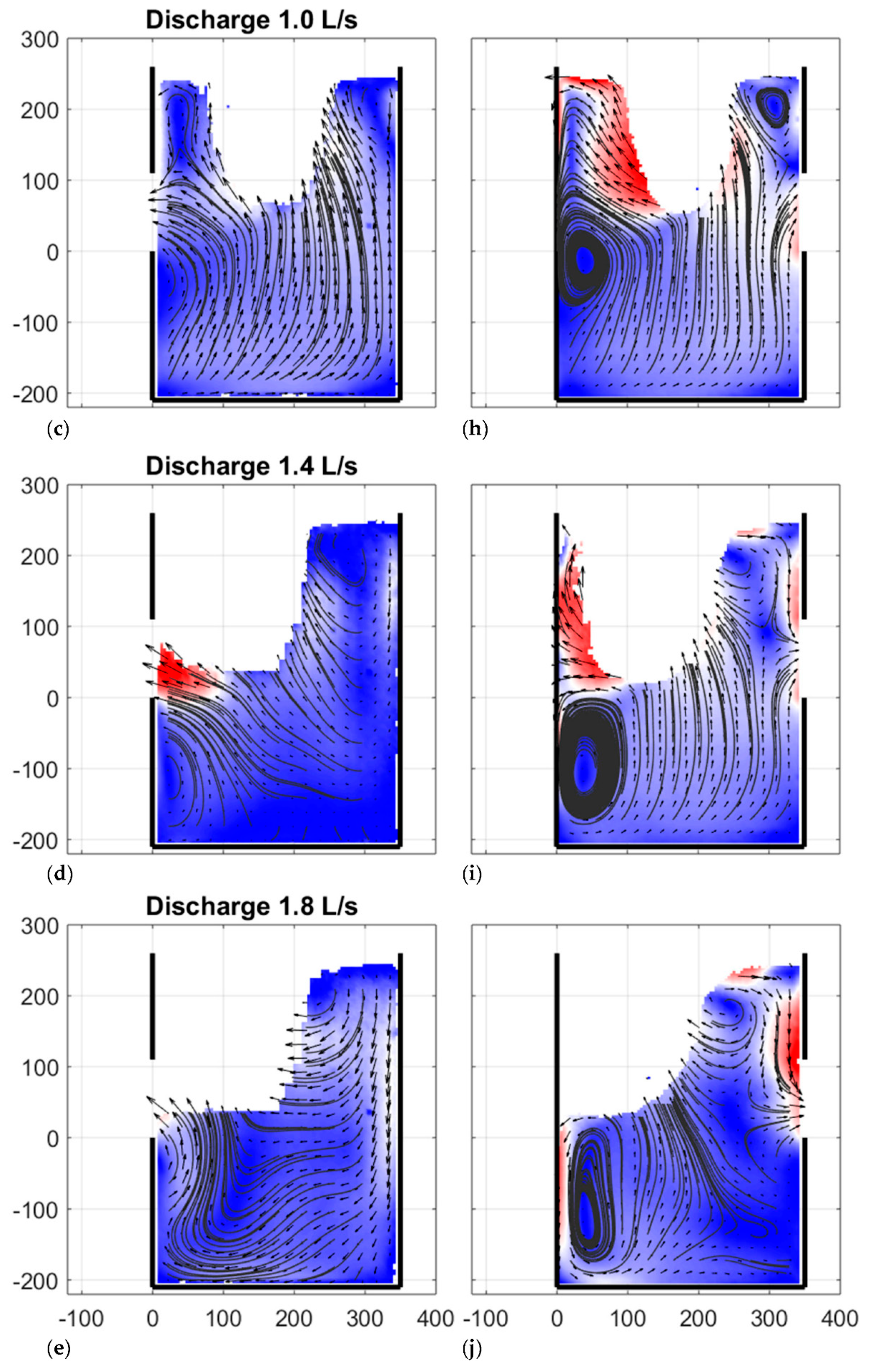
3.3. The Effect of the Discharge
3.4. The Effect of the Gully Pot Depth
3.5. The Effect of the Outlet Position
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Test Name | POI | Discharge (L/s) | Gully Pot Depth (m) | Outlet Position |
|---|---|---|---|---|
| F055DhalfV1 | P1 | 0.55 | 0.21 | Back |
| F075DhalfV1 | P1 | 0.75 | 0.21 | Back |
| F100DhalfV1 | P1 | 1.0 | 0.21 | Back |
| Bed1 F100DhalfV1 | P1 + bed 1 | 1.0 | 0.21 | Back |
| Bed2 F100DhalfV1 | P1 + bed 2 | 1.0 | 0.21 | Back |
| Bed3 F100DhalfV1 | P1 + bed 3 | 1.0 | 0.21 | Back |
| F140DhalfV1 | P1 | 1.4 | 0.21 | Back |
| F180DhalfV1 | P1 | 1.8 | 0.21 | Back |
| F055DfullV1 | P1 | 0.55 | 0.39 | Back |
| F075DfullV1 | P1 | 0.75 | 0.39 | Back |
| F100DfullV1 | P1 | 1.0 | 0.39 | Back |
| F140DfullV1 | P1 | 1.4 | 0.39 | Back |
| F180DfullV1 | P1 | 1.8 | 0.39 | Back |
| F055DhalfV2 | P2 | 0.55 | 0.21 | Back |
| F100DhalfV2 | P2 | 1.0 | 0.21 | Back |
| F180DhalfV2 | P2 | 1.8 | 0.21 | Back |
| F055DfullV2 | P2 | 0.55 | 0.39 | Back |
| F100DfullV2 | P2 | 1.0 | 0.39 | Back |
| F180DfullV2 | P2 | 1.8 | 0.39 | Back |
| F055DfullV3 | P3 | 0.55 | 0.39 | Back |
| F100DfullV3 | P3 | 1.0 | 0.39 | Back |
| F180DfullV3 | P3 | 1.8 | 0.39 | Back |
| F055DfullV4 | P4 | 0.55 | 0.39 | Back |
| F100DfullV4 | P4 | 1.0 | 0.39 | Back |
| F180DfullV4 | P4 | 1.8 | 0.39 | Back |
| F055DhalfV4 | P4 | 0.55 | 0.21 | Back |
| F100DhalfV4 | P4 | 1.0 | 0.21 | Back |
| F180DhalfV4 | P4 | 1.8 | 0.21 | Back |
| F055DfullV5 | P5 | 0.55 | 0.39 | Back |
| F100DfullV5 | P5 | 1.0 | 0.39 | Back |
| F180DfullV5 | P5 | 1.8 | 0.39 | Back |
| F055DhalfV5 | P5 | 0.55 | 0.21 | Back |
| F100DhalfV5 | P5 | 1.0 | 0.21 | Back |
| F180DhalfV5 | P5 | 1.8 | 0.21 | Back |
| F055DhalfV1 | P1 | 0.55 | 0.21 | Front |
| F075DhalfV1 | P1 | 0.75 | 0.21 | Front |
| F100DhalfV1 | P1 | 1.0 | 0.21 | Front |
| F140DhalfV1 | P1 | 1.4 | 0.21 | Front |
| F180DhalfV1 | P1 | 1.8 | 0.21 | Front |
| F055DfullV1 | P1 | 0.55 | 0.39 | Front |
| F075DfullV1 | P1 | 0.75 | 0.39 | Front |
| F100DfullV1 | P1 | 1.0 | 0.39 | Front |
| F140DfullV1 | P1 | 1.4 | 0.39 | Front |
| F180DfullV1 | P1 | 1.8 | 0.39 | Front |
| F055DfullV3 | P3 | 0.55 | 0.39 | Front |
| F100DfullV3 | P3 | 1.0 | 0.39 | Front |
| F180DfullV3 | P3 | 1.8 | 0.39 | Front |
| F055DfullV4 | P4 | 0.55 | 0.39 | Front |
| F100DfullV4 | P4 | 1.0 | 0.39 | Front |
| F180DfullV4 | P4 | 1.8 | 0.39 | Front |
| F055DhalfV4 | P4 | 0.55 | 0.21 | Front |
| F100DhalfV4 | P4 | 1.0 | 0.21 | Front |
| F180DhalfV4 | P4 | 1.8 | 0.21 | Front |
| F055DfullV5 | P5 | 0.55 | 0.39 | Front |
| F100DfullV5 | P5 | 1.0 | 0.39 | Front |
| F180DfullV5 | P5 | 1.8 | 0.39 | Front |
| F055DhalfV5 | P5 | 0.55 | 0.21 | Front |
| F100DhalfV5 | P5 | 1.0 | 0.21 | Front |
| F180DhalfV5 | P5 | 1.8 | 0.21 | Front |
References
- Young, R.A.; Wiersma, J.L. The role of rainfall impact in soil detachment and transport. Water Resour. Res. 1973, 9, 1629–1636. [Google Scholar] [CrossRef]
- Van Bijnen, M.; Korving, H.; Langeveld, J.G.; Clemens, F.H.L.R. Quantitative impact assessment of sewer condition on health risk. Water 2018, 10, 245. [Google Scholar] [CrossRef]
- Delleur, J.W. New results and research needs on sediment movement in urban drainage. Water Resour. Plan. Manag. 2001, 127, 186–193. [Google Scholar] [CrossRef]
- Chebbo, G.; Bachoc, A. Characterization of suspended solids in urban wet weather discharges. Water Sci. Technol. 1992, 25, 171–179. [Google Scholar] [CrossRef]
- Fulcher, G.A. Urban stormwater quality from a residential catchment. Sci. Total Environ. 1994, 146–147, 535–542. [Google Scholar] [CrossRef]
- Gromaire, M.C.; Garnaud, S.; Saad, M.; Chebbo, G. Contribution of different sources to the pollution of wet weather flows in combined sewers. Water Res. 2001, 35, 521–533. [Google Scholar] [CrossRef]
- Post, J.A.B.; Pothof, I.W.M.; Dirksen, J.; Baars, E.J.; Langeveld, J.G.; Clemens, F.H.L.R. Monitoring and statistical modelling of sedimentation in gully pots. Water Res. 2016, 88, 245–256. [Google Scholar] [CrossRef] [PubMed]
- De Man, H.; Van den Berg, H.H.J.L.; Leenen, E.J.T.M.; Schijven, J.F.; Schets, F.M.; Van der Vliet, J.C.; Van Knapen, F.; De Roda Husman, A.M. Quantitative assessment of infection risk from exposure to waterborne pathogens in urban floodwater. Water Res. 2014, 48, 90–99. [Google Scholar] [CrossRef]
- Ten Veldhuis, J.A.E.; Clemens, F.H.L.R. The efficiency of asset management strategies to reduce urban flood risk. Water Sci. Technol. 2011, 64, 1317–1324. [Google Scholar] [CrossRef]
- Chen, Y.; Cowling, P.; Polack, F.; Remde, S.; Mourdjis, P. Dynamic optimisation of preventative and corrective maintenance schedules for a large scale urban drainage system. Eur. J. Oper. Res. 2017, 257, 494–510. [Google Scholar] [CrossRef]
- Rietveld, M.W.J.; Clemens, F.H.L.R.; Langeveld, J.G. Monitoring and statistical modelling of the solids accumulation rate in gully pots. Urban Water J. 2020, 17, 549–559. [Google Scholar] [CrossRef]
- Butler, D.; Karunaratne, S.H.P.G. The suspended solids trap efficiency of the roadside gully pot. Water Res. 1995, 29, 719–729. [Google Scholar] [CrossRef]
- Rietveld, M.W.J.; Clemens, F.H.L.R.; Langeveld, J.G. Solids dynamics in gully pots. Urban Water J. 2020, 17, 669–680. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, D.Z.; Li, L. Numerical modeling on sediment capture in catch basins. Water Sci. Technol. 2018, 77, 1346–1354. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, D.Z.; Rajaratnam, N.; Van Duin, B. Experimental study of hydraulics and sediment capture efficiency in catchbasins. Water Sci. Technol. 2016, 74, 2717–2726. [Google Scholar] [CrossRef]
- Howard, A.K.; Mohseni, O.; Gulliver, J.S.; Stefan, H.G. Hydraulic analysis of suspended sediment removal from storm water in a standard sump. J. Hydraul. Eng. 2012, 138, 491–502. [Google Scholar] [CrossRef]
- Faram, M.; Harwood, R. A method for the numerical assessment of sediment interceptors. Water Sci. Technol. 2003, 47, 167–174. [Google Scholar] [CrossRef][Green Version]
- Westerweel, J.; Elsinga, G.E.; Adrian, R.J. Particle image velocimetry for complex and turbulent flows. Annu. Rev. Fluid Mech. 2013, 45, 409–436. [Google Scholar] [CrossRef]
- Drain, L.E. The Laser Doppler Techniques; Wiley-Interscience: Chichester, UK, 1980. [Google Scholar]
- Westerweel, J.; Scarano, F. Universal outlier detection for PIV data. Exp. Fluids 2005, 39, 1096–1100. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M.; Westerweel, J.; Boersma, B.J. Turbulence: Introduction to Theory and Application of Turbulent Flows; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Wilczek, M.; Narita, Y. Wave-number-frequency spectrum for turbulence from a random sweeping hypothesis with mean flow. Phys. Rev. E 2012, 86, 066308. [Google Scholar] [CrossRef] [PubMed]
- Beersma, J.; Versteeg, R. Basisstatistiek Voor Extreme Neerslag in Nederland; STOWA: Amersfoort, The Nederland, 2019. [Google Scholar]
- Heikkila, J.; Olli, S. A four-step camera calibration procedure with implicit image correction. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, 17–19 June 1997; IEEE: New York, NY, USA, 1997; pp. 1106–1112. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Avila, H.; Pitt, R.; Durrans, S.R. Factors affecting scour of previously captured sediment from stormwater catchbasin sumps. J. Water Manag. Model. 2008. [Google Scholar] [CrossRef]
- Terfous, A.; Hazzab, A.; Ghenaim, A. Predicting the drag coefficient and settling velocity of spherical particles. Powder Technol. 2013, 239, 12–20. [Google Scholar] [CrossRef]
- Avila, H.; Pitt, R.; Clark, S.E. Development of effluent concentration models for sediment scoured from catchbasin sumps. J. Irrig. Drain E. 2011, 137, 114–120. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rietveld, M.; de Rijke, D.; Langeveld, J.; Clemens, F. Sediment Morphology and the Flow Velocity Field in a Gully Pot: An Experimental Study. Water 2020, 12, 2937. https://doi.org/10.3390/w12102937
Rietveld M, de Rijke D, Langeveld J, Clemens F. Sediment Morphology and the Flow Velocity Field in a Gully Pot: An Experimental Study. Water. 2020; 12(10):2937. https://doi.org/10.3390/w12102937
Chicago/Turabian StyleRietveld, Matthijs, Demi de Rijke, Jeroen Langeveld, and Francois Clemens. 2020. "Sediment Morphology and the Flow Velocity Field in a Gully Pot: An Experimental Study" Water 12, no. 10: 2937. https://doi.org/10.3390/w12102937
APA StyleRietveld, M., de Rijke, D., Langeveld, J., & Clemens, F. (2020). Sediment Morphology and the Flow Velocity Field in a Gully Pot: An Experimental Study. Water, 12(10), 2937. https://doi.org/10.3390/w12102937







