Abstract
Nowadays, the estimation of volumetric soil water content (θ) through apparent dielectric permittivity (εa) is the most widely used method. The purpose of this study is to investigate the effect of the high iron content of two sandy loam soils on estimating their water content using two dielectric sensors. These sensors are the WET sensor operating at 20 MHz and the ML2 sensor operating at 100 MHz. Experiments on specific soil columns, in the laboratory, by mixing different amounts of water in the soils to obtain a range of θ values under constant temperature conditions were conducted. Analysis of the results showed that both sensors, based on manufacturer calibration, led to overestimation of θ. This overestimation is due to the high measured values of εa by both sensors used. The WET sensor, operating at a lower frequency and being strongly affected by soil characteristics, showed the greatest overestimation. The difference of εa values between the two sensors ranged from 14 to 19 units at the maximum actual soil water content (θm). Compared to the Topp equation, the WET sensor measures 2.3 to 2.8 fold higher value of εa. From the results, it was shown that the relationship θm-εa0.5 remained linear even in the case of these soils with high iron content and the multi-point calibration (CALALL) is a good option where individual calibration is needed.
1. Introduction
The knowledge of volumetric soil water content (θ) is crucial in the estimating of soil profile water balance and in the study of transport of salts and various agrochemicals in soils, as well as in irrigation water management. In recent decades, technologies for measuring water content in porous media have been remarkably developed. This development is based on the ability to measure soil apparent dielectric permittivity, εa, and to the fact that there is a relationship between εa and actual volumetric soil water content, θm. Relative complex permittivity (εr*) is composed of a real component and an imaginary component Equation (1):
where εr’ is the dielectric constant (the real part of relative permittivity), εr’’ (the imaginary part of relative permittivity) is the equivalent dielectric loss taking the conductive loss into consideration, and j = (−1)1/2. Volumetric soil water content is more directly related to εr’. For the Time Domain Reflectrometry (TDR) technique the real component εr’ of the relative permittivity is considered about equal to the εa. In case of inorganic porous media, it has been shown that εa can be precisely correlated with θ using the Topp equation Equation (2) [1,2]:
otherwise
Using TDR devices, the εa is measured through the transmission time of the electromagnetic wave along the device’s pins inserted into the soil. Since the dielectric constant is 80 for water, 1 for air and 2–5 for solid components of the soil, it is clear that the εa value of soil is mainly determined by θ.
Topp and Reynolds [3] gave a linear approach of the Equation (2):
In Equation (4), the slope of the linear relationship is related to the influence of clay and soil salinity, while the constant term is related to the electrical properties of the solid soil components. Soil salinity and clay percentage can affect the linearity of the relationship [4].
The high cost of TDR devices and the difficulties in waveform analysis have led to the development of commercial soil water sensors which calculate the θ through the εa using a different measurement way of εa [5,6,7]. Commercial dielectric sensors can be broadly classified as Frequency Domain (FD) or Amplitude Domain Reflectometry (ADR) sensors. The FD sensors include the Frequency Domain Reflectometry (FDR) and the capacitance sensors. The FDR sensor sends an electromagnetic wave into the measured medium (soil) and measures the frequency of the reflected wave, which varies with εa and θ [8]. With capacitance sensors, a medium’s εa is determined by measuring the charge time of a capacitor consisting of that medium, confined by the sensor’s prongs. ADR sensors infer the εa through measurement of voltage amplitude. The effective frequency (f) of commercial sensors, which ranges from approximately 10 to 150 MHz, is almost invariably lower than that of TDR, which ranges from approximately 300 to 1000 MHz [9]. The WET sensor (20 MHz), which belongs to the FDR category [10], calculates εa, soil bulk electrical conductivity and temperature in the same soil volume, while the ML2 sensor (100 MHz), which is based on ADR method, calculates only the εa utilizing the principle of the stationary wave [11,12]. These sensors have been used in many soil types and the relationship θm-εa0.5 has been shown to be linear with the slope and intercept coefficients vary depending on the soil type. Only in the case of sandy soils these coefficients are practically the same among different operating frequency sensors. However, it is known that soil properties such as type and amount of clay minerals, organic matter, content and forms of iron oxides affect the value of εa and consequently the sensor calibration equation. The soil type and especially the increased content of clay (mainly the clay type 2:1) significantly affect the εa value measured using low frequency sensors. Campbell [13] investigated the dielectric behavior of various soil types in a frequency range of 1–50 MHz and reported that the lower the frequency, the greater dependence on the soil type and the higher the apparent dielectric permittivity value.
From the abovementioned soil properties, the content and forms of soil iron oxides have not been extensively studied for their effects on εa and consequently on the estimation of θ. Roth et al. Study [14] presented results for the relationship θm-εa obtained by TDR measurements for two soils (Rhodic ferralsol) from Brazil. These soils contained 18.3% and 18.5% total iron, respectively, with unknown percentages of maghemite and magnetite. Results showed that the relationship θm-εa has a smaller slope compared to inorganic soils up to a θm = 0.2 m3m−3, while at higher soil water contents there is a convergence trend. However, these soils have a high content of clay and so it is not easy to estimate the particular effect of high iron content.
Robinson et al. [15] studied the effect of iron oxides (magnetite, hematite and goethite) on εa. Specifically, percentages of 5%, 10% and 15% by weight from each oxide form in an artificial porous medium composed by sand in various soil water content regimes were examined. They reported that the magnetite content compared to hematite and goethite seriously affects on εa in the case of TDR used, while in the case of capacitance probe (100 MHz) important role plays the iron oxide form and the length of sensor rods used. For TDR, the goethite content up to 15% did not affect the estimation of θ, whereas a hematite content of 15% led to a 6% overestimation of θ. However, in the case of 15% magnetite content, an overestimation of θ up to 60% was recorded. This effect is more pronounced with the increase of soil water content. In the case of capacitance probe at dry conditions, i.e. θm = 0, the effect of increased iron oxide content on εa is low. However, at saturation, when magnetite content is 15% w/w, the εa readings rose to 75 and 122 when the length of sensor rods is 10 and 5 cm, respectively, while in the pure sand the value of εa is 27. In the case where hematite content is 15% w/w, the increase of εa is minor for a 10 cm sensor rods length, while the increase of εa is significant (44) for a 5 cm sensor rods length. Correspondingly, in the case where goethite content is 15%, the values of εa are 135 and 23 when the length of sensor rods is 5 and 10 cm, respectively. Overall, from the study of Robinson et al. [15], it is clearly shown that between TDR and capacitance probe there is a completely different behavior when the content of three iron oxides in soil is high.
Van Dam et al. [16] reported from TDR field studies that goethite iron-oxide precipitates significantly lower the electromagnetic wave velocity of sediments. Measured variations in magnetic permeability do not explain this decrease. The TDR measurements show that apparent dielectric permittivity of the solid material is not altered significantly by the iron-oxide material. The amount of iron oxides appears to correlate with the volumetric water content, which is the result of differences in water retention capacity between goethite and quartz. These variations in water content control apparent dielectric permittivity and explain the observed variation in electromagnetic wave velocity.
Pettinelli et al. [17] reported that εa increases significantly as magnetite content increases and a complex behavior occurs, in a frequency range of 500 Hz–1MHz, which depends on different factors, i.e., shape, dimension and origin of the magnetic material. In international literature, there are no studies to investigate the effect of the increased iron content of soils on the estimation of volumetric water content for relative low-frequency sensors, such as WET (20 MHz) and ML2 (100 MHz), that are used in the application of irrigation in agricultural practice.
The purpose of this study is the investigation of the iron content effect of two sandy loam soils on the determination of their apparent dielectric permittivity and the estimation of their volumetric water content using the proposed manufactured equations of two dielectric sensors for inorganic soils. The linearity of the θm-εa0.5 relationship is also investigated when iron content of the soil is high.
2. Materials and Methods
2.1. WET and ML2 Sensors
The WET sensor [10] is a multi-parameter sensor consisting of the main body which contains the electronics and three sharpened, stainless steel rods 6.8 cm long, 3 mm in diameter and spaced 1.5 cm apart attached to it. The sensor measures the capacitance and conductance of the medium between the rods (usually soil) from changes in a generated 20 MHz signal. It directly measures the dielectric properties of the soil by generating a 20 MHz signal, which is applied to the central rod, the bulk electrical conductivity (σb) and soil temperature. The WET sensor, also, estimates volumetric water content and pore water electrical conductivity.
The ML2 Theta Probe [11] consists of an input/output cable, probe body and a sensing head. The sensing head has an array of four cylindrical rods, 60 mm long and 3 mm in diameter. Three outer rods form a triangle, with the fourth in the center. The outer rods are connected to instrument ground and form an electrical shield around the central rod, which transmits the signal in continuation from the probe body. The εa of the porous media is calculated as
where V denotes the voltage in Volts with a range of 0–1 Volts. This range corresponds to an approximate water content 0 to 0.6 m3m−3 and to a maximum square root of εa equal to 5.77, displayed on the screen of the probe.
It estimates volumetric water content by applying a 100 MHz signal via a specially designed transmission line whose impedance is changed as the impedance of the soil changes.
These sensors are used in combination to the soil water content meter HH2 [10] through which εa and θ values are obtained. Volumetric water content is calculated using a simple mixing formula that relates water content to the measured εa of the soil using the following Equation (6) [10]:
where α0, α1 are constants depended on the type of porous medium. The linearity of the θm-εa0.5 relationship has been documented in cases where θm is homogeneous in the soil volume used for measurement [5,18]. For inorganic porous media, parameter values as proposed by the manufacturer are 1.8 and 10.1 for WET sensor, and 1.6 and 8.4 for ML2 sensor.
2.2. Measurement of Physical and Chemical Properties of Soils
Two sandy loam soil samples were taken from Central Greece, (Beotia), transferred to the laboratory, air dried, ground and separated into <2 mm fraction using a 2 mm (fine earth) sieve. The water content of dried samples was determined by drying at 105 °C in order to allow correction of assay results. Soil texture was estimated using the Bouyoucos hydrometer method, organic matter was determined using a modified Walkley–Black method, the CaCO3-equivalent using the quantity of CO2 produced on reaction with HCl, the cation exchange capacity (CEC) and exchangeable bases were determined using ammonium acetate (NH4OAc (1 N, pH 7)) method. The methods used are described in detail in the Soil Survey Laboratory Methods Manual [19].
Free iron oxides (Fe2O3d) were extracted using the sodium dithionite-citrate (DCB) method [20], amorphous iron oxides (Fe2O3o) were extracted using ammonium oxalate method [21] and organically bound iron oxides (Fe2O3p) were extracted using the sodium pyrophosphate method [22]. Total iron was extracted by aqua regia digestion method [23]. The amount of crystalline iron oxides was estimated from the total iron minus amorphous iron oxides minus organically bound iron oxides. All iron concentrations were determined by atomic absorption spectrophotometry, using a Varian SpectrAA 300.
In order to estimate the soil salinity level, in both soil samples, the electrical conductivity of saturation paste extract (ECe) was determined [24].
2.3. Mineralogical Analysis
Mineralogical analysis was carried out by using an X-Ray Diffractometer of Siemens D 5005 type, with copper tube at 40 KV and 40 mA and graphite monochromatographe, at the Laboratory of Economic Geology and Geochemistry, Department of Geology and Geoenvironment, NKUA. The evaluation of the powder X-Ray Diffraction (XRD) pattern was performed by using Bruker EVA 10.0 program of the DIFFRACplus software package.
2.4. Measurement of Volumetric Water Content and Apparent Dielectric Permittivity of Soils
In all the experiments conducted, the actual soil water content, θm, ranged from oven dry to saturation in equal water content steps, Δθ = 0.05 m3m−3. To this end, air-dried soil samples were thoroughly mixed with different predetermined amounts of fresh water (EC = 0.28 dSm−1) taking care to get homogeneous water content. The obtained soil samples of various water content levels were packed in PVC columns with 10 cm height and 7 cm diameter in small portions and pressed with a 0.15 Kg rubber hammer to achieve homogeneous density distribution in the soil sample. The θm and dry bulk density of the soil samples were determined once again at the end of the experiment by weighing and oven drying. In addition, measurements were taken in the oven-dried soil samples (θm = 0 m3m−3). Using the above methodology, a sufficient number of εa, θm, and θ readings for the two soils examined were provided. Measurements were obtained by fully inserting vertically the WET and ML2 sensors into the soil samples.
The soil specific calibration of the sensors was performed using the following linear equation between the square root of εa and θm:
where the parameters a and b depend on the soil type. This equation has been widely applied for the calibration of TDR and other dielectric sensors [4,5,7,25,26,27,28].
Soil specific values for a and b parameters can be easily determined using two independent pairs of θm and εa values (two-point calibration, CAL). For simplicity reasons and in order to cover the entire range of possible θm values of the studied soil samples, the first εa measurement is taken at an oven-dried soil sample (i.e., θm = 0 m3m−3) and the second εa measurement is taken at a saturated soil sample (i.e., θm = θs) [28,29]. Optimal values for a and b can be also determined by linear regression between θm and εa0.5 using all the measured θm values (multi-point calibration, CALALL). In this study, soil specific calibration relationships for each soil studied were produced using both the above described methods.
Additionally, corresponding data of another sandy loam soil, referred in the study of Kargas et al. [6], using the same sensors are compared with the recent data received by the soils used in this study. More details about the properties of the soil and the experimental procedure can be found in Kargas et al. [6].
Additionally, a set of experiments where silica sand with bulk density of 1.68 gcm−3 was thoroughly mixed with appropriate amounts of soil 1 was carried out. So, sand-soil mixtures with five rates of soil 1 (100% sand, 75% sand and 25% soil 1, 50% sand and 50% soil 1, 25% sand and 75% soil 1, and 100% soil 1 v/v) were made. In each ratio of sand-soil mixture, the relationship between θm and εa for each sensor, according to the methodology described at the beginning of this subsection, was determined. With these experiments, it is possible to better assess the effect of iron content on εa in the case of the sensors tested.
2.5. Performance Evaluation Criteria
To evaluate the calibration equation the Root Mean Square Error (RMSE) performance evaluation criterion was used.
where Predi is the i th predicted value of the modeled parameter, Obsi is the corresponding observed value, and n is the total number of different observed − predicted values pairs. RMSE is expressed in the same units as the estimated parameter and values close to 0 indicate better performance.
Additionally, the coefficient of determination R2 was used. R2 ranges between 0 and 1, where values close to 0 indicate no correlation and values close to 1 indicate a strong correlation.
3. Results and Discussion
3.1. Physical and Chemical Soil Properties
The results of some physical and chemical properties for the two soils used are presented in Table 1.

Table 1.
Texture analysis, organic matter (%), content of CaCO3 (%) and cation exchange capacity (CEC) for the two soils used.
Additionally, the ECe values were determined 0.565 dSm−1 and 0.425 dSm−1 for the soil 1 and soil 2, respectively. These values indicated that the soil salinity level is very low and their effect on εa can be considered too low.
The content of free and amorphous or non-crystalline iron oxides as well as the organic matter-bound iron oxides and total iron oxides in two soil samples are presented in Table 2.

Table 2.
Content of different forms of iron oxides in two sandy loam soils used.
From the data showed in Table 2, it appears that both soils have high content of total iron.
In Figure 1 the XRD diagram of soil 1 is presented. The results of the XRD analysis revealed that calcite is the predominant mineral phase and quartz a major to medium constituent. Hematite and goethite occur as medium to minor mineral phases and their co-existence reveals secondary processes (e.g., weathering). Dolomite occurs as a medium to minor crystallic phase (probably attributed to the geological background formations of the area, such as Triassic dolomites and dolomitic limestones). Moreover, illite, chlorite (clinochlore, an iron-rich clay mineral), talc and smectites (montmorillonite and nontronite, an iron-rich smectite) were determined as minor to trace minerals.
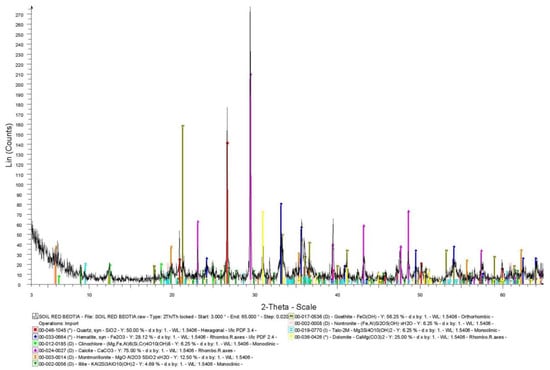
Figure 1.
XRD diagram of soil 1.
3.2. Relationship between Actual Soil Water Content and Apparent Dielectric Permittivity
In Figure 2 and Figure 3, the relationships θm-εa, where εa was measured by the WET and ML2 sensors and was also calculated from the Topp equation (Equation (3)) for soils 1 and 2, are presented. The widely accepted Topp equation was used as a reference equation since is independent on soil type, soil temperature and soluble salt content.
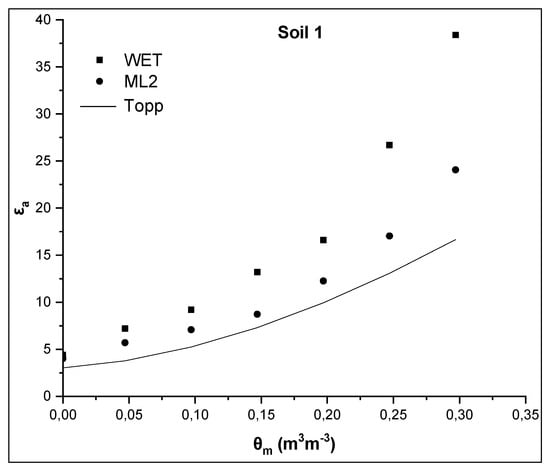
Figure 2.
Comparative presentation of relationships θm-εa obtained by the WET sensor, the ML2 sensor and the TOPP equation for soil 1.
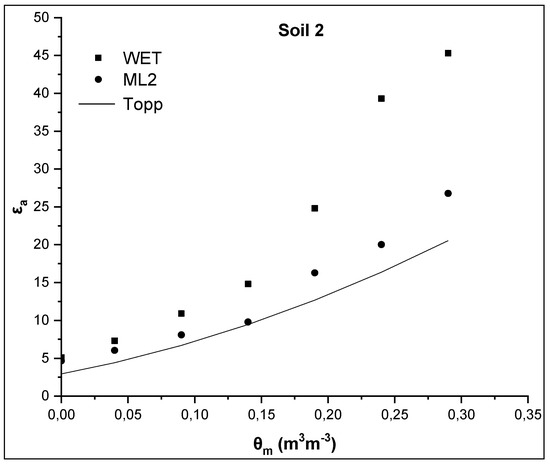
Figure 3.
Comparative presentation of relationships θm-εa obtained by the WET sensor, the ML2 sensor and the TOPP equation for soil 2.
As shown in Figure 2, εa values measured by the WET sensor for each θm are much higher than those predicted by the Topp equation for the same θm value. More specific, for the maximum value of actual soil water content θm = 0.297 m3m−3, εa values obtained by the WET sensor and the Topp equation are 38.4 and 16.7, respectively. Taking into account the εa value 38.4, the maximum θ value obtained by the WET sensor, using the manufacturer calibration (Equation (6)), is 0.435 m3m−3. Also, analogous phenomena, but to a less extent, are observed for the ML2 sensor (Figure 2). The ML2 sensor, which operates at higher frequency, measures lower values of εa as anticipated for the same θm [6]. For maximum θm, the εa value obtained by the ML2 sensor is 24, i.e. 14.4 units less than that obtained by the WET sensor, but 7 units greater than that from the Topp equation. Additionally, when the manufacturer calibration is applied using Equation (6) with α0 = 1.8 and α1 = 10.1 for the WET sensor and α0 = 1.6 and α1 = 8.4 for the ML2 sensor, an overestimation of soil water content for θm>0.2 m3m−3 and θm≥0 m3m−3 for the ML2 and the WET sensor, respectively, is observed.
In correspondence with soil 1, similar results for the soil 2 are presented in Figure 3. Specifically, εa values measured by the WET and the ML2 sensor are 45.3 and 26.8, respectively, for the maximum value of actual soil water content θm = 0.29 m3m−3, whereas the εa value calculated by the Topp equation is 16.1. Compared to soil 1, it appears that the difference between the εa values measured by the two sensors increases and their difference from the predicted εa value from the Topp equation increases too as soil water content increases.
The values of εa for θm = 0 m3m−3 are, then, examined. In case of soil 1, εa values are 4.4 and 4.02 for WET and ML2, respectively, for θm = 0 m3m−3, whereas the corresponding values for soil 2 are 5.1, and 4.65 for WET and ML2, respectively. These values are much higher than those calculated, on the basis of the manufacturer calibration, using Equation (6) for θm = 0 m3m−3. From Equation (6) assuming that θm = 0 m3m−3 then the soil apparent dielectric permittivity is calculated as εa = α02 = 1.82 = 3.24 for the WET sensor and 2.56 for the ML2 sensor. The corresponding value from the Topp equation (Equation (3)) is 3.03.
The high εa values measured by the two sensors in the two soils compared to those predicted by the Topp equation may be attributed to the high content of iron and especially to the content of hematite and goethite. Considering the semi-quantitative XRD analysis (Figure 1) and the analysis of different iron forms in soil 1 (Table 2), we can determine that the hematite and goethite content in crystalline phases is approximately 12% and 8%, respectively. Consequently, the sum of the crystalline phases of hematite and goethite is approximately 20%. In particular, the total iron oxides that participate in crystalline phases are: Total iron minus amorphous iron oxides minus organic matter-bound iron oxides (30.12-6.73-0.44 = 22.95%). The remaining percentage of ~3% (2.95%), may be attributed to the contribution of the iron-rich clay minerals (clinochlore and nontronite) as shown by XRD analysis.
Robinson et al. [15] reported that the effect of hematite and goethite on the estimation of εa from TDR measurements is clearly less than that of magnetite. However, in the case of capacitance probe (100 MHz) with a rods length of 5 cm and a hematite content of 15%, the effect is considerable (εa value rising from 27 in the saturated sand to 44) and even greater in the case of a goethite content of 15% (εa value rising from 27 in the saturated sand to 135). In soils 1 and 2 (Figure 2 and Figure 3) which contain hematite and goethite, the behavior of the WET sensor, that operates at 20 MHz and has a 6.8 cm rods length, is similar.
Thus, in the case of low-frequency FDR sensors (i.e. WET), the effect of high soil iron content and particular high content of hematite and goethite may be significant on the soil apparent dielectric permittivity measurement. However, from the present work, we cannot distinguish the particular contribution of hematite and goethite to the end result. Additionally, it could be noted the possible contribution of the clay minerals, such as smectite and chlorite, as it is shown from XRD analysis, on the high εa values. This issue needs further investigation to accurately assess the contribution of clay minerals.
Furthermore, the measurements of the soil bulk electrical conductivity (σb) using the WET sensor show that the high values of εa cannot be attributed to the salinity level of the soil samples since the maximum values of σb are 0.46 and 0.5 dSm−1 for soil 1 and soil 2, respectively. These low σb values in combination with the low ECe values (0.565 dSm−1 and 0.425 dSm−1 for the soil 1 and soil 2, respectively) showed that the effect of soil salinity may be considered negligible. It is mentioned that in this range of σb, none of the sensors was sensitive as the above σb values are much lower than the threshold 2 dSm−1 [6].
In order to enhance the results, the εa values measured by the two sensors and those ones of the sandy loam soil studied by Kargas et al. [6] with completely different mineralogical composition (most common constituent was illite with chlorite much less prominent), low soil salinity (with ECe = 0.655 dSm−1) and insignificant iron content (0.9%) were compared. In this case, the difference between the two sensors is approximately 4 dielectric units, at the maximum θm, and the difference between the WET sensor and the Topp equation is 5 dielectric units, while the difference between the ML2 sensor and the Topp equation is negligible (Figure 4). The values of εa, at the maximum θm, are 23 and 19 for the WET and the ML2, respectively, i.e., much lower than the values measured in Soil 1 and Soil 2, especially for the WET sensor which operates at low frequencies.
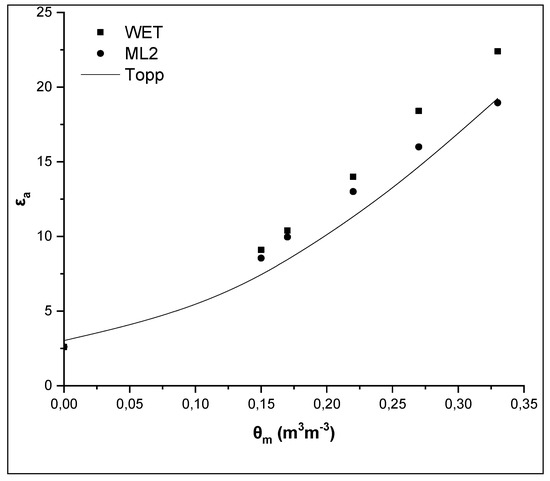
Figure 4.
Comparative presentation of the relationships θm-εa obtained by the WET sensor, the ML2 sensor and the Topp equation for a sandy loam soil (SL) studied by Kargas et al. (2014) [6] with low iron content.
From these results, it is confirmed that, due to the iron content difference, it is observed a great difference in εa between the sandy loam soil studied by Kargas et al. [6] and the two sandy loam soils examined in the present study. The high θ values obtained, in both soils studied, by the WET and ML2 sensors taking into consideration the manufacturer calibration, highlight that a specific calibration of the sensors is required for these soils. Results, also, show the influence of the soil mineralogical composition. Overall, it can be said that the soil texture alone is not an effective way to categorize soils in relation to sensors calibration, as in the case of the manufacturer calibration of WET and ML2 sensors.
3.3. Soil Specific Calibration
During the specific calibration process, the linearity of θm-εa0.5 relationship was investigated. In Figure 5, a comparative presentation between the θm-εa0.5 relationships obtained by the WET and ML2 sensors for soil 1 is presented, together with the respective manufacturer calibration, while in Table 3, the coefficients of these linear relationships (CALALL) are given.
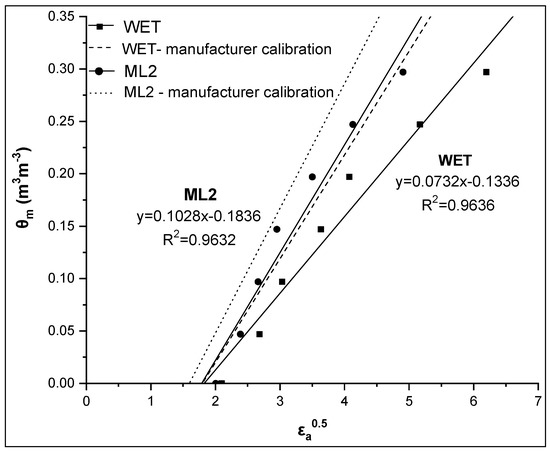
Figure 5.
Comparative presentation of the relationships θm-εa0.5 obtained by the WET and ML2 sensors for soil 1. The corresponding relationships using the manufacturer calibration are also given for both sensors.

Table 3.
Coefficients (slope (a) and intercept (-b)) of the linear relationship θm-εa0.5 obtained by the WET and ML2 sensors (CALALL) for the two sandy loam soils studied (Soil 1 and Soil 2). Additionally, the coefficients of a Sandy Loam (SL) soil studied by Kargas et al. [6] are presented.
As shown in Figure 5, the relationship θm-εa0.5 is strongly linear for both sensors used (high value of R2). However, in the case of the WET sensor, the coefficients of this linear relationship (slope and intercept) are smaller than those obtained by the Topp equation (i.e. slope = 0.115, intercept = –0.176), while in the case of the ML2 sensor, there is a difference mainly in the slope value. From RMSE values, it appears that the estimation of soil water content by the CALALL method is significantly improved using the specific calibration compared to the manufacturer calibration. Specifically, the RMSE values are 0.018 and 0.019 m3m−3 for the WET and the ML2 sensor, respectively, while the corresponding values taking into account the manufacturer calibration were 0.067 and 0.051 m3m−3, respectively. If we consider the RMSE value of 0.03 m3m−3 as a threshold to achieve a reliable calibration then it seems that the CALALL method is quite effective.
Similar findings for soil 2 are shown in Figure 6 and Table 3 (CALALL). In the case of soil 2, RMSE values by the CALALL method are 0.015 and 0.014 for the WET and the ML2 sensor, respectively. The corresponding values for manufacturer calibration were 0.123 and 0.086 m3m−3, respectively.
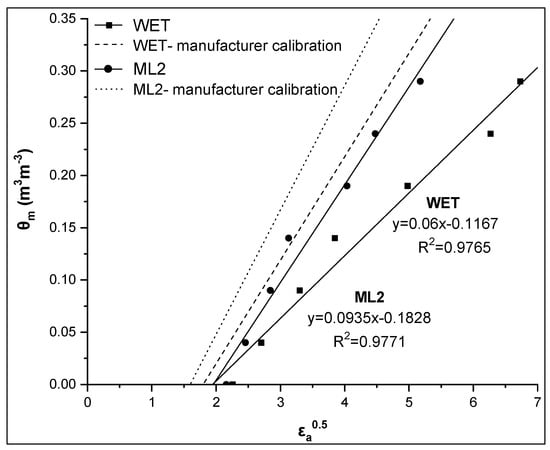
Figure 6.
Comparative presentation of the relationships θm-εa0.5 obtained by the WET and ML2 sensors for soil 2. The corresponding relationships using the manufacturer calibration are also given for both sensors.
Therefore, it is possible to overcome the problem of soil water content overestimation, due to the overestimation of εa values for this particular category of soils, using the specific calibration (CALALL) of sensors. Additionally, the two-point calibration method (CAL) appears to be effective, since RMSE values for soil 1 are 0.032 and 0.029 m3m−3 for WET and ML2, respectively, whereas for soil 2 are 0.019 and 0.023 m3m−3, respectively. Although, these values are higher than those of the CALALL method, they are less than the threshold value 0.03 m3m−3, with exception of soil 1 values for the WET sensor.
3.4. Sand-Soil Ratio
Figure 7 shows the relationship θm-εa for different sand-soil 1 ratios (v/v) in soil mixture studied using the WET sensor. The results showed the effect of soil 1 content on the εa value even in the case of a small percentage of soil 1 addition in soil mixture, i.e., 25% by volume. More specific, between the pure sand (100% sand) and the soil 1 (100% soil 1) there is a difference of 25 dielectric units at the maximum soil water content. Each 25% increase of the soil 1 in soil mixture leads to an increase of approximately 7 dielectric units, except in the case between the percentages 75% and 100% where the increase is less. Similar results were obtained by the ML2 sensor, where the increase of εa values is approximately 4 dielectric units for each percentage increase of the soil 1 in soil mixture by 25% (data not shown).
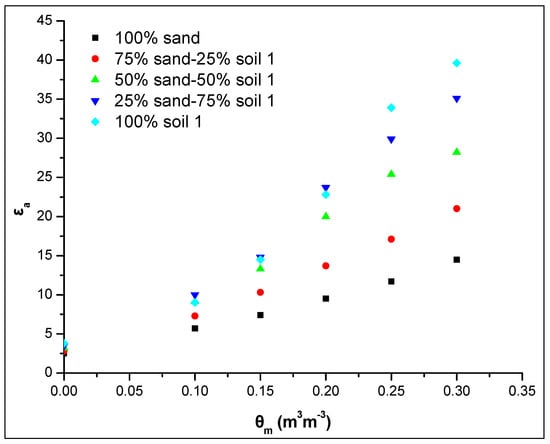
Figure 7.
Relationship between the apparent dielectric permittivity εa and the actual soil water content θm for five different ratios of the sand-soil mixture studied using the WET sensor.
Therefore, there is a strong positive correlation between the soil 1 content and εa. The smallest value is obtained in 100% sand and as the soil 1 percentage increases in the soil mixture the εa increases remarkably (Figure 7).
This underscores the need to account for the effect of soil iron content on sensor readings. This can be achieved by developing specific calibration equations as presented in Table 3.
Additionally, the strong linear correlation between εa and the soil 1 percentage in the soil mixture studied at various soil water contents and especially at the maximum actual soil water content value, i.e., θm = 0.297 m3m−3, (R2 = 0.9945) as shown in Figure 8 for the WET sensor, is noteworthy. This study’s findings clearly show that the addition of soil with high iron content results in higher apparent dielectric permittivity and thus, cause an overestimation of θ.
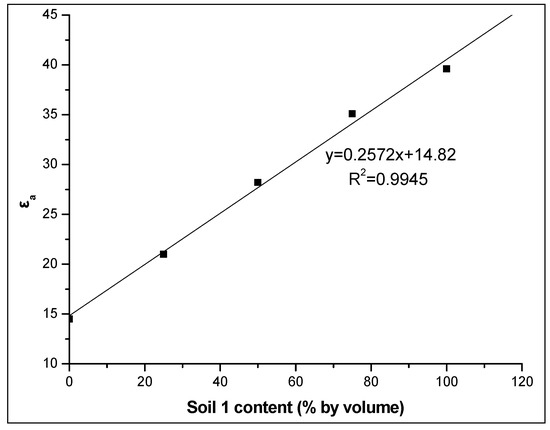
Figure 8.
Relationship between the apparent dielectric permittivity εa and the percentage of soil 1 in the soil mixture studied at the maximum actual soil water content using the WET sensor.
4. Conclusions
From the experiments conducted by using two dielectric sensors on two sandy loam soils, it is clearly shown that high iron content leads to high apparent dielectric permittivity values. Higher values of εa were determined when the measurements were made by the WET sensor, due to the fact that it operates at a lower frequency than the ML2. The high values of εa lead to an overestimation of soil water content in the case where the manufacturer calibration of the sensors is used. Soil water content near saturation is overestimated up to 60% using the WET sensor.
The problem of soil water content overestimation can be overcome by specific calibration (especially CALALL) of the sensors for the soils used. Even in these cases of soils, the relation θm-εa0.5 is linear, and the coefficients of this relationship for each soil can be easily determined. The coefficients for these soils are different from those obtained by the Topp equation and those proposed by the manufacturer for inorganic soils.
Further investigation is needed to distinguish the particular contribution of hematite and goethite to the higher values of the apparent dielectric permittivity.
Overall, our findings confirmed that iron content significantly affects the soil apparent dielectric permittivity and thus further investigation is needed under different soil types and environmental conditions.
Author Contributions
Conceptualization, G.K., P.L., M.A. and N.M.; Formal analysis, G.K., P.L., M.A. and N.M.; Methodology, G.K., P.L., M.A. and N.M.; Writing—review & editing, G.K., P.L., M.A. and N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Kargas, G.; Kerkides, P. Water content determination in mineral and organic porous media by ML2 theta probe. Irrig. Drain. 2008, 57, 435–449. [Google Scholar] [CrossRef]
- Topp, G.C.; Reynolds, W. Time domain reflectometry: A seminal technique for measuring mass and energy in soil. Soil Tillage Res. 1998, 47, 125–132. [Google Scholar] [CrossRef]
- Ferre, P.A.; Topp, G.C. Time domain reflectometry. In Methods of Soil Analysis; Part 4-Physical Methods; Soil Science Society of America, Inc.: Madison, WI, USA, 2002; pp. 434–446. [Google Scholar]
- Kargas, G.; Kerkides, P.; Seyfried, M.; Sgoumbopoulou, A. WET Sensor Performance in Organic and Inorganic Media with Heterogeneous Moisture Distribution. Soil Sci. Soc. Am. J. 2011, 75, 1244–1252. [Google Scholar] [CrossRef]
- Kargas, G.; Kerkides, P.; Seyfried, M. Response of Three Soil Water Sensors to Variable Solution Electrical Conductivity in Different Soils. Vadose Zone J. 2014, 13. [Google Scholar] [CrossRef]
- Kargas, G.; Soulis, K. Performance evaluation of a recently developed soil water content, dielectric permittivity, and bulk electrical conductivity electromagnetic sensor. Agric. Water Manag. 2019, 213, 568–579. [Google Scholar] [CrossRef]
- Hamed, Y.; Samy, G.; Persson, M. Evaluation of the WET sensor compared to time domain reflectometry. Hydrol. Sci. J. 2006, 51, 671–681. [Google Scholar] [CrossRef]
- Robinson, D.A.; Jones, S.B.; Wraith, J.M.; Or, D.; Friedman, S.P. A review of advances in dielectric and electrical conductivity measurement in soils using time domain reflectometry. Vadose Zone J. 2003, 2, 444–475. [Google Scholar] [CrossRef]
- Delta-T Devices. User Manual for the WET Sensor (Type WET-2); Delta-T Device Ltd.: Cambridge, UK, 2007. [Google Scholar]
- Delta-T Device. User Manual for the MML2 Sensor; Delta-T Device Ltd.: Cambridge, UK, 1999. [Google Scholar]
- Inoue, M.; Ahmed, B.O.; Saito, T.; Irshad, M. Comparison of Twelve Dielectric Moisture Probes for Soil Water Measurement under Saline Conditions. Am. J. Environ. Sci. 2008, 4, 367–372. [Google Scholar] [CrossRef]
- Campbell, J.E. Dielectric Properties and Influence of Conductivity in Soils at One to Fifty Megahertz. Soil Sci. Soc. Am. J. 1990, 54, 332–341. [Google Scholar] [CrossRef]
- Roth, C.H.; Malicki, M.A.; Plagge, R. Empirical evaluation of the relationship between soil dielectric constant and volumetric water content as the basis for calibrating soil moisture measurements by TDR. J. Soil Sci. 1992, 43, 1–13. [Google Scholar] [CrossRef]
- Robinson, D.A.; Bell, J.; Batchelor, C. Influence of iron minerals on the determination of soil water content using dielectric techniques. J. Hydrol. 1994, 161, 169–180. [Google Scholar] [CrossRef]
- Van Dam, R.; Schlager, W.; Dekkers, M.J.; Huisman, J.A. Iron oxides as a cause of GPR reflections. Geophys. 2002, 67, 536–545. [Google Scholar] [CrossRef]
- Pettinelli, E.; Vannaroni, G.; Cereti, A.; Pisani, A.R.; Paolucci, F.; Del Vento, D.; Dolfi, D.; Riccioli, S.; Bella, F. Laboratory investigations into the electromagnetic properties of magnetite/silica mixtures as Martian soil simulants. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]
- Kargas, G.; Kerkides, P. Performance of the theta probe ML2 in the presence of nonuniform soil water profiles. Soil Tillage Res. 2009, 103, 425–432. [Google Scholar] [CrossRef]
- Soil Survey Laboratory Methods Manual. Soil Survey Investigations Report No.42, Version 4.0, November 2004; United States Department of Agriculture, Natural Resources Conservation Service: Lincoln, NE, USA, 2004.
- Mehra, O.P. Iron Oxide Removal from Soils and Clays by a Dithionite-Citrate System Buffered with Sodium Bicarbonate. Clays Clay Miner. 1958, 7, 317–327. [Google Scholar] [CrossRef]
- Blakemore, L.C.; Searle, P.L.; Daly, B.K. Methods for Chemical Analysis of Soils; N.Z. Soil Bureau, Scientific Report 80; N.Z. Soil Bureau: Lower Hutt, New Zealand, 1987.
- Bascomb, C.L. Distribution of pyrophosphate-extractable iron and organic carbon in soils of various groups. J. Soil Sci. 1968, 19, 251–268. [Google Scholar] [CrossRef]
- Chen, M.; Ma, L.Q. Comparison of Three Aqua Regia Digestion Methods for Twenty Florida Soils. Soil Sci. Soc. Am. J. 2001, 65, 491–499. [Google Scholar] [CrossRef]
- U.S. Salinity Laboratory Staff. Diagnosis and Improvement of Saline and Alkali Soils; U.S. Salinity Laboratory Office: Washington, DC, USA, 1954.
- Ledieu, J.; De Ridder, P.; De Clerck, P.; Dautrebande, S. A method of measuring soil moisture by time-domain reflectometry. J. Hydrol. 1986, 88, 319–328. [Google Scholar] [CrossRef]
- White, I.; Knight, J.; Zegelin, S.; Topp, G. Comments on ‘Considerations on the use of time-domain reflectometry (TDR) for measuring soil water content’ by W.R. Whalley. Eur. J. Soil Sci. 1994, 45, 503–508. [Google Scholar] [CrossRef]
- Spaans, E.J.A.; Baker, J.M. The Soil Freezing Characteristic: Its Measurement and Similarity to the Soil Moisture Characteristic. Soil Sci. Soc. Am. J. 1996, 60, 13–19. [Google Scholar] [CrossRef]
- Kargas, G.; Soulis, K. Performance Analysis and Calibration of a New Low-Cost Capacitance Soil Moisture Sensor. J. Irrig. Drain. Eng. 2012, 138, 632–641. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Murdock, M.D. Measurement of soil water content with a 50 MHz soil dielectric sensor. Soil Sci. Soc. Amer. J. 2004, 68, 394–403. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).