A Modeling Comparison of Groundwater Potential Mapping in a Mountain Bedrock Aquifer: QUEST, GARP, and RF Models
Abstract
:1. Introduction
2. Materials and Methods
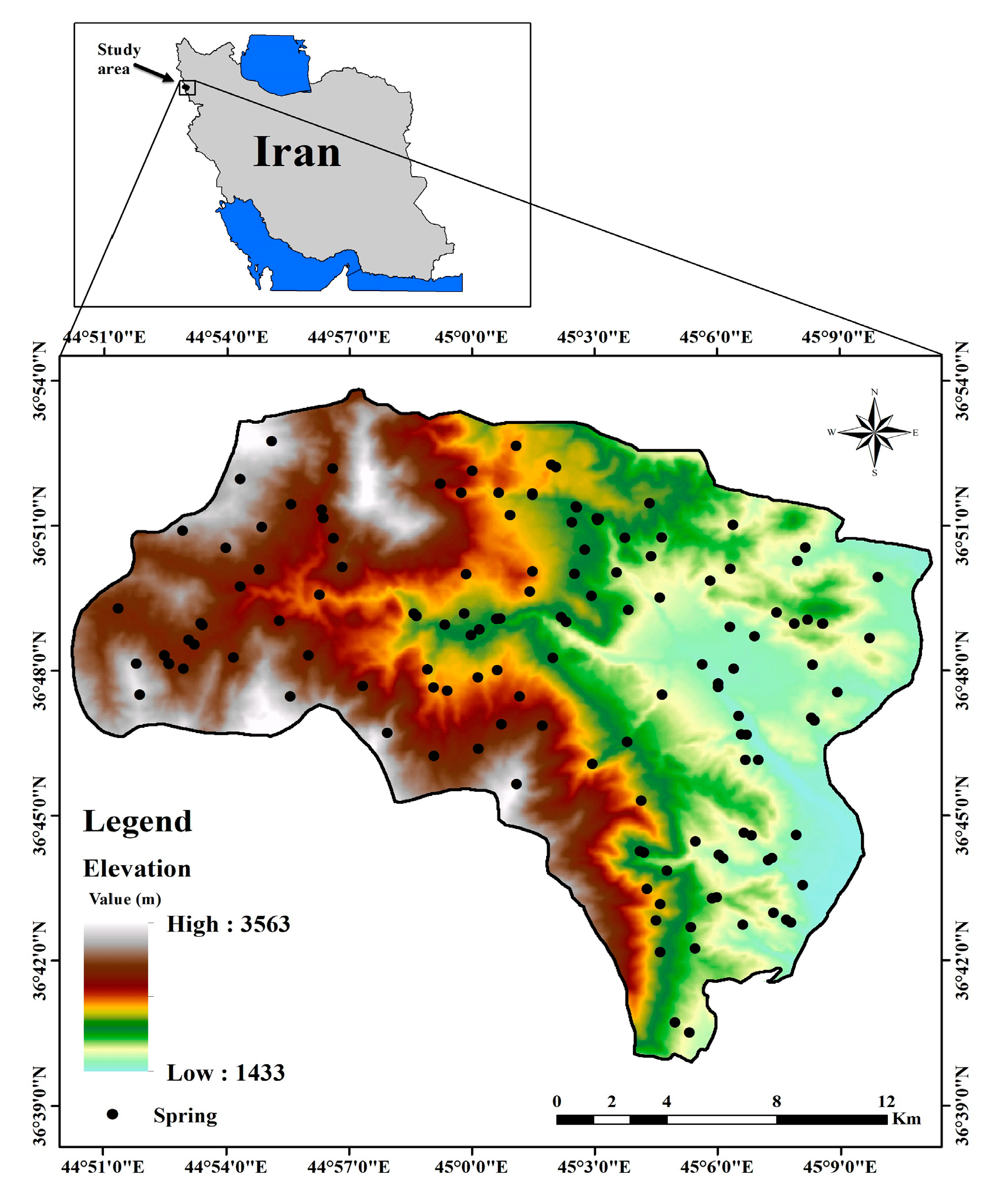
2.1. Description of the Study Area
2.2. Methodology
2.2.1. Springs Dataset
2.2.2. Geo-Environmental Factors
2.2.3. Description of Models
Genetic Algorithm for Rule-Set Production (GARP)
Quick Unbiased Efficient Statistical Tree (QUEST)
Random Forest (RF)
2.2.4. Accuracy Assessment of Models
3. Results
3.1. Multicollinearity Analysis of Predictive Factors
3.2. Application of the Models for Groundwater Potential Mapping
3.3. Accuracy of the Groundwater Potential Maps
3.4. Robustness Analysis
3.5. Importance Analysis of Predictive Factors
4. Discussion
5. Conclusions
- All three machine learning models showed good-excellent accuracy (AUC > 0.7) in prediction of groundwater potential, although there were some differences between the models in terms of predictive performance and robustness. Thus even when conducting model comparisons using clear criteria, such as prediction performance and robustness, understanding limitations and strengths remains somewhat difficult in model selection and identifying the best model. Here, RF showed the best performance based on two cutoff-dependent and cutoff–independent evaluation criteria, but exhibited slight sensitivity (lack of robustness) to changes in the training/validation data. In terms of pure prediction performance, GARP and QUEST showed slightly lower accuracy than RF. Therefore, RF provides the most accurate groundwater potential mapping, with acceptable robustness.
- Variable importance analysis demonstrated that RSP was the most important groundwater conditioning factor, followed by lithology factor, while slope, aspect, and plan curvature were the least important factors for modeling. These findings could be of practical help for water resources managers in handling the existing uncertain situation and understanding various aspects that affect groundwater potential.
- In future research, other metrics could be included in model comparisons, such as time spent in model generation and prediction calculation. A focus on DEM-derived factors and on obtaining high accuracy data could enhance the performance of the models. In order to raise the accuracy and reduce the uncertainties in models, hybrid modeling can be recommended, as it reduces some problems in classification models such as over-fitting.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magesh, N.S.; Chandrasekar, N.; Soundranayagam, J.P. Delineation of groundwater potential zones in Theni district, Tamil Nadu, using remote sensing, GIS and MIF techniques. Geosci. Front. 2012, 3, 189–196. [Google Scholar] [CrossRef] [Green Version]
- Naghibi, S.A.; Davoudi Moghaddam, D.; Kalantar, B.; Pradhan, B.; Kisi, O. A comparative assessment of GIS-based data mining models and a novel ensemble model in groundwater well potential mapping. J. Hydrol. 2017, 548, 471–483. [Google Scholar] [CrossRef]
- Rahmati, O.; Nazari Samani, A.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2014, 8, 7059–7071. [Google Scholar] [CrossRef]
- Yin, H.; Shi, Y.; Niu, H.; Xie, D.; Wei, J.; Lefticariu, L.; Xu, S. A GIS-based model of potential groundwater yield zonation for a sandstone aquifer in the Juye Coalfield, Shangdong, China. J. Hydrol. 2017, 557, 434–447. [Google Scholar] [CrossRef]
- Oh, H.J.; Kim, Y.S.; Choi, J.K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Davoodi Moghaddam, D.; Rezaei, M.; Pourghasemi, H.R.; Pourtaghie, Z.S.; Pradhan, B. Groundwater spring potential mapping using bivariate statistical model and GIS in the Taleghan watershed, Iran. Arab. J. Geosci. 2015, 8, 913–929. [Google Scholar] [CrossRef]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of evidence and artificial neural networks for potential groundwater spring mapping: An application to the Mt. Modino area (Northern Apennines, Italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Rahmati, O.; Melesse, A.M. Application of Dempster–Shafer theory, spatial analysis and remote sensing for groundwater potentiality and nitrate pollution analysis in the semi-arid region of Khuzestan, Iran. Sci. Total Environ. 2016, 568, 1110–1123. [Google Scholar] [CrossRef] [PubMed]
- Haghizadeh, A.; Davoodi Moghaddam, D.; Pourghasemi, H.R. GIS-based bivariate statistical techniques for groundwater potential analysis (an example of Iran). J. Earth Syst. Sci. 2017, 126, 109. [Google Scholar] [CrossRef] [Green Version]
- Ozdemir, A. Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C. GIS-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kordestani, M.D.; Naghibi, S.A.; Hashemi, H.; Ahmadi, K.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using a novel data-mining ensemble model. Hydrogeol. J. 2019, 27, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Pourghasemi, H.R.; Beheshtirad, M. Assessment of a data-driven evidential belief function model and GIS for groundwater potential mapping in the Koohrang Watershed, Iran. Geocarto Int. 2014, 30, 662–685. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; SamaniNeisani, N.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Hou, E.; Wang, J.; Chen, W. A comparative study on groundwater spring potential analysis based on statistical index, index of entropy and certainty factors models. Geocarto Int. 2018, 33, 754–769. [Google Scholar] [CrossRef]
- Al-Abadi, A.M.; Shahid, S. A comparison between index of entropy and catastrophe theory methods for mapping groundwater potential in an arid region. Environ. Monit. Assess. 2015, 187, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.J.; Walker, G.; Turner, J. Aquifer Sustainability Factor: A review of previous estimates. In Proceedings of the Groundwater 2010: The challenge of sustainable management, Canberra, Australia, 31 October–4 November 2010. [Google Scholar]
- Naghibi, A.; Pourghasemi, H.R. A comparative assessment between three machine learning models and their performance comparison by bivariate and multivariate statistical methods for groundwater potential mapping in Iran. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping, a case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Rahmati, O.; Davoudi Moghaddam, D.; Moosavi, V.; Kalantari, Z.; Samadi, M.; Lee, S.; Tien Bui, D. An Automated Python Language-Based Tool for Creating Absence Samples in Groundwater Potential Mapping. Remote Sens. 2019, 11, 1375. [Google Scholar] [CrossRef] [Green Version]
- Zabihi, M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Behzadfar, M. GIS-based multivariate adaptive regression spline and random forest models for groundwater potential mapping in Iran. Environ. Earth Sci. 2016, 75, 665. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Wang, X.; Bin Ahmad, B. Evaluating the usage of tree-based ensemble methods in groundwater spring potential mapping. J. Hydrol. 2020, 583, 124602. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S.M.; Jung, H.S. GIS-based groundwater potential mapping using artificial neural network and support vector machine models: The case of Boryeong city in Korea. Geocarto Int. 2018, 33, 847–861. [Google Scholar] [CrossRef]
- Pham, B.T.; Son, L.H.; Hoang, T.A.; Nguyen, D.M.; Tien Bui, D. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.D.; Pham, B.; Bui, Q.T.; Tran, C.T.; Panahi, M.; Ahmad, B.B.; et al. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef] [Green Version]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Tien Bui, D.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater Spring Potential Mapping Using Artificial Intelligence Approach Based on Kernel Logistic Regression, Random Forest, and Alternating Decision Tree Models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef] [Green Version]
- Tien Bui, D.; Shirzadi, A.; Chapi, K.; Shahabi, H.; Pradhan, B.; Pham, B.T.; Singh, V.P.; Chen, W.; Khosravi, K.; Bin Ahmad, B.; et al. A Hybrid Computational Intelligence Approach to Groundwater Spring Potential Mapping. Water 2019, 11, 2013. [Google Scholar] [CrossRef] [Green Version]
- Davoudi Moghaddam, D.; Rahmati, O.; Panahi, M.; Tiefenbacher, J.; Darabi, H.; Haghizadeh, A.; Torabi Haghighi, O.; Asadi Nalivan, O.; Tien Bui, D. The effect of sample size on different machine learning models for groundwater potential mapping in mountain bedrock aquifers. Catena 2020, 187, 104421. [Google Scholar] [CrossRef]
- Stockwell, D. The GARP modelling system: Problems and solutions to automated spatial prediction. Int. J. Geogr. Inf. Sci. Int. 1999, 13, 143–158. [Google Scholar] [CrossRef]
- Sut, N.; Simsek, O. Comparison of regression tree data mining methods for prediction of mortality in head injury. Expert Syst. Appl. 2011, 38, 15534–15539. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2000. [Google Scholar]
- Davoudi Moghaddam, D.; Pourghasemi, H.R.; Rahmati, O. Assessment of the Contribution of Geo-environmental Factors to Flood Inundation in a Semi-arid Region of SW Iran: Comparison of Different Advanced Modeling Approaches. In Natural Hazards GIS-Based Spatial Modeling Using Data Mining Techniques, Advances in Natural and Technological Hazards Research; Pourghasemi, H., Rossi, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 48, pp. 59–78. [Google Scholar]
- Geology Survey of Iran (GSI). Available online: https://gsi.ir/en (accessed on 5 October 1997).
- Voeckler, H.; Allen, D.M. Estimating regional-scale fractured bedrock hydraulic conductivity using discrete fracture network (DFN) modeling. Hydrogeol. J. 2012, 20, 1081–1100. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of GIS-based logistic regression: A case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef] [Green Version]
- Angileri, S.E.; Conoscenti, C.; Hochschild, V.; Märker, M.; Rotigliano, E.; Agnesi, V. Water erosion susceptibility mapping by applying stochastic gradient Treeboost to the Imera Meridionale River Basin (Sicily, Italy). Geomorphology 2016, 262, 61–76. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Choubin, B.; Rahmati, O.; Soleimani, F.; Alilou, H.; Moradi, E.; Alamdari, N. Regional Groundwater Potential Analysis Using Classification and Regression Trees. In Spatial Modeling in GIS and R for Earth and Environmental Sciences, 1st ed.; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 485–498. [Google Scholar]
- Aniya, M. Landslide-susceptibility mapping in the Amahata river basin, Japan. Ann. Assoc. Am. Geogr. 1985, 75, 102–114. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modeling: A review of hydrological, geomorphological and biological applications. Hydro. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Schlögl, M.; Matulla, C. Potential future exposure of European land transport infrastructure to rainfall-induced landslides throughout the 21st century. Nat. Hazards Earth Syst. Sci. 2018, 18, 1121–1132. [Google Scholar] [CrossRef] [Green Version]
- Peterson, A.T.; Ball, L.G.; Cohoon, K.P. Predicting distributions of Mexican birds using ecological niche modelling methods. Ibis 2002, 144, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Sanchez-Flores, E. GARP modeling of natural and human factors affecting the potential distribution of the invasives Schismus arabicus and Brassica tournefortii in ‘El Pinacate y Gran Desierto de Altar’ Biosphere Reserve. Ecolog. Model. 2007, 204, 457–474. [Google Scholar] [CrossRef]
- Boeckmann, M.; Joyner, T.A. Old health risks in new places? An ecological niche model for I. ricinus tick distribution in Europe under a changing climate. Health Place 2014, 30, 70–77. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y. Applying various algorithms for species distribution modelling. Integr. Zool. 2013, 8, 124–135. [Google Scholar] [CrossRef] [PubMed]
- Rattray, A.; Ierodiaconou, D.; Laurenson, L.; Burq, S.; Reston, M. Hydro-acoustic remote sensing of benthic biological communities on the shallow South East Australian continental shelf. Estuar. Coast. Shelf Sci. 2009, 84, 237–245. [Google Scholar] [CrossRef]
- Ture, M.; Tokatli, F.; Kurt, I. Using Kaplan–Meier analysis together with decision tree methods (C&RT, CHAID, QUEST, C4. 5 and ID3) in determining recurrence-free survival of breast cancer patients. Expert Syst. Appl. 2009, 36, 2017–2026. [Google Scholar]
- Lee, S.; Park, I. Application of decision tree model for the ground subsidence hazard mapping near abandoned underground coal mines. J. Environ. Manag. 2013, 127, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Ierodiaconou, D.; Monk, J.; Rattray, A.; Laurenson, L.; Versace, V.L. Comparison of automated classification techniques for predicting benthic biological communities using hydroacoustics and video observations. Cont. Shelf Res. 2011, 31, 28–38. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Motevalli, A.; Zakeri, M.A. Gully erosion modeling using GIS-Based data mining techniques in northern Iran: A comparison between boosted regression tree and multivariate adaptive regression spline. In Natural Hazards GIS-Based Spatial Modeling Using Data Mining Techniques, Advances in Natural and Technological Hazards Research; Pourghasemi, H., Rossi, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 48, pp. 1–26. [Google Scholar]
- Ture, M.; Kurt, I.; Kurum, A.T.; Ozdamar, K. Comparing classification techniques for predicting essential hypertension. Expert Syst. Appl. 2005, 29, 583–588. [Google Scholar] [CrossRef]
- Chou, J.S. Comparison of multilabel classification models to forecast project dispute resolutions. Expert Syst. Appl. 2012, 39, 10202–10211. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.W. Application of decision-tree model to groundwater productivity-potential mapping. Sustainability 2015, 7, 13416–13432. [Google Scholar] [CrossRef] [Green Version]
- Loh, W.Y.; Shih, Y.S. Split selection methods for classification trees. Stat. Sin. 1997, 7, 815–840. [Google Scholar]
- Breiman, L. Statistical modelling: The two cultures. Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Youssefi, S.; Sadhasivam, N.; Pourghasemi, H.R.; Ghaffari Nazarlou, H.; Golkar, F.; Tavangar, S.; Santosh, M. Groundwater spring potential assessment using new ensemble data mining techniques. Measurement 2020, 107652. [Google Scholar] [CrossRef]
- Hollister, J.W.; Milstead, W.B.; Kreakie, B.J. Modeling lake trophic state: A random forest approach. Ecosphere 2016, 7, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Pradhan, B.; Xu, C.; Bui, D.T. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Khosravi, K.; Nohani, E.; Maroufinia, E.; Pourghasemi, H.R. A GIS-based flood susceptibility assessment and its mapping in Iran: A comparison between frequency ratio and weights-ofevidence bivariate statistical models with multi-criteria decisionmaking technique. Nat. Hazards 2016, 83, 947–987. [Google Scholar] [CrossRef]
- Gaprindashvili, G.; Guo, J.; Daorueang, P.; Xin, T.; Rahimy, P. A new statistic approach towards landslide hazard risk assessment. Int. J. Geosci. 2014, 5, 38–49. [Google Scholar] [CrossRef] [Green Version]
- Pham, B.T.; Khosravi, K.; Prakash, I. Application and comparison of decision tree-based machine learning methods in landside susceptibility assessment at Pauri Garhwal Area, Uttarakhand, India. Environ. Process. 2017, 4, 711–730. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. Catena 2012, 96, 28–40. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Tien Bui, D.; Hoang, N.D. GIS-based spatial prediction of tropical forest fire danger using a new hybrid machine learning method. Ecol. Inform. 2018, 48, 104–116. [Google Scholar] [CrossRef]
- Ngoc-Thach, N.; Ngo, D.B.T.; Xuan-Canh, P.; Hong-Thi, N.; Thi, B.H.; NhatDuc, H.; Dieu, T.B. Spatial pattern assessment of tropical forest fire danger at Thuan Chau area (Vietnam) using GIS-based advanced machine learning algorithms: A comparative study. Ecol. Inform. 2018, 46, 74–85. [Google Scholar] [CrossRef]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Dayal, K.S.; Deo, R.C.; Mohammadi, F.; Davoudi Moghaddam, D.; Naghibi, S.A.; Bui, D.T. Machine learning approaches for spatial modeling of agricultural droughts in the south-east region of Queensland Australia. Stoten 2020, 699, 134230. [Google Scholar] [CrossRef] [PubMed]
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei Sardooi, E.; Nazari Samani, A.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P.A. Uncertainty in the environmental modelling process-A framework and guidance. Environ. Model. Softw. 2007, 22, 1543–1556. [Google Scholar] [CrossRef] [Green Version]
- Garosi, Y.; Sheklabadi, M.; Pourghasemi, H.R.; Besalatpour, A.A.; Conoscenti, C.; Van Oost, K. Comparison of differences in resolution and sources of controlling factors for gully erosion susceptibility mapping. Geoderma 2018, 330, 65–78. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef]
- Ye, Y.; Wu, Q.; Huang, J.Z.; Ng, M.K.; Li, X. Stratified sampling for feature subspace selection in random forests for high dimensional data. Pattern Recogn. 2013, 46, 769–787. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modelling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef] [Green Version]
- Li, W.K.; Guo, Q.H.; Elkan, C. Can we model the probability of presence of species without absence data? Ecography 2011, 34, 1096–1105. [Google Scholar] [CrossRef]
- Pearson, R.G.; Thuiller, W.; Araujo, M.B. Model-based uncertainty in species range prediction. J. Biogeogr. 2006, 33, 1704–1711. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Spatial prediction of flood susceptible areas using rule based decision tree (DT) and a novel ensemble bivariate and multivariate statistical models in GIS. J. Hydrol. 2013, 504, 69–79. [Google Scholar] [CrossRef]


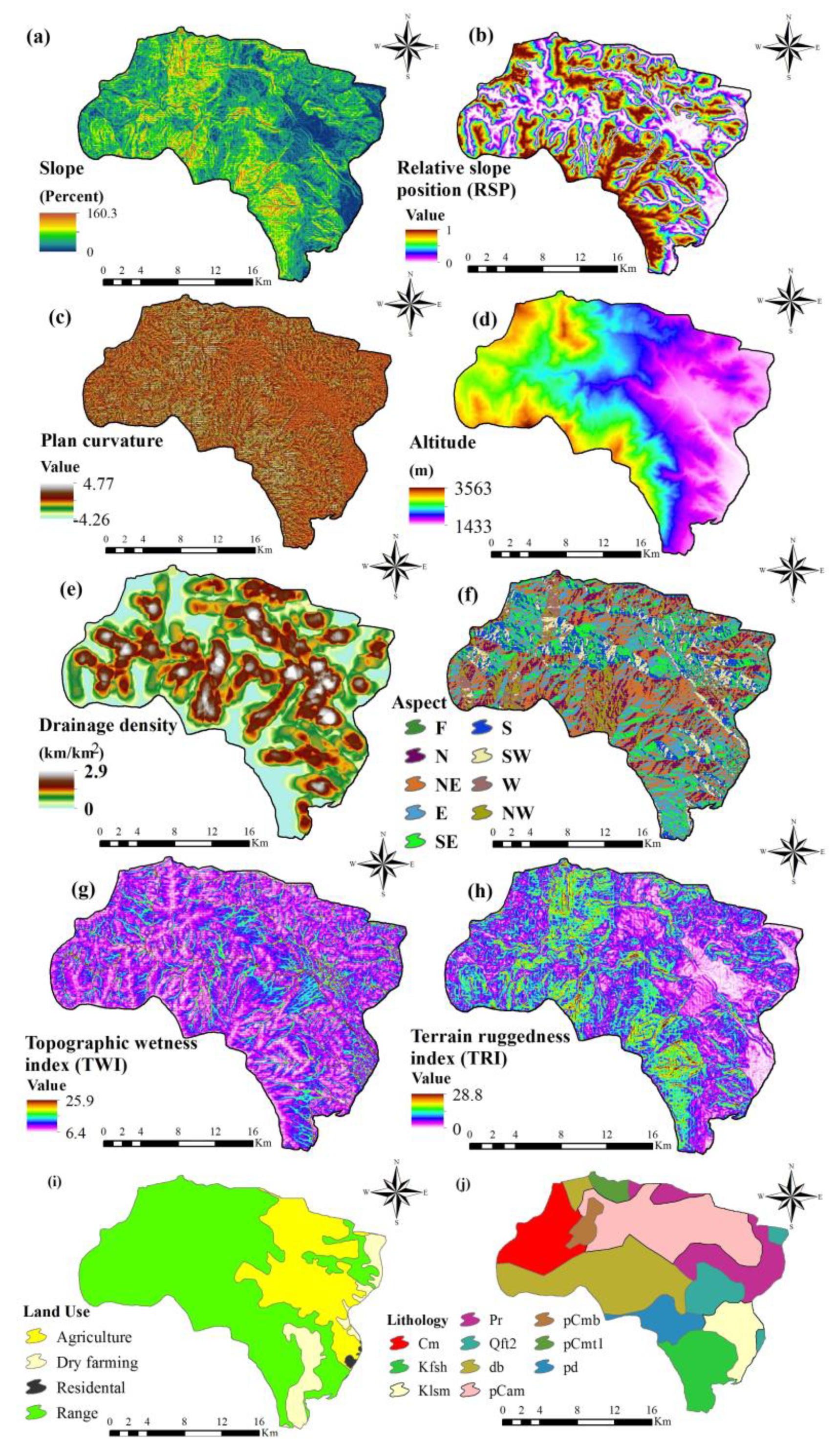





| Geological Unit | Description | Age | |
|---|---|---|---|
| pCmt1 | Medium-grade, regional metamorphic rocks (Amphibolite Facies) | Pre-Cambrian | Proterozoic |
| Pr | Dark grey medium-bedded to massive limestone (Ruteh Limestone) | Permian | Paleozoic |
| db | Diabase | Late Cretaceous | Mesozoic |
| Cm | Dark grey to black fossiliferous limestone with subordinate black shale (Mobarak FM) | Carboniferous | Paleozoic |
| pCam | Amphibolite | Pre-Cambrian | Proterozoic |
| pCmb | Marble | Pre-Cambrian | Proterozoic |
| Qft2 | Low level pediment fan and valley terrace deposits | Quaternary | Cenozoic |
| pd | Peridotite including harzburgite, dunite, lerzolite, and websterite | Triassic-Cretaceous | Mesozoic |
| Klsm | Marl, shale, sandy limestone, and sandy dolomite | Early Cretaceous | Mesozoic |
| Kfsh | Dark grey argillaceous shale | Cretaceous | Mesozoic |
| Factor | VIF | TOL |
|---|---|---|
| Relative slope position (RSP) | 2.256 | 0.563 |
| Lithology | 1.484 | 0.800 |
| Topographic wetness index (TWI) | 3.231 | 0.331 |
| Altitude | 3.547 | 0.238 |
| Drainage density | 1.833 | 0.906 |
| Terrain roughness index (TRI) | 2.993 | 0.410 |
| Slope | 1.550 | 0.956 |
| Aspect | 1.665 | 0.932 |
| Land use | 1.622 | 0.946 |
| Plan curvature | 2.837 | 0.544 |
| Class | GARP | QUEST | RF | |||
|---|---|---|---|---|---|---|
| Area (km2) | Area (%) | Area (km2) | Area (%) | Area (km2) | Area (%) | |
| Very low | 47.11 | 11.15 | 39.83 | 9.42 | 35.51 | 8.40 |
| Low | 115.15 | 27.24 | 75.77 | 17.92 | 82.26 | 19.46 |
| Medium | 107.38 | 25.40 | 57.45 | 13.59 | 91.04 | 21.54 |
| High | 119.72 | 28.32 | 81.45 | 19.27 | 87.97 | 20.81 |
| Very high | 33.35 | 7.89 | 168.20 | 39.79 | 125.93 | 29.79 |
| Evaluation Criteria | Dataset | Models | ||
|---|---|---|---|---|
| GARP | RF | QUEST | ||
| TSS | S1 | 0.81 | 0.88 | 0.79 |
| S2 | 0.86 | 0.94 | 0.74 | |
| S3 | 0.81 | 0.86 | 0.69 | |
| Mean | 0.82 | 0.89 | 0.74 | |
| AUC | S1 | 0.965 | 0.99 | 0.957 |
| S2 | 0.955 | 0.99 | 0.947 | |
| S3 | 0.952 | 1 | 0.943 | |
| Mean | 0.957 | 0.995 | 0.949 | |
| Evaluation Criteria | Dataset | Models | ||
|---|---|---|---|---|
| GARP | RF | QUEST | ||
| TSS | S1 | 0.79 | 0.81 | 0.70 |
| S2 | 0.81 | 0.91 | 0.69 | |
| S3 | 0.74 | 0.79 | 0.62 | |
| Mean | 0.78 | 0.83 | 0.67 | |
| AUC | S1 | 0.892 | 0.935 | 0.891 |
| S2 | 0.912 | 0.893 | 0.881 | |
| S3 | 0.925 | 0.946 | 0.899 | |
| Mean | 0.910 | 0.925 | 0.890 | |
| No. | Factor | Percentage Increase in Mean Square Error |
|---|---|---|
| 1 | Relative slope position, RSP | 82.6 |
| 2 | Lithology | 69.2 |
| 3 | Topographic wetness index, TWI | 55.1 |
| 4 | Altitude | 42.4 |
| 5 | Drainage density | 39.8 |
| 6 | Terrain ruggedness index, TRI | 35.3 |
| 7 | Slope | 31.2 |
| 8 | Aspect | 28.4 |
| 9 | Land use | 24.5 |
| 10 | Plan curvature | 20.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davoudi Moghaddam, D.; Rahmati, O.; Haghizadeh, A.; Kalantari, Z. A Modeling Comparison of Groundwater Potential Mapping in a Mountain Bedrock Aquifer: QUEST, GARP, and RF Models. Water 2020, 12, 679. https://doi.org/10.3390/w12030679
Davoudi Moghaddam D, Rahmati O, Haghizadeh A, Kalantari Z. A Modeling Comparison of Groundwater Potential Mapping in a Mountain Bedrock Aquifer: QUEST, GARP, and RF Models. Water. 2020; 12(3):679. https://doi.org/10.3390/w12030679
Chicago/Turabian StyleDavoudi Moghaddam, Davoud, Omid Rahmati, Ali Haghizadeh, and Zahra Kalantari. 2020. "A Modeling Comparison of Groundwater Potential Mapping in a Mountain Bedrock Aquifer: QUEST, GARP, and RF Models" Water 12, no. 3: 679. https://doi.org/10.3390/w12030679
APA StyleDavoudi Moghaddam, D., Rahmati, O., Haghizadeh, A., & Kalantari, Z. (2020). A Modeling Comparison of Groundwater Potential Mapping in a Mountain Bedrock Aquifer: QUEST, GARP, and RF Models. Water, 12(3), 679. https://doi.org/10.3390/w12030679







