A Perforated Baffle Design to Improve Mixing in Contact Tanks

Abstract

In this study, a perforated baffle design is proposed to improve mixing in contact tanks. Turbulent flow through the perforated baffle is studied at the perforation hole scale. The contribution of jets emerging from the perforations to the mixing process is evaluated in terms of standard mixing indexes for various perforation parameters, such as the solidity ratio and hole diameter. Based on numerical simulation results, the two sets of perforated baffles that yielded the highest performance were manufactured from polycarbonate and tracer studies were conducted on a laboratory model. Comparison of numerical and experimental results demonstrates that the numerical model developed is reliable in simulating the flow through the perforated baffles and the associated mixing level in the contact tank. Numerical simulations indicate that the jet flow structure through the perforated baffle penetrates to the recirculation zones in the neighboring chambers and turns the dead zones into active mixing zones. Furthermore, large scale turbulent eddies shed by the perforations contribute to the mixing process in the chambers of the tank. With the use of the perforated baffle design, it is shown that the hydraulic efficiency of the tank can be improved from average to superior according to the baffling factor, and the associated mixing in the proposed design can be improved by 31% according to the Morrill index.

1. Introduction

Raw water is delivered to contact tanks for chemical disinfection using chlorine or ozone as the last treatment process in water treatment plants. Conventionally, solid baffles are used in contact tanks to increase the residence time of water in the tank through the serpentine flow created. Serpentine flow increases the water–disinfectant contact time for the removal of pathogens and viruses from the water. This classical design yields an inefficient mixing environment due to the occurrence of recirculating dead zones and short-circuiting in the chambers of the mixing tank. The interaction of turbulent flow with the solid baffles significantly reduces the hydraulic and mixing efficiencies. As the disinfection efficiency is reduced, high disinfectant usage and energy consumption emerge as the negative outcomes of the disinfection process. These concerns have led researchers to design alternative mixing tank systems for the effective disinfection of potable water using less chemical and low energy consumption in municipal water treatment plants.

More recently, the slot-baffle design (SBD), proposed by Aral and Demirel [1,2], has considerably improved the mixing efficiency and reduced short-circuiting in the water treatment contact tank. Based on the Large Eddy Simulation (LES) studies, the SBD improved the mechanical mixing efficiency by 44%, the hydraulic efficiency by 44% and reduced the friction-induced energy losses by 43% [3]. Kizilaslan et al. [4] numerically investigated the performance of a full-scale chlorine contact tank (CCT), which is locally installed in a water treatment plant run by the Eskisehir municipality in Turkey. Performance assessment of the patented SBD [2] on the full-scale tank showed that the hydraulic efficiency shifted from average to high as Morrill (Mo) index approached 2, chlorine usage decreased by 19% and energy efficiency increased by 62%. Mixing performance of a vertical contact tank was numerically analyzed by Kizilaslan et al. [5] using horizontally placed baffles, where the porosity of the horizontal baffles were modeled using Darcy–Forchheimer equations. They concluded that this design could successfully reduce short-circuiting in the tank yielding a plug-flow condition along the chambers. For this case, the hydraulic efficiency was promoted from poor to good and the overall efficiency shifted from compromising (0.5 < AD < 1.75) to good (1.75 < AD < 3.5) according to the Aral–Demirel (AD) index [6,7].

Modifying baffle spacing [8,9,10,11,12,13,14,15], changing inlet configuration [9,10,14,15], placing turning vanes near the corners of the chamber baffles [10] and creating slim openings above and below the baffles [1,2,3,16] are other design alternatives that are reported in the literature. Using a solid turning vane apparatus or adding horizontal baffles in addition to the existing solid baffles reduces the effective mixing volume proportional to the volume of the tank, which is not desired. Another drawback of the use of additional solid structures inside the tank is that the interaction of turbulent flow with the solid structures increases friction-induced energy losses. In order to overcome these design problems, a porous baffle application has been recently introduced as a conceptual design to improve the hydraulic and mixing efficiencies of contact tanks [17]. In that study, sand–gravel mixture zones embedded in the vertical baffles were used to create the heterogeneous porous zones. Experimental and numerical studies have demonstrated that the sand–gravel porous baffle zones improved the hydraulic efficiency of the contact tank, and the mixing efficiency was improved by 28%, according to the Mo index. The use of sand–gravel porous zones has some drawbacks in operation, such as blocking of the pores, bacterial clogging and the need for frequent cleansing processes. Experimental studies are also available in the literature, where nanoscale micro-porous structures are used [18,19]. In these studies, the focus is on chemical aspects of the treatment process.

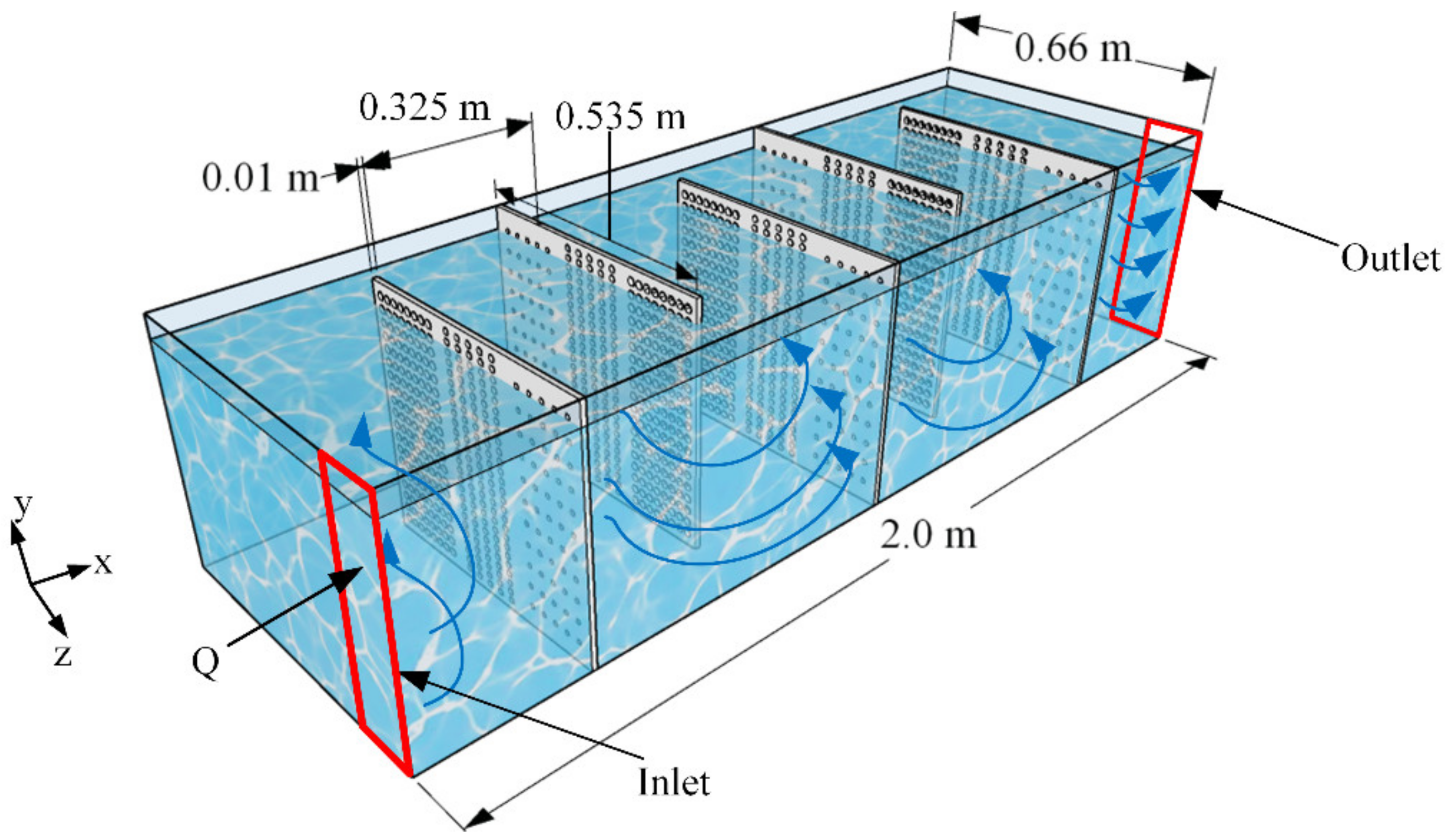
The main motivation of the present study is to design a perforated baffle that would mimic the performance of the previously investigated sand–gravel porous baffle concept as the perforated baffles replace the main solid wall baffles of the mixing tank. This approach would avoid the important limitations of the sand–gravel concept in practical applications. In the present work, experimental and numerical studies are carried out to investigate the contribution of the perforated baffle to the mixing performance of a multi-chambered contact tank, as shown in Figure 1. Highly resolved three-dimensional (3D) numerical models are used to solve the turbulent flow equations through the perforated baffles at a hole scale. The effect of the resulting jet flow structures formed in the chambers of the tank on mixing is evaluated for a conservative tracer. The study also includes an experimental investigation where two sets of perforated baffles with different perforations were manufactured and tracer studies were carried out on a laboratory scale contact tank. Numerical results are compared with the experimental results to show the reliability of the numerical model used. A series of flow and tracer simulations are performed for different perforations to optimize the proposed baffle design. The present experimental and numerical results are evaluated for practical implementation of the proposed perforated baffle design in field scale contact tanks.

2. Methods

A three-dimensional numerical model is employed for the simulation of turbulent flow through the perforated baffle at a hole scale in order to capture small jet-flow structures emerging from the holes. A numerical conservative tracer model is developed and used to evaluate the resulting efficiency index values. Experimental studies are carried out using two sets of perforated baffles to validate the numerical model and to demonstrate the practical implementation of the perforated baffle design on a physical model.

2.1. Computational Model

2.1.1. Flow Model

Incompressible and turbulent flow inside the contact tank is governed by the following continuity and momentum equations:

$$\frac{\partial U_i}{\partial x_i}=0,$$

(1)

$$\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_i}\left(v\frac{\partial U_i}{\partial x_j}-\overline{u_i^{\prime }}\overline{u_j^{\prime }}\right),$$

(2)

where $U_i$ is the average flow velocity in the i-direction, $u_i^{\prime }$ is fluctuating velocity components in the i-direction, ρ is the fluid density, p is the pressure, t is the time, $v$ is the kinematic viscosity, x_i and x_j are Cartesian coordinates. Reynolds-averaged Navier–Stokes (RANS) equations are closed using a k-ε turbulence closure model for the solution of turbulent flow in the contact tank. Reynolds stresses are approximated by the following Boussinesq hypothesis:

$$-\overline{u_i^{\prime }}\overline{u_j^{\prime }}=v_t\left(\frac{\partial U_j}{\partial x_i}+\frac{\partial U_i}{\partial x_j}\right)+\frac{2}{3}k{\delta }_{ij},$$

(3)

where δ_ij is the Kronecker delta, k is the turbulence kinetic energy, and $v_t$ is the turbulent viscosity, which is defined as,

$$v_t=C_{\mu }\frac{k}{{\epsilon }^2}$$

(4)

where C_μ is the model constant and selected as 0.09. Two transport equations are sequentially solved for $k$ and $\epsilon$ using appropriate boundary conditions.

2.1.2. Conservative Tracer Model

Efficiency of the contact tank is evaluated by means of tracer simulations for a conservative tracer. The following advection–diffusion equation is solved using the frozen flow concept to propagate the tracer on a predicted flow field:

$$\frac{\partial C}{\partial t}+u_j\frac{\partial C}{\partial x_j}=\frac{\partial }{\partial x_j}\left(D_t\frac{\partial C}{\partial x_j}\right),$$

(5)

where $D_t$ is the turbulent diffusivity and $C$ is the tracer concentration. Turbulent diffusivity is calculated as the ratio of the turbulent viscosity $\left(v_t\right)$ to the Schmidt number $\left(S{c}_t=0.7\right)$. In the conservative tracer analysis, a fixed volume of tracer is injected at the inlet and the concentration is observed at the outlet of the tank to obtain Residence Time Distribution (RTD) and cumulative RTD (CRTD) curves. These results are used to determine the hydraulic and mixing efficiency index values. Tracer injection time is selected to be less than 5% of the calculated MRT [20].

$$MRT=\frac{\forall }{Q}$$

(6)

where $\forall$ is the volume of the tank and $Q$ is the flow rate. The non-dimensionalized tracer concentration and cumulative concentrations are calculated from the following equations:

$$E\left(\theta \right)=\frac{C}{C_{init}\times \frac{T_{injection}}{\tau }}$$

(7)

and

$$F\left(\theta \right)={{\displaystyle \int }}_0^{\infty }E\left(\theta \right)d\theta ,$$

(8)

where C_init is the injected tracer concentration (C_init = 1), T_injection is the injection time, Ɵ = t/τ is the dimensionless time and τ is the MRT.

An open source CFD code OpenFOAM [21] is employed for the simulation of turbulent flow and tracer transport through the perforated baffles and the chambers. Second order numerical schemes are used for the discretization of convective and diffusive terms in the governing equations to reduce truncation errors.

2.1.3. Computational Domain and Boundary Conditions

In order to simulate flow through a perforated wall, a three-dimensional computational mesh is generated in two steps. A base mesh is first generated without baffles using the standard utility blockMesh to define dimensions and outer boundaries of the computational domain (Figure 2a). A structured mesh system is adopted in the base mesh, clustering smaller elements near the walls and top boundary to capture high gradients in the flow variables. Baffles are sketched using a free software SketchUp [22] and the surface geometry is exported as a stereo lithography (STL) format. Another standard utility snappyHexMesh is then used as the second step to generate hexahedra and split-hexahedra meshes for the corresponding surface geometry. The utility snappyHexMesh approximately conforms the mesh to the surface, iteratively refining the mesh near the curved surfaces with parallel computing, since morphing of the split-hex mesh may take a considerably long time on a single processor. The maximum allowable skewness and non-orthogonality of the mesh is optionally defined in the input file to reduce numerical errors arising from the calculation of gradients near the curved surfaces. Mesh is generated approximately in three hours using 28 processors (Intel E-5 2690 v4 2.60GHz) with parallel computing on a cloud-computing center. The resultant mesh in Figure 2b contains 13 million cells. However, the number of meshes may reach 27 million cells for the other cases studied, depending on the number of holes on the perforated baffles that are used in the study.

For closure of the mathematical model, appropriate boundary conditions are defined for the flow variables at the inlet, outlet, walls and top of the computational domain (Figure 1). The average flow velocity at the inlet is calculated as U_average = Q/A for a given flow rate Q and applied as a constant value along the flow direction. The following boundary conditions are used for the turbulence quantities at the inlet:

$$k=\frac{3}{2}{\left(UI\right)}^2,$$

(9)

$$\epsilon =C_{\mu }^{\frac{3}{4}}\frac{k^{1.5}}{l},$$

(10)

where $U$ is the average flow velocity at the inlet, $I$ is the turbulence intensity, which is set to 0.05 and $l$ is the turbulence length scale. Free-stream boundary conditions are applied at the outlet to allow the flow variables to leave the computational domain with no reflection. A no-shear condition is imposed for the velocity and a zero gradient boundary condition is used for the pressure on the smooth walls. The top boundary is treated as a symmetry boundary with no shear, since free-surface effects are neglected in the present problem. Unified wall functions are used for the turbulence kinetic energy k, specific turbulent dissipation rate ε and the turbulent viscosity $v_t$ on the walls.

2.2. Experimental Method

The chlorine contact tank, situated in the province of Eskisehir, was constructed using a 1:10 model scale in the laboratory [17]. The average flow rate of 80,000 m³/day in the prototype was converted to the laboratory model as 2.9 lt/s, according to the Froude similitude $\left(\frac{Q_{model}}{Q_{prototype}}={\left(\frac{1}{10}\right)}^{2.5}\right)$, which was appropriate to characterize the flow in the contact tank. Experimental studies were conducted using the flow conditions shown in

Table 1. Flow conditions used in the experimental studies.

Discharge (lt/s)	Water Depth (cm)	Wet Volume (m3)	MRT (s)	Injection Time (s)
2.93	48.5	0.63	215	10

on a laboratory model which was 4 m long, 66 cm in width and 75 cm in height. The flow rate was adjusted manually using a valve and measured with an ultrasonic flow meter mounted on the feeding pipe. The water depth in the tank was measured as 48.5 cm under steady-state flow conditions. As seen in Figure 3a, the laboratory-scale contact tank consists of ten chambers and baffles are removable to test different baffling configurations on the same experimental setup in [4].

Tracer studies were conducted on the physical model to validate the numerical model. The Rhodamine WT Dye was used as a conservative tracer, which was injected at the inlet of the chamber using a time adjustable syringe pump. Even though the laboratory model consists of ten chambers, numerical studies are performed on a six-chambered tank in order to reduce computational memory and time, since a periodical flow forms inside the baffled tank. To compare experimental and numerical results with no complications, the tracer was injected at the inlet of the third chamber and monitored by using Cyclops 7F fluorimeter at the outlet of the eighth chamber of the contact tank (Figure 3b) during the experimental studies. This approach also excluded the disturbance effects encountered near the inlet and enabled us to evaluate the effect of the perforated baffle design on the mixing performance independent of the inlet effects.

3. Results and Discussion

Prior to the experimental studies, numerical simulations were performed to determine which configuration yields the highest mixing performance. Flow and tracer simulations are carried out for seven designs with different perforation parameters, as summarized in

Table 2. Perforation parameters of baffle designs with varying open areas.

Design	Solidity Ratio (%)			Hole Diameter (cm)	Number of Holes
Design 1	Open Area	Section 1	90	1	110
		Section 2	80	1.3	130
		Section 3	70	1.6	128
Design 2	Open Area	Section 1	95	1	54
		Section 2	80	1.3	132
		Section 3	70	1.6	128
Design 3	Open Area	Section 1	95	1	55
		Section 2	85	1.2	114
		Section 3	75	1.4	140
Design 4	Open Area	Section 1	95	1	55
		Section 2	85	1.2	114
		Section 3	70	1.6	128
Design 5	Open Area	Section 1	95	1	55
		Section 2	75	1.4	140
		Section 3	70	1.6	128
Design 6	Open Area	Section 1	96	1	44
		Section 2	80	1.4	130
		Section 3	70	1.6	128
Design 7	Open Area	Section 1	95	1	55
		Section 2	80	1.4	130
		Section 3	65	1.6	152

. The two designs that gave the highest performance were selected and perforated baffles were constructed to conduct experimental studies on the laboratory setup identified above. The experimental studies consisted of tracer studies using the two highest performing designs. Numerical results are validated with the experimental measurements for this complex mixing system. After validation of the numerical model, the optimum perforation is determined for these designs using numerical simulations. To analyze the results in a systematic manner, the solidity ratio is defined as:

$$S=1-\frac{{{\displaystyle \sum }}_{i=1}^3{{\displaystyle \sum }}_{j=1}^{N_i}{A}_{ij}}{A_T}$$

(11)

where i denotes the zone number on the baffle since the baffle is composed of three zones having different perforations, $N_i$ is the number of holes on the ith zone, $A_{ij}$ is the area of the corresponding circular hole and $A_T$ is the total surface area of the baffle. As the solidity increases, the blockage effect of the perforated baffle increases and hence, permeation of the baffle reduces.

The effect of the hole size is then investigated, keeping the solidity of the baffle constant to optimize the proposed design. Numerical simulations consist of the simulation of flow inside the contact tank and the transport of the tracer over the corresponding flow field. The former includes the steady-state simulation of the turbulent flow using appropriate boundary conditions. The unsteady simulation of the flow through the narrow hole distribution would increase the simulation time extremely, even with the parallel computing platform we have used. Thus, this approach was not used. The approach used consists of the unsteady solution of the advection–diffusion equation over a steady-state flow field, since this equation includes spatial variations of velocity field and turbulent viscosity, which are predicted from the flow simulations.

3.1. Perforated Baffle Structures

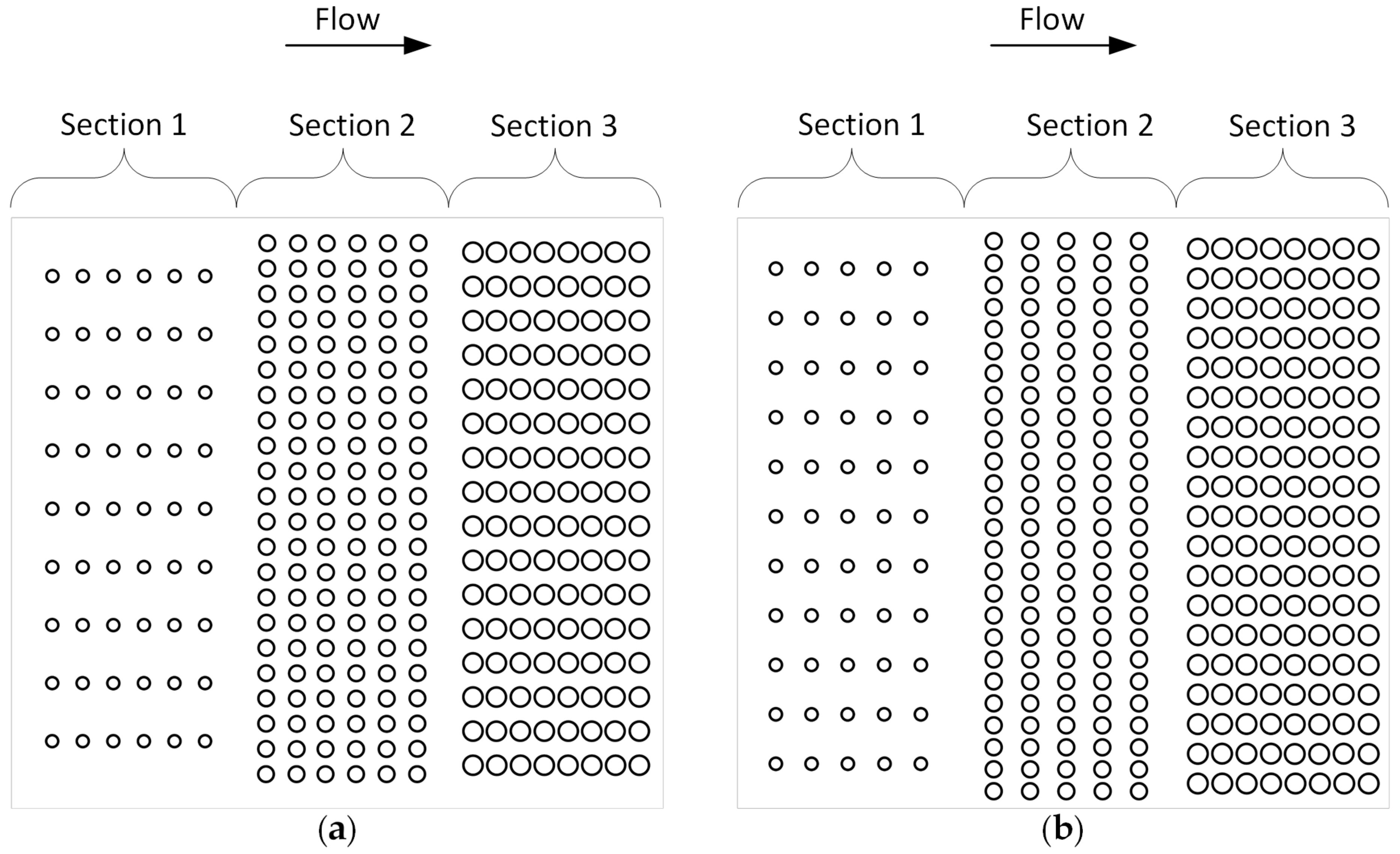
Perforated baffles have been designed in three sections with increasing perforation in the flow direction, like the porous baffle concept developed earlier [17]. The previous experimental and numerical studies revealed that decreasing the solidity ratio (S) of the porous baffle design in the flow direction increases the efficiency of the contact system, since the momentum and energy of the mean flow decreases due to the flow through the permeated sections of the baffle. Accordingly, baffles were designed in three sections in the flow direction such that each homogenous section had a different hole diameter and hole number for the corresponding solidity ratios. Baffles are sketched for different perforations and corresponding parameters, such as the open area, the hole diameter and the number of holes, which are given in Table 2, and were used to analyze the effect of perforation on mixing performance.

3.2. Numerical Results

Flow and tracer simulations were sequentially performed for the perforated designs, along with the conventional baffle design, to assess the improvement in mixing performance relying on the available indexes that are determined from the CRTD plot shown in Figure 4b. With the use of the conventional baffle design in the contact tank, the initial peak value observed in the RTD curve (Figure 4a) occurs at approximately θ = 0.4, which indicates that most of the tracer concentration leaves the tank with the jet flow in less time than the desired contact time. A second peak is observed in the conventional design near θ = 0.8. This is because some portion of the tracer that is trapped in the dead zones are observed at the outlet after a time delay in the conventional design. The second peak is not seen in the perforated designs since the dead zones are successfully converted to the active mixing zones with the effect of the jet flow regions created. Perforated baffles successfully eliminate recirculation zones and reduce the short-circuiting effects observed in the conventional design. Moreover, when the perforated baffle is used, the peak in the RTD plot shifts to the right and approaches to θ = 1, which is a strong indicator of the reduction of short-circuiting effects. Dimensionless hydraulic and mixing efficiency indexes are determined from CRTD curves, as given in

Table 3. Baffling classifications and factors [23].

Baffling Condition	θ10
Unbaffled	0.1
Poor	0.3
Average	0.5
Superior	0.7
Perfect (plug flow)	1.0

. As suggested by the US EPA [23], hydraulic performance of a contact tank can be classified according to the baffling factor θ₁₀, as given in Table 3.

The mixing efficiency can be evaluated with respect to several indexes such as Mo, dispersion (σ) and AD [6,7], which has been suggested (Equation (12)) for the evaluation of overall efficiency of contact tanks, since Mo index may give confusing results for some cases.

$$AD=\frac{{\theta }_{90}-1}{1-{\theta }_{10}},$$

(12)

Design 2 and Design 7 showed the highest performance, since both designs upgraded the tank to excellent class in terms of the baffling factor (Table 3). As given in

Table 4. Hydraulic and mixing efficiency indexes for conventional and perforated baffle designs.

Design	θ10	θ90	Mo	σ	AD
Conventional	0.547	2.486	4.545	0.14293	3.203
Design 1	0.768	1.894	2.466	0.08597	3.853
Design 2	0.8	1.914	2.392	0.07553	5.097
Design 3	0.784	1.885	2.404	0.07719	4.097
Design 4	0.798	2	2.506	0.07874	4.95
Design 5	0.797	1.895	2.378	0.07439	4.409
Design 6	0.799	1.968	2.463	0.07822	4.816
Design 7	0.807	1.838	2.277	0.07454	4.342

, Mo and dispersion indexes indicate that Design 7 has the highest mixing efficiency, since regulations recommend the Mo index to be close to 2 and the dispersion index should be close to 0 for a perfect mixing system. AD index shows that all perforated designs improved overall efficiency of the tank to the excellent classification (AD > 3.5) [6].

3.3. Experimental Results and Model Validation

Numerical simulations conducted for different perforated baffles demonstrated that Design 2 and Design 7 had the highest hydrodynamic performance among the considered designs according to the baffling factor [23]. Therefore, Design 2 and Design 7 were selected for further study. As shown in Figure 5, two sets of perforated baffles were manufactured from polycarbonate for the corresponding perforations. Baffles were carefully perforated using the water jet as a perforator, ensuring that each hole was completely circular. This forms the basis of the experimental system design.

Experimental tracer studies were conducted using the manufactured baffles and results are compared with the numerical simulation results in Figure 6. Distributions of RTD curves show high similarity between the result of experimental and numerical studies. The peak value observed in the RTD plot shifts to the right for the perforated baffle and approaches to unity in the horizontal axis, which is a strong indicator of the reduction of short-circuiting effects. Thus, raw water interacts with the conservative tracer for a longer period. As seen in Figure 6a, experimental measurements produce a wavy variation in the RTD plot which may be due to the large-scale energetic eddies in the wake of the baffles. On the other hand, Design 2 produces a higher θ₉₀ value in the CRTD curve (Figure 6b). The differences between CRTD curves are such that they do not contain significant deviations in hydraulic and mixing efficiency indexes.

3.4. Flow Analysis

Velocity vectors on a horizontal plane located at the mid-depth of the tank are compared for solid and perforated baffles in Figure 7. The large recirculation zone that covers most of the volume of the chambers reduces the effective mixing volume of the mean flow inside the chamber and results in a higher mean velocity magnitude to pass the desired flow rate through the small volume. Expectedly, water leaves the tank with higher tracer concentration within the main jet flow region resulting in a strong short-circuiting effect in the tank (Figure 7a). High velocity parcels also account for high friction-induced energy losses in the conventional contact tank design, whereas the jet flow through the perforated baffles penetrate in the recirculation zone in the neighboring chambers and turns the dead zones to active mixing zones (Figure 7b,c). Large-scale turbulent eddies shed by the circular holes on the perforated baffle also contribute to the mixing inside chambers. Perforated baffle design provides a flow transition between neighboring chambers that reduces the momentum of the jet in the flow direction. The proposed contact system with less main jet flow region and recirculation zones is expected to yield high hydraulic and mixing efficiencies. As can be seen in Figure 7b, the relatively higher solidity ratio used at the third section of Design 2 has created a stronger jet flow through the holes near the inlet of the tank. This observation shows that the dynamics of the perforated baffle system are strongly dependent on the distribution of the perforation over the baffle.

To analyze the flow structure that occurs in the tank in more detail, three-dimensional path-lines are visualized in Figure 8 for steady-state flow conditions. The path-lines show that the conventional tank design is under the influence of the jet flow since circulation zones induced by the solid walls cover most of the chambers. The perforated baffle was designed in three sections to prevent the injected tracer from leaving the tank before a desired time, since it contains less perforation and more solidity in the section where the jet momentum is high [17]. Perforated baffles eliminated the recirculating dead zones while creating new mixing zones in these regions.

3.5. Performance Analysis of the Perforated Baffle Design

Numerical simulations reveal that Design 7 increases hydraulic and mixing efficiencies of the present contact tank in a most effective way in comparison to the other designs analyzed in this study. Here, a performance analysis is carried out for Design 7 using the validated numerical model. Additional simulations of flow and tracer with different perforation parameters were used to investigate the effect of hole diameter and hole number on the efficiency without changing the solidity ratio. To achieve this goal, hole diameters were first increased at each section of the baffle in Design 7.1. Efficiency indexes indicated a reducing efficiency in terms of both hydraulic and mixing for this case. Thus, hole diameter is reduced in the remaining cases in

Table 5. Perforation parameters and calculated efficiency indexes for new designs.

Design	Hole Diameter (cm)	Number of Holes	θ10	Mo	σ	AD
Design 7	1	55	0.807	2.2776	0.07454
	1.4	130				4.342
	1.6	152
Design 7.1	1.51	25	0.7911	2.4544
	1.86	64			0.0806	4.507
	2.19	80
Design 7.2	0.54	192	0.8235	2.2745
	1.1	182			0.0718	4.960
	1.35	210
Design 7.3	0.54	192	0.8456	2.2776
	0.9	270			0.0698	6.013
	1.12	306
Design 7.4	0.47	250	0.8491	2.2346
	0.83	320			0.0692	5.947
	1.05	350

to optimize the efficiency of the perforated baffle. Variations of the efficiency indexes with the number of holes are also shown in Figure 9.

Figure 9 shows that the baffling factor increases, Mo index approaches 2 and dispersion index approaches 0, which are all indicators of improvement of hydraulic and mixing efficiencies when the number of holes increases. The AD index, which provides information on mixing and hydraulic efficiencies as a single parameter, indicates that the improvement in the efficiency of the contact tank is at an important level. The AD index value shows that perforated baffles in Table 5 are classified as excellent (AD > 3.5) [6]. All indexes show that the perforated baffle with small diameters and a high number of holes increases the efficiency of the contact system. Improvement in the efficiency becomes independent of the hole number when the hole number is greater than 800 (Figure 9). Considering the production cost in the perforation process, it would be appropriate to determine the optimum design using a formal optimization analysis, which is out of the scope of the current study.

The tracer results for the optimized design are compared with the conventional design in Figure 10. The RTD curve shows that the tracer and raw water remain in interaction for a longer period with the perforated baffle design. The second peak created by the tracer, trapped in the dead zones leaving the tank, disappears when perforated baffle design is used. Higher magnitude of the peak observed in the RTD plot corresponds to the formation of the bulk flow without recirculation zones in the perforated design. As a novel design, the perforated baffle produces significantly different RTD and CRTD plots.

4. Conclusions

The improvement of the mixing efficiency of disinfection contact tanks has been the subject of decades of research for public health and energy considerations. In this study, numerical and experimental analysis results are presented for the flow and tracer transport through perforated baffles in a multi-chambered contact tank with a focus on the practical implementation of the perforated baffle concept. Comparison of high-resolution numerical simulations with experimental results has shown that the numerical model developed accurately simulates the flow and tracer transport through the chambers of the tank. It was found that the jet flow through the perforated baffle penetrates the recirculating zone in the neighboring chambers and turns the dead zones into active mixing zones. Moreover, large scale turbulent eddies shed by the circular holes on the baffle create new mixing zones in the chambers of the tank.

A series of flow and tracer simulations performed on a laboratory scale contact tank demonstrate that the perforated baffle design enhances the hydraulic efficiency by 36% according to the baffling factor and mixing efficiency by 31% according to the Mo index. Various hole distributions are numerically studied, keeping the solidity ratio as constant. Simulation results show that the improvement in efficiency becomes independent of the hole number when the hole number is greater than 800 for the present contact tank. Considering the production cost in the perforation process, it would be appropriate to determine the optimum design using a formal optimization analysis, which is out of the scope of the current study. Instead of using metal as the manufacturing material of the perforated baffle, it is recommended to construct the perforated baffles from concrete, which is a standard procedure in contact tank construction in water treatment plants. This would provide long-term performance, while avoiding potential corrosion effects. If cost is not of concern, thick polycarbonate material may also be used in the construction of the perforated baffles, as was done in this study. This approach may provide flexibility in the design, since these perforated baffles may be changed depending on the discharge treated, which may vary seasonally. The proposed perforated baffle design can also be applied to the existing contact tanks by perforating the solid baffle using appropriate drilling techniques. The perforation levels necessary can be determined from CFD simulations on a field scale contact tank. To minimize the production costs and increase efficiency, it is recommended that each contact tank design should be evaluated individually, and optimum hole diameter and hole number should be determined for a range of flow rates, based on flow and tracer simulations similar to the cases reported in this study.