Simulation of a Water Distribution Network with Key Performance Indicators for Spatio-Temporal Analysis and Operation of Highly Stressed Water Infrastructure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study Description
2.2. Infrastructure and Data
2.3. Simulation of the WDN with EPANET
2.4. Water Consumption, Leakage and Other SIV Components Spatio-Temporal Distribution Simulation
2.4.1. Time-Pattern Spatio-Temporal Demands
2.4.2. Pressure-Dependent Spatio-Temporal Demands
2.5. Leakage Estimation and SIV Component Analysis
2.5.1. Daily Pressure Patterns
- (a)
- The recorded pressure time series by the three cellos were processed; outliers are removed and replaced with averaged values of the adjacent time slot records, and the quarterly time step is transformed to hourly time step by averaging the four records of every hour. The recorded data use refers to a time period from February 2015 to March 2017.
- (b)
- From the above profiles, average daily pressure profiles are constructed for each one of the three locations, by averaging horizontally the records that correspond to the same hour of the day for the whole month. Days of the same month but different year (e.g., all July days, independent of the year) are used for the construction of the respective month profile.
- (c)
- The average WDN pressure value of the monthly period is estimated through an EPANET initial run. This initial run holds the assumption of zero leakage, so the WDN pressure is expected to be overestimated. This is corrected through an iterative process, after the first estimation of leakage.
- (d)
- The cello pressure profiles are moved laterally in order to meet the average WDN pressure as estimated in the previous step.
- (e)
- The three produced WDN pressure profiles are averaged, so that a single WDN daily pressure profile is created for every month.
2.5.2. Estimation of Leakage Using the Night-Flow Approach
- (a)
- For this estimation, the following steps are implemented:
- (b)
- The quarterly flowrate PRV time series are processed, outliers are removed and missing values are inputted. The available time series refer to a period from January to December 2016.
- (c)
- Average flowrates for each 15 minutes are estimated separately for each month.
- (d)
- At the average flowrates diagrams, the lowest estimated value is identified, as well as the timeslot it occurred. This value is defined as the MNF.
- (e)
- The pressure at that timeslot for the WDN is estimated with an EPANET run. The assumption of zero leakage is made for this first EPANET run, but it is corrected through an iterative process after the first estimated leakage values are input in the EPANET runs.
- (f)
- The night consumption is estimated according to the empirical model.
- (a)
- The leakage is estimated as the subtraction of MNF-night consumption.where 49.6 m3/hr is the minimum of averaged recorded flowrates and it occurs in January 4.15 am time slot
- (b)
- The formula i is used to construct the leakage daily profiles (as suggested in [34]) according to the pressure profiles produced as described in Section 2.5.2, the night leakage and the respective night leakage pressure value. N1 is estimated equal to 1.08.
- (c)
- For the twelve produced leakage profiles (Figure 13), the leakage estimated is compared to the minimum recorded night flow. The estimated amount should be less or at most equal, assuming that there might be a quarter of night hours, especially in winter time that for such a small village the consumption is negligible, if not zero.
- (d)
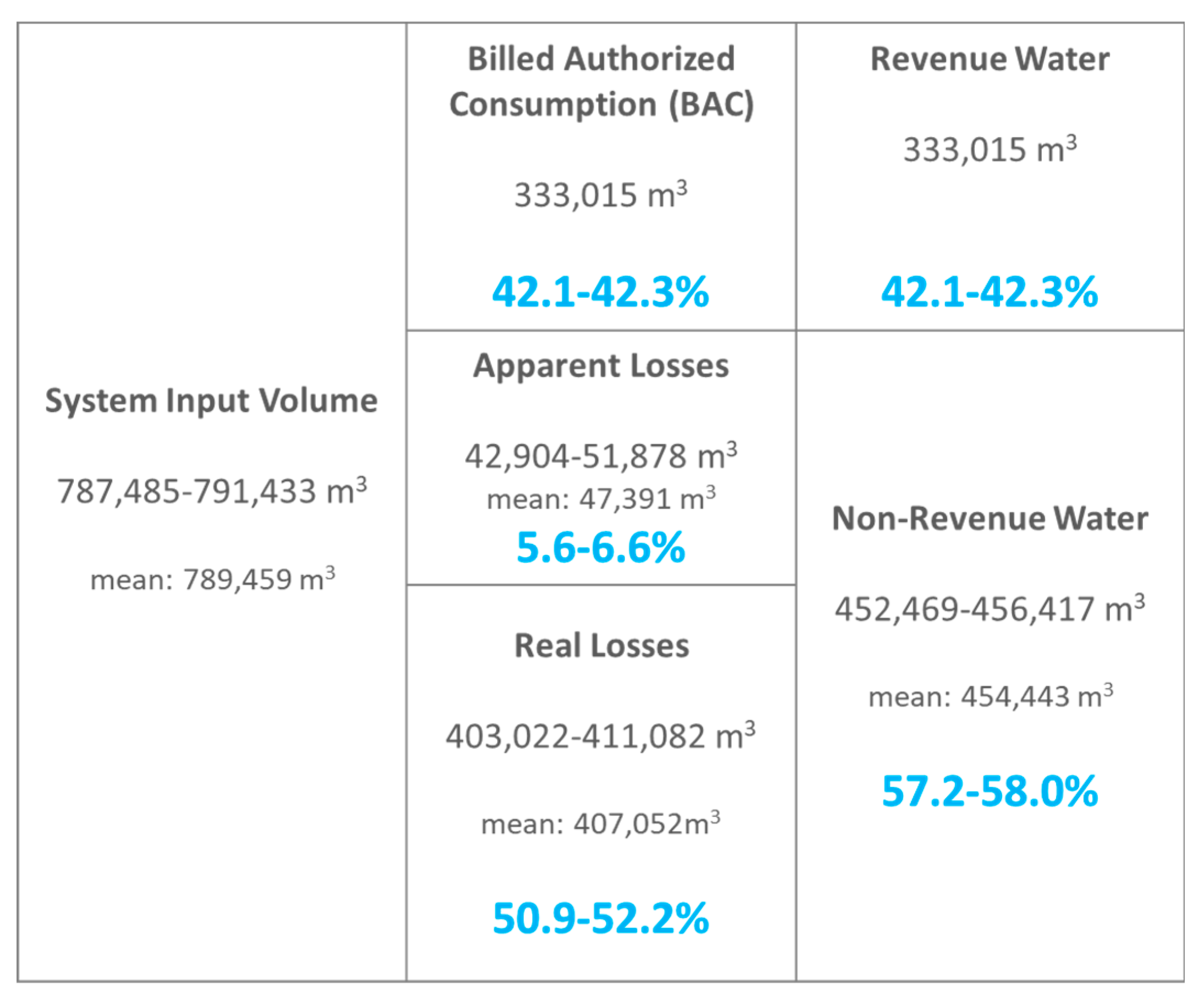
- The leakage is integrated for every one of the 12 months and a percentage of leakage over SIV is estimated.
- (e)
- The difference of NRW percentage and leakage percentage is considered as the decoupled apparent losses percentage at this iteration and is added to the billed consumption of each EPANET node for the next EPANET run iteration.
2.6. Pressure Management Scheme and Key Indicators for the Performance of the WDN
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- EEA. EEA SIGNALS 2018, Water Is Life; European Environmental Agency: Copenhagen, Denmark, 2018; ISBN 9789292139810. [Google Scholar]
- Raskin, P.; Gleick, P.H. Stockholm Environment Institute. In Water Futures: Assessment of Long-Range Patterns and Problems; Stockholm Environment Institute: Stockholm, Sweden, 1997; ISBN 9188714454. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S.; Papadopoulou, A.; Curk, B.C.; Karleusa, B. Estimating the Water Resources Vulnerability Index in the Adriatic Sea Region. Procedia Eng. 2016, 162, 476–485. [Google Scholar] [CrossRef] [Green Version]
- Kanakoudis, V.; Tsitsifli, S.; Papadopoulou, A.; Cencur Curk, B.; Karleusa, B. Water resources vulnerability assessment in the Adriatic Sea Region: The case of Corfu Island. Environ. Sci. Pollut. Res. 2017, 24, 20173–20186. [Google Scholar] [CrossRef] [PubMed]
- Sitarz, D. Agenda 21: The Earth Summit Strategy to Save Our Planet; Earthpress: Boulder, CO, USA, 1993. [Google Scholar]
- Colglazier, W. Sustainable development agenda: 2030. Science 2015, 349, 1048–1050. [Google Scholar] [CrossRef] [PubMed]
- Liemberger, R.; Wyatt, A. Quantifying the global non-revenue water problem. Water Sci. Technol. Water Supply 2019, 19, 831–837. [Google Scholar] [CrossRef]
- Lambert, A.O. International report: Water losses management and techniques. Water Sci. Technol. Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Almandoz, J.; Cabrera, E.; Arregui, F.; Cabrera, E.; Cobacho, R. Leakage Assessment through Water Distribution Network Simulation. J. Water Resour. Plan. Manag. 2005, 131, 458–466. [Google Scholar] [CrossRef]
- Cabrera, E.; Pellejero, I. Evaluation of leakage by means of night flow measurements and analytical discrimination. A comparative study. In Pumps, Electromechanical Devices and Systems Applied to Urban Water Management 1; Balkema Publisher: Lisse, The Netherlands, 2003; p. 327. [Google Scholar]
- Ismail, Z.; Puad, W.F.W.A. Non-Revenue Water Losses: A Case Study. Asian J. Water Environ. Pollut. 2007, 4, 113–117. [Google Scholar]
- Giustolisi, O.; Savic, D.; Kapelan, Z. Pressure-driven demand and leakage simulation for water distribution networks. J. Hydraul. Eng. 2008, 134, 626–635. [Google Scholar] [CrossRef] [Green Version]
- Tabesh, M.; Asadiyami Yekta, A.H.; Burrows, R. An integrated model to evaluate losses in water distribution systems. Water Resour. Manag. 2009, 23, 477–492. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S. Results of an urban water distribution network performance evaluation attempt in Greece. Urban Water J. 2010, 7, 267–285. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S. Water volume vs. revenues oriented water balance calculation for urban water networks: The Minimum Charge Difference component makes a difference! Proc. IWA Int. Spec. Conf. Water Loss 2010, 69, 27–30. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S. Using the bimonthly water balance of a non-fully monitored water distribution network with seasonal water demand peaks to define its actual NRW level: The case of Kos town, Greece. Urban Water J. 2014, 11, 348–360. [Google Scholar] [CrossRef]
- Cobacho, R.; Arregui, F.; Soriano, J.; Cabrera, E. Including leakage in network models: An application to calibrate leak valves in EPANET. J. Water Supply Res. Technol. AQUA 2015, 64, 130–138. [Google Scholar] [CrossRef] [Green Version]
- Sophocleous, S.; Savić, D.; Kapelan, Z. Leak Localization in a Real Water Distribution Network Based on Search-Space Reduction. J. Water Resour. Plan. Manag. 2019, 145, 04019024. [Google Scholar] [CrossRef]
- Makropoulos, C.K.; Natsis, K.; Liu, S.; Mittas, K.; Butler, D. Decision support for sustainable option selection in integrated urban water management. Environ. Model. Softw. 2008, 23, 1448–1460. [Google Scholar] [CrossRef]
- Rozos, E.; Makropoulos, C. Source to tap urban water cycle modelling. Environ. Model. Softw. 2013, 41, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Makropoulos, C.; Savíc, D.A. Urban hydroinformatics: Past, present and future. Water 2019, 11, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Puig, V.; Cembrano, G. Real-Time Control of Urban Water Cycle under Cyber-Physical Systems Framework. Water 2020, 12, 406. [Google Scholar] [CrossRef] [Green Version]
- Hellenic Statistical Authority. Population Housing Census. Available online: www.statistics.gr/en/2011-census-pop-hous (accessed on 25 February 2020). (In Greek).
- Kofinas, D.; Papageorgiou, E.; Laspidou, C.; Mellios, N.; Kokkinos, K. Daily multivariate forecasting of water demand in a touristic island with the use of artificial neural network and adaptive neuro-fuzzy inference system. In Proceedings of the 2016 International Workshop on Cyber-Physical Systems for Smart Water Networks (CySWater 2016), Vienna, Austria, 11 April 2016; pp. 37–42. [Google Scholar]
- Spyropoulou, A.; Lazarou, Y.G.; Laspidou, C. Mercury Speciation in the Water Distribution System of Skiathos Island, Greece. Proceedings 2018, 2, 668. [Google Scholar] [CrossRef] [Green Version]
- Rossman, L.A. EPANET 2 Users Manual; U.S. Environmental Protection Agency: Washington, DC, USA, 2000; ISBN EPA/600/R-00/057.
- Lambert, A.; Hirner, W. Losses from Water Supply Systems: A standard Terminology and Recommended Performance Measures; IWA: London, UK, 2000; Available online: waterfund.go.ke/watersource/Downloads/001.%20Losses%20from%20water%20supply%20systems.pdf (accessed on 10 January 2020).
- Alegre, H. Performance Indicators for Water Supply Systems. In Drought Management Planning in Water Supply Systems. Water Science and Technology Library; Cabrera, E., García-Serra, J., Eds.; Springer: Dordrecht, The Netherlands, 1999; Volume 32. [Google Scholar] [CrossRef]
- Germanopoulos, G. A technical note on the inclusion of pressure dependent demand and leakage terms in water supply network models. Civ. Eng. Syst. 1985, 2, 171–179. [Google Scholar] [CrossRef]
- Germanopoulos, G.; Jowitt, P.W. Leakage reduction by excess pressure minimization in a water supply network. Proc. Inst. Civ. Eng. Part 2 Res. Theory 1989, 87, 195–214. [Google Scholar] [CrossRef]
- Kofinas, D.; Mellios, N.; Laspidou, C. Spatial and temporal disaggregation of water demand and leakage of the water distribution network in Skiathos, Greece. In Proceedings of the MDPI AG in 2nd International Electronic Conference on Sensors and Applications Session Sensing Technologies for Water Resource Management, 5–30 November 2015; p. S7001. [Google Scholar] [CrossRef]
- Lambert, A. What Do We Know About Pressure: Leakage Relationships in Distribution Systems? In IWA Conf. on System Approach to Leakage Control and Water Distribution System Management; IWA: Brno, Czech Republic, 2000; pp. 1–8. Available online: http://www.geocities.ws/kikory2004/2_Lambert.pdf (accessed on 7 March 2020).
- Liemberger, R.; Farley, M. Developing a Non-Revenue Water Reduction Strategy Part 1: Investigating and Assessing Water Losses. In Proceedings of the IWA WWC2004 Conference, Marrakech, Morocco, January 2004; Available online: https://sswm.info/sites/default/files/reference_attachments/LIEMBERGER%20FARLEY%202004%20Developing%20a%20NRW%20Reduction%20Strategy.pdf (accessed on 20 January 2020).
- Fantozzi, M.; Lambert, A. Residential Night Consumption-Assessment, Choice of Scaling Units and Calculation of Variability. In Proceedings of the IWA Water Loss Conference, Manila, Philippines, 26–29 February 2012; pp. 26–29. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S.; Samaras, P.; Zouboulis, A.; Demetriou, G. Developing appropriate performance indicators for urban distribution systems evaluation at Mediterranean countries. Water Util. J. 2011, 1, 31–40. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S.; Samaras, P.; Arabatzis, S.; Banovec, P.; Zoumpoulis, A.; Argyriadou, I. Designing a user friendly EDSS tool for NRW reduction strategies prioritization: Developing a new set of Performance Indicators focused on the Mediterranean area. In Proceedings of the 3rd International Conference Environmental Management, Planning & Engineering (CEMEPE 2011), Skiathos, Greece, 19–24 June 2011; pp. 219–225. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S.; Samaras, P.; Zouboulis, A.; Banovec, P. A new set of water losses-related performance indicators focused on areas facing water scarcivty conditions. Desalin. Water Treat. 2013, 51, 2994–3010. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S.; Samaras, P.; Zoumpoulis, A.; Argyriadou, I. Water distribution system performance level integrated evaluation using new Performance Indicators based on a modified IWA Water Balance. In Proceedings of the 10th International Conference Hydroinformatics-HIC2012, Understanding Changing Climate and Environment and Finding Solutions, Hamburg, Germany, 14–18 July 2012. [Google Scholar]
- Farley, M.; Trow, S. Losses in Water Distribution Networks; IWA Publishing: London, UK, 2003. [Google Scholar]
- Laspidou, C.S.; Kofinas, D.T.; Mellios, N.K.; Witmer, M. Modelling the Water-Energy-Food-Land Use-Climate Nexus: The Nexus Tree Approach. Proceedings 2018, 2, 617. [Google Scholar] [CrossRef] [Green Version]
- Colombo, A.F.; Karney, B.W. Energy and costs of leaky pipes toward comprehensive picture. J. Water Resour. Plan. Manag. 2002, 128, 441–450. [Google Scholar] [CrossRef] [Green Version]
- Morley, M.S.; Tricarico, C. Pressure Driven Demand Extension for EPANET (EPANETpdd); University of Exeter: Exeter, UK, 2008. [Google Scholar]
- Moore, D.S.; Notz, W.I.; Flinger, M.A. The Basic Practice of Statistics, 6th ed.; W. H. Freeman and Company: New York, NY, USA, 2013. [Google Scholar]
- Stakiadis, G.; Papanikolaou, P. Reliability laboratory exploration of household water meters. In Proceedings of the 6th National Conference of EEDYP, Chania, Crete, Greece, 14–16 June 2007. (In Greek). [Google Scholar]
- Arregui, F.; Cabrera, E.; Cobacho, R.; García-Serra, J. Reducing Apparent Losses Caused By Meters Inaccuracies. Water Pract. Technol. 2015, 1. Available online: https://iwaponline.com/wpt/article/1/4/wpt2006093/29469/Reducing-Apparent-Losses-Caused-By-Meters (accessed on 16 April 2020). [CrossRef] [Green Version]
- Seago, C.J.; Mckenzie, R.S.; Liemberger, R. International Benchmarking of Leakage from Water Reticulation Systems In Paper to Leakage 2005 Conference, Halifax. 2005. Available online: http://www.miya-water.com/fotos/artigos/06_international_benchmarking_of_leakage_from_water_reticulation_systems_1017893235a325e2b03b5c.pdf (accessed on 5 February 2020).
- Lambert, A. Water Losses Management and Techniques International Report. Water Supply 2.4. Water Sci. Technol. 2002, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Laspidou, C.; Papageorgiou, E.; Kokkinos, K.; Sahu, S.; Gupta, A.; Tassiulas, L. Exploring patterns in water consumption by clustering. Procedia Eng. 2015, 119, 1439–1446. [Google Scholar] [CrossRef] [Green Version]
- Winarni, W. Infrastructure Leakage Index (ILI) as Water Losses Indicator. Civ. Eng. Dimens. 2009, 11, 126–134. [Google Scholar]
- Creaco, E.; Haidar, H. Multiobjective Optimization of Control Valve Installation and DMA Creation for Reducing Leakage in Water Distribution Networks. J. Water Resour. Plan. Manag. 2019, 145, 1–10. [Google Scholar] [CrossRef]
- Creaco, E.; Cunha, M.; Franchini, M. Using Heuristic Techniques to Account for Engineering Aspects in Modularity-Based Water Distribution Network Partitioning Algorithm. J. Water Resour. Plan. Manag. 2019, 145, 1–11. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Laspidou, C.; Morlando, F.; Santonastaso, G.F.; Kofinas, D. Spectral analysis and topological and energy metrics for water network partitioning of Skiathos island. Eur. Water 2017, 423–428. [Google Scholar]



















| Trimester | SIV (m3/hr) | SIV Standard Deviation for ±1% Accuracy Range | SIV Variance | BAC Variance | NRW = BAC Variance + SIV Variance | NRW Standard Deviation | NRW Accuracy Range |
|---|---|---|---|---|---|---|---|
| 1st 2011 | 45.2 | 0.23 | 0.05 | 0 | 0.05 | 0.23 | ±2.8 |
| 2nd 2011 | 67.1 | 0.34 | 0.12 | 0 | 0.12 | 0.34 | ±2.9 |
| 3rd 2011 | 104.3 | 0.53 | 0.28 | 0 | 0.28 | 0.53 | ±3.2 |
| 4th 2011 | 53.2 | 0.27 | 0.07 | 0 | 0.07 | 0.27 | ±2.4 |
| 1st 2012 | 52.4 | 0.27 | 0.07 | 0 | 0.07 | 0.27 | ±2.0 |
| 2nd 2012 | 73.2 | 0.37 | 0.14 | 0 | 0.14 | 0.37 | ±2.4 |
| 3rd 2012 | 109.0 | 0.56 | 0.31 | 0 | 0.31 | 0.56 | ±2.7 |
| 4th 2012 | 55.4 | 0.28 | 0.08 | 0 | 0.08 | 0.28 | ±1.8 |
| 1st 2013 | 54.0 | 0.28 | 0.08 | 0 | 0.08 | 0.28 | ±1.9 |
| 2nd 2013 | 75.3 | 0.38 | 0.15 | 0 | 0.15 | 0.38 | ±2.2 |
| 3rd 2013 | 109.5 | 0.56 | 0.31 | 0 | 0.31 | 0.56 | ±2.5 |
| 4th 2013 | 60.7 | 0.31 | 0.10 | 0 | 0.10 | 0.31 | ±1.7 |
| 1st 2014 | 60.7 | 0.31 | 0.10 | 0 | 0.10 | 0.31 | ±1.6 |
| 2nd 2014 | 83.0 | 0.42 | 0.18 | 0 | 0.18 | 0.42 | ±2.3 |
| 3rd 2014 | 111.6 | 0.57 | 0.32 | 0 | 0.32 | 0.57 | ±2.4 |
| 4th 2014 | 64.6 | 0.33 | 0.11 | 0 | 0.11 | 0.33 | ±1.9 |
| 1st 2015 | 63.7 | 0.33 | 0.11 | 0 | 0.11 | 0.33 | ±1.4 |
| 2nd 2015 | 86.5 | 0.44 | 0.19 | 0 | 0.19 | 0.44 | ±2.1 |
| 3rd 2015 | 119.7 | 0.61 | 0.37 | 0 | 0.37 | 0.61 | ±2.3 |
| 4th 2015 | 72.9 | 0.37 | 0.14 | 0 | 0.14 | 0.37 | ±1.5 |
| 1st 2016 | 67.0 | 0.34 | 0.12 | 0 | 0.12 | 0.34 | ±1.5 |
| 2nd 2016 | 92.9 | 0.47 | 0.22 | 0 | 0.22 | 0.47 | ±1.8 |
| 3rd 2016 | 125.7 | 0.64 | 0.41 | 0 | 0.41 | 0.64 | ±2.1 |
| 4th 2016 | 74.5 | 0.38 | 0.14 | 0 | 0.14 | 0.38 | ±1.5 |
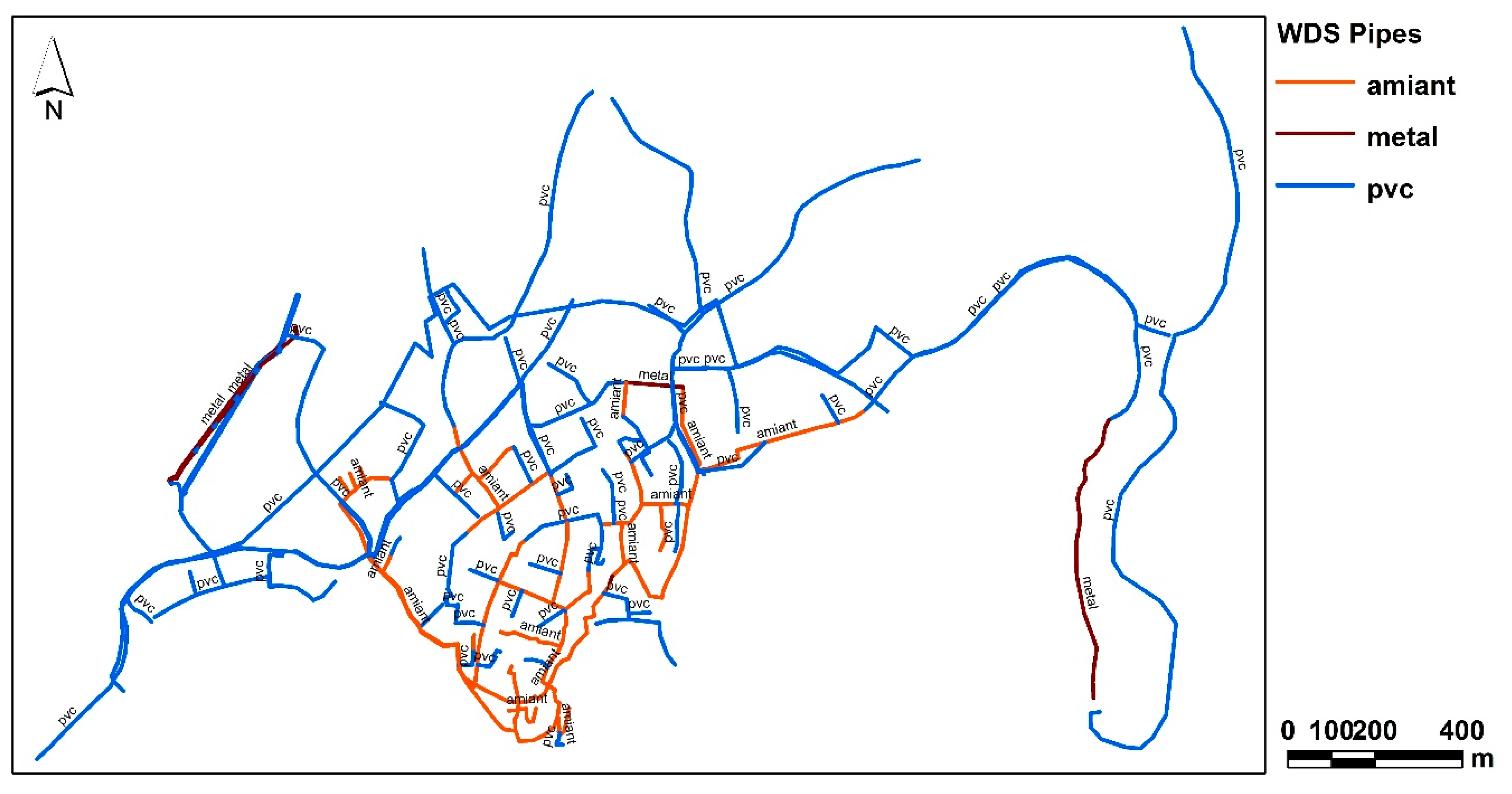
| Material | Length (m) | Length Proportion | Pressure Exponent | |||
|---|---|---|---|---|---|---|
| from | to | Average | N Partitioning | |||
| PVC | 12,266.7 | 0.64 | 0.40 | 1.85 | 1.13 | 0.72 |
| metal (cast-iron) | 1054.6 | 0.06 | 0.52 | 2.30 | 1.41 | 0.08 |
| amiant | 5833.2 | 0.3 | 0.78 | 1.04 | 0.91 | 0.28 |
| total | 19,154.5 | N = 1.08 | ||||
| Cello Location | Trimester | Simulated | Actual | % Error |
|---|---|---|---|---|
| Central point | January–March | 29.711 | 29.708 | 0.01 |
| April–June | 34.810 | 34.865 | −0.16 | |
| July–September | 33.371 | 33.236 | 0.41 | |
| October–December | 29.497 | 29.355 | 0,00 | |
| Eastern point | January–March | 62.384 | 61.913 | 0.76 |
| April–June | 67.442 | 67.486 | −0.07 | |
| July–September | 65.984 | 65.938 | 0.07 | |
| October–December | 62.173 | 61.752 | 0.68 | |
| Western point | January–March | 9.155 | 9.147 | 0.09 |
| April–June | 14.349 | 14.417 | −0.47 | |
| July–September | 13.056 | 12.991 | 0.50 | |
| October–December | 8.965 | 8.852 | 1.28 |
| UARL (IWA) (m3/hr) =(18 × total pipe length+0.8 × number of connections+25×length of connections) × × Average WDN pressure/24/1000 | 5.19 |
|---|---|
| Total pipe length (km) | 2187 (<5000, >3000) |
| Number of connections | 42 (>25) |
| Length of connections (km) | 10.94 |
| Average WDN pressure (m) | 53.5 |
| Length per connection (m/con) | 5 |
| CARL (m3/hr) as estimated by the bottom up methodology | 44.99 |
| ILI = CARL/UARL | 8.66 |
| Reported leaks and bursts (m3/hr) | 20.27 |
| Connection density (con./km) | 129 |
| Population | 6100 |
| Average night pressure (m) | 17 |
| Number of bursts in mains/year (min, max) | 5–10 |
| Number of bursts in mains/year | 7.5 |
| Number of bursts in distribution pipes/year | 180 |
| Flowrate for Reported main bursts (m3/hour/m pressure) | 0.24 |
| Flowrate for Reported distribution bursts (m3/hour/m pressure) | 0.032 |
| Repair duration (hr) | 48 |
| Unreported leaks and bursts (m3/hr) = CARL-reported leaks and bursts | 24.72 |
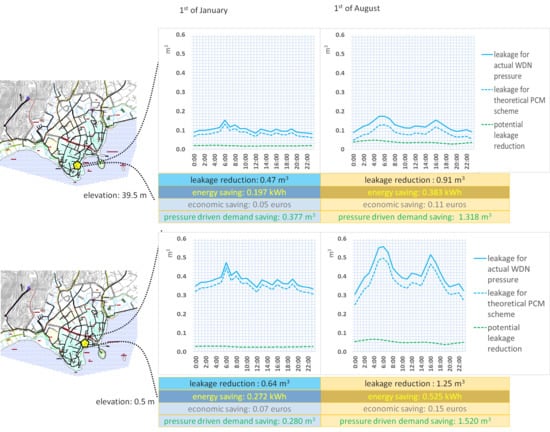
| Landzone | Hilly (39.5 m) | Coastal (0.5 m) | ||
|---|---|---|---|---|
| Network length | 60.34 m | 201.44 | ||
| Service connections | 25 | 8 | ||
| 1st of January | 1st of August | 1st of January | 1st of August | |
| LIV/network length (m3/d/m) | 0.073 | 0.124 | 0.064 | 0.113 |
| BAC/network length (m3/d/m) | 0.030 | 0.063 | 0.018 | 0.054 |
| Real Losses/network length (m3/d/m) | 0.041 | 0.050 | 0.045 | 0.050 |
| Apparent losses/network length (m3/d/m) | 0.002 | 0.012 | 0.001 | 0.009 |
| LIV/ service connections (m3) | 0.176 | 0.300 | 1.600 | 2.85 |
| BAC/ service connections (m3) | 0.072 | 0.152 | 0.450 | 1.362 |
| Real Losses/ service connection (m3) | 0.100 | 0.12 | 1.125 | 1.263 |
| Apparent Losses / per service connection (m3) | 0.004 | 0.028 | 0.025 | 0.238 |
| Trimester | Night Pressure Decrease (%) | Decrease in Pressure Fluctuation (%) | Energy Savings (kWh) | Economic Savings (Euro) | PDD Reduction (m3) |
|---|---|---|---|---|---|
| January–March | 9.5 | 43.2 | 3389 | 897 | 4786 |
| April–June | 19.2 | 41.2 | 7809 | 2067 | 17,462 |
| July–September | 17.6 | 38.7 | 7131 | 1888 | 25,968 |
| October–December | 9.28 | 47.8 | 3435 | 909 | 5514 |
| Annual | 13.9 | 42.7 | 21,763 | 5761 | 53,730 |
| Landzone | Hilly (39.5 m) | Coastal (0.5 m) | ||
|---|---|---|---|---|
| Service Connections | 25 | 8 | ||
| 1st of January | 1st of August | 1st of January | 1st of August | |
| PDD reduction in m3/m3 of BAC + Apparent losses | 0.199 | 0.293 | 0.074 | 0.119 |
| PDD reduction in m3/service connection | 0.015 | 0.053 | 0.035 | 0.190 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kofinas, D.; Ulanczyk, R.; Laspidou, C.S. Simulation of a Water Distribution Network with Key Performance Indicators for Spatio-Temporal Analysis and Operation of Highly Stressed Water Infrastructure. Water 2020, 12, 1149. https://doi.org/10.3390/w12041149
Kofinas D, Ulanczyk R, Laspidou CS. Simulation of a Water Distribution Network with Key Performance Indicators for Spatio-Temporal Analysis and Operation of Highly Stressed Water Infrastructure. Water. 2020; 12(4):1149. https://doi.org/10.3390/w12041149
Chicago/Turabian StyleKofinas, Dimitris, Rafal Ulanczyk, and Chrysi S. Laspidou. 2020. "Simulation of a Water Distribution Network with Key Performance Indicators for Spatio-Temporal Analysis and Operation of Highly Stressed Water Infrastructure" Water 12, no. 4: 1149. https://doi.org/10.3390/w12041149
APA StyleKofinas, D., Ulanczyk, R., & Laspidou, C. S. (2020). Simulation of a Water Distribution Network with Key Performance Indicators for Spatio-Temporal Analysis and Operation of Highly Stressed Water Infrastructure. Water, 12(4), 1149. https://doi.org/10.3390/w12041149