A Method to Improve the Flood Maps Forecasted by On-Line Use of 1D Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Methods
2.1.1. Foreword
- -
- the peak flow Q, which is the maximum value of the flow;
- -
- the flooding time T, that is the time when the Q > Q’;
- -
- the overflow volume Vf , that is the water volume exceeding the hydraulic capacity of the drainage system;
- -
- the mean overflow , which is simply the ratio between V and T.
2.1.2. Modeling of the Hydraulic Parameters
- -
- -
- -
- -
2.1.3. Flood Map Selection
- -
- the flood area A;
- -
- the flood volume V;
- -
- the flood depth (mean) D;
- -
- coordinates () of center of mass, wherewith , total number and coordinate north and east of each pixel image, and its depth value (Figure 3);
- -
- ratio between moment of inertia about the north and east directions (IgN, IgE), where:
- -
- polar moment of inertia, IgN + IgE;
- -
- centrifugal moment of inertia, ;
- -
- ratio between moment of inertia about north direction and polar moment of inertia ()
- -
- ratio between moment of inertia about east direction and polar moment of inertia ();
- -
- ratio between the difference between moments of inertia about east and north direction and polar moment of inertia ()
- -
- ratio between centrifugal moment of inertia and polar moment of inertia ().
2.1.4. The Similarity Algorithm Based on the “Ranking Approach”
2.1.5. Uncertainty Analysis of the Selected Map
2.2. Method Application to a Case Study (Corace Watershed, Calabria, Southern Italy)
2.2.1. Description of the Study Area
2.2.2. Construction of the Hydrological Database
2.3. Implementation of the 1D and 2D Models to the Case Study
2.3.1. Short Description of the SWMM Model
2.3.2. Parameterisation of the SWMM Model in the Corace Watershed
2.3.3. Short Description of the MIKE Models
2.3.4. Paramerisation of the MIKE Models in the Corace Watershed
2.3.5. Calibration and Validation of Models
3. Results and Discussion
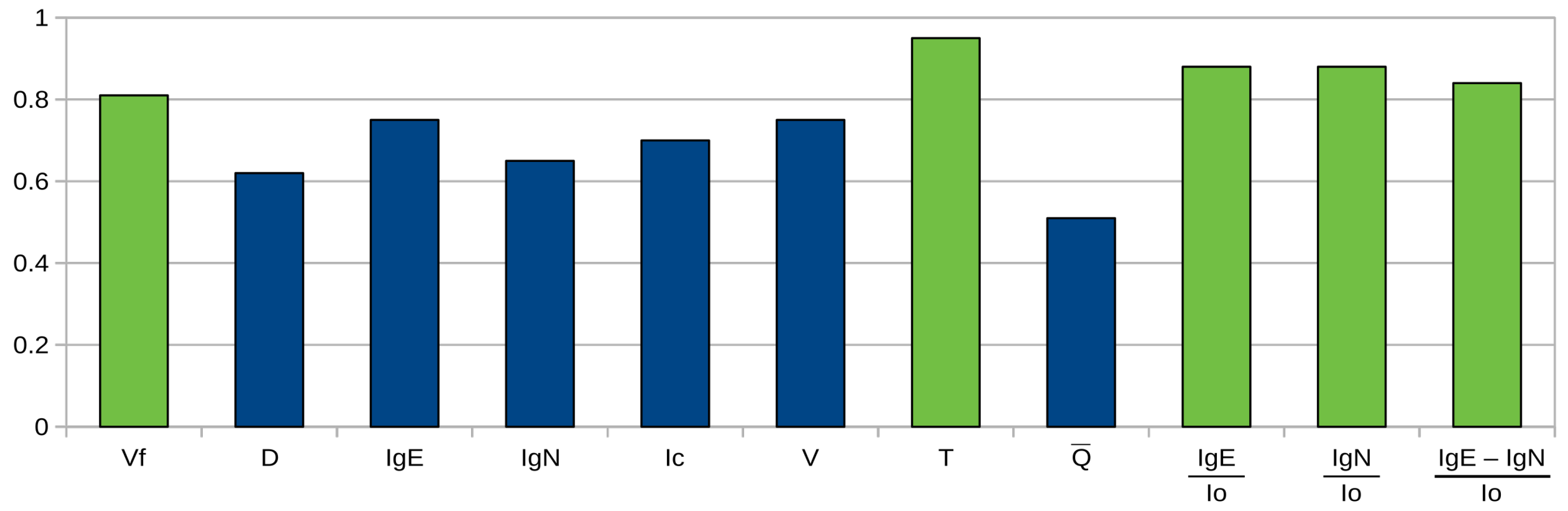
3.1. Comparison of the Hydraulic Parameters and 1D/2D Flood Maps
3.2. 2D Map Selection Using the Similarity Method
- -
- for 11 rainfall-runoff events, the minimum distance falls on the main diagonal of the rank matrix, giving a frequency of occurrence of 11/17 (64.7%);
- -
- this frequency increases to 12 over 17 events (that is, 70.6%), if we accept the possibility of selecting one of the two most similar 1D-2D maps;
- -
- finally, a frequency of 14/17 = 82.4% is achieved, if the tolerance limit increases to the three most similar 1D-2D maps.
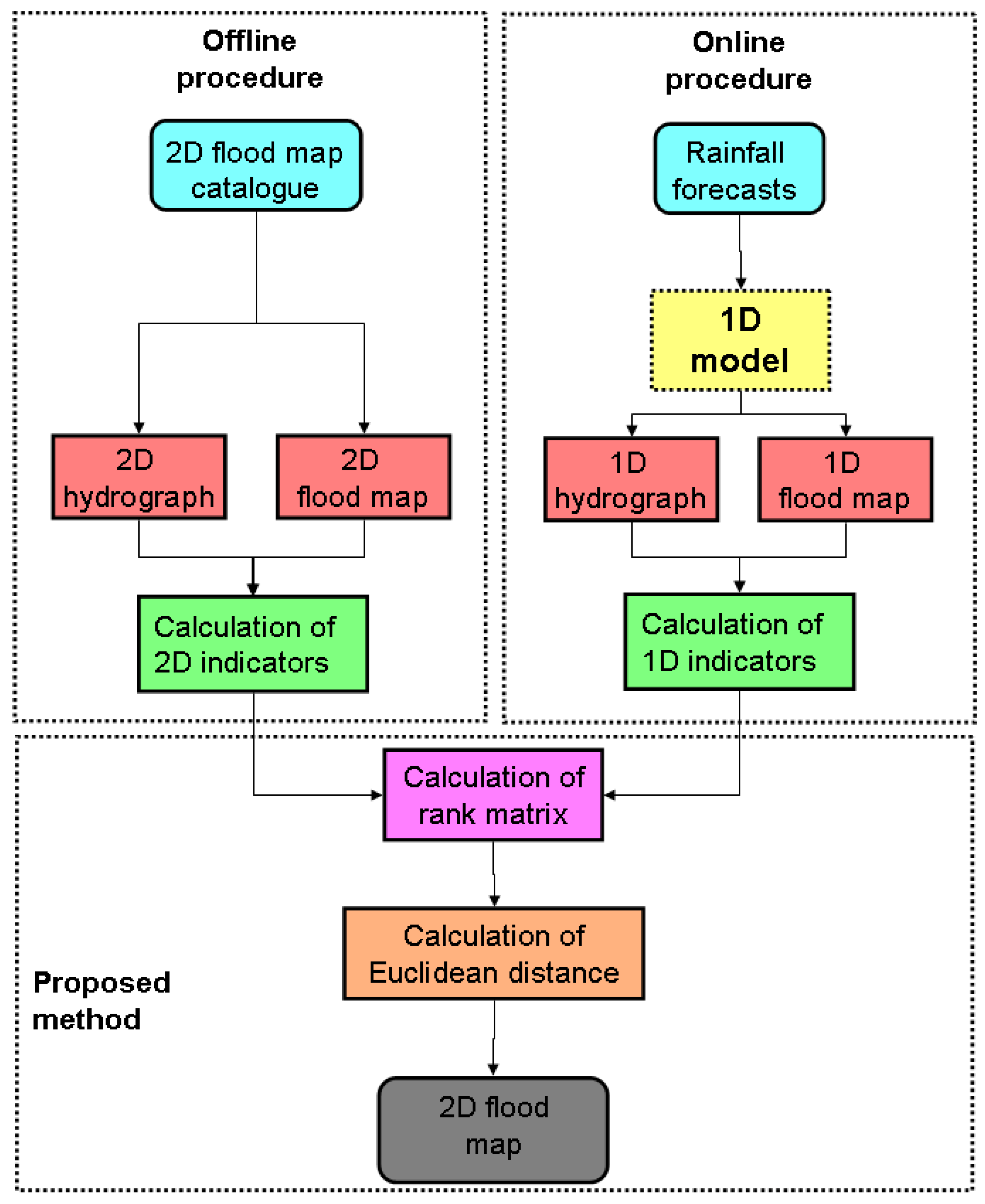
3.3. Proposal for the Method Implementation into an Online Early-Warning Platform for Flood Forecasting
- -
- offline preparation of the event catalogue consisting of flood maps produced by a 1D-2D model applied to a finite number of synthetic hyetographs;
- -
- construction of the forecasted hyetograph from weather radar predictions;
- -
- simulation of the corresponding hydrograph and 1D map using the 1D model for the forecasted event in real time;
- -
- calculation of the n indicators (see Section 2.1.3) used by the proposed method;
- -
- calculation of vector in ;
- -
- calculation of Euclidean distance among the vector of the forecasted events and all the vectors of maps catalogue , which provides the vector ∈;
- -
- calculation of the vector of the ranks of (distance data in ascending order);
- -
- selection of the map in the catalogue corresponding to the rank of (thus, having the minimum Euclidean distance from the 1D map) with the cumulative frequency .
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | |
| AMC | Antecedent Moisture Condition |
| CLC | Corine land cover, scale 1:100,000, 2006 |
| DEM | digital elevation model |
| DHI | Danish Hydraulic Institute |
| DTM | digital terrain model |
| HHUs | homogeneous hydrologically units |
| IDF | intensity-duration-frequency curve |
| LIDAR | laser imaging detection and ranging |
| MIKE | Danish Hydraulic Institute, 1995 |
| QGIS | QuantumGIS |
| SWMM | Storm Water Management Model |
| List of symbols | |
| A | flood area [m2] |
| CRM | Coefficient of Residual Mass [-] |
| D | flood depth (mean) [m] |
| E | coefficient of efficiency [-] |
| h | total precipitation depth [mm] |
| centrifugal moment of inertia [m3] | |
| ratio between centrifugal moment of inertia and polar moment of inertia | |
| moment of inertia about east direction [m3] | |
| ratio between the difference between moments of inertia about east and north direction and | |
| polar moment of inertia | |
| ratio between moment of inertia about east direction and polar moment of inertia | |
| moment of inertia about north direction [m3] | |
| ratio between moment of inertia about north direction and polar moment of inertia | |
| percent bias (-) | |
| Q | peak flow [m3s−1] |
| flow threshold [m3s−1] | |
| mean overflow [m3s−1] | |
| Root Mean Square Error | |
| r2 | coefficient of determination [-] |
| t | duration of precipitation [h] |
| T | flooding time [s] |
| return interval [years] | |
| watershed’s concentration time [h] | |
| V | flood volume [106 m3] |
| overflow volume [106 m3] | |
References
- UNISDR. 2018: Extreme weather events affected 60 million people. In Extreme Weather Events; United Nations Disaster Risk Reduction (UNISDR): New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, R.; Barrett, D.; Gao, L.; Zhou, M.; Renzullo, L.; Emelyanova, I. A spatial assessment framework for evaluating flood risk under extreme climates. Sci. Total Environ. 2015, 538, 512–523. [Google Scholar] [CrossRef]
- Sharifan, R.; Roshan, A.; Aflatoni, M.; Jahedi, A.; Zolghadr, M. Uncertainty and Sensitivity Analysis of SWMM Model in Computation of Manhole Water Depth and Subcatchment Peak Flood. Procedia Soc. Behav. Sci. 2010, 2, 7739–7740. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Altunkaynak, A. Comparative Case Study of Rainfall-Runoff Modeling between SWMM and Fuzzy Logic Approach. J. Hydrol. Eng. 2012, 17, 283–291. [Google Scholar] [CrossRef]
- Kreibich, H.; Van Den Bergh, J.; Bouwer, L.; Bubeck, P.; Ciavola, P.; Green, C.; Hallegatte, S.; Logar, I.; Meyer, V.; Schwarze, R.; et al. Costing natural hazards. Nat. Clim. Chang. 2014, 4, 303–306. [Google Scholar] [CrossRef]
- Mignot, E.; Li, X.; Dewals, B. Experimental modelling of urban flooding: A review. J. Hydrol. 2019, 568, 334–342. [Google Scholar] [CrossRef] [Green Version]
- Choi, K.; Ball, J. Parameter estimation for urban runoff modelling. Urban Water 2002, 4, 31–41. [Google Scholar] [CrossRef]
- Du, J.; Qian, L.; Rui, H.; Zuo, T.; Zheng, D.; Xu, Y.; Xu, C.Y. Assessing the effects of urbanization on annual runoff and flood events using an integrated hydrological modeling system for Qinhuai River basin, China. J. Hydrol. 2012, 464, 127–139. [Google Scholar] [CrossRef]
- Krebs, G.; Kokkonen, T.; Valtanen, M.; Koivusalo, H.; Setälä, H. A high resolution application of a stormwater management model (SWMM) using genetic parameter optimization. Urban Water J. 2013, 10, 394–410. [Google Scholar] [CrossRef]
- Sahoo, G.; Ray, C.; De Carlo, E. Calibration and validation of a physically distributed hydrological model, MIKE SHE, to predict streamflow at high frequency in a flashy mountainous Hawaii stream. J. Hydrol. 2006, 327, 94–109. [Google Scholar] [CrossRef]
- Loi, N.K.; Liem, N.D.; Tu, L.H.; Hong, N.T.; Truong, C.D.; Tram, V.N.Q.; Nhat, T.T.; Anh, T.N.; Jeong, J. Automated procedure of real-time flood forecasting in Vu Gia—Thu Bon river basin, Vietnam by integrating SWAT and HEC-RAS models. J. Water Clim. Chang. 2018, 10, 535–545. [Google Scholar] [CrossRef]
- Goodall, J.; Morsy, M.; Sadler, J. Real-Time Flood Prediction Using Data-Driven and Hydrodynamic Modeling Tools. Model. Manag. Extrem. Precip. 2017, 10, 535–545. [Google Scholar]
- Teng, J.; Jakeman, A.; Vaze, J.; Croke, B.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Follum, M.; Tavakoly, A.; Niemann, J.; Snow, A. AutoRAPID: A Model for Prompt Streamflow Estimation and Flood Inundation Mapping over Regional to Continental Extents. JAWRA J. Am. Water Resour. Assoc. 2016, 53. [Google Scholar] [CrossRef]
- Zheng, X.; Tarboton, D.G.; Maidment, D.R.; Liu, Y.Y.; Passalacqua, P. River Channel Geometry and Rating Curve Estimation Using Height above the Nearest Drainage. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 785–806. [Google Scholar] [CrossRef]
- Wang, X.; Kinsland, G.; Poudel, D.; Fenech, A. Urban flood prediction under heavy precipitation. J. Hydrol. 2019, 577, 123984. [Google Scholar] [CrossRef]
- Dottori, F.; Di Baldassarre, G.; Todini, E. Detailed data is welcome, but with a pinch of salt: Accuracy, precision, and uncertainty in flood inundation modeling. Water Resour. Res. 2013, 49, 6079–6085. [Google Scholar] [CrossRef]
- Paquier, A.; Mignot, E.; Bazin, P. From hydraulic modelling to urban flood risk. Procedia Eng. 2015, 115, 37–44. [Google Scholar] [CrossRef]
- Falconer, R.; Xia, J.; Liang, D.; Kvoka, D. Flood modelling and hazard assessment for extreme events in riverine basins. In Proceedings of the 37th IAHR World Congress 2017: Managing Water for Sustainable Development: Learning from the Past for the Future, Kuala Lumpur, Malaysia, 13–18 August 2017; Ghani, A., Ed.; International Assn for Hydro-Environment Engineering and Research (IAHR): Beijing, China, 2017. [Google Scholar]
- Rong, Y.; Zhang, T.; Zheng, Y.; Hu, C.; Peng, L.; Feng, P. Three-dimensional urban flood inundation simulation based on digital aerial photogrammetry. J. Hydrol. 2019, 584, 124308. [Google Scholar] [CrossRef]
- Patro, S.; Chatterjee, C.; Mohanty, S.; Singh, R.; Raghuwanshi, N. Flood inundation modeling using MIKE FLOOD and remote sensing data. J. Indian Soc. Remote Sens. 2009, 37, 107–118. [Google Scholar] [CrossRef]
- Aricò, C.; Filianoti, P.; Sinagra, M.; Tucciarelli, T. The FLO Diffusive 1D-2D Model for Simulation of River Flooding. Water 2016, 8, 200. [Google Scholar] [CrossRef] [Green Version]
- Phillips, B.; Yu, S.; Thompson, G.; Silva, N. 1D and 2D Modelling of Urban Drainage Systems using XP-SWMM and TUFLOW. In Proceedings of the 10th International Conference on Urban Drainage, Copenhagen, Denmark, 21–26 August 2005. [Google Scholar]
- Barco, J.; Wong, K.; Stenstrom, M. Automatic calibration of the U.S. EPA SWMM model for a large urban catchment. J. Hydraul. Eng. 2008, 134, 466–474. [Google Scholar] [CrossRef]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time urban flood forecasting and modelling—A state of the art. J. Hydroinform. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Jamali, B.; Löwe, R.; Bach, P.M.; Urich, C.; Arnbjerg-Nielsen, K.; Deletic, A. A rapid urban flood inundation and damage assessment model. J. Hydrol. 2018, 564, 1085–1098. [Google Scholar] [CrossRef]
- Lee, S.; Lee, S.; Lee, M.J.; Jung, H.S. Spatial Assessment of Urban Flood Susceptibility Using Data Mining and Geographic Information System (GIS) Tools. Sustainability 2018, 10, 648. [Google Scholar] [CrossRef] [Green Version]
- Zema, D.; Labate, A.; Martino, D.; Zimbone, S. Comparing Different Infiltration Methods of the HEC-HMS Model: The Case Study of the Mésima Torrent (Southern Italy). Land Degrad. Dev. 2017, 28, 294–308. [Google Scholar] [CrossRef]
- Bisht, D.; Chatterjee, C.; Kalakoti, S.; Upadhyay, P.; Sahoo, M.; Panda, A. Modeling urban floods and drainage using SWMM and MIKE URBAN: A case study. Nat. Hazards 2016, 84, 749–776. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G. Flood inundation mapping sensitivity to riverine spatial resolution and modelling approach. Nat. Hazards 2016, 83, 117–132. [Google Scholar] [CrossRef]
- Kourtis, I.; Bellos, V.; Tsihrintzis, V. Comparison of 1D-1D and 1D-2D urban flood models. In Proceedings of the 15th International Conference on Environmental Science and Technology, Rhodes, Greece, 31 August–2 September 2017. [Google Scholar]
- Leandro, J.; Chen, A.S.; Djordjević, S.; Savic, D. Comparison of 1D/1D and 1D/2D Coupled (Sewer/Surface) Hydraulic Models for Urban Flood Simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Leandro, J.; Djordjević, S.; Chen, A.; Savić, D.; Stanić, M. Calibration of a 1D/1D urban flood model using 1D/2D model results in the absence of field data. Water Sci. Technol. 2011, 64, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- Fortugno, D.; Boix-Fayos, C.; Bombino, G.; Denisi, P.; Quiñonero Rubio, J.; Tamburino, V.; Zema, D. Adjustments in channel morphology due to land-use changes and check dam installation in mountain torrents of Calabria (southern Italy). Earth Surf. Process. Landf. 2017, 42, 2469–2483. [Google Scholar] [CrossRef]
- Zema, D.; Lucas-Borja, M.; Carrá, B.; Denisi, P.; Rodrigues, V.; Ranzini, M.; Arcova, F.; de Cicco, V.; Zimbone, S. Simulating the hydrological response of a small tropical forest watershed (Mata Atlantica, Brazil) by the AnnAGNPS model. Sci. Total Environ. 2018, 636, 737–750. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huber, W.; Dickinson, R.; Rossman, L. EPA Storm Water Management Model, SWMM5. In Watershed Models; US Environmental Protection Agency (EPA): Washington, DC, USA, 2010. [Google Scholar] [CrossRef]
- Willmott, C.; Cort, J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 100, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Legates, D.; McCabe, G. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Loague, K.; Green, R. Statistical and graphical methods for evaluating solute transport models: Overview and application. J. Contam. Hydrol. 1991, 7, 51–73. [Google Scholar] [CrossRef]
- Zema, D.; Bingner, R.L.; Denisi, P.; Govers, G.; Licciardello, F.; Zimbone, S. Evaluation of runoff, peak flowand sediment yield for events simulated by the annagnps model in a belgian agricultural watershed. Land Degrad. Dev. 2012, 23, 205–215. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Báse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Garbrecht, J. Hydrologic simulation of little wrew using SWAT. JAWRA J. Am. Water Resour. Assoc. 2003, 39, 413–426. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.; Williams, J.; Dugas, W.; Srinivasan, R.; Hauck, L. Validation of the Swat Model on a Large Rwer Basin With Point and Nonpoint Sources. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Vieira, D.; Serpa, D.; Nunes, J.; Prats, S.; Neves, R.; Keizer, J. Predicting the effectiveness of different mulching techniques in reducing post-fire runoff and erosion at plot scale with the RUSLE, MMF and PESERA models. Environ. Res. 2018, 165, 365–378. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models. Part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Fernández, C.; Vega, J.; Vieira, D. Assessing soil erosion after fire and rehabilitation treatments in NW Spain: Performance of RUSLE and revised Morgan–Morgan–Finney models. Land Degrad. Dev. 2010, 21, 58–67. [Google Scholar] [CrossRef] [Green Version]
- Singh, J.; Knapp, H.; Arnold, J.; Demissie, M. Hydrological modeling of the Iroquois river watershed using HSPF and SWAT. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Gupta, H.; Sorooshian, S.; Yapo, P. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J.; Li, Z. Assessment and modelling of uncertainty in precipitation forecasts from TIGGE using fuzzy probability and Bayesian theory. J. Hydrol. 2019, 577, 123995. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Lu, W.; Zhang, J.; Zhou, J.; Guo, S. Streamflow forecast uncertainty evolution and its effect on real-time reservoir operation. J. Hydrol. 2016, 540, 712–726. [Google Scholar] [CrossRef]
- Chow, V.; Maidment, D.; Mays, L. Applied Hydrology; MacGraw-Hill: New York, USA, 1988. [Google Scholar]
- Kirpich, Z. Time of concentration of small watersheds. J. Civ. Eng. (ASCE) 1940, 10, 362. [Google Scholar]
- European Environment Agency. CORINE Land Cover; European Environment Agency (EEA): Copenhagen, Denmark, 2006. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc-2006 (accessed on 19 November 2019).
- Huber, W.C.; Dickinson, R. Storm Water Management Model, Version 4: Users Manual; Environmental Research Laboratory, EPA: Washington, DC, USA, 1988.
- Rossman, L. Storm Water Management Model User’s Manual Version 5.0; National Risk Management Research Laboratory: Washington, DC, USA, 2009. [Google Scholar]
- Gironás, J.; Roesner, L.; Rossman, L.; Davis, J. A new applications manual for the Storm Water Management Model (SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Gaál, L.; Szolgay, J.; Kohnová, S.; Hlavˇcová, K.; Parajka, J.; Viglione, A.; Merz, R.; Blöschl, G. Dependence between flood peaks and volumes: A case study on climate and hydrological controls. Hydrol. Sci. J. 2014, 60, 968–984. [Google Scholar] [CrossRef] [Green Version]
- Gaál, L.; Szolgay, J.; Kohnová, S.; Hlavčová, K.; Parajka, J.; Viglione, A.; Merz, R.; Blöschl, G. Relation entre pics et volumes de crues: Étude des déterminants climatiques et hydrologiques. Hydrol. Sci. J. 2015, 60, 968–984. [Google Scholar] [CrossRef] [Green Version]











| Parametres | Measuring Unit | Value | |
|---|---|---|---|
| Area | km2 | 294 | |
| Perimeter | km | 113 | |
| Shape coefficient | - | 1.86 | |
| Altitude (a.s.l.) | max | m | 1385 |
| mean | m | 565 | |
| min | m | 1 | |
| Drainage density | km/km2 | 4.32 | |
| Length of the main reach | km | 53.3 | |
| Concentration time | h | 7.4 | |
| Mean yearly precipitation | mm | 1279 | |
| Mean yearly temperature | °C | 12.9 | |
| Event | Hyetograph Type | [year] | [h] | h [mm] |
|---|---|---|---|---|
| A | IT | 5 | 7.6 | 86.6 |
| B | C | 500 | 1 | 87.6 |
| C | C | 500 | 7.6 | 290.1 |
| E | R | 50 | 12 | 168.3 |
| F | IT | 50 | 7.6 | 140.4 |
| G | R | 100 | 12 | 186.8 |
| H | R | 500 | 24 | 302.7 |
| I | R | 100 | 10 | 186.8 |
| L | R | 200 | 12 | 205.2 |
| M | C | 100 | 7.6 | 155.9 |
| N | R | 200 | 10 | 205.2 |
| O | R | 500 | 24 | 326.9 |
| P | C | 200 | 7.6 | 171.3 |
| Q | R | 500 | 12 | 231.0 |
| R | R | 500 | 10 | 231.0 |
| S | C | 500 | 7.6 | 193.4 |
| T | R | 500 | 24 | 348.1 |
| Sub-Watershed | [ha] | [mm] | [mm] | [%] | [s/m] | [s/m] | [%] | [%] | [%] | [m] | [-] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SR11 | 22.43 | 2.54 | 5 | 44.21 | 0.01 | 0.13 | 100 | 25 | 4.19 | 897.2 | 83.8 |
| SR14m2 | 15.78 | 2.54 | 5 | 35.00 | 0.01 | 0.13 | 100 | 25 | 4.86 | 631.2 | 82.0 |
| SR14m1 | 11.29 | 2.54 | 5 | 4.51 | 0.01 | 0.13 | 100 | 25 | 13.17 | 451.6 | 75.9 |
| SSD14 | 0.04 | 2.54 | 5 | 100.00 | 0.01 | 0.13 | 100 | 25 | 2.13 | 1.6 | 95.0 |
| SR03 | 21.71 | 2.54 | 5 | 25.73 | 0.01 | 0.13 | 100 | 25 | 2.50 | 868.4 | 80.2 |
| SR07 | 18.01 | 2.54 | 5 | 55.83 | 0.01 | 0.13 | 100 | 25 | 11.99 | 720.4 | 86.2 |
| SSD29 | 1.89 | 2.54 | 5 | 62.52 | 0.01 | 0.13 | 100 | 25 | 2.79 | 75.6 | 87.5 |
| SR02 | 24.89 | 2.54 | 5 | 40.89 | 0.01 | 0.13 | 100 | 25 | 6.11 | 995.6 | 83.2 |
| SSD27 | 1.84 | 2.54 | 5 | 78.80 | 0.01 | 0.13 | 100 | 25 | 1.90 | 73.6 | 90.8 |
| SR08 | 6.14 | 2.54 | 5 | 33.11 | 0.01 | 0.13 | 100 | 25 | 3.13 | 245.6 | 81.6 |
| SSD25 | 0.05 | 2.54 | 5 | 100.00 | 0.01 | 0.13 | 100 | 25 | 4.18 | 2.0 | 95.0 |
| SSD13 | 1.73 | 2.54 | 5 | 54.26 | 0.01 | 0.13 | 100 | 25 | 3.66 | 69.2 | 85.9 |
| SSD17 | 12.90 | 2.54 | 5 | 53.06 | 0.01 | 0.13 | 100 | 25 | 5.74 | 516.0 | 85.6 |
| SSD12 | 18.03 | 2.54 | 5 | 34.59 | 0.01 | 0.13 | 100 | 25 | 6.86 | 721.2 | 81.9 |
| SSD39_1 | 10.08 | 2.54 | 5 | 10.37 | 0.01 | 0.13 | 100 | 25 | 2.07 | 403.2 | 77.1 |
| SSD30 | 0.06 | 2.54 | 5 | 100.00 | 0.01 | 0.13 | 100 | 25 | 7.40 | 2.4 | 95.0 |
| SSD5 | 0.10 | 2.54 | 5 | 74.50 | 0.01 | 0.13 | 100 | 25 | 2.00 | 4.0 | 89.9 |
| SSD9 | 4.02 | 2.54 | 5 | 49.39 | 0.01 | 0.13 | 100 | 25 | 3.77 | 160.8 | 84.9 |
| SR01 | 11.42 | 2.54 | 5 | 0.12 | 0.01 | 0.13 | 100 | 25 | 9.79 | 456.8 | 75.0 |
| SR06 | 3.01 | 2.54 | 5 | 6.53 | 0.01 | 0.13 | 100 | 25 | 3.29 | 120.4 | 76.3 |
| SSD36 | 0.20 | 2.54 | 5 | 100.00 | 0.01 | 0.13 | 100 | 25 | 2.99 | 8.0 | 95.0 |
| SSD26 | 1.96 | 2.54 | 5 | 0.00 | 0.01 | 0.13 | 100 | 25 | 1.33 | 78.4 | 75.0 |
| SSD4 | 4.42 | 2.54 | 5 | 77.52 | 0.01 | 0.13 | 100 | 25 | 5.57 | 176.8 | 90.5 |
| SR05 | 6.47 | 2.54 | 5 | 1.11 | 0.01 | 0.13 | 100 | 25 | 2.45 | 258.8 | 75.2 |
| SSD24 | 0.41 | 2.54 | 5 | 85.07 | 0.01 | 0.13 | 100 | 25 | 3.16 | 16.4 | 92.0 |
| SSD8 | 21.57 | 2.54 | 5 | 47.11 | 0.01 | 0.13 | 100 | 25 | 7.42 | 862.8 | 84.4 |
| SR09 | 24.37 | 2.54 | 5 | 41.23 | 0.01 | 0.13 | 100 | 25 | 10.99 | 974.8 | 83.3 |
| SR10 | 2.67 | 2.54 | 5 | 44.02 | 0.01 | 0.13 | 100 | 25 | 3.43 | 106.8 | 83.8 |
| SR04 | 2.71 | 2.54 | 5 | 19.04 | 0.01 | 0.13 | 100 | 25 | 3.03 | 108.4 | 78.8 |
| SR12 | 7.52 | 2.54 | 5 | 44.21 | 0.01 | 0.13 | 100 | 25 | 4.06 | 300.8 | 83.8 |
| SSD34 | 1.58 | 2.54 | 5 | 53.67 | 0.01 | 0.13 | 100 | 25 | 3.46 | 63.2 | 85.7 |
| SSD38 | 0.11 | 2.54 | 5 | 55.45 | 0.01 | 0.13 | 100 | 25 | 3.87 | 4.4 | 86.1 |
| SSD35 | 1.27 | 2.54 | 5 | 100.00 | 0.01 | 0.13 | 100 | 25 | 2.56 | 50.8 | 95.0 |
| SSD22 | 4.66 | 2.54 | 5 | 49.35 | 0.01 | 0.13 | 100 | 25 | 4.59 | 186.4 | 84.9 |
| SSD11 | 0.33 | 2.54 | 5 | 100.00 | 0.01 | 0.13 | 100 | 25 | 8.32 | 13.2 | 95.0 |
| SSD39_2 | 13.16 | 2.54 | 5 | 0.00 | 0.01 | 0.13 | 100 | 25 | 1.18 | 526.4 | 75.0 |
| SSD33 | 2.14 | 2.54 | 5 | 53.86 | 0.01 | 0.13 | 100 | 25 | 6.67 | 85.6 | 85.8 |
| SSD37 | 0.99 | 2.54 | 5 | 99.29 | 0.01 | 0.13 | 100 | 25 | 4.12 | 39.6 | 94.9 |
| SR14 | 16.13 | 2.54 | 5 | 43.66 | 0.01 | 0.13 | 100 | 25 | 3.75 | 645.2 | 83.7 |
| SSD23 | 6.36 | 2.54 | 5 | 34.02 | 0.01 | 0.13 | 100 | 25 | 3.54 | 254.4 | 81.8 |
| SR11m | 7.36 | 2.54 | 5 | 41.26 | 0.01 | 0.13 | 100 | 25 | 3.21 | 294.4 | 83.3 |
| SSD23m | 5.25 | 2.54 | 5 | 37.38 | 0.01 | 0.13 | 100 | 25 | 3.74 | 210.0 | 82.5 |
| SR17 | 22.13 | 2.54 | 5 | 0.00 | 0.01 | 0.13 | 100 | 25 | 18.71 | 368.0 | 75.0 |
| SR15 | 2.04 | 2.54 | 5 | 0.00 | 0.01 | 0.13 | 100 | 25 | 1.78 | 55.6 | 75.0 |
| Sub-Watershed | [km2] | [h] | [mm] | [mm] | [-] | [h] | [-] | [-] |
|---|---|---|---|---|---|---|---|---|
| R01 | 0.114 | 0.85 | 15 | 150 | 0.3 | 500 | 0.7 | 0.5 |
| R02 | 0.249 | 1.87 | 15 | 150 | 0.59 | 500 | 0.7 | 0.5 |
| R03 | 0.217 | 2.2 | 15 | 150 | 0.48 | 500 | 0.7 | 0.5 |
| R04 | 0.027 | 0.52 | 15 | 150 | 0.43 | 500 | 0.7 | 0.5 |
| R05 | 0.065 | 1.22 | 15 | 150 | 0.31 | 500 | 0.7 | 0.5 |
| R06 | 0.03 | 0.48 | 15 | 150 | 0.35 | 500 | 0.7 | 0.5 |
| R07 | 0.18 | 1.32 | 15 | 150 | 0.69 | 500 | 0.7 | 0.5 |
| R08 | 0.061 | 0.77 | 15 | 150 | 0.53 | 500 | 0.7 | 0.5 |
| R09 | 0.244 | 2.65 | 15 | 150 | 0.59 | 500 | 0.7 | 0.5 |
| R10 | 0.027 | 0.65 | 15 | 150 | 0.61 | 500 | 0.7 | 0.5 |
| R11 | 0.224 | 1.63 | 15 | 150 | 0.61 | 500 | 0.7 | 0.5 |
| R11m | 0.074 | 1.13 | 15 | 150 | 0.59 | 500 | 0.7 | 0.5 |
| R12 | 0.075 | 1.08 | 15 | 150 | 0.61 | 500 | 0.7 | 0.5 |
| R14 | 0.161 | 0.93 | 15 | 150 | 0.61 | 500 | 0.7 | 0.5 |
| R14m1 | 0.113 | 1.18 | 15 | 150 | 0.33 | 500 | 0.7 | 0.5 |
| R14m2 | 0.158 | 1.35 | 15 | 150 | 0.55 | 500 | 0.7 | 0.5 |
| R15 | 0.02 | 0.68 | 15 | 150 | 0.3 | 500 | 0.7 | 0.5 |
| R17 | 0.221 | 1.18 | 15 | 150 | 0.3 | 500 | 0.7 | 0.5 |
| SD11 | 0.003 | 0.28 | 15 | 150 | 1 | 500 | 0.7 | 0.5 |
| SD12 | 0.18 | 1.57 | 15 | 150 | 0.54 | 500 | 0.7 | 0.5 |
| SD13 | 0.017 | 0.43 | 15 | 150 | 0.68 | 500 | 0.7 | 0.5 |
| SD14 | 0 | 0.05 | 15 | 150 | 1 | 500 | 0.7 | 0.5 |
| SD17 | 0.129 | 0.85 | 15 | 150 | 0.67 | 500 | 0.7 | 0.5 |
| SD22 | 0.047 | 0.92 | 15 | 150 | 0.65 | 500 | 0.7 | 0.5 |
| SD23 | 0.064 | 0.63 | 15 | 150 | 0.54 | 500 | 0.7 | 0.5 |
| SD23m | 0.053 | 0.75 | 15 | 150 | 0.56 | 500 | 0.7 | 0.5 |
| SD24 | 0.004 | 0.2 | 15 | 150 | 0.9 | 500 | 0.7 | 0.5 |
| SD25 | 0.001 | 0.07 | 15 | 150 | 1 | 500 | 0.7 | 0.5 |
| SD26 | 0.02 | 0.58 | 15 | 150 | 0.3 | 500 | 0.7 | 0.5 |
| SD27 | 0.018 | 0.45 | 15 | 150 | 0.85 | 500 | 0.7 | 0.5 |
| SD29 | 0.019 | 0.38 | 15 | 150 | 0.74 | 500 | 0.7 | 0.5 |
| SD30 | 0.001 | 0.1 | 15 | 150 | 1 | 500 | 0.7 | 0.5 |
| SD33 | 0.021 | 0.77 | 15 | 150 | 0.68 | 500 | 0.7 | 0.5 |
| SD34 | 0.016 | 0.37 | 15 | 150 | 0.68 | 500 | 0.7 | 0.5 |
| SD35 | 0.013 | 0.47 | 15 | 150 | 1 | 500 | 0.7 | 0.5 |
| SD36 | 0.002 | 0.12 | 15 | 150 | 1 | 500 | 0.7 | 0.5 |
| SD37 | 0.01 | 0.35 | 15 | 150 | 1 | 500 | 0.7 | 0.5 |
| SD38 | 0.001 | 0.08 | 15 | 150 | 0.69 | 500 | 0.7 | 0.5 |
| SD39_1 | 0.101 | 1.13 | 15 | 150 | 0.37 | 500 | 0.7 | 0.5 |
| SD39_2 | 0.132 | 1.33 | 15 | 150 | 0.3 | 500 | 0.7 | 0.5 |
| SD4 | 0.044 | 0.8 | 15 | 150 | 0.84 | 500 | 0.7 | 0.5 |
| SD5 | 0.001 | 0.12 | 15 | 150 | 0.82 | 500 | 0.7 | 0.5 |
| SD8 | 0.216 | 2.03 | 15 | 150 | 0.63 | 500 | 0.7 | 0.5 |
| SD9 | 0.04 | 0.48 | 15 | 150 | 0.65 | 500 | 0.7 | 0.5 |
| Synthetic | Q [m3s−1] | [Mm3] | T [h] | Q’ [m3s−1] | ||||
|---|---|---|---|---|---|---|---|---|
| Hydrograph | SWMM | MIKE | SWMM | MIKE | SWMM | MIKE | SWMM | MIKE |
| A | 214 | 383 | 0.00 | 0.00 | 0.0 | 0.0 | 0 | 0 |
| B | 228 | 507 | 0.00 | 0.09 | 0.0 | 0.4 | 0 | 58 |
| C | 531 | 802 | 0.13 | 0.71 | 0.5 | 0.9 | 74 | 210 |
| E | 643 | 546 | 2.54 | 1.54 | 4.8 | 5.8 | 148 | 74 |
| F | 356 | 792 | 1.88 | 3.05 | 2.5 | 4.5 | 209 | 190 |
| G | 756 | 614 | 4.81 | 3.09 | 6.0 | 7.2 | 223 | 120 |
| H | 818 | 521 | 15.40 | 4.40 | 16.3 | 16.0 | 263 | 77 |
| I | 868 | 718 | 5.82 | 4.42 | 6.0 | 7.0 | 269 | 175 |
| L | 879 | 682 | 7.49 | 4.85 | 7.3 | 8.2 | 287 | 164 |
| M | 820 | 861 | 3.80 | 5.88 | 4.5 | 5.8 | 235 | 280 |
| N | 1007 | 800 | 8.61 | 6.34 | 6.8 | 7.8 | 354 | 225 |
| O | 898 | 564 | 20.03 | 7.00 | 17.5 | 17.3 | 318 | 112 |
| P | 1019 | 956 | 6.05 | 7.34 | 5.0 | 6.1 | 336 | 335 |
| Q | 1046 | 776 | 11.70 | 7.58 | 8.8 | 9.3 | 371 | 226 |
| R | 729 | 915 | 3.40 | 9.23 | 5.0 | 8.7 | 189 | 294 |
| S | 1297 | 1104 | 9.51 | 9.41 | 5.3 | 6.4 | 503 | 408 |
| T | 968 | 602 | 24.22 | 9.42 | 18.3 | 18.3 | 369 | 143 |
| Hydraulic Variable | ||||||||
|---|---|---|---|---|---|---|---|---|
| Q | V | T | Q’ | |||||
| Model | SWMM | MIKE | SWMM | MIKE | SWMM | MIKE | SWMM | MIKE |
| Mean | 769 | 714 | 7.38 | 4.96 | 6.72 | 7.63 | 244 | 182 |
| Minimum | 214 | 383 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0 |
| Maximum | 1297 | 1104 | 24,22 | 9.42 | 18.25 | 18.28 | 503 | 408 |
| Standard Deviation | 296 | 187 | 7.01 | 3.19 | 5.64 | 5.35 | 135 | 107 |
| r2 | 0.34 | 0.42 | 0.97 | 0.39 | ||||
| RMSE | 241 | 5.87 | 1.29 | 121 | ||||
| CRM | 0.07 | 0.33 | −0.14 | 0.25 | ||||
| Syntetic | SWMM Model | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hyetograph | A | B | C | E | F | G | H | I | L | M | N | O | P | Q | R | S | T | |
| MIKE model | A | 9.2 | 15 | 32.5 | 5.6 | 26.9 | 15.3 | 16.1 | 29 | 25.1 | 33.2 | 38 | 20.8 | 40.3 | 37.5 | 44.6 | 45.9 | 27.3 |
| B | 11 | 13.2 | 30.5 | 5.4 | 26.4 | 15.3 | 15.9 | 28.8 | 24.8 | 32.1 | 37.8 | 20.4 | 39.4 | 37.3 | 44.2 | 45.1 | 27 | |
| C | 34.7 | 24.8 | 15.8 | 30.6 | 20.9 | 27.3 | 30.5 | 24.2 | 24.3 | 17.3 | 27.3 | 29.5 | 22.1 | 29.3 | 30.4 | 26.3 | 29.9 | |
| E | 11.1 | 13.3 | 28.2 | 2.2 | 21.9 | 8.9 | 10.1 | 23.3 | 18.6 | 27.3 | 32.1 | 14.1 | 34.2 | 31.2 | 38.3 | 39.8 | 20.5 | |
| F | 14.7 | 21 | 28.5 | 17.2 | 11.4 | 11.4 | 19.1 | 12.4 | 12.8 | 21.4 | 20.6 | 19.7 | 26 | 21.4 | 27.6 | 30.9 | 20.7 | |
| G | 16.2 | 17.5 | 27.1 | 9.8 | 18.5 | 4.4 | 6 | 17.8 | 12.1 | 22.6 | 26 | 7.4 | 28.8 | 24.3 | 31.8 | 34.1 | 13.1 | |
| H | 26.1 | 23.7 | 26.1 | 20.8 | 17.4 | 12.5 | 14.4 | 14.8 | 9.2 | 17.3 | 19.7 | 9.4 | 21.6 | 16.6 | 23.6 | 25.9 | 5.5 | |
| I | 21.8 | 25.7 | 28.8 | 19.9 | 13.4 | 11.1 | 15.7 | 7.5 | 5.2 | 17.6 | 15.1 | 13.4 | 21 | 13.7 | 21.4 | 25.5 | 12.2 | |
| L | 25.4 | 21 | 21.7 | 19.7 | 14.5 | 11.6 | 14.7 | 13.8 | 8.7 | 13.7 | 19.3 | 11.3 | 19.5 | 17.2 | 23.5 | 24.5 | 10.3 | |
| M | 28.6 | 23.2 | 17.9 | 26.4 | 7.3 | 19.4 | 25.5 | 11.6 | 13.6 | 7.5 | 14.6 | 23.3 | 12.4 | 16.7 | 19 | 17.7 | 21.4 | |
| N | 38.9 | 38.3 | 31.8 | 37.8 | 18.4 | 28.5 | 33.6 | 14.1 | 18.7 | 16.2 | 5.3 | 29.8 | 10.9 | 7.9 | 3.6 | 10.7 | 24.4 | |
| O | 31.4 | 27.9 | 25.6 | 26.4 | 17.6 | 17.7 | 19.9 | 14.4 | 10.9 | 14 | 16.3 | 14.8 | 16.7 | 13 | 18.7 | 20.4 | 9.3 | |
| P | 37.8 | 34.9 | 25.9 | 36.4 | 15.1 | 28 | 33.7 | 14.5 | 19.2 | 11.8 | 9.1 | 30.4 | 7.1 | 12.5 | 9.5 | 8.9 | 25.9 | |
| Q | 37.6 | 36.2 | 29.5 | 35.2 | 18 | 25.9 | 30 | 13.4 | 16.1 | 13.6 | 7.4 | 25.8 | 9.5 | 6 | 6.3 | 10.8 | 20 | |
| R | 19 | 23.5 | 28.6 | 20 | 10.7 | 12 | 18.8 | 8.2 | 9.1 | 19.4 | 16.1 | 18 | 23 | 16.7 | 23.2 | 27.4 | 17.5 | |
| S | 43.9 | 40.6 | 30.1 | 42.2 | 21.3 | 33.6 | 38.9 | 20.1 | 24.4 | 15.7 | 12.8 | 35 | 8.2 | 15.1 | 8.5 | 5.1 | 29.7 | |
| T | 35.6 | 32.1 | 27.1 | 30.9 | 19.6 | 22.1 | 24.4 | 16 | 14.2 | 14 | 15.3 | 19.3 | 14.5 | 11.7 | 15.8 | 17.2 | 13.4 | |
| Syntetic | SWMM Model | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hyetograph | A | B | C | E | F | G | H | I | L | M | N | O | P | Q | R | S | T | |
| MIKE model | A | 1 | 3 | 17 | 3 | 17 | 9 | 7 | 17 | 17 | 17 | 17 | 11 | 17 | 17 | 17 | 17 | 15 |
| B | 2 | 1 | 15 | 2 | 16 | 8 | 6 | 16 | 16 | 16 | 16 | 10 | 16 | 16 | 16 | 16 | 14 | |
| C | 12 | 10 | 1 | 12 | 13 | 14 | 14 | 15 | 14 | 10 | 14 | 14 | 11 | 14 | 13 | 11 | 17 | |
| E | 3 | 2 | 9 | 1 | 15 | 2 | 2 | 14 | 11 | 15 | 15 | 5 | 15 | 15 | 15 | 15 | 9 | |
| F | 4 | 5 | 10 | 5 | 3 | 4 | 9 | 4 | 7 | 13 | 12 | 9 | 13 | 12 | 12 | 13 | 10 | |
| G | 5 | 4 | 8 | 4 | 11 | 1 | 1 | 12 | 6 | 14 | 13 | 1 | 14 | 13 | 14 | 14 | 5 | |
| H | 9 | 9 | 6 | 9 | 7 | 7 | 3 | 10 | 4 | 9 | 11 | 2 | 10 | 8 | 11 | 10 | 1 | |
| I | 7 | 11 | 12 | 7 | 4 | 3 | 5 | 1 | 1 | 11 | 6 | 4 | 9 | 6 | 8 | 9 | 4 | |
| L | 8 | 6 | 3 | 6 | 5 | 5 | 4 | 6 | 2 | 4 | 10 | 3 | 8 | 11 | 10 | 8 | 3 | |
| M | 10 | 7 | 2 | 10 | 1 | 11 | 12 | 3 | 8 | 1 | 5 | 12 | 5 | 9 | 7 | 6 | 11 | |
| N | 16 | 16 | 16 | 16 | 10 | 16 | 15 | 7 | 12 | 8 | 1 | 15 | 4 | 2 | 1 | 3 | 12 | |
| O | 11 | 12 | 4 | 11 | 8 | 10 | 10 | 8 | 5 | 6 | 9 | 6 | 7 | 5 | 6 | 7 | 2 | |
| P | 15 | 14 | 5 | 15 | 6 | 15 | 16 | 9 | 13 | 2 | 3 | 16 | 1 | 4 | 4 | 2 | 13 | |
| Q | 14 | 15 | 13 | 14 | 9 | 13 | 13 | 5 | 10 | 3 | 2 | 13 | 3 | 1 | 2 | 4 | 8 | |
| R | 6 | 8 | 11 | 8 | 2 | 6 | 8 | 2 | 3 | 12 | 8 | 7 | 12 | 9 | 9 | 12 | 7 | |
| S | 17 | 17 | 14 | 17 | 14 | 17 | 17 | 13 | 15 | 7 | 4 | 17 | 2 | 7 | 3 | 1 | 16 | |
| T | 13 | 13 | 7 | 13 | 12 | 12 | 11 | 11 | 9 | 5 | 7 | 8 | 6 | 3 | 5 | 5 | 6 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filianoti, P.G.F.; Nicotra, A.; Labate, A.; Zema, D.A. A Method to Improve the Flood Maps Forecasted by On-Line Use of 1D Model. Water 2020, 12, 1525. https://doi.org/10.3390/w12061525
Filianoti PGF, Nicotra A, Labate A, Zema DA. A Method to Improve the Flood Maps Forecasted by On-Line Use of 1D Model. Water. 2020; 12(6):1525. https://doi.org/10.3390/w12061525
Chicago/Turabian StyleFilianoti, Pasquale G. F., Angelo Nicotra, Antonino Labate, and Demetrio A. Zema. 2020. "A Method to Improve the Flood Maps Forecasted by On-Line Use of 1D Model" Water 12, no. 6: 1525. https://doi.org/10.3390/w12061525
APA StyleFilianoti, P. G. F., Nicotra, A., Labate, A., & Zema, D. A. (2020). A Method to Improve the Flood Maps Forecasted by On-Line Use of 1D Model. Water, 12(6), 1525. https://doi.org/10.3390/w12061525






