Comparison of ERA5-Land and UERRA MESCAN-SURFEX Reanalysis Data with Spatially Interpolated Weather Observations for the Regional Assessment of Reference Evapotranspiration

Abstract

Reanalysis data are being increasingly used as gridded weather data sources for assessing crop-reference evapotranspiration (ET₀) in irrigation water-budget analyses at regional scales. This study assesses the performances of ET₀ estimates based on weather data, respectively produced by two high-resolution reanalysis datasets: UERRA MESCAN-SURFEX (UMS) and ERA5-Land (E5L). The study is conducted in Campania Region (Southern Italy), with reference to the irrigation seasons (April–September) of years 2008–2018. Temperature, wind speed, vapor pressure deficit, solar radiation and ET₀ derived from reanalysis datasets, were compared with the corresponding estimates obtained by spatially interpolating data observed by a network of 18 automatic weather stations (AWSs). Statistical performances of the spatial interpolations were evaluated with a cross-validation procedure, by recursively applying universal kriging or ordinary kriging to the observed weather data. ERA5-Land outperformed UMS both in weather data and ET₀ estimates. Averaging over all 18 AWSs sites in the region, the normalized BIAS (nBIAS) was found less than 5% for all the databases. The normalized RMSE (nRMSE) for ET₀ computed with E5L data was 17%, while it was 22% with UMS data. Both performances were not far from those obtained by kriging interpolation, which presented an average nRMSE of 14%. Overall, this study confirms that reanalysis can successfully surrogate the unavailability of observed weather data for the regional assessment of ET₀.

1. Introduction

Fresh water scarcity is one of the main issues examined by climate-change adaptation policies [1,2]. A common objective of climate change adaptation policies is to identify feasible water management strategies at regional and continental scales to secure the water required for food production, while preserving the ecosystems. This issue is particularly relevant in regions where agricultural irrigation is the main pressure on renewable water resources. In these regions, an assessment of water withdrawal for crop irrigation is fundamental to plan sustainable policies and implement better-informed decisions in water resource management.

Irrigation maps at global and continental scales have been developed for spatial statistics of agricultural water demand [3,4,5]. However their utility for planning water resources and climate adaptation polices is still limited [6]. In Europe, Regulation (EU) No 1303/2013, consistently with the Water Framework Directive (WFD, 2000/60/EC), has imposed to Member States the implementation of effective procedures for assessing irrigation water volumes, as a prerequisite for the exploitation of structural and investments funds within the EU Common Agricultural Policy [7].

Since direct accounting of irrigation water use is often not feasible, procedures based on crop-water-balance modeling have been proposed for a quantitative assessment of irrigation water use at regional scale [8,9,10,11,12,13,14]. In Mediterranean regions, where rainfall and groundwater capillary rise are negligible in the irrigation season (generally from April to September), evapotranspiration is the key variable of the crop water budget. To this end, the Italian Ministry for Agricultural Policy (MIPAAF) has established a set of guidelines to define estimation methodologies of irrigation volumes as an alternative to direct measurements (ministerial decree 31 July 2015). In order to uniform instruments and methodologies at the national scale, these guidelines catalog the procedures having a sound scientific basis, including those adopted by the irrigation advisory services, available in several Italian Regions [8]. In the case of collective irrigation schemes, the estimation methodology allows to consider the withdrawal water volumes coincident with the net irrigation requirements for crops in “standard” conditions as defined by the Food and Agriculture Organization of the United Nations (FAO)-56 study [14], accounting for the actual crop development.

Evapotranspiration is often estimated as a function of the daily reference crop evapotranspiration (ET₀), which is evapotranspiration from a well-watered hypothetical reference crop according to the FAO-56 Penman–Monteith equation [15].

A complete set of meteorological data—including air temperature, wind speed, solar radiation and relative humidity—is required for computing ET₀. Even in highly developed countries, ground weather stations recording variables with consistent accuracy over time are generally available only in a few sites, as part of relatively sparse monitoring networks or very often far from rural areas [16]. In some countries, such as Italy, data availability is also constrained by the fact that the monitoring networks are managed by several regional and national services, which adopt different policies in data storage and distribution.

In areas where a monitoring network is available, spatial interpolation procedures can be employed for assessing weather data at the ungauged sites as well as for generating regular gridded data for regional studies, e.g., [17,18,19]. In the spatial interpolation of nonlinear models such as ET₀, the best solution is to first interpolate the input variable (e.g., the weather variables) and then, calculate the model output (e.g., ET₀) [20]. This rule was verified by recent studies applied to the regional assessments of ET₀ [21,22,23,24].

Methods have been proposed for estimating ET₀ with a reduced set of variables, such as temperature [25] or temperature and radiation [26]. However, these methods introduce empirical parameters that need to be locally calibrated, e.g., [27,28] and then possibly regionalized [29,30,31]. Moreover, these empirical equations are more exposed to errors in case of non-stationarities as those induced by climate change [32].

To overcome the unavailability of ground data, radiometers mounted on satellite platforms, such as Meteosat second generation (MSG), have been also exploited for assessing downward solar radiation [33] and then combined with other sources of air temperature data for assessing ET₀, e.g., [34].

During the last decade, reanalysis products have been increasingly used as gridded data source for water resource management studies. Reanalysis data are produced by running updated versions of the numerical weather prediction models which sequentially assimilate observed atmosphere and surface data, to reconstruct land surface, oceans and atmosphere state variables of the past. Differently from gridded data derived by geostatistical spatial interpolation, the spatial structures of the weather variables (such a temperature, surface pressure and water vapor) are the result of the integration of the physical laws embedded into the numerical models.

Two aspects have been favoring the application of reanalysis data in water resources management studies [35]: (i) their consistency in space and time, covering several decades at global or regional scales; (ii) their free public availability by means of dedicated web platforms, which make these data ready to be used in standard formats, thus avoiding all those time-consuming procedures required for collecting and homogenizing weather station data from different service providers.

Examples of reanalysis are the National Center for Environmental Prediction–National Center for Atmospheric Research reanalysis (NCEP/NCAR) [36], the NASA-Modern Era Retrospective-Analysis for Research and Applications (MERRA) [37] and the ERA-Interim produced by the European Centre for Medium-range Weather Forecasts (ECMWF) [38].

A few studies have applied and compared reanalysis data for ET₀ estimates in different regions of the world. Boulard et al. [39] computed ET₀ by using ERA-Interim reanalysis, verifying their accuracy for water balance studies in northeastern France. Srivastava et al. [40] verified that ET₀ estimated with ERA-Interim, outperformed those obtained with NCEP/NCAR in England. These results were confirmed in similar studies conducted in the Iberian Peninsula [41]. As with all numerical weather products, reanalysis data must be bias-corrected prior to applying them to a specific region [42,43,44]. Paredes et al. [45] provided a comprehensive analysis of the impact of different bias correction methods applied to ERA-Interim reanalysis data for ET₀ estimates across Continental Portugal.

The spatial and temporal resolutions of reanalysis data, along with their reliability, have progressively increased thanks to the continuous advances in numerical weather modeling, computational and ICT tools, data assimilation techniques and increasing quality of atmosphere and ground data retrieved from satellite constellation [46].

In 2018 the UERRA-HARMONIE system was released, producing reanalysis data with a spatial resolution of 11 km over the entire European area [47]. The boundary conditions of UERRA-HARMONIE system are defined by the ERA-Interim reanalysis data which has a spatial resolution of 79 km. UERRA-HARMONIE covers the period from January 1961 until July 2019, when ERA-interim production ceased. UERRA-HARMONIE is integrated by a complementary surface analysis system, named MESCAN-SURFEX, which combines downscaled UERRA-HARMONIE reanalysis fields and additional surface observations, to produce a coherent surface analysis over Europe with a spatial resolution of 5.5 km [48].

In 2019 ERA5 reanalysis data were released, under the auspices of the Copernicus Climate Change Service [49]. ERA5 is the fifth generation of ECMWF global reanalysis, succeeding ERA-Interim and covering the entire globe from 1979 at a spatial resolution of about 31 km. In the same year, Copernicus Climate Change Service has also released ERA5-Land, produced by replaying the land component of the ERA5 climate reanalysis, but with a horizontal resolution of 9 km. The atmospheric forcing in ERA5-land are provided by land fields of ERA5 atmospheric variables. Specifically, ERA5 air temperature, air humidity and pressure used to run ERA5-Land are corrected to account for the altitude difference between the grid of the forcing and the higher-resolution grid of ERA5-Land, according to the so called ’lapse rate correction’ [50].

This study, for the first time, provides a comprehensive analysis of ET₀ estimate performances based on MESCAN-SURFEX and ERA5-Land weather data and compared them with ET₀ estimate performances obtained by spatially interpolating weather variables with geostatistical procedures. A geostatistical cross-validation procedure was designed and applied for evaluating ET₀ estimate performances based on the spatial interpolation of point observations. The study was conducted for Campania Region (Southern Italy), in the irrigation seasons of years 2008–2018.

2. Materials and Methods

2.1. Study Area

The study area is the Campania region, sited in Southern Italy, with an extension of about 14,000 km². Figure 1 shows the location of the region, bounded between the coastline of the Tyrrhenian Sea and the mountains of the Southern Apennines. The relief map, also displayed in Figure 1, reveals the topographic complexity of the study area, characterized by two main plains and by an irregular orography in proximity of the sea and in the inner part of the region, that highly influences the spatial variability of the weather [51].

The study area is characterized by Mediterranean climates with hot, dry summers, warm springs and mild, wet winters and autumns. Precipitations occur mostly in autumn and winter: the maximum monthly precipitations are recorded during November and December.

Although the actual duration of the irrigation season is determined by the weather variability and specific agricultural practices, irrigation in open fields generally starts in April and it lasts until the end of September. Thus, hereinafter the period from April 1st to September 30th will be referred to as irrigation season.

The region has been the focus area of several projects aiming at developing innovative technologies to support water resources management in agriculture, based on satellite remote sensing and numerical weather predictions [9,12,14,52]. It is also the demonstrative area of the EU-Horizon2020 project, LANDSUPPORT (https://www.landsupport.eu/), aiming at identifying sustainable management practices in agriculture.

A network of 18 automatic weather stations (AWSs) has been operating since 2008, recording hourly measurements of air temperature at 2 m, wind speed at 10 m, relative humidity at 2 m, global incoming solar radiation and barometric pressure. The locations of the stations are shown on the regional map in Figure 1, while details about their reference ID number, site name, elevation and coordinates are listed in

Table 1. List of the ground weather stations in the study area.

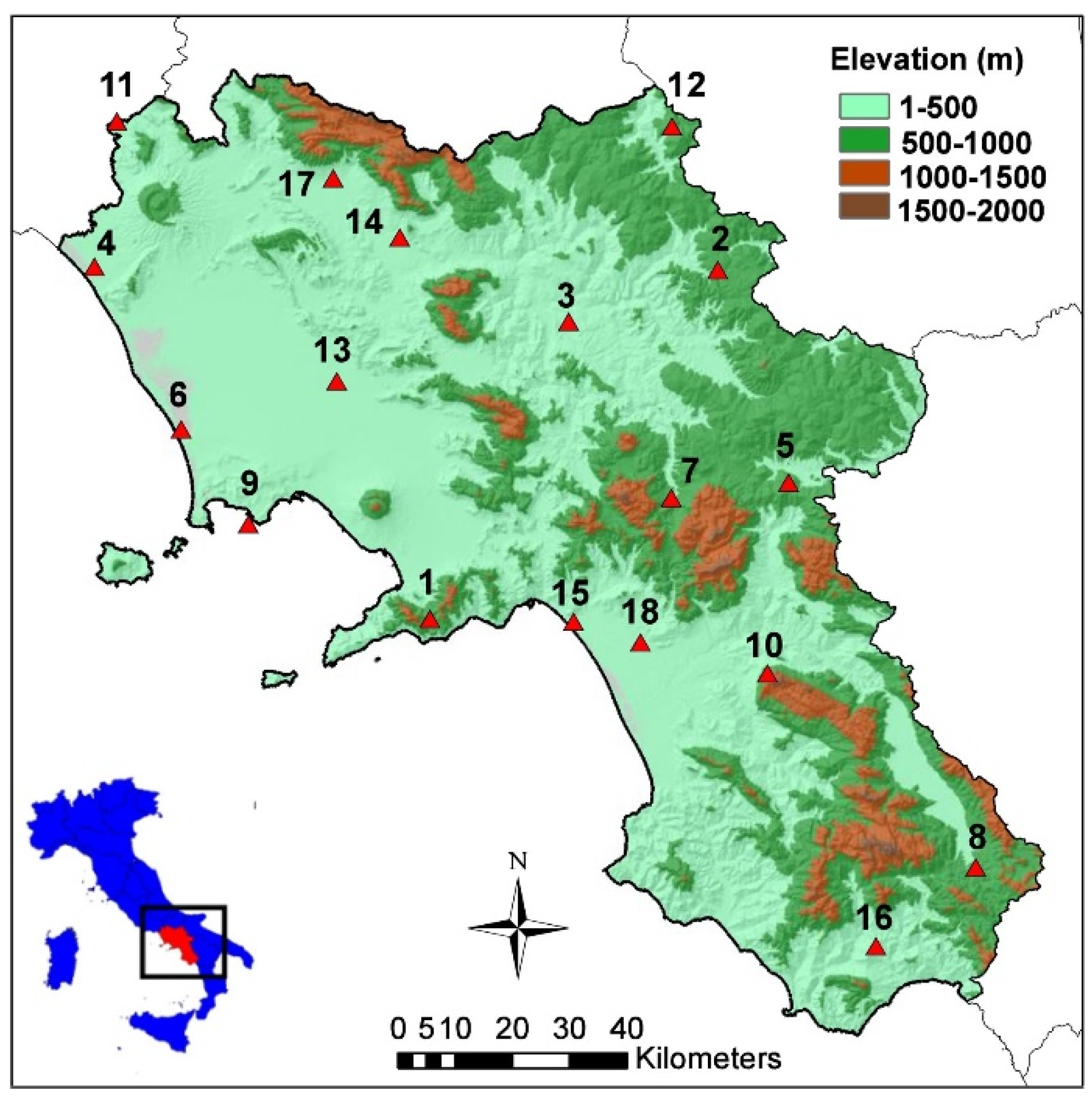
ID	Name	Elevation (m)	Latitude (°)	Longitude (°)
1	Agerola METEO	848	40°38′49″ N	14°32′28″ E
2	Ariano Irpino METEO	631	41°11′49″ N	15°8′10″ E
3	Benevento METEO	236	41°6′54″ N	14°49′30″ E
4	Cellole METEO	9	41°11′46″ N	13°50′17″ E
5	Conza della Campania METEO	770	40°51′43″ N	15°16′55″ E
6	Lago Patria METEO	1	4056′31″ N	14°1′19″ E
7	Montella METEO	515	40°50′17″ N	15°2′20″ E
8	Montesano Marcellana METEO	552	40°15′22″ N	15°39′50″ E
9	Nisida METEO	88	40°47′38″ N	14°9′50″ E
10	Postiglione METEO	660	40°33′43″ N	15°14′13″ E
11	Rocca d’Evandro METEO	62	41°25′30″ N	13°52′48″ E
12	S.Bartolomeo METEO	750	41°25′19″ N	15°2′28″ E
13	San Marco Evangelista METEO	31	41°1′12″ N	14°20′38″ E
14	S.Salvatore Telesino METEO	167	41°14′49″ N	14°28′23″ E
15	Salerno METEO	13	40°38′38″ N	14°50′13″ E
16	Torre Orsaia METEO	413	40°7′55″ N	15°27′32″ E
17	Alife	117	41°20′20″ N	14°20′2″ E
18	Battipaglia	64	40°36′40″ N	14°58′34″ E

. This network is managed by the Regional Hydrometeorological Service, as part of the larger hydrometeorological network, including additional 59 weather stations equipped with air temperature sensors at 2 m (Figure A1 in Appendix B).

Table 2. Weather data statistics for the irrigation seasons (April–September) of years 2008–2018.

Station	T (°C)		WS (m s−1)		VPD (kPa)		RS (W m−2)
ID	Mean	cv	Mean	cv	Mean	cv	Mean	cv
1	18.0	0.27	2.08	0.37	0.73	0.75	224	0.35
2	18.7	0.27	3.17	0.38	0.8	0.67	256	0.29
3	20.5	0.23	1.95	0.40	0.9	0.51	254	0.28
4	21.3	0.19	2.04	0.26	0.66	0.49	259	0.26
5	18.2	0.29	4.64	0.47	0.74	0.76	258	0.3
6	21.5	0.19	2.60	0.33	0.65	0.46	263	0.25
7	18.0	0.25	1.34	0.42	0.72	0.54	240	0.32
8	18.4	0.24	1.55	0.23	0.63	0.57	246	0.29
9	23.1	0.19	3.31	0.39	0.87	0.56	269	0.25
10	18.9	0.26	4.28	0.43	0.84	0.66	248	0.33
11	21.1	0.21	1.27	0.39	0.79	0.54	233	0.31
12	17.9	0.30	4.40	0.41	0.71	0.83	258	0.32
13	23.4	0.20	2.03	0.33	1.13	0.49	243	0.28
14	21.4	0.21	1.99	0.45	0.9	0.56	246	0.28
15	23.5	0.19	2.10	0.24	1.12	0.43	249	0.26
16	20.8	0.22	2.62	0.26	0.84	0.61	251	0.3
17	20.8	0.21	1.2	0.42	0.91	0.53	242	0.28
18	22.4	0.20	1.33	0.33	1.13	0.46	254	0.26

T—air temperature; WS—wind speed; RS—solar radiation; VPD—vapor pressure deficit; cv—variation coefficient.

illustrates the mean and coefficient of variation of daily weather data recorded at the 18 AWSs during the irrigation seasons of years 2008–2018, assumed as focus period in this study.

Mean air temperature, T, ranges between 17.85 °C and 23.50 °C with coefficients of variation (cv) from 0.19 to 0.30; wind speed, WS, ranges from 1.27 m s⁻¹ to 4.64 m s⁻¹ with cv from 0.23 to 0.47; solar radiation, RS, ranged from 224 W m⁻² to 269 W m⁻² with cv from 0.26 to 0.35.

The daily vapor pressure deficit (VPD) was computed by using daily mean air relative humidity data and the daily maximum and minimum temperatures according to the FAO irrigation and drainage study No. 56 [15] (pp. 36–40). The VPD ranged from 0.63 kPa to 1.13 kPa with coefficients of variation from 0.43 to 0.83.

2.2. Reanalysis Data

Meteorological reanalysis data provide an accurate description of the past weather by assimilating land surface and atmospheric observations from several sources into the most advanced numerical weather prediction models that obey physical laws, in order to create a complete and consistent climate dataset that covers several decades back in time and that is coherent both from physical and dynamic perspectives [53]. Reanalysis data are generally freely available on dedicated platforms of the web, released in regular grid formats, with a delay of few months from present.

In this study, we employed the most advanced reanalysis data produced in Europe, specifically optimized for the land surface: UERRA MESCAN-SURFEX (UMS) [54] and ERA5-Land (E5L) [50,55]. The former is a regional reanalysis model implemented for Europe within an European FP7 reanalysis preoperational project with the participation of the European Centre for Medium-Range Weather Forecasts (ECMWF), while the latter is a global atmospheric reanalysis model implemented by ECMWF. Both are freely available as products of the Copernicus Climate Change Service that holds the intellectual property rights of the raw data.

UERRA MESCAN-SURFEX is a downscaled surface analysis system of the UERRA-HARMONIE regional reanalysis forced by the global ERA-Interim reanalysis data [56] and its production ceased with the end of availability of ERA-interim (July 2019). It will be replaced by a new system called Copernicus European Regional ReAnalysis (CERRA). CERRA will be used to create a pan-European reanalysis, with very high resolution (5.5 km) forced by the global ERA5 reanalysis [57].

UERRA MESCAN-SURFEX has a spatial resolution of 5.5 km over Europe and covers the period January 1961–July 2019. Figure 2a shows its numerical grid over the study area. Daily mean values of air temperature at 2 m, wind speed at 10 m, relative humidity at 2 m, global incoming solar radiation and barometric pressure as well as maximum and minimum daily air temperature were computed by aggregating the six-hour forecasts available at 00, 06, 12 and 18 UTC.

ERA5-Land is a rerun of the land component of the ERA5 reanalysis, obtained by implementing a series of improvements with respect to ERA5, in order to make it more accurate for all types of land applications [58]. ERA5-Land runs at enhanced spatial resolution (9 km vs 31 km in ERA5), but it has the inconvenient that data, including atmospheric variables, are not provided for numerical grid points falling on sea surface. Thus, for land areas close to the coast, since they are not surrounded by four valid grid data values, the assessment of weather variables must rely on inland data only. Figure 2b shows the numerical grid of the E5L data: the gray dots refer to the grid points on the sea surface for which no data are available.

ERA5-Land data are produced with an hourly time-step. Thus, daily values were derived by collecting 24 values starting from 00 UTC every day. The available weather variables are air temperature at 2 m, wind speed at 10 m, global incoming solar radiation, barometric pressure and dew point temperature at 2 m. Instead of relative humidity, dew point temperature was then used for computing vapor pressure deficit.

For both E5L and UMS data, a simple bias correction technique was applied to temperature, vapor pressure deficit and solar radiation data to remove the systematic bias. Raw reanalysis data were corrected by subtracting the corresponding regional mean bias computed at the 18 AWSs. Both E5L and UMS data showed a systematic overestimation of temperature over the region that was corrected with the average regional error that was equal to 0.66 °C for E5L and 1.57 °C for UMS.

2.3. Geostatistical Interpolation of Ground Sensor Data and Cross-Validation for Evaluating Performances

Geostatistical interpolation is generally employed to estimate weather data over a regularly spaced prediction grid by using ground sensor measurements available over irregularly spaced networks [59]. Among the wide collection of geostatistical interpolation methods, ordinary kriging is the most used to interpolate weather data, such as wind speed [60,61], relative humidity [61] and solar radiation [62,63,64]. However, ordinary kriging only uses data available from observations and its performance greatly depends on the density of the available measuring network and the spatial structure of the variable of interest [65]. For this reason, in some other applications where an evident statistical correlation exists between the weather variable of interest and an auxiliary external variable sampled with a higher spatial resolution, regression kriging is preferred [66]. This is the case of temperature [66,67,68,69], which is highly correlated with the elevation.

Regression kriging [70] (also named residual kriging [71], mathematically equivalent to universal kriging, often said kriging with external drift [72]) couples a regression model of the variable of interest on auxiliary independent variables, with the ordinary kriging applied to the regression residuals.

Appendix A provides theoretical details of kriging estimation that can be exhaustively found in Journel & Huijbregts [73] and Cressie [74], among others.

In this study, we used (i) ordinary kriging—Equations (A1–A4)—for interpolating daily wind speed, relative humidity and solar radiation and (ii) regression kriging for daily mean, maximum and minimum air temperature. By implementing daily regression models of temperature with elevation, regression kriging requires the application of Equations (A1–A4) to the random field of the regression residuals, instead of the observed weather variable.

Then, the performances of kriging estimators were assessed by means of the cross-validation method [74,75]. Indeed, a very common way to assess the predictive ability of a statistical model and, specifically, of a spatial interpolation technique, such as kriging, is to test model results on a set of data that were not used for estimation. Cross-validation serves this scope and it is based on a jackknife kriging estimation of the variable of interest at a sampling site, obtained by applying the kriging interpolator to the variable observations available at the remaining sampling sites (leave-one-out cross-validation).

Then, after applying the described procedure for all sampling sites, i.e., 18 AWSs sites and weather variables, the (jackknife) kriging estimations were used for the performance analysis and to evaluate the predictive ability of kriging in deriving gridded data from weather observations in the study area.

2.4. Reference Evapotranspiration Model

The reference evapotranspiration is an important notion in hydrological and agricultural applications, able to describe the evaporative demand of the atmosphere [15]. It only depends on the weather data and it can be defined as the evapotranspiration under standard conditions of a hypothetical grass reference crop according to FAO irrigation and drainage study No. 56 [15].

In this study, daily reference evapotranspiration, ET₀, was computed by using daily weather data retrieved from ground sensors at AWS sites and, alternately, by using bias-corrected reanalysis data and spatially interpolated data from ground sensors by cross-validation.

ET₀ (mm day⁻¹) is computed with the FAO Penman–Monteith equation, as follows:

$${\mathrm{ET}}_0=\frac{1}{\lambda }\frac{\Delta \left({\mathrm{R}}_{\mathrm{n}}-\mathrm{G}\right)+\gamma \frac{900}{\mathrm{T}+273}\mathrm{WS}·\mathrm{VPD}}{\Delta +\gamma \left(1+0.34·\mathrm{WS}\right)}$$

(1)

where:

• $\lambda$ is the latent heat of vaporization;
• Δ is the slope of the vapor pressure curve (kPa °C⁻¹);
• γ is the psychometric constant (kPa °C⁻¹);
• T is the daily mean air temperature at 2 m height (°C) computed as the average between the daily maximum (T_max) and minimum (T_min) air temperature at 2 m height at the highest available temporal resolution of data;
• WS is the wind speed at 2 m height above ground (m s⁻¹) computed from the wind speed at 10 m above the ground by multiplying for a factor of about 0.75 given by the logarithmic equation of the wind speed profile [15];
• VPD is the daily vapor pressure deficit (kPa), computed as function of T_max and T_min and relative humidity, RH. If available, dew point temperature (T_dew) is used for computing VPD, instead of RH);
• R_n is the net radiation at the crop surface (MJ m⁻² day⁻¹) and G is the soil heat flux density (MJ m⁻² day⁻¹). The net radiation (R_n) was calculated as the difference between the incoming net shortwave radiation and the outgoing net long-wave radiation. The incoming net shortwave radiation is a fraction of the incoming shortwave solar radiation (RS), computed for the reference crop by setting the albedo equal to 0.23.

Table 3. Monthly statistics for Food and Agriculture Organization of the United Nations (FAO) Penman–Monteith reference evapotranspiration, ET₀ (mm day⁻¹), averaged over years 2008–2018.

Station	April		May		June		July		August		September
ID	Mean	cv	Mean	cv	Mean	cv	Mean	cv	Mean	cv	Mean	cv
1	2.56	0.42	3.08	0.34	4.04	0.23	4.29	0.20	3.31	0.30	2.22	0.28
2	2.70	0.33	3.43	0.29	4.62	0.23	5.16	0.20	4.08	0.25	2.72	0.28
3	2.75	0.28	3.59	0.24	4.66	0.18	5.04	0.16	4.05	0.22	2.77	0.22
4	2.70	0.25	3.57	0.20	4.43	0.17	4.71	0.12	3.90	0.19	2.86	0.19
5	2.68	0.45	3.34	0.36	4.64	0.25	5.31	0.23	4.23	0.28	2.85	0.40
6	2.75	0.26	3.69	0.19	4.66	0.16	4.85	0.13	3.98	0.19	2.97	0.20
7	2.47	0.32	3.09	0.29	4.12	0.20	4.38	0.17	3.36	0.23	2.30	0.29
8	2.59	0.32	3.18	0.28	4.12	0.19	4.46	0.16	3.60	0.21	2.41	0.24
9	3.18	0.28	4.08	0.22	5.16	0.17	5.54	0.14	4.67	0.22	3.58	0.21
10	2.91	0.40	3.47	0.36	4.74	0.25	5.33	0.21	4.38	0.27	3.13	0.30
11	2.65	0.29	3.33	0.26	4.29	0.20	4.59	0.16	3.63	0.24	2.21	0.28
12	2.52	0.43	3.20	0.36	4.51	0.27	5.29	0.25	4.20	0.31	2.68	0.40
13	3.12	0.28	3.90	0.24	4.93	0.20	5.15	0.14	4.18	0.23	3.04	0.22
14	2.94	0.32	3.59	0.27	4.56	0.22	4.90	0.17	4.07	0.25	2.85	0.23
15	3.05	0.25	4.00	0.20	4.99	0.15	5.29	0.11	4.30	0.20	3.13	0.18
16	2.99	0.36	3.55	0.30	4.52	0.22	5.05	0.16	4.33	0.23	3.16	0.27
17	2.63	0.29	3.30	0.26	4.26	0.21	4.56	0.17	3.72	0.22	2.62	0.21
18	2.87	0.26	3.71	0.21	4.69	0.15	4.96	0.12	4.03	0.20	2.92	0.18

reports monthly statistics averaged over years 2008–2018 for daily ET₀, computed with ground-based weather data at the 18 AWSs.

The mean daily ET₀ values over the region are 2.78 mm day⁻¹ in April, 3.51 mm day⁻¹ in May, 4.55 mm day⁻¹ in June, 4.94 mm day⁻¹ in July, 4.00 mm day⁻¹ in August and 2.80 mm day⁻¹ in September. The minimum mean value over a month of daily ET₀ is registered in September, 2.21 mm day⁻¹ and the maximum in July, 5.54 mm day⁻¹. The mean coefficient of variation is minimum in July, 0.17 and maximum in April, 0.32.

2.5. Statistical Indicators for Performance Analysis

The performance of the bias-corrected reanalysis data and of the spatially interpolated data, computed from ground sensors by cross-validation, were evaluated at each AWSs, by assuming the weather observations retrieved from the AWS sensors as benchmarks.

Similarly, for what concerns the reference evapotranspiration, the benchmark was assumed to be the reference evapotranspiration computed with Equation (1) by using the weather data retrieved from ground sensors as input variables. This benchmark ET₀ was, respectively compared with ET₀ computed by using the bias-corrected reanalysis weather data and the spatially interpolated weather data from ground sensors as input.

The performances were evaluated by computing the BIAS, which was used as an indicator of accuracy of data. and the root mean square error, RMSE, which gives insight about both accuracy and precision of data. These two statistical indicators were calculated as follows:

$$\mathrm{BIAS}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{X}}_{\mathrm{p}}^{\mathrm{i}}{-\mathrm{X}}_{\mathrm{b}}^{\mathrm{i}}\right)}{n}$$

(2)

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{X}}_{\mathrm{p}}^{\mathrm{i}}{-\mathrm{X}}_{\mathrm{b}}^{\mathrm{i}}\right)}^2}{n}}$$

(3)

where ${\mathrm{X}}_{\mathrm{p}}^{\mathrm{i}}$ and ${\mathrm{X}}_{\mathrm{b}}^{\mathrm{i}}$ are, respectively, the variable for which the performance evaluation is desired and the corresponding variables assumed as benchmark, at the i–th day; n denotes the number of examined days (183 days of the annual irrigation season multiplied by the 11 years analyzed, i.e., 2013 days in total). The more the BIAS differs from zero the less accurate is the estimate. The greater is the RMSE, the less are accuracy and precision of the estimates.

In the following, differences between the performance indicators were computed for comparing the performance of different methods each other. For comparing BIAS, the differences between the corresponding absolute values resulting from Equation (2) were computed.

When monthly analyses for the reference evapotranspiration were performed, the BIAS and RMSE were divided by the mean daily ET₀ on the examined j-th month computed over the analyzed years (values specified in Table 3), in order to consistently compare monthly performances.

These normalized indicators are hereinafter referred to as nBIAS and nRMSE, computed as follows for the j-month:

$$\mathrm{nBIAS}=\frac{1}{\overline{{\mathrm{X}}_o^j}}\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^k\left({\mathrm{X}}_{\mathrm{p}}^{j,i}{-\mathrm{X}}_{\mathrm{b}}^{j,i}\right)}{k}$$

(4)

$$\mathrm{nRMSE}=\frac{1}{\overline{{\mathrm{X}}_o^j}}\sqrt{\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^k{\left({\mathrm{X}}_{\mathrm{p}}^{j,i}{-\mathrm{X}}_{\mathrm{b}}^{j,i}\right)}^2}{k}}$$

(5)

where k refers to the number of days in the j-month of interest and $\overline{{\mathrm{X}}_o^j}$ is the mean observed value of the generic variable X in the examined j-month over the analyzed years at a specific site of interest. In the following, we express nBIAS and nRMSE in percent.

3. Results

3.1. Performance Analysis on Weather Data

A performance analysis of weather variables was conducted to better explain the performance of the target variable of this study, i.e., the reference evapotranspiration. This analysis may be also relevant for other applications, since it can guide the choice of the most suitable data source for the different set of weather variables, based on the corresponding statistical performance indicators.

Figure 3 shows the statistical performance indicators of the kriging estimator computed with Equations (2–3), where ${\mathrm{X}}_{\mathrm{p}}^{\mathrm{i}}$ are the spatially interpolated observed daily weather data obtained by cross-validation and ${\mathrm{X}}_{\mathrm{b}}^{\mathrm{i}}$ are the daily weather observations. Both indicators were computed over the reference period April–September of years 2008–2018 (2013 days).

In the case of air temperature, the kriging performances at each of the 18 reference AWSs were assessed by cross validation, after conditioning the kriging estimates to the observations at the remaining 76 temperature stations, i.e., the remaining 17 reference AWSs plus the additional 59 air temperature sensors, distributed across the region as depicted in Figure A1. In this way, we explicitly considered the availability of air temperature data with a much higher density than the other weather variables involved in ET₀ computations: a common scenario to many regions of the world. Appendix B shows the sensitivity of kriging interpolator to the density of the network for what concerns air temperature data. For all other weather variables, the kriging estimates at each AWSs where conditioned to just the remaining 17 AWSs, for which the corresponding observations were available.

In Figure 3a, the BIAS values are represented according to the color scale on the side: green corresponds to BIAS close to zero. In Figure 3b, the color scale ranges from blue to red, as RMSE runs from the minimum to maximum values.

Summarizing the main results depicted in Figure 3, temperature BIAS varies over the region from −0.8 °C to 1.6 °C, with a mean RMSE of 1.2 °C and a maximum RMSE of 2.0 °C. Wind speed BIAS varies from −1.66 m s⁻¹ to 2.19 m s⁻¹, with mean RMSE equal to 1.16 m s⁻¹ and maximum RMSE equal to 2.78 m s⁻¹. Solar radiation BIAS ranges from −30 W m⁻² to 20 W m⁻², with mean RMSE equal to 30 W m⁻² and a maximum RMSE at 53 W m⁻². VPD BIAS varies over the region from −0.19 kPa to 0.30 kPa, with a mean RMSE of 1.50 kPa and a maximum RMSE of 2.24 kPa. The worst performances in terms of RMSE are observed at AWSs n. 1, 9 and 13 for T, at AWSs n. 5, 10, 12 for WS, at AWSs n. 1, 10, 12 for RS and at AWSs n. 1, 6, 13 for VPD.

The performances considerably change across the region due to: (i) the irregularly spaced AWS network that may penalize some of the AWS sites, such n. 13; (ii) border effects that penalize the locations at the inland boundaries (AWSs n. 2, 5, 10, 12) of the region and along coastline (AWSs n. 1, 6, 9); (iii) complex topography, especially in proximity of the sea (AWS n. 1).

In relative terms, considering the statistics of weather observations over the irrigation seasons of years 2008–2018, kriging spatial interpolations provided the best performances with temperature, thanks to the strong correlation with the elevation taken as auxiliary variable. However, as illustrated in Appendix B, the density of the network in the case of temperature slightly influenced the kriging performances.

Figure 4 shows the performances of the two considered reanalysis datasets: UERRA MESCAN-SURFEX (UMS) and ERA5-Land (E5L). Temperature, vapor pressure deficit and solar radiation were bias-corrected as explained in Section 2.2.

The statistical performances were presented by means of BIAS and RMSE, as defined in Equations (2–3), where ${\mathrm{X}}_{\mathrm{p}}^{\mathrm{i}}$ are the bias-corrected daily reanalysis values for the variable of interest and ${\mathrm{X}}_{\mathrm{b}}^{\mathrm{i}}$ are the daily weather observations at the AWSs sensors. Figure 4 shows the differences between the computed performance indicators of each reanalysis dataset and the kriging estimator (as depicted in Figure 3), providing information about the convenience of using reanalysis datasets versus spatially interpolated ground sensor weather data. The benchmarks data for the computations of the BIAS and RMSE remain the daily weather observations at AWSs sensors.

Figure 4a shows the differences between the corresponding absolute BIAS, while Figure 4b shows the differences between the corresponding RMSE. Except for RMSE computed for RS, the color scales are built to range from negative values when kriging is performing better than reanalysis (blue on the color bar), to positive values when kriging is performing worse than reanalysis (red color on the color bar). In case of RS, the color scale represents only positive increasing values from blue to red.

Reanalysis and kriging show generally similar accuracies in temperature estimates (see T in Figure 4a), while kriging slightly outperforms reanalysis in term of RMSE (see T in Figure 4b). ERA5-Land shows generally more favorable RMSE values than UMS. AWS n.1 is a special case that deserves a note, since it is located on the ridge of the Sorrento’s Peninsula, characterized by high elevation in proximity of the coastline. The effect of this complex terrain features cannot be represented by the coarse spatial resolution of the numerical grid. Moreover, as shown in Figure 2b, E5L does not provide valid data grid points located in proximity of this coastal ridge. Any estimation at AWS n.1 must rely on bilinear interpolation of grid points located in the inland plain.

With respect to wind speed, both BIAS and RMSE show that kriging estimator outperforms reanalysis roughly in only half of the AWSs and that E5L outperforms UMS.

With respect to vapor pressure deficit and solar radiation, differences in BIAS and in RMSE show that kriging estimator outperforms reanalysis and that E5L outperforms UMS, which presents limitations in predicting solar radiation, as also reported in the UERRA user guide [56].

3.2. Performance Analysis on Reference Evapotranspiration

This section is focused on the performances of ET₀ averaged over the entire irrigation season of years 2008–2018. The following subsection will present monthly based results.

Figure 5 shows the average BIAS and RMSE of ET₀ in the period 2008–2018 for the whole region. The spread of the box plots refers to the variability of the statistical indicators among the 18 AWS sites. ET₀ was computed by, respectively using weather data from kriging interpolation, UERRA MESCAN-SURFEX (UMS) and ERA5-Land (E5L). Figure 5 reveals that ET₀ computed with weather data estimated by kriging is generally more accurate and precise than reanalysis data. However, the differences in ET₀ estimate performances among datasets are negligible: the differences in RMSE between kriging estimator and E5L are on average less than 3% of the mean daily ET₀ and the differences in RMSE between kriging estimator and UMS are on average less than 8% of the mean daily ET₀. The differences among databases are even smaller in terms of BIAS.

The BIAS of the daily ET₀ computed with kriging interpolated observations varies from −0.49 mm day⁻¹ to 0.59 mm day⁻¹ with a mean value of 0.04 mm day⁻¹; the RMSE from 0.32 mm day⁻¹ to 0.86 mm day⁻¹ with a mean value of 0.56 mm day⁻¹. The BIAS of the daily ET₀ computed with UMS weather data varies from −0.31 mm day⁻¹ to 0.51 mm day⁻¹ with a mean value of 0.08 mm day⁻¹; the RMSE from 0.70 mm day⁻¹ to 1.23 mm day⁻¹ with a mean value of 0.87 mm day⁻¹. The BIAS of the daily ET₀ computed with E5L weather data varies from −0.53 mm day⁻¹ to 0.55 mm day⁻¹ with a mean of 0.21 mm day⁻¹; the RMSE ranges from 0.44 mm day⁻¹ to 1.04 mm day⁻¹ with a mean of 0.67 mm day⁻¹.

Performance Analysis on Monthly Basis

This section presents ET₀ estimate performances on a monthly basis. The statistical indicators of Equations (4–5) are averaged for each month and normalized by the corresponding monthly mean of the daily ET₀ observed at each AWSs (Table 3).

Figure 6 shows the nBIAS and nRMSE of ET₀ computed by using weather data from kriging interpolation of ground sensor data.

The monthly statistical indicators are represented according to the color scale on the bottom. The markers’ size describes to the expected maximum interannual variability of the statistics, defined by p₇₅ + 1.5(p₇₅−p₂₅), where p₂₅ and p₇₅ are, respectively the 25th and 75th percentiles of the monthly values in the years 2008–2018.

The interannual variability of nRMSE is greater than that of the nBIAS. The months characterized by the worst performances in terms of nRMSE are April and September. June is the month that presents the best relative performances. However, the accuracy and precision of the estimates are very high: nBIAS ranges between −13% and 14% of the corresponding observed ET₀ monthly mean; nRMSE ranges between 8% and 21% of the corresponding observed ET₀ monthly mean, with an average nRMSE value of 14%.

As for Figure 4, Figure 7 presents the differences between ET₀ estimate performances of each reanalysis dataset and the corresponding performances of the kriging estimator (given by Figure 6).

Figure 7a shows the differences between absolute values of nBIAS, while Figure 7b between nRMSE: positive values (red color on the color bar) mean that the kriging estimator is performing better than reanalysis and negative values mean the opposite. In most cases, kriging estimator outperforms reanalysis data, but in the worst cases the increase of nBIAS and nRMSE is less than 15% for UMS and less than 10% for E5L.

E5L outperforms UMS in assessing reference evapotranspiration. However, both datasets show very high performances. For UMS, nBIAS ranges between −28% and 23% of the corresponding observed ET₀ monthly mean and nRMSE ranges between 11% and 32% of the corresponding observed ET₀monthly mean_, with an average value of 22%. For E5L, nBIAS ranges between −12% and 8% of the corresponding observed ET₀ monthly mean and nRMSE ranges between 7% and 27% of the corresponding observed ET₀ monthly mean, with an average value of 17%.

The most accurate and precise ET₀ estimates based on UMS and E5L occurs in July, which is also the month with highest ET₀ in the study region. UMS performances drop in April, May and slightly in September. When the aerodynamic term of Penman Monteith equation is prevalent over the radiation term, the uncertainty about VPD and wind speed exerts a major role in the estimation of ET₀. Hence, the performance of reanalysis models in April and May is influenced by the larger BIAS and RMSE (Figure 4).

4. Discussion and Conclusions

Regional maps of daily reference evapotranspiration are fundamental for addressing many water resources management issues, especially in those areas, such in Mediterranean regions, where significant freshwater abstractions are practiced for crop irrigation in the dry seasons [4]. The computation of FAO-56 daily reference evapotranspiration (ET₀) requires dataset of multiple weather variables, recorded by networks of automatic weather stations (AWSs). The spatial distribution of these AWSs is generally too coarse and irregular for assessing the spatial variability of weather variables, such as solar radiation and wind [76].

The availability of observed weather data is also hindered by the policy data access adopted by the hydrometeorological service providers. This study examined the case of the Campania Region (Southern Italy), where the Regional Hydrometeorological Service is operating a network of 18 automatic weather stations, recording a complete set of weather data since year 2008, across an area of 14,000 km². The spatial density of this network is relatively high if compared with those examined by previous studies on this topic: Paredes et al. [45] analyzed data of 24 stations in Portugal (about 92,000 km²) while Martins et al. [41] collected data observed at 130 station across the entire Iberian Peninsula (597,000 km²). Indeed, the access to observed weather data can be even more difficult for areas extending across regional or national boundaries. In Italy, for instance, weather monitoring networks are managed by regional and national services, without a common data sharing policy and data distribution platform [77]. Pan European gridded agrometeorological maps released to support the EU Common Agricultural Policy, are derived by interpolating observed weather data collected in the different Member States, with uneven distributions, not consistent with what would be required based on the topographic complexity (e.g., Agri4Cast Resources Portal, Gridded Agro-Meteorological Data in Europe [78]).

These constrains in the availability of observational weather data are the main motivations of the growing interest toward the application of reanalysis data in hydrological studies.

The quality of the reanalysis data is rapidly growing, thanks to the significant research efforts in providing temporally consistent combination of the most advanced numerical weather models and the available climate observations. This study examined the last two reanalysis products distributed by the Copernicus Climate Change Service: the pan-European regional reanalysis UERRA MESCAN-SURFEX (UMS) with a spatial resolution of 5.5 km; and the global land surface reanalysis ERA5-Land (E5L) with a spatial resolution of nine kilometers.

We found that ERA5-Land systematically outperformed UERRA MESCAN-SURFEX in reconstructing the historical weather variables required for computing ET₀. This result testifies that the choice of the gridded product should be not merely driven by its nominal spatial resolution. ERA5-Land benefits of the latest ERA5 global reanalysis, downscaled from 31 km to 9 m by applying the lapse rate correction to account for the influence of the altitude on the spatial structure of the weather variables. UMS is instead a downscaled product of UERRA-HARMONIE regional reanalysis at spatial resolution of 11 km, which boundary conditions were defined by the ERA-Interim global reanalysis, which production ceased in 2019, being substituted by the more advanced ERA5.

Reanalysis products are generally evaluated by point-to-point comparisons, consisting in assessing the difference between the observed data and the corresponding reanalysis value, obtained by linear interpolation of the reanalysis data at the numerical grid points surrounding the observation site, e.g., [41,45]. In this study, we aimed at assessing the reanalysis performances with what could be achieved by spatially interpolating AWSs observations, following established methods in regional scale analyses [75,79]. AWSs data were interpolated by universal kriging and ordinary kriging, combined with a cross validation procedure for retrieving the corresponding indicators of performances, which were then compared with the reanalysis products.

Reanalysis temperature and wind speed exhibited better performances than other variables, and comparable to those achieved by kriging interpolations (Figure 4). Indeed, as a general aspect of numerical weather predictions, prognostic variables such as temperature and wind speed, since they are directly derived by the numerical integration of dynamic laws of the atmosphere, are better predicted than diagnostic variables.

Our findings confirm that the numerical solar radiation reconstructions are most prone to error. UMS estimate errors of solar radiation were almost 2–3 times larger than E5L. UMS results were coherent with other studies that evidenced ERA-Interim tendency to overestimate solar radiation [45,80]. Improvement in solar radiation estimates is certainly one of the most desirable aspect from future reanalysis products, such as the upcoming Copernicus regional reanalysis for Europe (CERRA) [57], especially because solar radiation errors have the highest impact on the predicted evapotranspiration [52,81]. The availability of weather data on grid points located over the sea close to the coastline would be also desirable, to avoid the issue experienced when assessing weather conditions close to the coast with E5L (Figure 2b).

Still, ET₀ estimate performances based on the examined reanalysis data were satisfactory if compared with those obtained by spatially interpolating the observed data. Reanalysis-based ET₀ presented average nBIAS lower than 5%. Average nRMSE ranged from 17% with E5L to 22% with UMS. The values of these performance indicators were not far from those obtained by kriging interpolation: average nBIAS of 1% and average nRMSE of 14%.

ET₀ estimate performances based on E5L and UMS were better than those presented by Martins et al. [41] for the Iberian Peninsula based on NCEP/NCAR blended reanalysis data, and those presented by Parades et al. [45] for Continental Portugal based on the ERA-Interim.

Another interesting result is that differences in statistical performances between reanalysis- and observation-based ET₀ estimates were small: ET₀ predicted with E5L and the kriging estimator presented average differences in nRMSE smaller than 3%; while in the comparison between UMS and kriging estimator, the differences in nRMSE were smaller than 8%. The corresponding differences were even smaller and negligible in terms of nBIAS.

These outcomes confirm that for regions with limited past weather data archives or served by sparse and irregular monitoring networks, reanalysis data can be successfully exploited as a source of gridded weather data. Nevertheless, the availability of ground-based weather observations always represents an added value that must be used in combination (and not in substitution) with reanalysis data, to improve our knowledge of the past weather in a region.

A preliminary bias correction of the reanalysis products is always advisable if observational data are available in the region. In this study, we used a simple regionally uniform bias correction, applied to all variables except for wind speed, for which we did not find any systematic bias pattern, consistently with previous reports [82]. Indeed, the development of different procedures for improving the bias-correction has been the topic of several research studies [43,44,45,76]. However, we believe that this topic must be addressed in a more general research framework, aimed at evaluating the optimal integration of observational and reanalysis data for regional hydrological studies [76].