Pier Scour Prediction in Non-Uniform Gravel Beds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiments
2.1.1. Experimental Works from Literature Sources
2.1.2. Present Experimental Work
2.2. Predictive Approaches from Literature
2.2.1. Melville and Coleman’s Approach
2.2.2. Guo’s Approach
2.2.3. Kim et al.’s Approach
3. Results and Discussion
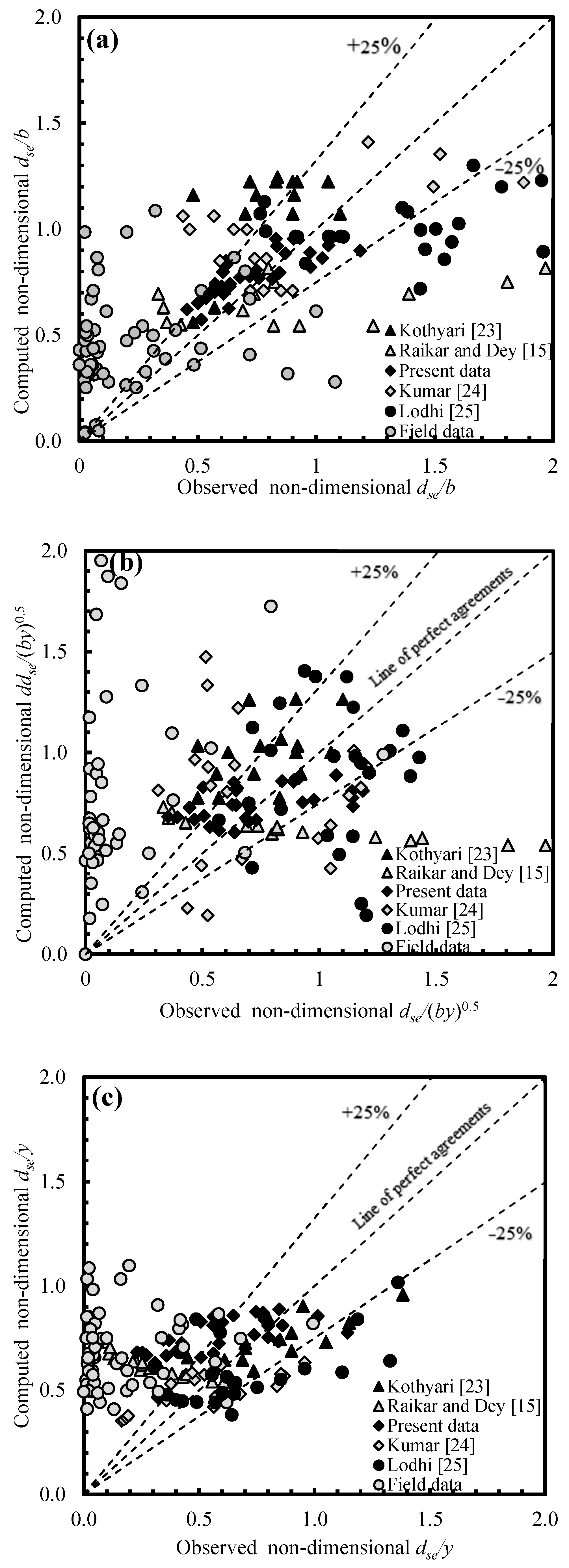
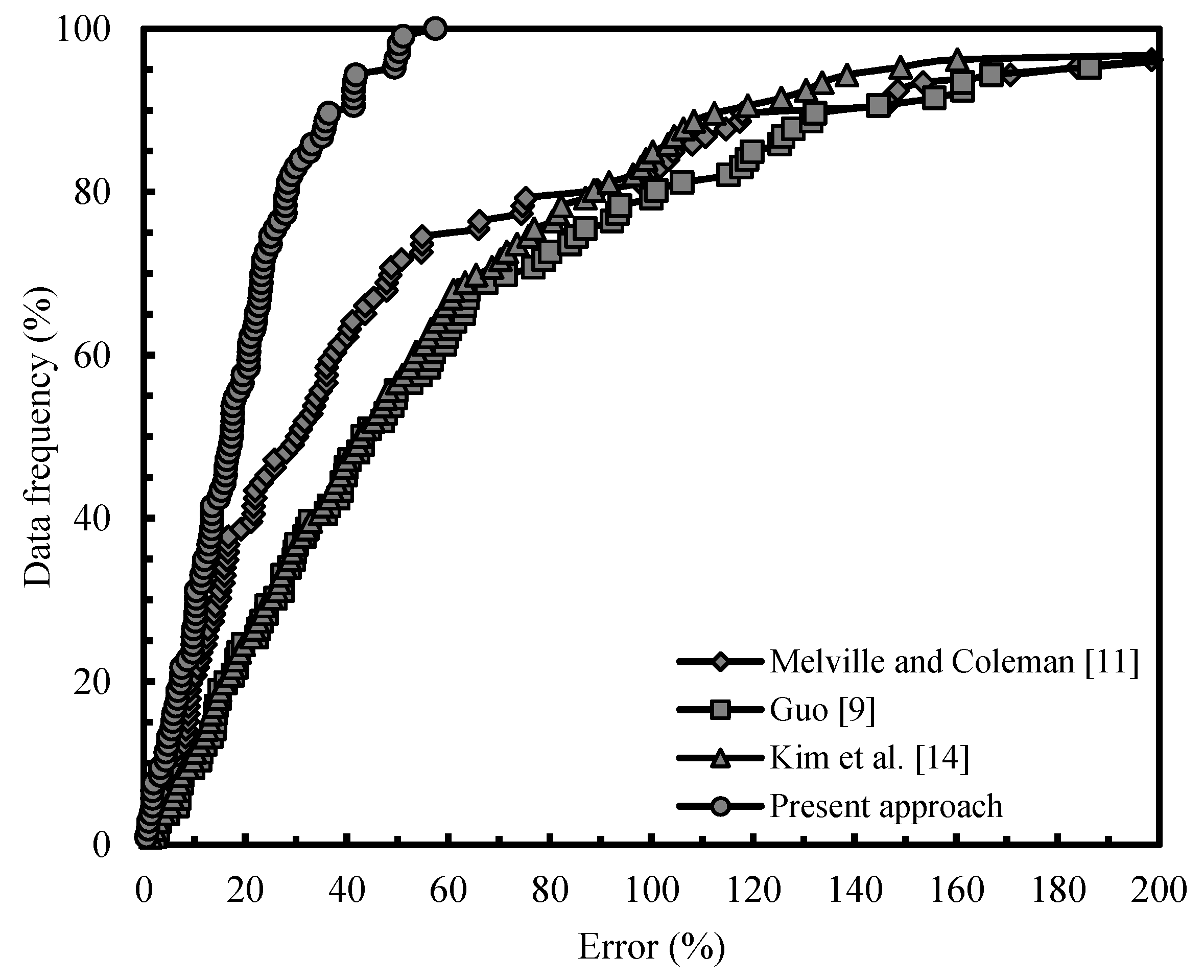
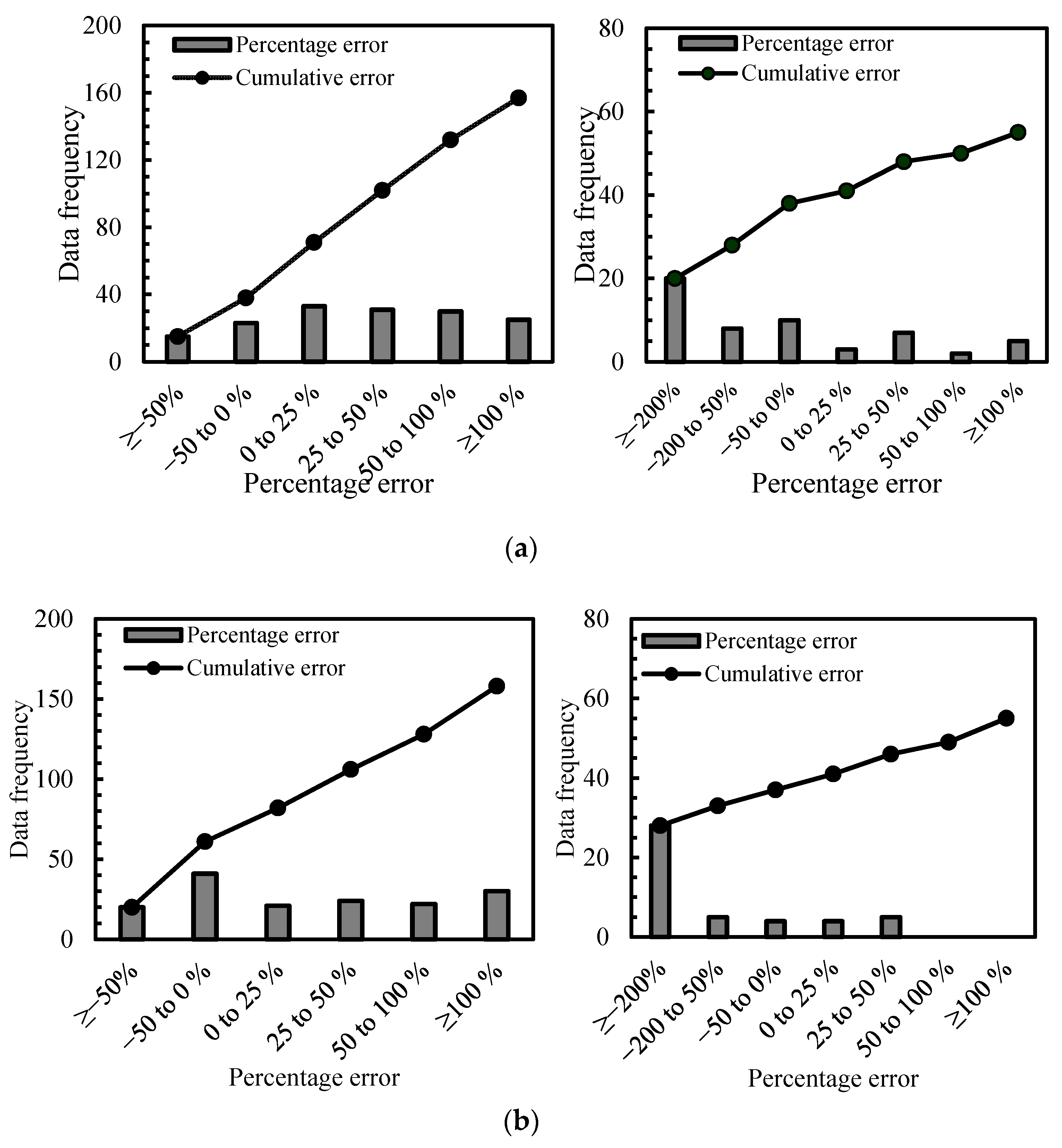
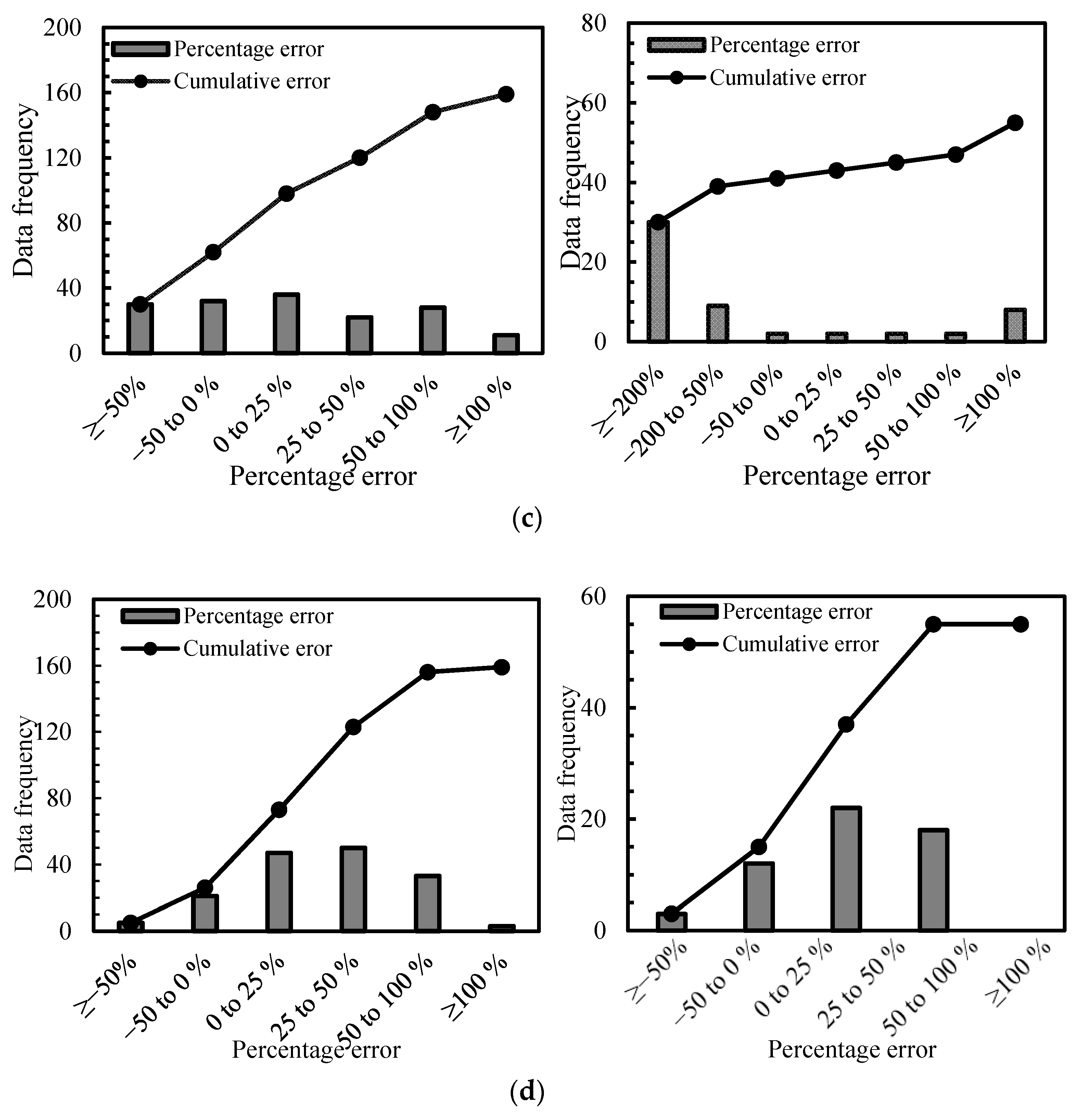
3.1. Comparative Analysis for Previous Approaches
3.2. A New Approach for the Maximum Equilibrium Scour Depth
3.2.1. Flow Depth–Pier Diameter Factor (Kby)
3.2.2. Flow Intensity Factor (KI)
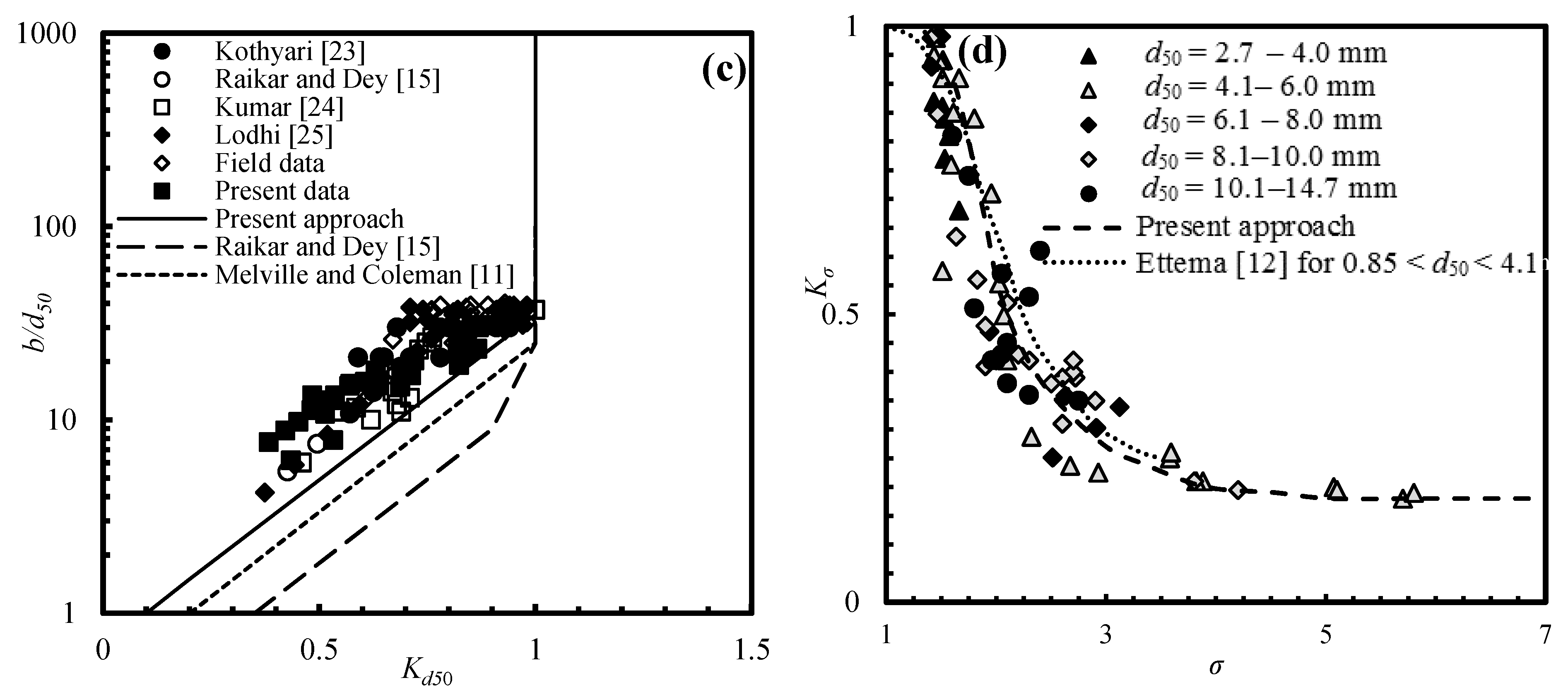
3.2.3. Gravel Size Factor (Kd50)
3.2.4. Effect of Non-Uniformity Factor (Kσ)
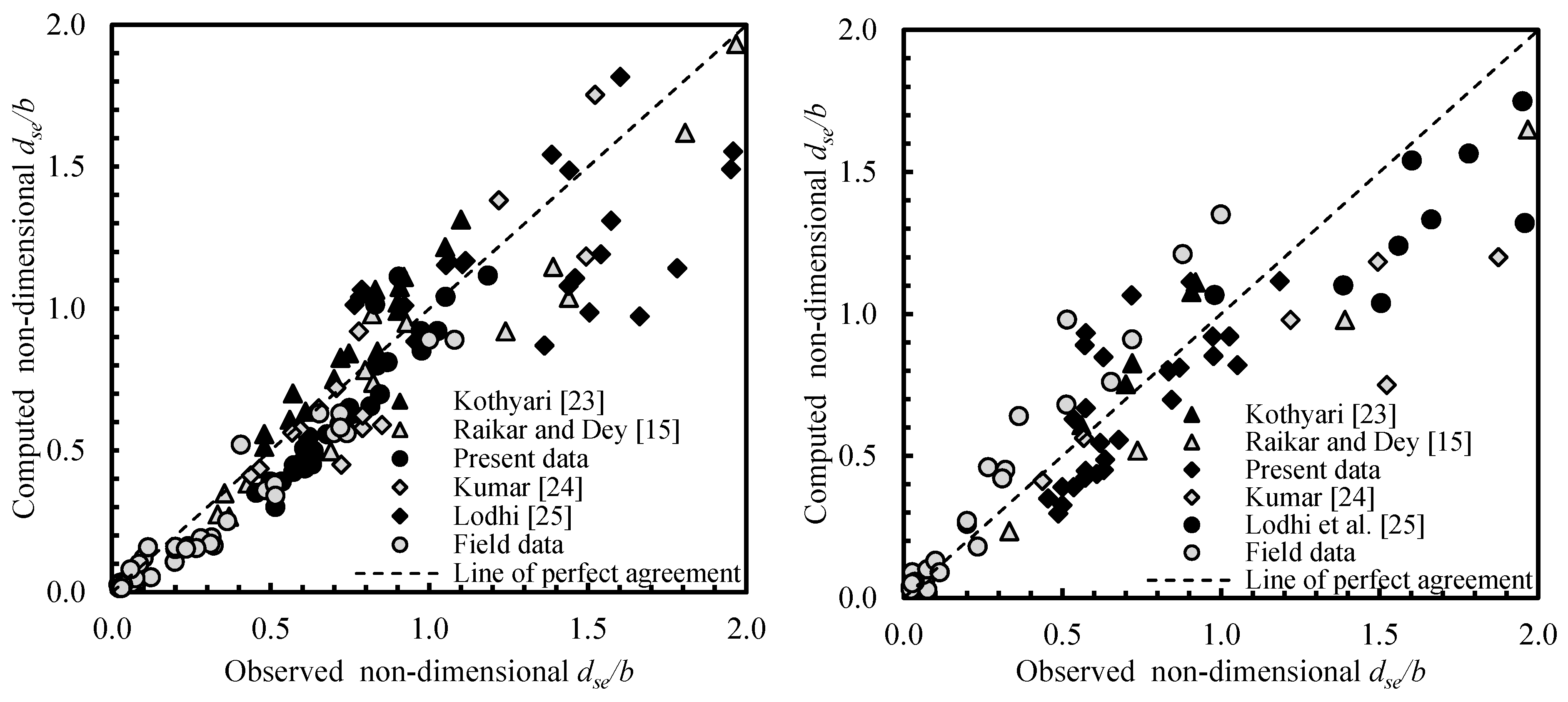
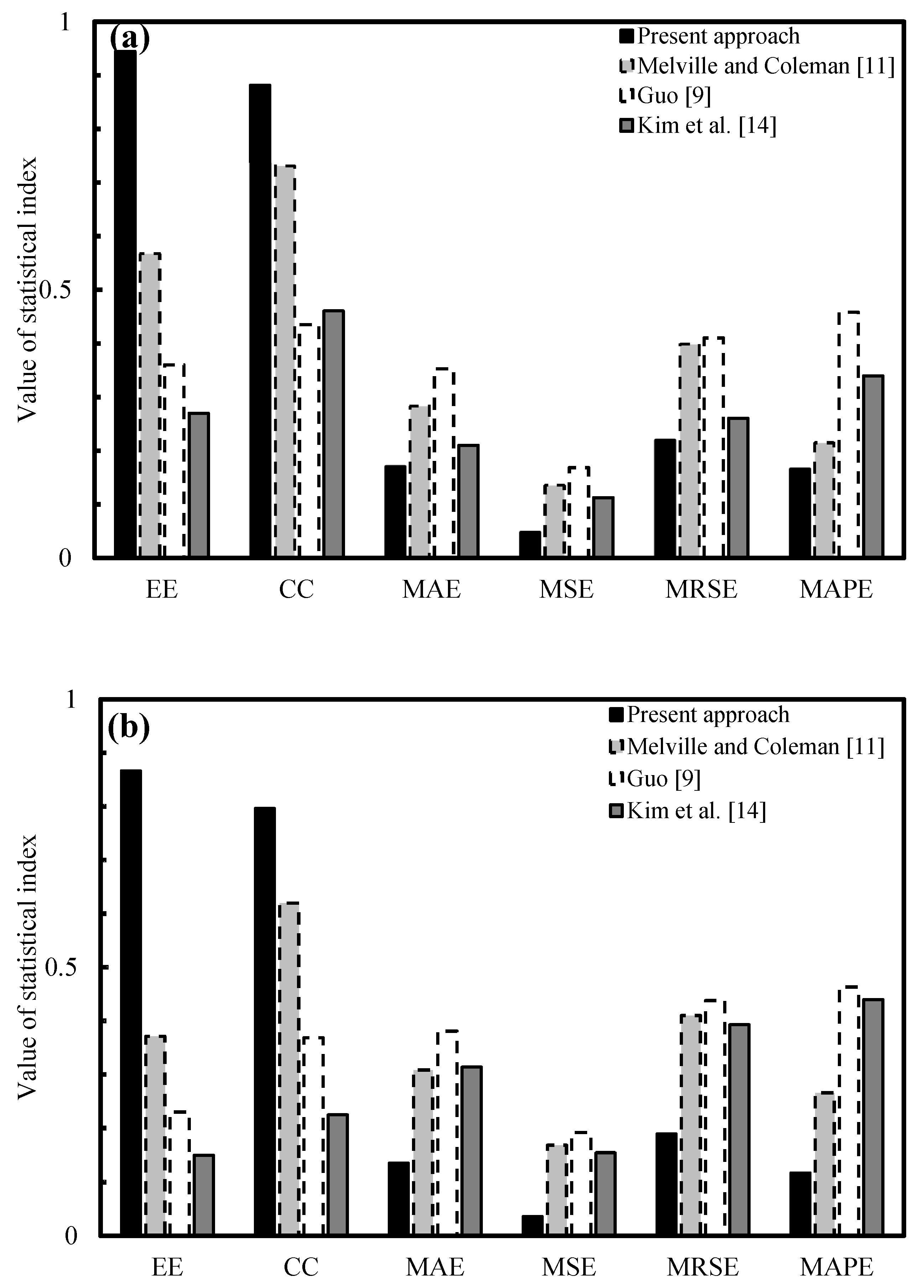
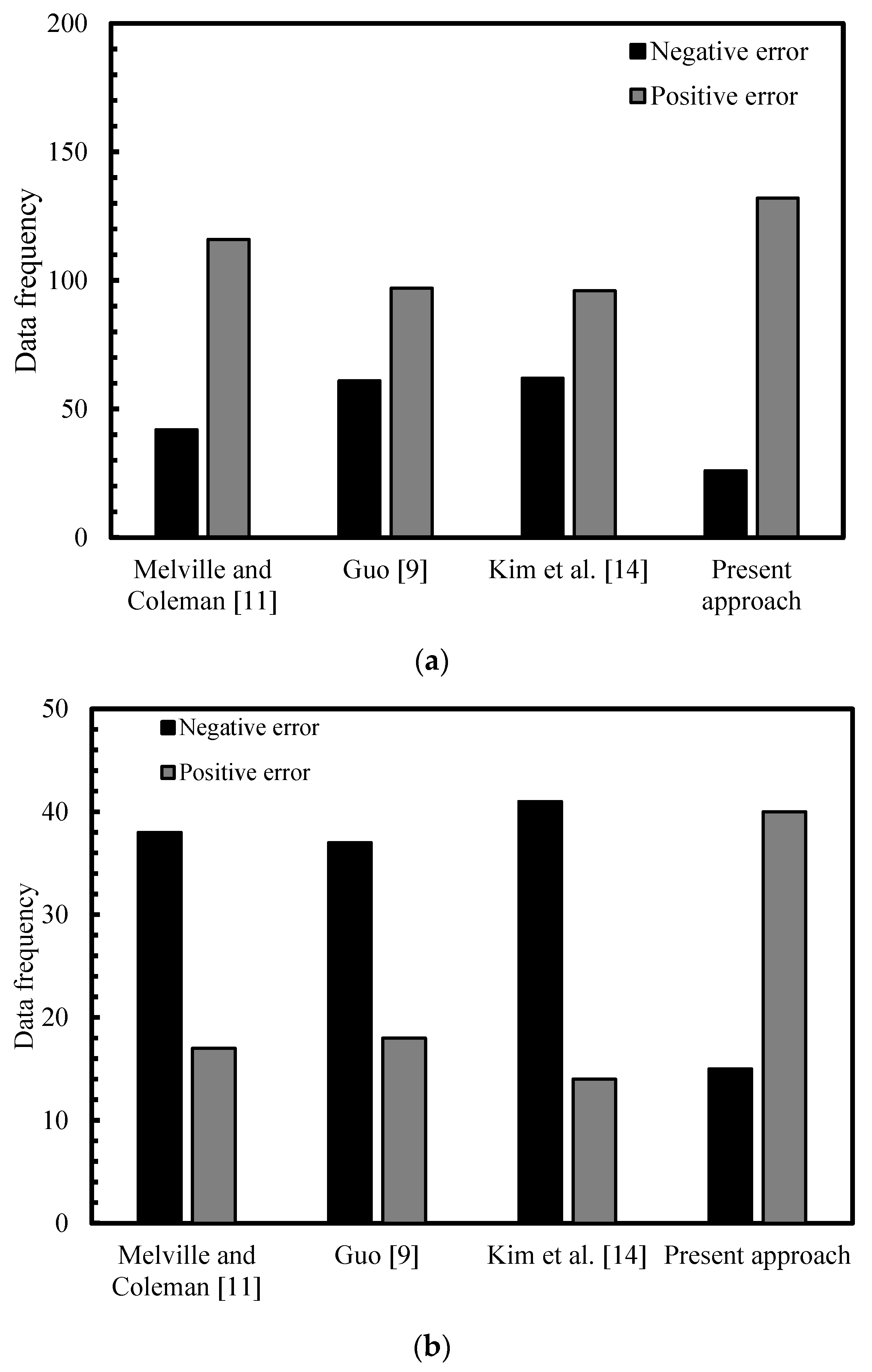
3.3. Error and Statistical Calculations
3.4. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Azamathulla, H.M.; Yusoff, M.A.M.; Hasan, Z.A. Scour below submerged skewed pipeline. J. Hydrol. 2014, 509, 615–620. [Google Scholar] [CrossRef]
- Qi, W.-G.; Gao, F.-P. Physical modeling of local scour development around a large-diameter monopile in combined waves and current. Coast. Eng. 2014, 83, 72–81. [Google Scholar] [CrossRef] [Green Version]
- Barbetta, S.; Camici, S.; Moramarco, T. A reappraisal of bridge piers scour vulnerability: A case study in the Upper Tiber River basin (central Italy). J. Flood Risk Manag. 2017, 10, 283–300. [Google Scholar] [CrossRef]
- Qi, M.; Li, J.; Chen, Q. Comparison of existing equations for local scour at bridge piers: Parameter influence and validation. Nat. Hazards 2016, 82, 2089–2105. [Google Scholar] [CrossRef]
- Qi, M.; Li, J.; Chen, Q. Applicability analysis of pier-scour equations in the field: Error analysis by rationalizing measurement data. J. Hydraul. Eng. ASCE 2018, 144, 04018050. [Google Scholar] [CrossRef]
- Decò, A.; Frangopol, D.M. Life-cycle risk assessment of spatially distributed aging bridges under seismic and traffic hazards. Earthq. Spectra 2013, 29, 127–153. [Google Scholar] [CrossRef]
- Brandimarte, L.; Paron, P.; Di Baldassarre, G. Bridge pier scour: A review of processes, measurements and estimates. Environ. Eng. Manag. J. 2012, 11, 975–989. [Google Scholar] [CrossRef]
- Richardson, E.V.; Davis, S.R. Evaluating Scour at Bridges—Hydraulic Engineering Circular No. 18; Report No. FHWA NHI 01-001; U.S. Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2001.
- Guo, J. Pier scour in clear water for sediment mixtures. J. Hydraul. Res. 2012, 50, 18–27. [Google Scholar] [CrossRef]
- Pu, J.H.; Tait, S.; Guo, Y.; Huang, Y.; Hanmaiahgari, P.R. Dominant features in three-dimensional turbulence structure: Comparison of non-uniform accelerating and decelerating flows. Environ. Fluid Mech. 2018, 18, 395–416. [Google Scholar] [CrossRef] [Green Version]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publications, LLC: Lone Tree, CO, USA, 2000. [Google Scholar]
- Ettema, R. Scour at Bridge Piers. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 1980. [Google Scholar]
- Coleman, S.E. Clearwater local scour at complex piers. J. Hydraul. Eng. ASCE 2005, 131, 330–334. [Google Scholar] [CrossRef]
- Kim, I.; Fard, M.Y.; Chattopadhyay, A. Investigation of a bridge pier scour prediction model for safe design and inspection. J. Bridge Eng. 2015, 20, 04014088. [Google Scholar] [CrossRef]
- Raikar, R.V.; Dey, S. Clear-water scour at bridge piers in fine and medium gravel beds. Can. J. Civ. Eng. 2005, 32, 775–781. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hager, W.H.; Oliveto, G. Generalized approach for clear-water scour at bridge foundation elements. J. Hydraul. Eng. ASCE 2007, 133, 1229–1240. [Google Scholar] [CrossRef]
- Jueyi, S.U.I.; Afzalimehr, H.; Samani, A.K.; Maherani, M. Clear-water scour around semi-elliptical abutments with armored beds. Int. J. Sediment Res. 2010, 25, 233–245. [Google Scholar]
- Abderrezzak, K.E.K.; Moran, A.D.; Mosselman, E.; Bouchard, J.P.; Habersack, H.; Aelbrecht, D. A physical, movable-bed model for non-uniform sediment transport, fluvial erosion and bank failure in rivers. J. Hydroenviron. Res. 2014, 8, 95–114. [Google Scholar] [CrossRef]
- Pournazeri, S.; Li, S.S.; Haghighat, F. A bridge pier scour model with non-uniform sediments. Proc. Inst. Civ. Eng. Water Manag. 2012, 167, 499–511. [Google Scholar] [CrossRef]
- Sharma, A.; Chavan, R.; Kumar, B. Multi-scale statistical characterization of migrating pier scour depth in non-uniform sand bed channel. Int. J. River Basin Manag. 2017, 15, 265–276. [Google Scholar] [CrossRef]
- Pandey, M.; Chen, S.C.; Sharma, P.K.; Ojha, C.S.P.; Kumar, V. Local Scour of Armor Layer Processes around the Circular Pier in Non-Uniform Gravel Bed. Water 2019, 11, 1421. [Google Scholar] [CrossRef] [Green Version]
- Pandey, M.; Valyrakis, M.; Qi, M.; Sharma, A.; Lodhi, A.S. Experimental assessment and prediction of temporal scour depth around a spur dike. Int. J. Sediment Res. 2020, 1–10. [Google Scholar] [CrossRef]
- Kothyari, U.C. Scour around Bridge Piers. Ph.D. Thesis, Indian Institute of Technology Roorkee, Roorkee, India, 1989. [Google Scholar]
- Kumar, A. Scour around Circular Compound Bridge Piers. Ph.D. Thesis, Indian Institute of Technology Roorkee, Roorkee, India, 2007. [Google Scholar]
- Lodhi, A.S. Scour around Spur Dikes and Bridge Piers Founded in Cohesive Sediment Mixtures. Ph.D. Thesis, Indian Institute of Technology Roorkee, Roorkee, India, 2015. [Google Scholar]
- Benedict, S.T.; Caldwell, A.W. A Pier-Scour Database: 2427 Field and Laboratory Measurements of Pier Scour; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2014.
- Pu, J.H.; Lim, S.Y. Efficient numerical computation and experimental study of temporally long equilibrium scour development around abutment. Environ. Fluid Mech. 2014, 14, 69–86. [Google Scholar] [CrossRef] [Green Version]
- Kothyari, U.C.; Ranga Raju, K.G. Scour around spur dikes and bridge abutments. J. Hydraul. Res. 2001, 39, 367–374. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Karna, N. Maximum scour depth around bridge pier in gravel bed streams. Nat. Hazards 2018, 91, 819–836. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng. ASCE 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Graf, W.H.; Altinakar, M.S. Fluvial Hydraulics—Flow and Transport Processes in Channels of Simple Geometry; John Wiley & Sons Ltd.: Chichester, UK, 1998; pp. 10–12. [Google Scholar]
- Ballio, F.; Teruzzi, A.; Radice, A. Constriction effects in clear-water scour at abutments. J. Hydraul. Eng. ASCE 2009, 135, 140–145. [Google Scholar] [CrossRef]
- Melville, B.W.; Sutherland, A.J. Design method for local scour at bridge piers. J. Hydraul. Eng. ASCE 1988, 114, 1210–1226. [Google Scholar] [CrossRef]
- Chiew, Y.M. Local Scour at Bridge Piers. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 1984. [Google Scholar]
- Baker, R.E. Local Scour at Bridge Piers in Non Uniform Sediment. Master’s of Philosophy Thesis, University of Auckland, Auckland, New Zealand, 1986. [Google Scholar]
- Pandey, M.; Lam, W.H.; Cui, Y.; Khan, M.A.; Singh, U.K.; Ahmad, Z. Scour around Spur Dike in Sand–Gravel Mixture Bed. Water 2019, 11, 1417. [Google Scholar] [CrossRef] [Green Version]
- Oliveto, G.; Marino, M.C. Temporal scour evolution at non-uniform bridge piers. Proc. Inst. Civ. Eng. Water Manag. 2017, 170, 254–261. [Google Scholar] [CrossRef]

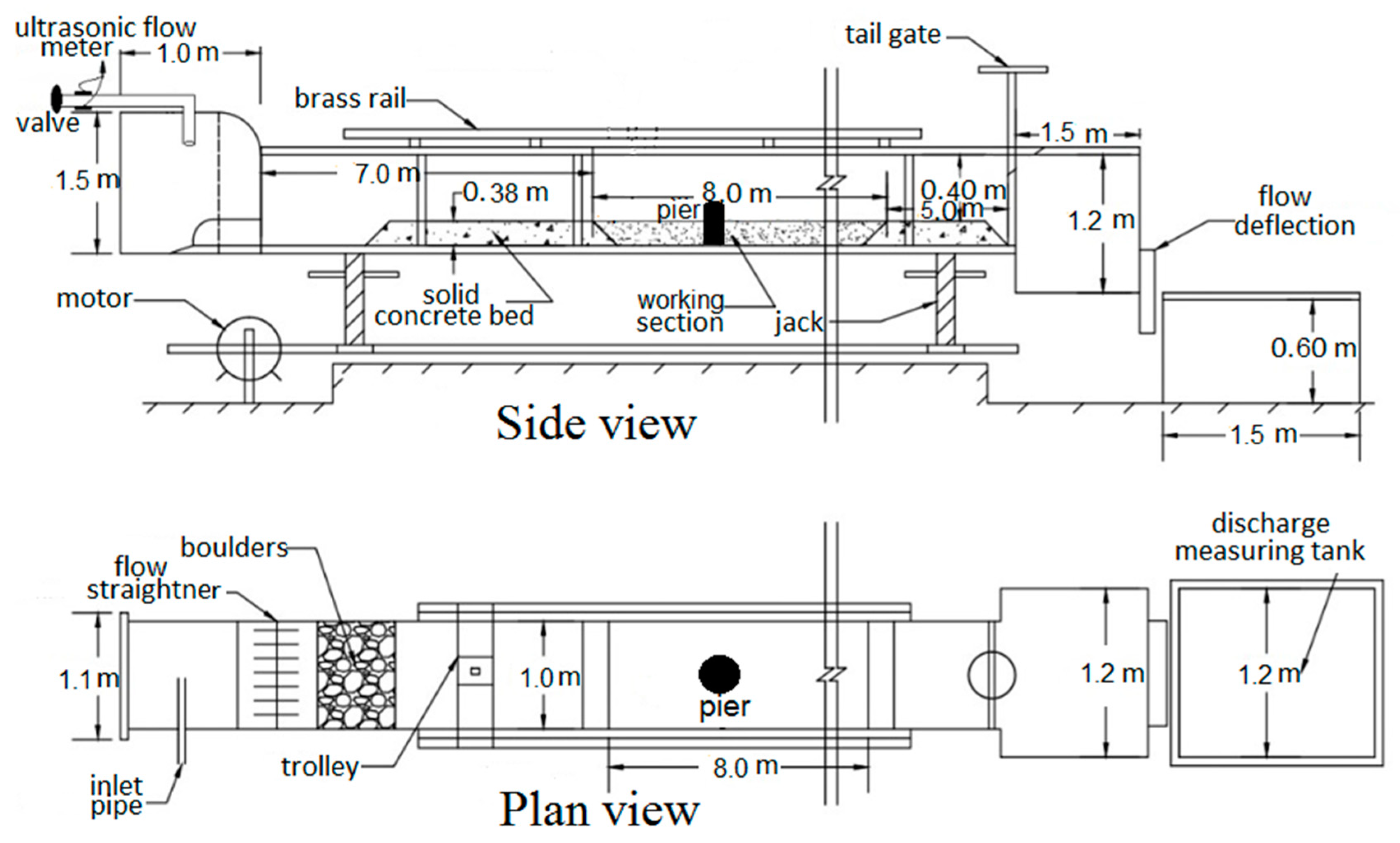

| Literature Source | Data Type | y (m) | U (m/s) | b (m) | d50 (mm) | σ | U/Uc |
|---|---|---|---|---|---|---|---|
| Raikar and Dey [15] | Lab | 0.25 | 0.76–1.10 | 0.03–0.08 | 4.10–14.25 | 1.43–2.90 | 0.66–0.96 |
| Kothyari [23] | Lab | 0.06–0.13 | 0.25–0.31 | 0.05–0.11 | 8.30 | 1.80 | 0.70–0.95 |
| Kumar [24] | Lab | 0.16–0.19 | 0.28–0.44 | 0.05–0.20 | 3.47–4.00 | 1.52–1.67 | 0.54–0.86 |
| Lodhi [25] | Lab | 0.08–0.25 | 0.30–1.10 | 0.08–0.12 | 2.70–5.53 | 1.43–1.51 | 0.60–0.95 |
| Benedict and Caldwell [26] | Field | 0.91–5.58 | 0.95–3.66 | 0.76–1.52 | 2.70–6.10 | 1.50–5.80 | 0.52–0.89 |
| Run | b (m) | d50 (m) | σ | y (m) | U (m/s) | U/Uc | dse (m) | te (h) | t* (h) |
|---|---|---|---|---|---|---|---|---|---|
| R1 | 0.066 | 0.00494 | 1.51 | 0.14 | 0.61 | 0.938 | 0.042 | 10 | 11.24 |
| R2 | 0.066 | 0.00494 | 1.51 | 0.13 | 0.55 | 0.846 | 0.035 | 12 | 10.98 |
| R3 | 0.066 | 0.00494 | 1.51 | 0.10 | 0.46 | 0.708 | 0.026 | 15 | 9.70 |
| R4 | 0.084 | 0.00494 | 1.51 | 0.14 | 0.61 | 0.938 | 0.071 | 11 | 10.28 |
| R5 | 0.084 | 0.00494 | 1.51 | 0.13 | 0.55 | 0.846 | 0.062 | 11 | 9.69 |
| R6 | 0.084 | 0.00494 | 1.51 | 0.10 | 0.46 | 0.708 | 0.032 | 14 | 11.06 |
| R7 | 0.115 | 0.00494 | 1.51 | 0.14 | 0.61 | 0.938 | 0.118 | 10 | 9.73 |
| R8 | 0.115 | 0.00494 | 1.51 | 0.13 | 0.55 | 0.846 | 0.111 | 12 | 11.04 |
| R9 | 0.115 | 0.00494 | 1.51 | 0.10 | 0.46 | 0.708 | 0.082 | 15 | 9.51 |
| R10 | 0.135 | 0.00494 | 1.51 | 0.14 | 0.61 | 0.938 | 0.160 | 11 | 8.66 |
| R11 | 0.135 | 0.00494 | 1.51 | 0.13 | 0.55 | 0.846 | 0.136 | 14 | 8.27 |
| R12 | 0.135 | 0.00494 | 1.51 | 0.10 | 0.46 | 0.708 | 0.089 | 15 | 8.25 |
| R13 | 0.066 | 0.00438 | 1.88 | 0.14 | 0.61 | 0.984 | 0.050 | 11 | 9.79 |
| R14 | 0.066 | 0.00438 | 1.88 | 0.13 | 0.58 | 0.935 | 0.042 | 12 | 10.04 |
| R15 | 0.066 | 0.00438 | 1.88 | 0.10 | 0.53 | 0.855 | 0.031 | 14 | 9.68 |
| R16 | 0.084 | 0.00438 | 1.88 | 0.14 | 0.61 | 0.984 | 0.082 | 10 | 8.86 |
| R17 | 0.084 | 0.00438 | 1.88 | 0.13 | 0.58 | 0.935 | 0.079 | 12 | 8.16 |
| R18 | 0.084 | 0.00438 | 1.88 | 0.10 | 0.53 | 0.855 | 0.062 | 15 | 7.62 |
| R19 | 0.115 | 0.00438 | 1.88 | 0.14 | 0.61 | 0.984 | 0.112 | 11 | 9.93 |
| R20 | 0.115 | 0.00438 | 1.88 | 0.13 | 0.58 | 0.935 | 0.101 | 12 | 9.72 |
| R21 | 0.115 | 0.00438 | 1.88 | 0.10 | 0.53 | 0.855 | 0.068 | 14 | 10.41 |
| R22 | 0.135 | 0.00438 | 1.88 | 0.14 | 0.61 | 0.984 | 0.142 | 14 | 9.64 |
| R23 | 0.135 | 0.00438 | 1.88 | 0.13 | 0.58 | 0.935 | 0.132 | 15 | 9.11 |
| R24 | 0.135 | 0.00438 | 1.88 | 0.10 | 0.53 | 0.855 | 0.078 | 13 | 10.80 |
| R25 | 0.066 | 0.00382 | 1.71 | 0.13 | 0.55 | 0.932 | 0.040 | 12 | 12.18 |
| R26 | 0.066 | 0.00382 | 1.71 | 0.12 | 0.49 | 0.831 | 0.031 | 14 | 12.26 |
| R27 | 0.066 | 0.00382 | 1.71 | 0.11 | 0.45 | 0.763 | 0.015 | 15 | 13.52 |
| R28 | 0.084 | 0.00382 | 1.71 | 0.13 | 0.55 | 0.932 | 0.052 | 12 | 13.44 |
| R29 | 0.084 | 0.00382 | 1.71 | 0.12 | 0.49 | 0.831 | 0.046 | 14 | 12.43 |
| R30 | 0.084 | 0.00382 | 1.71 | 0.11 | 0.45 | 0.763 | 0.029 | 16 | 14.56 |
| R31 | 0.115 | 0.00382 | 1.71 | 0.13 | 0.55 | 0.932 | 0.096 | 13 | 12.29 |
| R32 | 0.115 | 0.00382 | 1.71 | 0.12 | 0.49 | 0.831 | 0.060 | 15 | 14.75 |
| R33 | 0.115 | 0.00382 | 1.71 | 0.11 | 0.45 | 0.763 | 0.023 | 15 | 18.16 |
| R34 | 0.135 | 0.00382 | 1.71 | 0.13 | 0.55 | 0.932 | 0.112 | 12 | 13.11 |
| R35 | 0.135 | 0.00382 | 1.71 | 0.12 | 0.49 | 0.831 | 0.081 | 14 | 14.19 |
| R36 | 0.135 | 0.00382 | 1.71 | 0.11 | 0.45 | 0.763 | 0.049 | 15 | 17.65 |
| R37 | 0.066 | 0.00326 | 1.59 | 0.13 | 0.53 | 0.946 | 0.041 | 12 | 13.97 |
| R38 | 0.066 | 0.00326 | 1.59 | 0.12 | 0.48 | 0.857 | 0.036 | 14 | 13.25 |
| R39 | 0.066 | 0.00326 | 1.59 | 0.105 | 0.44 | 0.786 | 0.025 | 14 | 14.10 |
| R40 | 0.084 | 0.00326 | 1.59 | 0.13 | 0.54 | 0.964 | 0.073 | 12 | 12.73 |
| R41 | 0.084 | 0.00326 | 1.59 | 0.12 | 0.48 | 0.857 | 0.063 | 15 | 11.88 |
| R42 | 0.084 | 0.00326 | 1.59 | 0.105 | 0.44 | 0.786 | 0.035 | 14 | 15.01 |
| R43 | 0.115 | 0.00326 | 1.59 | 0.13 | 0.54 | 0.964 | 0.104 | 15 | 14.01 |
| R44 | 0.135 | 0.00326 | 1.59 | 0.13 | 0.54 | 0.964 | 0.122 | 15 | 14.90 |
| R45 | 0.135 | 0.01070 | 1.57 | 0.125 | 0.79 | 0.898 | 0.081 | 11 | 9.37 |
| R46 | 0.135 | 0.01070 | 1.57 | 0.125 | 0.76 | 0.864 | 0.072 | 11 | 9.80 |
| R47 | 0.135 | 0.01070 | 1.57 | 0.125 | 0.74 | 0.841 | 0.064 | 12 | 10.38 |
| R48 | 0.115 | 0.01070 | 1.57 | 0.125 | 0.79 | 0.898 | 0.070 | 10 | 8.67 |
| R49 | 0.115 | 0.01070 | 1.57 | 0.125 | 0.76 | 0.864 | 0.063 | 12 | 8.99 |
| R50 | 0.115 | 0.01070 | 1.57 | 0.125 | 0.74 | 0.841 | 0.051 | 12 | 10.12 |
| R51 | 0.084 | 0.01070 | 1.57 | 0.125 | 0.79 | 0.898 | 0.053 | 11 | 7.40 |
| R52 | 0.084 | 0.01070 | 1.57 | 0.125 | 0.76 | 0.864 | 0.045 | 10 | 7.97 |
| R53 | 0.084 | 0.01070 | 1.57 | 0.125 | 0.74 | 0.841 | 0.040 | 12 | 8.39 |
| R54 | 0.066 | 0.01070 | 1.57 | 0.125 | 0.79 | 0.898 | 0.034 | 10 | 7.60 |
| R55 | 0.066 | 0.01070 | 1.57 | 0.125 | 0.76 | 0.864 | 0.031 | 11 | 7.75 |
| R56 | 0.066 | 0.01070 | 1.57 | 0.125 | 0.74 | 0.841 | 0.022 | 11 | 9.13 |
| R57 | 0.115 | 0.00910 | 1.66 | 0.13 | 0.76 | 0.974 | 0.073 | 13 | 8.52 |
| R58 | 0.115 | 0.00910 | 1.66 | 0.13 | 0.74 | 0.949 | 0.069 | 12 | 8.63 |
| R59 | 0.115 | 0.00910 | 1.66 | 0.13 | 0.72 | 0.923 | 0.065 | 14 | 8.75 |
| R60 | 0.135 | 0.00910 | 1.66 | 0.13 | 0.74 | 0.949 | 0.110 | 13 | 6.88 |
| R61 | 0.135 | 0.00910 | 1.66 | 0.13 | 0.74 | 0.949 | 0.091 | 12 | 8.31 |
| R62 | 0.135 | 0.00860 | 1.63 | 0.13 | 0.74 | 0.974 | 0.097 | 12 | 8.71 |
| R63 | 0.135 | 0.00860 | 1.63 | 0.13 | 0.72 | 0.947 | 0.085 | 12 | 9.43 |
| R64 | 0.135 | 0.00860 | 1.63 | 0.13 | 0.70 | 0.921 | 0.077 | 13 | 9.88 |
| R65 | 0.115 | 0.00860 | 1.63 | 0.13 | 0.74 | 0.974 | 0.066 | 12 | 9.80 |
| R66 | 0.115 | 0.00860 | 1.63 | 0.13 | 0.70 | 0.921 | 0.056 | 13 | 10.38 |
| R67 | 0.115 | 0.00860 | 1.63 | 0.13 | 0.70 | 0.921 | 0.066 | 12 | 9.43 |
| R68 | 0.084 | 0.00860 | 1.63 | 0.13 | 0.74 | 0.974 | 0.045 | 10 | 8.95 |
| R69 | 0.084 | 0.00860 | 1.63 | 0.13 | 0.72 | 0.947 | 0.042 | 12 | 9.11 |
| R70 | 0.084 | 0.00860 | 1.63 | 0.13 | 0.70 | 0.921 | 0.039 | 13 | 9.30 |
| R71 | 0.066 | 0.00860 | 1.63 | 0.13 | 0.74 | 0.974 | 0.030 | 11 | 8.82 |
| R72 | 0.066 | 0.00860 | 1.63 | 0.13 | 0.72 | 0.947 | 0.025 | 12 | 9.52 |
| R73 | 0.066 | 0.00860 | 1.63 | 0.13 | 0.70 | 0.921 | 0.018 | 12 | 10.92 |
| R74 | 0.135 | 0.00750 | 1.56 | 0.13 | 0.73 | 0.973 | 0.101 | 10 | 9.87 |
| R75 | 0.135 | 0.00750 | 1.56 | 0.13 | 0.71 | 0.947 | 0.092 | 12 | 10.31 |
| R76 | 0.135 | 0.00750 | 1.56 | 0.13 | 0.69 | 0.920 | 0.084 | 14 | 10.72 |
| R77 | 0.115 | 0.00750 | 1.56 | 0.13 | 0.73 | 0.973 | 0.078 | 11 | 10.03 |
| R78 | 0.115 | 0.00750 | 1.56 | 0.13 | 0.71 | 0.947 | 0.069 | 12 | 10.65 |
| R79 | 0.115 | 0.00750 | 1.56 | 0.13 | 0.69 | 0.920 | 0.063 | 12 | 11.02 |
| R80 | 0.084 | 0.00750 | 1.56 | 0.13 | 0.73 | 0.973 | 0.048 | 12 | 9.85 |
| R81 | 0.084 | 0.00750 | 1.56 | 0.13 | 0.71 | 0.947 | 0.045 | 11 | 10.00 |
| R82 | 0.084 | 0.00750 | 1.56 | 0.13 | 0.69 | 0.920 | 0.044 | 11 | 9.87 |
| R83 | 0.066 | 0.00750 | 1.56 | 0.13 | 0.73 | 0.973 | 0.033 | 11 | 9.52 |
| R84 | 0.066 | 0.00750 | 1.56 | 0.13 | 0.71 | 0.947 | 0.037 | 12 | 8.70 |
| R85 | 0.066 | 0.00750 | 1.56 | 0.13 | 0.69 | 0.920 | 0.031 | 12 | 9.41 |
| Percentage Change | X | ΔX | ΔZ | A.S. | R.S. |
|---|---|---|---|---|---|
| 10% increment | Kσ | 0.034 | 0.057 | 1.66 | 2.67 |
| Kby | 0.089 | 0.046 | 0.51 | 2.17 | |
| Kd50 | 0.084 | 0.032 | 0.38 | 1.51 | |
| KI | 0.117 | 0.015 | 0.13 | 0.69 | |
| 10% reduction | Kσ | 0.034 | −0.041 | −1.18 | −1.92 |
| Kby | 0.089 | −0.037 | −0.42 | −1.78 | |
| Kd50 | 0.084 | −0.025 | −0.31 | −1.21 | |
| KI | 0.117 | −0.022 | −0.19 | −1.06 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, M.; Oliveto, G.; Pu, J.H.; Sharma, P.K.; Ojha, C.S.P. Pier Scour Prediction in Non-Uniform Gravel Beds. Water 2020, 12, 1696. https://doi.org/10.3390/w12061696
Pandey M, Oliveto G, Pu JH, Sharma PK, Ojha CSP. Pier Scour Prediction in Non-Uniform Gravel Beds. Water. 2020; 12(6):1696. https://doi.org/10.3390/w12061696
Chicago/Turabian StylePandey, Manish, Giuseppe Oliveto, Jaan H. Pu, P. K. Sharma, and C. S. P. Ojha. 2020. "Pier Scour Prediction in Non-Uniform Gravel Beds" Water 12, no. 6: 1696. https://doi.org/10.3390/w12061696
APA StylePandey, M., Oliveto, G., Pu, J. H., Sharma, P. K., & Ojha, C. S. P. (2020). Pier Scour Prediction in Non-Uniform Gravel Beds. Water, 12(6), 1696. https://doi.org/10.3390/w12061696








