Groundwater Parameter Inversion Using Topographic Constraints and a Zonal Adaptive Multiscale Procedure: A Case Study of an Alluvial Aquifer
Abstract
:1. Introduction
2. Groundwater Model and Calibration Procedure
2.1. The Groundwater Saturated Flow Model
2.2. The Groundwater Recharge and Vadose Zone Model
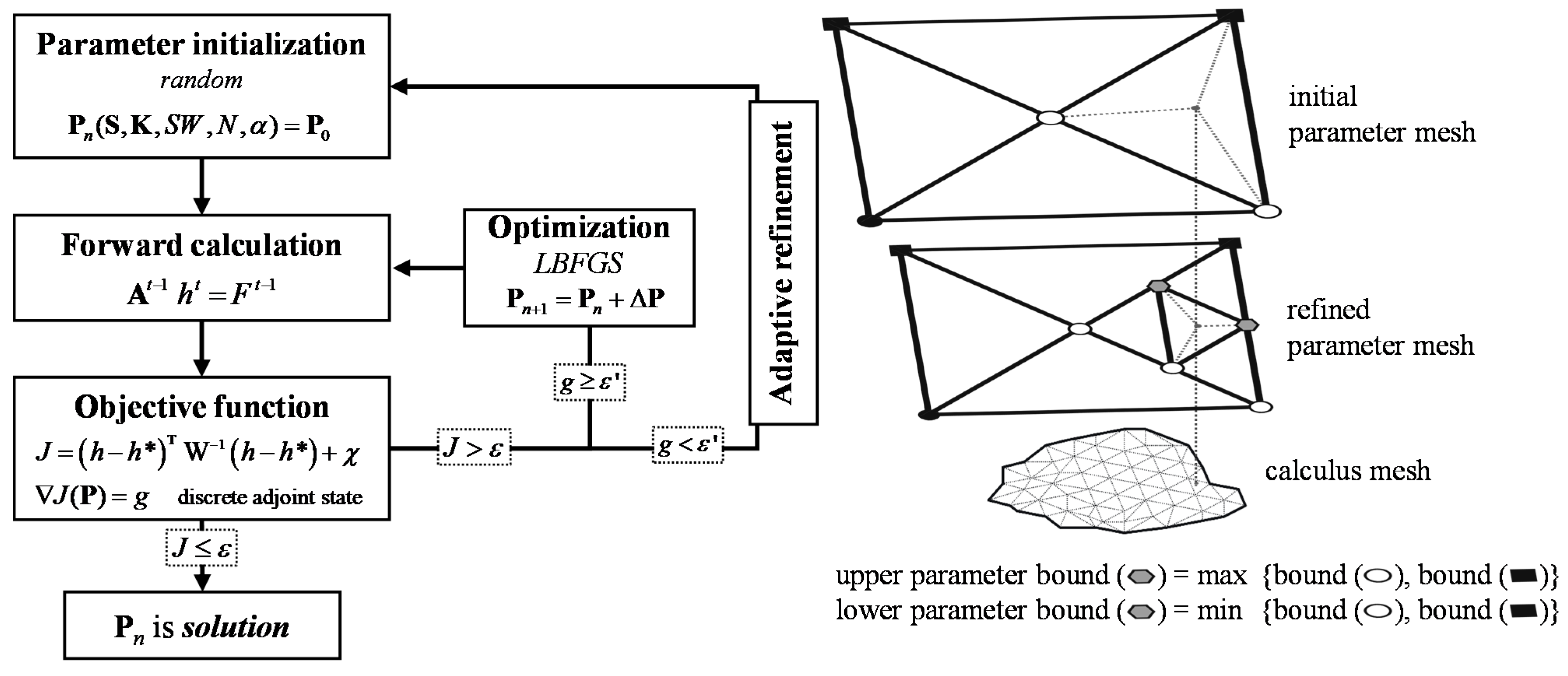
2.3. Model Calibration by Solving an Inverse Problem
2.4. Zoned Adaptive Multiscale Triangulation
3. Application to an Alluvial Aquifer
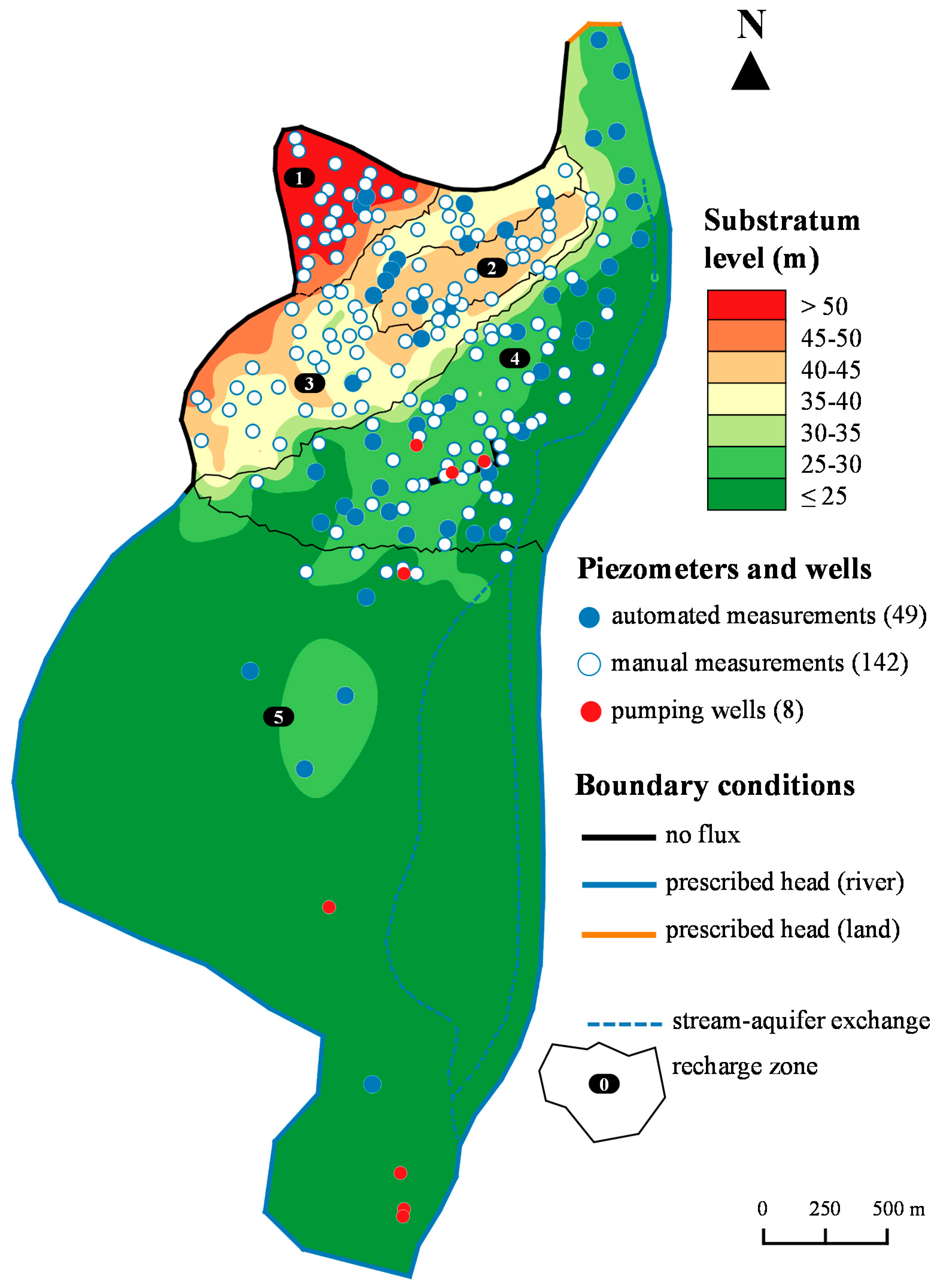
3.1. Description of the Study Area
3.2. Model Conceptualization and Required Parameters
4. Results and Discussion
4.1. Topographic Constraint (Criterion χ) Contribution
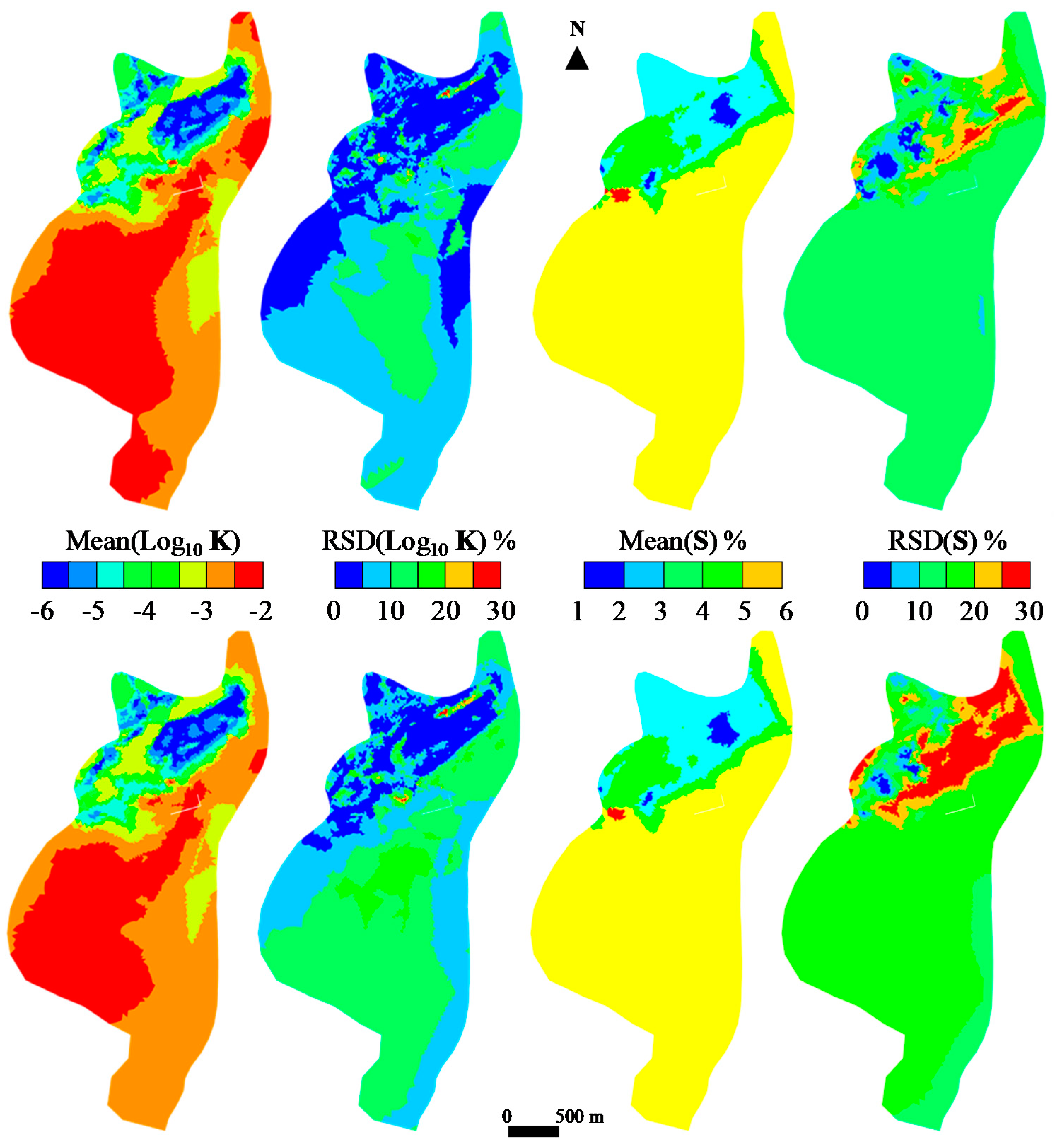
4.2. Choice of the Adjusting Criterion Threshold and Parameter Reliability
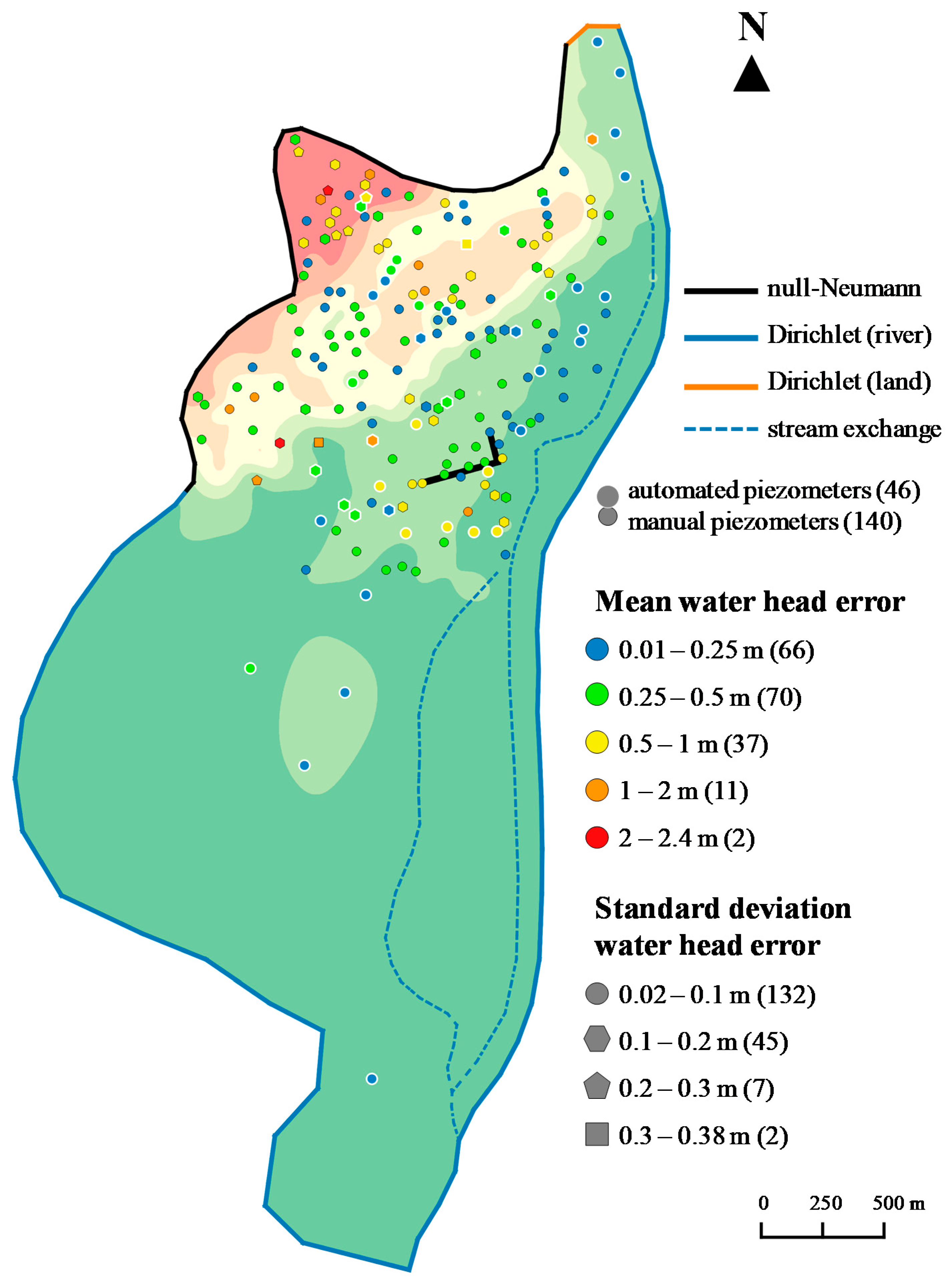
4.3. Piezometry and Water Balance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Carrera, J.; Neuman, S.P. Estimation of aquifer parameters under transient and steady state conditions: 1. maximum likelihood method incorporating prior information. Water Resour. Res. 1986, 22, 199–210. [Google Scholar] [CrossRef]
- Poeter, E.P.; Hill, M.C. Inverse models: A necessary next step in groundwater modeling. Ground Water 1997, 35, 250–260. [Google Scholar] [CrossRef]
- Yakowitz, S.; Duckstein, L. Instability in aquifer identification: Theory and case studies. Water Resour. Res. 1980, 16, 1045–1064. [Google Scholar] [CrossRef]
- McLaughlin, D.; Townley, L.R. A reassessment of the groundwater inverse problem. Water Resour. Res. 1996, 32, 1131–1161. [Google Scholar] [CrossRef] [Green Version]
- Hadamar, J. Le Problème de Cauchy et les Équations aux Dérivées Partielles Linéaires Hyperboliques; Herman: Paris, France, 1932. [Google Scholar]
- Sun, N.-Z.; Yeh, W.W.-G. Identification of parameter structure in groundwater inverse problem. Water Resour. Res. 1985, 21, 869–883. [Google Scholar] [CrossRef]
- Carrera, J.; Alcolea, A.; Medina, A.; Hidalgo, J.; Slooten, L.J. Inverse problem in hydrogeology. Hydrogeol. J. 2005, 13, 206–222. [Google Scholar] [CrossRef]
- Coats, K.H.; Dempsey, J.R.; Henderson, J.H. A new technique for determining reservoir description from field performance data. Soc. Pet. Eng. J. 1970, 10, 66–74. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Yeh, W.W.-G. Parameter identification in an inhomogeneous medium with the finite-element method. Soc. Pet. Eng. J. 1976, 16, 217–226. [Google Scholar] [CrossRef]
- Garay, H.L.; Haimes, Y.Y.; Das, P. Distributed parameter identification of groundwater systems by nonlinear estimation. J. Hydrol. 1976, 30, 47–61. [Google Scholar] [CrossRef]
- Certes, C.; de Marsily, G. Application of the pilot point method to the identification of aquifer transmissivities. Adv. Water Resour. 1991, 14, 284–300. [Google Scholar] [CrossRef]
- Tsai, F.T.-C.; Yeh, W.W.-G. Characterization and identification of aquifer heterogeneity with generalized parametrization and Bayesian estimation. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Hendricks Franssen, H.J.; Alcolea, A.; Riva, M.; Bakr, M.; van der Wiel, N.; Stauffer, F.; Guadagnini, A. A comparison of seven methods for the inverse modelling of groundwater flow: Application to the characterisation of well watchments. Adv. Water Resour. 2009, 32, 851–872. [Google Scholar] [CrossRef]
- Yeh, W.W.-G.; Yoon, Y.S. Aquifer parameter identification with optimum dimension in parametrization. Water Resour. Res. 1981, 17, 664–672. [Google Scholar] [CrossRef]
- Eppstein, M.J.; Dougherty, D.E. Simultaneous estimation of transmissivity values and zonation. Water Resour. Res. 1996, 32, 3321–3336. [Google Scholar] [CrossRef] [Green Version]
- Sun, N.-Z.; Yang, S.-L.; Yeh, W.W.-G. A proposed stepwise regression method for model structure identification. Water Resour. Res. 1998, 34, 2561–2572. [Google Scholar] [CrossRef]
- Lu, Z.; Robinson, B.A. Parameter identification using the level set method. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Lien, M.; Berre, I.; Mannseth, T. Combined adaptive multiscale and level-set parameter estimation. Multiscale Model. Simul. 2006, 4, 1349–1372. [Google Scholar] [CrossRef]
- Cardiff, M.; Kitanidis, P.K. Bayesian inversion for facies detection: An extensible level set framework. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Majdalani, S.; Ackerer, P. Identification of groundwater parameters using an adaptive multiscale method. Ground Water 2011, 49, 548–559. [Google Scholar] [CrossRef]
- Ackerer, P.; Trottier, N.; Delay, D. Flow in double-porosity aquifers: Parameter estimation using an adaptive multiscale method. Adv. Water Resour. 2014, 73, 108–122. [Google Scholar] [CrossRef]
- Hassane, M.M.; Ackerer, P. Groundwater flow parameter estimation using refinement and coarsening indicators for adaptive downscaling parameterization. Adv. Water Resour. 2017, 100, 139–152. [Google Scholar] [CrossRef]
- McDonald, M.G.; Harbaugh, A.W. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model; USGS: Washington, DC, USA, 1988. [Google Scholar]
- Crouzeix, M.; Raviart, P.-A. Conforming and nonconforming finite element methods for solving the stationary Stokes equations. Revue Française d’Automatique, Informatique, Recherche Opérationnelle. Mathématique 1973, 7, 33–75. [Google Scholar] [CrossRef]
- Simmers, I. Estimation of Natural Groundwater Recharge; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Richards, L. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Besbes, M.; De Marsily, G. From infiltration to recharge: Use of a parametric transfer function. J. Hydrol. 1984, 74, 271–293. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Neuman, S.P. Generalized scaling of permeabilities: Validation and effect of support scale. Geophys. Res. Lett. 1994, 21, 349–352. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Vila, X.; Carrera, J.; Girardi, J.P. Scale effects in transmissivity. J. Hydrol. 1996, 183, 1–22. [Google Scholar] [CrossRef]
- Kitanidis, P.K.; Lane, R.W. Maximum likelihood parameter estimation of hydrologic spatial processes by the Gauss-Newton method. J. Hydrol. 1985, 79, 53–71. [Google Scholar] [CrossRef]
- Carter, R.D.; Jemp, L.F.J.; Pierce, A.C.; Williams, D.L. Performance matching with constraints. Soc. Pet. Eng. J. 1974, 14, 187–196. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Townley, L.R.; Wilson, J.L. Computationally efficient algorithms for parameter estimation and uncertainty propagation in numerical models of groundwater flow. Water Resour. Res. 1985, 21, 1851–1860. [Google Scholar] [CrossRef]
- Pebesma, E.J.; Heuvelink, G.B.M. Latin Hypercube Sampling of Gaussian Random Fields. Technometrics 1999, 41, 303–312. [Google Scholar] [CrossRef]
- Rajabi, M.M.; Ataie-Ashtiani, B.; Janssen, H. Efficiency enhancement of optimized Latin hypercube sampling strategies: Application to Monte Carlo uncertainty analysis and meta-modeling. Adv. Water Resour. 2015, 76, 127–139. [Google Scholar] [CrossRef] [Green Version]
- Turc, L. Evaluation des besoins en eau d’irrigation, évapotranspiration potentielle. Ann. Agron. 1961, 12, 13–49. [Google Scholar]




| Temperature * | [°C] | 13.7 |
|---|---|---|
| Relative humidity * | [%] | 66.5 |
| Solar radiation * | [J·m−2·d−1] | 1333.5 |
| Rainfall | [mm·y−1] | 764.5 |
| Potential evapotranspiration ** | [mm·y−1] | 987 |
| River’s characteristic | Units | Western River * | Eastern River ** |
|---|---|---|---|
| Annual flow rate | [m3·s−1] | 17.5 | 1 540 |
| Monthly low flow (Summer) | [m3·s−1] | 2.4 | 1 050 |
| Monthly high flow (Fall–Winter) | [m3·s−1] | 46 | 1 850 |
| Marling (high flow–low flow level) | [cm] | 101 | 15 |
| Input | Units | Source | Scale |
|---|---|---|---|
| Rainfall/Evapotranspiration | [L3·T−1] | measured | element |
| Soil elevation | [L] | measured 1 | node |
| Imperviousness/Runoff ratio | [%] | measured 1 | element |
| Substratum level | [L] | interpolated 2 | node |
| Water head data | [L] | measured | local |
| Pumping rates | [L3·T−1] | measured | local |
| Initial water head conditions | [L] | calculated | edges |
| (No) flux boundary conditions | [L3·T−1] | estimated | edges |
| River/stream levels | [L] | measured 1 | edges |
| Recharge zonation/parameter ranges | estimated | according to geology, vadose depth, and piezometric signals | |
| ZAMT initial mesh/parameter ranges | estimated | according to geology and piezometric signals | |
| Zone | Soil Storage Capacity SWmax (cm) | Hydraulic Conductivity K (m·s−1) | Specific Yield S (−) |
|---|---|---|---|
| 1 | [1–2] | [10−6–10−4] | [0.01–0.03] |
| 2 | [1–2] | [10−6–10−5] | [0.01–0.03] |
| 3 | [1–2] | [10−5–10−3] | [0.01–0.04] |
| 4 | [3–5] | [5.10−4–10−2] | [0.03–0.06] |
| 5 | [8–15] | [5.10−4–10−2] | [0.03–0.06] |
| Sets of 150 Inversions | Mean Number of Time Steps Where Violation Occurs (over 175) | Mean Number of Edges Impacted by Time Step (over 19,544) | Average Magnitude of the Violation (in m) | Mean Final Number of Parameter Vertices |
|---|---|---|---|---|
| With χ | 174 | 158 | 0.28 | 1578 |
| Without χ | 175 | 871 | 1.83 | 871 |
| Threshold | 40 cm | 50 cm | ||
|---|---|---|---|---|
| Mean (cm) | RSD | Mean (cm) | RSD | |
| Zone 1 | 2.0 | 1.4% | 1.9 | 7.6% |
| Zone 2 | 1.0 | 1.5% | 1.1 | 15.3% |
| Zone 3 | 1.0 | 1.1% | 1.0 | 13.3% |
| Zone 4 | 3.2 | 7.8% | 3.4 | 12.0% |
| Zone 5 | 12.8 | 7.7% | 12.5 | 11.7% |
| Component | Min | Max | Mean | Total | Comments |
|---|---|---|---|---|---|
| Aquifer storage | 376 | 483 | 406 | - | |
| Recharge | 0.0 | 5.9 | 0.5 | 80 | 20% of the total rainfall |
| In/out at boundaries | −0.7 | 5.3 | 1.6 | 318 | 81% of the total aquifer input |
| Stream exchanges | −0.24 | −0.08 | −0.13 | −36 | |
| Pumping | constant | −1.3 | −370 | ||
| Water balance error | 0 | 0.2 | 0.02 | 2.1 | 0.6% of the average stored water |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rambourg, D.; Ackerer, P.; Bildstein, O. Groundwater Parameter Inversion Using Topographic Constraints and a Zonal Adaptive Multiscale Procedure: A Case Study of an Alluvial Aquifer. Water 2020, 12, 1899. https://doi.org/10.3390/w12071899
Rambourg D, Ackerer P, Bildstein O. Groundwater Parameter Inversion Using Topographic Constraints and a Zonal Adaptive Multiscale Procedure: A Case Study of an Alluvial Aquifer. Water. 2020; 12(7):1899. https://doi.org/10.3390/w12071899
Chicago/Turabian StyleRambourg, Dimitri, Philippe Ackerer, and Olivier Bildstein. 2020. "Groundwater Parameter Inversion Using Topographic Constraints and a Zonal Adaptive Multiscale Procedure: A Case Study of an Alluvial Aquifer" Water 12, no. 7: 1899. https://doi.org/10.3390/w12071899
APA StyleRambourg, D., Ackerer, P., & Bildstein, O. (2020). Groundwater Parameter Inversion Using Topographic Constraints and a Zonal Adaptive Multiscale Procedure: A Case Study of an Alluvial Aquifer. Water, 12(7), 1899. https://doi.org/10.3390/w12071899






