Probabilistic Prediction of Significant Wave Height Using Dynamic Bayesian Network and Information Flow
Abstract
1. Introduction
2. Theoretical Explanation
2.1. Dynamic Bayesian Network
- denotes the initial network, that is the CBN in each time slice. It contains the network structure and CPTs of nodes at the same time;
- denotes the transition network, which contains the structural arcs and the transition probability distribution of nodes in contiguous time slices.
2.2. Information Flow
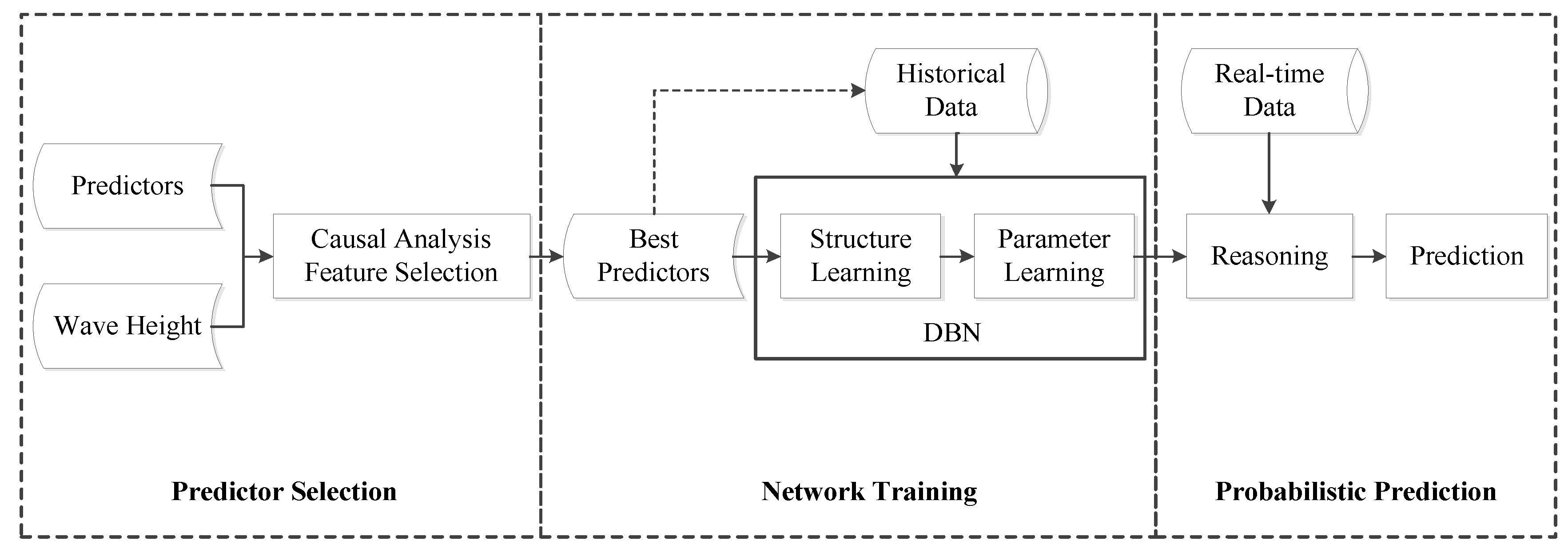
2.3. Model Formulation
- Predictor Selection: calculate IF between predictors and wave height to identify their causal relationships, and select the variables having significant causality with wave height as the best predictors.
- Network Training: discretize the data of variables (predictors and wave height); mine causal relationships among variables based on historical data and adjust arcs according to professional knowledge, establishing the initial network and transition network; learn the conditional probability and the transition probability using intelligent algorithms.
- Probabilistic Prediction: discretize the real-time data of predictors and input them as prior evidence; calculate the posterior probability distributions of wave height in different time slices for probabilistic prediction.
- More technical details and implementation processes are explained in the next section.
3. Experiment and Analysis
3.1. Description of Data
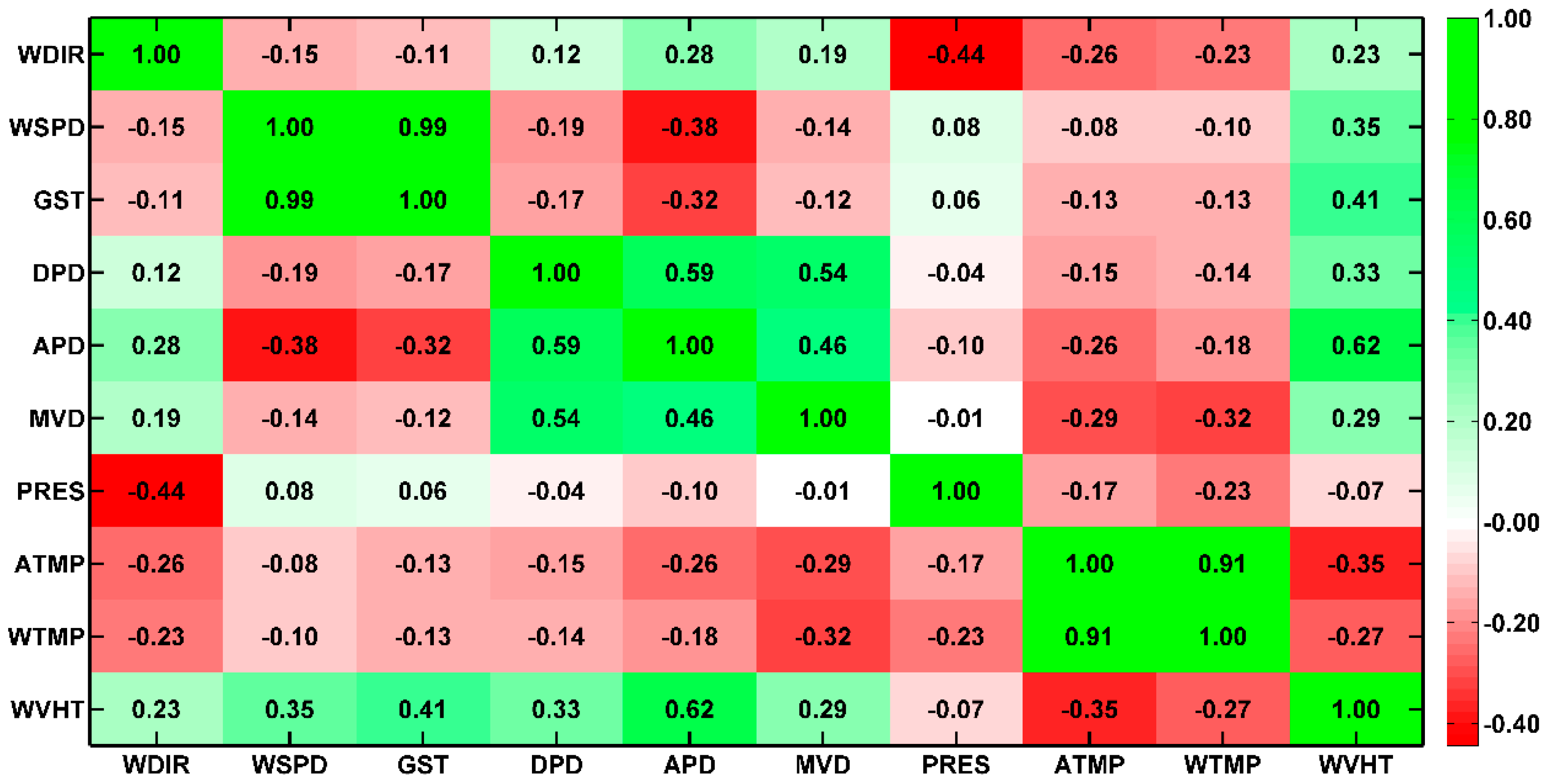
3.2. Predictor Selection
3.3. DBN Training
3.3.1. Data Discretization
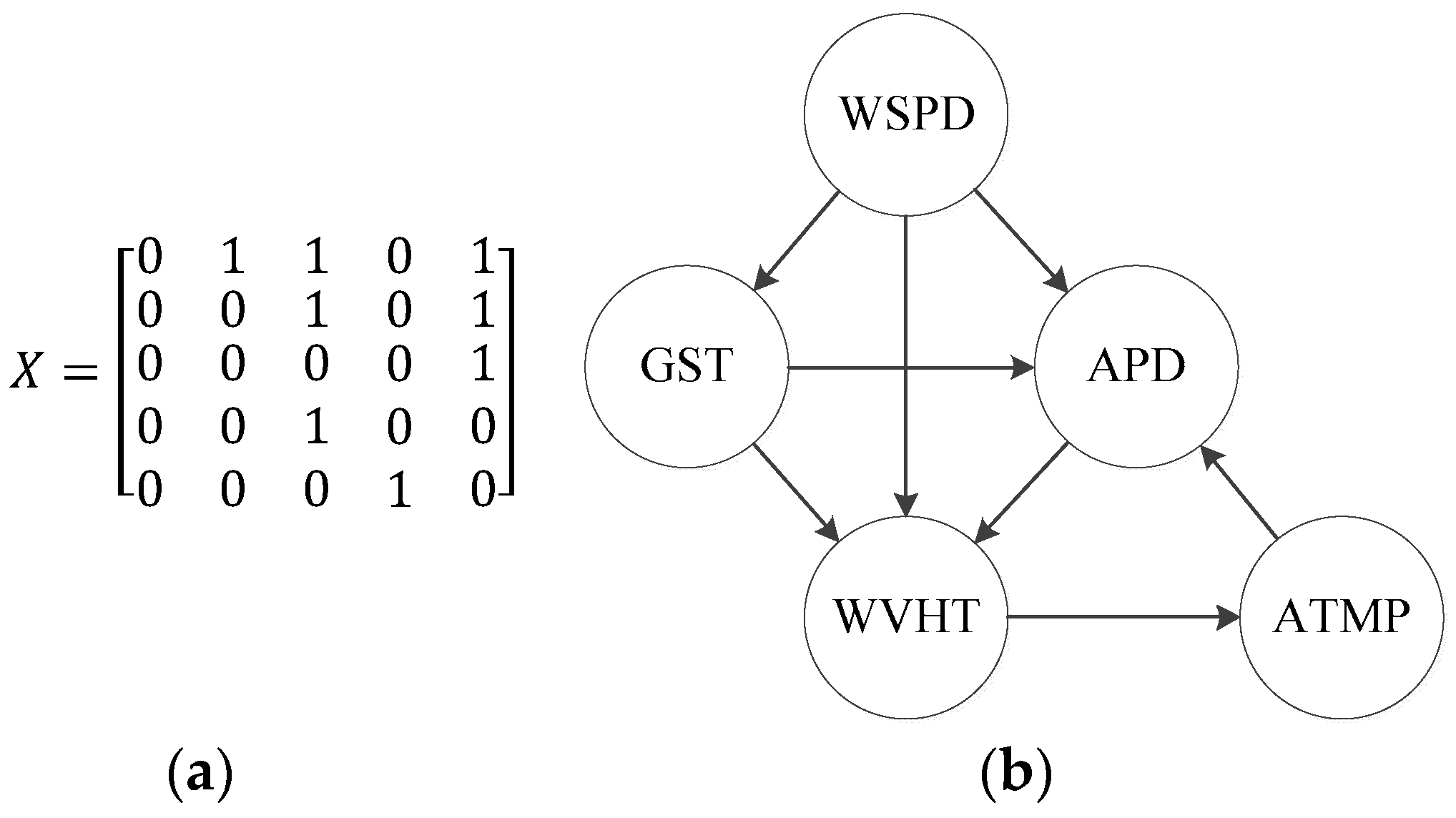
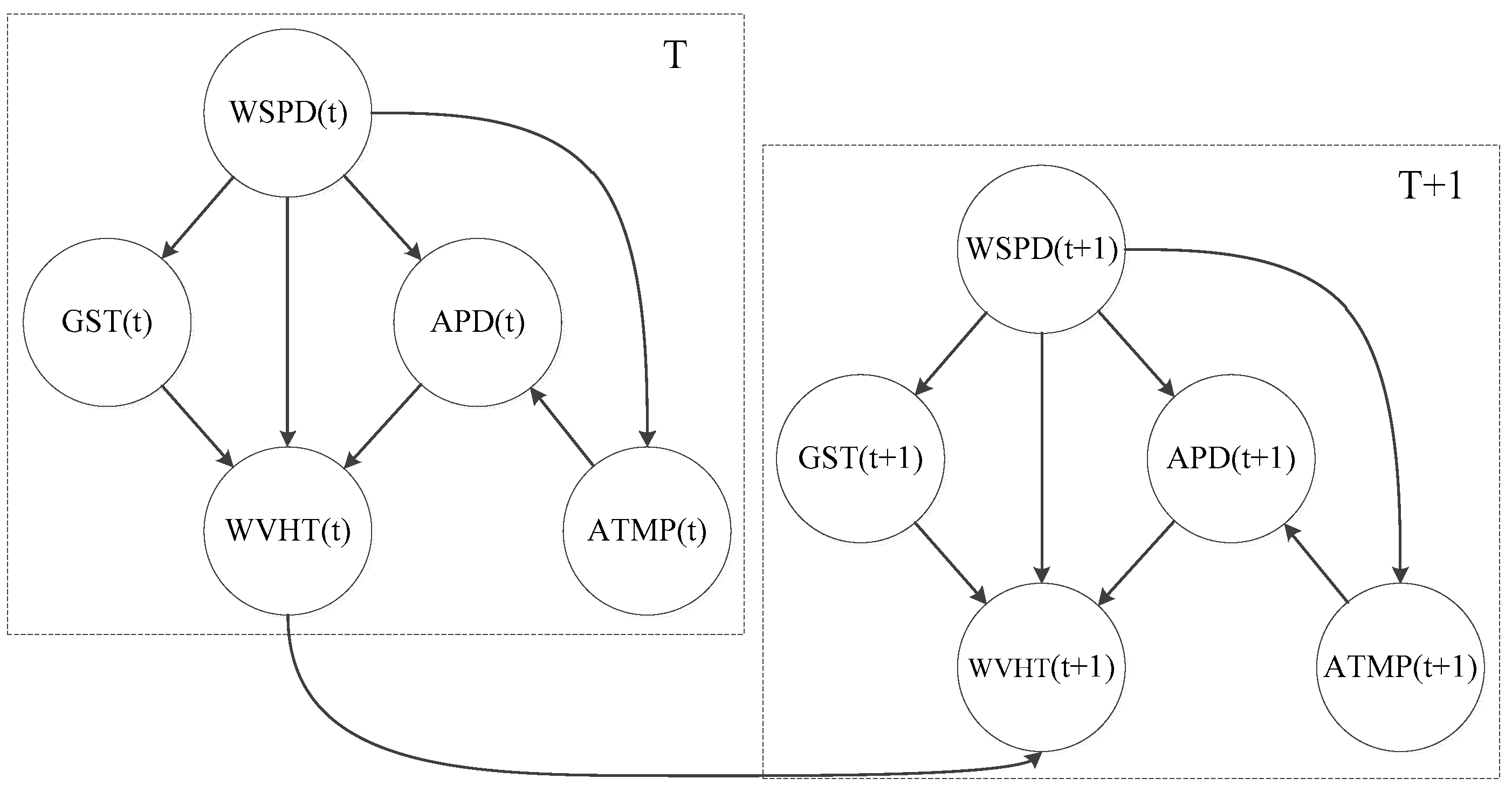
3.3.2. Structure Learning
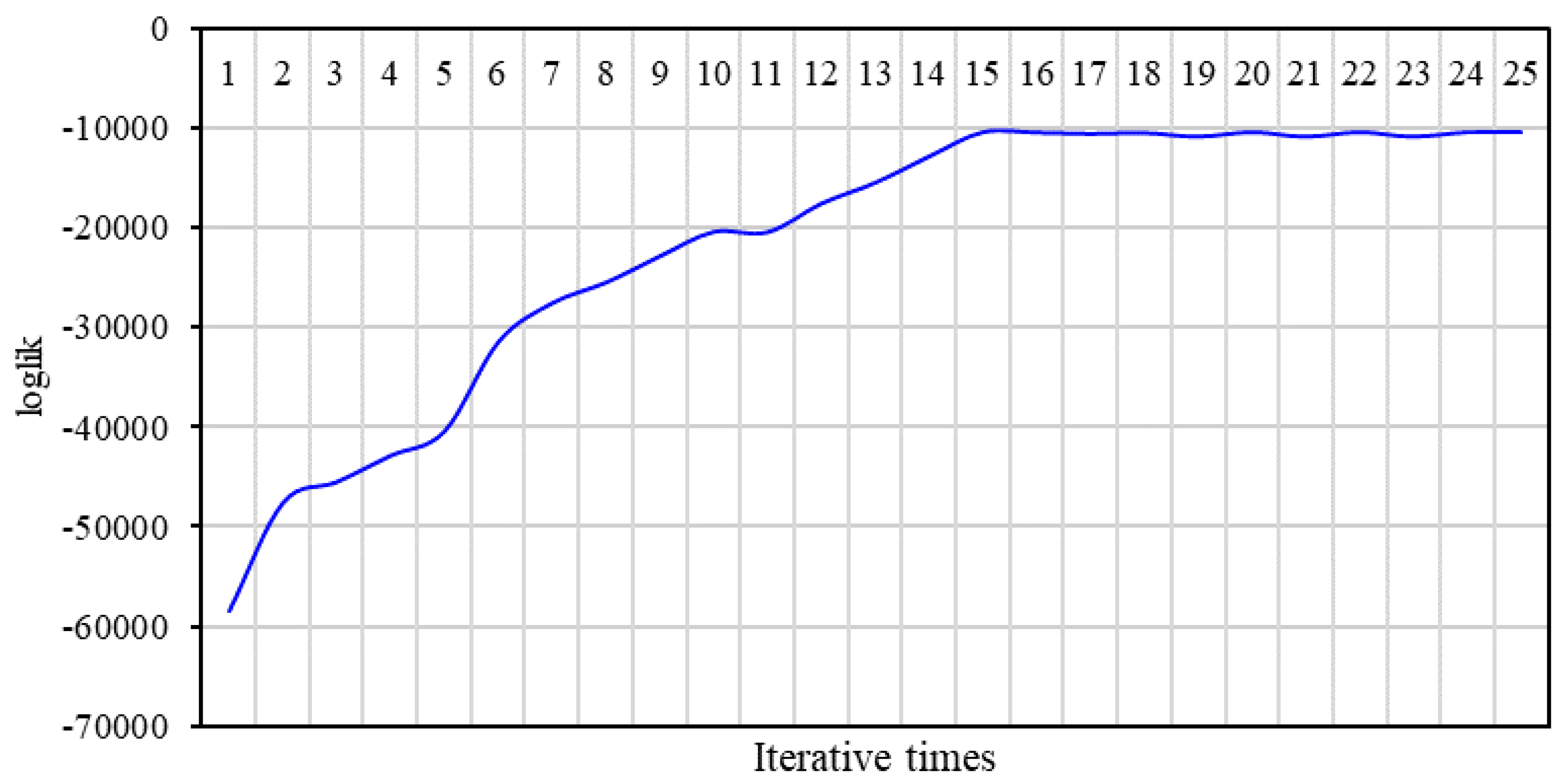
3.3.3. Parameter Learning
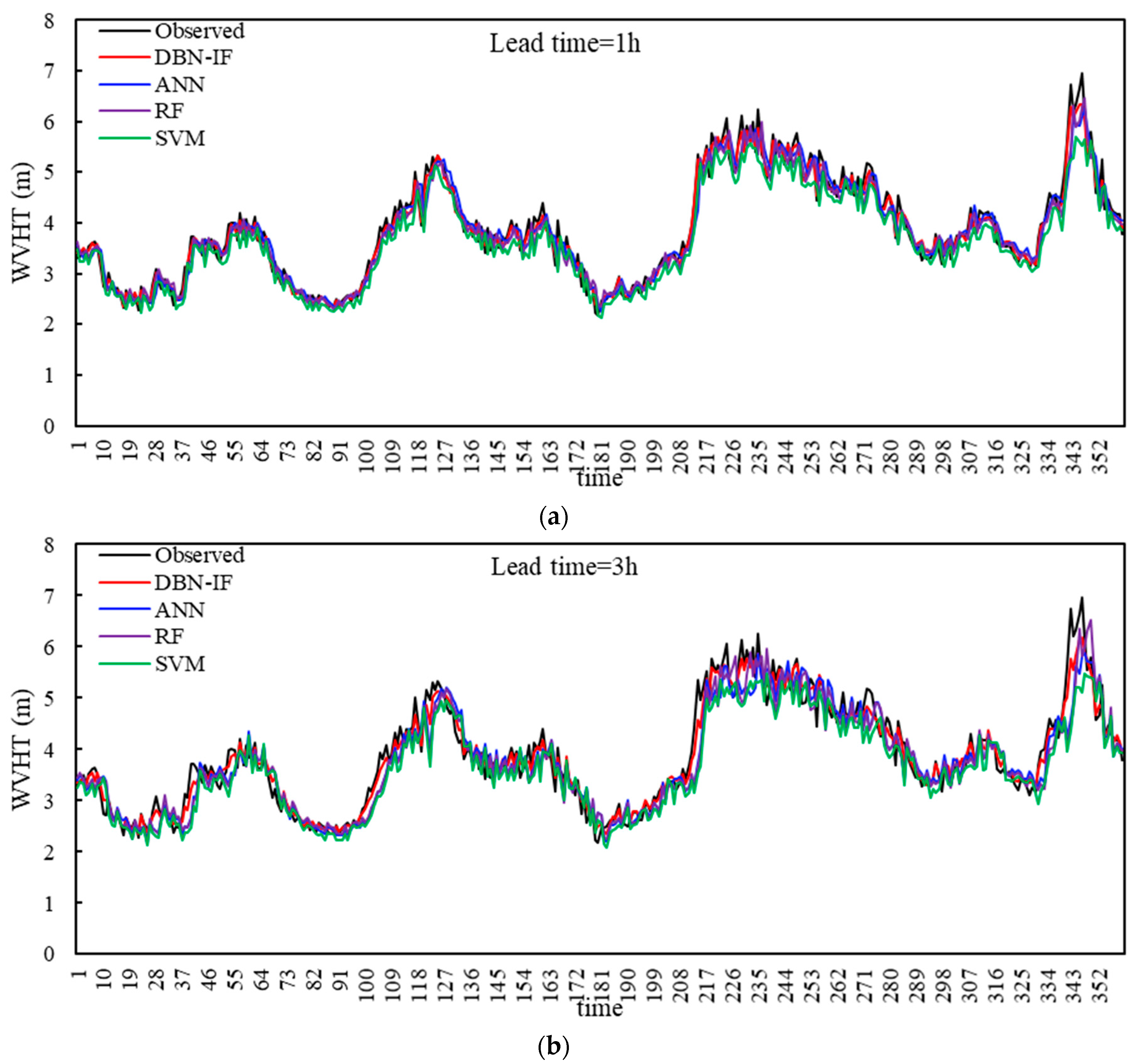
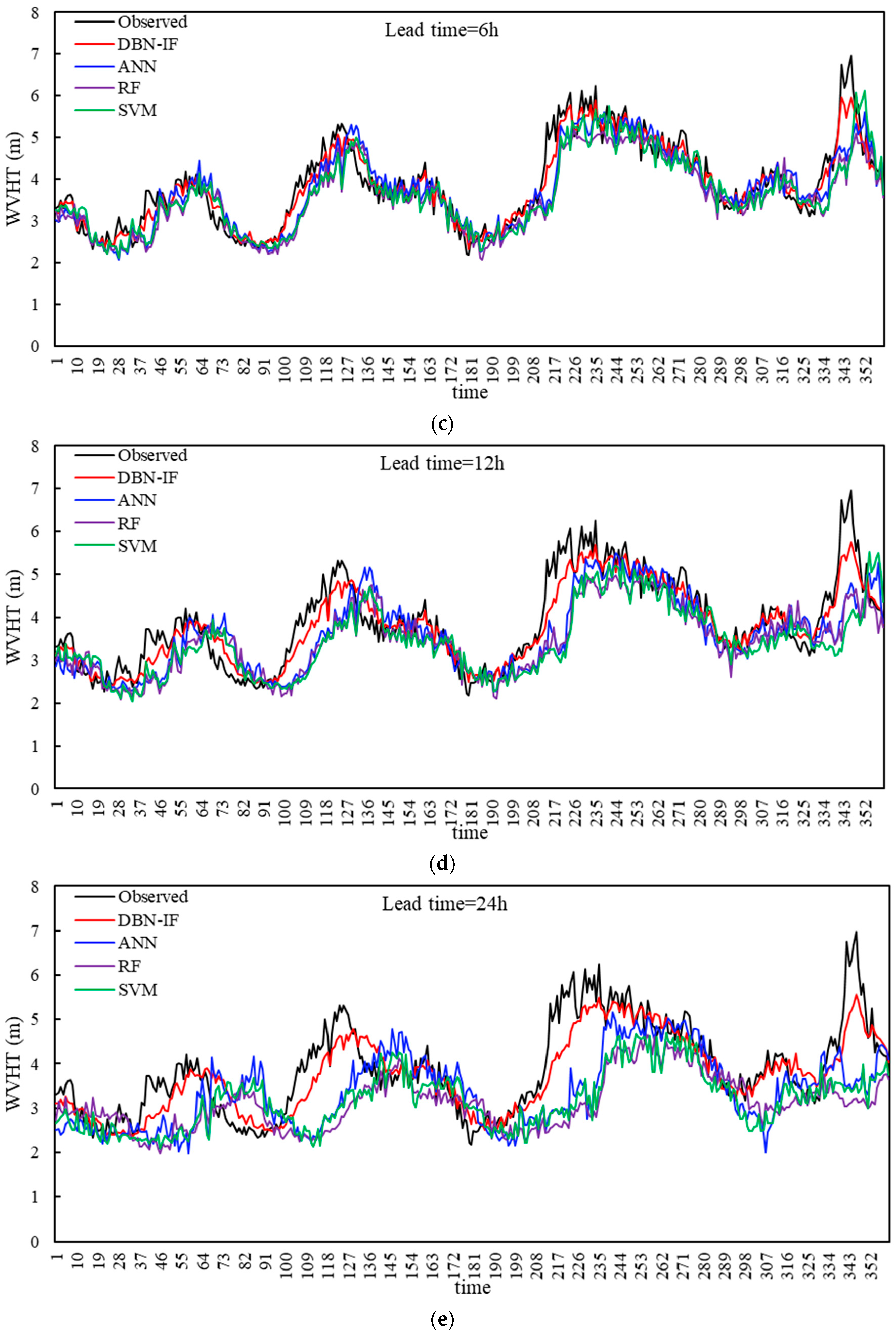
3.4. Results and Discussion
4. Conclusion
- Emphasis on screening of predictors. Different from the previous prediction models, the first step of our proposed model is to analyze and screen predictors. Use state-of-the-art IF theory instead of correlation coefficient or time-delay correlation coefficient to perform causal analysis between predictors and wave height to select the best predictors;
- Good interpretability of prediction model and ability to deal with uncertainty. Based on graph theory and probability theory, DBN can not only visualize the relationships among predictive variables but also quantitatively express the interactions with probability distributions. On the one hand, it handles the “Black Box” problem that ML algorithms such as ANN, SVM, and RF are difficult to explain. On the other hand, it deals with the uncertainty of nonlinear wave height time series through probability theory.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Time | Time Slices | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| State | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| State of Node WVHT | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 2.27 × 10−25 | 6.89 × 10−21 | 2.00 × 10−21 | 0 | 1.83 × 10−21 | 8.49 × 10−22 | 0 | |
| 3 | 0 | 0 | 2.10 × 10−15 | 2.84 × 10−13 | 7.23 × 10−13 | 4.16 × 10−11 | 9.81 × 10−13 | 3.89 × 10−13 | 2.52 × 10−12 | 7.36 × 10−11 | |
| 4 | 0 | 3.24 × 10−10 | 9.62 × 10−08 | 3.54 × 10−08 | 2.43 × 10−08 | 5.68 × 10−08 | 5.77 × 10−08 | 7.12 × 10−09 | 8.05 × 10−08 | 1.41 × 10−07 | |
| 5 | 0 | 4.59 × 10−05 | 2.75 × 10−05 | 2.66 × 10−05 | 1.06 × 10−05 | 2.70 × 10−06 | 3.17 × 10−06 | 7.63 × 10−06 | 6.06 × 10−06 | 7.43 × 10−06 | |
| 6 | 0.033 | 0.00582 | 0.001888 | 0.000699 | 0.000469 | 0.000305 | 0.000321 | 0.000459 | 0.000355 | 0.000522 | |
| 7 | 0.180059 | 0.157232 | 0.009649 | 0.0049 | 0.005205 | 0.005988 | 0.00946 | 0.011799 | 0.011033 | 0.01301 | |
| 8 | 0.402809 | 0.512611 | 0.231684 | 0.171305 | 0.208138 | 0.485044 | 0.3264 | 0.131721 | 0.176065 | 0.656672 | |
| 9 | 0.379515 | 0.298365 | 0.617647 | 0.543321 | 0.611694 | 0.187613 | 0.389711 | 0.758889 | 0.695046 | 0.133887 | |
| 10 | 0.004616 | 0.025927 | 0.136526 | 0.272912 | 0.174483 | 0.299568 | 0.222023 | 0.097124 | 0.117495 | 0.195903 | |
| 11 | 0 | 0 | 0.002578 | 0.006837 | 0 | 0.021479 | 0.052082 | 0 | 0 | 0 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
References
- Zheng, C.W.; Li, C.Y. Variation of the wave energy and significant wave height in the China sea and adjacent waters. Renew. Sustain. Energy Rev. 2015, 43, 381–387. [Google Scholar] [CrossRef]
- Zheng, C.W.; Wu, G.X.; Chen, X. CMIP5-based wave energy projection: Case studies of the South China Sea and the East China Sea. IEEE Access 2019, 31, 329–337. [Google Scholar] [CrossRef]
- Janssen, P. Progress in ocean wave forecasting. J. Comput. Phys. 2008, 227, 3572–3594. [Google Scholar] [CrossRef]
- Goda, Y. Revisiting Wilson’s formulas for simplified wind-wave prediction. J. Waterw. Port Coast. Ocean Eng. 2003, 129, 93–95. [Google Scholar] [CrossRef]
- Kamranzad, B.; Etemad-Shahidi, A.; Kazeminezhad, M.H. Wave height forecasting in Dayyer, the Persian Gulf. Ocean Eng. 2011, 38, 248–255. [Google Scholar] [CrossRef]
- Spanos, P. ARMA algorithms for ocean wave modeling. J. Energy Resour. Technol. 1983, 105, 300–309. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Özger, M. Temporal significant wave height estimation from wind speed by perceptron Kalman filtering. Ocean Eng. 2004, 31, 1245–1255. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Stefanakos, C. Fuzzy time series forecasting of nonstationary wind and wave data. Ocean Eng. 2016, 121, 1–12. [Google Scholar] [CrossRef]
- Deo, M.C.; Naidu, C.S. Real time forecasting using neural networks. Ocean Eng. 1998, 26, 191–203. [Google Scholar] [CrossRef]
- Lee, T.L. Neural network prediction of a storm surge. Ocean Eng. 2006, 33, 483–494. [Google Scholar] [CrossRef]
- Ozger, M. Significant wave height forecasting using wavelet fuzzy logic approach. Ocean Eng. 2010, 37, 1443–1451. [Google Scholar] [CrossRef]
- Shahabi, S.; Khanjani, M.J.; Kermani, M.R.H. Significant wave height modelling using a hybrid wavelet-genetic programming approach. KSCE J. Civil Eng. 2017, 21, 1–10. [Google Scholar] [CrossRef]
- Mahjoobi, J.; Mosabbeb, E.A. Prediction of significant wave height using regressive support vector machines. Ocean Eng. 2009, 36, 339–347. [Google Scholar] [CrossRef]
- Duan, W.Y.; Han, Y.; Huang, L.M.; Zhao, B.B.; Wang, M.H. A hybrid EMD-SVR model for the short-term prediction of significant wave height. Ocean Eng. 2016, 124, 54–73. [Google Scholar] [CrossRef]
- Mafi, S.; Amirinia, G. Forecasting hurricane wave height in Gulf of Mexico using soft computing methods. Ocean Eng. 2017, 146, 352–362. [Google Scholar] [CrossRef]
- Hatalis, K. Multi-step forecasting of wave power using a nonlinear recurrent neural network. In Proceedings of the IEEE Pes General Meeting, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar]
- Gasse, M.; Millioz, F.; Roux, E.; Garcia, D.; Liebgott, H.; Friboulet, D. High-quality plane wave compounding using convolutional neural networks. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1637–1639. [Google Scholar] [CrossRef]
- Cornejo-Bueno, L.; Nieto-Borge, J.C.; García-Díaz, P.; Rodríguez, G.; Salcedo-Sanz, S. Significant wave height and energy flux prediction for marine energy applications: A grouping genetic algorithm—Extreme learning machine approach. Renew. Energy 2016, 97, 380–389. [Google Scholar] [CrossRef]
- Weston, J.; Mukherjee, S.; Chapelle, O.; Pontil, M.; Vapnik, V. Feature selection for SVMs. Adv. Neural Inf. Process. Syst. 2000, 11, 526–532. [Google Scholar]
- Blum, A.L.; Langrey, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Prado-Cumplido, M.D.; Pérez-Cruz, F.; Bousoño-Calzón, C. Feature selection via genetic optimization. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2002; pp. 547–552. [Google Scholar]
- Landman, W.A.; Mason, S.J. Forecasts of near-global sea surface temperatures using canonical correlation analysis. J. Clim. 2001, 14, 3819–3833. [Google Scholar] [CrossRef]
- Juneng, L.; Tangang, F.T. Level and source of predictability of seasonal rainfall anomalies in Malaysia using canonical correlation analysis. Int. J. Climatol. 2008, 28, 1255–1267. [Google Scholar] [CrossRef]
- San Liang, X. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef]
- Li, M.; Liu, K.F. Causality-based attribute weighting via information flow and genetic algorithm for naive bayes classifier. IEEE Access 2019, 7, 150630–150641. [Google Scholar] [CrossRef]
- Schaefer, H. Entering the black box of neural networks. Methods Inf. Med. 2003, 42, 287–296. [Google Scholar]
- Liang, S.X. Normalizing the causality between time series. Phys. Rev. E 2015, 92, 022126. [Google Scholar] [CrossRef]
- Sun, J.; Sun, J. A dynamic Bayesian network model for real-time crash prediction using traffic speed conditions data. Transp. Res. Part C Emerging Technol. 2015, 54, 176–186. [Google Scholar] [CrossRef]
- Xiao, Q.; Chaoqin, C.; Li, Z. Time series prediction using dynamic Bayesian network. Optik 2017, 135, 98–103. [Google Scholar] [CrossRef]
- Li, M.; Liu, K.F. Application of intelligent dynamic Bayesian network with wavelet analysis for probabilistic prediction of storm track intensity index. Atmosphere 2018, 9, 224. [Google Scholar] [CrossRef]
- Pearl, J. From Bayesian networks to causal networks. In Mathematical Models for Handling Partial Knowledge in Artificial Intelligence; Springer: Berlin, Germany, 1995; pp. 157–182. [Google Scholar]
- Cussens, J. Bayesian network learning with cutting planes. arXiv 2012, arXiv:1202.3713v1. Available online: https://arxiv.org/abs/1202.3713 (accessed on 3 June 2012).
- Mao, J.Y.; Xie, H.R. Review of Wind-Wave Generation Mechanisms. Adv. Mar. Sci. 2019, 37, 533–542. [Google Scholar]
- Li, M.; Zhang, R.; Hong, M.; Bai, C. Improved structural learning algorithm of Bayesian network based on information flow. Syst. Eng. Electron. 2018, 465, 202–207. [Google Scholar]
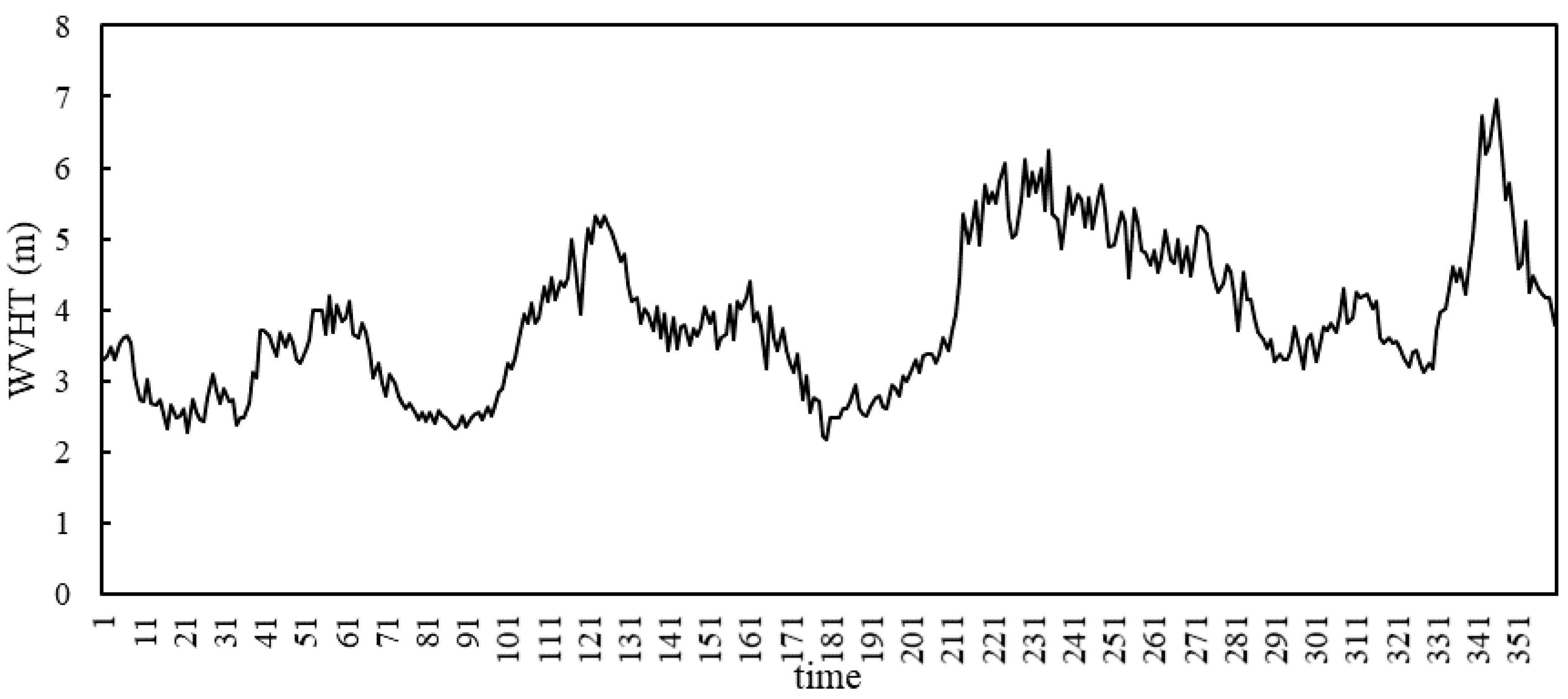



| Buoy: 51101 | Depth: 4849 m (24.361° N, 162.075° W) | ||
|---|---|---|---|
| Variables | Maximum | Average | Minimum |
| Wind direction (WDIR, °) | 360 | 117.947 | 1 |
| Wind speed (WSPD, m/s) | 15.4 | 6.908 | 0 |
| Gust speed (GST, m/s) | 20.4 | 8.506 | 0.2 |
| Dominant wave period (DPD, s) | 21.05 | 10.952 | 4.76 |
| Average wave period (APD, s) | 13.92 | 7.069 | 4.96 |
| Direction of wave at dominant period (MVD, °) | 360 | 173.408 | 1 |
| Sea level pressure (PRES, Pa) | 1026 | 1016.106 | 998.8 |
| Air temperature (ATMP, ℃) | 29.2 | 23.998 | 16.6 |
| Sea surface temperature (WTMP, ℃) | 30.2 | 25.082 | 20.8 |
| Significant wave height (WVHT, m) | 6.96 | 2.359 | 0.83 |
| Variable | WDIR | WSPD | GST | DPD | APD | MVD | PRES | ATMP | WTMP | |
|---|---|---|---|---|---|---|---|---|---|---|
| WVHT | IF | 0.0323 | 0.2488 | 0.3025 | 0.0977 | 0.1707 | 0.0794 | 0.0146 | 0.1117 | 0.0622 |
| CC | 0.2263 | 0.3472 | 0.4106 | 0.3287 | 0.6209 | 0.2928 | −0.0726 | −0.3543 | −0.2677 |
| The Best Predictors | Determinate Coefficient R2 | F |
|---|---|---|
| IF: GST + WSPD + APD + ATMP | 0.7934 | 4671.1564 |
| CC: APD + GST + ATMP + WSPD + DPD | 0.7061 | 2989.4381 |
| Variables | WSPD | GST | APD | ATMP | WVHT |
|---|---|---|---|---|---|
| Interval step | 0.5 m/s | 0.5 m/s | 0.5 s | 0.5 ℃ | 0.5 m |
| State number | 1–32 | 1–41 | 1–19 | 1–26 | 1–13 |
| Sample ID | WSPD | GST | APD | ATMP | WVHT |
|---|---|---|---|---|---|
| 1 | 7 | 18 | 21 | 7 | 7 |
| 2 | 8 | 20 | 23 | 8 | 7 |
| 3 | 8 | 22 | 27 | 8 | 6 |
| 4 | 8 | 19 | 23 | 9 | 7 |
| ... | ... | ... | ... | ... | ... |
| 8721 | 3 | 4 | 4 | 7 | 8 |
| 8722 | 4 | 7 | 8 | 8 | 6 |
| Input: | Training Data of Predictors and WVHT |
|---|---|
| Output: | Optimal DBN structure |
| Initialization: | Preprocess training data and set significant level |
| Causal analysis: | Calculate the IF between each two variables and analyze the causal relationships |
| Primitive structure: | Determine the arcs based on IF to obtain the primitive structure |
| Structure search: | Adopt GS algorithm to search for the optimal structure |
| (T + 1) | State of Node WVHT | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (T) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| State of node WVHT | 1 | 0.774 | 0.226 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0.012 | 0.873 | 0.115 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 0.056 | 0.855 | 0.089 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0.101 | 0.791 | 0.108 | 0.001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0.203 | 0.663 | 0.132 | 0.002 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 0 | 0.003 | 0.241 | 0.544 | 0.197 | 0.016 | 0 | 0 | 0 | 0 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0.264 | 0.536 | 0.172 | 0.024 | 0.004 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0.027 | 0.329 | 0.452 | 0.144 | 0.041 | 0.007 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.036 | 0.298 | 0.440 | 0.202 | 0.024 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.119 | 0.288 | 0.373 | 0.186 | 0.034 | 0 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.097 | 0.290 | 0.387 | 0.129 | 0.097 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.364 | 0.364 | 0.182 | 0.091 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.167 | 0.500 | 0.333 | |
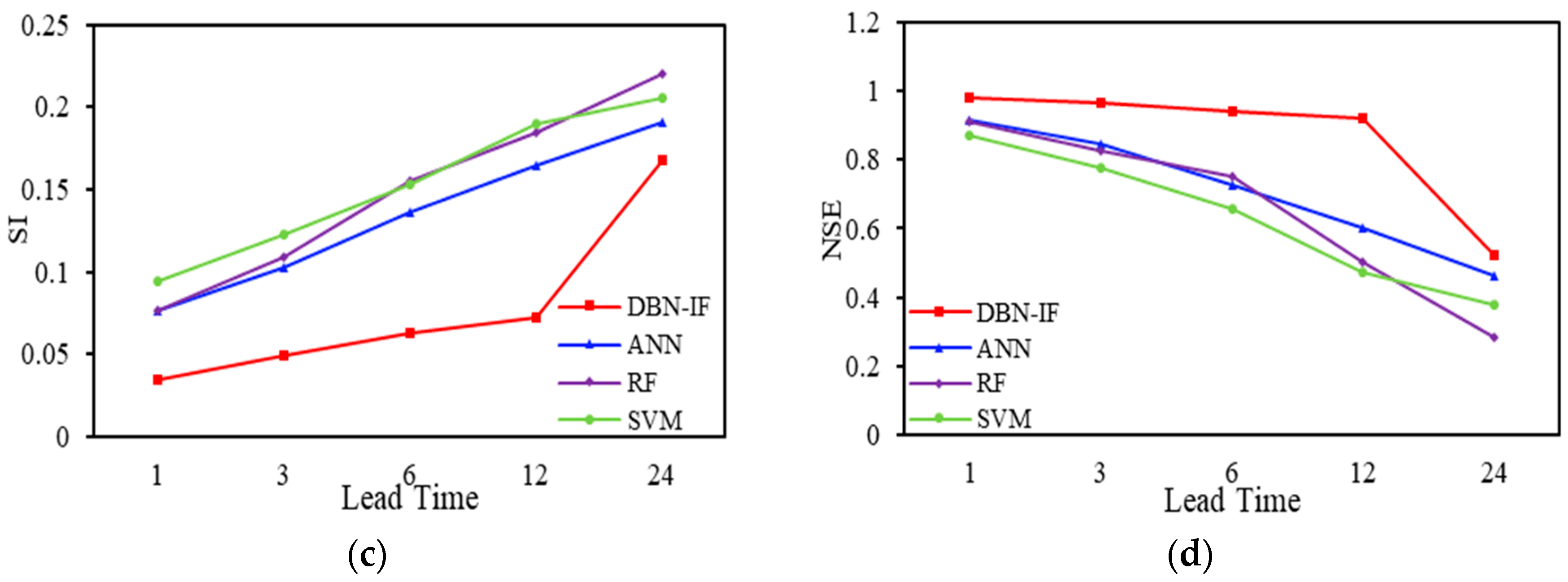
| Criteria | DBN-IF | ANN | RF | SVM |
|---|---|---|---|---|
| CC | 0.9927 | 0.9569 | 0.9585 | 0.9587 |
| RMSE | 0.1318 | 0.2948 | 0.2974 | 0.3641 |
| SI | 0.0341 | 0.0762 | 0.0769 | 0.0941 |
| NSE | 0.9829 | 0.9149 | 0.9134 | 0.8703 |
| Criteria | DBN-IF | ANN | RF | SVM |
|---|---|---|---|---|
| CC | 0.9839 | 0.9223 | 0.9251 | 0.9102 |
| RMSE | 0.1895 | 0.3987 | 0.4203 | 0.4759 |
| SI | 0.0491 | 0.1031 | 0.1087 | 0.1231 |
| NSE | 0.9648 | 0.8444 | 0.8272 | 0.7784 |
| Criteria | DBN-IF | ANN | RF | SVM |
|---|---|---|---|---|
| CC | 0.9334 | 0.8815 | 0.9024 | 0.8562 |
| RMSE | 0.2428 | 0.5272 | 0.6024 | 0.5935 |
| SI | 0.0628 | 0.1363 | 0.1557 | 0.1534 |
| NSE | 0.9423 | 0.7281 | 0.7524 | 0.6553 |
| Criteria | DBN-IF | ANN | RF | SVM |
|---|---|---|---|---|
| CC | 0.9142 | 0.8423 | 0.8981 | 0.8284 |
| RMSE | 0.2814 | 0.6356 | 0.7132 | 0.7346 |
| SI | 0.0727 | 0.1643 | 0.1844 | 0.1899 |
| NSE | 0.9225 | 0.6047 | 0.5023 | 0.4721 |
| Criteria | DBN-IF | ANN | RF | SVM |
|---|---|---|---|---|
| CC | 0.7523 | 0.6601 | 0.6932 | 0.6392 |
| RMSE | 0.6856 | 0.7427 | 0.8541 | 0.7965 |
| SI | 0.1676 | 0.1913 | 0.2208 | 0.2059 |
| NSE | 0.5248 | 0.4641 | 0.2862 | 0.3792 |
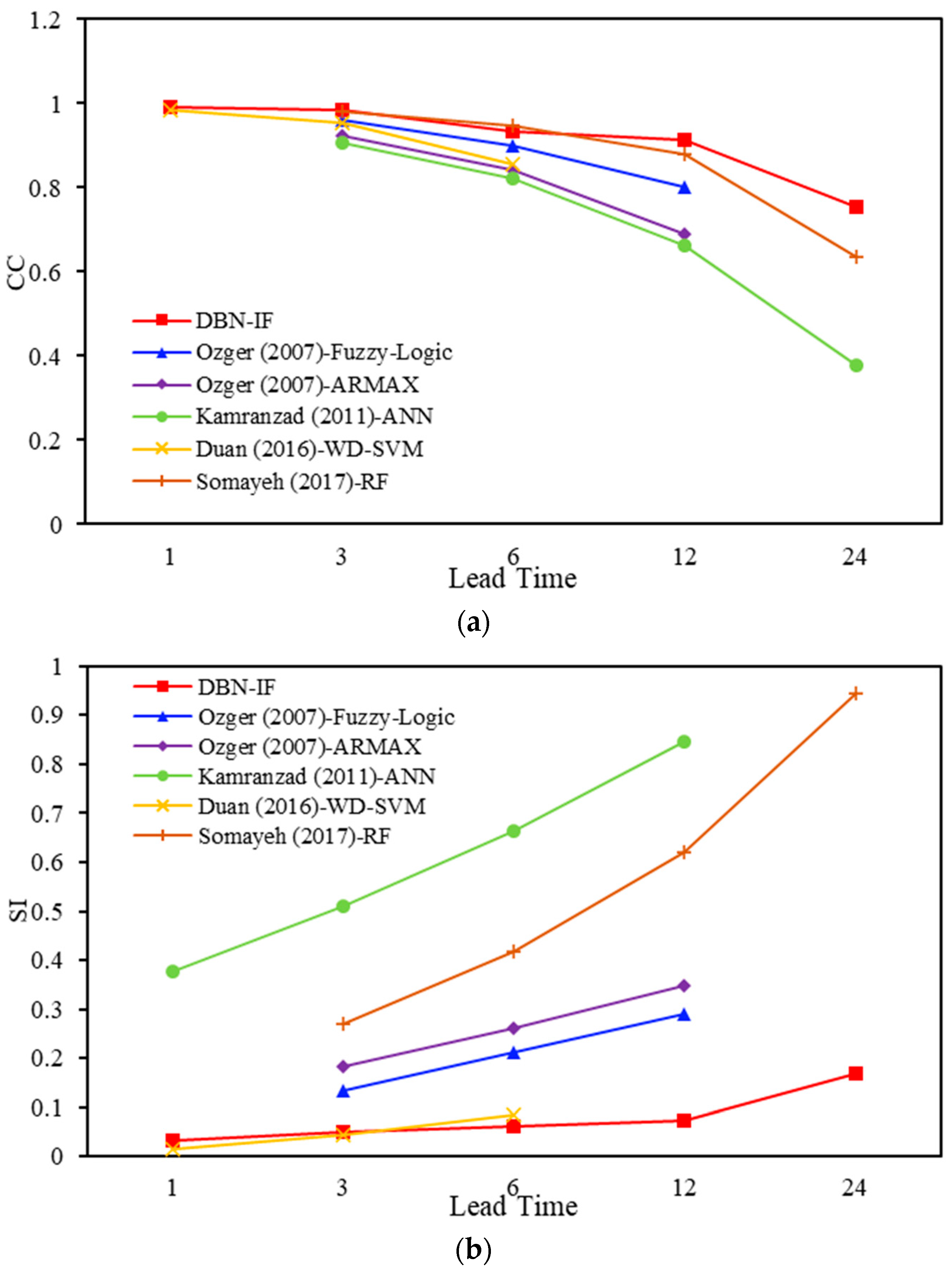
| Reference | Lead Time | CC | SI | Model | Predictors |
|---|---|---|---|---|---|
| Ozger [12] | 3 6 12 | 0.960 0.899 0.800 | 0.135 0.211 0.289 | Fuzzy-Logic | Wind speed Significant wave height |
| Ozger [12] | 3 6 12 | 0.925 0.842 0.690 | 0.184 0.260 0.349 | ARMAX | Wind speed Significant wave height |
| Kamranzad [5] | 3 6 12 24 | 0.907 0.820 0.663 0.379 | 0.378 0.511 0.663 0.845 | ANN | Friction velocity Wind direction Significant wave height Wave direction |
| Duan [15] | 1 3 6 | 0.986 0.954 0.855 | 0.014 0.044 0.086 | WD-SVM | Significant wave height |
| Somayeh [16] | 3 6 12 24 | 0.981 0.948 0.880 0.635 | 0.270 0.418 0.619 0.945 | RF | Wind speed Significant wave height Wave period Pressure Air temperature Water temperature Dew point |
| Criteria | DBN-IF | ANN | RF | SVM |
|---|---|---|---|---|
| CC | 0.9114 | 0.8672 | 0.8801 | 0.8542 |
| RMSE | 0.2165 | 0.3947 | 0.3851 | 0.4131 |
| SI | 0.1436 | 0.1758 | 0.1721 | 0.2164 |
| NSE | 0.9142 | 0.7561 | 0.7873 | 0.6983 |
| Criteria | DBN-IF | ANN | RF | SVM |
|---|---|---|---|---|
| CC | 0.8792 | 0.8211 | 0.8536 | 0.8147 |
| RMSE | 0.3489 | 0.4361 | 0.4253 | 0.5326 |
| SI | 0.1735 | 0.2083 | 0.1969 | 0.2945 |
| NSE | 0.8803 | 0.7206 | 0.7367 | 0.6714 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Liu, K. Probabilistic Prediction of Significant Wave Height Using Dynamic Bayesian Network and Information Flow. Water 2020, 12, 2075. https://doi.org/10.3390/w12082075
Li M, Liu K. Probabilistic Prediction of Significant Wave Height Using Dynamic Bayesian Network and Information Flow. Water. 2020; 12(8):2075. https://doi.org/10.3390/w12082075
Chicago/Turabian StyleLi, Ming, and Kefeng Liu. 2020. "Probabilistic Prediction of Significant Wave Height Using Dynamic Bayesian Network and Information Flow" Water 12, no. 8: 2075. https://doi.org/10.3390/w12082075
APA StyleLi, M., & Liu, K. (2020). Probabilistic Prediction of Significant Wave Height Using Dynamic Bayesian Network and Information Flow. Water, 12(8), 2075. https://doi.org/10.3390/w12082075





