An Integrated Approach for the Simulation Modeling and Risk Assessment of Coastal Flooding
Abstract
:1. Introduction
2. Model Testing Materials and Methods
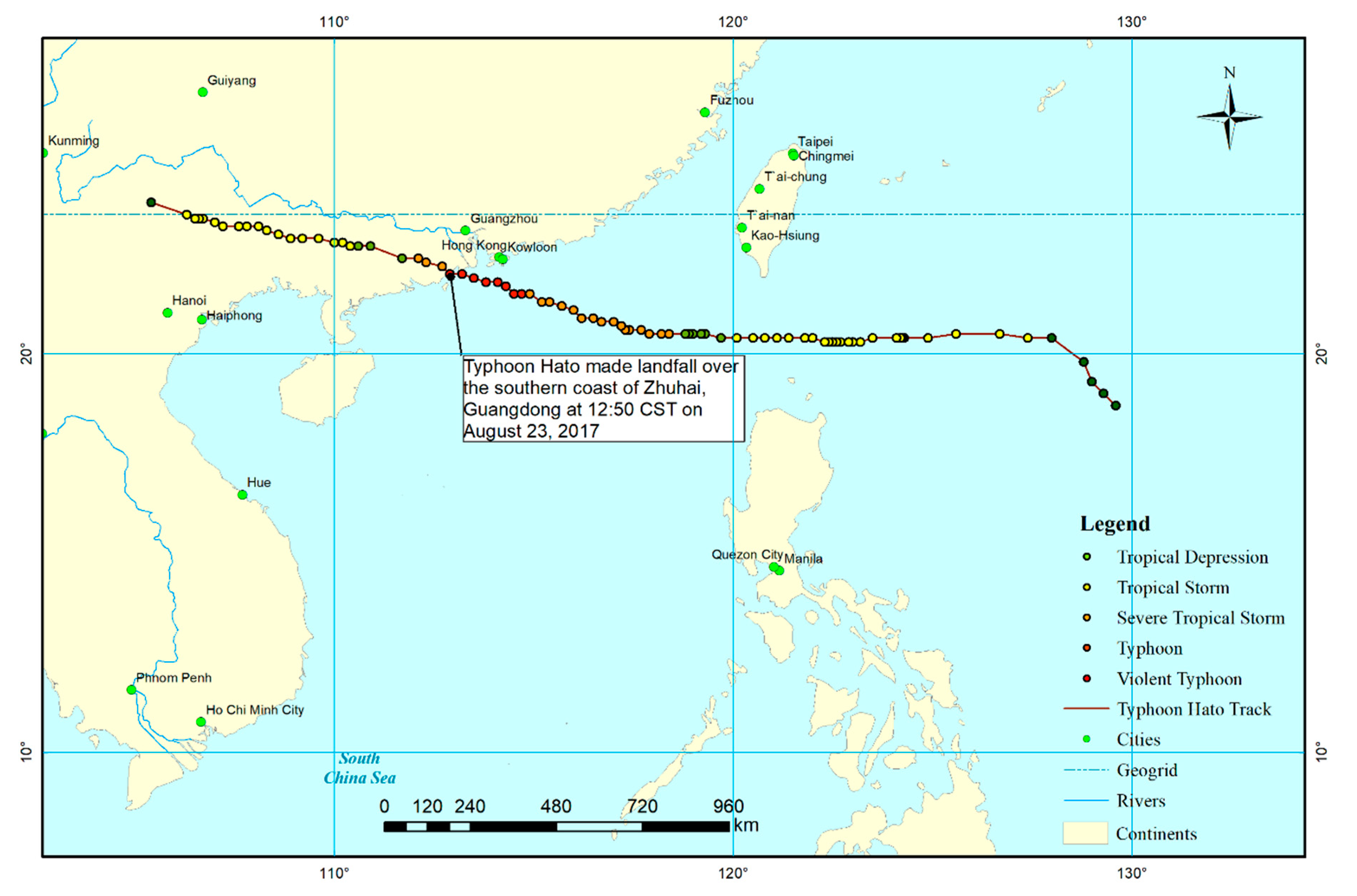
2.1. Case Background
2.2. Initial and Boundary Conditions for Model Testing
2.3. Methodology
2.3.1. Simplified Two-Dimensional Shallow Hydrodynamic Module
2.3.2. Physically-Based and Real-Time Risk Assessment Module
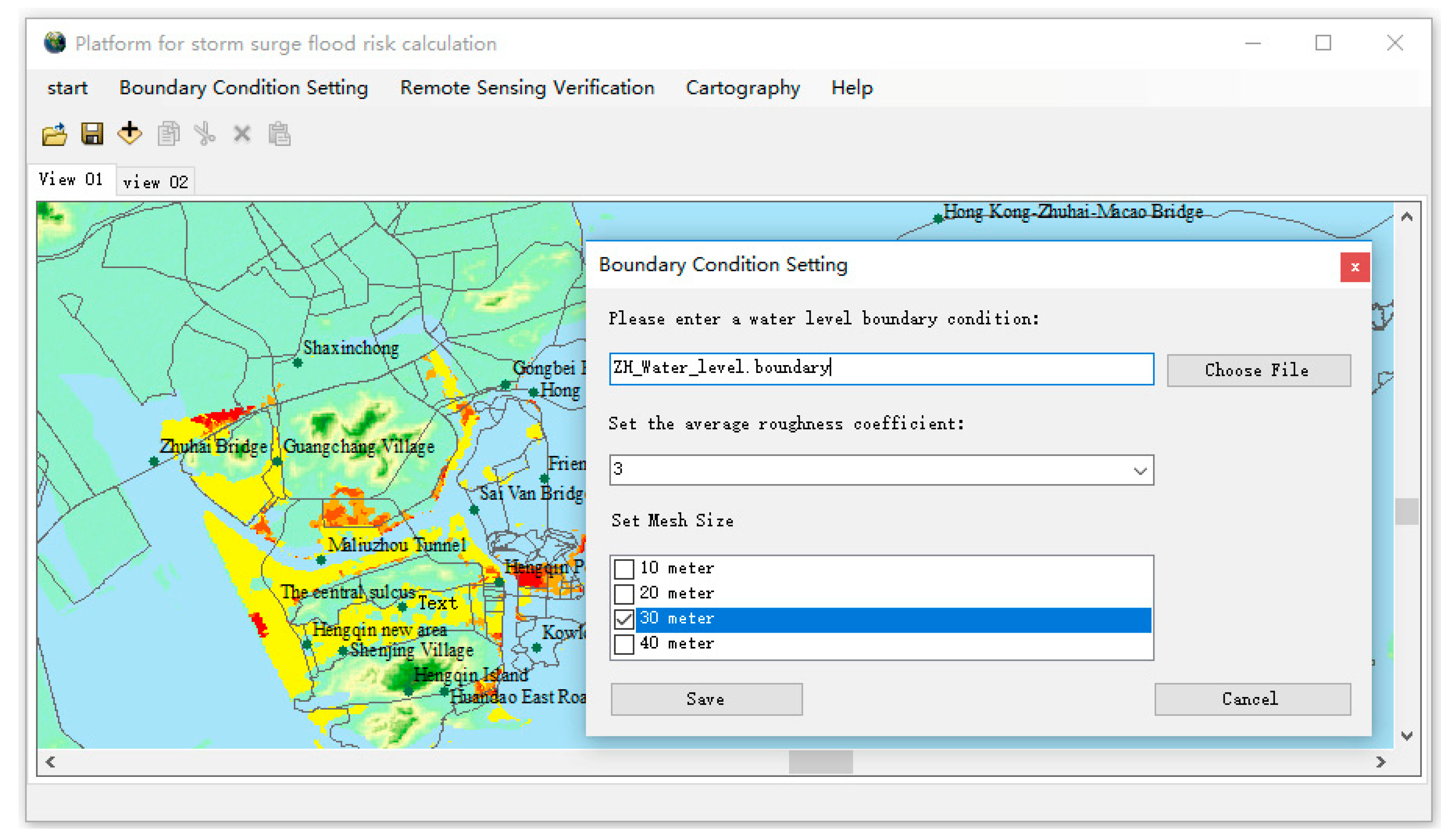
2.3.3. Calibration and Testing
3. Results and Discussions
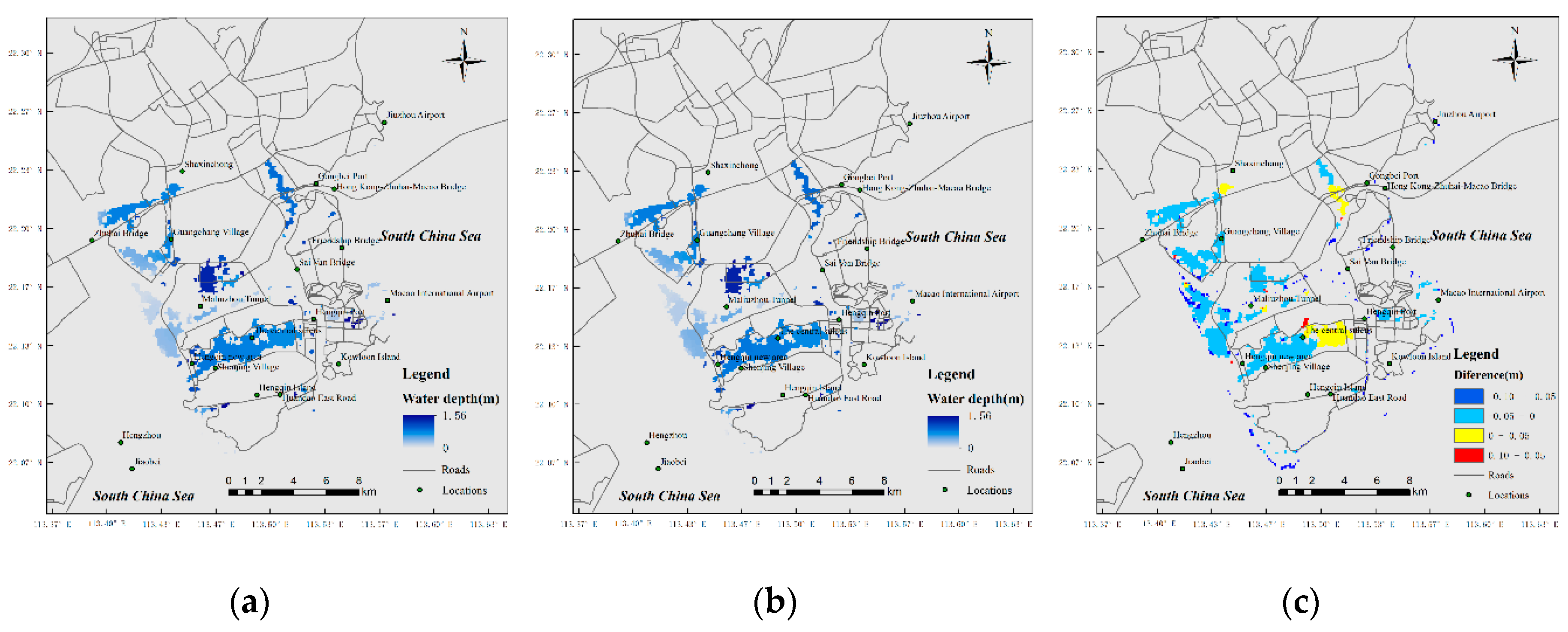
3.1. Comparison with MIKE 21 Simulation Results
3.2. Comparison of CA Model with Social Media-Based Dataset
3.3. Coastal Flood Risk Assessment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hallegatte, S.; Green, C.; Nicholls, R.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Burrus, R.; Dumas, C.; Graham, J. Hurricane risk and coastal property owner choices. Int. J. Disaster. Resil. Built. Environ. 2011, 2, 118–138. [Google Scholar] [CrossRef] [Green Version]
- Klerk, W.J.; Winsemius, H.C.; Van Verseveld, W.J.; Bakker, A.M.R.; Diermanse, F.L.M. The co-incidence of storm surges and extreme discharges within the Rhine–Meuse Delta. Environ. Res. Lett. 2015, 10, 035005. [Google Scholar] [CrossRef] [Green Version]
- Vousdoukas, M.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L. Projections of extreme storm surge levels along Europe. Clim. Dyn. 2016, 47, 3171–3190. [Google Scholar] [CrossRef] [Green Version]
- Androulidakis, Y.; Kombiadou, K.; Makris, C.; Baltikas, V.; Krestenitis, Y. Storm surges in the mediterranean sea: Variability and trends under future climatic conditions. Dyn. Atmos. Oceans. 2015, 71, 56–82. [Google Scholar] [CrossRef]
- Lin, N.; Emanuel, K. Grey swan tropical cyclones. Nat. Clim. Chang. 2015, 6, 106–111. [Google Scholar] [CrossRef] [Green Version]
- Schubert, C.E.; Busciolano, R.J.; Hearn, P.P.; Rahav, A.N.; Behrens, R.; Finkelstein, J.S.; Monti, J.; Simonson, A.E. Analysis of storm-tide impacts from Hurricane Sandy in New York. Available online: https://pubs.er.usgs.gov/publication/sir20155036 (accessed on 26 September 2019).
- Poulter, B.; Halpin, P. Raster modelling of coastal flooding from sea-level rise. Int. J. Geogr. Inf. Sci. 2008, 22, 167–182. [Google Scholar] [CrossRef]
- Lichter, M.; Felsenstein, D. Assessing the costs of sea-level rise and extreme flooding at the local level: A GIS-based approach. Ocean Coastal Manag. 2012, 59, 47–62. [Google Scholar] [CrossRef]
- Aerts, J.; Lin, N.; Botzen, W.; Emanuel, K.; de Moel, H. Low-probability flood risk modeling for New York City. Risk Anal. 2013, 33, 772–788. [Google Scholar] [CrossRef]
- Lloyd, S.; Kovats, R.; Chalabi, Z.; Brown, S.; Nicholls, R. Modelling the influences of climate change-associated sea-level rise and socioeconomic development on future storm surge mortality. Clim. Chang. 2015, 134, 441–455. [Google Scholar] [CrossRef]
- Gallien, T.; Schubert, J.; Sanders, B. Predicting tidal flooding of urbanized embayments: A modeling framework and data requirements. Coast. Eng. 2011, 58, 567–577. [Google Scholar] [CrossRef]
- Ramirez, J.; Lichter, M.; Coulthard, T.; Skinner, C. Hyper-resolution mapping of regional storm surge and tide flooding: Comparison of static and dynamic models. Nat. Hazards. 2016, 82, 571–590. [Google Scholar] [CrossRef]
- Bates, P.; Horritt, M.; Fewtrell, T. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Patro, S.; Chatterjee, C.; Mohanty, S.; Singh, R.; Raghuwanshi, N. Flood inundation modeling using MIKE FLOOD and remote sensing data. J. Indian Soc. Remote Sens. 2009, 37, 107–118. [Google Scholar] [CrossRef]
- Xia, J.; Guo, P.; Zhou, M.; Falconer, R.; Wang, Z.; Chen, Q. Modelling of flood risks to people and property in a flood diversion zone. J. Zhejiang Univ.-Sci. A 2018, 19, 864–877. [Google Scholar] [CrossRef]
- Prakash, M.; Rothauge, K.; Cleary, P. Modelling the impact of dam failure scenarios on flood inundation using SPH. Appl. Math. Model. 2014, 38, 5515–5534. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.; Stansby, P.; Mignosa, P. SPH modeling of shallow flow with open boundaries for practical flood simulation. J. Hydraul. Eng.-ASCE 2012, 138, 530–541. [Google Scholar] [CrossRef]
- Wang, X.; Sun, X.; Zhang, S.; Sun, R.; Li, R.; Zhu, Z. 3D simulation of storm surge disaster based on scenario analysis. Trans. Tianjin Univ. 2016, 22, 110–120. [Google Scholar] [CrossRef]
- A State of the Art Review on Mathematical Modelling of Flood Propagation. Available online: http://www.impact-project.net/cd/papers/print/008_pr_02-05-16_IMPACT_Alcrudo.pdf (accessed on 30 May 2020).
- McLusky, D.; Wolanski, E. Treatise on Estuarine and Coastal Science; Academic Press: Amsterdam, The Netherlands, 2011; pp. 441–458. [Google Scholar]
- Warren, I.; Bach, H. MIKE 21: A modelling system for estuaries, coastal waters and seas. Environ. Softw. 1992, 7, 229–240. [Google Scholar] [CrossRef]
- Madsen, H.; Jakobsen, F. Cyclone induced storm surge and flood forecasting in the northern Bay of Bengal. Coast. Eng. 2004, 51, 277–296. [Google Scholar] [CrossRef]
- Wang, J.; Gao, W.; Xu, S.; Yu, L. Evaluation of the combined risk of sea level rise, land subsidence, and storm surges on the coastal areas of Shanghai, China. Clim. Chang. 2012, 115, 537–558. [Google Scholar] [CrossRef]
- Wolfram, S. Computation theory of cellular automata. Commun. Math. Phys. 1984, 96, 15–57. [Google Scholar] [CrossRef]
- Zhou, C.; Sun, Z.; Xie, Y. Research of Geographical Cellular Automata; Science Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Murray, A.; Paola, C. A cellular model of braided rivers. Nature 1994, 371, 54–57. [Google Scholar] [CrossRef]
- Folino, G.; Mendicino, G.; Senatore, A.; Spezzano, G.; Straface, S. A model based on cellular automata for the parallel simulation of 3D unsaturated flow. Parallel Comput. 2006, 32, 357–376. [Google Scholar] [CrossRef]
- Mendicino, G.; Senatore, A.; Spezzano, G.; Straface, S. Three-dimensional unsaturated flow modeling using cellular automata. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Cai, X.; Li, Y.; Wu, W.; Wang, Y. Cellular automaton model of flood submergence based on bulk method. J. Hydroelectric. Eng. 2013, 32, 30–34. (In Chinese) [Google Scholar]
- Li, Y.; Gong, J.; Zhu, J.; Song, Y.; Hu, Y.; Ye, L. Spatiotemporal simulation and risk analysis of dam-break flooding based on cellular automata. Int. J. Geogr. Inf. Sci. 2013, 27, 2043–2059. [Google Scholar] [CrossRef]
- Guidolin, M.; Chen, A.; Ghimire, B.; Keedwell, E.; Djordjević, S.; Savić, D. A weighted cellular automata 2D inundation model for rapid flood analysis. Environ. Modell. Softw. 2016, 84, 378–394. [Google Scholar] [CrossRef] [Green Version]
- Dottori, F.; Todini, E. Developments of a flood inundation model based on the cellular automata approach: Testing different methods to improve model performance. Phys. Chem. Earth 2011, 36, 266–280. [Google Scholar] [CrossRef]
- Parsons, J.; Fonstad, M. A cellular automata model of surface water flow. Hydrol. Process. 2007, 21, 2189–2195. [Google Scholar] [CrossRef]
- 2017 State Oceanic Administration. Available online: http://gc.mnr.gov.cn/201806/t20180619_1798021.html (accessed on 30 May 2020).
- White, R.; Engelen, G. High resolution integrated modeling of the spatial dynamics of urban and regional systems. Comput. Environ. Urban Syst. 2000, 24, 383–400. [Google Scholar] [CrossRef] [Green Version]
- Li, X. Geographic Simulation System: Cellular Automata and Multi-Agent; Science Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Liu, S.K.; Li, X.; Li, S.; Yu, T. Numerical simulation of flood routing in Xiaoqinghe plain. Shuikexue Jinzhan 1991, 2, 188–193. (In Chinese) [Google Scholar]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review Article “Assessment of economic flood damage”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Wei, Y.M.; Jin, J.L.; Yang, C.J.; Huang, S.F.; Fan, Y.; Chen, D.Q. Theory of Risk Management of Flood Disaster; Science Press: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Yang, T.; Xie, J.; Li, G. A Social Media-based Dataset of Typhoon Disasters. 2017. Available online: http://www.scidb.cn/detail?dataSetId=633694461024534528&language=zh_CN&dataSetType=journal (accessed on 14 April 2020).










| Land Use | Mean | SD | Loss Rate Corresponding to Different Water Depths (%) | ||||
|---|---|---|---|---|---|---|---|
| (CNY/m2) | (CNY/m2) | 0–0.5 | 0.5–1.0 | 1.0–1.5 | 1.5–2.0 | >2.5 | |
| Cropland | 10.38 | 2.46 | 15 | 25 | 50 | 80 | 100 |
| Water | 21.97 | 4.54 | 1 | 2 | 3 | 5 | 7 |
| Forest | 0.88 | 0.23 | 2 | 5 | 10 | 15 | 25 |
| Building area | 5078.67 | 1267.44 | 8 | 12 | 17 | 22 | 27 |
| Development area | 646.94 | 150.89 | 3 | 7 | 10 | 14 | 21 |
| Statistical Parameter | Resolution (m) | ||||
|---|---|---|---|---|---|
| 10 | 25 | 50 | 100 | 200 | |
| RMSE (m) | 0.02 | 0.03 | 0.03 | 0.04 | 0.05 |
| R | 0.93 | 0.94 | 0.95 | 0.95 | 0.93 |
| Resolution (m) | ||||||
|---|---|---|---|---|---|---|
| 10 | 25 | 50 | 100 | 200 | ||
| Simulation Time (min) | MIKE | 37.02 | 10.35 | 3.27 | 2.60 | 1.98 |
| CA | 3.58 | 2.31 | 1.23 | 0.71 | 0.50 | |
| Collection Channel | Number of Photos | |||||
|---|---|---|---|---|---|---|
| Total | Correct | |||||
| 10 m | 25 m | 50 m | 100 m | 200 m | ||
| Sina-Weibo | 50 | 49 | 49 | 49 | 49 | 49 |
| 50 | 49 | 49 | 49 | 48 | 48 | |
| Baidu | 50 | 48 | 48 | 48 | 48 | 48 |
| Water Depth (m) | Cropland | Water | Forest | Building Area | Development Area | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Area (km2) | Loss (104 CNY) | Area (km2) | Loss (104 CNY) | Area (km2) | Loss (104 CNY) | Area (km2) | Loss (108 CNY) | Area (km2) | Loss (108 CNY) | |
| 0–0.5 | 0.33 | 51.38 | 9.95 | 218.60 | 0.58 | 1.02 | 3.34 | 13.57 | 1.66 | 0.32 |
| 0.5–1.0 | 0.44 | 114.18 | 7.69 | 337.90 | 0.55 | 2.42 | 3.16 | 19.26 | 1.98 | 0.90 |
| 1.0–1.5 | 0.35 | 181.65 | 5.06 | 333.50 | 1.32 | 11.62 | 2.31 | 19.95 | 2.41 | 1.56 |
| 1.5–2.0 | 0.33 | 274.03 | 3.63 | 398.76 | 1.45 | 19.14 | 1.55 | 17.32 | 2.94 | 2.66 |
| 2.0–2.5 | 0.33 | 342.54 | 5.43 | 835.08 | 1.34 | 29.48 | 2.00 | 27.43 | 6.50 | 8.83 |
| Total | 1.78 | 963.78 | 31.76 | 2123.84 | 5.24 | 63.68 | 12.36 | 97.53 | 15.49 | 14.27 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Sun, H. An Integrated Approach for the Simulation Modeling and Risk Assessment of Coastal Flooding. Water 2020, 12, 2076. https://doi.org/10.3390/w12082076
Zheng Y, Sun H. An Integrated Approach for the Simulation Modeling and Risk Assessment of Coastal Flooding. Water. 2020; 12(8):2076. https://doi.org/10.3390/w12082076
Chicago/Turabian StyleZheng, Yazhi, and Hai Sun. 2020. "An Integrated Approach for the Simulation Modeling and Risk Assessment of Coastal Flooding" Water 12, no. 8: 2076. https://doi.org/10.3390/w12082076






