Groundwater Flow-Modeling and Sensitivity Analysis in a Hyper Arid Region
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methods
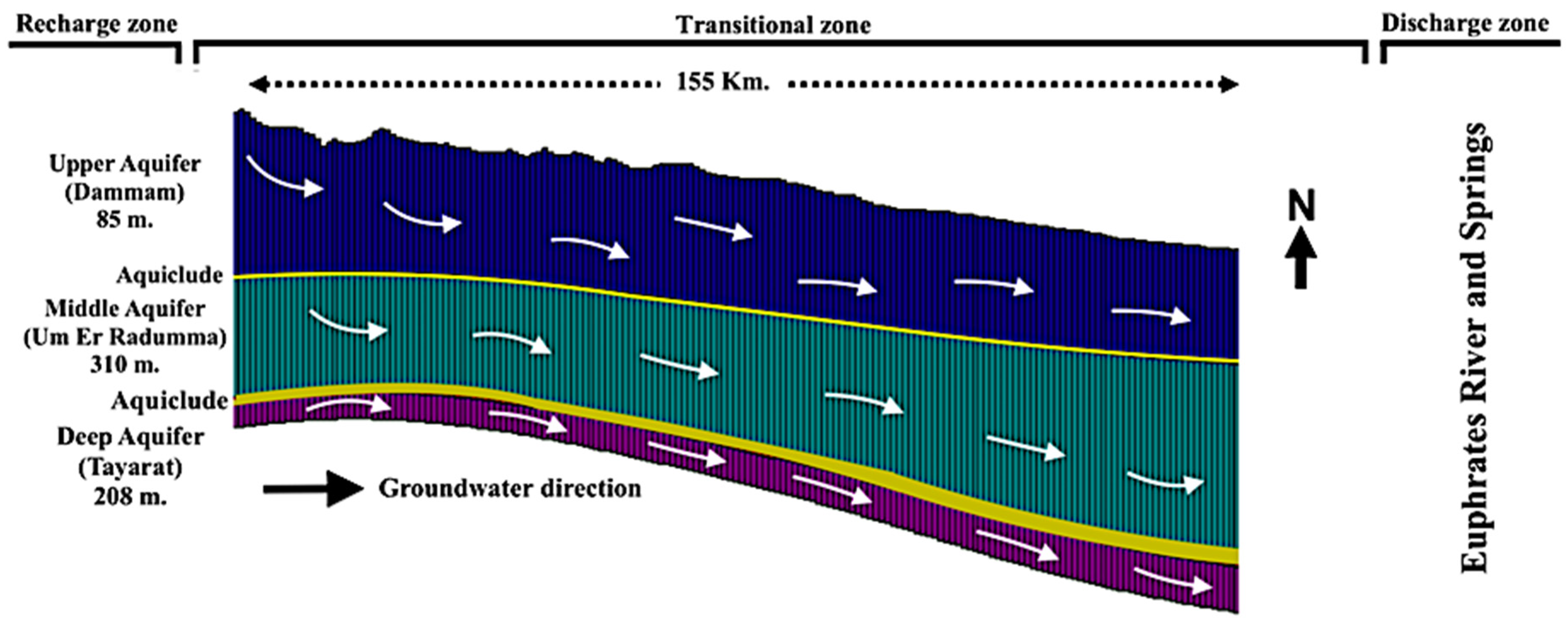
2.2. Properties and Initial Data
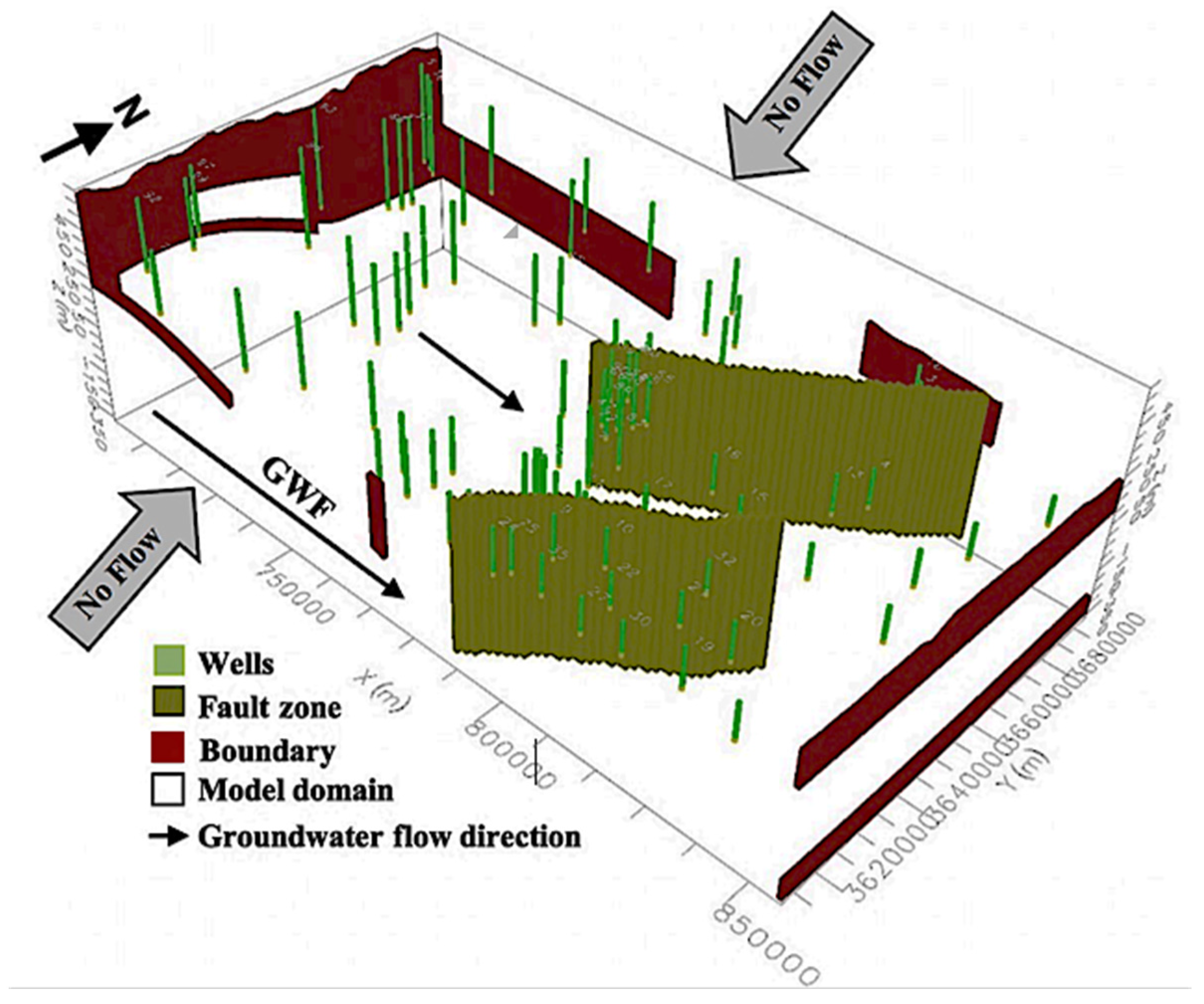
2.3. Boundary Conditions
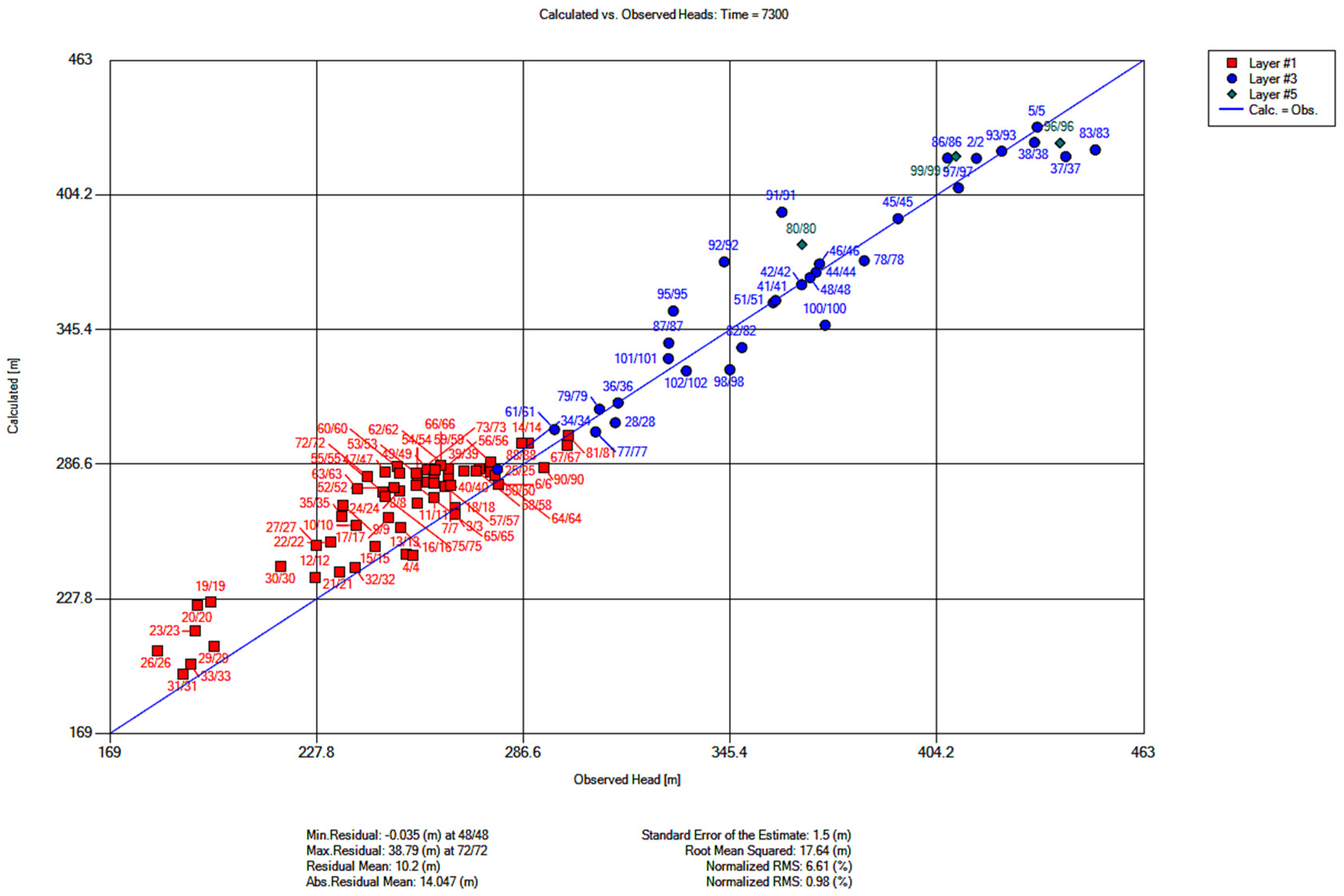
2.4. Model Calibration
3. Results and Discussion
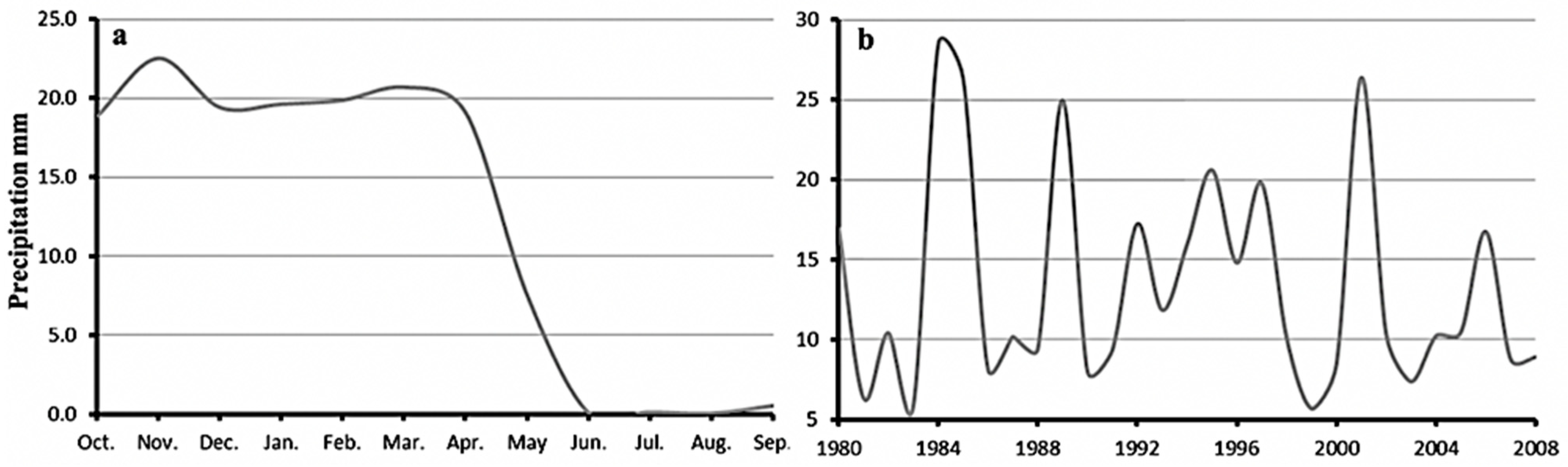
3.1. Groundwater Modeling
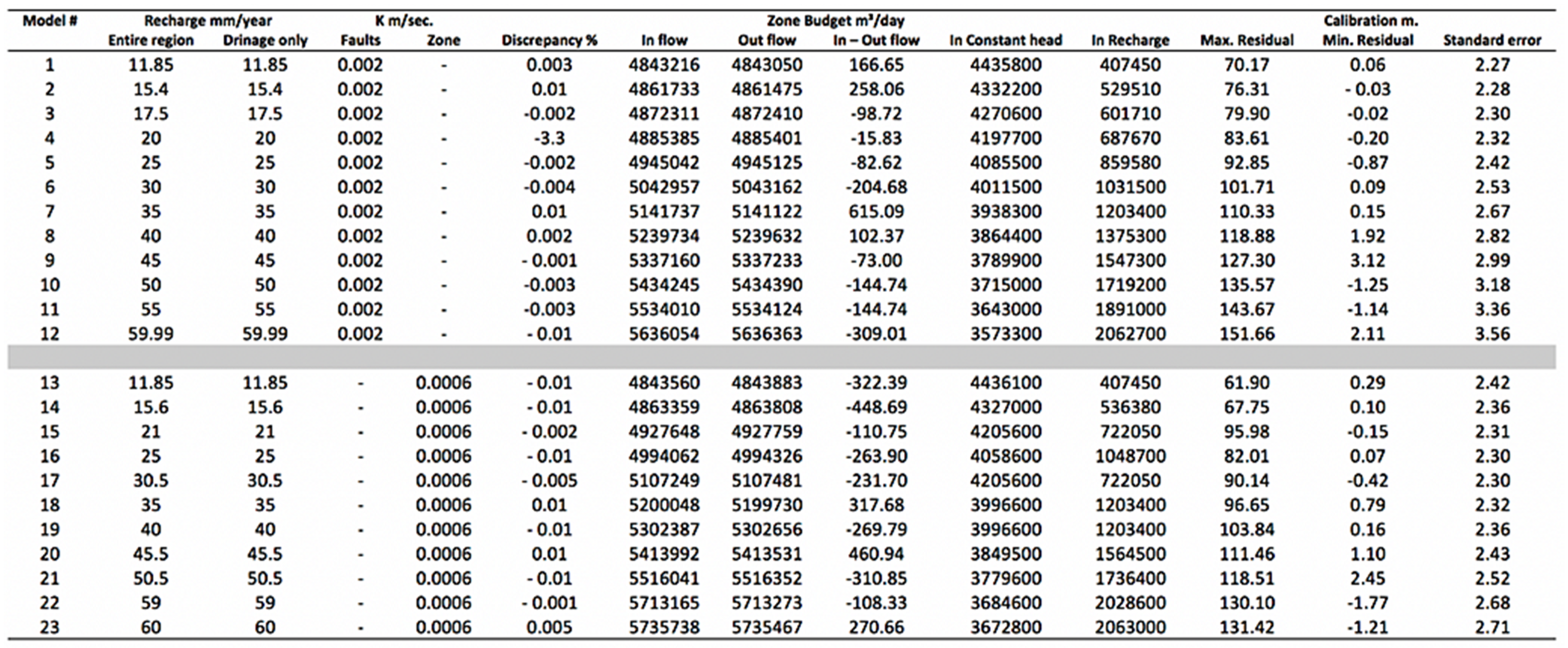
3.2. Model Sensitivity
3.3. Manual Calibration
3.4. Groundwater Harvesting
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press: Wyman Street, Waltham, MA, USA, 2015. [Google Scholar]
- Finch, J.W. Estimating Direct Groundwater Recharge Using a Simple Water Balance Model–Sensitivity to Land Surface Parameters. J. Hydrol. 1998, 211, 112–125. [Google Scholar] [CrossRef]
- Mehl, S.; Hill, M.C. Locally Refined Block-Centered Finite-Difference Groundwater Models: Evaluation of Parameter Sensitivity and the Consequences for Inverse Modelling and Predictions. Acta Univ. Carolina. Geol. 2002, 46, 199–203. [Google Scholar]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a Conduit Flow Process (CFP) for MODFLOW-2005: U.S. Geological Survey Techniques and Methods, Book 6, Chapter A24. 2008, p. 50. Available online: http://www.academia.edu/download/48243513/tm6-A24.pdf (accessed on 23 July 2020).
- Carrera-Hernández, J.J.; Smerdon, B.D.; Mendoza, C.A. Estimating Groundwater Recharge through Unsaturated Flow Modelling: Sensitivity to Boundary Conditions and Vertical Discretization. J. Hydrol. 2012, 452, 90–101. [Google Scholar] [CrossRef]
- Song, x.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; ×u, C. Global Sensitivity Analysis in Hydrological Modeling: Review of Concepts, Methods, Theoretical Framework, and Applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef] [Green Version]
- Xanke, J.; Jourde, H.; Liesch, T.; Goldscheider, N. Numerical Long-Term Assessment of Managed Aquifer Recharge from a Reservoir into a Karst Aquifer in Jordan. J. Hydrol. 2016, 540, 603–614. [Google Scholar] [CrossRef]
- Hanson, R.T.; Boyce, S.E.; Schmid, W.; Hughes, J.D.; Mehl, S.W.; Leake, S.A.; Maddock, T., III; Niswonger, R.G. One-Water Hydrologic Flow Model (MODFLOW-OWHM) (No. 6-A51); US Geological Survey: Preston, WV, USA, 2014.
- Hartmann, A. Experiences in Calibrating and Evaluating Lumped Karst Hydrological Models. Geol. Soc. Lond. Spec. Publ. 2018, 466, 331–340. [Google Scholar] [CrossRef]
- Bittner, A.K.; Ferraz, M.C. Reliability of Mesopic Measures of Visual Acuity and Contrast Sensitivity and their Correlation with Rod and Cone Function in Retinitis Pigmentosa. Ophthalmic Res. 2020, 63, 133–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarrazin, F. Understanding the Sensitivity of Karst Groundwater Recharge to Climate and Land Cover Changes at a Large-Scale. Ph.D. Thesis, University of Bristol, Bristol, UK, 2018. [Google Scholar]
- Teixeira Parente, M.; Bittner, D.; Mattis, S.A.; Chiogna, G.; Wohlmuth, B. Bayesian Calibration and Sensitivity Analysis for a Karst Aquifer Model Using Active Subspaces. Water Resour. Res. 2019, 55, 7086–7107. [Google Scholar] [CrossRef]
- NIC. Republic of Iraq National Investment Commission. 2004. Available online: http://www.iraq-jccme.jp/pdf/090416-4.pdf (accessed on 19 June 2020).
- Alrusheidat, J.; Aljaafreh, S. Climate change adaptation and technology transfer: The path to disaster risk reduction in the arid and semi-arid zones. The case of Jordan. New Medit 2016, 15, 2–7. [Google Scholar]
- Bishay, F. Towards Sustainable Agricultural Development in Iraq. The Transition from Relief, Rehabilitation and Reconstruction to Development. 2003. Available online: https://agris.fao.org/agris-search/search.do?recordID=XF2008434245 (accessed on 23 July 2020).
- Al-Muqdadi, S.W. Groundwater Investigation and Modeling-Western Desert of Iraq. Ph.D. Thesis, Technische Universität Bergakademie Freiberg, Freiberg, Germany, 2012. [Google Scholar]
- Al-Muqdadi, S.W.; Merkel, B.J. Automated Watershed Evaluation of Flat Terrain. J. Water Resour. Prot. 2011, 3, 892. [Google Scholar] [CrossRef] [Green Version]
- Adham, A.; Sayl, K.N.; Abed, R.; Abdeladhim, M.A.; Wesseling, J.G.; Riksen, M.; Fleskens, L.; Karim, U.; Ritsema, C.J. A Gis-Based Approach for Identifying Potential Sites for Harvesting Rainwater in the Western Desert of Iraq. Int. Soil Water Conserv. Res. 2018, 6, 297–304. [Google Scholar] [CrossRef]
- Al-Muqdadi, S.W.; Merkel, B.J. Interpretation of Groundwater Flow into Fractured Aquifer. Int. J. Geosci. 2012, 3, 357–364. [Google Scholar] [CrossRef] [Green Version]
- Consortium, Y. Hydrogeological Explorations and Hydrotechnical Work—Western Desert of Iraq. Blook7. (Directorate of Western Desert Development Projects. Baghdad, Iraq). Unpublished work. 1977. [Google Scholar]
- Jassim, S.Z.; Goff, J.C. (Eds.) Geology of Iraq; DOLIN, sro; Geological Society of London: London, UK, 2006. [Google Scholar]
- Buday, T.; Hak, J. The Geological Survey of the Western Part of the Western Desert. No. 1000; The State Company of Geological Survey and Mining: Baghdad, Iraq, 1980.
- Buday, T.; Jassim, S.Z. Tectonic Map of Iraq, Scale 1: 1000 000; GEOSURV: Baghdad, Iraq, 1984. [Google Scholar]
- Jawad, S.B.; Naom, F.H.; Zamil, H.I.; Mohammad, A.B. Hydrogeology of Groundwater aquifers in the Western Desert-West and Southwest of the Euphrates River. (Ministry of Irrigation. Baghdad. Iraq). Unpublished work. 2001. [Google Scholar]
- Winston, R.B. ModelMuse: A Graphical User Interface for MODFLOW-2005 and PHAST; US Geological Survey: Reston, VA, USA, 2009.
- SGS. UZF Unsaturated-Zone Flow Package. 2020. Available online: https://water.usgs.gov/nrp/gwsoftware/modflow2000/MFDOC/inde×.html?uzf_unsaturated_zone_flow_pack.htm (accessed on 30 June 2020).
- Diersch, H.J.G. WASY Software-FEFLOW Finite Element Subsurface Flow and Transport Simulation System Reference Manual; WASY: Berlin, Germany, 2002. [Google Scholar]
- Niswonger, R.G.; Panday, S.; Ibaraki, M. MODFLOW-NWT, a Newton Formulation for MODFLOW-2005. US Geol. Surv. Tech. Methods 2011, 6, 44. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the Us Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Department of the Interior: Washington, DC, USA; US Geological Survey: Reston, VA, USA, 2005; p. 6-A16.
- Golden Software, Inc. 809 14th Street, Golden, Colorado 80401-1866 USA. Available online: https://www.goldensoftware.com (accessed on 17 February 2016).
- Ministry of Water Resources, Groundwater Division and Database. Ministry of Water Resource, Iraq 2010, Unpublished. Available online: https://www.mowr.gov.iq (accessed on 8 February 2020).
- Doherty, J. PEST Model-Independent Parameter Estimation User Manual; Watermark Numerical Computing: Brisbane, Australia, 2004; Volume 3338, p. 3349. [Google Scholar]
- Chiang, W.H. 3D-Groundwater Modeling with PMWIN: A Simulation System for Modeling Groundwater Flow and Transport Processes; Springer Science & Business Media: Berlin, Germany, 2005. [Google Scholar]
- Smith, M.; Muñoz, G.; Sanz Alvarez, J. Irrigation Techniques for Small-Scale Farmers: Key Practices for DRR Implementers. 2014. Available online: http://www.fao.org/3/a-i3765e.pdf (accessed on 19 March 2020).
- Fernandes, C.; Corá, J.E.; Araújo, J.A.C.D. Reference Evapotranspiration Estimation inside Greenhouses. Sci. Agric. 2003, 60, 591–594. [Google Scholar] [CrossRef]

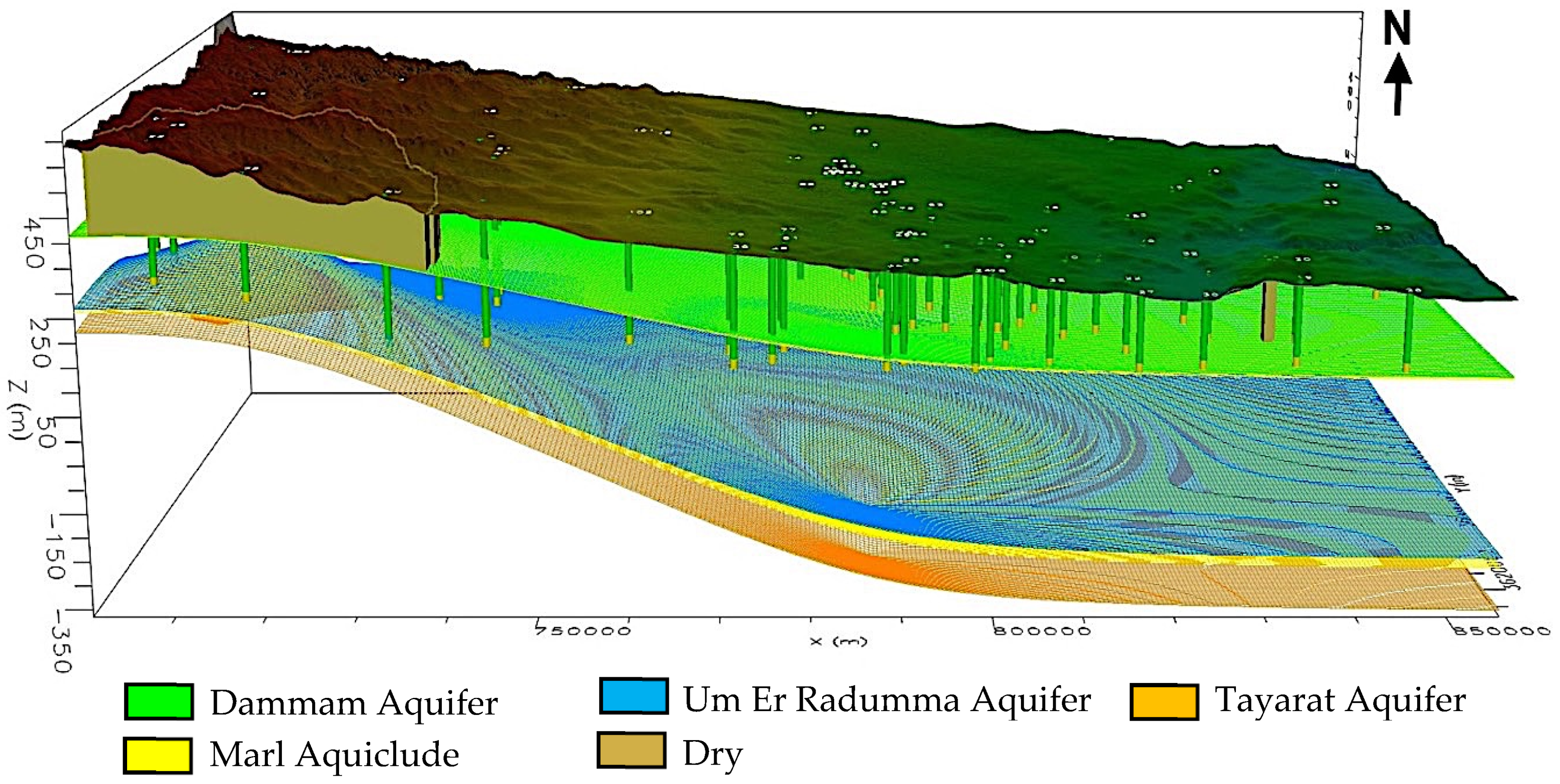
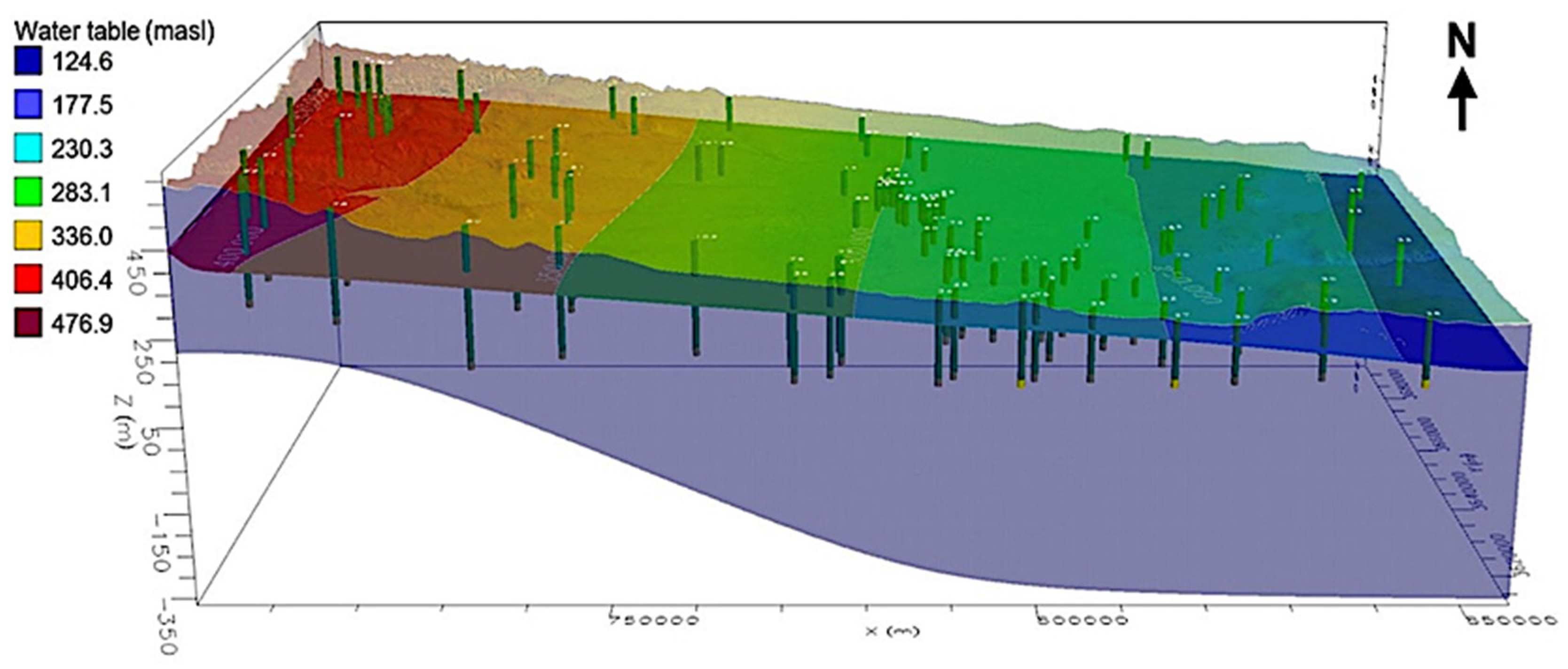
| Aquifer | Aquifer Type | Epoch | Thickness (m) | Transmissivity (m2/Day) | Storativity | Water Type | TDS (ppm) |
|---|---|---|---|---|---|---|---|
| Tayarat | Confined | Upper Cretaceous | 208 | 6851 | 1.2 × 10−4 | Cl-SO4 | 2271 |
| Um Er Radumma | Confined | Middle -Upper | 310 | 3683.5 | 6.0 × 10−3 | Na-SO4−Cl | 3956 |
| Dammam | Unconfined-Semiconfined | Middle Eocene | 85 | 19110 | 3.3 × 10−1 | Ca-Cl–SO4 | 3000 |
| Parameter | Type | Initial Value | Sensitivity/Iteration Number | Final Value | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| Kx_1 | Hyd. Conductivtiy (m/s) | 5.0 × 10−5 | 0.182 | 0.140 | 0.058 | 0.058 | 2.47 × 10−5 |
| Ky_1 | 5.0 × 10−5 | 0 | 0 | 0 | 0 | 5.0 × 10−5 | |
| Kx_2 | 1.0 × 10−4 | 1.174 | 1.031 | 1.178 | 1.178 | 4.11 × 10−5 | |
| Ky_2 | 1.0 × 10−4 | 0 | 0 | 0 | 0 | 1 × 10−4 | |
| Kx_3 | 1.0 × 10−3 | 0.019 | 0.014 | 0.012 | 0.012 | 1 × 10−3 | |
| Ky_3 | 1.0 × 10−3 | 0 | 0 | 0 | 0 | 1 × 10−3 | |
| Kx_4 | 1.0 × 10−5 | 0 | 0 | 0 | 0 | 1 × 10−5 | |
| Ky_4 | 1.0 × 10−5 | 0 | 0 | 0 | 0 | 1 × 10−5 | |
| Kx_5 | 3.0 × 10−4 | 1.040 | 1.261 | 1.296 | 1.296 | 1 × 10−3 | |
| Ky_5 | 3.0 × 10−4 | 0 | 0 | 0 | 0 | 1 × 10−4 | |
| Kx_6 | 5.0 × 10−4 | 0.473 | 0.439 | 0.25 | 0.25 | 1.33 × 10−5 | |
| Ky_6 | 5.0 × 10−4 | 0 | 0 | 0 | 0 | 5 × 10−4 | |
| Kx_7 | 8.0 × 10−4 | 0.919 | 0.909 | 0.91 | 0.91 | 1 × 10−3 | |
| Ky_7 | 8.0 × 10−4 | 0 | 0 | 0 | 0 | 8 × 10−4 | |
| Par001 | Groundwater Recharge (mm) | 1 | 0.353 | 0.406 | 0.574 | 0.574 | 5 |
| Par002 | 1 | 0.0046 | 0.0044 | 0.0056 | 0.0056 | 17 | |
| Par003 | 1 | 0.016 | 0.019 | 0.026 | 0.026 | 1 | |
| Par004 | 1 | 0.063 | 0.088 | 0.152 | 0.152 | 7 | |
| Model No. | Aquifers K | Aquiclude K | Model Respond | Maximum Residual m. | Slandered Error m. |
|---|---|---|---|---|---|
| 3 | 1.0 × 10−4 | 1.0 × 10−8 | run | 79.904 | 2.3 |
| 3-1 | 1.0 × 10−3 | 1.0 × 10−7 | run | 57.827 | 2.331 |
| 3-2 | 1.0 × 10−2 | 1.0 × 10−6 | Failed to run | - | - |
| 3-3 | 1.0 × 10 | 1.0 × 10−4 | run | 85.001 | 3.243 |
| 3-4 | 1.0 × 10−5 | 1.0 × 10−9 | Failed to run | - | - |
| 3-5 | 1.0 × 10−6 | 1.0 × 10−10 | Failed to run | - | - |
| Aquifer and Layer | Initial Value m/s | Calibrated m/s | ||
|---|---|---|---|---|
| Layer Nr. | Kx | Ky | Kx | Ky |
| 5 | 5.0 × 10−5 | 5.0 × 10−5 | 2.48 × 10−5 | 5.0 × 10−5 |
| 1-3-5 | 1.0 × 10−4 | 1.0 × 10−4 | 4.12 × 10−5 | 1.0 × 10−4 |
| 3 (Um Er Radumma Aquifer) | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 |
| 1 (Dammam Aquifer) | 3.0 × 10−4 | 3.0 × 10−4 | 1.0 × 10−3 | 3.0 × 10−4 |
| 5 (Tayarat Aquifer) | 5.0 × 10−4 | 5.0 × 10−4 | 1.34 × 10−5 | 5.0 × 10−4 |
| 1-3 | 8.0 × 10−4 | 8.0 × 10−4 | 1.0 × 10−3 | 8.0 × 10−4 |
| 2-4 (Aquiclude) | 1.0 × 10−8 | 1.0 × 10−8 | 1.0 × 10−8 | 1.0 × 10−8 |
| Recharge m3/Year | Total Rex. m3/Year | Rex. % | Rex. m3/Year | Total Area m2 | Rex. Area Covered % |
|---|---|---|---|---|---|
| 0.217 × 109 | 1.54 × 109 | 50 | 769 × 106 | 12.4 × 109 | 6.2 |
| 0.217 × 109 | 1.54 × 109 | 55 | 846 × 106 | 12.4 × 109 | 6.8 |
| 0.217 × 109 | 1.54 × 109 | 60 | 922 × 106 | 12.4 × 109 | 7.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Muqdadi, S.W.H.; Abo, R.; Khattab, M.O.; Abdulhussein, F.M. Groundwater Flow-Modeling and Sensitivity Analysis in a Hyper Arid Region. Water 2020, 12, 2131. https://doi.org/10.3390/w12082131
Al-Muqdadi SWH, Abo R, Khattab MO, Abdulhussein FM. Groundwater Flow-Modeling and Sensitivity Analysis in a Hyper Arid Region. Water. 2020; 12(8):2131. https://doi.org/10.3390/w12082131
Chicago/Turabian StyleAl-Muqdadi, Sameh W. H., Rudy Abo, Mohammed O. Khattab, and Firas M. Abdulhussein. 2020. "Groundwater Flow-Modeling and Sensitivity Analysis in a Hyper Arid Region" Water 12, no. 8: 2131. https://doi.org/10.3390/w12082131





