A New Approach for Optimizing Rain Gauge Networks: A Case Study in the Jinjiang Basin
Abstract
:1. Introduction
2. Material and Methods
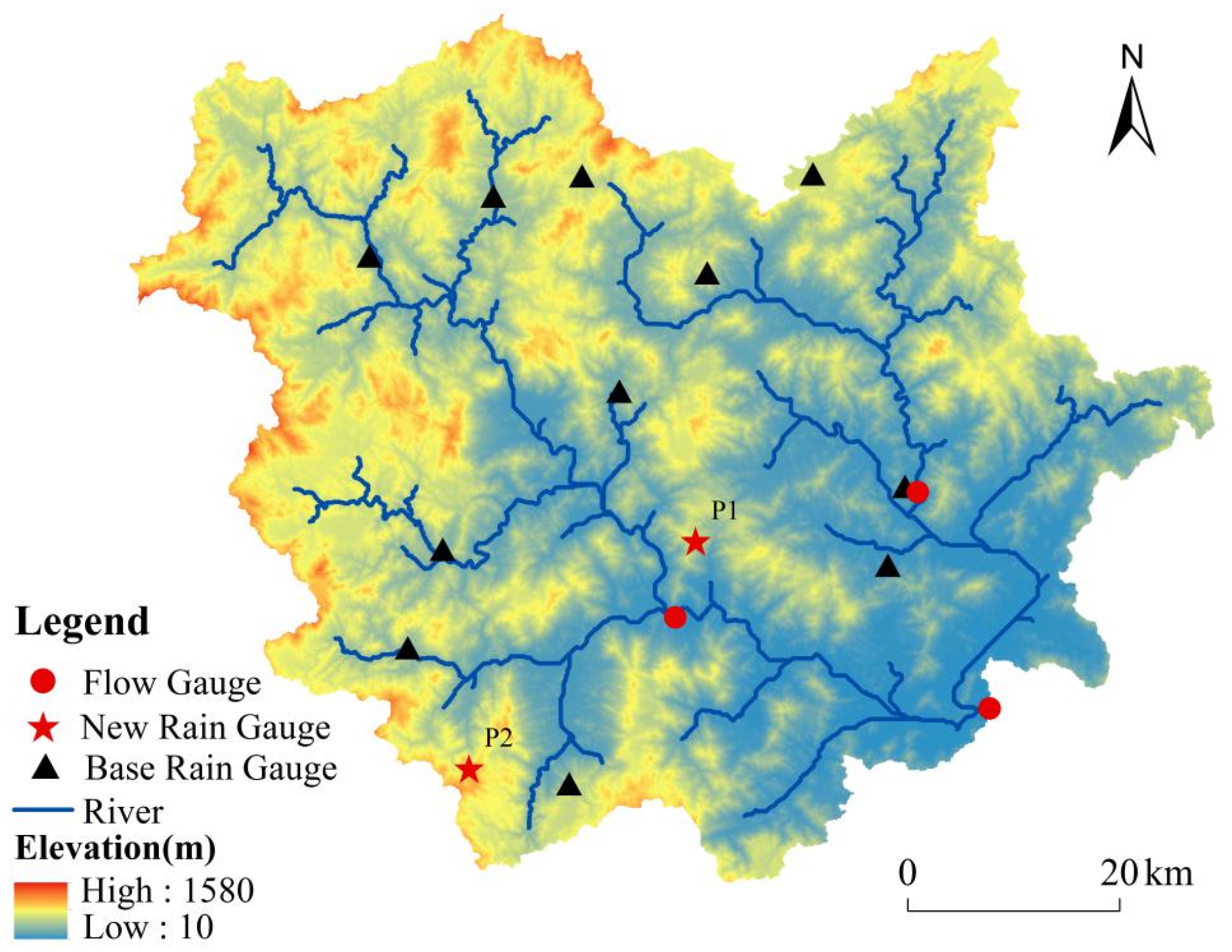
2.1. Study Area and Data
2.2. Methods
2.2.1. Ordinary Kriging
2.2.2. Spatial Correlation Approach
2.2.3. Determination of the New Rain Gauge Location Based on the OK
- Step 1:
- Based on average monthly rainfall from 2001 to 2010 of m base rain gauges, the KSE was obtained using OK interpolation [18].
- Step 2:
- Step 3:
- The center point of each grid within the basin was obtained by the Mean Center feature in ArcGIS 10.2.
- Step 4:
- The KSE of each grid was sorted from large to small, and the center points of the n grid with the larger summed KSE were determined as the location of the new rain gauges.
3. Results and Discussion
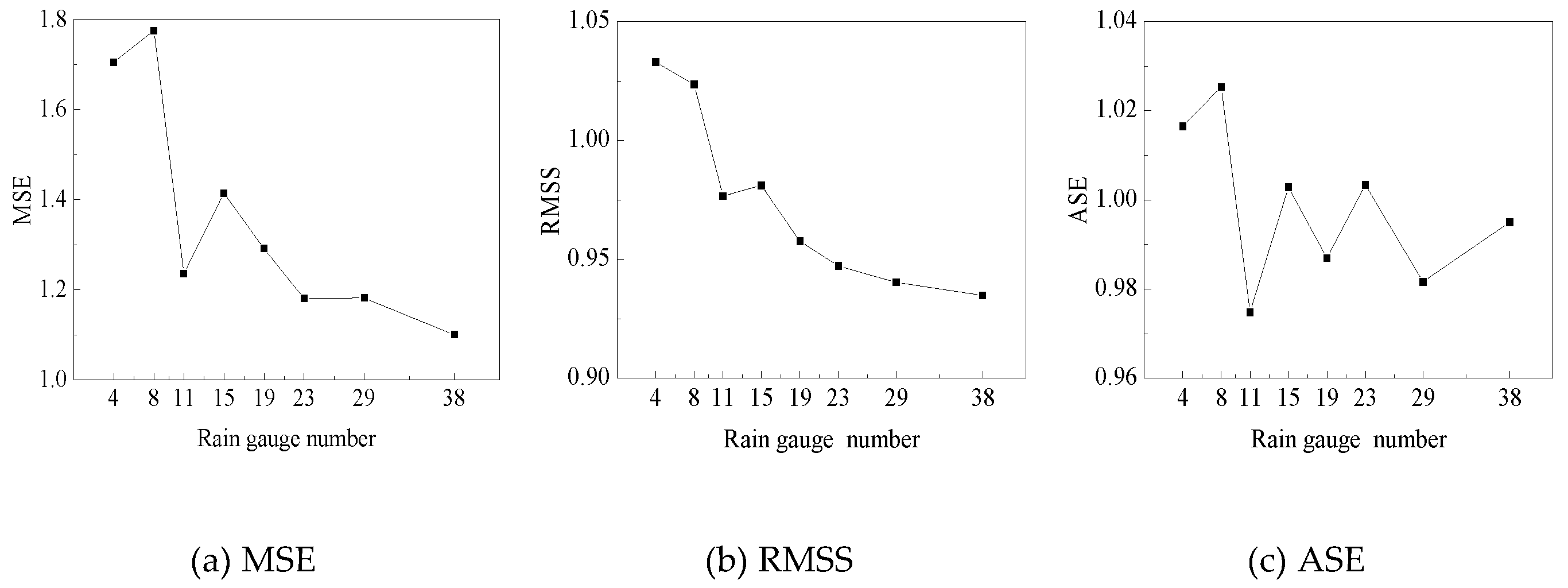
3.1. Selection of the Base Rain Gauge Network
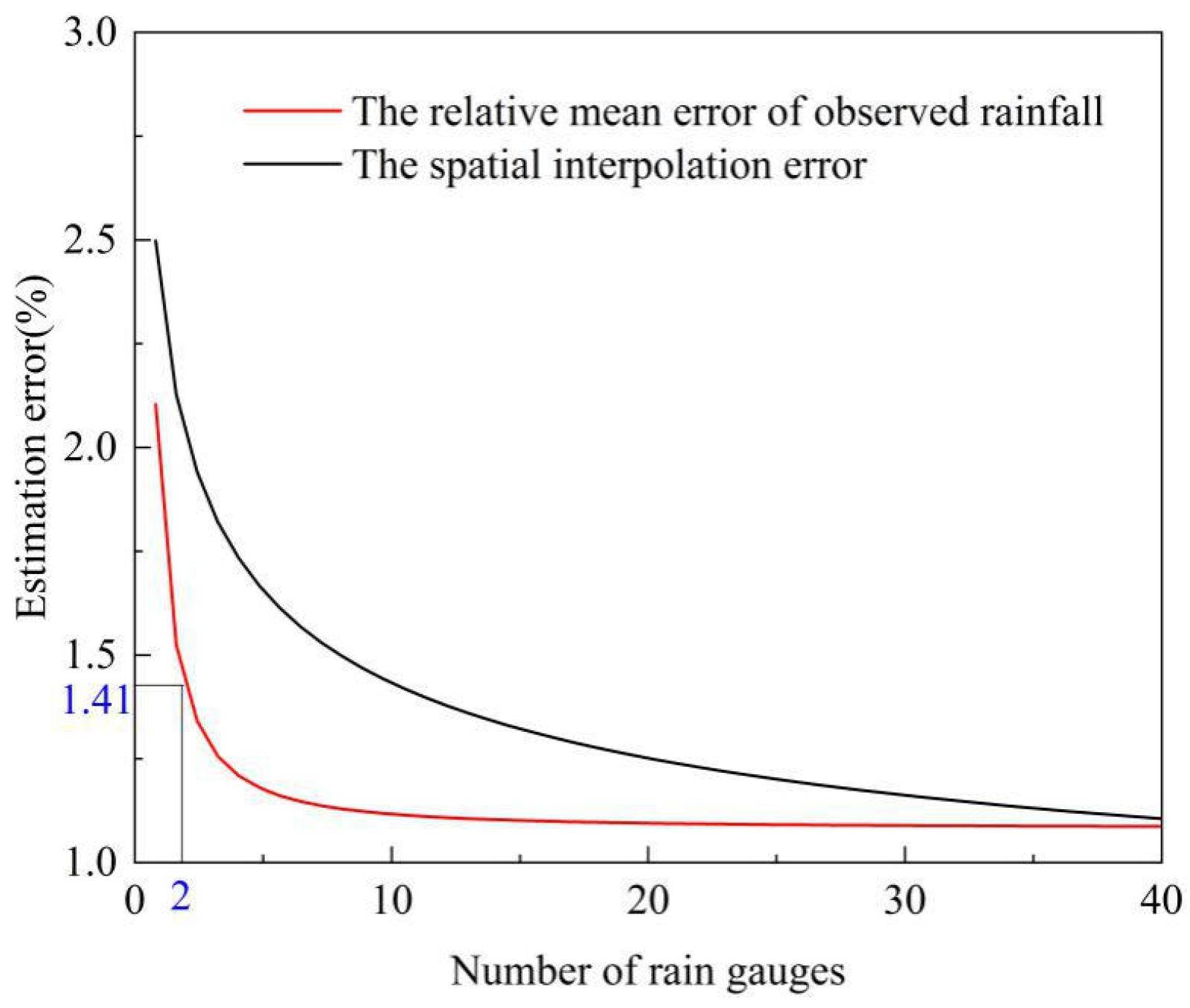
3.2. Number of New Rain Gauges Using the SCA
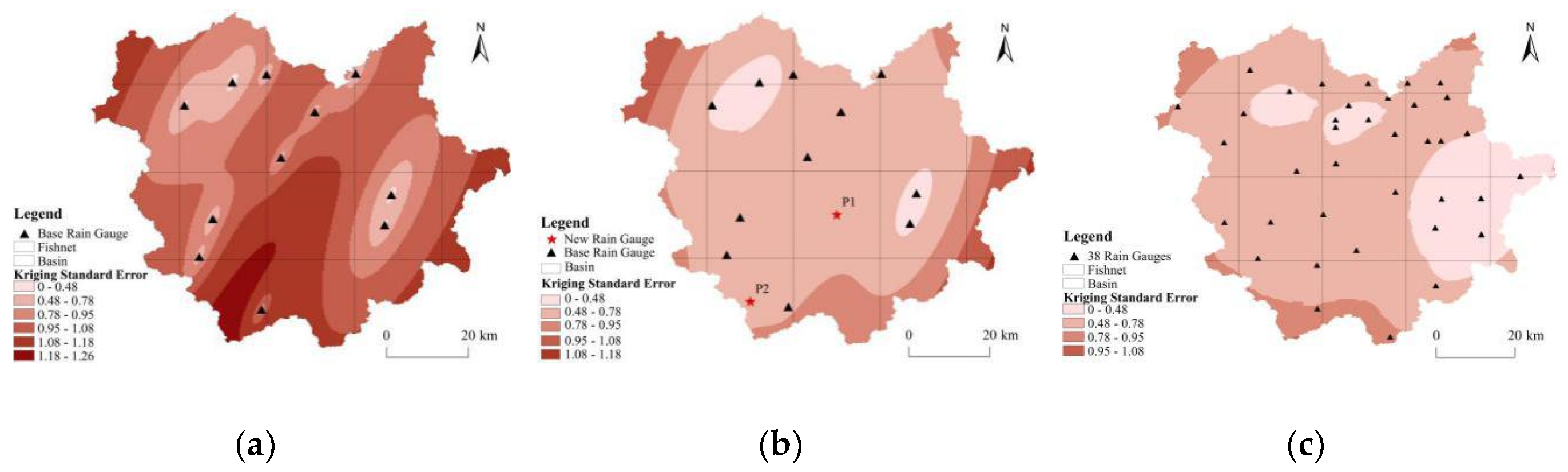
3.3. Location of New Rain Gauges Based on the OK
4. Conclusions
- (1)
- The OK method could not only identify the blank monitoring region with the highest rainfall error, but also determine the location of new rain gauges according to three cross-validation statistics (MSE, ASE, and RMSS). The SCA allowed the number of new rain gauges to be obtained. By coupling the OK and SCA, the redundant rain gauges were removed from the current rain gauge network, and new rain gauges in the blank monitoring region were determined.
- (2)
- The optimal rain gauge network provided more accurate rainfall estimates in comparison to the base network that was determined by the OK. The coupled OK–SCA could be appropriate for optimizing a rain gauge network in wet areas such as the Jinjiang Basin. A further study will assess how the optimized rain gauge network affects the simulation of hydrological process and the changes in hydrological model parameters.
Author Contributions
Funding
Conflicts of Interest
References
- Xu, H.; Xu, C.; Chen, H.; Zhang, Z.; Li, L. Assessing the influence of rain gauge density and distribution on hydrological model performance in a humid region of China. J. Hydrol. 2013, 505, 1–12. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.; Sælthun, N.; Xu, Y.; Zhou, B.; Chen, H. Entropy theory based multi-criteria resampling of rain gauge networks for hydrological modelling—A case study of humid area in southern China. J. Hydrol. 2015, 525, 138–151. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.; Jun, H. A study of the influence of the spatial distribution of rain gauge networks on areal average rainfall calculation. Water 2018, 10, 1635. [Google Scholar] [CrossRef] [Green Version]
- Bárdossy, A.; Das, T. Influence of rainfall observation network on model calibration and application. Hydrol. Earth Syst. Sci. 2008, 12, 77–89. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L.; Zou, X.; Chen, Y.; Chen, X.; Liu, J.; et al. A two-phase copula entropy-based multiobjective optimization approach to hydrometeorological gauge network design. J. Hydrol. 2017, 535, 228–241. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Seck, I.; Baelen, J. Geostatistical Merging of a Single-Polarized X-Band Weather Radar and a Sparse Rain Gauge Network over an Urban Catchment. Atmosphere 2018, 9, 496. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.; Wu, S.; Hsu, C.; Shen, J. An evaluation framework for identifying the optimal raingauge network based on spatiotemporal variation in quantitative precipitation estimation. Hydrol. Res. 2017, 48, 77–98. [Google Scholar] [CrossRef]
- Dai, Q.; Bray, M.; Zhuo, L.; Islam, T.; Han, D. A Scheme for Rain Gauge Network Design Based on Remotely Sensed Rainfall Measurements. J. Hydrometeorol. 2017, 18, 363–379. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.-Y.; Jie, M.-X.; Chen, J.; Guo, S.-L.; Liu, J. The effect of rain gauge density and distribution on runoff simulation using a lumped hydrological modelling approach. J. Hydrol. 2018, 563, 106–122. [Google Scholar] [CrossRef]
- Peleg, N.; Ben-Asher, M.; Morin, E. Radar subpixel-scale rainfall variability and uncertainty: Lessons learned from observations of a dense rain-gauge network. Hydrol. Earth Syst. Sci. 2013, 17, 2195–2208. [Google Scholar] [CrossRef] [Green Version]
- Shafiei, M.; Ghahraman, B.; Saghafian, B.; Pande, S.; Gharari, S.; Davary, K. Assessment of rain-gauge networks using a probabilistic GIS based approach. Hydrol. Res. 2014, 45, 551–562. [Google Scholar] [CrossRef] [Green Version]
- Yin, Z.; Liao, W.; Lei, X.; Wang, H.; Wang, R. Comparing the Hydrological Responses of Conceptual and Process-Based Models with Varying Rain Gauge Density and Distribution. Sustainability 2018, 10, 3209. [Google Scholar] [CrossRef] [Green Version]
- Singh, C.; Katpatal, Y. A GIS Based Design of Groundwater Level Monitoring Network Using Multi-Criteria Analysis and Geostatistical Method. Water Resour. Manag. 2017, 31, 4149–4163. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, X.; Chen, L.; Yuan, X.; Dong, H.; Yu, Y. Optimization of the basin hydrologic network based on multi-objective criteria. J. Hohai Univ. 2019, 47, 102–107. [Google Scholar]
- Stosic, T.; Stosic, B.; Singh, V.P. Optimizing streamflow monitoring networks using joint permutation entropy. J. Hydrol. 2017, 552, 306–312. [Google Scholar] [CrossRef]
- Wang, W.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L.; Zou, X.; Liu, J.; Zou, Y.; He, R. Optimization of rainfall networks using information entropy and temporal variability analysis. J. Hydrol. 2018, 559, 136–155. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, H.; Jiang, Y.; Lu, X.; Duan, H.; He, R. Comparison and analysis of different discrete methods and entropy-based methods in rain gauge network design. Water 2019, 11, 1357. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L.; Zou, X.; Liu, J.; Zou, Y.; He, R. A kriging and entropy-based approach to raingauge network design. Environ. Res. 2018, 161, 61–75. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Yilmaz, A.G.; Muttil, N. Optimal design of rain gauge network in the Middle Yarra River catchment, Australia. Hydrol. Process. 2015, 29, 2582–2599. [Google Scholar] [CrossRef] [Green Version]
- Barca, E.; Passarella, G.; Uricchio, V. Optimal extension of the rain gauge monitoring network of the Apulian Regional Consortium for Crop Protection. Environ. Monit. Assess. 2008, 145, 375–386. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wei, C.; Yeh, H. Rainfall network design using kriging and entropy. Hydrol. Process. 2010, 22, 340–346. [Google Scholar] [CrossRef]
- Nazaripour, H.; Mansouri, D. Rain gauge network evaluation and optimal design using spatial correlation approach in arid and semi-arid regions of Iran. Theor. Appl. Climatol. 2016, 129, 1255–1261. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yao, H.; Gao, L.; Chen, Y.; Liu, M. Non-linear relationship of hydrological drought responding to meteorological drought and impact of a large reservoir. J. Hydrol. 2017, 551, 495–507. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Xu, C.; Zhang, M.; Liu, M.; Gao, L. Toward Improved Calibration of SWAT Using Season-Based Multi-Objective Optimization: A Case Study in the Jinjiang Basin in Southeastern China. Water Resour. Manag. 2018, 32, 1193–1207. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y. Spatial interpolation of annual precipitation data in Cambodia based on geostatistics. Yangtze River. 2018, 49, 100–103. [Google Scholar]
- Chen, H.; Huo, R.; Zeng, Q.; Yang, W.; Chen, J.; Guo, S.; Xu, C. Comparative study on the influence of rain-gauge network on the uncertainty of hydrological modeling. Adv. Water Sci. 2019, 30, 34–44. [Google Scholar]
- Bayat, B.; Nasseri, M.; Hosseini, K.; Karami, H. Revisited rainfall network design: Evaluation of heuristic versus entropy theory methods. Arab. J. Geosci. 2018, 11, 561. [Google Scholar] [CrossRef]
- Haggag, M.; Elsayed, A.A.; Awadallah, A.G. Evaluation of rain gauge network in arid regions using geostatistical approach: Case study in northern Oman. Arab. J. Geosci. 2016, 9, 552. [Google Scholar] [CrossRef]
- Amin, M.A.; Torkan, G.; Eslamian, S.; Zareian, M.J.; Adamowski, J.F. Analysis of deterministic and geostatistical interpolation techniques for mapping meteorological variables at large watershed scales. Acta Geophys. 2019, 67, 191–203. [Google Scholar] [CrossRef]
- Foehn, A.; Hernández, J.G.; Schaefli, B.; Cesare, G.de. Spatial interpolation of precipitation from multiple rain gauge networks and weather radar data for operational applications in Alpine catchments. J. Hydrol. 2018, 563, 1092–1110. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, X.; Chen, H.; Xu, C.; Zeng, Q.; Xu, J. Influence of rain gauges network configuration on the accuracy of rainfall spatial interpolation and hydrological modeling. J. Yangtze River. Sci. Res. Inst. 2019, 36, 19–26. [Google Scholar]
- Kagan, R.L. Planning the spatial distribution of hydrometeorological stations to meet an error criterion. In Casebook on Hydrological Network Design Practice, III-1.2; WMO Publication: Geneva, Switzerland, 1972; Volume 324. [Google Scholar]
- Bakhtiaria, B.; Nekooamal Kermani, M.; Bordbarc, M.H. Rain Gauge Station Network Design for Hormozgan Province in Iran. Desert 2013, 18, 45–52. [Google Scholar]
- James, E.J.; Sreedharan, K.E. Design of rain-gauge network using spatial correlation for the Bharathapuzha basin on the Malabar Coast of India. In Integrated Design of Hydrological Networks, Proceedings of the Fourth International Symposium on Inventories, Budapest, Hungary, 25–29 August 1986; IAHS Press: Madrid, Spain, 1986; Volume 158. [Google Scholar]
- Ali, M.Z.M.; Othman, F. Rain gauge network optimization in a tropical urban area by coupling cross-validation with the geostatistical technique. Hydrol. Sci. J. 2018, 63, 474–491. [Google Scholar] [CrossRef]
- Jiang, X.; Ren, F.; Li, J.; Qiu, Y.; Ma, Z.; Cai, B. Characteristics and Preliminary Causes of Tropical Cyclone Extreme Rainfall Events over Hainan Island. Adv. Atmos. Sci. 2018, 35, 580–591. [Google Scholar] [CrossRef]
- Lin, Y.-F.; Wu, C.-C.; Yen, T.-H.; Huang, Y.-H.; Lien, G.-Y. Typhoon Fanapi (2010) and its Interaction with Taiwan Terrain-Evaluation of the Uncertainty in Track, Intensity and Rainfall Simulations. J. Meteorol. Soc. Jpn. 2020, 98, 93–113. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Chen, X.; Lin, M.; Chen, Y. Spatial and temporal Variations of Storm-floods in Xixi Watershed of Southeast Coastal Region. Mt. Res. 2017, 35, 488–495. [Google Scholar]
- Diodato, N. The influence of topographic co-variables on the spatial variability of precipitation over small regions of complex terrain. Int. J. Clim. 2005, 25, 351–363. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Q.; Hao, F. Impact of Network Density and Topography on Simulated Water and Sediment Yields. J. Soil Water Conserv. 2005, 19, 18–21. [Google Scholar]



| Density Degree | Percentage of Rain Gauges (%) | NRGs | Randomly Selecting Times | Rain Gauges Density (km2/Rain Gauge) |
|---|---|---|---|---|
| 1 | 10 | 4 | 100 | 1258.10 |
| 2 | 20 | 8 | 100 | 629.05 |
| 3 | 30 | 11 | 100 | 457.49 |
| 4 | 40 | 15 | 100 | 335.49 |
| 5 | 50 | 19 | 100 | 264.86 |
| 6 | 60 | 23 | 100 | 218.80 |
| 7 | 75 | 29 | 100 | 173.53 |
| 8 | 100 | 38 | 1 | 132.43 |
| Distance (km) | NRGs | MD | MC |
|---|---|---|---|
| 0~3 | 0 | 0 | 0 |
| 3~6 | 0 | 0 | 0 |
| 6~9 | 2 | 8.080 | 0.959 |
| 9~12 | 1 | 9.826 | 0.958 |
| 12~15 | 4 | 13.869 | 0.962 |
| 15~18 | 0 | 0 | 0 |
| 18~21 | 2 | 20.250 | 0.953 |
| 21~24 | 4 | 21.788 | 0.937 |
| 24~27 | 2 | 25.956 | 0.923 |
| 27~30 | 4 | 27.956 | 0.934 |
| 30~33 | 6 | 31.138 | 0.933 |
| 33~36 | 1 | 33.616 | 0.905 |
| 36~39 | 6 | 37.004 | 0.917 |
| 39~42 | 0 | 0 | 0 |
| 42~45 | 6 | 42.758 | 0.908 |
| 45~48 | 5 | 46.567 | 0.910 |
| 48~51 | 4 | 49.973 | 0.902 |
| 51~54 | 1 | 53.172 | 0.836 |
| 54~57 | 3 | 55.934 | 0.845 |
| 57~60 | 2 | 58.028 | 0.896 |
| 60~63 | 1 | 61.890 | 0.875 |
| Scenarios | Description | MSE | RMSE | ASE |
|---|---|---|---|---|
| N11 | The network of base 11 rain gauges | 1.5850 | 0.9503 | 0.9578 |
| N13_P1 | The network includes P1, P2 and the base 11 rain gauges | 1.4559 | 0.9620 | 0.8767 |
| N13_AX | The network includes Anxi, P2 and the base 11 rain gauges | 1.5173 | 0.9569 | 0.9207 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Chen, Y.; Chen, X.; Liu, M.; Gao, L.; Deng, H. A New Approach for Optimizing Rain Gauge Networks: A Case Study in the Jinjiang Basin. Water 2020, 12, 2252. https://doi.org/10.3390/w12082252
Wu H, Chen Y, Chen X, Liu M, Gao L, Deng H. A New Approach for Optimizing Rain Gauge Networks: A Case Study in the Jinjiang Basin. Water. 2020; 12(8):2252. https://doi.org/10.3390/w12082252
Chicago/Turabian StyleWu, Huifeng, Ying Chen, Xingwei Chen, Meibing Liu, Lu Gao, and Haijun Deng. 2020. "A New Approach for Optimizing Rain Gauge Networks: A Case Study in the Jinjiang Basin" Water 12, no. 8: 2252. https://doi.org/10.3390/w12082252
APA StyleWu, H., Chen, Y., Chen, X., Liu, M., Gao, L., & Deng, H. (2020). A New Approach for Optimizing Rain Gauge Networks: A Case Study in the Jinjiang Basin. Water, 12(8), 2252. https://doi.org/10.3390/w12082252







